金属学-扩散

固态扩散的实验(柯肯达尔效应 固态扩散的实验 柯肯达尔效应) 柯肯达尔效应 把Cu、Ni棒对焊，在焊接面上镶嵌上钨丝 作为界面标志。加热到高温并保温，界面标 志钨丝向纯Ni一侧移动了一段距离. 柯肯达尔效应:置换互溶组元所构成的扩散 柯肯达尔效应 偶中,由于两种原子以不同速度相对扩散,扩 散通量不相等造成标记面漂移的现象.
第八章
扩散
回 顾
金属的晶体结构 纯金属的结晶 二元合金 铁碳合金 三元相图 金属及合金的塑性变形 回复与再结晶
扩散:物质中原子（或分子）的迁移现象，它是 扩散 物质传输的一种方式. 原子的微观运动会引起物质的宏观流动,气体和 液体的扩散易察觉. 固态金属中同样存在扩散现象,且扩散是固体 中物质传递的唯一方式. 扩散是金属中的一个重要现象，是金属学的一 个重要领域，它与金属的加工、使用性能间存 在密切关系.
参考相图对新相进行分析 例如:铁在1000℃加热时被氧化，氧化层组织如图， 由表向内依次为：Fe2O3 、 Fe3O4 、 FeO、 Fe
反应扩散的特点: 反应扩散的特点 在相界面处产生浓度突变，浓度正好对应于相图 中相的极限溶解度。 原因：（可用相律F=C-P+1解释） 原因 扩散温度一定， F=C-P，在单相区，F=2-1=1， 自由度为1，即单相区浓度可变，存在浓度梯度 在两相区，F=2-2=0，即各相的浓度不能改变， 其大小分别相当于与其相邻的单相区浓度。 每个组元的化学位在两相区中的各点都相等，不 存在化学位梯度，扩散失去了驱动力，因此，二 元系的扩散层中不可能存在两相区。
上坡扩散的驱动力也可以是弹性应力梯度、电 位梯度或温度梯度。 如图,将均匀的单相固溶体Al-Cu合金方棒加以弹 性弯曲，在一定温度下加热后,发生上坡扩散。 上坡扩散的驱动力:应力梯度
3、根据扩散过程中是否出现新相进行分类 、 原子扩散 定义： 定义：在扩散过程中基体晶格始终不变,没有 新相产生，称为原子扩散。 反应扩散 定义： 定义：通过扩散，使固溶体内溶质组元浓度 超过固溶度极限而不断形成新相的过程.(属于 一种相变扩散) 反应扩散形成的新相，可以是新的固溶体,也 可以是各种化合物。
固态扩散是大量原子无序跃迁的统计结果 晶体的周期势场中,原子向各个方向跃迁几率相等,这 样,不会产生物质传输的宏观扩散效果. 若晶体周期场的势能曲线倾斜(图),则原子自左向右 跃迁的激活能为Q,自右向左的激活能为 Q＋ΔC.那么, 原子向右跳动的几率将大于向左跳动的几率.大量原 子的无序跃迁造成物质的定向迁移，即发生扩散. 扩散不是原子的定向跃迁,而是原子的随机无序跃迁
4、扩散要有驱动力 、 扩散过程是在驱动力作用下进行的，扩散的 驱动力不是浓度梯度,而是化学位梯度。 原因： 原因 ： 一些扩散过程沿着浓度降低的方向进 行，使浓度趋于均匀化，而另一些扩散过程 是沿着浓度升高的方向进行。 因此，浓度梯度并不是导致扩散的本质原因。 从热力学来看，等温等压条件下，不管浓度 梯度如何，组元原子总是从化学位高处自发 转移到化学位低处，当每种组元的化学位在 系统中各点都相等时，达到动态平衡。
置换原子的两种间隙扩散模型 顶替式和挤列式
2.换位扩散机理 换位扩散机理 在纯金属或置换固溶体中，原子可以通过 换位进行扩散，如图. 直接换位扩散机制:两原子 直接换位扩散机制 交换位置时须同时起跳,很难. 环形换位模型:显然环形旋转 环形换位模型 换位方式引起的晶格畸变要小 得多,故这种扩散机理是可能的.
1885年，菲克进行了固态原子从高浓度向低 浓度的扩散实验，表明：单位时间内通过垂 直于扩散方向的单位截面积的扩散流量与该 截面处的浓度梯度成正比。 称菲克第一定律，其数学表达式称扩散第一 dC 方程： J= -D dx J：扩散流量，扩散物质流过单位截面速度； D：扩散系数,反映扩散速度的物理量,是单位 浓度梯度时的扩散流量，D值越大,扩散越快。 ：体积浓度梯度， dC 负号：表示扩散流方向与浓度梯度方向相反 dx
二、菲克第二定律 非稳定态扩散:在扩散过程中，各处的浓度梯度 非稳定态扩散 不仅随距离x变化，而且随时间t变化。 描述非稳定态扩散中各截面浓度梯度与距离x 和时间t间的关系，要建立偏微分方程。 方法:在扩散通道中取相距dx 方法 的两个垂直于X轴的平面,割 取一微小体积进行质量平衡 运算,即该微小体积中的物质 增加率 ∂c 等于流入和流出 ∂t 该体积的流量差。
3 空位扩散机理 定义： 定义：通过扩散原子与空位交换位置来实现物质 的宏观迁移。 空位的存在，使周围邻近原子偏离平衡位置，势 能升高，从而使原子跳入空位所需跨越的势垒高 度降低，相邻原子就易于向空位跳动。是固态金属最可能采取的扩散机制
空位扩散是固态金属最可能采取的扩散机制 空位扩散是固态金属最可能采取的扩散机制 固态金属最可能 原因： 原因： 相互调位所需能量较大，难以实现。 环形换位必然使通过界面流入和流出的原子 数目相等，无法解释柯肯达尔效应。 基于柯肯达尔效应，以及实际晶体结构中存 在着一定数量点阵空位的事实，空位扩散可能 是置换固溶体的互扩散和纯金属的自扩散唯一 采取的方式。
三、固态金属扩散的条件 1、温度要足够高 、 固态扩散依靠原子热激活而进行。温度越高， 原子热振动越激烈，被激活而迁移的几率越大。 只要热力学温度不是零，总有部分原子被激活 而迁移。温度低时，原子被激活的几率很低， 表现不出物质输送的宏观效果，好象扩散过程 被“冻结”，不同物质扩散 “冻结”的温度不 同。 如,碳原子在室温下的扩散极其微弱，100℃以 上时较显著，而铁原子须在500℃以上才能扩 散。
二 、扩散机理 对于不同晶体结构的金属材料，原子的跳动方 式不同，故扩散机理随晶体结构的不同而变化。 原因: 原因:扩散不仅由原子的热运动所控制，还受 具体的晶体结构制约。 扩散需具备的条件: 扩散需具备的条件:能量条件与结构条件 扩散模型(按照单原子的跳动方式分) 扩散模型 间隙扩散机理 换位扩散机理 空位扩散机理
1.间隙扩散机理 间隙扩散机理 定义： 定义：扩散原子在点阵间隙位置间跃迁导致的扩散。 间隙固溶体中,溶质原子从其所占间隙位置跳到邻 近另一个空着的间隙位置 置换固溶体中,溶质或溶剂原子从原来所占据的平衡 位置跳到间隙位置，再跳到邻近其他间隙位置.
实现间隙扩散的条件: 实现间隙扩散的条件: 结构条件: 结构条件:扩散原子周围具备几何间隙位置 能量条件:克服跳动时周围阵点原子的阻力 能量条件 间隙固溶体中,溶质原子占据的间隙位置很少,大 部分是空的,可供间隙原子跳动,间隙扩散可能性大. 对置换固溶体,原子尺寸大,间隙很小,处于平衡位 置的原子要跳入很小的间隙位置,且还要通过两个 原子之间更小的间隙跳到另一个间隙位置，很难.
( )
(微小体积中积存物质量)=(流入-流出)物质量 设两平面截面积均为A，在某一时间间隔内流 入和流出微小体积的物质扩散流量为J1和J2。 由于 J 2 = ∂J dx + J 1
∂x
故物质的积存速率=
(2)
而物质的积存速率也可用体积浓度C的变化率 表示,则微小体积Adx内物质积存速率为 ∂ (CAdx ) ∂C = Adx (3) ∂t ∂t
2、根据扩散方向与浓度梯度方向相同与否分类 、 下坡扩散 沿着浓度降低的方向进行的扩散，使浓度趋于 均匀化。 例:铸锭的均匀化退火、渗碳、渗金属等。 上坡扩散 沿着浓度升高的方向进行的扩散，即由低浓度 向高浓度方向扩散，使浓度发生两极分化。 例 :将含碳量相近的碳钢与硅钢对焊，高温加 热，发现：碳由低浓度一侧向高浓度一侧扩散， 发生上坡扩散，扩散的驱动力为化学位梯度。
推广为三维空间普遍式:
D为常数
三、扩散应用举例 扩散第二定律普遍适用于一般的扩散过程。 扩散方程是偏微分方程，不能直接应用，必须 结合实际的扩散过程，运用具体的起始条件和 边界条件，求解后才能应用。 ∂C ∂ 2C 从 式可知,扩散第 =D 2 (6) ∂t ∂x 二定律是以浓度C为因变量，以距离x和时间t 为自变量得偏微分方程，方程的解由解析式 C＝f（x，t） 给出.
固态金属中原子的跃迁 固态金属中原子的跃迁 金属晶体中的原子按一定规律呈周期性重复排 列，每个原子都处于周期性规律变化的结合能 曲线的势能谷中，相邻原子间都隔着一个势垒Q, 因此它们不会合并，也很难换位。 但是，原子时刻进行着热振动，振动能量与温 度有关。当温度不变时，存在着能量起伏。 能量起伏的存在使部分原子具有足够高的能量, 跨越势垒,由原来平衡位置跃迁到相邻平衡位置。 只要热力学温度不是零度，原子就有热振动， 依靠能量起伏被热激活，以进行扩散迁移。 温度越高，原子迁移的几率越大。
扩散第一定律的说明: 扩散第一定律的说明 描述溶质原子的宏观移动与其浓度梯度的关系 将金属看作连续介质，建立微分方程求解，不 涉及金属内部的原子过程. 适用范围: 适用范围 稳态扩散，即在一定区域内，浓度和浓度梯度 不随时间变化，不考虑时间因素对扩散的影响. 但实际上稳态扩散的情况很少，大部分属于非 稳定态扩散，需要应用菲克扩散第二定律。
2、时间要足够长 、 原子在晶体中跃迁一次最多移动0.3-0.5nm的距 离，扩散1mm的距离须跃迁亿万次。且原子跃 迁的过程是随机的，所以，只有经过很长时间 才能造成物质的宏观定向迁移。 应用:快速冷却到低温，原子来不及被激活，使 应用 扩散过程“冻结”，就可以保持高温下的状态。 举例
3、扩散原子要固溶 、 扩散原子在基体金属中必须有一定固溶度，溶 入基体晶格形成固溶体，才能进行固态扩散。 例1：在水中滴墨水，可很快扩散均匀.但在水 中滴油，放置多久也不扩散均匀。 例2：铅不能固溶于铁，故钢可以在铅浴中加 热，获得光亮清洁表面，不用担心铅粘附钢材 表面。
第二节
扩散定律
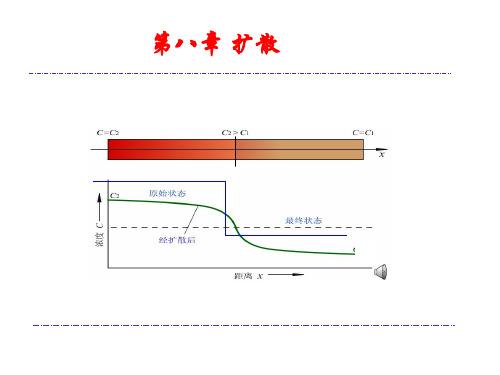
菲克第一定律（ 一 、 菲克第一定律 （ 研究扩散现象的宏观规律） 将两根不同溶质浓度的固溶体合金棒对焊， 加热到高温，则溶质原子将从浓度较高一端向浓 度较低一端扩散，并沿长度方向形成浓度梯度.
如在扩散过程中各处浓度C只随距离X变化，不 随时间t变化，则单位时间通过单位垂直截面的扩 散流量J对于各处都相等。 即：每一时刻从左边扩散来多少原子，就向右 边扩散走多少原子，没有盈亏，浓度不随时间变 化，这种扩散称稳定态扩散 稳定态扩散。 稳定态扩散