四川省成都市2020-2021学年高二上学期期末调研考试数学(理)试题 Word版含答案

合集下载

成都市成华区2020-2021学年上学期期末考试九年级数学试卷(一诊)(含答案)

成都市成华区2020~2021学年度上期期末学业水平阶段性监测九年级数学注意事项：1. 全卷分A卷和B卷，A卷满分100分，B卷满分50分；考试时间120分钟.2. 考生使用答题卡作答.3. 在作答前，考生务必将自己的姓名、考生号和座位号填写在答题卡上. 考试结束，监考人员将试卷和答题卡一并收回.4.选择题部分请使用2B铅笔填涂；非选择题部分请使用0.5毫米黑色墨水签字笔书写，字体工整、字迹清楚.5. 请按照题号在答题卡上各题目对应的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效.6. 保持答题卡面清洁，不得折叠、污染、破损等.A卷(共100分)第Ⅰ卷(选择题，共30分)一、选择题(本大题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上)1.一元二次方程22x x=的根为(A)0(B)2(C)0或2(D)0或2−2.下列图形中，是中心对称图形但不是轴对称图形的是(A)矩形(B)菱形(C)正方形(D)平行四边形3.如图所示的几何体，其俯视图是(A) (B) (C) (D)4.下列说法中，错误的是(A)菱形的对角线互相垂直(B)对角线互相垂直的四边形是菱形(C)矩形的四个内角都相等(D)四个内角都相等的四边形是矩形5.已知△ABC∽△DEF，相似比为2，且△ABC的面积为16，则△DEF的面积为(A)4(B)8(C)16(D)326. 一元二次方程2304y y −−=配方后可化为(A )21()12y +=(B )213()24y +=(C )213()24y −=(D )21()12y −=7. 若点1(1,)A y −，2(2,)B y ，3(3,)C y 在反比例函数6y x=−的图象上，则1y ，2y ，3y 的大小关系是(A )123y y y ＞＞ (B )231y y y ＞＞ (C )132y y y ＞＞ (D )321y y y ＞＞8. 如图，在△ABC 中，∠C ＝90°，则下列各式中正确的是(A )sin c b B =⋅(B )sin b c B =⋅(C )tan a b B =⋅(D )tan b c B =⋅第8题图第9题图第10题图9. 如图，在平行四边形ABCD 中，点F 是AD 上的点，AF ＝2FD ，直线BF 交AC 于点E ，交CD 的延长线于点G ，则BEEG的值为 (A )12(B )13(C )23(D )3410. 二次函数2y ax bx c =++(0a ≠)的对称轴是2x =，图象如图所示，下面四个结论： ①240b ac −＞；②0abc ＜；③40a b +=；④420a b c −+＞. 其中正确结论的个数是(A )4(B )3(C )2(D )1第Ⅱ卷(非选择题，共70分)二、填空题(本大题共4个小题，每小题4分，共16分，答案写在答题卡上) 11. 关于x 的一元二次方程220x x k +−=无实数根，则k 的取值范围是______.12. 在抛掷正六面体的试验中，正六面体的六个面分别标有数字1，2，3，4，5，6，在试验次数很大时，数字6朝上的频率的变化趋势接近的值是______.13. 将抛物线21y x =−+向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线的一般式为______.b14. 如图，在平行四边形ABCD 中，以点A 为圆心，AB 为半径作弧，交AD 于点F ，再分别以点B ，F 为圆心，大于12BF 为半径作弧，两弧相交于点G ，射线AG 交BC 于点E . 若BF ＝8，AB ＝5，则AE 的长为______.三、解答题(本大题共6个小题，共54分，解答过程写在答题卡上) 15. (本小题满分12分，每题6分)(1)计算：0115(π2021)2cos60()3−−−−++；(2)解方程：2(3)3(3)x x x −=−.16. (本小题满分6分)先化简，再求值：22224()2442x x x x x x x x +−−−÷−−+−，其中4tan 452sin 60x =+.为了解疫情期间网络学习的效果，某中学随机抽取了部分学生进行调查. 要求每位学生从“优秀”、“良好”、“一般”、“不好”四个等次中，选择一项作为评价网络学习的效果. 现将调查结果绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：(1)这题活动共抽查了______人；扇形统计图中，学习效果“一般”所对应的圆心角度数为______；请将条形统计图补充完整；(2)张老师在班上抽取了4名学生，其中学习效果“优秀”的1人，“良好”的2人，“一般”的1人，若从这4人中随机抽取2人，请用画树状图或列表法，求抽取的2人学习效果全是“良好”的概率.18. (本小题满分8分)在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的一、二号楼进行测高实践. 如图为实践时绘制的截面图，无人机从地面CD 的中点B 垂直起飞到达点A 处，测得一号楼顶部E 的俯角为55°，测得二号楼顶部F 的俯角为37°，此时航拍无人机的高度为60米，已知一号楼的高CE 为20米，求二号楼的高DF . (结果精确到米)(参考数据：sin 370.60≈，cos370.80≈，tan370.75≈，sin 550.82≈，cos550.57≈，tan 55 1.43≈.)效果人数(人)优秀良好一般不好如图，一次函数y kx b =+的图象与反比例函数my x=的图象相交于(1,2)A ，(,1)B n −两点. (1)求一次函数和反比例函数的表达式；(2)若点P 是x 轴上的点，△ABP 的面积是4，求点P 的坐标.20. (本小题满分10分)如图，点E 在菱形ABCD 的边AB 上滑动(不与A ，B 重合)，点F 在边CB 上，CF ＝AE ，DE 的延长线交CB 的延长线于点G ，DF 的延长线交AB 的延长线于点H .(1)求证：DE ＝DF ； (2)求证：2AB AE AH =⋅；(3)若点E 为边AB 的黄金分割点(AE EB ＞)，求证BH ＝AE .CB 卷(共50分)一、填空题(本大题共5个小题，每小题4分，共20分，答案写在答题卡上) 21. 关于x 的一元二次方程22(1)210a x x a −−+−=有一个根为0x =，则a ＝______.22. 如图，在44⨯的正方形网格(每个小正方形的边长都是1)中，△ABC 的顶点都在小正方形的格点上，则sin ACB ∠=______.第22题图第24题图第25题图23. 从1−，2，3−，4四个数中任取两个不同的数分别作为a ，b 的值，得到反比例函数aby x=，则这些反比例函数中，其图象在二、四象限的概率是______. 24. 如图，点B 是反比例函数12y x=(0x ＞)图象上一点，过点B 分别向坐标轴作垂线，垂足分别为A ，C . 反比例函数ky x=(0x ＞)的图象经过OB 的中点M ，与AB ，BC 分别交于点D ，E . 连接DE 并延长交x 轴于点F ，则△BDF 的面积是______.25. 如图，在66⨯的正方形网格中，每个小正方形的边长为1，已知Rt △ABC 是网格中的格点三角形，则该网格中与Rt △ABC 相似且面积最大的格点三角形的面积是____，符合条件的格点三角形共有____个. 二、解答题(本大题共3个小题，共30分，解答过程写在答题卡上) 26. (本小题满分8分)某水果商店销售一种进价为40元/千克的优质水果，若售价为50元/千克，则一个月可售出500千克；若售价在50元/千克的基础上每涨价1元，则月销售量就减少10千克.(1)当月利润为8000元时，每千克水果售价为多少元？(2)当每千克水果售价为多少元时，获得的月利润最大？月利润的最大值是多少？△ABC 中，AB ＝AC ，∠ABC ＝α，过点A 作直线MN ，使MN ∥BC ，点D 在直线MN 上(不与点A 重合)，作射线BD ，将射线BD 绕点B 顺时针旋转α后交直线AC 于点E .(1)如图1，点D 在射线AN 上，α＝60°，求证：AB ＋AD ＝AE ；(2)如图2，点D 在射线AN 上，α＝45°，线段AB ，AD ，AE 之间又有何数量关系？写出你的结论，并证明；(3)若α＝30°，∠ABE ＝15°，BC＝AD 的长.图1 图2 备用图E如图，抛物线24y ax bx =++(0a ≠)与x 轴交于点(1,0)A −和点(4,0)B ，与y 轴交于点C ，顶点为D ，连接AC ，BC ，BC 与抛物线的对称轴l 交于点E .(1)求抛物线的表达式；(2)点P 是第一象限内抛物线上的动点，连接PB ，PC ，若35PBC ABC S S =△△，求点P 的坐标；(3)点N 是对称轴l 右侧抛物线上的动点，在射线ED 上是否存在点M ，使得以点M ，N ，E 为顶点的三角形与△OBC 相似？若存在，直接写出点M 的坐标；若不存在，说明理由.成都市成华区2020—2021学年度上期期末学业水平阶段性监测九年级数学参考答案一．选择题（共10小题）1．C ．2．D ．3．A ．4．B ．5．A ．6．D ．7．C ．8．B ．9．C ．10．B ．二．填空题（共4小题）11．1k <-．12．16．13．222y x x =---．14．6．三．解答题（共5小题）15．解：（1）原式＝151+2+32-⨯＝8；（2）()3(23)0x x --=解得：x 1＝3，x 2＝23．16．17．18．19．20.B卷一．填空题（共5小题）21．1 ．22．4 5．23．2 3．24．9 2．25．10；16．二．解答题（共3小题）26．。

2020-2021学年四川省成都市锦江区九年级(上)期末数学试卷(一诊)

2020-2021学年四川省成都市锦江区九年级（上）期末数学试卷（一诊）一、选择题（共10个小题，每小题3分，满分30分）在下列小题中，均给出四个答案，其中有且只有一个正确答案，请将正确答案的字母代号在答题卡上涂黑，涂错或不涂均为零分．1．（3分）如图所示的几何体的俯视图是（）A．B．C．D．2．（3分）如图，在Rt△ABC中，∠C＝90°，sin A＝，BC＝3，则AC的长为（）A．3B．4C．5D．63．（3分）为满足人们对防疫物资的需求，某口罩加工厂增加设备，努力提高口罩生产量．2020年10月份该工厂的口罩产量为500万个，12月份产量为720万个，若口罩产量平均每月增长率为x，则可列方程为（）A．500（1+2x）＝720B．720（1﹣x）2＝500C．500（1+x2）＝720D．500（1+x）2＝7204．（3分）如图，在△ABC中，点D，E分别是边AB，AC的中点，若S△ADE＝4．则四边形BDEC的面积为（）A．4B．8C．12D．165．（3分）已知点（x1，y1），（x2，y2）都在反比例函数y＝的图象上，且0＜x1＜x2，则y1与y2的大小关系为（）A．y1＞y2B．y1≥y2C．y1＜y2D．y1≤y26．（3分）如图，在⊙O上有三点A，B，C，连接OA，OC，BA，BC，若∠ABC＝110°，则∠AOC的大小为（）A．70°B．110°C．130°D．140°7．（3分）已知，将△ABC沿AD折叠，点B的对应点B'落在边AC上（如图a），再将∠CAD对折，点A的对应点为A'，折痕为EF（如图b），再沿A'E所在直线剪下，则阴影部分展开后的形状为（）A．等腰三角形B．矩形C．菱形D．正方形8．（3分）将二次函数y＝x2﹣2x+1的图象向上平移3个单位长度，再向左平移2个单位长度，得到的抛物线的表达式为（）A．y＝x2﹣2x+3B．y＝x2﹣2x+4C．y＝x2+2x+3D．y＝x2+2x+4 9．（3分）如图，矩形ABCD的对角线AC，BD相交于点O，且∠AOD＝120°．过点A作AE⊥BD于点E，则BE：ED等于（）A．1：3B．1：4C．2：3D．2：510．（3分）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，下列结论：①abc＜0；②9a+3b+c＜0；③a＞；④若方程ax2+bx+c＝0两个根x1和x2，则3＜|x1﹣x2|＜4，其中正确的结论有（）A．①②③B．①②④C．①③④D．②③④二、填空题（共4个小题，每小题4分，满分16分）11．（4分）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tan C＝．12．（4分）已知关于x的一元二次方程x2﹣2（k﹣1）x+k2﹣1＝0有两个不相等的实数根，则k的取值范围是．13．（4分）用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若转盘a转出红色，转盘b转出蓝色即可配成紫色，则配成紫色的概率为．14．（4分）如图，四边形ABCD是正方形，按如下步骤操作：①分别以点A，D为圆心，以AD长为半径画弧，两弧交于点P，连接AP，DP；②连接BP，CP，则∠BPC＝．三、解答题（共6个小题，满分54）15．（12分）（1）计算：﹣tan60°+（）﹣1﹣|1﹣2cos30°|．（2）解方程：x2﹣4x﹣1＝0．16．（6分）“青年大学习”是共青团中央为组织引导广大青年，深入学习宣传贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学习行动．某校为了解九年级同学学习“青年大学习”的情况，随机抽取部分九年级同学进行了问卷调查，按照调查结果，将学习情况分为优秀、良好、合格、较差四个等级．学校绘制了如图不完整的统计图，根据图中信息解答下列问题：（1）将条形统计图补充完整；（2）若该校九年级有800名学生，请估计九年级学生“青年大学习”学习情况为“优秀”和“良好”的一共有多少名？（3）该校某班有3名同学（1名男同学、2名女同学）在调查中获得“优秀”等级，班主任将从这3名同学中随机选取2名同学，代表班级参加学校组织的“青年大学习”演讲大赛．请用列表或画树状图的方法，求所选两位同学恰好是1名男同学和1名女同学的概率．17．（8分）如图，在水平地面上，有一盏垂直于地面的路灯AB，在路灯前方竖立有一木杆CD．已知木杆长CD＝2.65米，木杆与路灯的距离BD＝5米，并且在C点测得灯源A 的仰角为44°．（结果保留1位小数：参考数据：sin44°≈0.69，cos44°≈0.72，tan44°≈0.97）（1）求路灯高AB大约是多少米？（2）请在图中画出木杆CD在灯光下的影子（用线段表示），并求出影长．18．（8分）如图1，在平行四边形ABCD中，过点A作AE⊥BC交BC于点E，连接ED ，且ED平分∠AEC．（1）求证：AE＝BC；（2）如图2，过点C作CF⊥DE交DE于点F，连接AF，BF，猜想△ABF的形状并证明．19．（10分）如图，直线y＝﹣x+4与x轴交于点A，与y轴交于点B，反比例函数y1＝（x＞0）的图象经过线段AB的中点C．（1）求反比例函数的表达式；（2）将直线y＝﹣x+4向右平移4个单位长度后得到直线y2＝ax+b，直线y2交x轴于点D，交反比例函数y1＝（x＞0）的图象于点E，F，连接CE，CF，求△CEF的面积；（3）请结合图象，直接写出不等式y1＜y2的解集．20．（10分）如图，在△ABC中，AB＝AC，以边BC为直径作⊙O，交AC于点D，连接AO，交BD于点E，交⊙O于点F，连接DF．（1）求证：∠CAO＝∠CBD；（2）求证：＝；（3）当△DEF为等腰三角形时，若BC＝4，求△DEF的面积．四、填空题（共5个小题，每小题4分，满分20分）21．（4分）设x1，x2是一元二次方程x2﹣3x﹣2＝0的两个实数根，则x12+3x1x2+x22的值为．22．（4分）如图，菱形ABCD的边长AB＝3，对角线BD＝4，点E，F在BD上，且BE＝DF＝，连接AE，AF，CE，CF．则四边形AECF的周长为．23．（4分）如图，点A，B是反比例函数y＝（x＞0）的图象上的两点，过点A作AC⊥x轴于点C，交直线OB于点D，连接OA．若点A的坐标为（3，1），OB＝BD，则sin ∠AOD＝．24．（4分）黄金分割是指把一条线段分割为两部分，使较短线段与较长线段的比等于较长线段与原线段的比，其比值等于．如图，在正方形ABCD中，点G为边BC延长线上一动点，连接AG交对角线BD于点H，△ADH的面积记为S1，四边形DHCG的面积记为S2．如果点C是线段BG的黄金分割点，则的值为．25．（4分）如图1，点E是等边△ABC的边BC上一点（不与点B，C重合），连接AE，以AE为边向右作等边△AEF，连接CF．若△ECF的面积（S）与BE的长（x）之间的函数关系如图2所示（P为图象顶点），则等边△ABC的边长AB＝．五、解答题（第26题满分30分，第27题满分30分，第28题满分30分）26．（8分）近年来，西部某民族聚居区扶贫工作小组结合当地实际，大力开发乡村旅游扶贫项目，积极挖掘乡村生态休闲、旅游观光、文化教育价值，发展乡村民宿．某民宿建有40个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆每天需对每个房间支出40元的各种费用，设每个房间的定价为x元，相应的住房数为y间．（1）求y与x的函数关系式；（2）求每个房间定价为多少元时，该民宿当天利润W最大？最大利润是多少？27．（10分）如图，在△ABC中，AB＝AC，∠BAC＝90°，BC＝14，过点A作AD⊥BC 于点D，E为腰AC上一动点，连接DE，以DE为斜边向左上方作等腰直角△DEF，连接AF．（1）如图1，当点F落在线段AD上时，求证：AF＝EF；（2）如图2，当点F落在线段AD左侧时，（1）中结论是否仍然成立？若成立，请证明；若不成立，请说明理由；（3）在点E的运动过程中，若AF＝，求线段CE的长．28．（12分）抛物线y＝ax2+bx﹣3（a≠0）的图象与x轴交于点B（﹣3，0），C（1，0），与y轴交于点A．（1）求抛物线的表达式和顶点坐标；（2）抛物线上是否存在一点D（不与点A，B，C重合），使得直线DA将四边形DBAC 的面积分为3：5两部分，若存在，求出点D的坐标；若不存在，请说明理由；（3）点P是抛物线对称轴上一点，在抛物线上是否存在一点Q，使以点P，Q，A，B为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．2020-2021学年四川省成都市锦江区九年级（上）期末数学试卷（一诊）参考答案与试题解析一、选择题（共10个小题，每小题3分，满分30分）在下列小题中，均给出四个答案，其中有且只有一个正确答案，请将正确答案的字母代号在答题卡上涂黑，涂错或不涂均为零分．1．（3分）如图所示的几何体的俯视图是（）A．B．C．D．【解答】解：从上边看是两个有公共边的矩形，如图所示：故选：A．2．（3分）如图，在Rt△ABC中，∠C＝90°，sin A＝，BC＝3，则AC的长为（）A．3B．4C．5D．6【解答】解：∵∠C＝90°，sin A＝＝，∴AB＝BC＝×3＝5，∴AC＝＝＝4．故选：B．3．（3分）为满足人们对防疫物资的需求，某口罩加工厂增加设备，努力提高口罩生产量．2020年10月份该工厂的口罩产量为500万个，12月份产量为720万个，若口罩产量平均每月增长率为x，则可列方程为（）A．500（1+2x）＝720B．720（1﹣x）2＝500C．500（1+x2）＝720D．500（1+x）2＝720【解答】解：设第11、12月份每月的平均增长率为x，则根据题意可得出方程为：500（1+x）2＝720；故选：D．4．（3分）如图，在△ABC中，点D，E分别是边AB，AC的中点，若S△ADE＝4．则四边形BDEC的面积为（）A．4B．8C．12D．16【解答】解：∵点D，E分别是边AB，AC的中点，∴DE＝BC，DE∥BC，∴△ADE∽△ABC，∴＝（）2＝，∴S△ABC＝16，∴四边形BDEC的面积＝16﹣4＝12，故选：C．5．（3分）已知点（x1，y1），（x2，y2）都在反比例函数y＝的图象上，且0＜x1＜x2，则y1与y2的大小关系为（）A．y1＞y2B．y1≥y2C．y1＜y2D．y1≤y2【解答】解：∵反比例函数y＝中的k＝5＞0，∴反比例函数y＝的图象经过第一、三象限，且在每一象限内y的值随x的值增大而减小．∵（x1，y1），（x2，y2），0＜x1＜x2，即这两点都位于第一象限，∴y1＞y2．故选：A．6．（3分）如图，在⊙O上有三点A，B，C，连接OA，OC，BA，BC，若∠ABC＝110°，则∠AOC的大小为（）A．70°B．110°C．130°D．140°【解答】解：在优弧AC上取一点D，连接AD，DC．∵∠B+∠D＝180°，∴∠D＝180°﹣110°＝70°，∴∠AOC＝2∠D＝140°，故选：D．7．（3分）已知，将△ABC沿AD折叠，点B的对应点B'落在边AC上（如图a），再将∠CAD对折，点A的对应点为A'，折痕为EF（如图b），再沿A'E所在直线剪下，则阴影部分展开后的形状为（）A．等腰三角形B．矩形C．菱形D．正方形【解答】解：阴影部分展开后如图所示，由折叠可得，∠AFE＝∠A'FE＝90°，AF＝A'F，EF＝E'F，∴AA'与EE'互相平分，AA'⊥EE'，∴四边形AEA'E'是菱形，故选：C．8．（3分）将二次函数y＝x2﹣2x+1的图象向上平移3个单位长度，再向左平移2个单位长度，得到的抛物线的表达式为（）A．y＝x2﹣2x+3B．y＝x2﹣2x+4C．y＝x2+2x+3D．y＝x2+2x+4【解答】解：∵y＝x2﹣2x+1＝（x﹣1）2，∴该抛物线的顶点坐标是（1，0），∴将二次函数y＝x2﹣2x+3的图象向上平移3个单位长度，向左平移2个单位长度得到抛物线的顶点坐标是（﹣1，3），∴平移后的抛物线相应的函数表达式为：y＝（x+1）2+3，即y＝x2+2x+4．故选：D．9．（3分）如图，矩形ABCD的对角线AC，BD相交于点O，且∠AOD＝120°．过点A 作AE⊥BD于点E，则BE：ED等于（）A．1：3B．1：4C．2：3D．2：5【解答】解：∵四边形ABCD是矩形，∴OA＝OB＝OD，∵∠AOD＝120°，∴∠AOB＝180°﹣120°＝60°，∴△AOB为等边三角形，∵AE⊥BD，∴BE＝OE＝OB，∴ED＝3BE，∴＝，故选：A．10．（3分）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，下列结论：①abc＜0；②9a+3b+c＜0；③a＞；④若方程ax2+bx+c＝0两个根x1和x2，则3＜|x1﹣x2|＜4，其中正确的结论有（）A．①②③B．①②④C．①③④D．②③④【解答】解：①抛物线对称轴在y轴右侧，则ab异号，而c＞0，则abc＜0，故结论正确；②由图象可知x＝3时，y＝9a+3b+c＜0，故结论正确；③∵﹣＝2，∴b＝﹣4a，∵x＝1时，y＝a+b+c＜0，∴﹣3a+c＜0，∴a＞，故结论正确；④若方程ax2+bx+c＝0两个根x1和x2，由图象可知，0＜x1＜1，3＜x2＜4，∴则2＜|x1﹣x2|＜4，故结论错误；故选：A．二、填空题（共4个小题，每小题4分，满分16分）11．（4分）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tan C＝．【解答】解：如图，过点A作AE⊥CB交CB的延长线于E．Rt△AEC中，tan C＝＝＝，故答案为：．12．（4分）已知关于x的一元二次方程x2﹣2（k﹣1）x+k2﹣1＝0有两个不相等的实数根，则k的取值范围是k＜1．【解答】解：根据题意得Δ＝4（k﹣1）2﹣4（k2﹣1）＞0，解得k＜1．故答案为k＜1．13．（4分）用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若转盘a转出红色，转盘b转出蓝色即可配成紫色，则配成紫色的概率为．【解答】解：画树状图如图：共有12个等可能的结果，其中配成紫色的结果有1个，∴配成紫色的概率为，故答案为：．14．（4分）如图，四边形ABCD是正方形，按如下步骤操作：①分别以点A，D为圆心，以AD长为半径画弧，两弧交于点P，连接AP，DP；②连接BP，CP，则∠BPC＝150°．【解答】解：根据作图过程可知：AD＝AP＝PD，∴△ADP是等边三角形，∴∠DAP＝∠ADP＝∠APD＝60°，∵四边形ABCD是正方形，∴AB＝AD＝DC，∠BAD＝∠ADC＝∠ABC＝∠BCD＝90°，∴AB＝AP，DP＝DC，∴∠ABP＝∠APB＝∠DPC＝∠DCP＝75°，∴∠BPC＝360°﹣60°﹣75°﹣75°＝150°．故答案为：150°．三、解答题（共6个小题，满分54）15．（12分）（1）计算：﹣tan60°+（）﹣1﹣|1﹣2cos30°|．（2）解方程：x2﹣4x﹣1＝0．【解答】解：（1）﹣tan60°+（）﹣1﹣|1﹣2cos30°|＝2﹣+2﹣|1﹣2×|＝2﹣+2+（1﹣）＝3；（2）x2﹣4x﹣1＝0，移项，得x2﹣4x＝1，配方，得x2﹣4x+4＝1+4，即（x﹣2）2＝5，解得x﹣2＝±，所以x1＝2+，x2＝2﹣．16．（6分）“青年大学习”是共青团中央为组织引导广大青年，深入学习宣传贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学习行动．某校为了解九年级同学学习“青年大学习”的情况，随机抽取部分九年级同学进行了问卷调查，按照调查结果，将学习情况分为优秀、良好、合格、较差四个等级．学校绘制了如图不完整的统计图，根据图中信息解答下列问题：（1）将条形统计图补充完整；（2）若该校九年级有800名学生，请估计九年级学生“青年大学习”学习情况为“优秀”和“良好”的一共有多少名？（3）该校某班有3名同学（1名男同学、2名女同学）在调查中获得“优秀”等级，班主任将从这3名同学中随机选取2名同学，代表班级参加学校组织的“青年大学习”演讲大赛．请用列表或画树状图的方法，求所选两位同学恰好是1名男同学和1名女同学的概率．【解答】解：（1）抽取的学生数为：24÷30%＝80（人）；抽取的学生中良好的人数为：80﹣24﹣16﹣8＝32（人），将条形统计图补充完整如图：（2）800×＝560（名），即估计九年级学生“青年大学习”学习情况为“优秀”和“良好”的一共有560名；（3）画树状图如图：共有6个等可能的结果，所选两位同学恰好是1名男同学和1名女同学的有4个，∴所选两位同学恰好是1名男同学和1名女同学的概率为＝．17．（8分）如图，在水平地面上，有一盏垂直于地面的路灯AB，在路灯前方竖立有一木杆CD．已知木杆长CD＝2.65米，木杆与路灯的距离BD＝5米，并且在C点测得灯源A的仰角为44°．（结果保留1位小数：参考数据：sin44°≈0.69，cos44°≈0.72，tan44°≈0.97）（1）求路灯高AB大约是多少米？（2）请在图中画出木杆CD在灯光下的影子（用线段表示），并求出影长．【解答】解：（1）过点C作CE⊥AB于E．在Rt△ACE中，∠ACE＝44°，CE＝BD＝5米，∴＝tan44°，∴AE＝EC•tan44°≈5×0.97≈4.85（米），∵EB＝CD＝2.65米，∴AB＝AE+EB＝4.85+2.65≈7.5（米）．（2）如图，延长AC交BD的延长线于F．则线段DF就是木杆CD在灯光下的影子，∵CE∥BF，∴∠CFD＝∠ACE＝44°，在Rt△CFD中，tan∠CFD＝，∴DF＝≈≈2.7（米）．即木杆CD在灯光下的影子为2.7米．18．（8分）如图1，在平行四边形ABCD中，过点A作AE⊥BC交BC于点E，连接ED ，且ED平分∠AEC．（1）求证：AE＝BC；（2）如图2，过点C作CF⊥DE交DE于点F，连接AF，BF，猜想△ABF的形状并证明．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，又∵AE⊥BC，∴∠AEC＝90°，又∵ED平分∠AEC，∴∠ADE＝∠CED＝45°，∴∠AED＝∠ADE，∴AE＝AD，∴AE＝BC；（2）△ABF是等腰直角三角形，证明：∵CF⊥DE，∴∠CFE＝90°，又∵∠CEF＝45°，∴∠ECF＝45°，∴∠FEC＝∠FCE＝∠AEF，∴EF＝CF，在△AEF和△BCF中，，∴△AEF≌△BCF（SAS），∴AF＝BF，∠AFE＝∠BFC，∴∠AFE﹣∠BFE＝∠BFC﹣∠BFE，即∠AFB＝∠EFC＝90°，∴△ABF是等腰直角三角形．19．（10分）如图，直线y＝﹣x+4与x轴交于点A，与y轴交于点B，反比例函数y1＝（x＞0）的图象经过线段AB的中点C．（1）求反比例函数的表达式；（2）将直线y＝﹣x+4向右平移4个单位长度后得到直线y2＝ax+b，直线y2交x轴于点D，交反比例函数y1＝（x＞0）的图象于点E，F，连接CE，CF，求△CEF的面积；（3）请结合图象，直接写出不等式y1＜y2的解集．【解答】解：（1）∵直线y＝﹣x+4与x轴交于点A，与y轴交于点B，∴A（6，0），B（0，4），∵线段AB的中点是C，∴C（3，2）．将C（3，2）代入y1＝（x＞0），得k＝3×2＝6，∴反比例函数的表达式为y1＝；（2）∵将直线y＝﹣x+4向右平移4个单位长度后得到直线y2＝ax+b，直线y2交x轴于点D，∴a＝﹣，D（10，0）．把D（10，0）代入y＝﹣x+b，解得b＝，∴直线EF的解析式为y2＝﹣x+．由，解得或，∴E（1，6），F（9，）．如图，过点C作CP∥y轴交EF于P，则P点的横坐标为3．将x＝3代入y2＝﹣x+，得y＝，∴CP＝，∴S△ECF＝S△ECP+S△PCF＝××（3﹣1）+××（9﹣3）＝+8＝；（3）由图象可得，不等式y1＜y2的解集为1＜x＜9．20．（10分）如图，在△ABC中，AB＝AC，以边BC为直径作⊙O，交AC于点D，连接AO，交BD于点E，交⊙O于点F，连接DF．（1）求证：∠CAO＝∠CBD；（2）求证：＝；（3）当△DEF为等腰三角形时，若BC＝4，求△DEF的面积．【解答】（1）证明：∵AB＝AC，OB＝OC，∴∠AOC＝90°，∴∠CAO+∠ACO＝90°，∵BC是⊙O的直径，∴∠BDC＝90°，∴∠CBD+∠BCD＝90°，∴∠CAO＝∠CBD；（2）证明：∵AB＝AC，OB＝CO，∴∠BAO＝∠CAO，又∵∠CAO＝∠CBD，∵∠BAO＝∠EBO，又∵∠AOB＝∠BOE，∴△AOB∽△BOE，∴，又∵OB＝OF，∴，∴，∴，即；（3）解：∵∠BDF＝∠BOF，∠BOF＝90°，∴∠BDF＝45°，∴∠ADF＝45°，又∵∠DFE＝∠ADF+∠F AD，∴∠DFE＞45°，连接BF，∵OB＝OF，∴∠OBF＝∠OFB＝45°，又∵∠BEO＝∠OFB+∠FBE，∴∠BEO＞45°，∴∠DEF＝∠BEO＞45°，在△DEF中，∠EDF＝45°，∠DFE＞45°，∠DEF＞45°，∴DE≠EF，DF≠EF，∴若△DEF是等腰三角形，则只有一种情况：DE＝DF．∴∠DFE＝∠DEF，连接EC，FC，∵∠DEC+2∠BEO＝180°，∴∠DEC+2∠DEF＝180°，又∵∠EDF+2∠DEF＝180°，∴∠DEC＝∠EDF＝45°，又∵∠EDC＝90°，∴∠DCE＝45°，∴DE＝DC，又∵∠ADE＝∠BDC＝90°，∠EAD＝∠CBD，∴△ADE≌△BDC（ASA），∴AE＝BC＝4，又∵OF＝BC＝2，，∴，∴EF＝4﹣2或EF＝4+2（大于2，舍去），∴EO＝2﹣2，过点D作DG⊥EF于点G，∴EG＝EF＝2﹣，DG∥BC，∴△DGE∽△BOE，∴，∴，∴DG＝，∴＝＝2﹣2四、填空题（共5个小题，每小题4分，满分20分）21．（4分）设x1，x2是一元二次方程x2﹣3x﹣2＝0的两个实数根，则x12+3x1x2+x22的值为7．【解答】解：由题意，得：x1+x2＝3，x1x2＝﹣2；原式＝（x1+x2）2+x1x2＝9﹣2＝7．故答案为：7．22．（4分）如图，菱形ABCD的边长AB＝3，对角线BD＝4，点E，F在BD上，且BE＝DF＝，连接AE，AF，CE，CF．则四边形AECF的周长为4．【解答】解：如图，连接AC，交BD于O，∵四边形ABCD是菱形，∴AC⊥BD，BO＝BD＝＝，在Rt△ABO中，AO＝＝＝1，又∵BE＝，∴EO＝﹣＝，在Rt△AOE中，AE＝＝＝，同理可得，CE＝CF＝AF＝，∴四边形AECF的周长4．故答案为：4．23．（4分）如图，点A，B是反比例函数y＝（x＞0）的图象上的两点，过点A作AC⊥x轴于点C，交直线OB于点D，连接OA．若点A的坐标为（3，1），OB＝BD，则sin ∠AOD＝．【解答】解：∵AD⊥x轴，A（3，1），∴OC＝3，点D的横坐标为3，将点A（3，1）代入反比例函数y＝中得，k＝3×1＝3，∴反比例函数的解析式为y＝，如图，过点B作BH⊥AD于H，∵AD⊥x轴，∴BH∥OC，∵OB＝BD，∴CH＝DH，∴BH是△OCD的中位线，∴BH＝OC＝，当x＝时，y＝＝2，∴点H（3，2），点B的坐标为（，2），∴直线OB的解析式为y＝x，∴D（3，4），∴OD＝5，AD＝3，过点A作AG⊥OD于G，∴S△AOD＝AD•OC＝OD•AG，∴AG＝＝＝，∵OA＝＝，在Rt△AGO中，sin∠AOD＝＝＝，故答案为：．24．（4分）黄金分割是指把一条线段分割为两部分，使较短线段与较长线段的比等于较长线段与原线段的比，其比值等于．如图，在正方形ABCD中，点G为边BC延长线上一动点，连接AG交对角线BD于点H，△ADH的面积记为S1，四边形DHCG的面积记为S2．如果点C是线段BG的黄金分割点，则的值为或．【解答】解：∵四边形ABCD是正方形，∴AB＝CB，AD∥BC，∠ABH＝∠CBH＝45°，∴△ABD的面积＝△AGD的面积，又∵BH＝BH，∴△AHB≌△CHB（SAS），∴△AHB的面积＝△DHG的面积，∴S2＝△GBH的面积，∵AD∥BC，∴△ADH∽△GBH，∴＝（）2，分两种情况：①点C是线段BG的黄金分割点，BC＞CG，则AD＝BC＝BG，∴＝（）2＝（）2＝；②点C是线段BG的黄金分割点，BC＜CG，则AD＝BC＝BG，∴＝（）2＝（）2＝；综上所述，如果点C是线段BG的黄金分割点，则的值为或；故答案为：或．25．（4分）如图1，点E是等边△ABC的边BC上一点（不与点B，C重合），连接AE，以AE为边向右作等边△AEF，连接CF．若△ECF的面积（S）与BE的长（x）之间的函数关系如图2所示（P为图象顶点），则等边△ABC的边长AB＝4．【解答】解：过点F作FM⊥BC，交BC延长线于M，设AB＝a．∵AB＝AC，AE＝AF，∠BAC＝∠EAF，∴∠BAE＝∠CAF，∴△BAE≌△CAF（SAS），∴BE＝CF＝x，∠ACF＝∠B＝60°，∴FM＝CF•sin60°＝x，∴S＝•（a﹣x）•x＝﹣x2+ax，∵﹣＜0，∴当x＝a时，S的值最大，∴E为BC中点，AE⊥BC，∴∠AEF＝60°，∴∠FEM＝90°﹣60°＝30°，∴FM＝EF＝AE，在Rt△ABE中，AE＝，∴FM＝AE＝AB，∵EC＝BC＝AB，∴，∴AB＝，法二：过点F作FM⊥BC，交BC延长线于M，当E在BC的中点时，F最高，此时面积最大，在E为BC中点，AE⊥BC，∴∠AEF＝60°，∴∠FEM＝90°﹣60°＝30°，∴FM＝EF＝AE，在Rt△ABE中，AE＝，∴FM＝AE＝AB，∵EC＝BC＝AB，∴，∴AB＝，故答案为：4．五、解答题（第26题满分30分，第27题满分30分，第28题满分30分）26．（8分）近年来，西部某民族聚居区扶贫工作小组结合当地实际，大力开发乡村旅游扶贫项目，积极挖掘乡村生态休闲、旅游观光、文化教育价值，发展乡村民宿．某民宿建有40个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆每天需对每个房间支出40元的各种费用，设每个房间的定价为x元，相应的住房数为y间．（1）求y与x的函数关系式；（2）求每个房间定价为多少元时，该民宿当天利润W最大？最大利润是多少？【解答】解：（1）由题意得：y＝40﹣＝﹣0.1x+58，∴y与x的函数关系式为y＝﹣0.1x+58；（2）由题意得：W＝（x﹣40）（﹣0.1x+58）＝﹣0.1（x﹣310）2+7290，∵a＝﹣0.1＜0，∴当x＝310时，W最大＝7290元．∴每个房间定价为310元时，该民宿当天利润W最大，最大利润是7290元．27．（10分）如图，在△ABC中，AB＝AC，∠BAC＝90°，BC＝14，过点A作AD⊥BC 于点D，E为腰AC上一动点，连接DE，以DE为斜边向左上方作等腰直角△DEF，连接AF．（1）如图1，当点F落在线段AD上时，求证：AF＝EF；（2）如图2，当点F落在线段AD左侧时，（1）中结论是否仍然成立？若成立，请证明；若不成立，请说明理由；（3）在点E的运动过程中，若AF＝，求线段CE的长．【解答】（1）证明：∵AB＝AC，∠BAC＝90°，AD⊥BC，∴∠CAD＝45°，∵△EFD是等腰直角三角形，∴∠EFD＝∠AFE＝90°，∴∠AEF＝180°﹣∠CAD﹣∠AFE＝45°，∴∠EAF＝∠AEF，∴AF＝EF；（2）解：当点F落在线段AD左侧时，（1）中结论AF＝EF仍然成立，理由如下：如图2，取AC的中点G，连接DG，FG，在Rt△ADC中，∴DG＝CG＝AG，∴∠GDC＝∠C＝45°，∴∠DGC＝90°，∴△DGC是等腰直角三角形，∵△DFE是等腰直角三角形，∴＝，∵∠FDG＝∠FDE+∠EDG＝45°+∠EDG，∠EDC＝∠GDC+∠EDG＝45°+∠EDG，∴∠FDG＝∠EDC，∴△FDG∽△EDC，∴∠FGD＝∠ECD＝45°，∴∠FGA＝45°，在△FGA和△FGD中，，∴△FGA≌△FGD（SAS），∴AF＝DF，∵DF＝EF，∴AF＝EF；（3）在Rt△ABC中，BC＝14，D是BC中点，∴AD＝7，取AC的中点G，连接DG，FG，设直线FG与AD相交于点P，由（2）可知∠FGD＝45°＝∠GDC，∴FG∥DC，∴GP⊥AD且AP＝DP＝PG＝AD＝，在Rt△APF中，AP＝，AF＝，∴PF＝＝＝，①如图2，当点F落在线段AD左侧时，FG＝4，∵△FDG∽△EDC，∴＝，∴EC＝4；②如图3，当点F落在线段AD的右侧时，∴FG＝PG﹣PF＝DP﹣PF＝3.5﹣0.5＝3，同理得△FDG∽△EDC，∴＝，∴EC＝3．综上，EC的长是4或3．28．（12分）抛物线y＝ax2+bx﹣3（a≠0）的图象与x轴交于点B（﹣3，0），C（1，0），与y轴交于点A．（1）求抛物线的表达式和顶点坐标；（2）抛物线上是否存在一点D（不与点A，B，C重合），使得直线DA将四边形DBAC 的面积分为3：5两部分，若存在，求出点D的坐标；若不存在，请说明理由；（3）点P是抛物线对称轴上一点，在抛物线上是否存在一点Q，使以点P，Q，A，B为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx﹣3（a≠0）的图象与x轴交于点B（﹣3，0），C（1，0），∴，解得：，∴该二次函数的解析式是y＝x2+2x﹣3，∵y＝x2+2x﹣3＝（x+1）2﹣4，∴顶点坐标为（﹣1，﹣4）；（2）解法一：如图1，将x＝0代入y＝x2+2x﹣3中得：y＝﹣3，∴A（0，﹣3），设D（m，m2+2m﹣3），设直线AD的解析式为：y＝kx+n，则，解得：，∴直线AD的解析式为：y＝（m+2）x﹣3，∴直线AD与x轴的交点E的坐标为（，0），∴＝＝＝＝＝，①当＝时，，解得：m＝﹣4，m2+2m﹣3＝5，∴D（﹣4，5）；②当＝时，＝，解得：m＝﹣8，m2+2m﹣3＝45，∴D（﹣8，45）；综上，点D的坐标是（﹣4，5）或（﹣8，45）；解法二：∵直线DA将四边形DBAC的面积分为3：5两部分，∴＝或＝，①当时，E（﹣，0），则直线AE的解析式为：y＝﹣2x﹣3，∴x2+2x﹣3＝﹣2x﹣3，解得：x1＝0（舍），x2＝﹣4，∴D（﹣4，5）；②当＝时，同理得：D（﹣8，45）；综上，点D的坐标是（﹣4，5）或（﹣8，45）；（3）分三种情况：①如图2，以AB为边时，四边形ABPQ是平行四边形，∵抛物线的对称轴是：x＝﹣1，∴P的横坐标为﹣1，∵A（0，﹣3），B（﹣3，0），∴Q的横坐标为2，当x＝2时，y＝22+2×2﹣3＝5，∴Q（2，5）；②如图3，以AB为边时，四边形ABQP是平行四边形，同理得Q（﹣4，5）；③如图4，以AB为对角线时，四边形AQBP是平行四边形，同理得Q（﹣2，﹣3）；综上，点Q的坐标为（2，5）或（﹣4，5）或（﹣2，﹣3）．。

2021-2022学年四川省成都市蓉城高中教育联盟高二上学期期末考试联考地理试卷带讲解

【12题详解】
该区地下水含盐量高，长期灌溉后，地下水水位上升，加之蒸发旺盛，易造成土壤盐碱化，无法继续进行耕作，造成弃耕，C对，D错；根据材料泰地区年均降水量180毫米，且等高线稀疏，地形平坦，不容易产生水土流失，A错；材料和图并没有反应景泰川灌区出现土地沙化区域，B错。故选C。
【13题详解】
根据上题分析可知，景泰川灌区因土壤次生盐碱化导致弃耕，“抬土造田”使表层土壤与地下水位的高差增大，减弱盐碱化。黄淮平原某些地区海拔低，地下水位高，春秋季节蒸发旺盛，土壤次生盐碱化严重，故采取“抬土造田”与景泰川灌区最相似，B对；珠江三角洲在地势低洼的积水区域因地制宜，发展基塘农业，A错；长江三角洲河网密布，发展水稻种植，渔业等，不需“抬土造田”，C错；制约着青藏高原发展农业的主要因素是热量不足，而不是土壤次生盐碱化，D错。故选B。
蓉城高中教育联盟2021～2022学年度上期高中2020级期未联考
地理
一、选择题:本题共25小题，每小题2分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
下图为某区域等高线地形图，据此完成下面小题。
1.图中山脊走向为（）
A.东一西走向B.南一北走向C.东北一西南走向D.西北一东南走向
14.该国河流水文特征的描述正确的是（）
A.径流量大，汛期较长B.含沙量大，流速快C.有结冰期，汛期出现在春季D.无结冰期，流速慢
15.该国地势特征为（）
A.西北高东南低B.西南高东北低C.东北高西南低D.东南高西北低
16.若该国木材产品运往我国，最短的航线将是（）
A.好望角一莫桑比克海峡一苏伊士运河B.直布罗陀海峡一霍尔木兹海峡一马六甲海峡
【点睛】形成盐碱土要有两个条件：一是气候干旱和地下水位高（高于临界水位）。地下水都含有一定的盐份，如其水面接近地面，而该地区又比较干旱，由于毛细作用上升到地表的水蒸发后，便留下盐分。日积月累，土壤含盐量逐渐增加，形成盐碱土。二是地势低洼，没有排水出路。洼地水份蒸发后，即留下盐份，也形成盐碱地。

2020-2021学年四川省成都市某校初一(上)期中考试数学试卷

2020-2021学年四川省成都市某校初一(上）期中考试数学试卷一、选择题1. −15的绝对值是( )A.5B.15C.−5 D.−152. 地球上的海洋面积约为361000000km2，用科学记数法可表示为（）A.361×106km2B.36.1×107km2C.0.361×109km2D.3.61×108km23. 如图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体“着”相对的面上的汉字是（）A.冷B.静C.应D.考4. 一袋大米的质量标识为“10±0.15千克”，则下列大米中质量合格的是（）A.9.80千克B.10.16千克C.9.90千克D.10.21千克5. 某物体从不同方向看到的三种视图如图所示，那么该物体是（）A.长方体B.圆锥体C.正方体D.圆柱体6. 若单项式−2x m y3与5x2y n−1是同类项，则m+n的值是( )A.5B.6C.7D.−77. 在式子a2+2, 1x ，ab2，xy2, −8m2，32中，整式有( )A.6个B.5个C.4个D.3个8. 已知|a−2|+(b+3)2=0，则ab的值是（）A.−6B.6C.−9D.99. 笔记本每本m元，圆珠笔每支n元，买x本笔记本和y支圆珠笔共需()元A.mx+nyB.(m+n)(x+y)C.nx+myD.mn(x+y)10. 实数a，b在数轴上的位置如图所示，则下列各式正确的是()A.a−b>0B.a+b>0C.ab<0D.ab>0二、填空题如果向东走5m，记作+5m；那么向西走10m，记作________m.比较大小：−35_______−32（填“>”或“<”）．单项式−2a3b3的系数是________，次数是________.如果对于任何非零有理数a，b定义一种新的运算“★”如下：a★b=ba−1，则−4★2的值为________．代数式2x2+x的值是2，则代数式8x2+4x−3的值是________.若a，b互为相反数，m，n互为倒数，c是最大的负整数，则5a+|c|+(4mn)2+5b=__________.如图，一个边长为2的正方形和等腰直角三角形的一边重合，组成了一个平面图形，如果将它绕AB所在直线按逆时针方向旋转180∘，得到一个几何体，则这个几何体的体积为________.(圆锥的体积公式为：V圆锥=13πr2ℎ)下列图形是将等边三角形按一定规律排列，则第5个图形中所有等边三角形的个数有________．如图，在数轴上原点为O，点P表示的数为30，点Q表示的数为120，甲、乙两只小虫分别从O，P两点出发，沿直线匀速爬向点Q，最终达到点Q.已知甲每分钟爬行60个单位长度，乙每分钟爬行30个单位长度，则在此过程中，甲、乙两只小虫相距10个单位长度时的爬行时间为________分钟.三、解答题计算：(1)(+18)−(+6)−(+19)−(−12)；(2)(54−76)×(−87)；(3)−22+3×(−1)2021−9÷(−3).化简：(1)3m+2n−5m−n；(2)a+(a−5b)−2(a−2b).分别画出图中几何体从正面、左面、上面看到的这个几何体的形状图．先化简，再求值：2(x2y+xy)−3(x2y−xy)+2x2y，其中x=1，y=−1.如图，大小两个正方形的边长分别为a，b．(1)用含a，b的代数式表示阴影部分的面积S；(2)如果a=8，b=6，求阴影部分的面积．出租车司机小张某天上午营运全是在东西走向的政府大道上进行的，规定向东为正，向西为负，他这天上午的行程是（单位：km）：+15，−3，+16，−11，+10，−12，+4，−15，+16，−18．(1)将最后一名乘客送达目的地时，小张距上午出发点的距离是多少千米？在出发点的什么方向？(2)若汽车耗油量为0.6L/km，出车时，邮箱有油72.2L，若小张将最后一名乘客送达目的地，再返回出发点，问：小张今天下午是否需要加油？若要加油，至少需要加多少油才能返回出发点？若不用加油，请说明理由．2016年第三次G20财长和央行行长会议在成都举行，订制某品牌茶叶作为纪念品，该品牌茶叶加工厂接到一周生产任务为182kg，计划平均每天生产26kg，由于各种原因实际每天产量与计划量相比有出入，某周七天的生产情况记录如下（超产为正、减产为负）：+3，−2，−4，+1，−1，+6，−5(1)这一周的实际产量是多少kg？(2)若该厂工人工资实行每日计件工资制，按计划每生产1kg茶叶50元，若超产，则超产的每千克奖20元；若每天少生产1kg，则扣除10元，那么该厂工人这一周的工资总额是多少？观察下列各式，解答问题：第1个等式：22−12=2×1+1=3；第2个等式：32−22=2×2+1=5；第3个等式：42−32=2×3+1=7；⋯(1)根据以上规律，第4个等式：________；第n个等式：________；（n为整数，且n≥1）(2)（写出必要的过程）利用以上规律：①计算20012−20002的值；②求3+5+7+⋯+1999的值．如图，已知数轴上原点为O，点B表示的数为−4，A在B的右边，且A与B的距离是11，动点P从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P，Q同时出发，设运动时间为t(t>0)秒．(1)写出数轴上点A表示的数________，点P表示的数________（用含t的代数式表示），点Q表示的数________（用含t的代数式表示）；(2)问点P与点Q何时到点O距离相等？(3)若点D是数轴上一点，点D表示的数是x，是否存在整数x，使得|x−7|+|x+4|=15？如果存在，直接写出x的值：如果不存在，说明理由．参考答案与试题解析2020-2021学年四川省成都市某校初一(上）期中考试数学试卷一、选择题1.【答案】B【考点】绝对值【解析】绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．【解答】解：根据负数的绝对值是它的相反数，得|−15|=15.故选B.2.【答案】D【考点】科学记数法--表示较大的数【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．【解答】解：361000000=3.61×108.故选D.3.【答案】B【考点】正方体相对两个面上的文字【解析】利用正方体及其表面展开图的特点解题．【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“静”与面“着”相对，面“沉”与面“应”相对，“冷”与面“考”相对．故选B.4.【答案】C【考点】正数和负数的识别【解析】根据“10±0.15千克”，可算出合格范围，再根据合格范围，选出答案．【解答】解：∵10−0.15=9.85（千克），10+0.15=10.15（千克），∴合格范围为：9.85∼10.15千克.结合选项，只有C选项的大米质量合格.故选C.5.【答案】D【考点】由三视图判断几何体【解析】根据三视图的知识，主视图以及左视图都是矩形，俯视图为一个圆，故易判断该几何体为圆柱．【解答】解：根据从正面看和从左面看是矩形，从上面看是圆，符合这样条件的物体应该是圆柱体．故选D．6.【答案】B【考点】同类项的概念【解析】根据同类项的概念即可求出m与n的值．【解答】解：所含字母相同，相同字母的指数相同的单项式是同类项.由题意可知：m=2，n−1=3，∴m=2，n=4，∴m+n=2+4=6故选B.7.【答案】B【考点】整式的概念【解析】单项式和多项式统称为整式．【解答】解：单项式和多项式统称整式.1x的分母中有未知数，是分式；a2+2 ，ab2 ，xy2 ，−8m2 ，32是整式，共5个.故选B．8.【答案】A【考点】列代数式求值非负数的性质：偶次方非负数的性质：绝对值【解析】此题暂无解析【解答】解：根据题意得，a−2=0，b+3=0，解得a=2，b=−3，ab=−6.故选A．9.【答案】A【考点】列代数式【解析】先求出买x本笔记本的钱数和买y支圆珠笔的钱数，再把两者相加即可．【解答】解：笔记本每本m元，买x本笔记本，需要mx元，圆珠笔每支n元，买y支圆珠笔，需要ny元，则买x本笔记本和y支圆珠笔共需(mx+ny)元.故选A．10.【答案】C【考点】数轴【解析】根据数轴判断出a、b的取值范围，再根据有理数的乘除法，减法运算对各选项分析判断后利用排除法求解．【解答】解：由图可知，a<0<b，−a>b.∵ a<0<b，∴a−b<0，故A选项错误；∵−a>b，∴a+b<0，故B选项错误；∵a<0<b，∴ab<0，故C选项正确；∵a<0<b，∴ab<0，故D选项错误．故选C.二、填空题【答案】−10【考点】正数和负数的识别【解析】此题暂无解析【解答】解：如果向东走5m，记作+5m；那么向西走10m，记作−10m.故答案为：−10.【答案】>【考点】有理数大小比较【解析】两个负数比较大小，绝对值大的反而小，因此比较这两个数的绝对值即可．【解答】解：∵|−35|=35=610，|−32|=32=1510，610<1510，∴−35>−32．故答案为：>.【答案】−23,4【考点】单项式的系数与次数【解析】直接利用单项式定义以及单项式次数与系数的定义分析得出即可．【解答】解：单项式−2a3b3的系数是−23，次数是3+1=4.故答案为：−23；4.【答案】−32【考点】有理数的加法有理数的乘法定义新符号【解析】根据题中的新定义将所求式子化为普通运算，计算即可得到结果．【解答】解：根据题意：−4★2=2−4−1=−32．故答案为：−32.【答案】5【考点】列代数式求值【解析】先将8x2+4x−3变形为4(2x2+x)−3的形式，然后将2x2+x整体代入即可．【解答】解：原式=8x2+4x−3=4(2x2+x)−3，∵2x2+x=2，∴原式=4×2−3=5．故答案为：5．【答案】17【考点】有理数的混合运算倒数相反数【解析】根据a、b互为相反数，m、n互为倒数，x是最大的负整数，可以求得a+b、mn、x的值，从而可以求得所求式子的值．【解答】解：∵a，b互为相反数，∴a+b=0.∵m，n互为倒数，∴ mn=1.∵c是最大的负整数，∴c=−1，∴5a+|c|+(4mn )2+5b=5(a+b)+|c|+(4mn ) 2=0+1+16=17.故答案为：17.【答案】16π3【考点】平面图形旋转得到立体图形问题【解析】根据题意可知该几何体是由半个圆柱和半个圆锥组成，根据题目中的数据分别计算出两部分的体积，最后求和即可. 【解答】解：根据题意，这个几何体的体积为V=12×22×2π+12×13×22×2π=16π3.故答案为：16π3.【答案】485【考点】规律型：图形的变化类【解析】由图可以看出：第一个图形中5个正三角形，第二个图形中5×3+2=17个正三角形，第三个图形中17×3+2=53个正三角形，由此得出第四个图形中53×3+2=161个正三角形，第五个图形中161×3+ 2=485个正三角形．【解答】解：第一个图形正三角形的个数为5，第二个图形正三角形的个数为5×3+2=2×32−1=17，第三个图形正三角形的个数为17×3+2=2×33−1=53，第四个图形正三角形的个数为53×3+2=2×34−1=161，第五个图形正三角形的个数为161×3+2=2×35−1=485．如果是第n个图，则有2×3n−1个.故答案为：485．【答案】23或43或83【考点】数轴【解析】分三种情况，甲追上乙前、甲追上乙后和乙距Q点10个单位，分别列式求解即可.【解答】解：设爬行时间为x分钟，分三种情况：①甲追上乙前：依题意可得30+30x−60x=10，解得x=23；②甲追上乙后：依题意可得60x−(30+30x)=10，解得x=43；③当甲到达Q点时，t=12060=2，当乙到达Q点时，t=120−3030=3，∴当甲到达Q点时乙还没有到Q点，∴当甲到达Q点，乙距Q点10个单位时依题意得30+30x=120−10,解得x =83.综上：甲、乙两只小虫相距10个单位长度时的爬行时间为23或43或83分钟. 故答案为：23或43或83. 三、解答题【答案】解：(1)原式=18−6−19+12=5 . (2)原式=54×(−87)−76×(−87) =−107+43=−221 .(3)原式=−4−3+3=−4 . 【考点】有理数的加减混合运算有理数的混合运算有理数的乘方【解析】（1）原式=18−6−19+12=5 . （2）解：原式=54×(−87)−76×(−87)=−107+43=−221.（3）解：=−4−3+3=−4 . 【解答】解：(1)原式=18−6−19+12=5 . (2)原式=54×(−87)−76×(−87)=−107+43=−221.(3)原式=−4−3+3=−4 . 【答案】解：(1)原式=3m −5m +2n −n =−2m +n .(2)原式=a +a −5b −2a +4b =a +a −2a +4b −5b =−b . 【考点】合并同类项【解析】无无【解答】解：(1)原式=3m −5m +2n −n =−2m +n .(2)原式=a +a −5b −2a +4b =a +a −2a +4b −5b =−b .【答案】解：根据题意画图如下：【考点】作图-三视图【解析】由已知条件可知，主视图有4列，每列小正方数形数目分别为1，1，3，1；左视图有3列，每列小正方形数目分别为3，1，1；俯视图有4列，每列小正方体的数目分别为1，3，1，1，据此可画出图形．【解答】解：根据题意画图如下：【答案】解：原式=2x 2y +2xy −3x 2y +3xy +2x 2y =x 2y +5xy .将x =1，y =−1代入，原式=12×(−1)+5×1×(−1) =−1−5 =−6．【考点】整式的混合运算——化简求值【解析】【解答】解：原式=2x2y+2xy−3x2y+3xy+2x2y=x2y+5xy.将x=1，y=−1代入，原式=12×(−1)+5×1×(−1)=−1−5=−6．【答案】解：(1)∵大小两个正方形的边长分别为a，b，∴阴影部分的面积为：S=a2+b2−12a2−12(a+b)⋅b=12a2+12b2−12ab.(2)∵a=8，b=6，∴S=12×82+12×62−12×8×6=32+18−24=26．【考点】列代数式列代数式求值【解析】（1）依据阴影部分的面积等于两个正方形的面积之和减去空白部分的面积，即可用含a、b的代数式阴影部分的面积S；（2）把a＝8，b＝6，代入代数式，即可求阴影部分的面积．【解答】解：(1)∵大小两个正方形的边长分别为a，b，∴阴影部分的面积为：S=a2+b2−12a2−12(a+b)⋅b=12a2+12b2−12ab.(2)∵a=8，b=6，∴S=12×82+12×62−12×8×6=32+18−24=26．【答案】解：(1)15−3+16−11+10−12+4−15+16−18=2（km）. 答：小张距上午出发点的距离是2km，在出发点的东方.(2)需加油.72.2−0.6×(15+3+16+11+10+12+4+15+16+18+2) =72.2−0.6×122=72.2−73.2=−1(L).答：至少加油1L才能返回出发地．【考点】正数和负数的识别有理数的加法有理数的混合运算【解析】（1）根据有理数的加法运算，可得答案；（2）根据行车就耗油，可得耗油量，根据耗油量与油量的差，可得答案．【解答】解：(1)15−3+16−11+10−12+4−15+16−18=2（km）.答：小张距上午出发点的距离是2km，在出发点的东方.(2)需加油.72.2−0.6×(15+3+16+11+10+12+4+15+16+18+2)=72.2−0.6×122=72.2−73.2=−1(L).答：至少加油1L才能返回出发地．【答案】解：(1)∵七天的生产情况记录如下（超产为正、减产为负）：+3，−2，−4，+1，−1，+6，−5，∴七天的生产情况实际值为：29kg，24kg，22kg，27kg，25kg，32kg，21kg．∴一周总产量：29+24+22+27+25+32+21=180(kg)．答：这一周的实际产量是180kg.(2)26×50+3×20+(26−2)×50+10×(−2)+(26−4)×50+(−4)×10+26×50+1×20+(26−1)×50+(−1)×10+26×50+6×20+(26−5)×50+(−5)×10=8580（元）.答：该厂工人这一周的工资总额是8580元．【考点】正数和负数的识别有理数的混合运算【解析】（1）根据（1）中结果，算出金额，再将一周的超产、减产相加乘以10元，求出二者之和即可以得出答案．【解答】解：(1)∵七天的生产情况记录如下（超产为正、减产为负）：+3，−2，−4，+1，−1，+6，−5，∴七天的生产情况实际值为：29kg，24kg，22kg，27kg，25kg，32kg，21kg．∴一周总产量：29+24+22+27+25+32+21=180(kg)．答：这一周的实际产量是180kg.(2)26×50+3×20+(26−2)×50+10×(−2)+(26−4)×50+(−4)×10+26×50+1×20+(26−1)×50+(−1)×10+26×50+6×20+(26−5)×50+(−5)×10=8580（元）.答：该厂工人这一周的工资总额是8580元．【答案】52−42=2×4+1=9,(n+1)2−n2=2n+1(2)①原式=2×2000+1=4001；②∵10002−9992=2×999+1=1999，∴3+5+7+⋯+1999=22−12+32−22+42−32+⋯+10002−9992=−12+10002=999999.【考点】规律型：数字的变化类有理数的混合运算【解析】此题暂无解析【解答】解：(1)分别为52−42=2×4+1=9；(n+1)2−n2=2n+1．故答案为：52−42=2×4+1=9；(n+1)2−n2=2n+1．(2)①原式=2×2000+1=4001；②∵10002−9992=2×999+1=1999，∴3+5+7+⋯+1999=22−12+32−22+42−32+⋯+10002−9992=−12+10002=999999.【答案】7,−4+2t,7−3t(2)点P与点Q到点O距离相等，即：|−4+2t|=|7−3t|，①−4+2t=7−3t，则：5t=11，∴ t=115；②−4+2t+7−3t=0，3−t=0，∴ t=3.综上所述：当t=115或t=3时，点P与点Q到点O距离相等．(3)∵ 15>|7−(−4)|，∴12(15−11)=2，7+2=9，−4−2=−6，∴ x的值为9或−6．【考点】数轴列代数式绝对值【解析】【解答】解：(1)A：−4+11=7，P：−4+2t，Q：7−3t.则点A表示的数为7，点P表示的数为−4+2t，点Q表示的数为7−3t. 故答案为：7；−4+2t；7−3t.(2)点P与点Q到点O距离相等，即：|−4+2t|=|7−3t|，①−4+2t=7−3t，则：5t=11，∴ t=115；②−4+2t+7−3t=0，3−t=0，∴ t=3.综上所述：当t=115或t=3时，点P与点Q到点O距离相等．(3)∵ 15>|7−(−4)|，∴12(15−11)=2，7+2=9，−4−2=−6，∴ x的值为9或−6．。

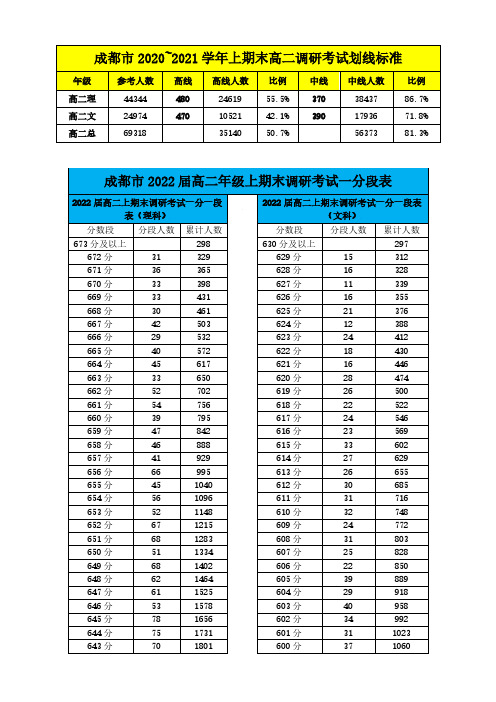
成都市2022届高二年级上期末调研考试一分段表和划线标准

126
6027
599 分
116
6143
598 分
127
6270
597 分
125
6395
596 分
120
6515
595 分
159
6674
594 分
117
6791
593 分
117
6908
592 分
134
7042
591 分
132
7174
590 分
136
7310
589 分
149
7459
588 分
128
7587
2022 届高二上期末调研考试一分一段
表（理科）
分数段
分段人数累计人数
642 分
74
1875
641 分
57
1932
640 分
78
2010
639 分
73
2083
638 分
81
2164
637 分
82
2246
636 分
79
2325
635 分
87
2412
634 分
74
2486
633 分
88
2574
632 分
51
1334
649 分
68
1402
648 分
62
1464
647 分
61
1525
646 分
53
1578
645 分
78
1656
644 分
75
1731
643 分
70
1801
2022 届高二上期末调研考试一分一段表（文科）

2020-2021学年四川省遂宁二中高二上学期半期考试数学(理)试题

遂宁二中2020-2021学年高二上学期半期考试数学（理科）试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

总分150分。

考试时间120分钟。

第Ⅰ卷（选择题，满分60分）注意事项：1．答题前，考生务必将自己的姓名、班级、考号用毫米的黑色墨水签字笔填写在答题卡上。

并检查条形码粘贴是否正确。

2．选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上，非选择题用毫米黑色墨水签字笔书写在答题卡对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

3．考试结束后，将答题卡收回。

一、选择题（本大题共12小题，每小题5分，共计60分。

在每小题给出的四个选项中，只有一项是符合题目要求。

） 1．过点()2,M a -和(),4N a 的直线的斜率为1，则实数a 的值为（）A. 1B. 2C. 1或4D. 1或22．已知圆()()221 221:C x y ++-=，圆 ()()222 2516:C x y -+-= ，则圆C 1与圆C 2的位置关系是（）A. 相离B. 相交C. 外切D. 内切 3．平行线0943=-+y x 和620x my ++=的距离是（）A ．58 B ．2 C ．511 D ．57 4．设有直线m ，n 和平面α，β，下列四个命题中，正确的是（） A ．若m ∥α，n ∥α，则m ∥n B ．若m ?α，n ?α，m ∥β，l ∥β，则α∥β C ．若α⊥β，m ?α，则m ⊥β D ．若α⊥β，m ⊥β，m ⊄α，则m ∥α5．对于a ∈R ，直线（x +y ﹣1）﹣a （x +1）=0恒过定点P ，则以P 为圆心，5为半径的圆的方程是（）A ． 5)2()1(22=-++y xB ．5)2()1(22=+++y xC ．5)2()1(22=++-y xD ．5)2()1(22=-+-y x6．设P 是圆(x －3)2＋(y ＋1)2＝4上的动点，Q 是直线x ＝－3上的动点，则|PQ |的最小值为（）A ．6B ．4C ．3D ．27．半径为R 的半圆卷成一个圆锥，则它的体积为（）A ．324πR 3B ．38πR 3C ．525πR 3D ．58πR 38．已知,x y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩，若z ax y =+的最大值为4，则a = （）A ．3B ．-3C ．-2D ．29．如图，正四棱柱ABCD —A 1B 1C 1D 1中，AA 1=2AB ，则异面直线A 1B 与AD 1所成角的余弦值为（）A ．51 B ．52C ．53D ．5410．某三棱锥的三视图如图所示，则该三棱锥的表面积是（）A ．2＋ 5B ．4＋ 51A 1B 1C 1DA BCDC ．2＋2 5D ．511．在三棱锥A BCD -中,1,AB AC ==2DB DC ==,3AD BC ==,则三棱锥A BCD -的外接球表面积为（）A ．πB ．7π4C ．7πD ．4π 12．N 为圆x 2+y 2=1上的一个动点，平面内动点M （x 0，y 0）满足|y 0|≥1且∠OMN=30°（O 为坐标原点），则动点M 运动的区域面积为（）A ．334-πB ．3238-π C ．332+π D ．334+π第Ⅱ卷（非选择题，共90分）二、填空题：本大题四小题，每小题5分，共20分。

选修2-1学霸必刷题空间向量与立体几何(选择题、填空题)

空间向量与立体几何（选择题、填空题）一、单项选择题1．（江西省赣州市赣县第三中学2020-2021学年高二8月入学考试）已知点(,1,2)A x 和点(2,3,4)B ，且AB =x 的值是（）A ．6或2-B ．6或2C ．3或4-D ．3-或4【答案】A【解析】AB ==()2216x -=，解得：2x =-或6x =．故选A2．（2020江西省新余期末质量检测）在空间直角坐标系中，已知P(－1，0，3)，Q(2，4，3)，则线段PQ 的长度为( )A B ．5C D 【答案】B【解析】由题得2(3,4,0),35PQ PQ =∴=+=，所以线段PQ 的长度为5．故答案为B3．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）已知空间向量()3,1,3m =，()1,,1n λ=--，且//m n ，则实数λ=（）A ．13- B ．-3 C ．13D ．6【答案】A【解析】因为//m n ，所以,m n R μμ=∈，即：()3,1,3m ==(),,n μλμμμ--=，所以3,1μλμ=-=，解得13λ=-．故选A ．4．（江西省新余一中、宜春一中2021届高二联考）如图所示，在正方体1111ABCD A B C D -中，O 是底面正方形ABCD 的中心，M 是1D D 的中点，N 是11A B 的中点，则直线NO ，AM 的位置关系是（）A ．平行B ．相交C ．异面垂直D ．异面不垂直【答案】C【分析】建立空间直角坐标系，写出NO 与AM 的坐标，即可判断位置关系．【解析】建立空间直角坐标系，如图所示．设正方体的棱长为2，则(2,0,0)A ，(0,0,1)M ，(1,1,0)O ，(2,1,2)N ，∴(1,0,2)NO =--，(2,0,1)AM =-．∵0NO AM ⋅=，∴直线NO ，AM 的位置关系是异面垂直．故选: C5．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）已知空间四边形ABCD 的每条边和对角线的长都等于a ，点,E F 分别是,BC AD 的中点，则AE AF ⋅的值为（） A ．2aB ．212aC ．214a D 2 【答案】C【分析】由题意可得11()22AB AC AE AF AD ⋅=+⋅，再利用两个向量的数量积的定义求得结果．【解析】11()22AB AC AE AF AD ⋅=+⋅1()4AB AD AC AD =⋅+⋅ ()22211cos60cos6044a a a ︒︒=+=，故选C. 6．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）已知M ，N 分别是四面体OABC 的棱OA ，BC 的中点，点P 在线段MN 上，且2MP PN =，设向量OA a =，OBb =，OC c =则OP =（）A ．111666a b c ++B ．111333a b c ++C ．111633a b c ++D ．111366a b c ++【答案】C【解析】如图所示，连接ON ，∵OP ON NP =+，1()2ON OB OC =+，所以13NP NM =，NM OM ON =-，12OM OA =，∴13OP ON NP ON NM =+=+121()333ON OM ON ON OM =+-=+21()32OB OC =⨯+1132OA +⨯111633OA OB OC =++111633a b c =++．故选C ． 7．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）若两条不重合直线1l 和2l 的方向向量分别为()11,0,1ν=-，()22,0,2ν=-，则1l 和2l 的位置关系是（） A ．平行 B ．相交 C ．垂直D ．不确定【答案】A【解析】因为两条不重合直线1l 和2l 的方向向量分别为()11,0,1ν=-，()22,0,2ν=-，所以212v ν=-，即2ν与1v 共线，所以两条不重合直线1l 和2l 的位置关系是平行，故选A8．（山东省滕州市第一中学2020-2021学年高二9月开学收心考试）设,x y R ∈，向量()()(),1,1,1,,1,2,4,2,a x b y c ===-且,//a c b c ⊥，则a b +=（）A ．BC ．3D ．4【答案】C【分析】根据向量垂直和平行的坐标表示求得参数,x y ，再求向量模长即可．【解析】()//,241,2,1,21b c y y b ∴=-⨯∴=-∴=-，，(),1210,1a b a b x x ⊥∴⋅=+⋅-+=∴=，()()1,112,1,2a a b ∴=∴+=-，，(2213a b ∴+=+-=，故选C ．9．（江西省宜春市2016-2017学年高二上学期期末统考理）如图所示，在空间四边形OABC 中，OA a OB b OC c ==＝，，，点M 在OA 上，且2,OM MA N =为BC 中点，则MN =（）A ．121232a b c -+B ．211322a b c -++ C ．111222a b c +-D ．221b 332a c -+-【答案】B【解析】由向量的加法和减法运算：12211()23322MN ON OM OB OC OA a b c =-=+-=-++．故选B10．（陕西省商洛市商丹高新学校2019-2020学年高二下学期4月学情质量检测数学（理））如图，已知正方体ABCD A B C D ''''-，点E 是A C ''的中点，点F 是AE 的三等分点，且12AF EF =，则AF =（）A ．1122AA AB AD '++ B ．111222AA AB AD '++ C ．111266AA AB AD '++D ．111366AA AB AD '++【答案】D【解析】∵点E 是A C ''的中点，点F 是AE 的三等分点，且12AF EF =， ∴111111()333236AF AE AA A E AA A C AA A C ⎛⎫''''''''==+=+=+ ⎪⎝⎭ 11()36AA A B A D '''''=++111366AA AB AD '=++，故选D ． 11．（安徽省六安市舒城中学2020-2021学年高二上学期开学考试数学（文）试题）如图，四个棱长为1的正方体排成一个正四棱柱，AB 是一条侧棱，()1,2,,8i P i =是上底面上其余的八个点，则()1,2,,8i AB AP i ⋅=⋅⋅⋅的不同值的个数为（）A ．8B ．4C ．2D ．1【答案】D【解析】()2i i i AB AP AB AB BP AB AB BP ⋅=⋅+=+⋅，AB ⊥平面286BP P P ，i AB BP ∴⊥，i AB BP ∴⋅=，21i AB AP AB ∴⋅==，则()1,2,,8i AB AP i ⋅=⋅⋅⋅的不同值的个数为1个，故选D .12．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）点P (1，2，3）关于xOy 平面的对称点的坐标为（） A ．(－1，2，3) B ．(1，－2，－3) C ．(－1，－2，－3) D ．(1，2，－3)【答案】D【分析】关于xOy 平面对称的点的,x y 坐标不变，只有z 坐标相反．【解析】点P (1，2，3）关于xOy 平面的对称点的坐标为(1,2,)3-．故选D ．13．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）若向量(2,0,1)a =-，向量(0,1,2)b =-，则2a b -=（）A ．(4,1,0)-B ．(4,1,4)--C ．(4,1,0)-D ．(4,1,4)--【答案】C【分析】根据题意求出2(4,0,2)a=-，再根据向量的减法坐标运算，由此即可求出结果．【解析】因为向量(2,0,1)a =-，向量(0,1,2)b =-，则2(4,0,2)a =-，则2(4,0,2)(0,1,2)(4,1,0)a b -=---=-，故选C ．14．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）已知正方体1111ABCD A B C D -，点E 是上底面11A C 的中心，若1AE AA xAB yAD =++，则x y +等于（） A ．13B ．12C ．1D ．2【答案】C【解析】如图，()111111112AE AA A E AA A B A D =+=++ ()11111222AA AB AD AA AB AD =++=++，所以12x y ==，所以1x y +=．故选C15．（江苏省南京市秦淮区2019-2020学年高一下学期期末）空间直角坐标系O xyz -中，已知两点()11,2,1P -，()22,1,3P -，则这两点间的距离为（）A BC ．D ．18【答案】B【解析】根据题意，两点()11,2,1P -，()22,1,3P -，则12||PP =B ．16．（湖北省恩施高中2020届高三下学期四月决战新高考名校交流卷（B ））已知向量()1,2a =，()3,b x =，()1,1c y =--，且//a b ，b c ⊥，则x y ⋅的值为（）A ．6B ．32 C ．9D ．132-【答案】C【解析】∵//a b ，∴60x -=，6x =，∴向量()3,6b =， ∵b c ⊥，∴()3610y -+-=，∴32y =，∴9x y ⋅=．故选C ． 17．（四川省绵阳市2019-2020学年高二下学期期末教学质量测试数学（理）试题）在空间直角坐标系中，若()1,1,0A ，()13,0,12AB =，则点B 的坐标为（） A ．()5,1,2-- B ．()7,1,2- C ．()3,0,1 D ．()7,1,2【答案】D【分析】首先设出点(,,)B x y z ，利用向量坐标公式以及向量相等的条件得到等量关系式，求得结果．【解析】设(,,)B x y z ，所以(1,1,)2(3,0,1)(6,0,2)AB x y z =--==，所以16102x y z -=⎧⎪-=⎨⎪=⎩，所以712x y z =⎧⎪=⎨⎪=⎩，所以点B 的坐标为(7,1,2)，故选D ．18．（广东省云浮市2019-2020学年高二上学期期末）如图，在三棱锥P ABC -中，点D ，E ，F 分别是AB ，PA ，CD 的中点，设PA a =，PB b =，PC c =，则EF =（）A ．111442a b c --B ．111442a b c -+ C ．111442a b c +-D ．111442a b c -++【答案】D 【解析】点D ，E ，F 分别是AB ，PA ，CD 的中点，且PA a =，PB b =，PC c =，∴()11112224EF EP PC CF PA PC CD PA PC CA CB =++=-++=-+++()1111124442PA PC PA PC PB PC PA PB PC =-++-+-=-++111442a b c =-++．故选D ．19．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）一个向量p 在基底{},,a b c 下的坐标为()1,2,3，则p 在基底{},,a b a b c +-下的坐标为（）A ．31322⎛⎫- ⎪⎝⎭，，B ．31322⎛⎫- ⎪⎝⎭，， C ．13322⎛⎫- ⎪⎝⎭，，D ．13322⎛⎫- ⎪⎝⎭，，【答案】B【解析】因为向量p 在基底{},,a b c 下的坐标为()1,2,3，所以23p a b c =++，设p 在基底{},,a b a b c +-下的坐标为(),,x y z ，所以()()()()p x a b y a b zc x y a x y b zc =++-+⇒++-+，有13223x y x y x z +=⎧⎪-=⇒=⎨⎪=⎩，12y，3z =，p 在基底{},,a b a b c +-下的坐标为31,,322⎛⎫- ⎪⎝⎭．故选B ．20．（湖北省武汉襄阳荆门宜昌四地六校考试联盟2020-2021学年高三上学期起点联考）如图，直四棱柱1111ABCD A B C D -的底面是菱形，12AA AB ==，60BAD ∠=︒，M 是1BB 的中点，则异面直线1A M 与1B C所成角的余弦值为（）A． B ．15- C ．15D．5【答案】D【分析】用向量1,,AB BC BB 分别表示11,AM BC ，利用向量的夹角公式即可求解．【解析】由题意可得221111111111,5,2A M AB B M AB BB A M A B B M=+=-=+=221111,2BC BC BB B C BC BB =-=+=，()211111111111cos ,AB BB BC BB AB BC BB A M B C A M B C A M B C⎛⎫-⋅-⋅+ ⎪⋅⎝〈〉===0122cos604⨯⨯+⨯==故选D21．（河北省石家庄市第二中学2020-2021学年高二上学期8月线上考试（二））长方体1111ABCD A B C D -中，11,2,AB AD AA E ===为棱1AA 的中点，则直线1C E 与平面11CB D 所成角的余弦值为（） A．9 B．9CD ．23【答案】A【解析】根据题意，建立如图所示直角坐标系：则1C E (1,1,1)=--，设平面11B D C 的法向量为n (,,)x y z =，则100n B D n BC ⎧⋅=⎪⎨⋅=⎪⎩可得：020x y x z --=⎧⎨--=⎩，取n (2,2,1)=--，则1,cos n C E =11n C E nC E⋅9==，设直线1C E 与平面11B D C 的夹角为θ，则9sin θ=，9cos θ==．故选A ． 22．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）已知点()1,1,A t t t --，()2,,B tt ，则A ，B 两点的距离的最小值为A．10 B．5C．5D ．35【答案】C【分析】由两点之间的距离公式求得AB 之间的距离用t 表示出来，建立关于t 的函数，转化为求函数的最小值．【解析】因为点()1,1,A t t t --，()2,,B t t ，所以22222(1)(21)()522AB t t t t t t =++-+-=-+，有二次函数易知，当15t =时，取得最小值为95，AB ∴，故选C ．23．（湖南省邵阳市邵东县第十中学2020届高三下学期模拟考试数学（文）试题）如图，在正方体1111ABCD A B C D -中，M ，N 分别是棱AB ，1BB 的中点，点P 在对角线1CA 上运动．当△PMN 的面积取得最小值时，点P 的位置是（）A ．线段1CA 的三等分点，且靠近点1AB ．线段1CA 的中点C ．线段1CA 的三等分点，且靠近点CD ．线段1CA 的四等分点，且靠近点C【答案】B【解析】设正方体的棱长为1，以A 为原点，1,,AB AD AA 分别为,,x y z 轴，建立空间直角坐标系，如图所示：则1(,0,0)2M ，1(1,0,)2N ，MN 的中点31(,0,)44Q ，1(0,0,1)A ，(1,1,0)C ，则1(1,1,1)AC =-，设(,,)P t t z ，(1,1,)PC t t z =---，由1AC 与PC 共线，可得11111t t z---==-，所以1t z =-，所以(1,1,)P z z z --，其中01z ≤≤，因为||(1PM ==||(11)(1PN z =--+=所以||||PM PN =，所以PQ MN ⊥，即||PQ 是动点P 到直线MN 的距离，由空间两点间的距离公式可得||PQ ===12c =时，||PQ 取得最小值4，此时P 为线段1CA 的中点，由于||4MN =为定值，所以当△PMN 的面积取得最小值时，P 为线段1CA 的中点．故选B24．（云南省梁河县第一中学2019-2020学年高二7月月考数学（理）试题）长方体1111ABCD A B C D -中，12AB AA ==，1AD =，E 为1CC 的中点，则异面直线1BC 与AE 所成角的余弦值为（）A BCD ．【答案】B【分析】以点A 为坐标原点，AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法可求得异面直线1BC 与AE 所成角的余弦值．【解析】以点A 为坐标原点，AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系A xyz -，则()0,0,0A 、()2,0,0B 、()12,1,2C 、()2,1,1E ，()2,1,1AE =，()10,1,2BC =，111cos ,6AE BC AE BC AEBC ⋅<>===⋅．因此，异面直线1BC 与AE ．故选B ． 25．（广西桂林市2019-2020学年高二下学期期末质量检测数学（理））在正方体ABCD --A 1B 1C1D 1中，E 是C 1C 的中点，则直线BE 与平面B 1BD 所成角的正弦值为( ) A．5-B．5C ．D 【答案】B【分析】以D 为坐标原点，以DA 为x 轴，以DC 为y 轴，以1DD 为z 轴，建立空间直角坐标系，利用向量法能求出直线BE 与平面1B BD 所成角的正弦值．【解析】以D 为坐标原点，以DA 为x 轴，以DC 为y 轴，以1DD 为z 轴，建立如图空间直角坐标系，设正方体的棱长为2，则()000D ，，，()220B ，，，()1222B ，，，()021E ，，， ∴() 220BD =--，，，()1 002BB =，，，() 201BE =-，，，设平面1B BD 的法向量为() ,,x n y z =，∵ n BD ⊥，1n BB ⊥， ∴22020x y z --=⎧⎨=⎩，令y 1=，则() 110n =-，，，∴10cos ,n BE n BE n BE ⋅==⋅，设直线BE 与平面1B BD 所成角为θ，则10sin cos ,5n BE θ==，故选B ．26．（陕西省商洛市商丹高新学校2020届高三下学期考前适应性训练理科）如图在平行六面体1111ABCD A B C D -中，底面ABCD 是边长为1的正方形，侧棱12AA =且1160A AD A AB ∠=∠=︒，则1AC =（）A ． BC ．D 【答案】B【解析】因为底面ABCD 是边长为1的正方形，侧棱12AA =且1160A AD A AB ∠=∠=︒，则2=1AB ，2=1AD ，21=4AA ，0AB AD ⋅=，111cos 1AB AA AB AA A AB ⋅=⋅⋅∠=，111cos 1AD AA AD AA A AD ⋅=⋅⋅∠=，则1AC 1AB AD AA =++()1222111222AB AD AA AB AA AB AD AD AA =+++⋅+⋅+⋅==，故选B ．27．（2020届上海市七宝中学高三高考押题卷）已知MN 是正方体内切球的一条直径，点P 在正方体表面上运动，正方体的棱长是2，则PM PN →→⋅的取值范围为（） A ．[]0,4 B ．[]0,2 C ．[]1,4D ．[]1,2【答案】B【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-，根据正方体的特点可确定PO →的最大值和最小值，代入即可得到所求范围．【解析】设正方体内切球的球心为O ，则1OM ON ==，2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，MN 为球O 的直径，0OM ON →→∴+=，1OM ON →→⋅=-，21PM PN PO →→→∴⋅=-，又P 在正方体表面上移动，∴当P 为正方体顶点时，PO →P 为内切球与正方体的切点时，PO →最小，最小值为1，[]210,2PO →∴-∈，即PM PN →→⋅的取值范围为[]0,2．故选B ．【点睛】本题考查向量数量积的取值范围的求解问题，关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题．28．（湖北省荆门市2019-2020学年高二下学期期末）在平行六面体ABCD A B C D ''''-中，若2AC x AB y BC z CC →→→→''=++，则x y z ++=（）A ．52B ．2C ．32D ．116【答案】A【解析】由空间向量的线性运算，得AB BC AC AC CC CC →→→→→→⎛⎫=+=++ ⎪⎭'''⎝，由题可知，2AC x AB y BC z CC →→→→''=++，则1,1,21x y z ===，所以11,2y z ==， 151122x y z ∴++=++=．故选A ．29．（安徽省六校教育研究会2020-2021学年高三上学期第一次素质测试理科）如图，在直三棱柱111ABC A B C -中，已知90ABC ∠=︒，P 为侧棱1CC 上任意一点，Q 为棱AB 上任意一点，PQ 与AB 所成角为α，PQ 与平面ABC 所成的角为β，则α与β的大小关系为（）A ．αβ=B ．αβ<C ．αβ>D ．不能确定【答案】C【分析】建立空间直角坐标系设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥，利用空间向量法分别求得cos ,cos αβ，然后根据(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦，利用余弦函数的单调性求解．【解析】建立如图所示空间直角坐标系：设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥，则()(),,,0,,0QP x y z QB y =-=-，所以2222,,QP QB y QP x y z QB y ⋅==++=，所以2cos QP QB QP QBx zα⋅==⋅+又(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦，sin QP CP QPβ⋅==所以cos β=cos cos βα>，因为cos y x = 在0,2π⎛⎫⎪⎝⎭上递减，所以αβ>，故选C 30．（江西省赣州市赣县第三中学2019-2020学年高二6月份考试数学（理）试题）如图，在四棱柱1111ABCD A B C D -中，底面ABCD 为正方形，侧棱1AA ⊥底面ABCD ，3AB =，14AA =，P 是侧面11BCC B 内的动点，且1AP BD ⊥，记AP 与平面11BCC B 所成的角为θ，则tan θ的最大值为（）A ．43B ．53 C ．2D ．259【答案】B【分析】建立空间直角坐标系，利用向量法能求出线面角的正切值的最大值．【解析】以1,,DA DC DD 所在直线分别为,,x y z 轴，建立空间直角坐标系，设(,3,)P x z ，则1(3,3,),(3,3,4)AP x z BD =-=--，11,0AP BD AP BD ⊥∴⋅=，33(3)3340,4x z z x ∴---⨯+=∴=，||BP ∴==9255=， ||5tan ||3AB BP θ∴=，tan θ∴的最大值为53．故选B ．31．（江西省赣州市赣县第三中学2019-2020学年高二6月份考试数学（理）试题）如图，在棱长都相等的正三棱柱111ABC A B C -中，D 是棱1CC 的中点，E 是棱1AA 上的动点．设AE x =，随着x 增大，平面BDE 与底面ABC 所成锐二面角的平面角是（）A ．增大B ．先增大再减小C ．减小D ．先减小再增大【答案】D【解析】设正三棱柱111ABC A B C -棱长为2，,02AE x x =≤≤，设平面BDE 与底面ABC 所成锐二面角为α，以A 为坐标原点，过点A 在底面ABC 内与AC 垂直的直线为x 轴，1,AC AA 所在的直线分别为,y z 轴建立空间直角坐标系，则(0,2,1),(0,0,),(3,1,1),(0,2,1)B D E x BD ED x =-=-，设平面BDE 的法向量(,,)m s t k =，则m BD m ED⎧⊥⎨⊥⎩，即02(1)0t k t x k ⎧++=⎪⎨+-=⎪⎩，令k =33,1t x s x =-=+，所以平面BDE的一个法向量(m x=+-，底面ABC的一个法向量为(0,0,1)n =，cos|cos,|m nα=<>==当1(0,)2x∈，cosα随着x增大而增大，则α随着x的增大而减小，当1(,2)2x∈，cosα随着x增大而减小，则α随着x的增大而增大．故选D．32．（山东省滕州市第一中学2020-2021学年高二9月开学收心考试）已知空间直角坐标系O xyz-中，()1,2,3OA =，()2,1,2OB =，()1,1,2OP =，点Q在直线OP上运动，则当QA QB⋅取得最小值时，点Q 的坐标为（）A．131,,243⎛⎫⎪⎝⎭B．133,,224⎛⎫⎪⎝⎭C．448,,333⎛⎫⎪⎝⎭D．447,,333⎛⎫⎪⎝⎭【答案】C【分析】设(,,)Q x y z，根据点Q在直线OP上，求得(,,2)Qλλλ，再结合向量的数量积和二次函数的性质，求得43λ=时，QA QB⋅取得最小值，即可求解．【解析】设(,,)Q x y z，由点Q在直线OP上，可得存在实数λ使得OQ OPλ=，即(,,)(1,1,2)x y zλ=，可得(,,2)Qλλλ，所以(1,2,32),(2,1,22)QA QB λλλλλλ=---=---，则2(1)(2)(2)(1)(32)(22)2(385)QA QB λλλλλλλλ⋅=--+--+--=-+，根据二次函数的性质，可得当43λ=时，取得最小值23-，此时448(,,)333Q ．故选C ．【点睛】本题主要考查了空间向量的共线定理，空间向量的数量积的运算，其中解答中根据向量的数量积的运算公式，得关于λ的二次函数是解答的关键，着重考查运算与求解能力．33．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）如图该几何体由半圆柱体与直三棱柱构成，半圆柱体底面直径BC ＝4，AB ＝AC ，∠BAC ＝90°，D 为半圆弧的中点，若异面直线BD 和AB 1所成角的余弦值为23，则该几何体的体积为（）A ．16+8πB ．32+16πC ．32+8πD ．16+16π【答案】A【解析】设D 在底面半圆上的射影为1D ，连接1AD 交BC 于O ，设1111A D B C O ⋂=．依题意半圆柱体底面直径4,,90BC AB AC BAC ==∠=︒，D 为半圆弧的中点，所以1111,AD BC A D B C ⊥⊥且1,O O 分别是下底面、上底面半圆的圆心．连接1OO ，则1OO 与上下底面垂直，所以11,,OO OB OO OA OA OB ⊥⊥⊥，以1,,OB OA OO 为,,x y z 轴建立空间直角坐标系，设几何体的高为()0h h >，则()()()()12,0,0,0,2,,0,2,0,2,0,B D h A B h -，所以()()12,2,,2,2,BD h AB h =--=-，由于异面直线BD 和1AB 所成的角的余弦值为23，所以11238BD AB BD AB ⋅==⋅，即2222,16,483h h h h ===+．所以几何体的体积为2112442416822ππ⨯⨯⨯+⨯⨯⨯=+．故选A.34．（安徽省阜阳市太和第一中学2020-2021学年高二（平行班）上学期开学考试）在正方体1111ABCD A B C D -中，直线1BC 与平面1A BD 所成角的余弦值为（）A ．24B ．23 C ．3 D ．3 【答案】C【分析】分别以1,,DA DC DD 为,,x y z 轴建立如图所示空间直角坐标系，求出直线的方向向量和平面的法向量后可得所求线面角的余弦值．【解析】分别以1,,DA DC DD 为,,x y z轴建立如图所示空间直角坐标系，设正方体的棱长为1，可得()()()()110,0,0,1,1,0,0,1,1,1,0,1D B C A ∴()()()111,0,1,1,0,1,1,1,0BC A D BD =-=--=--，设(),,n x y z =是平面1A BD 的一个法向量，∴100n A D n BD ⎧⋅=⎨⋅=⎩，即00x z x y +=⎧⎨+=⎩，取1x =，得1y z ==-，∴平面1A BD 的一个法向量为()1,1,1n =--，设直线1BC 与平面1A BD 所成角为θ， ∴11126sin cos ,323BC nBC n BC nθ⋅-=〈〉===⨯， ∴23cos 1sin θθ=-1BC 与平面1A BD 所成角的余弦值是33，故选C.【点睛】用向量法求二面角大小的两种方法：（1）分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小即为二面角的大小；（2）分别求出二面角的两个半平面的法向量，然后通过两个法向量的夹角得到二面角大小，解题时要注意结合图形判断出所求的二面角是锐角还是钝角．35．（2020届重庆市第一中学高三下学期6月模拟数学（理）试题）如图所示，在正方体1111ABCD A B C D -中，点P 是底面1111D C B A 内（含边界）的一点，且//AP 平面1DBC ，则异面直线1A P 与BD 所成角的取值范围为（）A ．3,44ππ⎡⎤⎢⎥⎣⎦B ．,42ππ⎡⎤⎢⎥⎣⎦C ．,32ππ⎡⎤⎢⎥⎣⎦D ．2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【解析】过A 作平面α平面1DBC ，点P 是底面1111D C B A 内（含边界）的一点，且//AP 平面1DBC ，则P ∈平面α，即P 在α与平面1111D C B A 的交线上，连接111,,AB AD B D ，11DD BB =，则四边形11BDD B 是平行四边形，11B D BD ∴，11B D ∴平面1DBC ，同理可证1AB ∥平面1DBC ，∴平面11AB D ∥平面1DBC ，则平面11AB D 即为α，点P 在线段11B D 上，以D 为坐标原点，1,,DA DC DD 建立如图坐标系，设正方体棱长为1，则()0,0,0D ，()1,1,0B ，()1,0,0A ，设(),,1P λλ，[]0,1λ∈， ()1,1,0DB ∴=，()1,,1AP λλ=-，21DB AP λ∴⋅=-，2DB =，2AP λ=，设1A P 与BD 所成角为θ，则cos 2DB APDB APθ⋅===⋅ ==12λ=时，cos θ取得最小值为0，当0λ=或1时，cos θ取得最大值为12，10cos 2θ∴≤≤，则32ππθ≤≤．故选C ． 36．（重庆市第八中学2020届高三下学期第五次月考数学（理）试题）如图，矩形ABCD 中，2AB AD ==E 为边AB 的中点，将ADE 沿直线DE 翻折成1A DE △．在翻折过程中，直线1A C 与平面ABCD 所成角的正弦值最大为（）A．4B ．6C．14D【答案】A【解析】分别取DE ，DC 的中点O ，F ，则点A 的轨迹是以AF 为直径的圆，以,OA OE 为,x y 轴，过O 与平面AOE 垂直的直线为z 轴建立坐标系，则()2,1,0C -，平面ABCD 的其中一个法向量为n = (0，0．1)，由11A O =，设()1cos ,0,sin A αα，则()1cos 2,1,sin CA αα=+-，记直线1A C 与平面ABCD 所成角为θ，则11sin 4cos ||CA nCAn θ⋅===⋅设315cos ,,sin 222t αθ⎡⎤=+∈=≤=⎢⎥⎣⎦ 所以直线1A C 与平面ABCD ，故选A ．二、多项选择题37．（江苏省南京市秦淮中学2019-2020学年高二（美术班）上学期期末）对于任意非零向量()111,,a x y z =，()222,,b x y z =，以下说法错误的有( )A ．若a b ⊥，则1212120x x y y z z ++=B ．若//a b ，则111222x y z x y z == C ．cos ,a b =><D ．若1111===x y z ，则a为单位向量【答案】BD【解析】对于A 选项，因为a b ⊥，则1212120a b x x y y z z ⋅=++=，A 选项正确；对于B 选项，若20x =，且20y ≠，20z ≠，若//a b ，但分式12x x 无意义，B 选项错误；对于C 选项，由空间向量数量积的坐标运算可知cos ,a b =><，C 选项正确；对于D 选项，若1111===x y z，则211a =+=，此时，a 不是单位向量，D 选项错误．故选BD ．38．（2020届百师联盟高三开学摸底大联考山东卷）下面四个结论正确的是（） A ．向量(),0,0a b a b ≠≠，若a b ⊥，则0a b ⋅=．B ．若空间四个点P ，A ，B ，C ，1344PC PA PB =+，则A ，B ，C 三点共线． C ．已知向量()1,1,a x =，()3,,9b x =-，若310x <，则,a b 为钝角．D ．任意向量a ，b ，c 满足()()a b c a b c ⋅⋅=⋅⋅．【答案】AB【解析】由向量垂直的充要条件可得A 正确；1344PC PA PB =+，∴11334444PC PA PB PC -=-即3AC CB =，∴A ，B ，C 三点共线，故B 正确；当3x =-时，两个向量共线，夹角为π，故C 错误；由于向量的数量积运算不满足结合律，故D 错误．故选AB.39．（广东省中山市2019-2020学年高一下学期期末）在空间直角坐标系中，下列结论正确的是（） A ．点()2,1,4-关于x 轴对称的点的坐标为()2,1,4 B ．到()1,0,0的距离小于1的点的集合是()(){}222,,11x y z x y z -++<C ．点()1,2,3与点()3,2,1的中点坐标是()2,2,2D ．点()1,2,0关于平面yOz 对称的点的坐标为()1,2,0- 【答案】BCD【解析】对于选项A ：点()2,1,4-关于x 轴对称的点的坐标为()2,1,4---，所以A 不正确；对于选项B ：点(),,x y z到()1,0,0的距离小于11<，所以B 正确；对于选项C ：点()1,2,3与点()3,2,1的中点坐标是()132231,,2222,2,2⎛⎫=⎪⎝⎭+++，所以C 正确；对于选项D ：由点(),,x y z 关于平面yOz 对称的点的坐标为(),,x y z -，所以D 正确．故选B C D ．40．（山东省威海市文登区2019-2020学年高二上学期期末）正方体1111ABCD A B C D -的棱长为a ，则下列结论正确的是（）A ．211AB AC a ⋅=- B ．212BD BD a ⋅= C ．21AC BA a⋅=- D ．212AB AC a ⋅=【答案】BC【解析】如下图所示：对于A 选项，()2211AB AC AB AC AB AB AD AB a ⋅=⋅=⋅+==，A 选项错误；对于B ，()()()()2221112BD BD AD AB BD DD AD AB AD AB AA AD AB a ⋅=-+=--+=+=，B 选项正确；对于C 选项，()()2211AC BA AB AD AA AB AB a ⋅=+⋅-=-=-，C 选项正确；对于D 选项，()2211AB AC AB AB AD AA AB a ⋅=⋅++==，D 选项错误．故选BC ．41．（福建省泉州市普通高中2019-2020学年毕业班第一次质量检查（理））如图，正方体1111ABCD A B C D -的棱长为1，E 是1DD 的中点，则（）A ．直线1//BC 平面1A BD B ．11B C BD ⊥C ．三棱锥11C B CE -的体积为13D ．异面直线1B C 与BD 所成的角为60︒【答案】ABD【解析】如图建立空间直角坐标系，()0,0,0A ，()1,0,0B ，()1,1,0C ，()0,1,0D ，()10,0,1A ，()11,0,1B ，()11,1,1C ，()10,1,1D ，10,1,2⎛⎫ ⎪⎝⎭E ，()1B C 0,1,1=-，()11,1,1BD =-，()1,1,0BD =-，()11,0,1BA =-，所以()111011110B C BD =-⨯+⨯+-⨯=，即11BC BD ⊥，所以11B C BD ⊥，故B 正确；()11011101B C BD =-⨯+⨯+-⨯=，12B C =，2BD =，设异面直线1B C 与BD 所成的角为θ，则111cos 2B C BD B C BDθ==，又0,2πθ⎛⎤∈ ⎥⎝⎦，所以3πθ=，故D 正确；设平面1A BD 的法向量为(),,n x y z =，则1·0·0n BA n BD ⎧=⎨=⎩，即0x y x z -+=⎧⎨-+=⎩，取()1,1,1n =，则()10111110n B C =⨯+⨯+⨯-=，即1C n B ⊥，又直线1B C ⊄平面1A BD ，所以直线1//B C 平面1A BD ，故A 正确；111111111111113326C B CE B C CE C CE V B C S V -∆-===⨯⨯⨯⨯=⋅，故C 错误；故选ABD.42．（海南省海南中学2019-2020学年高三第四次月考）如图所示，正方体1111ABCD A B C D -中，1AB =，点P 在侧面11BCC B 及其边界上运动，并且总是保持1AP BD ⊥，则以下四个结论正确的是（）A ．113P AA D V -=B ．点P 必在线段1BC 上C ．1AP BC ⊥D ．//AP 平面11AC D【答案】BD 【解析】对于A ，P 在平面11BCC B 上，平面11//BCC B 平面1AA D ，P ∴到平面1AA D 即为C 到平面1AA D 的距离，即为正方体棱长，1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△，A 错误；对于B ，以D 为坐标原点可建立如下图所示的空间直角坐标系：则()1,0,0A ，(),1,P x z ，()1,1,0B ，()10,0,1D ，()11,1,1B ，()0,1,0C()1,1,AP x z →∴=-，()11,1,1BD →=--，()11,0,1B C →=--，1AP BD ⊥，1110AP BD x z →→∴⋅=--+=，x z ∴=，即(),1,P x x ，(),0,CP x x →∴=，1CP x B C →→∴=-，即1,,B P C 三点共线，P ∴必在线段1B C 上，B 正确；对于C ，()1,1,AP x x →=-，()11,0,1BC →=-，111AP BC x x →→∴⋅=-+=，AP ∴与1BC 不垂直，C 错误；对于D ，()11,0,1A ，()10,1,1C ，()0,0,0D ，()11,0,1DA →∴=，()10,1,1DC →=，设平面11AC D 的法向量(),,n x y z →=，1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩，令1x =，则1z =-，1y =，()1,1,1n →∴=-， 110AP n x x →→∴⋅=-+-=，即AP n →→⊥，//AP ∴平面11ACD ，D 正确．故选BD ． 43．（福建省宁德市2019-2020学年高二上学期期末考试）如图所示，棱长为1的正方体1111ABCD A B C D-中，P 为线段1A B 上的动点（不含端点），则下列结论正确的是（）A ．平面11D A P ⊥平面1A APB ．1AP DC ⋅不是定值 C ．三棱锥11BD PC -的体积为定值 D ．11DC D P ⊥【答案】ACD【解析】A ．因为是正方体，所以11D A ⊥平面1A AP ，11D A ⊂平面11D A P ，所以平面11D A P ⊥平面1A AP ，所以A 正确；B ．11111111()AP DC AA A P DC AA DC A P DC ⋅=+⋅=⋅+⋅ 11112cos 45cos901212AA DC A P DC =+=⨯⨯=，故11AP DC ⋅=，故B 不正确； C ．1111B D PC P B D C V V --=，11B D C 的面积是定值，1//A B 平面11B D C ，点P 在线段1A B 上的动点，所以点P 到平面11B D C 的距离是定值，所以1111B D PC P B D C V V --=是定值，故C 正确； D ．111DC A D ⊥，11DC A B ⊥，1111A D A B A =，所以1DC ⊥平面11A D P ，1D P ⊂平面11A D P ，所以11DC D P ⊥，故D 正确．故选ACD44．（山东省济南莱芜市第一中学2019-2020学年高二下学期第一次质量检测）关于空间向量，以下说法正确的是（）A ．空间中的三个向量，若有两个向量共线，则这三个向量一定共面B ．若对空间中任意一点O ，有111632OP OA OB OC =++，则P ，A ，B ，C 四点共面 C ．设{},,a b c 是空间中的一组基底，则{},,a b b c c a +++也是空间的一组基底 D ．若0a b ⋅<，则,a b 是钝角【答案】ABC【解析】对于A 中，根据共线向量的概念，可知空间中的三个向量，若有两个向量共线，则这三个向量一定共面，所以是正确的；对于B 中，若对空间中任意一点O ，有111632OP OA OB OC =++，根据空间向量的基本定理，可得,,,P A B C 四点一定共面，所以是正确的；对于C 中，由{},,a b c 是空间中的一组基底，则向量,,a b c 不共面，可得向量,a b b c ++，c a +也不共面，所以{},,a b b c c a +++也是空间的一组基底，所以是正确的；对于D 中，若0a b ⋅<，又由,[0,]a b π∈，所以,(,]2a b ππ∈，所以不正确．故选ABC ．45．（河北省沧州市盐山中学2019-2020学年高一下学期期末）若长方体1111ABCD A B C D -的底面是边长为2的正方形，高为4，E 是1DD 的中点，则（）A ．11B E A B ⊥B ．平面1//B CE 平面1A BDC ．三棱锥11C B CE -的体积为83D ．三棱锥111C B CD -的外接球的表面积为24π【答案】CD【解析】以1{,,}AB AD AA 为正交基底建立如图所示的空间直角坐标系，则 (0,0,0)A ，(2,0,0)B ，(2,2,0)C ，(0,2,0)D ，1(0,0,4)A ，1(2,0,4)B ，(0,2,2)E ，所以1(2,2,2)B E =--，1(2,0,4)A B =-，因为1140840B E A B ⋅=-++=≠，所以1B E 与1A B 不垂直，故A 错误； 1(0,2,4)CB =-，(2,0,2)CE =-，设平面1B CE 的一个法向量为111(,,)n x y z =，则由100n CB n CE ⎧⋅=⎨⋅=⎩，得1111240220y z x z -+=⎧⎨-+=⎩，所以11112y z x z =⎧⎨=⎩，不妨取11z =，则11x =，12y =，所以(1,2,1)n =，同理可得设平面1A BD 的一个法向量为(2,2,1)m =，故不存在实数λ使得n λm =，故平面1B CE 与平面1A BD 不平行，故B 错误；在长方体1111ABCD A B C D -中，11B C ⊥平面11CDD C ，故11B C 是三棱锥11B CEC -的高，所以111111111184223323三棱锥三棱锥CEC C B CE CEC B V V S B C --==⋅=⨯⨯⨯⨯=△，故C 正确；三棱锥111C B CD -的外接球即为长方体1111ABCD A B C D -的外接球，故外接球的半径2R ==所以三棱锥111C B CD -的外接球的表面积2424S R ππ==，故D 正确．故选CD ．46．（山东省济南市2019-2020学年高二下学期末考试）如图，棱长为的正方体1111ABCD A B C D -中，P 为线段1A B 上的动点（不含端点），则下列结论正确的是（）A ．直线1D P 与AC 所成的角可能是6π B ．平面11D A P ⊥平面1A AP C ．三棱锥1D CDP -的体积为定值D ．平面1APD 截正方体所得的截面可能是直角三角形【答案】BC【解析】对于A ，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，()()()10,0,1,1,0,0,0,1,0D A C ，设()()1,,01,01P a b a b <<<< ()()11,,1,1,1,0D P a b AC =-=-，(111cos ,01D P AC D P AC D P ACa b ⋅==<++-1301,01,,24a b D P AC ππ<<<<∴<<∴直线D 1P 与AC 所成的角为,42ππ⎛⎫⎪⎝⎭，故A 错误；对于B ，正方体ABCD ﹣A 1B 1C 1D 1中，A 1D 1⊥AA 1，A 1D 1⊥AB ， ∵AA 1AB ＝A ，∴A 1D 1⊥平面A 1AP ，∵A 1D 1⊥平面D 1A 1P ，∴平面D 1A 1P ⊥平面A 1AP ，故B 正确；对于C ，1111122CDD S=⨯⨯=，P 到平面CDD 1的距离BC ＝1， ∴三棱锥D 1﹣CDP 的体积：111111326D CDP P CDD V V --==⨯⨯=为定值，故C 正确；对于D ，平面APD 1截正方体所得的截面不可能是直角三角形，故D 错误；故选BC ．47．（江苏省苏州中学园区校2020-2021学年高三上学期8月期初调研）如图，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且12EF =，则下列结论中正确的是（）A ．线段11B D 上存在点F ，使得AC AF ⊥ B ．//EF 平面ABCD C ．AEF 的面积与BEF 的面积相等 D ．三棱锥A BEF -的体积为定值【答案】BD【解析】如图，以C 为坐标原点建系CD ，CB ，1CC 为x ，y ，z 轴，()1,1,0A ，()0,0,0C ，()1,1,0AC =--，1B F B λ=11D ，即()()0,1,11,1,0x y z λ---=-,∴x λ=，1y λ=-，1z =，∴(),1,1F λλ-，()1,,1AF λλ=--,()()11010AC AF λλ⋅=--++=≠， ∴AC 与AF 不垂直，A 错误．E ，F 都在B ，D 上，又11//BD B D ，∴//EF BD ，BD ⊂平面ABCD ，EF ⊄平面ABCD ，∴//EF 平面ABCD ，B 正确AB 与EF 不平行，则1A B 与EF 的距离相等，∴AEF BEF S S ≠△△，∴C 错误A 到BEF 的距离就是A 到平面11BDDB 的距离，A 到11BDD B 的距离为22AC =1111224BEF S =⨯⨯=△，∴1134224A BEF V -=⨯⨯=是定值，D 正确．故选BD ．48．（江苏省扬州市宝应中学2020-2021学年高三上学期开学测试）在正三棱柱ABC A B C '''-中，所有棱长为1，又BC '与B C '交于点O ，则（）A ．AO =111222AB AC AA '++ B ．AO B C '⊥C ．三棱锥A BB O '-D ．AO 与平面BB ′C ′C 所成的角为π6【答案】AC【解析】由题意，画出正三棱柱ABC A B C '''-如图所示，向量()()111222AO AB BO AB BC BB AB AC AB AA ''=+=++=+-+ 111222AB AC AA '=++，故选项A 正确；在AOC △中，1AC =，22OC，1OA ==， 222OA OC AC +≠，所以AO 和B C '不垂直，故选项B 错误；在三棱锥A BB O '-中，14BB O S '=，点A 到平面BB O '的距离即ABC 中BC 边上的高，所以h =以111334A BB O BB O V S h ''-==⨯=C 正确；设BC 中点为D ，所以AD BC ⊥，又三棱柱是正三棱柱，所以AD ⊥平面BB C C ''，所以AOD ∠即AO 与平面BB ′C ′C 所成的角，112cos 12OD AOD OA ∠===，所以3AOD π∠=，故选项D 错误．故选AC49．（山东省泰安肥城市2020届高三适应性训练（一））如图四棱锥P ABCD -，平面PAD ⊥平面ABCD ，侧面PAD 是边长为ABCD 为矩形，CD =Q 是PD 的中点，则下列结论正确的是（）A ．CQ ⊥平面PADB ．PC 与平面AQC所成角的余弦值为3C ．三棱锥B ACQ -的体积为D ．四棱锥Q ABCD -外接球的内接正四面体的表面积为【答案】BD【解析】取AD 的中点O ，BC 的中点E ，连接,OE OP ，因为三角形PAD 为等边三角形，所以OP AD ⊥，因为平面PAD ⊥平面ABCD ，所以OP ⊥平面 ABCD ，因为AD OE ⊥，所以,,OD OE OP 两两垂直，所以，如下图，以O 为坐标原点，分别以,,OD OE OP 所在的直线为x 轴，y 轴，z 轴，建立空间直角坐标系，则(0,0,0),(O D A ，(P C B ，因为点Q 是PD 的中点，所以Q ，平面PAD 的一个法向量为(0,1,0)m =，6(QC =，显然 m 与QC 不共线，所以CQ 与平面PAD 不垂直，所以A 不正确；3632(6,23,32),(,0,),(26,PC AQ AC =-==，设平面AQC 的法向量为(,,)n x y z =，则3602260n AQ x zn AC ⎧⋅==⎪⎨⎪⋅=+=⎩，令=1x ，则y z ==(1,2,3)n =--，设PC 与平面AQC 所成角为θ，则21sin 36n PC n PCθ⋅===，所以22cos 3θ=，所以B 正确；三棱锥B ACQ -的体积为1132B ACQ Q ABC ABCV V S OP --==⋅ 1116322=⨯⨯⨯=，所以C 不正确；设四棱锥Q ABCD -外接球的球心为)M a ，则MQ MD =，所以22222222a a ⎛⎫⎛++-=++ ⎪ ⎪ ⎝⎭⎝⎭，解得0a =，即M 为矩形ABCD 对角线的交点，所以四棱锥Q ABCD -外接球的半径为3，设四棱锥Q ABCD -外接球的内接正四面体的棱长为x ，将四面体拓展成正方体，其中正四面体棱为正方体面的对角线，故正方体的棱长为2x ，所以2236⎫=⎪⎪⎝⎭，得224x =，所以正四面体的表面积为244x ⨯=，所以D 正确．故选BD.50．（山东省滕州市第一中学2020-2021学年高二9月开学收心考试）在四面体P ABC -中，以上说法正确的有（）A ．若1233AD AC AB =+，则可知3BC BD = B ．若Q 为△ABC 的重心，则111333PQ PA PB PC =++C ．若0PA BC =，0PC AB =，则0PB AC =D ．若四面体P ABC -各棱长都为2，M N ，分别为,PA BC 的中点，则1MN = 【答案】ABC 【解析】对于A ，1233AD AC AB =+，32AD AC AB ∴=+， 22AD AB AC AD ∴-=- ， 2BD DC ∴=，3BD BD DC BC ∴=+=即3BD BC ∴=，故A 正确；对于B ，Q 为△ABC 的重心，则0QA QB QC ++=，33PQ QA QB QC PQ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=，3PA PB PC PQ ∴++=，即111333PQ PA PB PC ∴=++，故B 正确；对于C ，若0PA BC =，0PC AB =，则0PA BC PC AB +=，()0PA BC PC AC CB ∴++=，0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=，()0PA PC BC PC AC ∴-+= 0CA BC PC AC ∴+=，0AC CB PC AC ∴+=()0AC PC CB ∴+=，0AC PB ∴=，故C 正确；对于D ，111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+==2MN ∴=D 错误．故选ABC.三、填空题51．（辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考）O 为空间中任意一点，A ，B ，C 三点不共线，且3148OP OA OB tOC =++，若P ，A ，B ，C 四点共面，则实数t ＝_________．。

四川省成都市武侯外国语学校2020-2021学年高二英语上学期期末试题含解析

四川省成都市武侯外国语学校2020-2021学年高二英语上学期期末试题含解析一、选择题1. I'm sure you'd rather she returned home, ____?A. wouldn't youB. shouldn't youC. didn't sheD. couldn't you参考答案：A2. --May I pick a flower in the garden?--No, you _________.A. needn’t B mustn’t C. can’t D. won’t参考答案：B3. My MP4 player isn’t in my bag. Where I have put it?A. wouldB. mustC. shouldD. can参考答案：D略4. He has_____great interest in____history, especially______history of_____Tang Dynasty.A. a; 不填; 不填; theB. a; the; the; 不填C. a; 不填; the; theD. 不填; 不填; the; 不填参考答案：D5. --Good afternoon. Can I help you?--My bike is broken. I’d like to have it______, sir.A. repairedB. repairingC. to repairD. to be repaired参考答案：A 略6. ---- How can I find you in the large crowd?---- _______ down the street and you will see me wearing a red shawl.A. If walkingB. To walkC. WalkD. Walking参考答案：C略7. The documentary film “Under the Dome” released by the famous journalist Chai Jing reminds us that it’s high time the Chinese government ______ air pollution in China.A. addressesB. addressedC. will addressD. address参考答案：B考查虚拟语气。

2020-2021学年四川省成都市高考数学三诊试卷(理科)及答案解析

四川省成都市高考数学三诊试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知田径队有男运动员56人，女运动员42人，若按男女比例用分层抽样的方法，从全体运动员中抽出14人参加比赛，则抽到女运动员的人数为（）A．2 B．4 C．6 D．82．命题“∀x∈（﹣1，+∞），ln（x+1）＜x”的否定是（）A．∀x∉（﹣1，+∞），ln（x+1）＜x B．∀x0∉（﹣1，+∞），ln（x0+1）＜x0C．∀x∈（﹣1，+∞），ln（x+1）≥x D．∃x0∈（﹣1，+∞），ln（x0+1）≥x03．已知复数z=﹣i（其中i为虚数单位），则|z|=（）A．3 B．C．2 D．14．已知α，β是空间中两个不同的平面，m为平面β内的一条直线，则“α⊥β”是“m⊥α”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．已知向量，满足=2，•=﹣3，则在方向上的投影为（）A．B． C．D．6．某工厂用A、B两种配件生产甲、乙两种产品，每生产一件甲产品需用4个A配件耗时1h，每生产一件乙产品需用4个B配件耗时2h，该厂每天最多可从配件厂获得24个A配件和16个B配件，每天生产总耗时不超过8h．若生产一件甲产品获利3万元，生产一件乙产品获利4万元，则通过恰当的生产安排，该工厂每天可获得的最大利润为（）A．24万元B．22万元C．18万元D．16万元7．执行如图所示的程序框图，若依次输入m=，n=0.6﹣2，p=，则输出的结果为（）A．B．C．0.6﹣2 D．8．某学校食堂旱餐只有花卷、包子、面条和蛋炒饭四种主食可供食用，有5名同学前去就餐，每人只选择其中一种，且每种主食都至少有一名同学选择．已知包子数量不足仅够一人食用，甲同学肠胃不好不会选择蛋炒饭，则这5名同学不同的主食选择方案种数为（）A．144 B．132 C．96 D．489．定义在（1，+∞）上的函数f（x）同时满足：①对任意的x∈（1，+∞）恒有f（3x）=3f（x）成立；②当x∈（1，3]时，f（x）=3﹣x．记函数g（x）=f（x）﹣k（x﹣1），若函数g（x）恰好有两个零点，则实数k的取值范围是（）A．（2，3）B．[2，3）C．D．10．已知O为坐标原点，双曲线C：﹣=1（a＞0，b＞0）的左焦点为F（﹣c，0）（c＞0），以OF为直径的圆交双曲线C的渐近线于A，B，O三点，且（+）=0，若关于x的方程ax2+bx﹣c=0的两个实数根分别为x1和x2，则以|x1|，|x2|，2为边长的三角形的形状是（）A．钝角三角形B．直角三角形C．锐角三角形D．等腰直角三角形二、填空题：（大题共5小题，每小题5分，共25分.11．计算：sin65°cos35°﹣sin25°sin35°= ．12．一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥（底面是正方形，从顶点向底面作垂线，垂足为底面中心的四棱锥）形容器，O为底面ABCD的中心，则侧棱SC与底面ABCD所成角的余弦值为．13．已知椭圆C：+=1（0＜n＜16）的两个焦点分别为F1，F2，过F1的直线交椭圆C于A，B两点，若|AF2|+|BF2|的最大值为10，则n的值为．14．若直线2ax+by﹣1=0（a＞﹣1，b＞0）经过曲线y=cosπx+1（0＜x＜1）的对称中心，则+的最小值为．15．函数f（x）=（a＞0，b＞0），因其图象类似于汉字“囧”字，被称为“囧函数”，我们把函数f（x）的图象与y轴的交点关于原点的对称点称为函数f（x）的“囧点”，以函数f（x）的“囧点”为圆心，与函数f （x）的图象有公共点的圆，皆称函数f（x）的“囧圆”，则当a=b=1时，有下列命题：①对任意x∈（0，+∞），都有f（x）＞成立；∈（，），使f（x0）＜tanx0成立；②存在x③函数f（x）的“囧点”与函数y=lnx图象上的点的最短距离是；④函数f（x）的所有“囧圆”中，其周长的最小值为2π．其中的正确命题有（写出所有正确命题的序号）．三、解答题：本大题共6小题，满分75分.解答应写出文字说明、证明过程或演算步骤.16．已知函数f（x）=sin2x+2sin（x+）cos（x+）+．（1）求函数f（x）的单调递增区间；（2）在△ABC中，内角A，B，C的对边分别为a，b，c，角A满足f（A）=1+，若a=3，sinB=2sinC，求b的值．17．如图，在三棱台DEF﹣ABC中，已知底面ABC是以AB为斜边的直角三角形，FC⊥底面ABC，AB=2DE，G，H分别为AC，BC的中点．（1）求证：平面ABED∥平面GHF；（2））若BC=CF=AB=1，求二面角A﹣DE﹣F的余弦值．18．某高校一专业在一次自主招生中，对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试，结果如表：语言表达能力一般良好优秀人数逻辑思维能力一般 2 2 1良好 4 m 1优秀 1 3 n由于部分数据丢失，只知道从这20名参加测试的学生中随机抽取一人，抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为．（1）从参加测试的语言表达能力良好的学生中任意抽取2名，求其中至少有一名逻辑思维能力优秀的学生的概率；（2）从参加测试的20名学生中任意抽取2名，设语言表达能力优秀或逻辑思维能力优秀的学生人数为X，求随机变量X的分布列及其均值．19．已知数列{a n}的前n项和为S n，且3S n+a n﹣3=0，n∈N*．（1）求数列{a n}的通项公式；（2）设数列{b n}满足b n=，求T n=，求使T n≥成立的n 的最小值．20．已知一动圆经过点M（2，0），且在y轴上截得的弦长为4，设动圆圆心的轨迹为曲线C．（1）求曲线C的方程；（2）过点N（1，0）任意作相互垂直的两条直线l1，l2，分别交曲线C于不同的两点A，B和不同的两点D，E．设线段AB，DE的中点分别为P，Q．①求证：直线PQ过定点R，并求出定点R的坐标；②求|PQ|的最小值．21．已知函数f（x）=e x，其中e=2.71828…为自然对数的底数．（1）设函数g（x）=（x2+ax﹣2a﹣3）f（x），a∈R．试讨论函数g（x）的单调性；（2）设函数h（x）=f（x）﹣mx2﹣x，m∈R，若对任意，且x1＞x2都有x2h（x1）﹣x1h （x2）＞x1x2（x2﹣x1）成立，求实数m的取值范围．四川省成都市高考数学三诊试卷（理科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知田径队有男运动员56人，女运动员42人，若按男女比例用分层抽样的方法，从全体运动员中抽出14人参加比赛，则抽到女运动员的人数为（）A．2 B．4 C．6 D．8【考点】分层抽样方法．【分析】先求出每个个体被抽到的概率，再用女运动员的人数乘以此概率，即得所求．【解答】解：每个个体被抽到的概率等于=，则样本中女运动员的人数为42×=6．故选：C．2．命题“∀x∈（﹣1，+∞），ln（x+1）＜x”的否定是（）A．∀x∉（﹣1，+∞），ln（x+1）＜x B．∀x0∉（﹣1，+∞），ln（x0+1）＜x0C．∀x∈（﹣1，+∞），ln（x+1）≥x D．∃x0∈（﹣1，+∞），ln（x0+1）≥x0【考点】命题的否定．【分析】根据全称命题的否定是特称命题即可得到结论．【解答】解：∵全称命题的否定是特称命题，∴命题“∀x∈（﹣1，+∞），ln（x+1）＜x”的否定是：“∃x0∈（﹣1，+∞），ln（x0+1）≥x0”，故选：D．3．已知复数z=﹣i（其中i为虚数单位），则|z|=（）A．3 B．C．2 D．1【考点】复数求模．【分析】利用复数代数形式的乘除运算化简，然后代入复数模的公式得答案．【解答】解：∵z=﹣i=，∴|z|=．故选：A．4．已知α，β是空间中两个不同的平面，m为平面β内的一条直线，则“α⊥β”是“m⊥α”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】利用充分条件和必要条件的定义进行判断．【解答】解：由平面与平面垂直的判定定理知如果m为平面β内的一条直线，且m⊥α，则α⊥β，反之，α⊥β时，若m平行于α和β的交线，则m∥α，所以不一定能得到m⊥α，所以“α⊥β”是“m⊥α”的必要不充分条件．故选B．5．已知向量，满足=2，•=﹣3，则在方向上的投影为（）A．B． C．D．【考点】平面向量数量积的运算．【分析】根据平面向量数量积的定义与投影的定义，进行计算即可．【解答】解：∵||=2，•（﹣）=﹣3，∴•﹣=•﹣22=﹣3，∴•=1，∴向量在方向上的投影为=．故选：C．6．某工厂用A、B两种配件生产甲、乙两种产品，每生产一件甲产品需用4个A配件耗时1h，每生产一件乙产品需用4个B配件耗时2h，该厂每天最多可从配件厂获得24个A配件和16个B配件，每天生产总耗时不超过8h．若生产一件甲产品获利3万元，生产一件乙产品获利4万元，则通过恰当的生产安排，该工厂每天可获得的最大利润为（）A．24万元B．22万元C．18万元D．16万元【考点】简单线性规划．【分析】根据条件建立不等式组即线性目标函数，利用图象可求该厂的日利润最大值．【解答】解：设甲、乙两种产品分别生产x、y件，工厂获得的利润为z又已知条件可得二元一次不等式组：目标函数为z=3x+4y，由，可得，利用线性规划可得x=6，y=1时，此时该厂的日利润最大为z=3×6+4=22万元，故选：B．7．执行如图所示的程序框图，若依次输入m=，n=0.6﹣2，p=，则输出的结果为（）A．B．C．0.6﹣2 D．【考点】程序框图．【分析】模拟执行程序，可得该流程图的作用是求出m、n、p中的最小数，化简比较三个数即可得解．【解答】解：根据题意，该流程图的作用是求出m、n、p中的最小数，并将此最小的数用变量x表示并输出，由于，m==，n=0.6﹣2=，p==，可得，＞＞，即：n＞m＞p．故选：A．8．某学校食堂旱餐只有花卷、包子、面条和蛋炒饭四种主食可供食用，有5名同学前去就餐，每人只选择其中一种，且每种主食都至少有一名同学选择．已知包子数量不足仅够一人食用，甲同学肠胃不好不会选择蛋炒饭，则这5名同学不同的主食选择方案种数为（）A．144 B．132 C．96 D．48【考点】计数原理的应用．【分析】分类讨论：甲选花卷，则有2人选同一种主食，剩下2人选其余主食；甲不选花卷，其余4人中1人选花卷，方法为4种，甲包子或面条，方法为2种，其余3人，有1人选甲选的主食，剩下2人选其余主食，或没有人选甲选的主食，相加后得到结果【解答】解：分类讨论：甲选花卷，则有2人选同一种主食，方法为C42C31=18，剩下2人选其余主食，方法为A22=2，共有方法18×2=36种；甲不选花卷，其余4人中1人选花卷，方法为4种，甲包子或面条，方法为2种，其余3人，若有1人选甲选的主食，剩下2人选其余主食，方法为3A22=6；若没有人选甲选的主食，方法为C32A22=6，共有4×2×（6+6）=96种，故共有36+96=132种，故选：B．9．定义在（1，+∞）上的函数f（x）同时满足：①对任意的x∈（1，+∞）恒有f（3x）=3f（x）成立；②当x∈（1，3]时，f（x）=3﹣x．记函数g（x）=f（x）﹣k（x﹣1），若函数g（x）恰好有两个零点，则实数k的取值范围是（）A．（2，3）B．[2，3）C．D．【考点】函数零点的判定定理．【分析】根据题中的条件得到函数的解析式为：f（x）=3m+1﹣x，x∈（3m，3m+1]，在直角坐标系中画出f（x）的图象和直线y=k（x﹣1），根据函数的图象、题意、斜率公式求出实数k的范围．【解答】解：因为对任意的x∈（1，+∞）恒有f（3x）=3f（x）成立，所以f（t）=3f（），取x∈（3m，3m+1]，则∈（1，3]，因为当x∈（1，3]时，f（x）=3﹣x，所以f（）=3﹣，则f（x）=…=3m f（）=3m+1﹣x，且y=k（x﹣1）的函数图象是过定点（1，0）的直线，在直角坐标系中画出f（x）的图象和直线y=k（x﹣1）：因为函数g（x）=f（x）﹣k（x﹣1），且函数g（x）恰好有两个零点，所以f（x）的图象和直线y=k（x﹣1）恰好由两个交点，由图得，直线y=k（x﹣1）处在两条红线之间，且过（3，6）的直线取不到，因，，所以k的范围是[，3），故选：D．10．已知O为坐标原点，双曲线C：﹣=1（a＞0，b＞0）的左焦点为F（﹣c，0）（c＞0），以OF为直径的圆交双曲线C的渐近线于A，B，O三点，且（+）=0，若关于x的方程ax2+bx﹣c=0的两个实数根分别为x1和x2，则以|x1|，|x2|，2为边长的三角形的形状是（）A．钝角三角形B．直角三角形C．锐角三角形D．等腰直角三角形【考点】双曲线的简单性质．【分析】运用向量的加减运算和数量积的性质可得|AF|=|AO|，△AOF为等腰直角三角形，求得渐近线的斜率，进而得到c=a，方程ax2+bx﹣c=0即为x2+x﹣=0，求得两根，求得平方，运用余弦定理，即可判断三角形的形状．【解答】解：由（+）=0，可得（+）•（﹣）=0，即有2﹣2=0，即|AF|=|AO|，△AOF为等腰直角三角形，可得∠AOF=45°，由渐近线方程y=±x，可得=1，c=a，则关于x的方程ax2+bx﹣c=0即为x2+x﹣=0，即有x1x2=﹣，x1+x2=﹣1，即有x12+x22=1+2＜4，可得以|x1|，|x2|，2为边长的三角形的形状是钝角三角形．故选：A．二、填空题：（大题共5小题，每小题5分，共25分.11．计算：sin65°cos35°﹣sin25°sin35°= ．【考点】两角和与差的正弦函数．【分析】由条件利用诱导公式、两角而和的余弦公式，求得所给式子的值．【解答】解：sin65°cos35°﹣sin25°sin35°=cos25°cos35°﹣sin25°sin35°=cos（25°+35°）=cos60°=，故答案为：．12．一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥（底面是正方形，从顶点向底面作垂线，垂足为底面中心的四棱锥）形容器，O为底面ABCD的中心，则侧棱SC与底面ABCD所成角的余弦值为．【考点】直线与平面所成的角．【分析】连接OC，则∠SCO为侧棱SC与底面ABCD所成角，根据图1可知棱锥底面边长为6，斜高为4，从而棱锥的侧棱长为5．于是cos∠SCO=．【解答】解：由图1可知四棱锥的底面边长为6，斜高为4．∴棱锥的侧棱长为5．连接OC，∵SO⊥平面ABCD，∴∠SCO为侧棱SC与底面ABCD所成的角．∵AB=BC=6，∴OC=AC=3．∴cos∠SCO==．故答案为：．13．已知椭圆C：+=1（0＜n＜16）的两个焦点分别为F1，F2，过F1的直线交椭圆C于A，B两点，若|AF2|+|BF2|的最大值为10，则n的值为12 ．【考点】椭圆的简单性质．【分析】由题意可知椭圆是焦点在x轴上的椭圆，利用椭圆定义得到|BF2|+|AF2|=16﹣|AB|，再由过椭圆焦点的弦中通径的长最短，可知当AB垂直于x轴时|AB|最小，把|AB|的最小值，代入|BF2|+|AF2|=16﹣|AB|，由|BF2|+|AF2|的最大值等于10，列式求n的值．【解答】解：由0＜n＜16可知，焦点在x轴上，由过F1的直线l交椭圆于A，B两点，由椭圆的定义可得|BF2|+|AF2|+|BF1|+|AF1|=2a+2a=4a=16，即有|BF2|+|AF2|=16﹣|AB|．当AB垂直x轴时|AB|最小，|BF2|+|AF2|值最大，此时|AB|===，即为10=16﹣，解得n=12．故答案为：12．14．若直线2ax+by﹣1=0（a＞﹣1，b＞0）经过曲线y=cosπx+1（0＜x＜1）的对称中心，则+的最小值为．【考点】基本不等式．【分析】曲线y=cosπx+1（0＜x＜1）的对称中心为，可得：a+b=1．（a＞﹣1，b＞0）．再利用“乘1法”与基本不等式的性质即可得出．【解答】解：曲线y=cosπx+1（0＜x＜1）的对称中心为，∴+b﹣1=0，化为：a+b=1（a＞﹣1，b＞0）．∴+=（a+1+b）=≥=，当且仅当a=2﹣3，b=4﹣2时取等号．故答案为：．15．函数f（x）=（a＞0，b＞0），因其图象类似于汉字“囧”字，被称为“囧函数”，我们把函数f（x）的图象与y轴的交点关于原点的对称点称为函数f（x）的“囧点”，以函数f（x）的“囧点”为圆心，与函数f （x）的图象有公共点的圆，皆称函数f（x）的“囧圆”，则当a=b=1时，有下列命题：①对任意x∈（0，+∞），都有f（x）＞成立；∈（，），使f（x0）＜tanx0成立；②存在x③函数f（x）的“囧点”与函数y=lnx图象上的点的最短距离是；④函数f（x）的所有“囧圆”中，其周长的最小值为2π．其中的正确命题有②③④（写出所有正确命题的序号）．【考点】函数的图象．【分析】利用特殊值法，研究函数的值域，单调性，和零点问题，以及导数的几何意义，利用数形结合的方法进行判断．【解答】解：当a=1，b=1时，函数f（x）=，①当x=时，f（）==﹣2，=2，故f（x）＞不成立，故①不正确；=时，f（）=＜0，tan=1，故存在x0∈（，），使f（x0）＜tanx0成立，故②正②当x确；③则函数f（x）=与y轴交于（0，﹣1）点，则“囧点”坐标为（0，1），设y=lnx，则y′=，设切点为（x0，lnx0），∴切线的斜率k=，当“囧点”与切点的连线垂直切线时，距离最短，∴•=﹣1，解得x0=1，∴切点坐标为（1，0），故函数f（x）的“囧点”与函数y=lnx图象上的点的最短距离是=，故③正确，④令“囧圆”的标准方程为x2+（y﹣1）2=r2，令“囧圆”与f（x）=图象的左右两支相切，则切点坐标为（，）、（﹣，）、此时r=；令“囧圆”与f（x）=图象的下支相切则切点坐标为（0，﹣1）此时r=2，故函数f（x）的所有“囧圆”中，其周长的最小值为2π，故④正确，综上所述：其中的正确命题有②③④，故答案为：②③④三、解答题：本大题共6小题，满分75分.解答应写出文字说明、证明过程或演算步骤.16．已知函数f（x）=sin2x+2sin（x+）cos（x+）+．（1）求函数f（x）的单调递增区间；（2）在△ABC中，内角A，B，C的对边分别为a，b，c，角A满足f（A）=1+，若a=3，sinB=2sinC，求b的值．【考点】三角函数中的恒等变换应用；余弦定理．【分析】（1）由诱导公式与辅助角公式得到f（x）的解析式，由此得到单调增区间．（2）由f（A）=1+，得A=，由恒等式得到B=，所以得到b．【解答】解：（1）∵f（x）=sin2x+2sin（x+）cos（x+）+．=sin2x+sin（2x+）+．=2sin（2x+）+，由﹣+2kπ≤2x+≤2kπ+，得：﹣+kπ≤x≤kπ+，（k∈Z），∴函数f（x）的单调递增区间是[﹣+kπ，kπ+]，（k∈Z）．（2）∵f（A）=1+，∴A=，∵sinB=2sinC=2sin（﹣B），∴cosB=0，即B=，∴由正弦定理得：=，∴b=．17．如图，在三棱台DEF﹣ABC中，已知底面ABC是以AB为斜边的直角三角形，FC⊥底面ABC，AB=2DE，G，H分别为AC，BC的中点．（1）求证：平面ABED∥平面GHF；（2））若BC=CF=AB=1，求二面角A﹣DE﹣F的余弦值．【考点】二面角的平面角及求法；平面与平面平行的判定．【分析】（1）推导出四边形BHFE是平行四边形，从而BE∥HF，从而∥平面GHF，BE∥平面GHF，由此能证明平面ABED∥平面GHF．（2）以C为原点，分别以CA，CB，CF所在的直线为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣DE﹣F的余弦值．【解答】证明：（1）由已知得三棱台DEF﹣ABC中，AB=2DE，∴，∵G，H分别为AC，BC的中点．，∴AB∥GH，EF∥BH，EF=BH，∴四边形BHFE是平行四边形，∴BE∥HF，∵AB⊄平面GHF，HF⊂平面GHF，∴AB∥平面GHF，BE∥平面GHF，又AB∩BE=B，AB，BE⊂平面ABED，∴平面ABED∥平面GHF．解：（2）由已知，底面ABC是以AB为斜边的直角三角形，即AC⊥BC，又FC⊥底面ABC，∴以C为原点，分别以CA，CB，CF所在的直线为x轴，y轴，z轴，建立空间直角坐标系，取AB=2，由BC=CF=，得BC=CF=1，AC=，则A（），C（0，0，0），B（0，1，0），F（0，0，1），E（0，，1），D（，0，1），平面DEF的一个法向量=（0，0，1），设平面ABED的法向量=（x，y，z），，=（﹣，），由，取x=2，得=（2，2），cos＜＞===，由图形得二面角A﹣DE﹣F的平面角是钝角，∴二面角A﹣DE﹣F的余弦值为﹣．18．某高校一专业在一次自主招生中，对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试，结果如表：语言表达能力一般良好优秀人数逻辑思维能力一般 2 2 1良好 4 m 1优秀 1 3 n由于部分数据丢失，只知道从这20名参加测试的学生中随机抽取一人，抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为．（1）从参加测试的语言表达能力良好的学生中任意抽取2名，求其中至少有一名逻辑思维能力优秀的学生的概率；（2）从参加测试的20名学生中任意抽取2名，设语言表达能力优秀或逻辑思维能力优秀的学生人数为X，求随机变量X的分布列及其均值．【考点】离散型随机变量及其分布列；列举法计算基本事件数及事件发生的概率．【分析】（1）语言表达能力优秀或逻辑思维能力优秀的学生共有（6+n）名，由题意得，从而n=2，m=4，由此利用对立事件概率计算公式能求出从参加测试的语言表达能力良好的学生中任意抽取2名，其中至少有一名逻辑能力优秀的学生．（Ⅱ）随机变量X的可能取值为0，1，2，分别求出相应的概率，由此能求出X的分布列及E（X）．【解答】解：（1）用A表示“从这20名参加测试的学生中随机抽取一人，抽到语言表达能力优秀或逻辑思维能力优秀的学生”，∵语言表达能力优秀或逻辑思维能力优秀的学生共有（6+n）名，∴P（A）=，解得n=2，∴m=4，用B表示“从参加测试的语言表达能力良好的学生中任意抽取2名，其中至少有一名逻辑能力优秀的学生”，∴P（B）=1﹣=．（Ⅱ）随机变量X的可能取值为0，1，2，∵20名学生中，语言表达能力优秀或逻辑思维能力优秀的学生人数共有名，∴P（X=0）==，P（X=1）==，P（X=2）==，∴X的分布列为：X 0 1 2PE（X）==．19．已知数列{a n}的前n项和为S n，且3S n+a n﹣3=0，n∈N*．（1）求数列{a n}的通项公式；（2）设数列{b n}满足b n=，求T n=，求使T n≥成立的n 的最小值．【考点】数列的求和；数列递推式．【分析】（1）通过3S n+a n﹣3=0与3S n﹣1+a n﹣1﹣3=0作差，进而可知数列{a n}是首项为、公比为的等比数列，利用公式计算即得结论；（2）通过（1）及3S n+a n﹣3=0计算可知b n=﹣n﹣1，裂项可知=﹣，进而并项相加即得结论．【解答】解：（1）∵3S n+a n﹣3=0，∴当n=1时，3S1+a1﹣3=0，即a1=，又∵当n≥2时，3S n﹣1+a n﹣1﹣3=0，∴3a n+a n﹣a n﹣1=0，即a n=a n﹣1，∴数列{a n}是首项为、公比为的等比数列，故其通项公式a n=•=3•；（2）由（1）可知，1﹣S n+1=a n+1=，∴b n==﹣n﹣1，∵==﹣，∴T n==﹣+﹣+…+﹣=﹣，由T n≥可知，﹣≥，化简得：≤，解得：n≥2016，故满足条件的n的最小值为2016．20．已知一动圆经过点M（2，0），且在y轴上截得的弦长为4，设动圆圆心的轨迹为曲线C．（1）求曲线C的方程；（2）过点N（1，0）任意作相互垂直的两条直线l1，l2，分别交曲线C于不同的两点A，B和不同的两点D，E．设线段AB，DE的中点分别为P，Q．①求证：直线PQ过定点R，并求出定点R的坐标；②求|PQ|的最小值．【考点】轨迹方程．【分析】（1）利用一动圆经过点M（2，0），且在y轴上截得的弦长为4，建立方程，即可求曲线C的方程；（2）①设A，B两点坐标分别为（x1，y1），（x2，y2），直线l1的方程为y=k（x﹣1）（k≠0），与抛物线方程联立，利用韦达定理可求点P，Q的坐标，进而可确定直线PQ的方程，即可得到结论．②由①|PQ|2=（2k﹣）2+（2k+）2=4[（k2+）2+（k2+）﹣2]，换元利用基本不等式求|PQ|的最小值．【解答】解：（1）设圆心C（x，y），则x2+4=（x﹣2）2+y2，化简得y2=4x，∴动圆圆心的轨迹的方程为y2=4x．（2）①设A，B两点坐标分别为（x1，y1），（x2，y2），由题意可设直线l1的方程为y=k（x﹣1）（k≠0），与y2=4x联立得k2x2﹣（2k2+4）x+k2=0．△=（2k2+4）2﹣4k4=16k2+16＞0，x1+x2=2+，y1+y2=k（x1+x2﹣2）=．所以点P的坐标为（1+，）．由题知，直线l2的斜率为﹣，同理可得点Q的坐标为（1+2k2，﹣2k）．当k≠±1时，有1+≠1+2k2，此时直线PQ的斜率k PQ=．所以，直线PQ的方程为y+2k=（x﹣1﹣2k2），整理得yk2+（x﹣3）k﹣y=0，于是，直线PQ恒过定点E（3，0）；当k=±1时，直线PQ的方程为x=3，也过点E（3，0）．综上所述，直线PQ恒过定点E（3，0）．②由①|PQ|2=（2k﹣）2+（2k+）2=4[（k2+）2+（k2+）﹣2]，记k2+=t∵k2+≥2，∴t≥2，∴|PQ|2=4[（t+）2﹣]，∴t=2，即k=±1时，|PQ|的最小值为4．21．已知函数f（x）=e x，其中e=2.71828…为自然对数的底数．（1）设函数g（x）=（x2+ax﹣2a﹣3）f（x），a∈R．试讨论函数g（x）的单调性；（2）设函数h（x）=f（x）﹣mx2﹣x，m∈R，若对任意，且x1＞x2都有x2h（x1）﹣x1h （x2）＞x1x2（x2﹣x1）成立，求实数m的取值范围．【考点】利用导数研究函数的单调性；导数在最大值、最小值问题中的应用．【分析】（1）先求函数g（x）的解析式，求导，根据a的取值，分别解关于x的不等式g′（x）＞0，g′（x）＜0即可；（2）根据已知条件将其转化成，+x1＞+x2，且x1＞x2，构造辅助函数F（x）=﹣（m﹣1）x﹣1，求导，分离变量求得m≤+1，在x∈[，2]上恒成立，构造辅助函数，求导，利用函数的单调性，求得函数的最小值，即可求得m的取值范围．【解答】解：（1）g（x）=e x（x2+ax﹣2a﹣3），a∈R．∴g′（x）=e x[x2+（a+2）x﹣a﹣3]，=a（x﹣1）（x+a+3），当a=﹣4时，g′（x）=a（x﹣1）2≥0，∴g（x）在R上单调递减，当a＞﹣4时，由g′（x）＞0，解得x＜﹣a﹣3或x＞1，∴g（x）在（﹣∞，﹣a﹣3），（1，+∞）上单调递增，由g′（x）＞0，解得﹣a﹣3＜x＜1，∴g（x）在（﹣a﹣3，1）上单调递减；当a＜﹣4时，由g′（x）＞0，解得x＜1或x＞﹣a﹣3，∴g（x）在（﹣∞，1），（﹣a﹣3，+∞）上单调递增，由g′（x）＞0，解得1＜x＜﹣a﹣3，∴g（x）在（1，﹣a﹣3）上单调递减，综上所述：当a=﹣4时，g（x）在R上单调递减；当a＞﹣4时，g（x）在（﹣∞，﹣a﹣3），（1，+∞）上单调递增，在（﹣a﹣3，1）上单调递减；当a＜﹣4时，g（x）在（﹣∞，1），（﹣a﹣3，+∞）上单调递增，在（1，﹣a﹣3）上单调递减．（2）h（x）=f（x）﹣mx2﹣x=e x﹣mx2﹣x，，∴x2h（x1）﹣x1h（x2）＞x1x2（x2﹣x1），∴﹣＞x2﹣x1，不等式﹣＞x2﹣x1，等价于+x1＞+x2，且x1＞x2，记F（x）==﹣（m﹣1）x﹣1，∴F（x）在[，2]上单调递增，F′（x）=﹣（m﹣1）≥0在x∈[，2]上恒成立，m≤+1，在x∈[，2]上恒成立，记P（x）=+1，∴P′（x）=＞0，∴P（x）在[，2]上单调递增，P（x）min=P（）=1﹣2．∴实数m的取值范围为（﹣∞，1﹣2]．。

2023-2024学年四川省成都市高二上册期末调研考试数学(理)试题(含解析)

2023-2024学年四川省成都市高二上册期末调研考试数学(理)试题第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.双曲线2214y x -=的渐近线方程为（）A.12y x =±B.14y x =±C.2y x=± D.4y x=±【正确答案】C【分析】根据给定双曲线方程直接求出其渐近线方程即可.【详解】双曲线2214y x -=的渐近线方程为.2y x=±故选：C2.在空间直角坐标系Oxyz 中，点(4,1,9)P 到点(2,4,3)Q 的距离为（）A.5B.6C.7D.8【正确答案】C【分析】根据空间两点的距离坐标公式即可.【详解】根据空间两点的距离坐标公式可得.7PQ ==故选：C3.在一次游戏中，获奖者可以获得5件不同的奖品，这些奖品要从编号为1-50号的50种不同奖品中随机抽取确定，用系统抽样的方法为获奖者抽取奖品编号，则5件奖品的编号可以是（）A.3，13，23，33，43 B.11，21，31，41，50C.3，6，12，24，48 D.3，19，21，27，50【正确答案】A【分析】根据系统抽样的知识求得正确答案.【详解】依题意，组距为50105=，所以A 选项符合，BCD 选项不符合.故选：A4.命题“0m ∀∈≤N ”的否定是（）A.00m ∃∉≥NB.00m ∃∈>NC.00m ∃∈≤ND.0m ∀∈>N 【正确答案】B【分析】利用含有一个量词的命题的否定的定义判断.【详解】解：因为命题0m ∀∈≤N 是全程量词命题，所以其否定是存在量词命题，即00m ∃∈>N ，故选：B5.若,,a b c ∈R ，则“a b >”是“a c b c +>+”的（）A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件【正确答案】C【分析】根据充要条件的定义即可判断.【详解】根据不等式的性质可得a b a c b c >⇔+>+，∴“a b >”是“a c b c +>+”的充要条件.故选：C6.已知直线:0l Ax By C ++=（A ，B 不同时为0），则下列说法中错误的是（）A.当0B =时，直线l 总与x 轴相交B.当0C =时，直线l 经过坐标原点O C.当0A C ==时，直线l 是x 轴所在直线D 当0AB ≠时，直线l 不可能与两坐标轴同时相交【正确答案】D【分析】根据直线的知识对选项进行分析，从而确定正确答案.【详解】依题意，直线:0l Ax By C ++=（A ，B 不同时为0）.A 选项，当0B =时，0A ≠，直线方程可化为Cx A=-，此时直线l 总与x 轴有交点，A 选项正确.B 选项，当0C =时，直线方程为0Ax By +=，此时直线l 经过原点O ，B 选项正确.C 选项，当0A C ==时，0B ≠，直线方程可化为0y =，此时直线l 是x 轴所在直线，C 选项正确.D 选项，当0AB ≠时，如10x y -+=，直线l 过点()()1,0,0,1-，即直线l 与两坐标轴同时相交，D 选项错误.故选：D.7.执行如图所示的程序语句，若输入5x =，则输出y 的值为（）INPUTx IF x<0THEN y=-x+1ELSE y=-x^2+3END IF PRINTy ENDA.4B.7C.22- D.28-【正确答案】C【分析】分析程序框图的运行过程知，本题的功能为计算并输出分段函数21,03,0x x y x x -+<⎧=⎨-+≥⎩的值，因为输入5x =，所以执行的是23y x =-+，进而可得解.【详解】由算法语句知，该程序的功能是计算并输出分段函数21,03,0x x y x x -+<⎧=⎨-+≥⎩的值，当5x =时，满足0x ≥，∴执行23y x =-+，∴输出的y 值为22-．故选：C8.已知F 是抛物线24y x =的焦点，M 是抛物线上一点，且满足120OFM ∠=︒（O 为坐标原点），则FM 的值为（）A.4B.3C. D.2【正确答案】A【分析】设FM t =，求得M 点坐标并代入抛物线方程，从而求得t ，也即求得FM .【详解】依题意，()1,0F ，设FM t =，由于120OFM ∠=︒，不妨设M 在第一象限，则()1cos60,sin 60M t t +︒︒，即131,22M t ⎛⎫+⎪ ⎪⎝⎭，将M 点坐标代入24y x =得2314142t t ⎛⎫=+ ⎪⎝⎭，即()()238160,4340t t t t --=-+=，由于0t >，所以4t =，即4FM =.故选：A9.已知圆221:(2)(1)9O x y -+-=和直线:10l x y -+=.若圆2O 与圆1O 关于直线l 对称，则圆2O 的方程为（）A.22(3)9x y -+= B.22(3)9x y +-=C.22(2)(3)9x y -+-= D.22(3)(2)9x y -+-=【正确答案】B【分析】求出圆1O 的圆心关于直线l 的对称点，即为圆2O 的圆心坐标，进而可得圆2O 的方程．【详解】圆2O 与圆1O 关于直线l 对称，则圆心()12,1O 与圆()2,O a b 关于:10l x y -+=对称可得211022112a bb a ++⎧-+=⎪⎪⎨-⎪=-⎪-⎩，化简得3030a b a b -+=⎧⎨+-=⎩，解得0,3a b ==又两圆半径相等，故圆2O 的方程为22(3)9x y +-=故选：B10.已知13,22m ⎡⎤∈-⎢⎣⎦，命题2:2320p m m --≤，命题22:1623x y q m m +=--表示焦点在x 轴上的椭圆.则下列命题中为真命题的是（）A.p q ∧ B.p q∨ C.p q⌝∨ D.p q⌝∧【正确答案】B【分析】首先判断命题p 、q 的真假，再根据复合命题的真假性判断即可.【详解】解：由22320m m --≤，即()()2120m m +-≤，解得122m -≤≤，因为13,22⎡⎤-⎢⎥⎣⎦1,22⎡⎤-⎢⎥⎣⎦，所以命题p 为真命题，则p ⌝为假命题，若方程221623x ym m +=--表示焦点在x 轴上的椭圆，则60230623m m m m ->⎧⎪->⎨⎪->-⎩，解得332m <<，又13,22m ⎡⎤∈-⎢⎥⎣⎦，所以命题q 为假命题，则q ⌝为真命题，所以p q ∧为假命题，p q ∨为真命题，p q ⌝∨为假命题，p q ⌝∧为假命题.故选：B11.在平面直角坐标系xOy 内，对任意两点()11,A x y ，()22,B x y ，定义A ，B 之间的“曼哈顿距离”为1212AB x x y y =-+-，记到点O 的曼哈顿距离小于或等于1的所有点(,)x y 形成的平面区域为Ω.现向221x y +=的圆内随机扔入N 粒豆子，每粒豆子落在圆内任何一点是等可能的，若落在Ω内的豆子为M 粒，则下面各式的值最接近圆周率的是（）A.N MB.2N MC.3N MD.4N M【正确答案】B【分析】设(),P x y ，根据1OP ≤得1x y +≤，作出平面区域Ω，根据几何概型计算求解即可.【详解】设(),P x y ，则|1|P y O x =+≤，当0,0x y ≤≥时，1x y +≤；当0,0x y ≥<时，1x y -≤；当0,0x y <≥时，1x y -+≤；当0,0x y <<时，1x y --≤.则平面区域Ω为下图中的四边形ABCD及其内部，其面积为2S ==，根据几何概型公式可得：2πM N =，2πN M∴=.故选：B12.已知有相同焦点1F ，2F 的椭圆22122:1(0)x y C a b a b+=>>与双曲线22222:1(0,0)x y C m n m n-=>>在第一象限的交点为A ，若2AOF △（O 为坐标原点）是等边三角形，则abmn的值为（）A.2+B.2C.232D.223+【正确答案】A【分析】根据已知图形特征结合椭圆，双曲线中,a b c ，关系及公交点求解即可.【详解】2AOF △（O 为坐标原点）是等边三角形，260°AOF ∠=且21OA OF OF ==，则2190°F AF ∠=，且122F F c =，则21,AF c AF ==，))121221,21,a AF AF c m AF AF c =+==-=-)2222221322c b a c c c ⎛⎫+⎪=-=-= ⎪⎝⎭，)2222221322c n c m c c ⎛⎫- ⎪=-=-= ⎪⎝⎭所以22b n =，即得b n =，所以112423222cab a a mn m m++=====+故选：A第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡上.13.椭圆22110036x y +=上一点P 与它的一个焦点的距离等于6，那么点P 与另一个焦点的距离等于______.【正确答案】14【分析】设左、右焦点为12,F F ,利用椭圆的定义即得解.【详解】设左、右焦点为12,F F ,设1||6PF =，由题得10,a =因为12||||2210=20PF PF a +==⨯，所以2||14PF =.所以点P 与另一个焦点的距离等于14.故1414.为了解某校高三学生的数学成绩，随机地抽查了该校100名高三学生的期中考试数学成绩，得到频率分布直方图如图所示.请根据以上信息，估计该校高三学生数学成绩的中位数为______.（结果保留到小数点后两位）【正确答案】71.67【分析】依据频率分布直方图，计算0.5p =时对应的数值，即为中位数.【详解】解：()0.0050.04100.450.5+⨯=< ，()0.0050.040.03100.750.5++⨯=> ，所以中位数在[)70,80之间，设中位数为m ，则有700.03100.50.4510m -⨯⨯=-，所以57071.673m =+≈故答案为.71.6715.甲，乙两人下棋，若两人下成和棋的概率是13，甲获胜的概率是14，则乙获胜的概率是______.【正确答案】512【分析】利用互斥事件概率加法公式直接求解．【详解】解：甲，乙两人下棋，两人下成和棋的概率是13，甲获胜的概率是14，∴乙获胜的概率11134512P =--=．故512．16.已知双曲线22221(0,0)x y a b a b-=>>的左，右焦点1F ，2F ，经过1F 斜率为的直线l 与双曲线的左支相交于P ，Q 两点.记12PF F △的内切圆的半径为a ，则双曲线的离心率为______.1或212+【分析】分两种情况求解离心率，设内切圆圆心为T，分别与三边相切于,,M N H，连接1TF，计算得到212HF HF c+=，1HF c a=-，得到1tan aTF Hc a∠=-，根据二倍角公式得到212ee e-=-解得答案.【详解】当P点在第二象限时，设内切圆圆心为T，分别与三边相切于,,M N H，连接1TF，2121212PF PF NF MF HF HF a-=-=-=，又212HF HF c+=，1HF c a=-，则1tan aTF Hc a∠=-，直线1PF的斜率为221ac aac a-=⎛⎫- ⎪-⎝⎭，整理得到：212ee e-=-1e=+或212e=-（舍去）.当P点在第三象限时，同理设内切圆圆心为T，分别与三边相切于,,M N H，连接1TF，2121212PF PF NF MF HF HF a-=-=-=，又212HF HF c+=，1HF c a=-，则1tan aTF Hc a∠=-，直线1PF的斜率为221ac aac a--=⎛⎫- ⎪-⎝⎭，整理得到：212e e e -=-12e =+或1e =.1+或212+三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.已知点(4,2)P -，直线:3450l x y --=.（1）求经过点P 且与直线l 平行的直线的方程；（2）求经过点P 且与直线l 垂直的直线的方程.【正确答案】（1）34200x y -+=（2）43100x y ++=【分析】（1）设出所求平行直线的方程，利用P 点坐标求得正确答案.（2）利用点斜式求得所求直线的方程.【小问1详解】设经过点P 且与直线l 平行的直线的方程为340x y C -+=，将()4,2P -代入得1280,20C C --+==，所以所求直线方程为34200x y -+=【小问2详解】直线:3450l x y --=的斜率为34，与直线l 垂直的直线的斜率为43-，所以经过点P 且与直线l 垂直的直线的方程为()4243y x -=-+，即43100x y ++=.18.甲，乙两台机床同时生产一种零件，统计5天中两台机床每天所出的次品件数，数据如下图：（1）判断哪台机床的性能更稳定，请说明理由；（2）从甲机床这五天的数据中任意抽取两天的数据，求至多有一天的次品数超过1件的概率.【正确答案】（1）乙机床更稳定，理由见解析；（2）910【分析】（1）计算甲、乙两种机床的生产次品的平均数和方差，说明稳定性；（2）分别计算从五天中任意抽取两天的方法种数和这两天中至多有一天次品数超过1的方法种数，利用古典概型公式计算概率即可.【小问1详解】甲机床的次品数为0,1,0,2,2，平均数为1，方差为()()()()()22222101110121210.85⎡⎤⨯-+-+-+-+-=⎣⎦；乙机床的次品数为.1，平均数为1，方差为()()()()()22222111011121110.45⎡⎤⨯-+-+-+-+-=⎣⎦；∴甲、乙两个机床生产的次品的平均数相等，甲机床次品数的方差大于乙机床次品数的方差，所以乙机床性能更稳定.【小问2详解】设从五天的数据中抽取两天，至多有一天的次品数超过1件为事件A ，则从甲机床这五天的数据中任意抽取两天的数据，抽取的方法有25C 10n ==种，至多有一天的次品数超过1件()211332C C C 9n A =+=，则()910P A =.19.已知圆22:60A x y x +-=与直线32x =相交于M ，N 两点.（1）求||MN 的长；（2）设圆C 经过点M ，N 及(2,2)B .若点P 在圆C 上，点Q 在圆A 上，求||PQ 的最大值.【正确答案】（1）（2）7+【分析】（1）根据圆的方程确定圆心与半径，求圆心到直线的距离，结合直线与圆相交弦长公式求解即可得||MN 的长；（2）根据圆C 经过点M ，N ，可得圆心在圆心C 在x 轴上，设(),0C a ，半径为1r ，即可求得圆C 的方程，再根据两圆上动点距离最值即可得||PQ 的最大值.【小问1详解】圆22:60A x y x +-=化成标准方程为()2239x y -+=，则圆心为()3,0A ，半径3r =，圆A 与直线32x =相交于M ，N 两点，则圆心A 到直线32x =的距离为33322d =-=，所以MN ===【小问2详解】由于圆A 与直线32x =相交于M ，N 两点，所以333333,2222M N ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，或333333,2222N M ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，，又圆C 经过点M ，N ，则圆心C 在x 轴上，设(),0C a ，半径为1r ，则1CM CB r ==，1r ==，解得11,a r =-=则圆()22:113C x y ++=，若点P 在圆C 上，点Q 在圆A上，所以max 1||437PQ AC r r =++=++=+.20.某工厂统计2022年销售网点数量与售卖出的产品件数的数据如下表：销售网点数x （单位：个）1719202123售卖出的产品件数y （单位：万件）2122252730假定该工厂销售网点的个数与售卖出的产品件数呈线性相关关系，（1）求2022年售卖出的产品件数y （单位：万件）关于销售网点数x （单位：个）的线性回归方程；（2）根据（1）中求出的线性回归方程，预测2022年该工厂建立40个销售网点时售卖出的产品件数.参考公式：()()()112211ˆn niii ii i nniii i x x y y x y nxybx x xnx ====---==--∑∑∑∑，ˆˆa y bx=-.【正确答案】（1）167.ˆyx =-；（2）约57万件.【分析】（1）由参考公式可算出销售网点数x （单位：个）的线性回归方程；（2）将40x =代入由（1）算得的回归方程可得答案.【小问1详解】由题，可得1719202123205x ++++==，2122252730255y ++++==，51172119222025212723302532i ii x y==⨯+⨯+⨯+⨯+⨯=∑，5222222117192021232020ii x==++++=∑.则22532520253216202020520ˆ.b-⨯⨯===-⨯，2520167.ˆa =-⨯=-.故回归方程为.167.ˆyx =-【小问2详解】将40x =代入回归方程，则64757ˆy=-=.故2022年该工厂建立40个销售网点时售卖出的产品件数约57万件.21.已知椭圆2222:1(0)x y E a b a b +=>>经过点12⎫⎪⎭，离心率为2.（1）求椭圆E 的方程；（2）设经过右焦点2F 的两条互相垂直的直线分别与椭圆E 相交于A ，B 两点和C ，D 两点.求四边形ACBD 的面积的最小值.【正确答案】（1）2214x y +=（2）3225【分析】（1）依题意得到关于a 、b 、c 的方程组，解得即可；（2）首先求出右焦点坐标，当直线AB 的斜率不存在或为0时直接求出四边形的面积，当直线AB 的斜率存在且不为0时，设直线(:AB y k x =-，()11,A x y ，()22,B x y ，联立直线与椭圆方程，消元、列出韦达定理，利用弦长公式表示出AB ，同理得到CD ，最后由面积公式及基本不等式计算可得.【小问1详解】依题意可得2222231142a b c e a c a b⎧+=⎪⎪⎪==⎨⎪=-⎪⎪⎩，解得21a b c ⎧=⎪=⎨⎪=⎩，所以椭圆方程为2214x y +=.【小问2详解】由（1）可知)2F ，当直线AB 的斜率不存在或为0时，1141222ACBDS AB CD =⋅=⨯⨯=，其中通径为221b a=，当直线AB 的斜率存在且不为0时，设直线(:AB y k x =-，()11,A x y ，()22,B x y ，则直线(1:CD y x k=-，由(2214y k x xy ⎧=-⎪⎨⎪+=⎩消去y 得()2222141240k x x k +-+-=，()()()()222224141241610k kk ∆=--+⨯-=+>，所以212214x x k+=+，212212414k x x k -=+，所以AB =()224114k k +==+，同理可得()2222141414114k k CD k k ⎛⎫⎛⎫-+ ⎪ ⎪ ⎪+⎝⎭⎝⎭==+⎛⎫+⋅- ⎪⎝⎭，所以()()222281121414ACBDSk k k kAB CD =⋅+⨯⨯++=+，因为()()()()()222222214425114424k k k k k ⎡⎤++++⎢⎥++≤=⎢⎥⎣⎦，所以()()22221322525148ACBD S k k +≥=⨯+，当且仅当1k =±时等号成立，综上可得四边形ACBD 的面积的最小值为3225.22.已知点(1,0)F ，经过y 轴右侧一动点A 作y 轴的垂线，垂足为M ，且||||1AF AM -=.记动点A 的轨迹为曲线C .（1）求曲线C 的方程；（2）设经过点(1,0)B -的直线与曲线C 相交于P ，Q 两点，经过点(1,)((0,2)D t t ∈，且t 为常数）的直线PD 与曲线C 的另一个交点为N ，求证：直线QN 恒过定点.【正确答案】（1）()240y x x =>（2）证明见解析【分析】（1）设()(),0A x y x >，根据距离公式得到方程，整理即可；（2）设()11,P x y 、()22,Q x y 、()33,N x y ，表示出直线PQ 的方程，由点()1,0B -在直线PQ 上，代入可得124y y =，同理可得()13231y y ty y y ++=，再表示出直线QN ，代入可得()()()131441y y ty y x +-=-，即可得到直线QN 过定点坐标.【小问1详解】解：设()(),0A x y x >，则()0,M y ，因为||||1AF AM -=1x -=，又0x>1x =+，整理得()240y x x =>.【小问2详解】证明：设()11,P x y 、()22,Q x y 、()33,N x y ，所以121222121212444PQ y y y y k y y x x y y --===-+-，所以直线PQ 的方程为()11124y y x x y y -=-+，因为点()1,0B -在直线PQ 上，所以()111241y x y y -=--+，即21112414y y y y ⎛⎫-=-- ⎪+⎝⎭，解得124y y =①，同理可得直线PN 的方程为()11134y y x x y y -=-+，又()1,D t 在直线PN 上，所以()111341t y x y y -=-+，易得1y t ≠，解得()13231y y ty y y ++=②，所以直线QN 的方程为()22234y y x x y y -=-+，即()23234y y y x y y +=+③，将②式代入③式化简得()1311234y y ty y x y y y +=+，又124y y =，即()131344y y ty y x y +=+，即()()()131441y y ty y x +-=-，所以直线QN 恒过定点41,t ⎛⎫ ⎪⎝⎭.。

2020-2021学年四川省成都市成华区二年级上学期期末数学试卷及答案解析

2020-2021学年四川省成都市成华区二年级上学期期末数学试卷一、我会算。

（20分）1．（20分）我会算。

3×5＝9÷9＝8×9＝28÷4＝5×7＝21÷7＝6×9＝5×7＝9×6＝45÷5＝4×6＝36+24＝36÷4＝7+7＝2×8＝9×3﹣3＝5×4﹣4＝6+6+6＝4+4+4+4＝32+16＝二、我会填。

（每空1分，共24分）2．（1分）5个6相加的和是。

3．（3分）4×7读作，表示个相加。

4．（1分）一根长绳20米，剪了4次，平均每段长米。

5．（4分）7+7+7+7＝×，8×4﹣8＝×。

6．（4分）填上合适的单位。

（米或厘米）房子宽约5。

粉笔长约7。

大树高约8。

杯子高约9。

7．（4分）横线上最大能填几？9×＜70×6＜508×＜604×＜188．（4分）在〇里填上“＞”“＜”或“＝”。

7×8〇8×71米〇99厘米91﹣25〇91﹣3940厘米+70厘米〇100米9．（1分）3张10元人民币+1张50元人民币+4张1元人民币＝元。

10．（2分）21÷3＝7表示21里面有个。

三、竖式计算。

（12分）11．（12分）竖式计算23+46+27＝96﹣38﹣37＝68+32﹣19＝97﹣48+32＝四、画一画，圈一圈。

（7分）12．（3分）画一条线，它的长度为3cm的两倍。

13．（4分）用两种方法在图上表示算式。

2×7＝。

五、判断。

（5分）14．（1分）计算3×8和4×6用的是同一句口诀。

（判断对错）15．（1分）4×7＝3×7+7＝4×6+6。

（判断对错）16．（1分）在计算87﹣35+41时，可以先计算35+41＝76，再算87﹣76＝11。

成都市2020~2021学年度上期期末高二年级调研考试语文试题及参考答案

C．最后一段就不同学科对经典阅读的看法进行了具体的对比分析,提出了理科如何开展
通识教育的问题.
D．文章结构清晰,从理解人类处境、扩大认知视野、关联生活与传统等角度探讨了通识教
育的重要意义.
３．根据原文内容,下列说法不正确的一项是(
３分)
我们今天遭遇到的一些困境,
有
可
能
在
人类文明不同处境下也出现过,阅读经典或许
系,教科书与专业研究文献成为阅读的主体.通识教育在理科要怎么做? 可能还需要自然
科学领域的专家和学者一起来探索.
(摘编自李猛«经典阅读、通识教育与美好生活»)
１．下列关于原文内容的理解和分析,正确的一项是(
３分)
中国当代读者对柏拉图等人的作品产生共鸣的根本原因是,
太相信了传统中的道理,以至于没法在现代社会中幸存下来,所以慢慢会把原来文明中建立
的读书、智慧和生活的关系给斩断了.所以现代中国得找到办法把它们重新联系起来,这种
联系的方式,无论在学术上,还是在教育中,都需要许多尝试和探索.通识教育的努力,特别
高二调研考试语文试题第
１页(共８页)
是通过深入到经典这个层面的努力,有助于实现这点.
代中国来说更为重要.我ቤተ መጻሕፍቲ ባይዱ知道,中华文明传统在近代遭到很强的质疑,而且新来的文明传
统直到今天还与中国人的生活有很多隔膜之处,现代中国的文明处境在今天是未定的.这
才需要通识教育给我们在面临今天的社会、经济、文化、心理等所有问题时提供一个更大的
这些作品表达了对较为重
A．

四川省成都市2019-2020学年高二上学期期末调研考试化学试卷

．．．．“ ”化学试题本试卷选择题和非选择题两部分。

第I 卷(选择题)1 至 4 页，第 II 卷(非选择题)4 至 6页，共 6 页，满分 100 分，考试时间 90 分钟。

注意事项：1.答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。

2.答选择题时，必须使用 2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3.答非选择题时，必须使用 0.5 毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

5.考试结束后，只将答题卡交回。

第 I 卷(选择题，共 40 分)本卷共 20 题，每题 2 分，共 40 分。

每题只有一个选项符合题意。

1.《礼记·内则》记载：冠带垢，和灰清漱；衣裳垢，和灰清浣。

古人洗涤衣裳冠带，所用的就是草木灰浸泡的溶液。

下列说法错误的是A 草木灰的主要成分是 H 2CO 3B.洗涤利用了草木灰溶液的碱性C.洗涤时加热可增强去油污能力D.草木灰做肥料时可与铵态氮肥混合施用2.下列仪器在中和热测定实验中不会用到的是A.温度计B.量筒C.分液漏斗D.环形玻璃搅拌棒3.配制 FeCl 3 溶液时，将 FeCl 3 固体溶解在较浓的盐酸中，再加水稀释。

下列说法正确的是A.较浓盐酸可有效抑制 Fe 3＋水解B.稀释过程中 FeCl 3 水解程度增大，c(H ＋)增大C.FeCl 3 溶液中存在 Fe 3＋＋3H 2O ＝Fe(OH)3↓＋3H ＋D.FeCl 3 溶液显黄色，没有 Fe(OH)3 存在 4.下列事实不能用勒夏特列原理解释的是A 常温下将 pH ＝4 的醋酸溶液稀释 10 倍，pH<5B.H 2、I 2(g)、HI 平衡体系加压后颜色变深C.利用 TiCl 4 水解制备 TiO 2 时，需加入大量水并加热D.向 Mg(OH)2 悬浊液中滴加 FeCl 3 溶液，有红褐色沉淀生成5.水煤气变换反应的能量变化如右图。

2020-2021学年高二上学期期末考试数学试卷(含解析)

2020-2021学年高二上学期期末考试数学试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．若3324A 10A n n =，则n =（）A ．1B ．8C ．9D ．102．期末考试结束后，某班要安排6节课进行试卷讲评，要求课程表中要排入语文、数学、英语、物理、化学、生物共六节课，如果第一节课只能排语文或数学，最后一节不能排语文，则不同的排法共有（） A ．192种B ．216种C ．240种D ．288种3．一台X 型号自动机床在一小时内不需要工人照看的概率为0.8，有4台这种型号的自动机床各自独立工作，则在一小时内至多2台机床需要工人照看的概率是（） A ．0.1536B ．0.1808C ．0.5632D ．0.97284．某市气象部门根据2021年各月的每天最高气温平均值与最低气温平均值（单位：℃）数据，绘制如下折线图：那么，下列叙述错误的是（）A ．各月最高气温平均值与最低气温平均值总体呈正相关B ．全年中，2月份的最高气温平均值与最低气温平均值的差值最大C ．全年中各月最低气温平均值不高于10℃的月份有5个D ．从2021年7月至12月该市每天最高气温平均值与最低气温平均值都呈下降趋势5．若()2N 1,X σ~，则()0.6827P X μσμσ-<≤+=，(22)0.9545P X μσμσ-<≤+=，已知()21,3X N ~，则(47)P X <≤=（）A ．0.4077B ．0.2718C ．0.1359D ．0.04536．为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了100位居民进行调查，经过计算()200.01P K k ≥=，根据这一数据分析，下列说法正确的是（）A ．有1%的人认为该栏目优秀；B ．有1%的把握认为该栏目是否优秀与改革有关系；C ．有99%的把握认为电视栏目是否优秀与改革有关系；D ．没有理由认为电视栏目是否优秀与改革有关系.7．若1021001210)x a a x a x a x =++++，则012310a a a a a -+-++的值为．A 1B 1C ．101)D ．101)8．关于()72x +的二项展开式，下列说法正确的是（） A ．()72x +的二项展开式的各项系数和为73B ．()72x +的二项展开式的第五项与()72x +的二项展开式的第五项相同C ．()72x +的二项展开式的第三项系数为4372CD ．()72x +的二项展开式第二项的二项式系数为712C9．如图，某建筑工地搭建的脚手架局部类似于一个3×2×3的长方体框架，一个建筑工人欲从A 处沿脚手架攀登至B 处，则其最近的行走路线中不连续向上攀登的概率为（）A ．528B ．514C ．29D ．1210．三棱锥P ABC -中P A ､PB ､PC 两两互相垂直，4PA PB +=，3PC =，则其体积（） A ．有最大值4B ．有最大值2C ．有最小值2D ．有最小值4二、填空题11．最小二乘法得到一组数据(),(1,2,3,4,5)i i x y i =的线性回归方程为ˆ23yx =+，若5125ii x==∑，则51i i y ==∑___________.12．某班举行的联欢会由5个节目组成,节目演出顺序要求如下: 节目甲不能排在第一个,并且节目甲必须和节目乙相邻.则该班联欢会节目演出顺序的编排方案共有____种. 13．若随机变量X 的概率分布如表，则表中a 的值为______.14．设随机变量ξ~B (2，p )，若P (ξ≥1)=59，则D (ξ)的值为_________.15．已知等差数列{}n a 中，33a =，则1a 和5a 乘积的最大值是______.16．某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了5个问题就晋级下一轮的概率为___________.17．经统计，在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下：则该营业窗口上午9点钟时，至少有2人排队的概率是_____．18．点A ，B ，C 在球O 表面上，2AB =，BC =90ABC ∠=︒，若球心O 到截面ABC的距离为___________.19．如图，在三棱柱111ABC A B C -中，四边形11AAC C 是边长为4的正方形，平面ABC ⊥平面11AAC C ，3AB =，5BC =.（℃）求证：1AA ⊥平面；（℃）若点E 是线段的中点，请问在线段是否存在点E ，使得面11AAC C ？若存在，请说明点E 的位置，若不存在，请说明理由；（℃）求二面角的大小.20．四根绳子上共挂有10只气球,绳子上的球数依次为1,2,3,4，每枪只能打破一只球,而且规定只有打破下面的球才能打上面的球,则将这些气球都打破的不同打法数是________.三、解答题21．已知集合(){}()12,,,|,1,2,,1nn i R x x x x R i n n =∈=≥，定义n R 上两点()12,,,n A a a a ，()12,,,n B b b b 的距离()1,ni i i d A B a b ==-∑.（1）当2n =时，以下命题正确的有__________（不需证明）： ℃若()1,2A ，()4,6B ，则(),7d A B =；℃在ABC 中，若90C =∠，则()()()222,,,d A C d C B d A B ⎡⎤⎡⎤⎡⎤+=⎣⎦⎣⎦⎣⎦； ℃在ABC 中，若()(),,d A B d A C =，则B C ∠=∠;（2）当2n =时，证明2R 中任意三点A B C ，，满足关系()()(),,,d A B d A C d C B ≤+；（3）当3n =时，设()0,0,0A ，()4,4,4B ，(),,P x y z ，其中x y z Z ∈，，，()()(),,,d A P d P B d A B +=.求满足P 点的个数n ，并证明从这n 个点中任取11个点，其中必存在4个点，它们共面或者以它们为顶点的三棱锥体积不大于83.22．今年4月，教育部办公厅印发了《关于加强义务教育学校作业管理的通知》，规定初中学生书面作业平均完成时长不超过90分钟．某市为了更好地贯彻落实“双减”工作要求，作教育决策，该市教育科学研究院就当前全市初三学生每天完成书面作业时长抽样调查，结果是学生书面作业时长（单位：分钟）都在区间[]50,100内，书面作业时长的频率分布直方图如下：(1)若决策要求：在国家政策范围内，若当前初三学生书面作业时长的中位数估计值大于或等于平均数（计算平均数时，同一组中的数据用该区间的中点值代表）估计值，则减少作业时长；若中位数估计值小于平均数，则维持现状．请问：根据这次调查，该市应该如何决策？(2)调查统计时约定：书面作业时长在区间[]90,100内的为A 层次学生，在区间[)80,90内的为B 层次学生，在区间[70,80)内的为C 层次学生，在其它区间内的为D 层次学生．现对书面作业时长在70分钟以上（含70分钟）的初三学生，按作业时长出现的频率用分层抽样的方法随机抽取8人，再从这8人中随机抽取3人作进一步调查，设这3人来自X 个不同层次，求随机变量X 的分布列及数学期望．23．国家文明城市评审委员会对甲､乙两个城市是否能入围“国家文明城市”进行走访调查.派出10人的调查组.先后到甲､乙两个城市的街道､社区进行问卷调查，然后打分（满分100分）.他们给出甲､乙两个城市分数的茎叶图如图所示：(1)请你用统计学的知识分析哪个城市更应该入围“国家文明城市”，请说明理由；(2)从甲､乙两个城市的打分中各抽取2个，在已知有大于80分的条件下，求抽到乙城市的分数都小于80分的概率；(3)从对乙城市的打分中任取2个，设这2个分数中不小于80分的个数为X，求X的分布列和期望.参考答案：1．B【分析】根据排列数的运算求解即可.【详解】由332A 10A n n =得，2(21)(22)10(1)(2)n n n n n n --=--，又3,n n *≥∈N ，所以2(21)5(2)n n -=-，解得8n =，所以正整数n 为8．故选：B. 2．B【分析】对第一节课的安排进行分类讨论，结合分步乘法计数原理和分类加法计数原理可得结果.【详解】分以下两种情况讨论：℃若第一节课安排语文，则后面五节课的安排无限制，此时共有55A 种；℃若第一节课安排数学，则语文可安排在中间四节课中的任何一节，此时共有444A 种.综上所述，不同的排法共有54544216A A +=种.故选：B. 3．D【详解】设在一个小时内有ξ台机床需要工人照看，则ξ～B (4,0.2)，所以P (ξ≤2)＝04C (0.8)4＋14C (0.8)3×0.2＋24C (0.8)2×(0.2)2＝0.972 8. 故选D 4．D【分析】利用折线图可以判断选项ABC 正确，从2021年7月至12月该市每天最高气温平均值与最低气温平均值，先上升后下降，所以选项D 错误.【详解】解：由2021年各月的每天最高气温平均值和最低气温平均值（单位：C)︒数据，绘制出的折线图，知：在A 中，各月最高气温平均值与最低气温平均值为正相关，故A 正确；在B 中，全年中，2月的最高气温平均值与最低气温平均值的差值最大，故B 正确；在C 中，全年中各月最低气温平均值不高于10C ︒的月份有1月，2月，3月，11月，12月，共5个，故C 正确；在D 中，从2021年7月至12月该市每天最高气温平均值与最低气温平均值，先上升后下降，故D 错误. 故选：D ． 5．C【分析】由题意，得(47)(2)P X P X μσμσ<≤=+<≤+，再利用3σ原则代入计算即可.【详解】℃()21,3X N ~，由()0.6827P X μσμσ-<≤+=，(22)0.9545P X μσμσ-<≤+=，℃1(47)(2)(0.95450.6827)0.13592P X P X μσμσ<≤=+<≤+=-=.故选：C 6．C【分析】利用独立性检验的基本原理即可求出答案．【详解】解：℃()200.01P K k ≥=表示“电视栏目是否优秀与改革没有关系”的概率，℃有99%的把握认为电视栏目是否优秀与改革有关系，故选：C ．【点睛】本题主要考查独立性检验的基本应用，准确的理解判断方法是解决本题的关键，属于基础题． 7．D【详解】分析：令1021001210())f x x a a x a x a x ==++++，再求f(-1)的值得解.详解：令1021001210())f x x a a x a x a x ==++++，1001210(1)1)f a a a a -==-+++．故答案为D ．点睛：（1）本题主要考查二项式定理中的系数求法问题，意在考查学生对这些基础知识的掌握水平.(2) 二项展开式的系数0123,,,,n a a a a a ⋅⋅⋅的性质：对于2012()?··n n f x a a x a x a x =++++，0123(1)n a a a a a f ++++⋅⋅⋅+=， 0123(1)(1)n n a a a a a f -+-+⋅⋅⋅+-=-.8．A【分析】利用赋值法求出展开式各项系数和，即可判断A ，根据二项式展开式的通项，即可判断B 、C 、D ；【详解】解：()72x +展开式的通项为7172rrr r T C x -+=⋅⋅，故第二项的二项式系数为177C =，故D 错误；第三项的系数为2572C ⋅，故C 错误；()72x +的展开式的第五项为43472C x ⋅⋅，()72x +的展开式的第五项为44372C x ⋅⋅，故B 错误；令1x =则()7723x +=，即()72x +的二项展开式的各项系数和为73，故A 正确；故选：A 9．B【解析】将问题抽象成“向左三次，向前两次，向上三次”，计算出总的方法数，然后利用插空法计算出最近的行走路线中不连续向上攀登的事件数，最后根据古典概型概率计算公式，计算出所求概率.【详解】从A 的方向看，行走方向有三个：左、前、上. 从A 到B 的最近的行走线路，需要向左三次，向前两次，向上三次，共8次.所以从A 到B 的最近的行走线路，总的方法数有88332332560A A A A =⋅⋅种. 不连续向上攀登的安排方法是：先将向左、向前的安排好，再对向上的方法进行插空.故方法数有：53563232200A C A A ⨯=⋅.所以最近的行走路线中不连续向上攀登的概率为200556014=. 故选：B【点睛】本小题主要考查古典概型的计算，考查有重复的排列组合问题，考查插空法，属于中档题. 10．B【分析】依题意可得1113332P ABC PABV PC SPA PB -=⋅=⨯⨯⋅再利用基本不等式计算可得；【详解】解：依题意21111132332222P ABCPABPA PB V PC S PA PB PA PB -+⎛⎫=⋅=⨯⨯⋅=⋅≤= ⎪⎝⎭，当且仅当2PA PB ==时取等号，所以()max 2P ABC V -=，故选：B11．65【分析】由最小二乘法得到的线性回归方程过点(),x y ，代入即可解决【详解】由5125i i x ==∑可知，数据的平均数2555x ==，又线性回归方程ˆ23yx =+过点(),x y ，所以25313y =⨯+=，故51551365i i y y ===⨯=∑故答案为：65 12．42【分析】由题意可知，甲可排在第二、三、四、五个，再根据甲、乙相邻，分别计算. 【详解】由题意可知，甲可排在第二、三、四、五个，当甲排在第二、三、四个时，甲乙相邻，有22A 种排法，将甲乙当做一个整体，剩下三个节目全排列，共3×22A ×33A =36种当甲排在第五个时，甲乙相邻，只有一种排法，剩下三个节目全排列，共33A =6种综上，编排方案共36+6=42种【点睛】本题考查了分类计数原理，分类时要注意不重不漏；解决排列问题时，相邻问题常用捆绑法，特殊位置要优先考虑. 13．0.2【解析】利用概率和为1可求出答案. 【详解】由随机变量X 的概率分布表得： 0.20.30.31a +++=，解得0.2a =. 故答案为：0.2【点睛】本题考查的是分布列的性质，较简单. 14．49【分析】由二项分布的特征，先求出13p =，套公式即可求出D (ξ). 【详解】因为随机变量ξ~B (2，p )，且P (ξ≥1)=59，所以P (ξ≥1)=()11P ξ-<= ()10P ξ-==()25119p --=. 解得：13p =. 所以D (ξ)()12412339np p =-=⨯⨯=.故答案为：4915．9【分析】设出公差，根据等差数列的性质，表示出15,a a ，再列式即可求得结果. 【详解】因为{}n a 是等差数列，设公差为d ，可得13532,2a a d a a d =-=+，于是得()()2153322949a a a d a d d =-+=-≤，当且仅当d =0，即153a a ==时，取得最大值. 故答案为：9.【点睛】本题考查等差数列的下标和性质，属基础题. 16．1443125##0.04608 【分析】认真分析该选手所有可能的答题情况，是本题的关键【详解】由该选手恰好回答了5个问题就晋级下一轮，说明他第4、第5两个问题是连续答对的，第3个问题没有答对，第1和第2两个问题也没有全部答对，即他答题结果可能有三种情况：⨯⨯⨯√√或⨯√⨯√√或√⨯⨯√√，根据独立事件同时发生的概率公式，可得该选手恰好回答了5个问题就晋级下一轮的概率为0.20.20.20.80.8+0.20.80.20.80.8+0.80.20.20.80.8=0.04608⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯故答案为：0.04608 17．0.74【详解】试题分析：x 表示人数，(2)(2)(3)(4)(5)P x P x P x P x P x ≥==+=+=+≥0.30.30.10.040.74=+++=.考点：互斥事件的概率.18．【分析】根据截面圆性质，先求出截面圆半径，然后由求得球半径，从而求得体积．【详解】因为2AB =，BC =90ABC ∠=︒，所以4AC ==，所以三角形外接圆半径22ACr ==，又球心O 到截面ABC 的距离为R =球体积为(334433V R ππ==⨯=．故答案为：．19．（℃）（℃）（℃）见解析【详解】试题分析：（℃）由正方形的性质得1AC AA ⊥，然后由面面垂直的性质定理可证得结果；（℃）当点E 是线段1AB 的中点时，利用中位线定理可得1DE AC ，进而得出DE 面11AAC C ；（℃）利用二面角的定义先确定11C AC ∠是二面角111C A B C --的平面角，易求得11tan C A C ∠，从而求得二面角的平面角为的度数．试题解析：（℃）因为四边形11AAC C 为正方形，所以1AC AA ⊥．因为平面ABC ⊥平面11AAC C ，且平面ABC ⋂平面11AAC C AC =，所以1AA ⊥平面ABC ．（℃）当点E 是线段1AB 的中点时，有DE 面11AAC C ，连结1AB 交1AB 于点E ，连结BC ，因为点E 是1AB 中点，点⊄是线段DE 的中点，所以1DE AC ．又因为BC ⊂面11AAC C ，11A C 面11AAC C ，所以DE 面11AAC C .（℃）因为1AA ⊥平面ABC ，所以.又因为，所以面11AAC C ，所以11A B ⊥面11AAC C ，所以11A B ⊥1A C ，11A B ⊥11A C ，所以11C AC ∠是二面角111C A B C --的平面角，易得，所以二面角111C A B C --的平面角为45°.考点：1、线面垂直的判定；2、线面平行的判定；2、二面角．【方法点睛】立体几何中的探索性问题主要是对平行、垂直关系的探究，对条件和结论不完备的开放性问题的探究．解决这类问题时一般根据探索性问题的设问，假设其存在并探索出结论，然后在假设下进行推理，若得到合乎情理的结论就肯定假设，若得到矛盾就否定假设． 20．12600【详解】问题等价于编号为1,2,3,10的10个小球排列，其中2,3号，4,5,6号，7,8,9,10号的排列顺序是固定的，据此可得：将这些气球都打破的不同打法数是101023423412600A A A A =⨯⨯. 21．（1）℃；（2）证明见解析；（3）125n =，证明见解析．【解析】（1）℃根据新定义直接计算．℃根据新定义，写出等式两边的表达式，观察它们是否相同，即可判断；℃由新定义写出等式()(),,d A B d A C =的表达式，观察有无AB AC =；（2）由新定义，写出不等式两边的表达式，根据绝对值的性质证明；（3）根据新定义，及绝对值的性质得P 点是以AB 为对角线的正方体的表面和内部的整数点，共125个，把它们分布在五个平面(0,1,2,3,4)z =上，这五个面一个面取3个点，相邻面上取一个点，以它们为顶点构成三棱锥（能构成时），棱锥的体积不超过83，然后任取11点中如果没有4点共面，但至少有一个平面内有3个点．根据这3点所在平面分类讨论可得．【详解】（1）当2n =时，℃若()1,2A ，()4,6B ，则(),41627d A B =-+-=，℃正确；℃在ABC 中，若90C =∠，则222AC BC AB +=，设112233(,),(,),(,)A x y B x y C x y ，所以222222131323231212()()()()()()x x y y x x y y x x y y -+-+-+-=-+-而()2221212121221212()()()2)),((x x y y x x y y d A x B x y y =⎡⎤⎣-+-+⎦=--+--， ()()22,,d A C d C B ⎡⎤⎡⎤+=⎣⎦⎣⎦22221313232313132323()()()()2()()2()()x x y y x x y y x x y y x x y y -+-+-+-+--+--，但1313232312122()()2()()2()()x x y y x x y y x x y y --+--=--不一定成立，℃错误； ℃在ABC 中，若()(),,d A B d A C =，在℃中的点坐标，有12121313x x y y x x y y -+-=-+-，但1212131322x x y y x x y y -⋅-=-⋅-不一定成立，因此AB AC =不一定成立，从而B C ∠=∠不一定成立，℃错误．空格处填℃（2）证明：设112233(,),(,),(,)A x y B x y C x y ，根据绝对值的性质有132312x x x x x x -+-≥-，132312y y y y y y -+-≥-，所以(,)(,)(,)d A C d B C d A B +≥．,（3）(,)12d A B =，44,44,44x x y y z z +-≥+-≥+-≥，所以(,)(,)12d A P d B P +≥，当且仅当以上三个等号同时成立，(,)(,)12d A P d B P +=又由已知()()(),,,d A P d P B d A B +=，℃04,04,04x y z ≤≤≤≤≤≤，又,,x y z Z ∈，℃,,0,1,2,3,4x y z =，555125⨯⨯=，点P 是以AB 为对角线的正方体内部（含面上）的整数点，共125个，125n =．这125个点在0,1,2,3,4z z z z z =====这五面内．这三个平面内，一个面上取不共线的3点，相邻面上再取一点构成一个三棱锥．则这个三棱锥的体积最大为118441323V =⨯⨯⨯⨯=，现在任取11个点，若有四点共面，则命题已成立，若其中无4点共面，但11个点分在5个平面上至少有一个平面内有3个点（显然不共线），若这三点在1,2,3z z z ===这三个平面中的一个上，与这个面相邻的两个面上如果有一点，那么这一点与平面上的三点这四点可构成三棱锥的四个顶点，其体积不超过83，否则还有8个点在平面0z =和4z =上，不合题意，若这三个点在平面0z =或5z =上，不妨设在平面0z =，若在平面1z =在一个点，则同样四点构成的三棱锥体积不超过83，否则剩下的8个点在2,3,4z z z ===三个平面上，只能是3，3，2分布，不管哪一种分布都有四点构成的三棱锥体积不超过83，综上，任取11个点，其中必存在4个点，它们共面或者以它们为顶点的三棱锥体积不大于83.【点睛】关键点点睛：本题新定义距离(,)d A B ，解题关键是利用新定义转化为绝对值，利用绝对值的性质解决一些问题．本题还考查了抽屉原理，11个放在5个平面上，至少有一个平面内至少有3点，由此分类讨论可证明结论成立． 22．(1)该市应该作出减少作业时长的决策； (2)分布列见解析；期望为167.【分析】（1）根据题意，结合频率分布直方图，分别求出中位数和平均数，即可求解；（2）根据题意，结合分层抽样以及离散型随机变量的分布列与期望求法，即可求解. (1)作业时长中位数的估计值为直方图中等分面积的线对立的值，设为x ．0.01100.01100.02100.5⨯+⨯+⨯<． 0.01100.01100.02100.03100.5⨯+⨯+⨯+⨯>，()0.01100.01100.02100.03800.5x ∴⨯+⨯+⨯+⨯-=．解得2503x =，即中位数的故计值2503分钟．又作业时长平均数估计值为0.0110550.0110650.021075⨯⨯+⨯⨯+⨯⨯ 2500.0310850.031095813+⨯⨯+⨯⨯=<．因为中位数的估计值2503分钟大于平均数估计值81分钟，所以，根据这次调查，该市应该作出减少作业时长的决策. (2)由题，作业时长在70分钟以上（含70分钟）为[90.100]，[80,90)，[70,80)三个区间，其频率比为3：3：2，分别对应A ，B ，C 三个层次．根据分层抽样的方法，易知各层次抽取的人数分别为3，3，2，因此X 的所有可能值为1，2，3．因为333821(1)28C P X C ⨯===，111233389(3)28C C C P X C ⋅⋅===， 121221333232382229(2)14C C C C C C P X C ⨯⋅+⨯⋅+⨯⋅===，所以X 的分在列为：故数学期望19916()1232814287E X =⨯+⨯+⨯=. 23．(1)乙城市更应该入围“国家文明城市”．理由见解析． (2)425； (3)分布列见解析，期望为1．【分析】（1）根据得分的平均值与方差说明，极差最值也可用来说明；（2）记抽到的数据中有大于80分为事件A ，甲城市抽到的分数有大于80分为事件B ，乙城市抽到的分数有大于80分为事件C ，由()()(|)()()P AC P C P C A P A P A ==计算；（2）X 的可能值是0,1,2，分别求得概率得概率分布列，由期望公式计算出期望． (1)乙城市更应该入围“国家文明城市”．理由如下：由茎叶图，计算两个城市的得分的均值为甲：6365987910x +++==，乙：6568927910y +++==，均值相等，方差为甲：222211[(16)(14)19]13610s =-+-++=，乙：222221[(14)(11)13]59.810s =-+-++=，甲的方差远大于乙的方差，说明乙的得分较稳定，甲极其不稳定，因此乙城市更应该入围“国家文明城市”． (2)记抽到的数据中有大于80分为事件A ，甲城市抽到的分数有大于80分为事件B ，乙城市抽到的分数有大于80分为事件C ，262102()13C P B C =-=，252107()19C P C C =-=，2725()1(1)(1)3927P A =--⨯-=，7()()9P AC P C ==，所以()()()()749(|)1(|)111252527P AC P C P C A P C A P A P A =-=-=-=-=；(3)乙城市10个人中5个大于80分，5个小于80，X 的可能是0,1,2，252102(0)9C P X C ===，11552105(1)9C C P X C ===，252102(2)9C P X C ===，所以X 的分布列为：52()12199E X =⨯+⨯=．。

成都市高2015届高二调研考试试题数学(理)

高二数学试题（理科）一、选择题：本大题共10小题，每个题5分，共50分．1．已知空间向量a (1,0,1)=，b (2,1,1)=--，则+=a b ( )（A ）(1,1,0)- （B ）(1,0,1)- （C ）(1,1,1)- （D ）(1,1,0) 2．下列说法正确的是 ( ) （A ）不可能事件没有概率（B ）必然事件的概率为0 （C ）随机事件的概率不大于1 （D ）随机事件的概率可以小于03．如图，''''A B C D 为各边与坐标轴平行的正方形ABCD 的直观图，若''3A B =，则原正方形的面积是（）（A ）9 （B ）36 （C ）9或36 （D ）92或9244．如图是甲、乙两名篮球运动员每场比赛得分情况的茎叶图，则甲得分的众数、乙得分的中位数分别是 ( )（A ）14分，25分（B ）32分，25分（C ）32分，26分（D ）14分，26分5．如图，在平行四边形ABCD 中，点E 为边CD 上一定点，若在平行四边形ABCD 内部随机取一个点Q ，则点Q 取自ABE ∆内部的概率等于（）（A ）14 （B ）13 （C ）12 （D ）236．某厂节能降耗技术改造后，生产某产品过程中记录的产量x (吨)与相应的生产能耗y (吨)的几组对应数据如下表：x1 2 3 4 y2t34.5根据上表提供的数据，求得y 关于x 的线性回归方程为ˆy＝0.8x ＋1，那么表中t 的值为（）（A ）2.8 （B ）2.7 （C ）2.6 （D ）2.5 7．执行如图所示的程序框图，如果输出的S =111111+112123⨯+⨯⨯+111112310+⨯⨯⨯⋅⋅⋅⨯ ，则输入的N 的值应该是（）（A ）12 （B ）11 （C ）10 （D ）9甲乙 4 0 8 4 4 1 2 5 85 4 2 36 52 2 6 9 2 13 2 3 49 5 4 1第4题图DACBE第5题图C'D'A'B'第3题图第7题图8．一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(0,0,0)，(3,0,3)，(0,3,3)，(3,2,0)，若以yOz 为投影面画出该三棱锥的正视图，则得到的正视图为（）（A ）（B ）（C ）（D ）9．设l ，m ，n 是三条不同的直线，α，β是两个平面，则下列命题不．正确．．的是( )（A ）若,m n 是两条异面直线，l m ⊥，l n ⊥，n α⊂，m β⊂且α∥β，则l α⊥ （B ）若,m n 是两条异面直线，n α⊂，m β⊂，m ∥α且n ∥β，则α∥β （C ）若l ⊥α，l m ⊥，l n ⊥，n β⊂，m β⊂，则//αβ（D ）若//l α，l β⊂，m αβ= ，n α⊄，//n m ，则//l n10．已知区域2{(,)|04}x y y x Ω=≤≤-，函数2()()1x x af x a a a -=--，其中 0a >且1a ≠，集合2{0|(1)(1)0}A m f m f m =>-+-≤，区域{(,)M x y =∈Ω |2,}y mx m m A =+∈，向区域Ω上随机投一点P ，点P 落在区域M 内的概率()P M =( )（A ）14ππ- （B ）22ππ- （C ）22π- （D ）14π-二、填空题：本大题共5小题，每个题5分，共25分．11．某班有男生30名，女生20名，采用分层抽样的方法从这50名学生中抽取一个容量为5的一个样本，则应抽取的男生人数为____________．12．阅读如图所示的程序，若输入的t 的值为6，则执行程序后输出的结果是________．INPUT t IF t<＝4 THEN c ＝0.2 ELSEc ＝0.2＋0.1*(t －3) END IF PRINT c END第12题图第14题图 13．三棱柱ABC A B C -111中，上、下两底面共有111111,,,,,AB BC CA A B B C C A 六条棱，从中任选两条棱，它们所在直线是异面直线的概率为_________．14．如图，四面体PABC 四顶点P 、A 、B 、C 均落在球O 的球面上，且2AC BC ==，90ACB ∠= ，AP BP AB ==，PC AC ⊥．那么球O 的体积是____________．ACBP15．如图，正方体 1111D C B A ABCD -，棱长为a ，有下列命题： ①P 点在BDC ∆1所在平面上运动，棱锥11D AB P -体积不变；②若点M N L 、、分别是线段A B A D A A 11111、、上与端点不重合的三个动点，则MNL ∆必为锐角三角形；③若Q 为AA 1的中点，G 为底面A B C D 1111（包含边界）内的一个动点，且始终满足GQ A C ⊥1，则动点G 的轨迹长度为23a ； ④若垂直于1AC 的平面α由点1A 移动至点C ，则截正方体得到的多边形只能是三角形或六边形，且所得多边形面积和周长的最大值分别为233324a a 和. 其中下正确的命题有_________．（写出所有正确命题的序号）三、解答题：本大题共6小题，共75分．解答过程应写明文字说明、证明过程或推演步骤．16．（本小题满分12分）如图，棱长为1的正方体ABCD -A 1B 1C 1D 1中．（Ⅰ）求异面直线1A D 与AC 所成角的大小；（Ⅱ）求证：平面1ACB ⊥平面11BB D D ．17．（本小题满分12分）袋中共有6个除颜色以外完全相同的小球，其中有标记为A ，B 的红球2个，标记为a ，b ，c ，d 的白球4个，若从中任意选取2个球．（Ⅰ）记{,}A a （不考虑顺序）为一种选取结果，试写出所有选取结果，并指出所有结果的个数；（Ⅱ）试求所选的两个球中至少有一个红球的概率．ABCDD 1C 1B 1A 1QG第15题图BD 1C 1 B 1A 1CDA第16题图18．（本小题满分12分）如图，在四棱柱1111A B C DA B C D -中，底面A B C D是平行四边形，其中111111A A A D A B ===，111160AA D AA B ∠=∠=︒，1111D A A B ⊥，点M 在11A B 上，且112AM MB =，N 为1AD 中点．（Ⅰ）若11A B ＝a ，11A D ＝b ，1A A＝c ，试用a ，b ，c 表示MN ；（Ⅱ）求线段MN 的长．19．（本小题满分12分）教育部、国家体育总局和共青团中央共同号召全国各级各类学校要广泛、深入地开展全国亿万大中学生阳光体育运动．为此，某校学生会对高二年级学生2013年6月这一个月时间内参加体育运动的情况进行统计，随机抽取了M 名学生作为样本，得到这M 名学生该月参加体育运动总时间的小时数．根据此数据作出了频数与频率的统计表和频率分布直方图（如图①）如下：分组序号 2013年6月参加体育运动总时间（小时）组中值（i a ）频数频率()i f1 [20,25)22.5 10 0.252 [25,30) 27.5 25n 3 [30,35) 32.5 mp4 [35,40)37.5 2 0.05合计——M1D 1C 1B 1A 1N A DBCM第18题图a频率/组距2025303540参加体育运动小时数O（Ⅰ）求出表中M ，p 及图①中a 的值；（Ⅱ）现以这M 人为样本来估计总体，若该校高二学生有720人，试估计该校高二学生在2013年6月参加体育运动总时间不超过30小时的人数；（Ⅲ）该校数学兴趣小组利用算法流程（如图②），对样本数据作进一步统计分析，求输出的S 的值．20．（本小题满分13分）将图①所示的直角梯形ABEF （图中数字表示对应线段的长度）沿直线CD折成直二面角，连接部分线段后围成一个空间几何体，如图②所示．（Ⅰ）证明：BE ∥平面ADF ；（Ⅱ）求平面BEF 与平面ABCD 所成锐二面角的正切值；（Ⅲ）求空间几何体ABCDFE 的表面积．第20题图第19题图图②图①图②图①21．（本小题满分14分）如图，在四面体A BCD -中，AD ⊥平面BCD ，BC CD ⊥，2AD =，22BD =．M是AD 的中点，P 是BM 的中点．（Ⅰ）若45BDC ∠=︒，求直线CD 与平面ACB 所成角的大小；（Ⅱ）若二面角C BM D --的大小为60︒，求BDC ∠的大小；（Ⅲ）若CD x =，对任意[1,2]x ∈，则线段BD 上是否存在点E ，使得平面CPE ⊥平面CMB ？若存在，设BE y =，试写出y 关于x 的函数表达式，并求出y 的最大值；若不存在，说明理由．第21题图。

四川省成都七中2020-2021学年上学期高二10月阶段性考试物理试卷 (含答案)

物理试题考试时间：100分钟满分：110分一、单项选择题（本题包括8个小题，每小题3分，共24分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的。

）1．下列说法正确的是( )A ．根据电场强度的定义式E ＝F q，可知电场中某点的电场强度和试探电荷的电荷量成反比 B ．根据电容的定义式C ＝Q U，可知电容器的电容与极板所带电荷量成正比 C ．根据真空中点电荷的电场强度公式E ＝k Q r 2，可知电场中某点的电场强度与场源点电荷所带电荷量成正比D ．根据电势差的定义式U AB ＝W AB q，可知电场中A 、B 两点间的电势差与将试探电荷从A 点移动到B 点电场力做的功成正比 2．某电场的电场线分布如图中实线所示，以下说法正确的是() A ．b 点场强大于c 点场强B ．b 、c 两点电势相等C ．电子在b 点的电势能大于在c 点的电势能D ．若某点电荷只在电场力作用下沿虚线由 a 点运动到d 点，则该电荷必带正电3．如图所示，在粗糙绝缘的水平地面上放置一带正电的物体甲，现将另一个也带正电的物体乙沿着以甲为圆心的竖直平面内的圆弧由M 点缓慢移动到N 点，若此过程中甲始终保持静止，甲、乙两物体可视为质点，则下列说法正确的是( )A ．乙的电势能先增大后减小B ．甲对地面的压力先增大后减小C ．甲受到地面的摩擦力不变D ．甲受到地面的摩擦力先增大后减小4．如图所示，由两块相互靠近的平行金属板组成的平行板电容器的极板N 与静电计相接，极板M 接地。

用静电计测量平行板电容器两极板间的电势差U 。

在两板相距一定距离d 时，给电容器充电，静电计指针张开一定角度。

在整个实验过程中，保持电容器所带电量Q 不变，下面哪些操作将使静电计指针张角变小( ) A ．将M 板向下平移B ．将N 板向上平移C ．在M 、N 之间插入云母板（介电常数ε>1）D ．将M 板沿水平向左方向远离N 板5．空间P 、Q 两点处固定电荷量绝对值相等的点电荷，其中Q 点处为正电荷，P 、Q 两点附近电场的等势线分布如图所示，a 、b 、c 、d 、e 为电场中的5个点，设无穷远处电势为0，则() A ．e 点的电势大于0 B ．a 点和b 点的电场强度相同C ．b 点的电势等于c 点的电势D ．负电荷从a 点移动到d 点时电势能增加N 静电计四川成都七中2020-2021学年度上学期高二10月阶段性考试11．如图所示，两块水平放置的平行正对金属板a 、b 与电池相连，在距离两板等远的M 点有一个带电液滴处于静止状态。

成都市2021-2021学年高二上期期末调研考试数学试题(word)

四川省成都市2021-2021学年高二上学期期末学业质量监测数学(理)试题（时间120分钟，满分150分）第Ⅰ卷（选择题，共 50 分）一、选择题：（本大题共10小题，每小题5分，满分50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．某校开设街舞选修课程，在选修的学生中，有男生28人，女生21人，若采用分层抽样的方法从中抽出一个容量为14的样本，则应抽取的女生人数为（） A ．9 B ．8 C ．7 D ．62．已知向量m 同时垂直于不共线向量a 和b ，若向量2n a b =+，则（）A ．//m nB ．m n ⊥C ．m 和n 既不平行也不垂直D ．以上三种情况都有可能 3．设,,m n l 是空间中三条不重合的直线，则下列命题中正确的是（）A ．若//,m n n l ⊥，则m l ⊥B ．若,m n n l ⊥⊥，则//m lC ．若,m n 共面，n 于l 共面，则m 于l 共面D ．若,m n 异面，n 于l 异面，则m 于l 异面 4．如图所示的程序是计算函数()y f x =函数值的程序，若输入的x 值为4，则输出的y 值为（）A ．17B ．3C ．3-D ．17-5．如图，在正方体1111ABCD A B C D -中，棱长2AB =，点E 是棱11C D 的中点，则异面直线1B E 和1BC 所成角的余弦值为（）A ．155B ．105C ．1510D ．10107．如图是某城市的一个艺术雕塑几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．264B ．228C ．192D ．1568．某设备的使用年限x 与所支出的维修费用y 的统计数据如下表：根据上表可得回归直线方程为：^^0.8y x a =+，据此模型预测，若使用年限为8年，估计维修费用约为A ．10.2万元B ．10.6万元C ．11.2万元D ．11.6万元9．如图，在二面角AB αβ--的棱上有,A B 两点，直线,AC BD 分别在这个二面角的两个半平面内，且都垂直于AB ，已知4,6,8,217AB AC BD CD ====，则直线CD 与平面α所成角的正弦值为（） A ．69734 B ．35164 C ．69764 D ．3513410．用随机数模拟的方法估计圆周率π的值的程序框图如图所示，P 表示输出的结果，则图中空白框应填（）A ．100MP = B ．600MP = C ．100NP = D ．600N P =第II 卷（非选择题，共 100 分）二．填空题：（本大题共5小题，每小题5分，共25分，把答案填在题中横线上。

四川省成都市2020-2021学年高二英语上学期期末调研考试试题

四川省成都市2020-2021学年高二英语上学期期末调研考试试题本试卷分选择题和非选择题两部分。

第I卷（选择题）1至8页，第Ⅱ卷（非选择题9至10页，共10页，满分150分，考试时间120分钟。

注意事项：1.答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3.答非选择题时，必须使用0. 5毫米黑色笔迹的签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

5.考试结束后，只将答题卡交回。

第I卷（100分）第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题;每小题1.5分，满分7. 5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. Who will come to the party?A. The man.B. The woman.C. Barry.2. How does the woman feel?A. Unsure.B. Confident.C. Anxious.3. What are the speakers mainly talking about?A. The local area.B. Coffee shops.C. The weekend plan.4. What does the man suggest?A. Taking more photos.B. Admiring the scenery.C. Continuing travelling.5. Where did Samantha go?A. A museum.B. A concert.C. A cinema.第二节（共15小题;每小题1. 5分，满分22. 5分）听下面5段对话或独白。