第二章 滤波器
合集下载
卡尔曼滤波器

Ak (xk1 xˆk1 H kCk Ak (xˆk1 xk1) k1 H kCk Akk1 H k vk
(I H kCk ) Ak (xk1 xˆk1) (I H kCk )k1 H k vk
(I H kCk ) Ak (xk1 xˆk1) k1 H kvk
(2.5.17)
精品文档
第二章 维纳滤波和卡尔曼滤波
所以(xˆskuǒ1yǐ) 仅依赖于xk-1,vk-1,而与vk不相关,即 E[(xk1 xˆk1)vkT ] E[vk (xk1 xˆk1)T ] 0 (2.5.18)
E[(xk1 xˆk1)kT1] E[k1(xk1 xˆk1)T ] 0 (2.5.19)
(2.5.24)
令
U T (Pk'CkT )T Ck Pk'T Ck Pk'
(2.5.25)
精品文档
第二章 维纳滤波和卡尔曼滤波
定义:设A∈Cn×n是Hermite矩阵,如果对任意0≠x∈Cn,都有 xHAx>0,则A是Hermite正定阵; 若xHAx≥0,则A是Hermite半正定阵.
定理(dìnglǐ):设A∈ Cn×n 是Hermite矩阵,则下列条件等价 (1)A是Hermite矩阵,AH=A (2)A的特征值全为正实数 (3)存在矩阵P ∈Cn×n,使得A=PHP
(3) 卡尔曼滤波采取的误差准则仍为估计误差的均方值最小。
精品文档
第二章 维纳滤波和卡尔曼滤波 2.5.1 卡尔曼滤波的状态方程(fāngchéng)和量测方程(fāngchéng)
假设某系统k时刻的状态变量为xk,状态方程(fāngchéng)和量 测方程(fāngchéng)(也称为输出方程(fāngchéng))表示为
LC带通滤波器的设计与仿真设计毕业设计(论文)

1.3.2 国内外投入滤波器产业概况................................6
1.3.3 滤波器的前景....................................................7
1.3.4几种新型滤波器介绍..........................................8
●阻带滤波器:它的阻带限定在两个有限频率ƒ1与ƒ2之间,阻带两侧都有通带。
1.1.2 滤波器的种类
根据使用的波段和元件的不同,滤波器有很多种类,而且随着技术的发展,种类还在不断增加。总的来说,滤波器可分为两大类:无源滤波器和有源滤波器。
在无源滤波器中,所使用的是无源元件。他们在个体或组合的情况下,能够把一种形式的能量变换为另一种形式,并重新变回到原来的形式,换言之,它们必须是谐振性的。例如,在一个LC谐振电路中,在电容器的电场和电感线圈的磁场之间不断发生着能量的反复交换。因此,如果两个不同储能装置当相互偶合时,能够以很小的损耗实现能量的交换,它们就可以被利用为滤波器元件。
结束语.................................................................................43
致谢....................................................................................45
摘要
随着电子信息的发展,滤波器作为信号处理的不可缺少的部分,也得到了迅速的发展。LC滤波器作为滤波器的一个重要组成部分,它的应用相当的广泛。因此对于它的设计也受到人们的广泛关注。如何设计利用简单的方法设计出高性能的LC滤波器是人们一直研究的课题。
1.3.3 滤波器的前景....................................................7
1.3.4几种新型滤波器介绍..........................................8
●阻带滤波器:它的阻带限定在两个有限频率ƒ1与ƒ2之间,阻带两侧都有通带。
1.1.2 滤波器的种类
根据使用的波段和元件的不同,滤波器有很多种类,而且随着技术的发展,种类还在不断增加。总的来说,滤波器可分为两大类:无源滤波器和有源滤波器。
在无源滤波器中,所使用的是无源元件。他们在个体或组合的情况下,能够把一种形式的能量变换为另一种形式,并重新变回到原来的形式,换言之,它们必须是谐振性的。例如,在一个LC谐振电路中,在电容器的电场和电感线圈的磁场之间不断发生着能量的反复交换。因此,如果两个不同储能装置当相互偶合时,能够以很小的损耗实现能量的交换,它们就可以被利用为滤波器元件。
结束语.................................................................................43
致谢....................................................................................45
摘要
随着电子信息的发展,滤波器作为信号处理的不可缺少的部分,也得到了迅速的发展。LC滤波器作为滤波器的一个重要组成部分,它的应用相当的广泛。因此对于它的设计也受到人们的广泛关注。如何设计利用简单的方法设计出高性能的LC滤波器是人们一直研究的课题。
有源电力滤波器使用说明书

3.4.1 滤除谐波...................................................................................................................................6 3.4.2 补偿无功...................................................................................................................................6 3.5 APF 有源电力滤波器性能....................................................................................................................7 3.5.1 电气性能...................................................................................................................................7 3.5.2 保护功能:...............................................................................................................................7 第四章.APF 有源电力滤波器的组成和功能.....................................................................................
信号检测与估计 第二章 匹配滤波
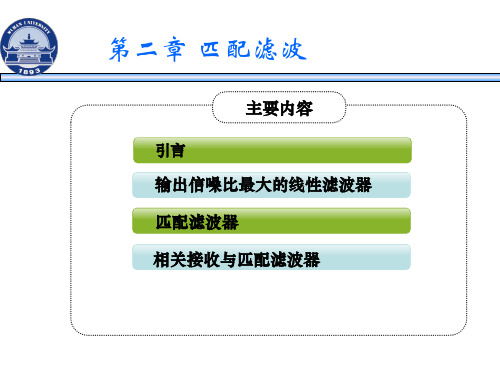
jt1
代表一个雷达回波信号,α及τ 是未知的参量或随机变量
S 1 ( ) a S ( ) e
j ( t1 )
j
caS ( )e
aH ( )e
j t1 ( t0 )
t1与to在输入信号结束后可以任选,如果取t1 = to+τ
H 1 ( ) a H ( )
2 j ( t t0 )
j t
d d
j arg H ( ) arg S ( ) t
e
d
arg H ( )
补偿了输入信号的
arg S ( )
§2.3
匹配滤波器
滤波器内部和外部产生的随机噪声(可等效为系统输入端 的噪声), 其功率谱宽度往往大于系统的通频带。
H ( ) Gn ( ) d
2
S ( )
2
Gn ( )d来自A ( ) H ) G n ( ) e (
j t 0
cB ( ) c
*
S ( )
*
G n ( )
H ) c (
S ( )
*
G n ( )
e
j t 0
输出波形
最大输出信噪比
*
G n ( )
e
j t 0
arg H ( ) arg S ( ) t 0
第一项与信号相频特性反相 第二项与频率成线性关系
s0 (t ) 1 2 1 2 1 2
H )()e ( S H )() ( S e S ( ) Gn ( )
取t0=(L-1)T+τ,令
H 1 ) cS1 ( )e (
代表一个雷达回波信号,α及τ 是未知的参量或随机变量
S 1 ( ) a S ( ) e
j ( t1 )
j
caS ( )e
aH ( )e
j t1 ( t0 )
t1与to在输入信号结束后可以任选,如果取t1 = to+τ
H 1 ( ) a H ( )
2 j ( t t0 )
j t
d d
j arg H ( ) arg S ( ) t
e
d
arg H ( )
补偿了输入信号的
arg S ( )
§2.3
匹配滤波器
滤波器内部和外部产生的随机噪声(可等效为系统输入端 的噪声), 其功率谱宽度往往大于系统的通频带。
H ( ) Gn ( ) d
2
S ( )
2
Gn ( )d来自A ( ) H ) G n ( ) e (
j t 0
cB ( ) c
*
S ( )
*
G n ( )
H ) c (
S ( )
*
G n ( )
e
j t 0
输出波形
最大输出信噪比
*
G n ( )
e
j t 0
arg H ( ) arg S ( ) t 0
第一项与信号相频特性反相 第二项与频率成线性关系
s0 (t ) 1 2 1 2 1 2
H )()e ( S H )() ( S e S ( ) Gn ( )
取t0=(L-1)T+τ,令
H 1 ) cS1 ( )e (
(中文)第二章 卡尔曼滤波器

两个步骤递归计算就构成了最优的贝叶斯估计。遗憾的是,式和在很多场合
下没有可分解的计算方法,所以它们只是一个理论上的解。基于特定分布的
假设,如高斯分布可以获得最优估计的解析的计算方法 。
卡尔曼滤波
卡尔曼滤波器认为后验概率在任何时刻都是高斯分布的,这样由均
值和方差就可以完全确定其概率分布。可以证明,如果 p xk1 | z1:k1 是高 斯的,那么要使 p xk | z1:k 也是高斯的话,隐含了下面的假设:
结构框图
计算步骤
Pn a2 n 1 Q
Gn
R
cPn c2Pn
n 1 cGn Pn
sˆn n a sˆn 1n 1Gnxn acsˆn 1n 1
Initiation sˆ00,0 P1 G1 1, sˆ11
信号矢量:例1
(同时估计若干个信号)
si n aisi n 1 wi n , i 1, 2, , q
2.2 维纳滤波器的迭代实现
信号模型和测量模型: sn asn 1 wn xn csn vn
因果IIR维纳滤波器 (前面推导结果):
sˆ n n , sˆ n n 1 , xˆ n n 1
分别代表用n时刻以及n-1时刻及以 前所有数据对s(n)和x(n)的估计值
迭
代
差分方程
形
sˆn n f sˆn 1n 1Gnxn
使用观察值更新预测(求后 验分布均值)
mk|k mk|k1 Kk zk Hk mk|k 1
求估计误差功率(求后验分 布方差)
Pk|k Pk|k 1 Kk Hk Pk|k 1
初始估计:m0|0 P0|0
2.4 卡尔曼滤波器扩展(非线性)
1。Extended Kalman Filter(EKF)
现代电路基础理论第二章二阶有源RC滤波器

非理想网络函数 H ~( s ) H ( s ) H ( s ) H ( s ) ( 1 H ( s )) H ( s )
三、同相放大器
运放的增益为A(s),则
Vn (s)
Vo (s) R1 R2
R2
V o(s)A (s)[V i(s) V n(s)]
Vo(s)[1R A 1 (s )R R2 2]A(s)Vi(s)
s
2 p
当z p时,幅频特性具有性对。称 当p z时,低通陷波;p 当z时,
高通陷波。
5.全通滤波器 AP
H(s)=H0
D(s) D(s)
二阶 AP
H
(s)
s2 s2
p
Q
p
Q
s s
2 p
2 p
2arD g (j) 2arc Q t a p 2 p n 2
第三节 运算放大器
2.2 按所处理信号:
➢ 按所处理的信号:模拟滤波器和数字滤波器。
➢ 数字滤波器:与模拟滤波器相对应,在离散系统中广泛应用数字滤 波器。它的作用是利用离散时间系统的特性对输入信号波形或频率 进行加工处理。
➢按所通过信号的频段:低通、高通、带通、带阻和全通滤 波器。
➢低通滤波器(low-pass filter)是容许低于截至频率的信号通过, 但 高于截止频率的信号不能通过的电子滤波装置。 ➢高通滤波器(High-pass filter)是容许高于截至频率的信号通过, 但 低于截止频率的信号不能通过的电子滤波装置。 ➢带通滤波器(Band-pass filter)是容许非零起始频率特定有限范围内 的信号通过, 但通带两侧的信号受到抑制的电子滤波装置。 ➢阻带滤波器(Band-reject filter)是让一定频率范围内的信号受到抑制, 但高于和低于这一频率范围外的信号通过的电子滤波装置。
三、同相放大器
运放的增益为A(s),则
Vn (s)
Vo (s) R1 R2
R2
V o(s)A (s)[V i(s) V n(s)]
Vo(s)[1R A 1 (s )R R2 2]A(s)Vi(s)
s
2 p
当z p时,幅频特性具有性对。称 当p z时,低通陷波;p 当z时,
高通陷波。
5.全通滤波器 AP
H(s)=H0
D(s) D(s)
二阶 AP
H
(s)
s2 s2
p
Q
p
Q
s s
2 p
2 p
2arD g (j) 2arc Q t a p 2 p n 2
第三节 运算放大器
2.2 按所处理信号:
➢ 按所处理的信号:模拟滤波器和数字滤波器。
➢ 数字滤波器:与模拟滤波器相对应,在离散系统中广泛应用数字滤 波器。它的作用是利用离散时间系统的特性对输入信号波形或频率 进行加工处理。
➢按所通过信号的频段:低通、高通、带通、带阻和全通滤 波器。
➢低通滤波器(low-pass filter)是容许低于截至频率的信号通过, 但 高于截止频率的信号不能通过的电子滤波装置。 ➢高通滤波器(High-pass filter)是容许高于截至频率的信号通过, 但 低于截止频率的信号不能通过的电子滤波装置。 ➢带通滤波器(Band-pass filter)是容许非零起始频率特定有限范围内 的信号通过, 但通带两侧的信号受到抑制的电子滤波装置。 ➢阻带滤波器(Band-reject filter)是让一定频率范围内的信号受到抑制, 但高于和低于这一频率范围外的信号通过的电子滤波装置。
有源电力滤波器

为克服无源滤波器的缺点,人们做了大量研究与实践,其中具有代表意 义的为有源电力滤波技术。从国内外目前的使用情况来看,有源电力滤波器 将是以后进行谐波消除和无功补偿的一个重要发展方向。
1.2 有源电力滤波器的特点
与无源滤波器不同,有源电力滤波器(ActivePowerFilter:APF)为一种能够 动态消谐波并且可以补偿无功的电力电子设备,其完全可以消除频率与幅值都 变化的谐波和无功,同时能够弥补PPF的不足,而且能够得到比PPF更好的补 偿效果。
无源滤波器具有如下缺点: (1)只能滤除特定次谐波,且滤波特性受系统参数的影响较大,易和系统发生 并联谐振,导致谐波放大,降低系统的稳定性。 (2)由于电网的阻抗和谐波频率随着电力系统的运行状况不断发生改变,而滤 波特性又过于依赖电网参数,所以给LC参数的设计带来了麻烦。 (3)滤波要求和无功补偿要求有时难以同时满足要求。 (4)LC可能会与电网阻抗发生串联谐振,而电网中的某次谐波电压可能使无 源电力滤波装置中产生较大的谐波电流。 (5)消耗较多的有效材料,增大了体积。
因此串联有源电力滤波器作用:动态调节电压即补偿系统电压的快速升 降,还可以补偿系统谐波,系统电压畸变与不对称等功能。
2.2 并联型有源电力滤波器的基本拓扑结构
AC
图3并联型有源电力滤波器的基本拓扑结构
并联型有源电力滤波器与系统并联等效为一个受控电流源,如图3所示。 有源滤波器向系统注入与谐波电流大小相等方向相反的电流,从而达到滤波 的目的。并联型有源电力滤波器主要适用于电流源型感性负载的谐波补偿, 技术上已相当成熟,工业上已投入使用的有源电力滤波器多采用此方
如图1所示有源滤波器与无源滤波器结构图
无源滤波器
有源电力滤波器
图1有源滤波器与无源滤波器结构
1.2 有源电力滤波器的特点
与无源滤波器不同,有源电力滤波器(ActivePowerFilter:APF)为一种能够 动态消谐波并且可以补偿无功的电力电子设备,其完全可以消除频率与幅值都 变化的谐波和无功,同时能够弥补PPF的不足,而且能够得到比PPF更好的补 偿效果。
无源滤波器具有如下缺点: (1)只能滤除特定次谐波,且滤波特性受系统参数的影响较大,易和系统发生 并联谐振,导致谐波放大,降低系统的稳定性。 (2)由于电网的阻抗和谐波频率随着电力系统的运行状况不断发生改变,而滤 波特性又过于依赖电网参数,所以给LC参数的设计带来了麻烦。 (3)滤波要求和无功补偿要求有时难以同时满足要求。 (4)LC可能会与电网阻抗发生串联谐振,而电网中的某次谐波电压可能使无 源电力滤波装置中产生较大的谐波电流。 (5)消耗较多的有效材料,增大了体积。
因此串联有源电力滤波器作用:动态调节电压即补偿系统电压的快速升 降,还可以补偿系统谐波,系统电压畸变与不对称等功能。
2.2 并联型有源电力滤波器的基本拓扑结构
AC
图3并联型有源电力滤波器的基本拓扑结构
并联型有源电力滤波器与系统并联等效为一个受控电流源,如图3所示。 有源滤波器向系统注入与谐波电流大小相等方向相反的电流,从而达到滤波 的目的。并联型有源电力滤波器主要适用于电流源型感性负载的谐波补偿, 技术上已相当成熟,工业上已投入使用的有源电力滤波器多采用此方
如图1所示有源滤波器与无源滤波器结构图
无源滤波器
有源电力滤波器
图1有源滤波器与无源滤波器结构
维纳滤波

(1894~1964) 维纳9岁小学毕业
表了一篇关于集合论的论文,将关系的理论 简化为类的理论的论文,在数理逻辑的发展 中占据一席之地。1919年维纳到麻省理工学 院数学系任教直至退休。1932年任正教授。
不満12岁中学毕业。 提出维纳滤波理论,开创了维纳信息论,创
立控制论。第二次世界大战期间,为了解决
第二章 维纳(Wiener)滤波
维纳生平
18岁获哈佛大学哲学博士学位。先后留学英 国剑桥大学和德国哥丁根大学,在罗索、哈 代、希尔伯特等著名数学家指导下研究逻辑 和数学。
罗索鼓励维纳选择把数学和物理、工程学结 合起来的研究方向。
1913年19岁维纳在<剑桥哲学学会会刊>发
N.维纳 (Norbert Wiener )
维纳滤波不能实时处理,其最大缺点是: 仅适用于一维平稳随机信号。这是由于 采用频域设计法所造成的。
因此,人们逐渐转向在时域内直接设计 最佳滤波器的方法。
11、维纳滤波器的应用
(1)通信的信道均衡器 (2)系统辨识 (3)最优线性预测
(1)通信的信道均衡器
在通信系统中,为了在接收器端补偿信 道传输引入的各种畸变,在对接收信号 进行检测之前,通过一个滤波器对信道 失真进行校正,这个滤波器称为信道均 衡器。
防空火力控制和雷达噪声滤波问题,1942年
建立维纳滤波理论。
本章内容
维纳滤波器的时域解 维纳滤波器的Z域解 维纳滤波器的预测器
第一节 引言
1、线性最佳滤波
滤波理论是估计理论的一个重要组成部分。 最佳线性估计理论:维纳滤波和卡尔曼滤波
理论,即:在线性滤波的前提下,以最小均 方误差为最佳准则。 采用最小均方误差准则的原因:其理论分析 比较简单,且可得到解析的结果。
表了一篇关于集合论的论文,将关系的理论 简化为类的理论的论文,在数理逻辑的发展 中占据一席之地。1919年维纳到麻省理工学 院数学系任教直至退休。1932年任正教授。
不満12岁中学毕业。 提出维纳滤波理论,开创了维纳信息论,创
立控制论。第二次世界大战期间,为了解决
第二章 维纳(Wiener)滤波
维纳生平
18岁获哈佛大学哲学博士学位。先后留学英 国剑桥大学和德国哥丁根大学,在罗索、哈 代、希尔伯特等著名数学家指导下研究逻辑 和数学。
罗索鼓励维纳选择把数学和物理、工程学结 合起来的研究方向。
1913年19岁维纳在<剑桥哲学学会会刊>发
N.维纳 (Norbert Wiener )
维纳滤波不能实时处理,其最大缺点是: 仅适用于一维平稳随机信号。这是由于 采用频域设计法所造成的。
因此,人们逐渐转向在时域内直接设计 最佳滤波器的方法。
11、维纳滤波器的应用
(1)通信的信道均衡器 (2)系统辨识 (3)最优线性预测
(1)通信的信道均衡器
在通信系统中,为了在接收器端补偿信 道传输引入的各种畸变,在对接收信号 进行检测之前,通过一个滤波器对信道 失真进行校正,这个滤波器称为信道均 衡器。
防空火力控制和雷达噪声滤波问题,1942年
建立维纳滤波理论。
本章内容
维纳滤波器的时域解 维纳滤波器的Z域解 维纳滤波器的预测器
第一节 引言
1、线性最佳滤波
滤波理论是估计理论的一个重要组成部分。 最佳线性估计理论:维纳滤波和卡尔曼滤波
理论,即:在线性滤波的前提下,以最小均 方误差为最佳准则。 采用最小均方误差准则的原因:其理论分析 比较简单,且可得到解析的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高 频 电 子 线 路
并联谐振回路的相对幅频特性和相对相频特性
v ( )
1 Q2 ( 1
1 1/ 2
0 )2 0
Q1>Q2 Q1 Q2
0 v ( ) arctgQ ( ) 0
Q1>Q2 Q1 0 Q2
/2
-/2 0
0 B
Q值增大→选择性更好
13
高 频 电 子 线 路
2.3.1 LC串、并联谐振回路
• 阻抗特性(导纳特性)。 • 谐振特性和回路谐振频率。 • 频率特性(幅频特性与相频特性)。 (什么是谐波抑制度 ϒ ) • 信号源和负载特性。 (包括阻抗变换电路)
14
高 频 电 子 线 路
LC串并联谐振回路
LC谐振回路是最简单也是最基本的LC滤波器电路。 并联谐振回路 L • 储能元件(电感和电容)并联 Ig CV o • 电流驱动,电压输出 R • 传输函数具有阻抗的量纲
< 0 ,呈容性 > 0 ,呈感性
高 频 电 子 线 路
27
3.谐振特性
并联回路谐振时,流过其电抗支路的电流IL、 IC 比激励电流Ig大Q倍,故并联谐振又称电流谐 振。所以品质因数 Q 易测量。
并联谐振时(
Q值很高),输出最大电压:
Vo max ( jo ) I g ( jo ) RP
延时信号:
x1 (t ) A cos1 (t ) x(t ) A cos (t )
附加相移:
延时量:
/
5
高 频 电 子 线 路
系统的相位延时与群延时
系统传输函数: H ( j ) H ( j ) e j ( )
一个角频率为ω 的正弦信号) ( Z P j) ( j ) Ig
串联谐振回路:电压驱动,电流输出
1 V s ( j ) Z (j)
R
Io
L
I o ( j )
VS
C
15
高 频 电 子 线 路
自由振荡现象:R、L、C电路具有自由振荡现象。
C2
V+
V1 = 0 V2 = 1 TD = 0 TR = 0 TF = 0 PW = 100u PER =
V1 R1
di 1 L Ri idt 0 dt C
1)R=0,等幅振荡; 2)R<0,增幅振荡; L 2 3)R>0,减幅振荡( R< ); C L 4)R> 2 ,没有振荡。
C
V-
L1 1 2
1.0V
0
0.5V
0V 0s V(C2:1,0) Time 40us 80us 120us 160us 200us
P
R 1 1 ( s )2 0 1 2 LC L Q
0
1 LC 为回路无阻尼振荡角频率。
当 Q >>1 时:
P 0
回路空载(固有)品质因数 Q (易测量) 意义:表征回路谐振过程中一个周期的电抗元 件的储能与电阻元件耗能状况的比值。
1 Q Rs
L 0 L 1 C Rs 0CRs
1 RS 1 1 1 P 1 o 1 2 1 L LC L LC Q 2 RS C
2
其中
o
1 LC
Q
1 RS
L o L 1 C RS oCRS
22
Vo max I g ( j p ) RP
高 频 电 子 线 路
回路谐振角频率: P
Rs
23
特性阻抗 :
L 1 0 L C 0C
高 频 电 子 线 路
Ig
ZP( j) R s
Ig
L
C
ZP ( j) RP
IL L
IC
C
使网络阻抗(ZP(jω))相等进行等效
RP (1 Q ) RS Q 2 RS
2 Q 1
Q 1 1 (1 )L L 2 Q
Vo ( j ) 1 v ( j ) 0 Vo ( j 0 ) 1 jQ ( )
0
v ( )
Vo ( j ) Vo ( j 0 )
1 1 Q2 (
0 )2 0
29
0 v ( ) arctgQ ( ) 0
18
高 频 电 子 线 路
3)R<0,增幅振荡
40
20
0
-20 0s V(C2:1,0) 20us I(C2) 40us Time 60us 80us 100us 110us
19
高 频 电 子 线 路
4)R> 2
1.0
L C
,没有振荡。
0.5
0
-0.5 0s V(C2:1,0) I(C2) Time 50us 100us 150us 200us
16
高 频 电 子 线 路
1)R=0,等幅振荡
1.0
0.5
0
-0.5 0s V(C2:1,0) I(C2) Time 50us 100us 150us 200us
0
1 LC 为回路自然角频率。
17
高 频 电 子 线 路
2)R>0,减幅振荡( R<
2
L C
)
1.0
0.5
0
-0.5 0s V(C2:1,0) I(C2) Time 50us 100us 150us 200us
2.2.2 滤波器的分类
按其幅频特性可分为: 低通(LPF)、高通(HPF)、带通(BPF) 和带阻(BEF)滤波器。
9
高 频 电 子 线 路
按其所用器件的特点可分为无源和有源滤波器。
无源滤波器:由无源器件构成。 电阻,电感和电容组成的RLC滤波器。
晶体滤波器是利用石英晶体薄片构成。 声表面波滤波器(SAW):利用压电效应构成的。 有源滤波器:指在所构成的滤波器中,除无源器件外 还含有放大器等有源电路。
25
高 频 电 子 线 路
并联回路的阻抗特性
Z ( j )
p()
RP
2
o
o
2
= 0 ,呈纯电阻且阻值最大
> 0 ,呈容性 < 0 ,呈感性
高 频 电 子 线 路
26
串联回路的阻抗特性
Z ( j )
p()
2
RP
p()
o
o
2
= 0 ,呈纯电阻且阻值最小
RC有源滤波器(含有运算放大器)。 开关电容滤波器(SCF)。
按处理的信号形式可分为模拟滤波器,数字滤 波器和抽样数据滤波器等。
10
高 频 电 子 线 路
滤波器按幅度频率特性可分为:低通,高通,带通 和带阻滤波器 H ( j ) H ( j ) 低通
1
1
高通
0
H ( j ) 1 带通
p 0
目录
高 频 电 子 线 路
3
2.2.1滤波器的特性
V(s) 输入 i vi (t) 阻抗
滤波器
h(t) ,H(s)
输出 Vo ( s) 阻抗 v0 (t )
时域特性: vo (t ) h( )vi (t )d 复频域传输函数:
Vo ( s ) N ( s ) b0 s m b1 s m 1 bm H ( s) n Vi ( s ) D( s ) s a1 s n1 a n
Q值增大→斜率的绝对值增大
30
单位谐振曲线可表示选择性好坏。
高 频 电 子 线 路
串联谐振回路的相对幅频特性和相对相频特性
i ( j )
i ( )
1 Q2 (
I o ( j ) I o ( j 0 )
1
1 jQ (
1 1/ 2
0 )2 0
Q1>Q2 Q1 Q2
传输函数(传输阻抗)
1 Rs jL 1 s Vo ( j ) jC jC Z P ( j ) 1 1 I g ( j ) Rs jL RS j L jC C 谐振:
R
jL
– 回路电压与输入激励电流同相位 X ( j ) 0 P – 回路呈纯阻特性
LP
串联与并联回路Q值相同 o L 1 RP Q oCRP RS oCRS o L
24
高 频 电 子 线 路
2.并联回路端阻抗的模和相角随频率变化的关系为:
1 Z P ( j ) YP ( j )
RP
0 2 1 Q ( ) 0
2
0 P ( ) arctgQ( ) 0
0) 0 () arctgQ( 0 ) i 0
Q1>Q2 Q1 Q2
1
/2
0 -/2
0
0 B
Q值增大→选择性更好
Q值增大→斜率的绝对值增大
31
高 频 电 子 线 路
通频带(BW):当保持外加信号的幅值不变而改变其 频率时, 将并联回路端电压值(串联回路电流值)下降为 谐振值的 2 时对应的频率范围称为回路的通频带。 1
( ) p ( )
d ( ) g ( ) d
附加相移
一群不同频率的信号通过滤波器产生的延时 问题——群延时
6
高 频 电 子 线 路
群延时与线性失真
群延时描述的是一群不同频率的信号通过滤波器后 所产生的时间延迟,它是在指定频率范围内,相频特性 曲线在不同频率处的斜率。
并联谐振回路的相对幅频特性和相对相频特性
v ( )
1 Q2 ( 1
1 1/ 2
0 )2 0
Q1>Q2 Q1 Q2
0 v ( ) arctgQ ( ) 0
Q1>Q2 Q1 0 Q2
/2
-/2 0
0 B
Q值增大→选择性更好
13
高 频 电 子 线 路
2.3.1 LC串、并联谐振回路
• 阻抗特性(导纳特性)。 • 谐振特性和回路谐振频率。 • 频率特性(幅频特性与相频特性)。 (什么是谐波抑制度 ϒ ) • 信号源和负载特性。 (包括阻抗变换电路)
14
高 频 电 子 线 路
LC串并联谐振回路
LC谐振回路是最简单也是最基本的LC滤波器电路。 并联谐振回路 L • 储能元件(电感和电容)并联 Ig CV o • 电流驱动,电压输出 R • 传输函数具有阻抗的量纲
< 0 ,呈容性 > 0 ,呈感性
高 频 电 子 线 路
27
3.谐振特性
并联回路谐振时,流过其电抗支路的电流IL、 IC 比激励电流Ig大Q倍,故并联谐振又称电流谐 振。所以品质因数 Q 易测量。
并联谐振时(
Q值很高),输出最大电压:
Vo max ( jo ) I g ( jo ) RP
延时信号:
x1 (t ) A cos1 (t ) x(t ) A cos (t )
附加相移:
延时量:
/
5
高 频 电 子 线 路
系统的相位延时与群延时
系统传输函数: H ( j ) H ( j ) e j ( )
一个角频率为ω 的正弦信号) ( Z P j) ( j ) Ig
串联谐振回路:电压驱动,电流输出
1 V s ( j ) Z (j)
R
Io
L
I o ( j )
VS
C
15
高 频 电 子 线 路
自由振荡现象:R、L、C电路具有自由振荡现象。
C2
V+
V1 = 0 V2 = 1 TD = 0 TR = 0 TF = 0 PW = 100u PER =
V1 R1
di 1 L Ri idt 0 dt C
1)R=0,等幅振荡; 2)R<0,增幅振荡; L 2 3)R>0,减幅振荡( R< ); C L 4)R> 2 ,没有振荡。
C
V-
L1 1 2
1.0V
0
0.5V
0V 0s V(C2:1,0) Time 40us 80us 120us 160us 200us
P
R 1 1 ( s )2 0 1 2 LC L Q
0
1 LC 为回路无阻尼振荡角频率。
当 Q >>1 时:
P 0
回路空载(固有)品质因数 Q (易测量) 意义:表征回路谐振过程中一个周期的电抗元 件的储能与电阻元件耗能状况的比值。
1 Q Rs
L 0 L 1 C Rs 0CRs
1 RS 1 1 1 P 1 o 1 2 1 L LC L LC Q 2 RS C
2
其中
o
1 LC
Q
1 RS
L o L 1 C RS oCRS
22
Vo max I g ( j p ) RP
高 频 电 子 线 路
回路谐振角频率: P
Rs
23
特性阻抗 :
L 1 0 L C 0C
高 频 电 子 线 路
Ig
ZP( j) R s
Ig
L
C
ZP ( j) RP
IL L
IC
C
使网络阻抗(ZP(jω))相等进行等效
RP (1 Q ) RS Q 2 RS
2 Q 1
Q 1 1 (1 )L L 2 Q
Vo ( j ) 1 v ( j ) 0 Vo ( j 0 ) 1 jQ ( )
0
v ( )
Vo ( j ) Vo ( j 0 )
1 1 Q2 (
0 )2 0
29
0 v ( ) arctgQ ( ) 0
18
高 频 电 子 线 路
3)R<0,增幅振荡
40
20
0
-20 0s V(C2:1,0) 20us I(C2) 40us Time 60us 80us 100us 110us
19
高 频 电 子 线 路
4)R> 2
1.0
L C
,没有振荡。
0.5
0
-0.5 0s V(C2:1,0) I(C2) Time 50us 100us 150us 200us
16
高 频 电 子 线 路
1)R=0,等幅振荡
1.0
0.5
0
-0.5 0s V(C2:1,0) I(C2) Time 50us 100us 150us 200us
0
1 LC 为回路自然角频率。
17
高 频 电 子 线 路
2)R>0,减幅振荡( R<
2
L C
)
1.0
0.5
0
-0.5 0s V(C2:1,0) I(C2) Time 50us 100us 150us 200us
2.2.2 滤波器的分类
按其幅频特性可分为: 低通(LPF)、高通(HPF)、带通(BPF) 和带阻(BEF)滤波器。
9
高 频 电 子 线 路
按其所用器件的特点可分为无源和有源滤波器。
无源滤波器:由无源器件构成。 电阻,电感和电容组成的RLC滤波器。
晶体滤波器是利用石英晶体薄片构成。 声表面波滤波器(SAW):利用压电效应构成的。 有源滤波器:指在所构成的滤波器中,除无源器件外 还含有放大器等有源电路。
25
高 频 电 子 线 路
并联回路的阻抗特性
Z ( j )
p()
RP
2
o
o
2
= 0 ,呈纯电阻且阻值最大
> 0 ,呈容性 < 0 ,呈感性
高 频 电 子 线 路
26
串联回路的阻抗特性
Z ( j )
p()
2
RP
p()
o
o
2
= 0 ,呈纯电阻且阻值最小
RC有源滤波器(含有运算放大器)。 开关电容滤波器(SCF)。
按处理的信号形式可分为模拟滤波器,数字滤 波器和抽样数据滤波器等。
10
高 频 电 子 线 路
滤波器按幅度频率特性可分为:低通,高通,带通 和带阻滤波器 H ( j ) H ( j ) 低通
1
1
高通
0
H ( j ) 1 带通
p 0
目录
高 频 电 子 线 路
3
2.2.1滤波器的特性
V(s) 输入 i vi (t) 阻抗
滤波器
h(t) ,H(s)
输出 Vo ( s) 阻抗 v0 (t )
时域特性: vo (t ) h( )vi (t )d 复频域传输函数:
Vo ( s ) N ( s ) b0 s m b1 s m 1 bm H ( s) n Vi ( s ) D( s ) s a1 s n1 a n
Q值增大→斜率的绝对值增大
30
单位谐振曲线可表示选择性好坏。
高 频 电 子 线 路
串联谐振回路的相对幅频特性和相对相频特性
i ( j )
i ( )
1 Q2 (
I o ( j ) I o ( j 0 )
1
1 jQ (
1 1/ 2
0 )2 0
Q1>Q2 Q1 Q2
传输函数(传输阻抗)
1 Rs jL 1 s Vo ( j ) jC jC Z P ( j ) 1 1 I g ( j ) Rs jL RS j L jC C 谐振:
R
jL
– 回路电压与输入激励电流同相位 X ( j ) 0 P – 回路呈纯阻特性
LP
串联与并联回路Q值相同 o L 1 RP Q oCRP RS oCRS o L
24
高 频 电 子 线 路
2.并联回路端阻抗的模和相角随频率变化的关系为:
1 Z P ( j ) YP ( j )
RP
0 2 1 Q ( ) 0
2
0 P ( ) arctgQ( ) 0
0) 0 () arctgQ( 0 ) i 0
Q1>Q2 Q1 Q2
1
/2
0 -/2
0
0 B
Q值增大→选择性更好
Q值增大→斜率的绝对值增大
31
高 频 电 子 线 路
通频带(BW):当保持外加信号的幅值不变而改变其 频率时, 将并联回路端电压值(串联回路电流值)下降为 谐振值的 2 时对应的频率范围称为回路的通频带。 1
( ) p ( )
d ( ) g ( ) d
附加相移
一群不同频率的信号通过滤波器产生的延时 问题——群延时
6
高 频 电 子 线 路
群延时与线性失真
群延时描述的是一群不同频率的信号通过滤波器后 所产生的时间延迟,它是在指定频率范围内,相频特性 曲线在不同频率处的斜率。
