机械分离与固体流态化习题解答
浙江大学化工原理(过程工程与控制乙) 2009ppe-chap3_2

100 % ; 100 %
p
压 降 : 好 , 一 般 在 5002000Pa 左 右 小
2009-1-28
zhumingqiao@
2.离心沉降设备
B
旋 液 分离 器:
净化气体 含尘
特点:与旋风分离器相比, 直 径 小 、 锥 形 部 分 长 Why?
气体 A
D
尘粒
标准型旋风分离器
zhumingqiao@
二、影响沉降的因素
(Influencing factors for settling process)
1. 干 扰沉 降
由于干扰作用,实际沉降速度 小于自由沉降速度。
2.非球形颗粒的沉降
球 形 度 越 小, 沉 降速 度 越小
颗粒的位向对沉降速度也有影响
2 ut 2 mg 1 dp 0 D p 2 4 3 2 2 d p p g1 d p D u t 0 6 p 8
ut
R e p = d p u t / 1 或 2
4d
图 3 -1 5
曳力系数与雷诺数关系
2. 离 心 沉 降 速 度
2 2
centrifugal
离心力 F c ma
c
离 心 加速 度 a c= r=u /r 不 是常 量
加速度很小,可近似作为匀速沉降处理
浮力 F b m a c
p
沉 降 过 程 没 有 匀 速 段 , 但 在 小 颗 粒 沉 降 时 , 曳力 F D
1.重力沉降设备
什么条件?
ut
d
2 p
p
g
18
思 考 3 : 要 想 使 某 一 粒 度 的 颗 粒 在 降 尘 室 中 被 1 0 0 % 除 去 ,必 须 满 足
化工基本知识修订版天津大学
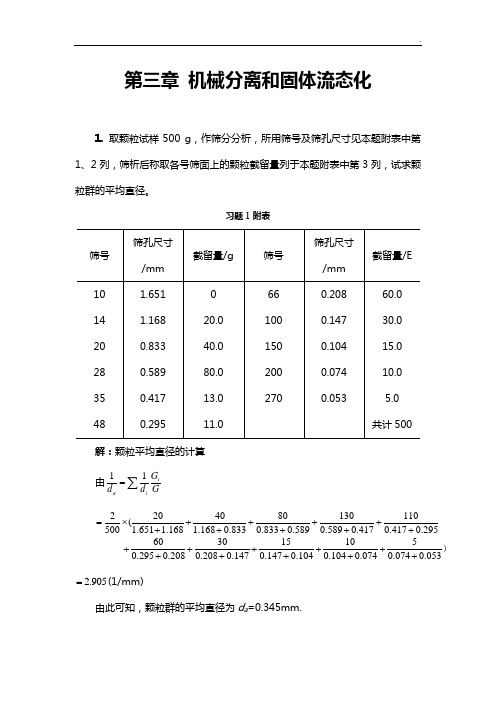
第三章 机械分离和固体流态化1. 取颗粒试样500 g ,作筛分分析,所用筛号及筛孔尺寸见本题附表中第1、2列,筛析后称取各号筛面上的颗粒截留量列于本题附表中第3列,试求颗粒群的平均直径。
习题1附表解:颗粒平均直径的计算 由11ia i G d d G=∑ 2204080130110(500 1.651 1.168 1.1680.8330.8330.5890.5890.4170.4170.2956030151050.2950.2080.2080.1470.1470.1040.1040.0740.0740.053=⨯+++++++++++++++++++ )2.905=(1/mm)由此可知,颗粒群的平均直径为d a =0.345mm.2. 密度为2650 kg/m 3的球形石英颗粒在20℃空气中自由沉降,计算服从斯托克斯公式的最大颗粒直径及服从牛顿公式的最小颗粒直径。
解:20C 时,351.205/, 1.8110kg m Pa s ρμ-==⨯⋅空气对应牛顿公式,K 的下限为69.1,斯脱克斯区K 的上限为2.62 那么,斯脱克斯区:max 57.4d m μ===min 1513d m μ==3. 在底面积为40 m 2的除尘室内回收气体中的球形固体颗粒。
气体的处理量为3600 m 3/h ,固体的密度3/3000m kg =ρ,操作条件下气体的密度3/06.1m kg =ρ,黏度为2×10-5 Pa ·s 。
试求理论上能完全除去的最小颗粒直径。
解:同P 151.例3-3在降尘室中能被完全分离除去的最小颗粒的沉降速度u t , 则 36000.025/4003600s t V u m s bl ===⨯ 假设沉降在滞流区,用斯托克斯公式求算最小颗粒直径。
min17.5d um ===核算沉降流型:6min 517.5100.025 1.06R 0.0231210t et d u ρμ--⨯⨯⨯===<⨯ 假设合理。
第三章化工原理_修订版_天津大学_
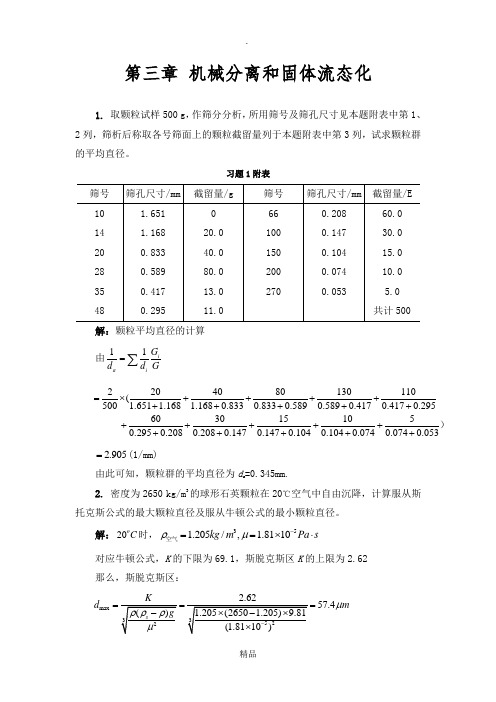
第三章 机械分离和固体流态化1. 取颗粒试样500 g ,作筛分分析,所用筛号及筛孔尺寸见本题附表中第1、2列,筛析后称取各号筛面上的颗粒截留量列于本题附表中第3列,试求颗粒群的平均直径。
习题1附表解:颗粒平均直径的计算 由11ia i G d d G=∑ 2204080130110(500 1.651 1.168 1.1680.8330.8330.5890.5890.4170.4170.2956030151050.2950.2080.2080.1470.1470.1040.1040.0740.0740.053=⨯+++++++++++++++++++ )2.905=(1/mm)由此可知,颗粒群的平均直径为d a =0.345mm.2. 密度为2650 kg/m 3的球形石英颗粒在20℃空气中自由沉降,计算服从斯托克斯公式的最大颗粒直径及服从牛顿公式的最小颗粒直径。
解:20C o 时,351.205/, 1.8110kg m Pa s ρμ-==⨯⋅空气对应牛顿公式,K 的下限为69.1,斯脱克斯区K 的上限为2.62 那么,斯脱克斯区:max 57.4d mμ===min 1513d m μ==3. 在底面积为40 m 2的除尘室内回收气体中的球形固体颗粒。
气体的处理量为3600 m 3/h ,固体的密度3/3000m kg =ρ,操作条件下气体的密度3/06.1m kg =ρ,黏度为2×10-5 P a·s。
试求理论上能完全除去的最小颗粒直径。
解:同P 151.例3-3在降尘室中能被完全分离除去的最小颗粒的沉降速度u t , 则 36000.025/4003600s t V u m s bl ===⨯ 假设沉降在滞流区,用斯托克斯公式求算最小颗粒直径。
min17.5d um ===核算沉降流型:6min 517.5100.025 1.06R 0.0231210t et d u ρμ--⨯⨯⨯===<⨯假设合理。
化工原理第二版答案解析

第三章 机械分离和固体流态化2. 密度为2650 kg/m 3的球形石英颗粒在20℃空气中自由沉降,计算服从斯托克斯公式的最大颗粒直径及服从牛顿公式的最小颗粒直径。
解:20C 时,351.205/, 1.8110kg m Pa s ρμ-==⨯⋅空气对应牛顿公式,K 的下限为69.1,斯脱克斯区K 的上限为2.62那么,斯托克斯区:max 57.4d m μ===min 69.11513d m μ==3. 在底面积为40 m 2的除尘室内回收气体中的球形固体颗粒。
气体的处理量为3600 m 3/h ,固体的密度3/3000m kg =ρ,操作条件下气体的密度3/06.1m kg =ρ,黏度为2×10-5P a·s。
试求理论上能完全除去的最小颗粒直径。
解:在降尘室中能被完全分离除去的最小颗粒的沉降速度u t ,则 36000.025/4003600s t V u m s bl ===⨯ 假设沉降在滞流区,用斯托克斯公式求算最小颗粒直径。
min 17.5d um === 核算沉降流型:6min 517.5100.025 1.06R 0.0231210t et d u ρμ--⨯⨯⨯===<⨯ 假设合理。
求得的最小粒径有效。
4. 用一多层降尘室除去炉气中的矿尘。
矿尘最小粒径为8m μ,密度为4000kg/m 3。
除尘室长 4.1 m 、宽 1.8 m 、高4.2 m ,气体温度为427℃,黏度为3.4×10-5 P a·s,密度为0.5 kg/m 3。
若每小时的炉气量为2160标准m 3,试确定降尘室内隔板的间距及层数。
解:由气体的状态方程PV nRT = 得''s s T V V T =,则气体的流量为: '34272732160 1.54/2733600s V m s +=⨯= 1.540.2034/1.8 4.2s t V u m s bH ===⨯ 假设沉降发生在滞流区,用斯托克斯公式求最小粒径。
化工习题解析

课后解析化工原理学院:环境与化学工程学院班级:化学工程与工艺1201班学号:姓名:日期: 2014年6月20日第一章流体流动2.在本题附图所示的储油罐中盛有密度为 960 ㎏/㎥的油品,油面高于罐底 6.9 m,油面上方为常压。
在罐侧壁的下部有一直径为 760 mm 的圆孔,其中心距罐底 800 mm,孔盖用14mm的钢制螺钉紧固。
若螺钉材料的工作应力取为39.23×106 Pa ,问至少需要几个螺钉?分析:罐底产生的压力不能超过螺钉的工作应力即P油≤σ螺解:P螺 = ρgh×A = 960×9.81×(9.6-0.8) ×3.14×0.762150.307×103 Nσ螺 = 39.03×103×3.14×0.0142×nP油≤σ螺得 n ≥ 6.23取 n min= 7至少需要7个螺钉3.某流化床反应器上装有两个U 型管压差计,如本题附图所示。
测得R1 = 400 mm , R2 = 50 mm,指示液为水银。
为防止水银蒸汽向空气中扩散,于右侧的U 型管与大气连通的玻璃管内灌入一段水,其高度R3= 50 mm。
试求A﹑B两处的表压强。
分析:根据静力学基本原则,对于右边的U管压差计,a–a′为等压面,对于左边的压差计,b–b′为另一等压面,分别列出两个等压面处的静力学基本方程求解。
解:设空气的密度为ρg,其他数据如图所示a–a′处 P A + ρg gh1 = ρ水gR3 + ρ水银ɡR2由于空气的密度相对于水和水银来说很小可以忽略不记即:P A = 1.0 ×103×9.81×0.05 + 13.6×103×9.81×0.05= 7.16×103 Pab-b′处 P B + ρg gh3 = P A + ρg gh2 + ρ水银gR1P B = 13.6×103×9.81×0.4 + 7.16×103=6.05×103Pa4. 本题附图为远距离测量控制装置,用以测定分相槽内煤油和水的两相界面位置。
化工原理习题及参考答案

第三章机械分离一、名词解释每题2分1.非均相混合物物系组成不同,分布不均匀,组分之间有相界面2.斯托克斯式3.球形度s非球形粒子体积相同的球形颗粒的面积与球形颗粒总面积的比值4.离心分离因数离心加速度与重力加速度的比值5.临界直径dc离心分离器分离颗粒最小直径6.过滤利用多孔性介质使悬浮液中液固得到分离的操作7.过滤速率单位时间所产生的滤液量8.过滤周期间歇过滤中过滤、洗涤、拆装、清理完成一次过滤所用时间9.过滤机生产能力过滤机单位时间产生滤液体积10.浸没度转筒过滤机浸没角度与圆周角比值二、单选择题每题2分1、自由沉降的意思是_______;A颗粒在沉降过程中受到的流体阻力可忽略不计B颗粒开始的降落速度为零,没有附加一个初始速度C颗粒在降落的方向上只受重力作用,没有离心力等的作用D颗粒间不发生碰撞或接触的情况下的沉降过程D2、颗粒的沉降速度不是指_______;A等速运动段的颗粒降落的速度B加速运动段任一时刻颗粒的降落速度C加速运动段结束时颗粒的降落速度D净重力重力减去浮力与流体阻力平衡时颗粒的降落速度B3、对于恒压过滤_______;A滤液体积增大一倍则过滤时间增大为原来的2倍B滤液体积增大一倍则过滤时间增大至原来的2倍C滤液体积增大一倍则过滤时间增大至原来的4倍D当介质阻力不计时,滤液体积增大一倍,则过滤时间增大至原来的4倍D4、恒压过滤时,如介质阻力不计,滤饼不可压缩,过滤压差增大一倍时同一过滤时刻所得滤液量___; A增大至原来的2倍B增大至原来的4倍倍D增大至原来的倍C5、以下过滤机是连续式过滤机_______;A箱式叶滤机B真空叶滤机C回转真空过滤机D板框压滤机C6、过滤推动力一般是指______;A过滤介质两边的压差B过滤介质与滤饼构成的过滤层两边的压差C滤饼两面的压差D液体进出过滤机的压差B7、回转真空过滤机中是以下部件使过滤室在不同部位时,能自动地进行相应的不同操作:______; A转鼓本身B随转鼓转动的转动盘C与转动盘紧密接触的固定盘D分配头D8、非球形颗粒的当量直径的一种是等体积球径,它的表达式为______;A d p=6V/A此处V为非球形颗粒的体积,A为非球形颗粒的表面积B d p=6V/1/3C d p=4V/1/2D d p=kV/1/3k为系数与非球形颗粒的形状有关B9、在讨论旋风分离器分离性能时,分割直径这一术语是指_________;A旋风分离器效率最高时的旋风分离器的直径B旋风分离器允许的最小直径C旋风分离器能够50%分离出来的颗粒的直径D能保持滞流流型时的最大颗粒直径C10、在离心沉降中球形颗粒的沉降速度__________;A只与d p,p,,u T,r,μ有关B只与d p,p,u T,r有关C只与d p,p,u T,r,g有关D只与d p,p,u T,r,k有关题中u T气体的圆周速度,r旋转半径,k分离因数A11、降尘室没有以下优点______________;A分离效率高B阻力小C结构简单D易于操作A12、降尘室的生产能力__________;A只与沉降面积A和颗粒沉降速度u T有关B与A,u T及降尘室高度H有关C只与沉降面积A有关D只与u T和H有关A13、回转真空过滤机的过滤介质阻力可略去不计,其生产能力为5m3/h滤液;现将转速度降低一半,其他条件不变,则其生产能力应为____________;A5m3/hB2.5m3/hC10m3/hD3.54m3/h D14、要除去气体中含有的5μ~50μ的粒子;除尘效率小于75%,宜选用;A除尘气道B旋风分离器C离心机D电除尘器B15、等压过滤的滤液累积量q与过滤时间τ的关系为______________;B16、过滤基本方程是基于____________推导出来的;A滤液在过滤介质中呈湍流流动B滤液在过滤介质中呈层流流动C滤液在滤渣中呈湍流流动D滤液在滤渣中呈层流流动D17、一般而言,旋风分离器长、径比大及出入口截面小时,其效率,阻力;A高B低C大D小A18、在板框过滤机中,如滤饼不可压缩,介质阻力不计,过滤时间增加一倍时,其过滤速率为原来的_____________;A2倍B1/2倍C1/2倍D4倍C19、在长为L m,高为H m的降尘室中,颗粒的沉降速度为u T m/s,气体通过降尘室的水平流速为u m/s,则颗粒能在降尘室内分离的条件是:____;A L/u<H/u LB L/u T<H/uC L/u T≥H/uD L/u≥H/u TD20、粒子沉降受到的流体阻力________;A恒与沉降速度的平方成正比B与颗粒的表面积成正比C与颗粒的直径成正比D在滞流区与沉降速度的一次方成正比D21、板框压滤机中,最终的滤液流率是洗涤液流率的_______;Δp E=Δp w,μ=μwA一倍B一半C四倍D四分之一C22、球形度形状系数恒小于或等于1,此值越小,颗粒的形状离球形越远,球形度的定义式可写为______;A=V p/V,V为非球形粒子的体积,V p为球形粒子的体积B=A p/A,A为非球形粒子的表面积,A p为与非球形粒子体积相同的球形粒子的表面积C=a p/a,a为非球形粒子的比表面积,a p为球形粒子的比表面积D=6a p/d B23、“在一般过滤操作中,实际上起到主要介质作用的是滤饼层而不是过滤介质本身”,“滤渣就是滤饼”则_______;A这两种说法都对B两种说法都不对C只有第一种说法正确D只有第二种说法正确A24、旋风分离器的总的分离效率是指__________;A颗粒群中具有平均直径的粒子的分离效率B颗粒群中最小粒子的分离效率C不同粒级直径范围粒子分离效率之和D全部颗粒中被分离下来的部分所占的质量分率D25、降尘室的生产能力由________决定;A降尘室的高度和长度B降尘室的高度C降尘室的底面积D降尘室的体积C26、在板框过滤机中,如滤饼不可压缩,介质阻力不计,黏度增加一倍时,对同一q值,过滤速率为原来的_____________;A2倍B1/2倍C1/2倍D4倍B27、回转真空过滤机洗涤速率与最终过滤速率之比为;AlB1/2 C1/4D1/3 A28、以下说法是正确的;A过滤速率与S过滤面积成正比B过滤速率与S2成正比C滤速率与滤液体积成正比D过滤速率与滤布阻力成反比B29、板框压滤机中;A框有两种不同的构造B板有两种不同的构造C框和板都有两种不同的构造D板和框都只有一种构造B30、助滤剂应具有以下性质;A颗粒均匀、柔软、可压缩B颗粒均匀、坚硬、不可压缩C粒度分布广、坚硬、不可压缩D颗粒均匀、可压缩、易变形B三、填空题每题2分1、一球形石英颗粒,在空气中按斯托克斯定律沉降,若空气温度由20℃升至50℃,则其沉降速度将; 下降2、降尘室的生产能力与降尘室的和有关;长度宽度3、降尘室的生产能力与降尘室的无关;高度4、在除去某粒径的颗粒时,若降尘室的高度增加一倍,则沉降时间;增加一倍5、在除去某粒径的颗粒时,若降尘室的高度增加一倍,气流速度;减少一倍6、在除去某粒径的颗粒时,若降尘室的高度增加一倍,生产能力;不变7、在滞流层流区,颗粒的沉降速度与颗粒直径的次方成正比;28、在湍流区,颗粒的沉降速度与颗粒直径的次方成正比;1/29、在过滤的大部分时间中,起到了主要过滤介质的作用;滤饼10、过滤介质阻力忽略不计,滤饼不可压缩,则恒速过滤过程中滤液体积由V l增多至V2=2V l时,则操作压差由ΔP l增大至ΔP2=;2ΔP l11、已知q为单位过滤面积所得滤液体积V/S,q e为V e/S,V e为过滤介质的当量滤液体积滤液体积为V e时所形成的滤饼层的阻力等于过滤介质的阻力,在恒压过滤时,测得Δ/Δq=3740q+200则过滤常数K=;12、已知q为单位过滤面积所得滤液体积V/S,q e为V e/S,V e为过滤介质的当量滤液体积滤液体积为V e时所形成的滤饼层的阻力等于过滤介质的阻力,在恒压过滤时,测得Δ/Δq=3740q+200则过滤常数q e=;13、最常见的间歇式过滤机有和;板框过滤机叶滤机14、在一套板框过滤机中,板有种构造,框种构造;2115、板框过滤机在过滤阶段结束的瞬间,设框已充满,则在每一框中,滤液穿过厚度为;框的厚度16、板框过滤机在过滤阶段结束的瞬间,设框已充满,在洗涤时,洗涤液穿过厚度为;框厚度之半17、板框过滤机在过滤阶段结束的瞬间,设框已充满,在洗涤时,洗涤液穿过的滤布面积等于;框的内面积18、旋风分离器性能的好坏,主要以来衡量;临界粒径的大小19、离心分离设备的分离因数定义式为Kc=;u T2/gR或u r/u t20、当介质阻力不计时,回转真空过滤机的生产能力与转速的次方成正比;1/221、间歇过滤机的生产能力可写为Q=V/,此处V为;一个操作循环中得到的滤液体积22、间歇过滤机的生产能力可写为Q=V/,此处表示一个操作循环所需的;总时间23、一个过滤操作周期中,“过滤时间越长,生产能力越大”的看法是否正确不正确的24、一个过滤操作周期中,“过滤时间越短,生产能力越大”的看法是否正确不正确的25、一个过滤操作周期中,过滤时间有一个值;最适宜26、一个过滤操作周期中,最适宜的过滤时间指的是此时过滤机生产能力;最大27、对不可压缩性滤饼dV/d 正比于ΔP 的次方,对可压缩滤饼dV/d 正比于ΔP 的次方;11-s28、对恒压过滤,介质阻力可以忽略时,过滤量增大一倍,则过滤速率为原来的;二分之一29、对恒压过滤,当过滤面积增大一倍时,如滤饼不可压缩,则过滤速率增大为原来的倍;对恒压过滤,当过滤面积增大一倍时,如滤饼可压缩,则过滤速率增大为原来的倍;4430、转鼓沉浸度是与的比值1转鼓浸沉的表面积转鼓的总表面积31、按ψ=A p/A 定义的球形度此处下标p 代表球形粒子,最大值为___;越小则颗粒形状与球形相差越___;1大32、将固体物料从液体中分离出来的离心分离方法中,最常见的有和;将固体物料从液体中分离出来的离心分离设备中,最常见的为;离心过滤离心沉降离心机33、在Stokes 区,颗粒的沉降速度与颗粒直径的_____次方成正比;在牛顿区,颗粒的沉降速度与颗粒直径的______次方成正比;21/234、一个过滤操作周期中,“过滤时间越长生产能力越大”的看法是,“过滤时间越短,生产能力越大”的看法是;过滤时间有一个值,此时过滤机生产能力为______;不正确的不正确的最适宜最大35、含尘气体通过长为4m,宽为3m,高为1m 的除尘室,已知颗粒的沉降速度为0.03m/s,则该除尘室的生产能力为s m 3;0.36m 3/s四、问答题每题3分1、影响回转真空过滤机生产能力的因素有哪些过滤介质阻力可忽略当过滤介质阻力可忽略时2Q KA n ϕ=2/K p r φμ=∆可见,影响因素有:转筒的转速、浸没度、转筒尺寸、操作压强及处理物料的浓度及特性;2、有一旋风分离器,在正常的速度和阻力的范围内操作,但除尘效率不够满意,现在仓库里还有一个完全相同的旋风分离器,有人建议将这台备用的旋风分离器与正在用的那一台一起并联使用,问这种措施能否提高除尘效率为什么不行;因为速度降低,离心惯性力减小,使除尘效率下降;3、恒压过滤时,如加大操作压力或提高滤浆温度,过滤速率会发生什么变化为什么由d q /d t =Δp /rΦμq +q e 知,加大操作压力,过滤速率变大;提高滤浆温度,使滤液黏度降低,过滤速率增大;4、临界直径dc 及分割直径d 50,可以表示旋风分离器的分离性能,回答d c 与d 50的含义是什么d c 旋风分离器的分离分离颗粒最小直径;d 50分离效率50%时颗粒直径5、由过滤基本方程d q /d t =Δp /rΦμq +q e 分析影响过滤速率的因素影响过滤速率的因素有:①物性参数,包括悬浮液的性质φ、μ及滤饼特性r ;②操作参数Δp ;③设备参数q e6、试说明滤饼比阻的意义比阻r 表示滤饼对过滤速率的影响,其数值的大小反映滤液通过滤饼层的难易程度;五、计算题每题10分1、某板框过滤机框空的长、宽、厚为250mm×250mm×20mm,框数为8,以此过滤机恒压过滤某悬浮液,测得过滤时间为与15min 时的滤液量分别为0.15m 3及0.20m 3,试计算过滤常数K ;解:过滤面积A =8×2××=1.0 m 22分已知:τ1==0.15 m 3τ2=15min V 2=0.20 m 3∵V 2+2VVe =KA 2τ4分可得+2×=K×12×1+2×=K×12×1521、2式联立,解得K =0.0030 m 2/min=×10-5 m 2/s4分2、以板框压滤机恒压过滤某悬浮液,过滤面积10m 2,操作压差×105Pa;每一循环过滤15min 得滤液2.91m 3;过滤介质阻力不计;(1) 该机生产能力为4.8m 3/h 滤液,求洗涤、装拆总共需要的时间及过滤常数K ;(2) 若压差降至×104Pa,过滤时间及过滤量不变,其他条件不变,需多大过滤面积设滤饼不可压缩;3如改用回转真空过滤机,转一圈得滤液0.2m 3,转速为多少才可以维持生产能力不变解:1∵V 2=KA 2τ即=K ×102×15∴K =×10-3 m 2/min又Q =V /∑τ即60=15+τw +τD∴τw +τD =4分2V 2=KA 2τA 2=V 2/Kτ4分3Q =60=×nn-r/min ∴n =min2分3、用某叶滤机恒压过滤钛白水悬浮液;滤叶每侧过滤面积为2m 2,共10只滤叶;测得:过滤10min 得滤液1.31m 3;再过滤10min 共得滤液1.905m 3;已知滤饼与滤液体积比n =;试问:1过滤至滤饼厚为21mm 即停止,过滤时间是多少2若滤饼洗涤与辅助时间共45min,其生产能力是多少以每小时得的滤饼体积计解:1∵V 2+2VVe =KA 2t由题意得+2×=KA 2×10a+2×=KA 2×20ba 、b 联立,解得KA 2=0.2076 m 6/min,Ve=0.1374 m 33分又A =10×2×=13.12m 2过滤终了时,共得滤液量V E =×=2.755 m 3由+2××=,∴t E =3分2生产能力=nV E /t E +t w +t 辅=×+45=×10-3 m 3/min=0.194 m 3/h 滤饼4分4、在3×105Pa 的压强差下对钛白粉在水中的悬浮液进行过滤实验,测得过滤常数K=5×10-5m 2/s 、q e =0.01m 3/m 2,又测得滤饼体积与滤液体积之比v=;现拟用有38个框的BMY50/810-25型板框压滤机处理此料浆,过滤推动力及所用滤布也与实验用的相同;试求:1过滤至框内全部充满滤渣所需的时间;2过滤完毕,以相当于滤液量1/10的清水进行洗涤,求洗涤时间;3若每次卸渣、重装等全部辅助操作共需15min,求每台过滤机的生产能力以每小时平均可得多少m 3滤饼计;解:1所需过滤时间A=×2×38=49.86m 2V c =××38=0.6233m 2()()2251120.156320.15630.01551510e q qq s K θ-=+=+⨯⨯=⨯4分 2洗涤时间30.10.156349.86/1.87410416s -=⨯⨯⨯=4分3生产能力30.62333600 1.2025514181560c Q m ⨯==++⨯滤饼/h2分 5、用板框过滤机过滤某悬浮液,一个操作周期内过滤20分钟后共得滤液4m 3滤饼不可压缩,介质阻力可略;若在一个周期内共用去辅助时间30分钟,求:(1) 该机的生产能力2若操作表压加倍,其它条件不变物性,过滤面积,过滤时间与辅助时间,该机生产能力提高了多少 解:滤饼不洗涤(1) 4分(2) 6分6、对某悬浮液进行恒压过滤;已知过滤时间为300s 时,所得滤液体积为0.75m 3,且过滤面积为1m 2,恒压过滤常数K=510-3m2/s;若要再得滤液体积0.75m 3,则又需过滤时间为多少2:2e q q K θ+=解由q 3分223225103000.750.625220.75e e q q K K q q θθ-=--⨯⨯-∴===⨯得q q 3分 2232 1.520.62515825510825300525e q q K sθθ-++⨯⨯===⨯=-=q 4分 7、一小型板框压滤机有框10块,长宽各为0.2m,在2at 表压下作恒压过滤共二小时滤框充满共得滤液160l,每次洗涤与装卸时间为1hr,若介质阻力可忽略不计,求:1过虑常数K,洗涤速率;2若表压增加一倍,其他条件不变,此时生产能力为若干解:15分A=××10×2=0.8m 225分故生产能力为1+1=0.08m 3/h8、某板框压滤机的过滤面积为0.4 m 2,在恒压下过滤某悬浮液,4hr 后得滤液80 m 3,过滤介质阻力可略去不计;试求:①若其它情况不变,但过滤面积加倍,可得多少滤液②若其它情况不变,但操作时间缩短为2hr,可得多少滤液③若在原表压下过滤4hr 后,再用5m 3水洗涤滤饼,需多长洗涤时间设滤液与水性质相近; 解:13分23分34分9、一小型板框过滤机,过滤面积为0.1m 2,恒压过滤某一种悬浮液;得出下列过滤议程式:q+102=250θ+0.4式中q 以l/m 2,θ以分钟计;试求:1经过249.6分钟获得滤液量为多少2当操作压力加大1倍,设滤饼不可压缩同样用249.6分钟将得到多少滤液量;解:1)4.0(250)10(2+=+θq当6.249=θ分时q=240L/M 2V=240×0;1=24L 5分2,P='K2P='K2343=⨯=5分5.LV3.341.0。
第3章机械分离与固体流态化(1)详解
16
小液滴行为与刚球相似; 稍大液滴内部形成环流使终端速度大于刚球; 考 滴径继续增大,液滴明显变形,终端速度小于刚球; 滴径大于某临界值时,液滴不停摆动,终端速度随直
研 导
径的增加有所降低。 辅 【例题】
假设一液滴与一固体球的体积和密度都相同,并且在同一流 体中自由沉降,则下列哪种液滴受到的曳力小于流体对固体 球的曳力( B)中科院07 B 有内部环流的球形液滴; A 刚性小液滴; C 曲折运动的椭球形液滴;
9B dc Nu i s
29
三点假设:
考 研 辅 导
(1)颗粒与气体在旋风分离器内的切线速度ut恒定,且等于 进口处的气速ui; (2)颗粒沉降过程中穿过的气流的最大厚度等于进气口宽度B; (3)颗粒与气流的相对运动为层流。
25
(三)离心沉降原理 依靠惯性离心力的作用而实现的沉降过程 考 1. 沉降速度
研 辅 导
ur
4d s ut2 3 r
离心加速度ar=2r=ut2/r 不是常量 颗粒运动半径不断变化,所以离心沉降速度总是 变化,加速度很小时可近似作为匀速沉降处理。 颗粒的真实运动速度是 ur与 ut 的合速度。
(2)无因次K判别流型法
13
K 2.62
层流区
考 研
s g K d 2
3
2.62 K 69.1 过渡区 K 69.1
湍流区
辅 4. 影响沉降速度的因素 导 包括:颗粒的因素,包括尺寸、形状、密度、是否
变形等;介质的因素,包括流体的状态(气体还是 液体)、密度、粘度等;环境因素,包括温度(影 响密度、粘度)、压力、颗粒的浓度(浓度达到一 定程度时发生干扰沉降等);设备因素,体现为壁 面效应。
化工原理讨论与答疑
第一章流体流动问1-1.如图所示,在两个压强不同的密闭容器A,B内充满了密度为的液体,两容器的上部与下部分别连接两支规格相同的U行管水银压差计,连接管内充满密度为的液体。
试回答:(1)p M和p N的关系;(2)判断1-2,2-3,3-4及5-6,6-7,7-8等对应截面上的压强是否相等;(3)两压差计读数R与H的关系。
答:(1)p M>p N。
(2)1-2,3-4,5-6,6-7为等压面(连续的同一介质在同一水平面上)。
(3)R和H相等。
证明:则又则由于所以即R=H问1-2.本题附图中所示的高位槽液面维持恒定,管路中ab和cd两段的长度、直径及粗糙度均相同。
某液体以一定流量流过管路,液体在流动过程中温度可视为不变。
问:(1)液体通过ab和cd两管段的能量损失是否相等?(2)此两管段的压强差是否相等?并写出它们的表达式;(3)两U管压差计的指示液相同,压差计的读数是否相等?答:(1)由于管路及流动情况完全相同,故。
(2)两管段的压强不相等。
在a、b两截面间列柏努利方程式并化简,得到式中表示a、b两截面间的垂直距离(即直管长度),m。
同理,在c、d两截面之间列柏努利方程并化简,得到(3)压差计读数反映了两管段的能量损失,故两管段压差计的读数应相等。
问1-3.上题图示的管路上装有一个阀门,如减小阀门的开度。
试讨论:(1)液体在管内的流速及流量的变化情况;(2)直管阻力及的变化情况;(3)液体流经整个管路系统的能量损失情况。
答:(1)关小阀门,局部阻力加大,管内流速及流量均变小。
(2)直管阻力减小,摩擦系数变大(Re变小)。
(3)整个管路系统的能量损失不变,即(包括出口阻力)问1-4.如本题附图所示,槽内水面维持不变,水从B、C两支管排出,各管段的直径、粗糙度阀门型号均相同,但>槽内水面与两支管出口的距离均相等,水在管内已达完全湍流状态。
试分析:(1)两阀门全开时,两支管的流量是否相等?(2)若把C支管的阀门关闭,这时B支管内水的流量有何改变?(3)当C支管的阀门关闭时,主管路A处的压强比两阀全开时是增加还是降低?答:(1)C支管流动阻力大,管内流速及流量均小于B支管。
新版化工原理习题答案(03)第三章_非均相混合物分离与固体流态化_题解
第三章非均相混合物分离及固体流态化1 .颗粒在流体中做自由沉降,试计算(1)密度为2 650 kg/m3,直径为0.04 mm的球形石英颗粒在 20 C 空气中自由沉降,沉降速度是多少? ( 2 )密度为2 650 kg/m 3,球形度 0.6的非球形颗粒在 20 C 清水中的沉降速度为 0.1 m/ s ,颗粒的等体积当量直径是多少? ( 3)密度为7 900 kg/m 的液体中沉降150 mm 所需的时间为解:(1 )假设为滞流沉降,则:d 2( s)U t—183 20.04 10 3 1818 1.81 10 5核算流型:查附录20 C 空气31.205kg/m,1.81 10 5 Pa s ,所以,Re du t1.205 0.1276 0.04 10 3 1.81 10 50.34 所以,原假设正确,沉降速度为(2 )采用摩擦数群法 0.1276 m/s s g 2 3 3 U t4 1.81 105 2650 Re 1- 1依 0.6, Re 1 431.9 , ,0.3 1.81 10 5 d e1.205 0.1(3 )假设为滞流沉降,得:d 2( s )g 18u t0.13431.9查出:Utde / R q ( 4.506105m 451.205 9.81 3 1.2052所以:其中u t h 0.15 7.32m s 0.02049m s 将已知数据代入上式得: 0.006352 7900 1600 9.81Pa s 18 0.02049 6.757Pa s核算流型 Re 4 O'00635O'02049 16006.7572 •用降尘室除去气体中的固体杂质,降尘室长 球形颗粒,密度为 3000 kg/m3。
气体的处理量为 0.030815 m , 3000 宽5 m ,高4.2 m ,固体杂质为(标准)m 3/h 。
试求理论上能完3,直径为6.35 mm 的钢球在密度为 1 600 kg/m7.32 s ,液体的黏度是多少?18 2650 12059^ms 0.1276ms全除去的最小颗粒直径。
化工原理(1)-作业题文
绪论1.从基本单位换算入手,将下列物理量的单位换算为SI单位。
(1) 水的粘度μ=0.00856g/(cm⋅s)(2) 密度ρ=1386kgf⋅s2/m4(3) 某物质的比热容c p=0.24BTU/(lb⋅︒F)(4) 传质系数K G=34.2kmol/(m2⋅h⋅atm)(5) 表面张力σ=74dyn/cm(6) 导热系数λ=1kcal/(m⋅h⋅K)2. 湿物料原来含水16%(wt%),在干燥器中干燥至含水0.8%,试求每吨物料干燥出的水量。
第一章流体流动1. 已知甲地区的平均大气压力为85.30kPa,乙地区的平均大气压力为101.33kPa,在甲地区的某真空设备上装有一个真空表,其读数为20kPa。
若改在乙地区操作,真空表的读数为多少才能维持该设备的绝对压力与甲地区操作时相同?2. 用一复式U管压差计测定水流管道A、B两点的压差,压差计的指示液为汞,两段汞柱之间放的是水,今若测得h1=1.2m,h2=1.3m,R1=0.9m,R2=0.95m,问管道中A、B两点间的差压∆p AB为多少?(先推导关系式,再进行数字运算)。
第2题图3. 在稳定流动系统中,水连续从粗管流入细管。
粗管内径d1=10cm,细管内径d2=5cm,当流量为4×10-3m3/s时,求粗管内和细管内水的流速?4.高位槽内的水面高于地面8m,水从φ108×4mm的管路中流出,管路出口高于地面2m。
在本题中,水流经系统的能量损失可按h f=6.5u2计算,其中u为水在管内的流速,试计算:(1)A-A截面处水的流速;(2)出口水的流量,以m3/h计。
第4题图5. 将高位槽内料液向塔内加料。
高位槽和塔内的压力均为大气压。
要求料液在管内以0.5m/s 的速度流动。
设料液在管内压头损失为1.2m (不包括出口压头损失),试求高位槽的液面应该比塔入口处高出多少米?6. 用泵将贮槽中密度为1200kg/m 3的溶液送到蒸发器内,贮槽内液面维持恒定,其上方压强为101.33×103Pa ,蒸发器上部的蒸发室内操作压强为26670Pa (真空度),蒸发器进料口高于贮槽内液面15m ,进料量为20m 3/h ,溶液流经全部管路的能量损失为120J/kg ,求泵的有效功率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
后卸渣、清理、重装等共需40min,球每台压滤机的生产能力,以
平均每小时可得到的滤饼体积计。
• 3-7
• 在实验室内用一片过滤面积为0.05 m2滤液在
36KPa(绝)下进行吸滤。在300s内共吸出
400cm3滤液,再过600s,又吸出400cm3滤液,求 (1)减压过滤下的过滤常数K和qe ;(2)估算
洗涤时间
例题 在实验装置中过滤钛白的水悬浮液,过滤压力为0.3MPa,求
得过滤常数为:K=5×10-5m2/s,qe=0.01m3/m2。又测出滤饼体积与滤
液体积之比c=0.08m3/m3先要用工业型板框压滤机过滤同样的料液, 过滤压力、所用的滤布亦与实验时相同。滤框长与宽均为810mm, 厚度为45mm,共有26个框,过滤面积为33m2,框内总容量为 0.760mm。 试计算:(1)过滤进行到框内全部充满滤饼所需的过滤时间(2) 过滤后用总滤液体积的1/10清水进行洗涤,求洗涤时间(3)洗涤
净化气体
含尘气体 粉尘
隔板
多层隔板降尘室示意图
当降尘室用水平隔板分为N层,则每层高度为H/N。水平速 度u不变。此时: 尘粒沉降高度为原来的1/N倍; 降尘室生产能力为原来的N倍 utc降为原来的1/N倍 (utc= Vs / bl) ; 临界粒径为原来的 1/ N 倍; 一般可分离20μm以上的颗粒。多层隔板降尘室排灰不方便。
•
(3)颗粒与气流的相对运动为层流,
由假设(1)、(3)可推出气流中颗粒的离心沉降速度:
Ρ比Ρs小很多故略去,用 进口速度代替切线速度
由假设(2)可得到颗粒到达器壁所需沉降时间:
令气体进入排气管以前在器内旋转的圈数为N,则运行的 距离为2πrmN,故停留时间:
若某种尺寸的颗粒所需的沉降时间恰好等于停留时间,则该颗粒就 是理论上能被完全分离下来的最小颗粒。即临界粒径
下过滤,某种悬浮液。4h后得滤液80m3,过滤介质
阻力忽略不计。求
(1)当其它情况不变,过滤面积加倍,可得滤液多少? (2)当其它情况不变,操作时间缩短为2h,可得滤 液多少? (3)若过滤4h后,再用5m3性质与滤液相近的水洗涤 滤饼,问需多少洗涤时间?
第四节 固体流态化
• 流态化是一种使固体颗粒层通过与流体接触而具有类似于流体某
四、离心沉降设备
旋风分离器是常用的气固系离
心分离设备。标准型旋风分离 器的结构如左图: • 工作原理:含尘气体自进风口 切向引入,在分离器内受器壁
约束做由上向下,再由下向上
的螺旋运动,然后从中心管引
出。在上、下螺旋运动过程中, 尘粒与气体发生相对运动被甩 向器壁后顺壁石掉落至灰斗,
这样尘粒得以与气体分离。
上,摇动或振动一定的时间。颗粒就按粒径从大到小分别
被截留在不同的筛盘上。若得知一种颗粒能通过某一号筛
而截留于相邻的另一号孔眼较小的筛上,则这一颗粒的直
径便可视为等于此两号筛孔宽度的算术平均值。将截留在
每个筛面上的颗粒取出称重,即可算出每一号筛上所截留
的样品质量分率。
第二节、沉降分离
一、重力沉降原理
些表观特性的过程
• 一. 固体流态化的基本概念
• 如果流体自下而上地流过颗粒层,则根据流速的不同,会出现三 种不同的情况。
u 离心力F离 d p s T 6 R 2 uT 3 浮力F浮 d p 6 R
3
2
u
阻力 Fd
浮力 Fb
离心力 Fc
阻力F阻
4
dp
2
ur 2
2
若这三个力达到平衡,则有
2 2
颗粒在离心力场中的受力分析
2
3 uT 3 uT 2 ur d p s d p s d p 0 6 R 6 R 4 2
含尘气体进入降尘室后,因流道截面积扩大而速度减慢,只要 颗粒能够在气体通过的时间内降至室底,便可从气流中分离出来。
沉降运动时间< 气体停留时间→分离
• 颗粒在降尘室停留的时间时间为: 位于降尘室最高点的颗粒沉降至室底需要的时间为:
分离满足的条件:
分离所需最低沉降速度: 降沉室的生产能力与其高度无关。 能被分离的最小颗径: (若斯托克斯定律适用)
一、过滤方式
深层过滤
过滤
滤饼过滤
二、过滤设备
• • • • • (1)压滤机 (2)叶滤机 (3)转筒真空过滤机 板框过滤机 (1)结构与工作原理
• • • • • • • •
1-非洗涤板; 2-滤框; 3-洗涤板; 四角均开孔 滤布—框的两侧 组装: 1-2-3-2-1-2-3-2-1-2-3-2-1 过滤 滤浆由总管入框 框内形成滤饼 滤液穿过滤 饼和滤布 经每板上旋塞排出(明流) • 从板流出的滤液汇集于某总管排出(暗流) • 洗涤
4.恒压过滤方程
积分式 或者 若过滤介质阻力可忽略不计,则上式可简化 为:
3.过滤常数的实验测定
恒压过滤方程同除以Kq
试验中记录下不同过滤时间θ内的单位面积滤液量q,将 θ/q对 q作图,可得一直线,直线斜率=1/K,截距=2qe/K 或 对过滤方程进行微分 微分用增量代替 连续测定θ,q,算出一系列Δθ及对应Δq,将Δθ/Δq对q作图,得 一直线,直线斜率=2/K,截距=2qe/K。
第三章 机械分离与固体流态化
李富霞
一、概述
• 混合物分为两大类:
均相物系:溶液和混合气体
下册介绍:气体吸收、液体蒸馏、液液萃 取、固体干燥、结晶、吸附、膜分离
悬浮液、乳浊液、 泡沫液 非均相物系: 含尘气体、含雾气 体 机械方法:沉降、过滤
一、单颗粒的几何特性参数
颗粒最基本的特性:大小(粒径)、形状、表面积
解得
• 二、分离效率 (1)粒级效率 指某一粒径的颗粒被分离的质量分数
(2)总分离效率 指单位时间内被除去的固体颗粒质量占进入分离 器的全部颗粒质量的分率。 (3)压降
第三节 过滤
以某种多孔物质为介质,在外力的作用下,使悬浮液中的液体通
过介质的孔道,而固体颗粒被截留在介质上,从而实现固液分离 的单元操作。
• 2.基本参数
• ① 空隙率ε:床层的空隙体积/床层的总体积 • ② 比表面积a:颗粒表面积/颗粒体积 • ③ 孔道(细管)当量直径de。
④ 滤液流速u1:
过滤速度是指单位时间内通过单位过滤面积的滤液 体积
3.过滤速度
u—瞬时过滤速度,m/s V—滤液体积,m3 A—过滤面积,m2 q—单位过滤面积所得的滤液量,m3/m2,q=V/A θ—过滤时间,s
(1)自由沉降
重力:
Hale Waihona Puke 浮力:阻力:式中 ζ ----阻力系数,无因次; A ----颗粒在垂直于其运动方向 的平面上的投影面积,其值为A= ,m2; u0----颗粒相对于流体的降落速度, m/s。
根据牛顿第二定律有:
代入公式得:
m-----颗粒的质量 ,kg; a------加速度,m/s2 θ------时间 ,s。 沉降刚开始时速度为零,因此阻力也为零,故加速度a有 最大值,颗粒加速下降。沉降过程中阻力随速度增加而增大 直至速度达到某一数值后,三力平衡,即合力为零。此时, 加速度为零,颗粒开始做匀速运动。可见,以上过程可分为
横穿洗涤:
洗涤液由总管入板
滤布 滤框 滤饼 滤布 非洗涤板
排出洗涤面=(1/2)过滤面积
置换洗涤:
洗涤液行程与滤液相同。洗涤面=过滤面 间歇操作——装合、过滤、洗涤、卸渣、整理
三、过滤的基本理论
• 1.颗粒床层的物理模型与基本参数
• 颗粒床层→ 一组平行细管--流体通道 • ① 细管内表面之和=滤饼内颗粒的全部表面 • ② 细管的全部流动空间=滤饼内的全部空隙体积
1. 球形颗粒
体积v=(π/6)dp3 表面积 s=πdp2 2. 非球形颗粒 (1)常用的参量: ①等体积当量直径de,v:与非球形颗粒体积相等的球的直径。 m3 m2
比表面积为a=s/v=6/dp
1/m
dp 球形颗粒的直径,m
de,v=(6v/π)1/3
v为非球形颗粒的体积。
S
②球形度ψ :与非球形颗粒体积相等的球的表面积与该颗粒表面积之比。 ψ=πd2e,v/s 为非球形颗粒的表面积。 (2)非球形颗粒的体积、表面积、比表面积 体积v=(π/6) d3e,v m3 表面积s=πd2e,v/ψ m2 比表面积a=s/v=6/ψde,v 1/m
例 采用降尘室回收常压炉气中所含球形固体颗粒。 降尘室底面积为10㎡,高1.6m。操作条件下气体 密度为0.5kg/m3,粘度为2×10-5Pa· s,颗粒密度 为3000 kg/m3。气体体积流量为5m3/s。试求: 可完全回收的最小颗粒直径;
三、离心沉降原理
离心沉降:依靠惯性离心力的作用而实现的沉降过程
试差法
对于小颗粒,假设Re0﹤2,用stokes公式求u0 → 校验Re0 不符合,重新假设。 (2)干扰沉降 自由沉降条件:颗粒沉降时彼此相距较远,互不干扰;容 器壁对颗粒沉降的阻滞作用可以忽略。 干扰沉降:颗粒间距离很小,即使没有相互接触,一个颗 粒沉降时也会受到其他颗粒的影响 方法:干扰沉降速度可用自由沉降速度的计算方法计算, 只是要根据颗粒的浓度对所用的流体的密度及黏度进行 校正。
两阶段,先加速后匀速。
沉降速度的计算
• 等速段中颗粒相对于流体的运动速度u0 • 沉降速度的关系式:
使用上式计算沉降速度要先知道阻力系数ζ
因次分析→
①层流区(Stokes区)
斯托克 斯定律
②过渡区(Al len区)
艾伦 公式
③湍流区(牛顿区) 500<Re0<200000
牛顿 公式
④Re0>2×105 ζ急剧下降。 阻力系数骤然下降,层流边界层→湍流边界层,分离点后移,尾 流区收缩,形体阻力突然下降,近似取 ζ=0.1
