立体几何
数学立体几何公式

数学立体几何公式
以下是一些常见的数学立体几何公式:
1. 棱柱表面积公式:A=LH+2S(其中L为底面周长,H为柱高,S为底面面积)。
2. 棱柱体积公式:V=SH(其中S为底面面积,H为柱高)。
3. 圆柱表面积公式:A=LH+2S=2πRH+2πR^2(其中L为底面周长,H为柱高,S为底面面积,R为底面圆半径)。
4. 圆柱体积公式:V=SH=πR^2H(其中S为底面面积,H为柱高,R为底面圆半径)。
5. 球体表面积公式:A=4πR^2(其中R为球体半径)。
6. 球体体积公式:V=4/3πR^3(其中R为球体半径)。
7. 圆锥表面积公式:A=1/2sL+πR^2(其中s为圆锥母线长,L为底面周长,R为底面圆半径)。
8. 圆锥体积公式:V=1/3SH=1/3πR^2H(其中S为底面面积,H为圆锥高,R为底面圆半径)。
9. 正方体体积公式:V=a^3(其中a为正方体的边长)。
10. 长方体体积公式:V=lwh(其中l为长度,w为宽度,h为高度)。
这些公式是解决立体几何问题的基础,能帮助我们更好地理解和计算空间几何体的性质。
立体几何的意义及价值

立体几何的意义及价值立体几何作为数学中的一个重要分支,研究的是三维空间中的图形和体积。
它不仅具有理论意义,还有着广泛的应用价值。
本文将从几何的意义和价值两个方面来探讨立体几何的重要性。
一、几何的意义立体几何作为几何学的一个分支,研究的是空间中的图形和体积。
它以点、线、面为基本元素,通过组合和运算来描述和分析三维空间中的物体。
立体几何通过几何图形的性质和关系,揭示了空间中的规律和结构,具有深远的意义。
立体几何的意义在于它帮助我们认识和理解三维空间。
人类生活在三维空间中,而立体几何正是研究这个空间的工具。
通过学习立体几何,我们可以掌握空间中图形的构造和性质,了解物体的形状、大小和位置关系。
这有助于我们更好地认识和理解我们所处的世界。
立体几何的意义在于它培养了我们的几何思维和空间想象力。
立体几何不同于平面几何,它需要我们在三维空间中进行思考和推理。
通过解决立体几何问题,我们可以培养和发展我们的几何思维能力,提高我们的空间想象力。
这对于我们在日常生活和工作中解决问题和创新具有重要的意义。
立体几何的意义还在于它与其他学科的关联。
立体几何与代数、物理等学科有着密切的联系。
在代数学中,立体几何可以通过向量和坐标的运算来描述和分析;在物理学中,立体几何可以用来研究物体的形状和运动。
因此,学好立体几何对于我们在其他学科中的学习和研究也是十分重要的。
二、几何的价值立体几何不仅具有理论意义,更有着广泛的应用价值。
它在现实生活和各个行业中都发挥着重要作用。
立体几何在建筑和设计领域有着广泛的应用。
建筑师和设计师需要通过立体几何的知识来构思和设计建筑物和产品。
他们需要考虑物体的形状、大小和位置关系,合理利用空间,使设计更加美观和实用。
立体几何为他们提供了有力的工具和方法。
立体几何在工程和制造领域也有着重要的应用。
工程师和制造商需要通过立体几何的知识来设计和制造各种零部件和产品。
他们需要考虑物体的形状、结构和材料等因素,以确保产品的质量和性能。
立体几何公式

立体几何公式立体几何是研究空间中尺寸、形状、位置等几何性质的分支学科。
在立体几何中,有许多重要的公式能够帮助我们计算不同立体体量、表面积、角度和长度等物理量。
本文将详细介绍一些常用的立体几何公式,包括点、线、面、体、角、球、圆锥、圆柱、圆盘等多个几何形状。
1. 点:- 点的坐标:点的坐标可由一组数字表示,通常使用(x, y, z)表示三维空间中的点。
- 两点间的距离:两点间的距离可使用勾股定理计算,公式为:d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ -z₁)²)。
2. 线:- 线段长度:线段的长度可以通过两点间的距离公式计算得出。
- 直线方程:直线可以使用一般式、点斜式或两点式等多种形式表示。
3. 面:- 面积:不同形状的面积计算公式略有不同,其中包括矩形的面积(A = l × w)、三角形的面积(A = 1/2 × b × h)、圆形的面积(A = πr²)等。
- 周长:周长是封闭几何图形的边界长度。
4. 体:- 体积:体积是三维几何图形的容积大小,如矩形的体积(V = l × w × h)和球的体积(V = 4/3 × πr³)等。
- 表面积:表面积是指三维几何图形的外部面积大小,如矩形的表面积(A = 2lw + 2lh + 2wh)和球的表面积(A = 4πr²)等。
5. 角:- 角度:角度是表示两条辐射线之间夹角的度量单位,常用度(°)表示。
- 三角函数:包括正弦、余弦、正切等三角函数,可用于计算角的各种相关性质。
6. 球:- 球的体积:V = 4/3 × πr³。
- 球的表面积:A = 4πr²。
7. 圆锥:- 圆锥的体积:V = 1/3 × πr²h。
- 圆锥的侧面积:A = πrl。
立体几何的基本概念

立体几何的基本概念立体几何是几何学的一个重要分支,研究物体的形状、大小、相对位置及其性质等问题。
在立体几何中,有一些基本概念是我们必须了解的。
本文将为您介绍一些立体几何的基本概念。
1. 点、线和面在立体几何中,点是最基本的概念,它没有大小和形状,只有位置。
线是由点组成,具有长度但没有宽度和厚度。
面是由线组成,具有长度和宽度,没有厚度。
这三个基本概念是构成立体几何的基础。
2. 多面体多面体是由平面多边形组成的立体图形。
常见的多面体有立方体、四面体、六面体等。
立方体是一种具有六个面的多面体,每个面都是一个正方形。
四面体是一种具有四个面的多面体,其中三个面相交于一点,称为顶点。
六面体是一种具有六个面的多面体,每两个面都平行。
3. 对称性对称性是立体几何中常见的概念,指一个物体在某一变换下保持不变。
常见的对称性有平面对称和中心对称。
平面对称是指一个物体在某个平面上对称,即该平面将物体分为两部分,两部分互为镜像。
中心对称是指一个物体围绕一个点旋转180度后重合。
4. 体积和表面积体积是指立体图形所占的空间大小,它是立体图形所有部分的容积之和。
常见的计算体积的公式有立方体的体积公式、圆柱的体积公式等。
表面积是指立体图形外部的总面积,常见的计算表面积的公式有正方体的表面积公式、立方体的表面积公式等。
5. 平行投影和透视投影在立体几何中,我们通常用平行投影和透视投影来描述立体图形。
平行投影是指物体中的平行线经过投影后仍然保持平行。
透视投影是指从视点处看立体图形时,远离视点的物体较近离视点的物体更小,两条平行线投影到视平面上时不再平行。
6. 空间几何关系在立体几何中,我们还需要了解一些空间几何关系,如垂直、平行、相交等。
垂直是指两条线或两个面相交成直角。
平行是指两条线或两个面永不相交。
相交是指两条线或两个面有一个或多个公共点。
通过了解这些基本概念,我们可以更好地理解立体几何,解决与立体图形相关的问题。
掌握这些基本概念是学习和应用立体几何的基础,希望本文对您有所帮助。
高中立体几何八大定理

高中立体几何八大定理
1、直线与平面平行的判定定理
如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行。
2、直线与平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
3、平面与平面平行的判定定理
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
4、平面与平面平行的性质定理
如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行。
5、直线与平面垂直的判定定理
如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面。
6、直线与平面垂直的性质定理
若两条直线垂直于同一个平面,则这两条直线平行。
7、平面与平面垂直的判定定理
如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
8、平面与平面垂直的性质定理
如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面。
立体几何知识点

立体几何知识点立体几何知识点概述1. 立体图形的基本概念- 体积与表面积- 多面体、旋转体的定义和分类2. 多面体- 棱柱和棱锥- 正方体和长方体- 正棱锥和正棱台- 棱镜和棱镜体- 多面体的体积和表面积公式- 棱柱体积公式:V = Bh(B为底面积,h为高)- 棱锥体积公式:V = (1/3)Bh(B为底面积,h为高) - 正多面体的表面积公式:A = 面积单位 * 面数3. 旋转体- 圆柱、圆锥和圆台- 体积公式:V = πr²h(r为半径,h为高)- 球体- 体积公式:V = (4/3)πr³- 表面积公式:A = 4πr²- 旋转椭球体和旋转抛物面4. 空间几何图形的性质- 线面关系- 平行与垂直- 线面角和面面角- 面面关系- 平行与相交- 二面角- 体积与表面积的计算5. 立体图形的构造- 利用基本几何体构造复杂图形- 几何体的切割与组合6. 空间向量与立体几何- 空间向量的基本概念- 向量的加法、数乘、数量积和向量积 - 利用空间向量解决立体几何问题7. 立体几何的应用- 建筑设计- 工程测量- 计算机图形学8. 立体几何的解题技巧- 利用对称性- 转化与化归- 空间想象能力的培养9. 典型例题解析- 计算多面体和旋转体的体积与表面积 - 解决线面、面面关系问题- 空间向量在立体几何中的应用10. 立体几何的数学思想- 空间直观与抽象- 几何变换- 极限与微积分初步以上是立体几何的主要知识点概述,每个部分都包含了该领域的核心概念、公式、性质和应用。
在实际教学或学习中,应根据具体情况深入探讨每个部分的细节,并结合实际问题进行练习和应用。
立体几何八大定理
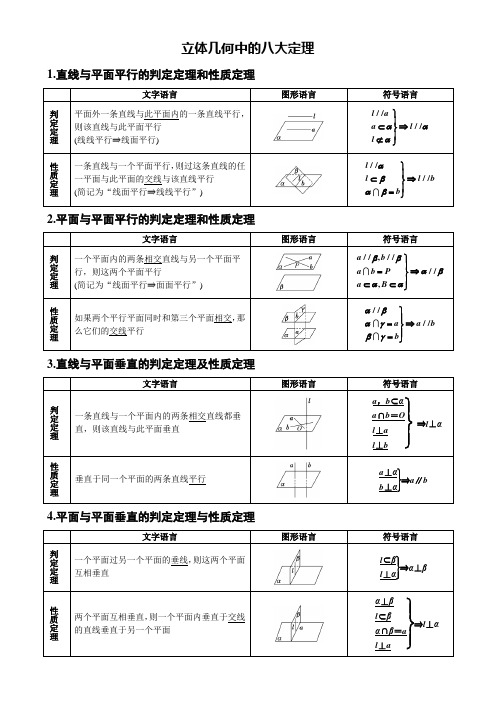
立体几何中的八大定理1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)////l aa llααα⎫⎪⊂⇒⎬⎪⊄⎭性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)////ll l bbαβαβ⎫⎪⊂⇒⎬⎪=⎭2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)//,////,a ba b Pa Bββαβαα⎫⎪=⇒⎬⎪⊂⊂⎭性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行////a a bbαβαγβγ⎫⎪=⇒⎬⎪=⎭3.直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a,b⊂αa∩b=Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b4.平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面互相垂直⎭⎪⎬⎪⎫l⊂βl⊥α⇒α⊥β性质定理两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl⊂βα∩β=al⊥a⇒l⊥α。
立体几何基本定理与公式

立体几何基本定理与公式
立体几何基本定理与公式包括以下几个方面:
1. 欧拉定理:对于任何一个凸多面体,其顶点数、边数和面数满足顶点数+面数=边数+2。
2. 平面角和定理:一个凸多面体的每个面的角和等于360度。
3. 球面面积公式:一个球面的面积等于4πr^2,其中r为球的
半径。
4. 球体体积公式:一个球体的体积等于(4/3)πr^3,其中r为球
的半径。
5. 正方体体积公式:一个正方体的体积等于边长的立方。
6. 矩形体积公式:一个矩形的体积等于长度乘以宽度乘以高度。
7. 棱柱体积公式:一个棱柱的体积等于底面积乘以高度。
8. 棱锥体积公式:一个棱锥的体积等于底面积乘以高度的一半。
9. 圆锥体积公式:一个圆锥的体积等于底面积乘以高度的三分之一。
10. 圆柱体积公式:一个圆柱的体积等于底面积乘以高度。
