“胡不归模型”——中考最值专题.doc
九年级培优专题:经典几何模型——“胡不归”

经典几何模型——“阿氏圆”与“胡不归” 一.“胡不归”模型典故从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路。
由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径 A →B (如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭。
邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?…何以归”。
这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问题”。
二.“胡不归”模型建立如图所示,已知sin ∠MBN =k ,点 P 为角∠MBN 其中一边 BM 上的一个动点,点A 在射线BM 、BN 的同侧,连接AP ,则当“PA +k ·PB ”最小时,P 点的位置如何确定? 分析:本题的关键在于如何确定“k ·PB ”的大小,过点P 作 PQ ⊥BN 垂足为Q ,则 k ·PB =PB ·sin ∠MBN =PQ , “PA +k ·PB ”的最小值转化为求“PA +PQ ”的最小值,即A 、P 、Q 三点共线时最小。
三.“胡不归”模型破解策略“胡不归”构造某角正弦值等于系数k (k 小于1)当k 值大于1时,则提取k ,构造某角正弦值等于系数k1 起点构造所需角(k =sin ∠CAE )→过终点作所构角边的垂线→利用垂线段最短解决四.“胡不归”典型例题讲解1.四边形ABCD 是菱形,AB =6,且∠ABC =60°,M 为对角线BD (不含B 点)上任意一点,则 AM +21BM 的最小值为 . 变式思考:(1)本题如要求“2AM +BM ”的最小值你会求吗?(2)本题如要求“AM +BM +CM ”的最小值你会求吗?A DBC 沙 砾 地 带2.如图,等腰△ABC 中,AB =AC =3,BC =2,BC 边上的高为AO ,点D为射线AO 上一点,一动点P 从点A 出发,沿AD -DC 运动,动点P 在AD 上运动速度3个单位每秒,动点P 在CD 上运动的速度为1个单位每秒,则当AD = 时,运动时间最短为 秒.3.如图,在菱形ABCD 中,AB =6,且∠ABC =150°,点P 是对角线AC 上的一个动点,则P A +2PB 的最小值为 .用费马点思想做下试试4.如图,在△ACE 中,CA =CE ,∠CAE =30°,⊙O 经过点C ,且圆的直径AB 在线段AE 上。
最值模型之胡不归(学生版)-中考数学专题解析

最值模型之胡不归“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。
1.当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“饮马问题”模型来处理,即可以转化为轴对称问题来处理(见专题08);2.当k取任意不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路。
此类问题的处理通常以动点P所在图像的不同来分类,一般分为2类研究。
即点P在直线上运动和点P 在圆上运动。
(1)其中点P在直线上运动的类型称之为“胡不归”问题;(2)点P在圆周上运动的类型称之为“阿氏圆”问题(见专题11)。
胡不归:【模型建立】如图1:P是直线BC上的一动点,求PA+k·PB的最小值。
【作法】1.作∠CBE=α,使sinα=k,则PD=k·OP(图2)2.当AD最短,AD⊥BE时,则P为要求点。
(图3)AD长即为PA+k·PB的最小值.简记:胡不归,正弦作个角,作高求长即可.特别提醒:当k>1时,kAP+BP=k AP+1k BP按常规模型算即可1∠AOB=30°,OM=2,D为OB上动点,求MD+12OD的最小值.2(1)【问题探究】如图1,点E是等边△ABC高AD上的一定点,请在AB上找一点F,使EF=12AE,并说明理由;(2)【问题解决】如图2,在△ACD中,CO⊥AD,垂足为O,若AD=32,AC=2,OC=3,点P在OC上,求DP+12PC的最小值.(3)【问题拓展】如图3,△ABC中,AB=AC=10,tan∠A=2,BE⊥AC于点E,D是线段BE上的一个动点,求CD+ 55BD的最小值.1.实战训练1一.选择题(共8小题)1如图,在△ABC 中,P 为平面内的一点,连接AP 、PB 、PC ,若∠ACB =30°,AC =8,BC =10,则4PA +2PB +23PC 的最小值是()A.489B.36C.410+25+67D.1610-102如图,△ABC 为等边三角形,BD 平分∠ABC ,AB =2,点E 为BD 上动点,连接AE ,则AE +12BE 的最小值为()A.1B.2C.3D.23如图,在平面直角坐标系中,抛物线y =-49x 2+83x 与x 轴的正半轴交于点A ,B 点为抛物线的顶点,C 点为该抛物线对称轴上一点,则3BC +5AC 的最小值为()A.24B.25C.30D.364如图,在等边△ABC 中,AB =6,点E 为AC 中点,D 是BE 上的一个动点,则CD +12BD 的最小值是()A.3B.33C.6D.3+35如图,在菱形ABCD中,AB=AC=6,对角线AC、BD相交于点O,点M在线段AC上,且AM= 2,点P是线段BD上的一个动点,则MP+12PB的最小值是()A.2B.23C.4D.436如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB的中点,P为边CD上一动点,则AP+12CP的最小值为()A.1B.2C.3D.27如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +55BD的最小值是()A.25B.45C.53D.108如图,在菱形ABCD中,∠ABC=60°,E是边BC的中点,P是对角线BD上的一个动点,连接AE,AP,若AP+12BP的最小值恰好等于图中某条线段的长,则这条线段是()A.ABB.AEC.BDD.BE2二.填空题(共9小题)1如图,AC垂直平分线段BD,相交于点O,且OB=OC,∠BAD=120°.(1)∠ABC=.(2)E为BD边上的一个动点,BC=6,当AE+12BE最小时BE=2 .2如图,在△ABC中,∠A=90°,∠C=30°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.3如图,在平面直角坐标系中,直线y=-x+4的图象分别与y轴和x轴交于点A和点B.若定点P的坐标为(0,63),点Q是y轴上任意一点,则12PQ+QB的最小值为3 .4如图,直线y=x-3分别交x轴、y轴于B、A两点,点C(0,1)在y轴上,点P在x轴上运动,则2PC+PB的最小值为.5如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=4 3,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是 649 s.6如图,在平面直角坐标系中,二次函数y=x2-2x+c的图象与x轴交于A、C两点,与y轴交于点B (0,-3),若P是x轴上一动点,点D(0,1)在y轴上,连接PD,则C点的坐标是,2PD+PC的最小值是.7如图,四边形ABCD是菱形,AB=4,且∠BAD=30°,P为对角线AC(不含A点)上任意一点,则DP+12AP的最小值为.8如图,四边形ABCD中,AB=62,∠ABC=45°,E是BD上一点,若∠ABD=15°,则AE+12BE的最小值为.9如图,矩形OABC中,点A、C分别在x轴,y轴的正半轴上,且OA=3,AB=1,点P为线段OA上一动点,则12OP+PB最小值为.3三.解答题(共5小题)1如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(0,-3),C(2,0),其对称轴与x轴交于点D.(1)求二次函数的表达式及其顶点坐标;(2)点M为抛物线的对称轴上的一个动点,若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,求点M的坐标;(3)若P为y轴上的一个动点,连接PD,求12PB+PD的最小值.2如图抛物线y=ax2+bx-4与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C.(1)求抛物线解析式.(2)连接BC,点P为BC下方上一动点,连接BP,CP.当△PBC的面积最大时,求点P的坐标和△PBC 面积的最大值.(3)点N为线段OC上一点,连接AN,求AN+12CN的最小值.3如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c与x轴交于点A、B两点,其中A(1,0),与y轴交于点C(0,3).(1)求抛物线解析式;(2)如图1,过点B作x轴垂线,在该垂线上取点P,使得△PBC与△ABC相似,请求出点P坐标;(3)如图2,在线段OB上取一点M,连接CM,请求出CM+12BM的最小值.4(1)【问题探究】如图1,点E是等边△ABC高AD上的一定点,请在AB上找一点F,使EF=12AE,并说明理由;(2)【问题解决】如图2,在△ACD中,CO⊥AD,垂足为O,若AD=32,AC=2,OC=3,点P在OC上,求DP+12PC的最小值.(3)【问题拓展】如图3,△ABC中,AB=AC=10,tan∠A=2,BE⊥AC于点E,D是线段BE上的一个动点,求CD+ 55BD的最小值.。
中考数学几何最值模型 专题06 胡不归模型(学生版+解析版)

胡不归模型从前,有一个小伙子在外地当学徒,当他得知在家乡的年老父亲病危的消息后,便立即启程日夜赶路。
由于思念心切,他选择了全是沙砾地带的直线路径A--B (如图所示:A 是出发地,B 是目的地,AC 是一条驿道,而驿道靠目的地的一侧全是沙砾地带),当他赶到父亲眼前时,老人已去世了,邻舍告诉小伙子时告诉说,老人在弥留之际还不断喃喃地叨念:胡不归?胡不归?一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BCV V +的值最小.V 2V 1MNCBA121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =, 即求BC +kAC 的最小值.构造射线AD 使得sin ∠DAN =k ,CH /AC =k ,CH =kAC .CH=kACsin α=CH AC=kHDαA BCNM模型讲解将问题转化为求BC +CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.MNCBAαDH在求形如“PA +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“PA +kPB ”型问题转化为“PA +PC ”型.方法点拨题型特征:PA+kPB (P 的运动轨迹为直线)1、将所求线段和改写为“PA+a b PB”的形式(a b <1,若a b>1,提取系数,转化为小于1的形式解决)。
2、在PB 的一侧,PA 的异侧,构造一个角度α,使得sinα=ab3、最后利用两点之间线段最短及垂线段最短解题例题演练1.如图,在△ABC中,∠A=15°,AB=2,P为AC边上的一个动点(不与A、C重合),连接BP,则AP+PB的最小值是()A.B.C.D.2【解答】解:如图,在△ABC内作∠MBA=30°过点A作AE⊥BM于点E,BM交AC于点P,∵∠BAC=15°,∴∠APE=45°∴EP=AP当BP⊥AE时,则AP+PB=PE+PB的值最小,最小值是BE的长,在Rt△ABE中,∠ABE=30°,AB=2∴BE=AB•cos30°=.∴AP+PB的最小值是.故选:B.2.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4,点D、F分别是边AB,BC上的动点,连接CD,过点A作AE⊥CD交BC于点E,垂足为G,连接GF,则GF+FB的最小值是()A.B.C.D.【解答】解:延长AC到点P,使CP=AC,连接BP,过点F作FH⊥BP于点H,取AC中点O,连接OG,过点O作OQ⊥BP于点Q,∵∠ACB=90°,∠ABC=30°,AB=4∴AC=CP=2,BP=AB=4∴△ABP是等边三角形∴∠FBH=30°∴Rt△FHB中,FH=FB∴当G、F、H在同一直线上时,GF+FB=GF+FH=GH取得最小值∵AE⊥CD于点G∴∠AGC=90°∵O为AC中点∴OA=OC=OG=AC∴A、C、G三点共圆,圆心为O,即点G在⊙O上运动∴当点G运动到OQ上时,GH取得最小值∵Rt△OPQ中,∠P=60°,OP=3,sin∠P=∴OQ=OP=∴GH最小值为故选:C.强化训练1.如图,AC是圆O的直径,AC=4,弧BA=120°,点D是弦AB上的一个动点,那么OD+BD的最小值为()A.B.C.D.2.如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE 上的一个动点,则CD+BD的最小值是.3.如图,△ABC中,AB=AC=10,tan A=3,CD⊥AB于点D,点E是线段CD的一个动点,则BE+CE的最小值是.4.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形点E为△BCD围成的区域(包括各边)的一点过点E作EM∥AB,交直线AC于点M作EN∥AC交直线AB于点N,则AN+AM的最大值为.5.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D、E分别是边BC、AC上的两个动点,且DE=4,P是DE的中点,连接P A,PB,则P A+PB 的最小值为.6.如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.7.如图,在菱形ABCD中,AB=6,点E是对角线BD上的一动点,且∠BCD =120°,则EB+EC+AE的最小值是.1.(2021•眉山中考真题)如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+PB的最小值是.胡不归模型从前,有一个小伙子在外地当学徒,当他得知在家乡的年老父亲病危的消息后,便立即启程日夜赶路。
胡不归模型整理
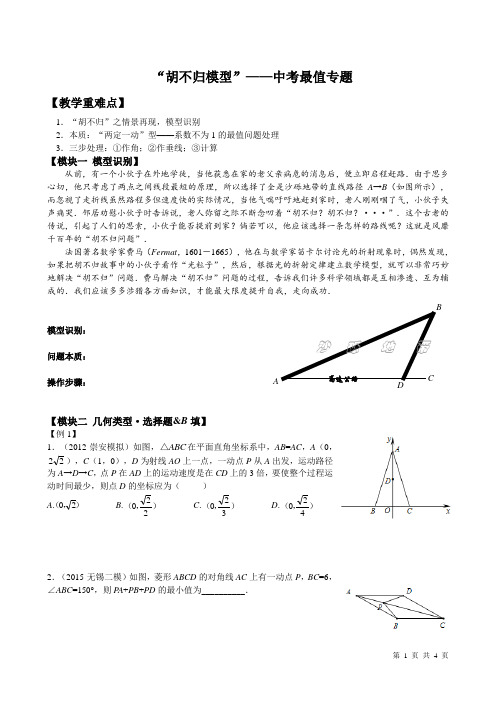
“胡不归模型”——中考最值专题【教学重难点】 1.“胡不归”之情景再现,模型识别 2.本质:“两定一动”型——系数不为1的最值问题处理3.三步处理:①作角;②作垂线;③计算【模块一 模型识别】从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路.由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径A →B (如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭.邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?···”.这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问题”.法国著名数学家费马(Fermat ,1601-1665),他在与数学家笛卡尔讨论光的折射现象时,偶然发现,如果把胡不归故事中的小伙子看作“光粒子”,然后,根据光的折射定律建立数学模型,就可以非常巧妙地解决“胡不归”问题.费马解决“胡不归”问题的过程,告诉我们许多科学领域都是互相渗透、互为辅成的.我们应该多多涉猎各方面知识,才能最大限度提升自我,走向成功.模型识别:问题本质: 操作步骤:【模块二 几何类型·选择题&B 填】【例1】1.(2012·崇安模拟)如图,ABC △在平面直角坐标系中,AB =AC ,A (0,22),C (1,0),D 为射线AO 上一点,一动点P 从A 出发,运动路径为A →D →C ,点P 在AD 上的运动速度是在CD 上的3倍,要使整个过程运动时间最少,则点D 的坐标应为( )A .),(20B . ),(220C . ),(320D . ),(4202.(2015·无锡二模)如图,菱形ABCD 的对角线AC 上有一动点P ,BC =6,∠ABC =150°,则P A +PB +PD 的最小值为__________.高速公路 A D B C沙 砾 地 带【模块三 A 20圆综合】【例2】(2015·内江)如图,在ACE △中,CA =CE ,∠CAE =30°,⊙O 经过点C ,且圆的直径AB 在线段AE 上.(1)试说明CE 是⊙O 的切线;(2)若ACE △中AE 边上的高为h ,试用含 h 的代数式表示⊙O 的直径AB ;(3)设点D 是线段AC 上任意一点(不含端点),连接OD ,当21CD +OD 的最小值为6时,求⊙O 的AB 的长.【模块三 二次函数综合·压轴】【例3】(2014·成都改编)如图,已知抛物线(2)(4)8k y x x =+-(k 为常数,k >0)与x 轴从左至右依次交于点A 、B ,与y 轴交于点C ,经过点B 的直线b x y +-=33与抛物线的另一个交点为D . (1)若点D 的横坐标为-5,求抛物线的函数关系式;(2)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A 出发,沿线段AF 以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止,当点F 的坐标为多少时,点M 在整个运动过程中用时最少?【例4】(2015·日照改编)如图,抛物线n mx x y ++=221与直线321+-=x y 交于A 、B 两点,交x 轴于D 、C 两点,连接AC 、BC ,已知A (0,3),C (3,0).(1)抛物线的函数关系式为____________________,tan ∠BAC =__________;(2)设E 为线段AC 上一点(不含端点),连接DE ,一动点M 从点D 出发,沿线段DE 以每秒一个单位的速度运动到E 点,再沿线段EA 以每秒2个单位的速度运动到点A 后停止,当点E 的坐标是多少时,点M 在整个运动过程中用时最少?【例5】(2016·徐州改编)如图,在平面直角坐标系中,二次函数y =ax 2+bx +c 的图像经过点A (-1,0), B (0,-3),C (2,0),其中对称轴与x 轴交于点D .(1)求二次函数的表达式及其顶点坐标;(2)若P 为y 轴上的一个动点,连接PD ,则PD PB +21的最小值为__________.【例6】(2016·随州改编)已知抛物线))(1)(3(≠-+=axxay,与x轴从左至右依次相交于A、B两点,与y轴交于点C,经过点A的直线bxy+-=3与抛物线的另一个交点为D.(1)若点D的横坐标为2,则抛物线的函数关系式为____________________;(2)在(1)的条件下,设点E是线段AD上一点(不含端点),连接BE,一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒332个单位运动到点D停止,问当点E的坐标为多少时,点Q运动的时间最少?。
特殊的平行四边形中的最值模型-胡不归模型(解析版)

特殊的平行四边形中的最值模型--胡不归模型胡不归模型可看作将军饮马衍生,主要考查转化与化归等的数学思想,近年在中考数学和各地的模拟考中常以压轴题的形式考查,学生不易把握。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:点到线的距离垂线段最短。
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.补充知识:在直角三角形中锐角A 的对边与斜边的比叫做∠A 的正弦,记作sin A ,即sin A =∠A 的对边斜边。
若无法理解正弦,也可考虑特殊直角三角形(含30°,45°,60°)的三边关系。
【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使AC V 2+BC V 1的值最小.(注意与阿氏圆模型的区分)1)AC V 2+BC V 1=1V 1BC +V 1V 2AC,记k =V 1V 2,即求BC +kAC 的最小值.2)构造射线AD 使得sin ∠DAN =k ,CH AC=k ,CH =kAC ,将问题转化为求BC +CH 最小值.3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“PA +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“PA +kPB ”型问题转化为“PA +PC ”型.(若k >1,则提取系数,转化为小于1的形式解决即可)。
中考数学几何最值模型第2讲胡不归问题

1
∴Rt△FHB中, = 2
∵Rt△OPQ中,∠P=60°,OP=3,sin∠P= =
3
∴OQ= 2 P=
故选:C.
3 3
-1
2
A
O
C
1
∴当G、F、H在同一直线上时, GF + 2 =GF+FH取得最小值
∵AE⊥CD于点G,∴∠AGC=90°
1
∴ OD + 的最小值为 3。
2
故选B.
3
2
D. 1 + 5
K
E
M
举一反三
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4,点D、F分别是边AB、BC上的动点,连接CD,过点A作
1
AE⊥CD交BC于点E,垂足为G,连接GF,则GF + 2 的最小值是( C )
A
A. 3 − 1
0, − 3
程的时间最短,则点G的坐标为______.
y
【解答】解:如图作GM⊥AB于点M,设电子虫在CG上的速度
为V,电子虫走完全程的时间 =
AC
CG
+
2
1 AG
+
2
=
,
1
B O
C
x
在Rt△AMG中,GM = 2 ,
y
1
∴电子虫走完全程的时间t = GM + ,
A
当C,G,M共线时,且CM⊥AB时,GM+CG最短,
∴BC= 2 + C 2 =
12 + 2 − 3
2
A
G
P
= 6 − 2,
中考数学经典几何模型之胡不归最值模型(解析版)

中考数学经典几何模型之胡不归最值模型(解析版)在数学中,经典几何模型是考试中经常出现的题型之一。
其中,胡不归最值模型是一种常见的最值问题。
这类问题通常涉及到形如“PA+kP”的式子,可以分为两类问题:胡不归问题和阿氏圆问题。
胡不归问题的故事源于一个少年外出求学,得知父亲病危后,他立即赶回家。
虽然他所在的位置到家的路上有一片砂石地,但他仍然义无反顾地走了这条路。
当他到家时,父亲已经去世了,他深感悔恨并痛哭流涕。
邻居告诉他,父亲在临终前一直念叨着“胡不归?胡不归?……”(“胡”同“何”)。
这个故事启发我们思考如何求解“PA+kP”型问题中的最值。
以胡不归问题为例,我们需要求解一个动点P在直线MN 外的运动速度为V1,在直线MN上运动的速度为V2,且V1<V2,A、B为定点,点C在直线MN上,确定点C的位置使得AC+BC的值最小,即求BC+kAC的最小值。
为了解决这个问题,我们可以构造射线AD使得sin∠DAN=k,即CH=kAC。
这样,我们可以将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小。
在解决“PA+kP”型问题时,关键是构造与kP相等的线段,将“PA+kP”型问题转化为“PA+PC”型。
而这里的P必须是一条方向不变的线段,方能构造定角利用三角函数得到kP的等线段。
举个例子,如图所示,在△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值为5.这个问题的关键在于处理“CD+BD”的式子,考虑tanA=2,△ABE三边之比为1:2:5,sin ABE⊥AB交AB于H点,则DH=BD/5.通过构造HD,我们可以将问题转化为求CD+CH的最小值,其中CH=kAC,k=sin∠DAN=BD/5.过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即CD+BD的最小值为5.综上所述,胡不归最值模型是一类常见的最值问题。
中考数学特殊的平行四边形中的最值模型胡不归模型

特殊的平行四边形中的最值模型--胡不归模型胡不归模型可看作将军饮马衍生,主要考查转化与化归等的数学思想,近年在中考数学和各地的模拟考中常以压轴题的形式考查,学生不易把握。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:点到线的距离垂线段最短。
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?” 看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.补充知识:在直角三角形中锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即斜边的对边A A ∠=sin 。
若无法理解正弦,也可考虑特殊直角三角形(含30°,45°,60°)的三边关系。
【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21A CBC V V +的值最小.(注意与阿氏圆模型的区分)1)121121=V A C B C B C A C V V V V ⎛⎫++ ⎪⎝⎭,记12V kV =,即求BC +kAC 的最小值.2)构造射线AD 使得sin ∠DAN =k ,C H kA C=,CH =kAC ,将问题转化为求BC +CH 最小值.3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“P A +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“P A +kPB ”型问题V 1V 2V 1驿道砂石地ABCV 2V 1MNCBA转化为“P A+PC”型.(若k>1,则提取系数,转化为小于1的形式解决即可)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“胡不归模型”——中考最值专题(一)
【教学重难点】
1.“胡不归”之情景再现,模型识别
2.本质:“两定一动”型——系数不为 1 的最值问题处理
3.三步处理:①作角;②作垂线;③计算
【模块一模型识别】
从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路.由于思乡
心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径A→ B(如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声
痛哭.邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?···”.这个古老的传
说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千
百年的“胡不归问题”.
法国著名数学家费马( Fermat,1601-1665),他在与数学家笛卡尔讨论光的折射现象时,偶然发现,如果把胡不归故事中的小伙子看作“光粒子”,然后,根据光的折射定律建立数学模型,就可以非常巧妙
地解决“胡不归”问题.费马解决“胡不归”问题的过程,告诉我们许多科学领域都是互相渗透、互为辅
成的.我们应该多多涉猎各方面知识,才能最大限度提升自我,走向成功.
B 模型识别:
沙砾地带问题本质:
操作步骤: A 高速公路 D C
B 填】
【模块二几何类型·选择题 &
【例 1】
1.( 2012·崇安模拟)如图,△ABC 在平面直角坐标系中,= ,( 0, 2 2 ),(1, 0),D 为射
AB AC A C
线上一点,一动点
P 从A 出发,运动路径为→ → ,点P 在上的运动速度是在上的 3 倍,要使AO A D C AD CD
整个过程运动时间最少,则点D的坐标应为()
A.(0,2)
B.(,2 )
C. (0,2 )
D. (0,2 )
2 4
3
2.( 2015 ·无锡二模)如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则PA+PB+PD 的最小值为 __________.
【模块三A20 圆综合】
【例 2】( 2015·内江)如图,在 △ACE 中, CA =CE , CAE =30°,⊙ O 经过点 C ,且圆的直径 AB 在线段
AE 上.
( 1)试说明 CE 是⊙ O 的切线;
( 2)若 △ ACE 中 AE 边上的高为 h ,试用含 h 的代数式表示⊙ O 的直径 AB ;
( 3)设点 D 是线段 AC 上任意一点 (不含端点) ,连接 OD ,当 1
CD +OD 的最小值为 6 时,求⊙ O 的 AB 的长.
2
【模块三 二次函数综合·压轴】
【例 3】( 2014·成都改编)如图,已知抛物线
y
k
( x 2)(x 4)
(k 为常数, k >0)与 x 轴从左至右依次
8
交于点 A 、B ,与 y 轴交于点 C ,经过点 B 的直线 y
3
x b 与抛物线的另一个交点为 D .
3
( 1)若点 D 的横坐标为- 5,求抛物线的函数关系式;
( 2)在( 1)的条件下,设 F 为线段 BD 上一点(不含端点),连接 AF ,一动点 M 从点 A 出发,沿线段 AF 以每秒 1 个单位的速度运动到 ,再沿线段 FD 以每秒 2 个单位的速度运动到 D 后停止, 当点 F 的坐标为多
F
少时,点 M 在整个运动过程中用时最少?
【例 4】( 2015·日照改编)如图,抛物线
y 1 x 2 mx n 与直线 y
1
x 3 交于 A 、B 两点,交 x
2
2
轴于 D 、 C 两点,连接 AC 、 BC ,已知 A (0, 3), C ( 3, 0).
(1)抛物线的函数关系式为 ____________________ , tan ∠BAC=__________;
(2)设E为线段AC上一点(不含端点),连接DE,一动点 M从点 D出发,沿线段 DE以每秒一个单位的
速度运动到 E 点,再沿线段 EA以每秒 2 个单位的速度运动到点 A 后停止,当点 E 的坐标是多少时,点 M 在整个运动过程中用时最少?
【例 5】( 2016·徐州改编)如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图像经过点A(-1,0),B(0,-3), C(2,0),其中对称轴与 x 轴交于点 D.
( 1)求二次函数的表达式及其顶点坐标;
( 2)若P为y轴上的一个动点,连接PD,则1
PB PD的最小值为__________.2
【例 6】( 2016·随州改编)已知抛物线y a(x 3)( x 1)(a 0),与x轴从左至右依次相交于A、 B 两点,与 y 轴交于点 C,经过点 A 的直线y 3x b 与抛物线的另一个交点为D.
( 1)若点 D 的横坐标为 2,则抛物线的函数关系式为 ____________________ ;
( 2)在( 1)的条件下,设点
E 是线段 AD 上一点(不含端点),连接 BE ,一动点 Q 从点 B 出发,沿线段
BE 以每秒 1 个单位的速度运动到点
,再沿线段
以每秒
2 3
个单位运动到点
D 停止,问当点
E 的坐标
E
ED
3
为多少时,点 Q 运动的时间最少?。
