三年级数学的不规则图形求面积练习
三年级 不规则图形面积的计算

第十讲:面积的实际应用知识梳理【知识要点】1、周长:封闭图形一周的长度,是它的周长。
长方形的周长 =(长+宽)×2正方形的周长 = 边长×42、面积:物体的表面或封闭图形的大小就是它们的面积。
边长是1厘米的正方形的面积是1平方厘米。
边长是1分米的正方形的面积是1平方分米边长是1米的正方形的面积是1平方米长方形的面积 = 长×宽正方形的面积 = 边长×边长3、一个图形剪掉一部分,面积一定会减少,但周长不一定会减少。
4、掌握换算的方法(1)高级单位化成低级单位:高级单位的数×进率大单位化小单位添0,如2平方米=(200)平方分米(想:平方米大,所以是大化小添0,因为1平方米=100平方分米,应该在2后面添两个0.)(2)低级单位聚成高级单位:低级单位的数÷进率小单位化大单位去0,如20000平方米=(2)公顷,(想:平方米小,所以是小化大去0,因为1公顷=10000平方米,应该去掉2后面的四个0.)5、周长相等的两个长方形,面积不一定相等。
面积相等的两个长方形,周长也不一定相等。
6、长方形和正方形的面积相等时,正方形的周长小。
7、长方形和正方形的周长相等时,正方形的面积大。
(如用同样长的绳子围成的正方形面积比长方形的面积大)面积单位换算1平方千米 = 100公顷 1公顷=10000 平方米 1平方米=100 平方分米 1平方分米=100平方厘米【例题一】小林要从左边的纸上剪下一个最大的正方形。
剩下部分是什么图形?它的面积是多少平方厘米?【拓展训练】一个长方形,长16分米,宽12分米,在这个长方形上尽可能剪下一个正方形,正方形的面积是多少?剩下图形的面积是多少?【例题二】求下列图形的周长。
12厘米 15厘米 15厘米12厘米 12厘米 9米10米 3米4米【拓展训练】(单位:cm )【例题三】李奶奶家房子东面有一块长方形菜地,菜地一边紧挨着墙壁(如右图),少先队员们要给李奶奶的菜地围上篱笆,需要准备多长的篱笆?这块菜地的面积是多少平方米?【拓展训练】李大爷靠东墙围了一个羊圈,算出这个羊圈的占地面积?如果要砌上围墙,围墙的长度应该是多少米?【例题四】一块面积有72平方分米的长方形台布,长9分米,它的宽是多少?57 522 18米 3米 墙18 25米东墙【拓展训练】一块正方形的喷水池的周长是20米,它的边长是多少米?面积是多少平方米?【例题五】3平方米=()平方分米 5平方分米=()平方厘米700平方厘米=()平方分米600平方分米=()平方厘米30平方分米=()平方厘米 8000平方分米=()平方米【拓展训练】1、教室地面的面积大约是60(),也就是6000()。
三年级人教版不规则图形的面积剪纸练习

不规则图形的面积是数学中的一个重要内容,通过剪纸练习,可以帮助三年级的学生更好地理解和掌握这个概念。
下面,我将为大家介绍一些有趣的不规则图形剪纸练习,帮助学生们巩固所学知识。
1.剪纸练习-蝴蝶材料:彩纸、剪刀、胶水步骤:1)将彩纸折叠成半,再将半张纸对折成四分之一,然后将对角线连接成一个三角形。
2)在三角形的一侧切几个小缺口,类似蝴蝶的翅膀形状。
3)展开纸片,将两片相同的图形叠在一起,用胶水固定。
4)测量蝴蝶的面积。
要求学生通过测量蝴蝶的面积,了解不规则图形的面积计算方法。
可以引导学生先将整张纸平铺成一个长方形,再通过将小三角形切割并移动,形成一个矩形或多边形,从而计算出不规则图形的面积。
2.剪纸练习-树材料:彩纸、剪刀、胶水步骤:1)将彩纸对折成半张纸,然后将半张纸再对折成四分之一张纸。
2)在纸的底部画出一个树冠的形状,再画出一个长方形的树干。
3)将纸沿着轮廓线剪下。
4)展开纸,将两片相同的图形叠在一起,用胶水固定。
5)测量树的面积。
这个练习可以帮助学生们理解不规则图形的面积计算方法。
可以引导学生们将纸张展开,形成一个长方形,再通过对纸的折叠和剪切,形成一个近似长方形的形状,从而计算出树的面积。
3.剪纸练习-小鸟材料:彩纸、剪刀、胶水步骤:1)将彩纸对折成半张纸,然后将半张纸再对折成四分之一张纸。
2)在纸的底部画出一个小鸟的形状。
3)将纸沿着轮廓线剪下。
4)展开纸,将两片相同的图形叠在一起,用胶水固定。
5)测量小鸟的面积。
这个练习可以帮助学生们通过剪纸的方式,掌握不规则图形的面积计算方法。
可以引导学生们将纸片展开,通过切割和移动,形成一个近似长方形的形状,从而计算出小鸟的面积。
通过上述的不规则图形剪纸练习,三年级的学生们可以通过实际操作,了解不规则图形的面积计算方法。
在练习中,引导学生们注意规范测量,合理剪切,以及记录计算过程等,培养他们的观察力、动手能力以及实际问题解决能力。
同时,还可以通过比较不同图形的面积大小,培养学生对数量和大小的认识,以及对几何概念的理解。
小学三年级下册数学“求图形面积”的10种方法,考试必考题型

小学三年级下册数学“求图形面积”的10种方法,考试必考题型!实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如:下图,求阴影部分的面积。
三年级下册数学素材方法技巧练——求不规则图形的面积

方法技巧练——求不规则图形的面积
莹莹的爸爸是一名设计师,爸爸绘制了这样几幅图(单位:米)。
1.工厂厂房俯视图(从工厂上方看工厂)。
请你算一算这个工厂厂房占地面积是多少平方米?
想:可以将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
2.办公楼正面图(从正面看办公楼)。
(单位:米)
办公楼正面墙贴瓷砖,贴瓷砖的面积是多少平方米?
想:可以用大面积-小面积求出不规则图形的面积。
3.一块花圃的设计图。
长35米、宽25米的长方形地中间纵横留着两条1米的互相垂直的小路,其余部分是花圃,花圃的面积是多少?
想:将图形中某一部分割下来平行移动到一个恰当的位置,使之组合成一个新的基本规则图形。
方法技巧练——求不规则图形的面积
1.15×18+(40-15)×35=1145(平方米)(方法不唯一)
2.52×20-18×17=734(平方米)
3.(35-1)×(25-1)=816(平方米)。
三年级下册数学求不规则图形的面积

1、你有什么好的方法计算所给图形的面积呢?(单位:厘米)
方法一:采用分割法,可给原图分成两个长方形(图1或图2),两个长方形的总面积就是所求的面积.
图1面积是:4×(9+3)+9×3=75(平方厘米)
图2面积是:(9+4)×3+9×4=75(平方厘米)
方法二:采用补图法,如果补上一个边长是9厘米的正方形(图3),就成了一个大长方形.因此用这个长方形的面积减去所补正方
形的面积,就是要求的图形面积
图3面积是:
(4+9)×(9+3)-9×9=75(平方厘米)
2、如图是学校操场一角,请计算它的面积(单位:米)
【解析】可以在图中添上一条辅助线,把多边形切割成上下两个长方形或左右两个长方形;也可以把多边形补充完整,成为一个长方形;
方法一:
30×40+20×(30+40)=2600(平方米)
方法二:
20×30+40×(20+30)=2600(平方米)
方法三:
(40+30)×(20+30)-30×30=2600(平方米)。
小学三年级数学上册易错题面积计算及答案(必考题)

小学三年级数学上册易错题面积计算及答案(必考题)1、计算下面图形的周长.2、计算下面图形的周长.(单位:厘米)(1) (2)(3) (4)3、求下面图形的周长.4、根据图形列式计算。
5、计算下面图形的周长。
(单位:)(1)(2)6、计算下面各图形的面积。
7、计算下面图形的周长.8、先测量所需要的数据,再算出每个图形的周长。
(取整毫米数)(1)(2)9、计算下面各图形的面积。
(单位:厘米)10、计算下面菜地和果园的面积。
菜地面积:果园面积:11、计算下面各图形的周长.(单位:厘米)12、下图是由一个边长是7厘米的大正方形和一个边长是2厘米的小正方形拼成的,求它的周长。
13、计算下面图形的周长(单位:厘米)。
(1)(2)14、你能计算出下面图形的面积吗?(单位:厘米)(提示:长方形的面积=长×宽正方形的面积=边长×边长)15、计算下面各个图形的周长。
参考答案1、(2+5)×2=14(厘米)2、(1)21厘米(2)154厘米 (3)54厘米(4)28厘米3、(41+16)×2=114(厘米)(1+3)×2=8(厘米)25×4=100(米)4、6 85、19cm,20cm6、1728cm2;1849cm27、(18+19)×2=74(米)15×4=60(分米)8、(1)70毫米;(2)84毫米9、64平方厘米;78平方厘米10、100平方米220平方米11、22厘米,20厘米,28厘米,38厘米12、32厘米13、(1)18厘米;(2)92厘米14、36平方厘米 25平方厘米15、74cm;52cm;48cm。
【北师大版】三年级数学下册五面积:什么是面积练习
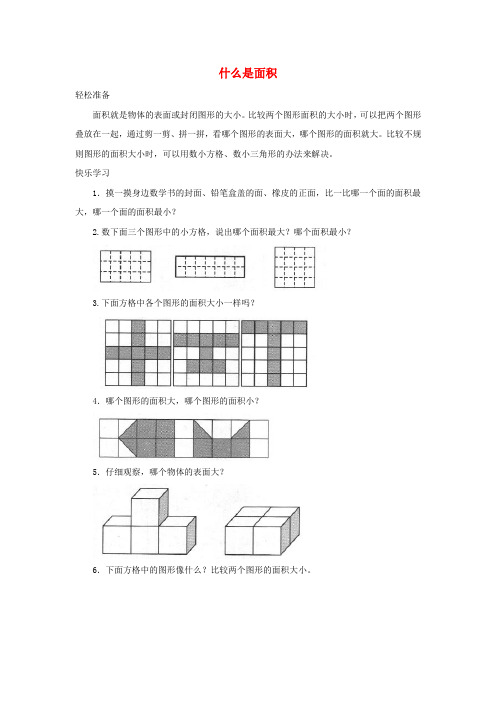
什么是面积
轻松准备
面积就是物体的表面或封闭图形的大小。
比较两个图形面积的大小时,可以把两个图形叠放在一起,通过剪一剪、拼一拼,看哪个图形的表面大,哪个图形的面积就大。
比较不规则图形的面积大小时,可以用数小方格、数小三角形的办法来解决。
快乐学习
1.摸一摸身边数学书的封面、铅笔盒盖的面、橡皮的正面,比一比哪一个面的面积最大,哪一个面的面积最小?
2.数下面三个图形中的小方格,说出哪个面积最大?哪个面积最小?
3.下面方格中各个图形的面积大小一样吗?
4.哪个图形的面积大,哪个图形的面积小?
5.仔细观察,哪个物体的表面大?
6.下面方格中的图形像什么?比较两个图形的面积大小。
7.下面图形的面积哪个大?
8.数一数每个图形的面积等于几个方格那么大。
9.在下面的方格里画一个正方形和一个三角形,使正方形面积正好是三角形面积的2倍。
10.填空。
图②的面积是图①面积的( )倍,图③的面积是图①面积的( )倍。
拓展提高
11.下面两个图形的面积哪个大?
12.设计几个你喜欢的图案,画在下面的方格里,要求它们的面积都要等于7个方格。
13.下面三个图形中,哪两个图形的面积相等?请把面积相等的两个图形涂上蓝色。
14.利用方格网数出下面图形的面积。
答案与点拨
3.一样
4.左边的大,右边的小。
5.左边物体表面大。
6.像桌子和椅子,两个图形的面积同样大。
7.右边图形面积大。
8.每个图形的面积都是8个方格。
10. 4 3
11.左边图形面积大。
三年级分割法求面积例题

三年级分割法求面积例题三年级分割法求面积例题在数学中,分割法是一种常用的方法来求解形状复杂的图形的面积。
这种方法将复杂的图形分割成较简单的几何形状,然后通过计算这些简单形状的面积,最终得到整个图形的面积。
下面是一个三年级的分割法求面积的例题,让我们一起来解决它吧!例题:小明有一块不规则形状的地板,他想知道这块地板的面积。
他将这块地板进行分割,如图所示。
```A-----------B-----------C| | || | || | || | |D-----------E-----------F| | || | || | || | |G-----------H-----------I```小明将地板分割成了9个小正方形区域,每个小正方形的边长都为2米。
他已经知道其中两个小正方形的面积分别为4平方米和9平方米。
请你帮助小明计算整个地板的面积是多少平方米。
解题思路:我们可以先计算出这两个已知小正方形的面积,然后再将它们相加得到部分面积。
接下来,我们需要计算剩余的7个小正方形的面积并相加,得到整个地板的面积。
解题步骤:1. 已知小正方形ABEF的面积为4平方米,边长为2米,所以ABEF 的面积为2 * 2 = 4平方米。
2. 已知小正方形CEFI的面积为9平方米,边长为3米,所以CEFI 的面积为3 * 3 = 9平方米。
3. 将ABEF和CEFI的面积相加得到部分面积,即4平方米 + 9平方米 = 13平方米。
4. 剩余的7个小正方形的边长都为2米,所以它们的面积都为2 * 2 = 4平方米。
5. 将剩余7个小正方形的面积相加得到整个地板的面积,即7 * 4平方米 = 28平方米。
6. 所以整个地板的面积为13平方米 + 28平方米 = 41平方米。
答案:这块地板的面积为41平方米。
通过这个例题,我们可以看到分割法是一种简单且有效的方法来求解复杂图形的面积。
在实际生活中,我们可以将地图、房间布局等各种形状的图形都通过分割法来求解其面积。
