北师大数学七年级下册 第二章平行线与相交线 期末复习
北师大七年级数学下册 相交线与平行线 期末复习

七年级数学(下) 期末复习知识点整理相交线1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表: 图形 顶点 边的关系 大小关系 对顶角∠1与∠2 有公共顶点∠1的两边与∠2的两边互为反向延长线对顶角相等 即∠1=∠2邻补角∠3与∠4有公共顶点∠3与∠4有一条边公共,另一边互为反向延长线。
∠3+∠4=180°注意点:⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2、垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:如图所示:AB ⊥CD ,垂足为O⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:垂线段最短。
3、垂线的画法:⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的1 2 4 3 A B C DO另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4、点到直线的距离直线外一点到这条直线的垂线段的长度,叫做点到直线的距离 记得时候应该结合图形进行记忆。
如图,PO ⊥AB ,同P 到直线AB 的距离是PO 的长。
北师版七下数学第二章相交线与平行线末复习

P
a
b
c
A
B
(6)平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
A
D
性质3:两直线平行,同旁内角互补.
41 2
3
B
C
(7)平行线的判定:
判定1:同位角相等,两直线平行.
判定2:内错角相等,两直线平行.
A
D
判定3:同旁内角互补,两直线平行.
3.下列图形中,由AB∥CD,能得到∠1=∠2的是
( B)
4. 如图,直线L1∥L2,则∠α为( D )
A.150° B.140° C.130° D.120°
5.(1)如图,已知∠1=∠2,试判断a、b的位置
关系.(2)直线a//b,∠1=∠2吗?为什么?
解:(1)a∥b.理由: 因为∠1=∠2,又因为∠2=∠3(对顶 角 相 等 ) , 所 以 ∠ 1 = ∠ 3 , 所 以 a∥b (同位角相等两直线平行). (2)∠1=∠2.理由:因为a∥b,所以 ∠1=∠3(两直线平行,同位角相等).又 因为∠2=∠3(对顶角相等).所以∠1 =∠2.
6.如图,已知△ABC,AD⊥BC于D,E为AB上一点, EF⊥BC于F,DG//BA交CA于G.∠1与∠2相等吗? 为什么?
解:∠1=∠2.理由: 因为AD⊥BC,FE⊥BC, 所以∠EFB=∠ADB=90°,所以EF//AD, 所以∠2=∠3, 因为DG//BA,所以∠3=∠1,所以∠1=∠2.
P
AB
O
l C
性质2:连接直线外一点与直线上各点的所有线段 中,垂线段最短.
(5)平行线:在同一平面内,不相交的两条直线
北师大版七年级数学下册第二章相交线与平行线期末证明题综合复习练习题
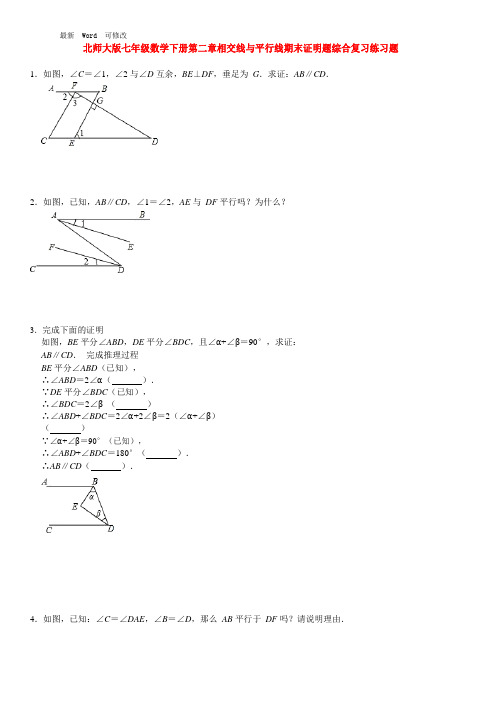
北师大版七年级数学下册第二章相交线与平行线期末证明题综合复习练习题1.如图,∠C=∠1,∠2 与∠D 互余,BE⊥DF,垂足为G.求证:AB∥CD.2.如图,已知,AB∥CD,∠1=∠2,AE 与DF 平行吗?为什么?3.完成下面的证明如图,BE 平分∠ABD,DE 平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.完成推理过程BE 平分∠ABD(已知),∴∠ABD=2∠α().∵DE 平分∠BDC(已知),∴∠BDC=2∠β ()∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)()∵∠α+∠β=90°(已知),∴∠ABD+∠BDC=180°().∴AB∥CD().4.如图,已知:∠C=∠DAE,∠B=∠D,那么AB 平行于DF 吗?请说明理由.5.如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB 与EF 的位置关系,并说明理由.6.如图,四边形ABCD 中,AD∥BC,F 为AB 边上一点,且∠ADF=∠CDB,射线DF、CB 相交于点E,∠BFE =∠CBD,求证:AB∥CD.7.如图,直线AB 和直线BC 相交于点B,连接AC,点D、E、H 分别在AB、AC、BC 上,连接DE、DH,F 是DH 上一点,已知∠1+∠3=180°(1)求证:∠CEF=∠EAD;(2)若DH 平分∠BDE,∠2=α,求∠3 的度数.(用α表示).8.如图,已知∠1=∠BDC,∠2+∠3=180°,(1)问 AD 与 EC 平行吗?试说明理由;(2)若DA 平分∠BDC,CE⊥AE 于E,∠1=70°,试求∠FAB 的度数.9.如图,在四边形ABCD 中,分别取AB,CD 延长线上的一点E 和F,连接EF,分别交BC,AD 于点G 和H,若∠1=∠2,∠A=∠C,求证:∠E=∠F.10.如图,已知AB∥CD,∠A=40°.点P 是射线AB 上一动点(与点A 不重合),CE、CF 分别平分∠ACP 和∠DCP 交射线AB 于点E、F.(1)求∠ECF 的度数;(2)随着点 P 的运动,∠APC 与∠AFC 之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;(3)当∠AEC=∠ACF 时,求∠APC 的度数.11.已知直线CD⊥AB 于点O,∠EOF=90°,射线OP 平分∠COF.(1)如图1,∠EOF 在直线CD 的右侧:①若∠COE=30°,求∠BOF 和∠POE 的度数;②请判断∠POE 与∠BOP 之间存在怎样的数量关系?并说明理由.(2)如图2,∠EOF 在直线CD 的左侧,且点E 在点F 的下方:①请直接写出∠POE 与∠BOP 之间的数量关系;②请直接写出∠POE 与∠DOP 之间的数量关系.12.如图,∠1+∠2=180°,∠A=∠C,DA 平分∠BDF.(1)A E 与FC 会平行吗?说明理由;(2)A D 与BC 的位置关系如何?为什么?(3)B C 平分∠DBE 吗?为什么.13.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C 的度数.14.如图,在三角形ABC 中,点D、G 分别为边BC、AB 上的点,DE⊥AC 于点E,BF⊥AC 于点F,连接FG,且∠BFG+∠BDE=180°.(1)求证:DE∥BF;(2)猜想∠AGF 与∠ABC 的数量关系,并证明你的猜想.15.思考:填空,并探究规律如图1,图2,OA∥EC,OB∥ED,∠AOB=30°,则图1 中∠CED=°;图2 中∠CED=°;用一句话概括你发现的规律证明:请利用图1,图 2 证明你发现的规律;应用:已知∠AOB=80°,∠CED=x°,OA∥CE,OB∥ED,则x 的值为(直接写出答案).16.如图1,BC⊥AF 于点C,∠A+∠1=90°.(1)求证:AB∥DE;(2)如图2,点P 从点A 出发,沿线段AF 运动到点F 停止,连接PB,PE.则∠ABP,∠DEP,∠BPE 三个角之间具有怎样的数量关系(不考虑点P 与点A,D,C 重合的情况)?并说明理由.17.如图1,已知l1∥l2,点A,B 在直线l1 上,点C,D 在l2 上,连接AD,BC.AE,CE 分别是∠BAD,∠BCD的平分线,∠1=70°,∠2=30°.(1)求∠AEC 的度数;(2)如图2,将线段AD 沿线段CD 方向平移,其他条件不变,求∠AEC 的度数.18.阅读下面材料:小明遇到这样一个问题:如图1,AC∥BD,点E 为直线AC 上方一点,连接CE、DE,猜想∠C、∠D、∠E 的数量关系,并证明.小明发现,可以过点E 作MN∥AC 来解决问题,如图2,请你完成解答;用学过的知识或参考小明的方法,解决下面的问题:如图3,AB∥CD,P 是平面内一点,连接AP、CP,使AP∥BD,∠APC=100°,BM、CM 分别平分∠ABD、∠DCP 交于点M,求∠M 的度数.19.如图,已知AB∥DC,BF 平分∠ABE,CF 平分∠DCE,BF 与CF 相交于F(1)如图①,若∠F=30°,求∠E 的度数;(2)如图②,若设∠F=α,∠E=β,请你猜想α与β之间的关系(直接写出结果不用说明理由);(3)在图③中,(2)中α与β之间的关系是否仍然成立?若成立说明理由,若不成立写出它们之间的关系,并说明理由.20.如图1,AB∥CD,点E 是直线AB、CD 之间的一点,连接EA、EC.(1)探究猜想:①若∠A=20°,∠C=50°,则∠AEC=.②若∠A=25°,∠C=40°,则∠AEC=.③猜想图1 中∠EAB、∠ECD、∠AEC 的关系,并证明你的结论(提示:作EF∥AB).(2)拓展应用:如图2,AB∥CD,线段MN 把ABCD 这个封闭区域分为I、Ⅱ两部分(不含边界),点E 是位于这两个区域内的任意一点,请直接写出∠EMB、∠END、∠MEN 的关系.21.(1)如图①,若AB∥CD,求∠B+∠D+∠E1 的度数?(2)如图②,若AB∥CD,求∠B+∠D+∠E1+∠E2 的度数?(3)如图③,若AB∥CD,求∠B+∠D+∠E1+∠E2+∠E3 的度数?(4)如图④,若AB∥CD,猜想∠B+∠D+∠E1+∠E2+…+∠E n 的度数?22.如图 1,MN ∥PQ ,直线 AD 与 MN 、PQ 分别交于点 A 、D ,点 B 在直线 PQ 上,过点 B 作 BG ⊥AD ,垂足为点G .(1)求证:∠MAG +∠PBG =90°;(2)若点 C 在线段 AD 上(不与 A 、D 、G 重合),连接 BC ,∠MAG 和∠PBC 的平分线交于点 H ,请在图 2 中补全图形,猜想并证明∠CBG 与∠AHB 的数量关系;(3)若直线 AD 的位置如图 3 所示,(2)中的结论是否成立?若成立,请证明;若不成立,请直接写出∠CBG 与∠AHB 的数量关系.1、最困难的事就是认识自己。
北师大版七年级数学下册第二章 相交线与平行线 期末单元提高复习试题(PDF版,无答案)
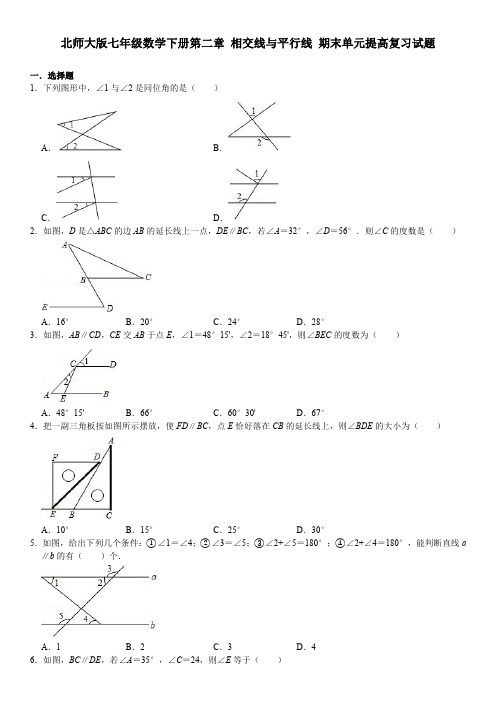
是多少度?
28.如图,已知,BC∥OA,∠C=∠OAB=100°,试回答下列问题: (1)如图 1,求证:OC∥AB; (2)如图 2,点 E、F 在线段 BC 上,且满足∠EOB=∠AOB,并且 OF 平分∠BOC: ①若平行移动 AB,当∠BOC=6∠EOF 时,求∠ABO;
②若平行移动 AB,
请你根据图形完成以下问题:
(1)如图 1,如果 AB∥CD,BE∥DF,那么∠1 与∠2 的关系是
;
如图 2,如果 AB∥CD,BE∥DF,那么∠1 与∠2 的关系是
;
(2)根据(1)的探究过程,我们可以得到结论:如果一个角的两边与另一个角3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的 3 倍少 40°,则这两个角分别
15.如图,CD∥AB,AC⊥BC,∠ACD=60°,那么∠B 的度数是__________. 16.如图,若 AB∥CD,CD∥EF,那么∠BCE 等于__________.
三、解答题
17.如图,在△ABC 中,∠A=∠B,D、E 是边 AB 上的点,DG∥AC,EF∥BC,DG、EF 相交于点 H.
;
(2)由(1)猜想∠ACB 与∠DCE 的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE 的角度所有可能的值(不必说明理由);
若不存在,请说明理由.
23.(1)如图 1,已知 AB∥CD,那么图 1 中∠PAB、∠APC、∠PCD 之间有什么数量关系?并说明理由. (2)如图 2,已知∠BAC=80°,点 D 是线段 AC 上一点,CE∥BD,∠ABD 和∠ACE 的平分线交于点 F,请利 用(1)的结论求图 2 中∠F 的度数.
北师大版七年级数学下册第二章相交线与平行线复习课件

因为S△ABC = 1/2 AB×CD 所=以C1D=/2.24cmAC×BC
4.你能求出点C到AB的距离吗?你是
怎样做的?小组合作交流.
等面积法
三线八角:
C
两条直线AB与CD被第三条
3
E 1
直线EF所截,形成:
75
D
(2)
解:∵AD//BC(已知)
∴∠2+∠4=180°
A1
D
4
(两直线平行,同旁内角互补) 2
3
又∵∠1=∠4(对顶角相等)
B
C
∴∠1+∠2=180°(等量代换)
已知AB∥CD,E为平面内一点(E不在AB和CD
上),连接AE,CE,探索∠AEC与∠A,∠C之间
的关系。
情况1
E在AB与CD之间且向内凹
的度数。
DC
1 25 7
3 46 AE B
16.如图,两平面镜所成的角为 ∠1,一束光线由点P发出,经 OB,OA两次反
后(,1∠)1=P1Q2与0°R∠CP平Q行B吗=4?0° B
变式 P
(2)要使 PQ与RC平行 Q
C
必须改变∠1和∠PQB任何一个角的度
数,问要改变哪一个角?这个角改变
后度数是多少?
EB与AD一定平行吗?”。 ❖小王说“一定平行”;
D
E1
❖而小李说“不一定平行”。
❖你更赞同谁的观点?
❖为什么?
A
B
C
E2
操作与解释
二、强化知识、技能训练
1.(1)若∠1=50 °,
则∠2 =___5_0_°__
ED
∠BOC=__1_3_0_°__
七年级下册第二章相交线与平行线复习总结(全)
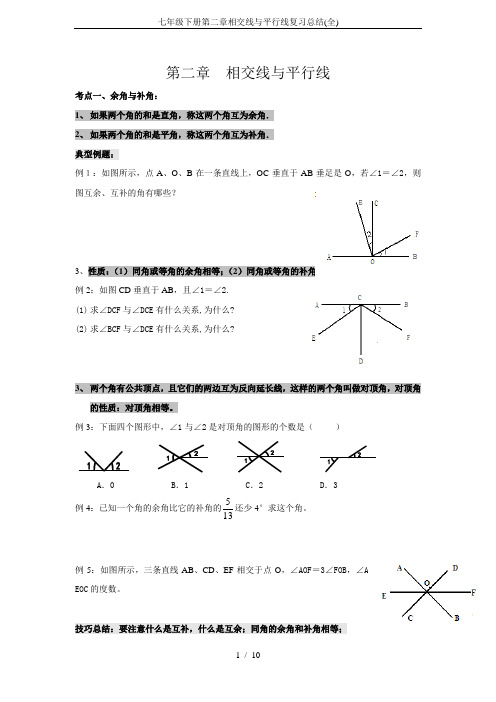
第二章 相交线与平行线考点一、余角与补角:1、 如果两个角的和是直角,称这两个角互为余角.2、 如果两个角的和是平角,称这两个角互为补角. 典型例题:例1:如图所示,点A 、O 、B 在一条直线上,OC 垂直于AB 垂足是O ,若∠1=∠2,则图互余、互补的角有哪些?3、性质:(1)同角或等角的余角相等;(2)同角或等角的补角相等。
例2:如图CD 垂直于AB ,且∠1=∠2. (1) 求∠DCF 与∠DCE 有什么关系,为什么? (2) 求∠BCF 与∠DCE 有什么关系,为什么?3、 两个角有公共顶点,且它们的两边互为反向延长线,这样的两个角叫做对顶角,对顶角的性质:对顶角相等。
例3:下面四个图形中,∠1与∠2是对顶角的图形的个数是( )12121212A .0B .1C .2D .3 例4:已知一个角的余角比它的补角的135还少4°求这个角。
例5:如图所示,三条直线AB 、CD 、EF 相交于点O ,∠AOF =3∠FOB ,∠AOC=90°,求∠EOC 的度数。
技巧总结:要注意什么是互补,什么是互余;同角的余角和补角相等;对应的课堂练习:一、填空题1.如图1,直线l1与l2相交,∠1=50°,则∠2=_________,∠3=_________.图1 图22.如图2,直线AB与CD相交于O点,且∠AOD=90°,则∠AOC=_________=_________ =_________=_________.3.如图3,若AO⊥CO,BO⊥DO,∠BOC=150°,则∠DOC=________,∠AOD=________.图3 图44.如图4,直线AB与CD相交于O,∠EOD=90°,正确填写下列两角关系的名称.∠1与∠2:______________________________________________________∠2与∠3:______________________________________________________∠2与∠4:______________________________________________________∠1与∠4:______________________________________________________三、选择题1.两条直线相交于一点,则共有对顶角的对数为()A.1对B.2对C.3对D.4对2.下面说法正确的个数为()①对顶角相等②相等的角是对顶角③若两个角不相等,则这两个角一定不是对顶角④若两个角不是对顶角,则这两个角不相等A.1个B.2个C.3个D.4个3.若∠1和∠2互余,∠2与∠3互余,∠1=40°,则∠3等于( ) A.40°B.130°C.50°D.140°4.如图,∠1和∠2是对顶角的图形有( )A.(1)(3)B.(2)(3)C.(3)D.(3)(4)一、判断题1.若∠1+∠2=90°,则∠1与∠2互余.( )2.若∠A 与∠B 互补,则∠A +∠B =180°.( )3.若∠1与∠2互补,∠2与∠3互补,则∠1与∠3互补.( )4.若∠AOB +∠BOC =180°,则点A 、O 、C 必在同一直线上.( )5.若∠α+∠β+∠γ=90°,则∠α、∠β、∠γ互余.( ) 四、解答题1.如图,AO ⊥BO ,直线CD 经过点O ,∠AOC =30°,求∠BOD 的度数.考点二、探索直线平行的条件同位角的特征:(1)在被截两直线的同旁;(2)在截线的两旁 内错角的特征:(1)在被截两直线之间;(2)在截线的两旁 同旁内角的特征:(1)在被截两直线之间;(2)在截线的同旁 例1:如图,写出图中的同位角、内错角和同旁内角。
2023年北师大版七年级下册数学期末复习第二章相交线与平行线

A
B
C
D
2. 如图,对顶角共有( B ) A.1对 B.2对 C.3对 D.4对
·数学
·数学
【例3】如图,直线a,b,c两两相交,∠1=60°,∠3= 28°,则∠4= 28° .
·数学
3.如图是一把剪刀,其中∠1=120°,则∠2= 120° , 其理由是 对顶角相等 .
·数学
知识要点3 补角 【例4】(1)如图,直线a与直线c相交于点O,∠1的度数是 ( D)
·数学
12.如图,∠2的内错角是( C ) A.∠2 B.∠3 C.∠4 D.∠5
·数学
·数学
【例13】如图,直线a,b被直线c所截,则下列说法中错误 的是( B ) A.∠1与∠2是邻补角 B.∠2与∠3是对顶角 C.∠2与∠4是同位角 D.∠3与∠4是同旁内角
·数学
13.如图,已知直线a,b被直线c所截,则∠1和∠2是一对 ( D) A.对顶角 B.同位角 C.内错角 D.同旁内角
15.如图,能判定EC∥AB的条件是( D ) A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE
·数学
·数学
【例16】如图,下列条件中能判定a∥b的是( D ) A.∠1+∠4=180° B.∠1+∠3=180° C.∠1=∠5 D.∠3+∠4=180°
·数学
变式练习 16.如图,∠1,∠2,…,∠8是两条直线a,b被直线c所截 后形成的八个角,则能够判定直线a∥b的是( B ) A.∠3+∠4=180° B.∠1+∠8=180° C.∠5+∠7=180° D.∠2+∠6=180°
·数学
·数学 5.若∠1+∠2=90°,∠1=23°,则∠2= 67° .
2022-2023学年北师大版数学七年级下册 第二章 相交线与平行线 期末复习题
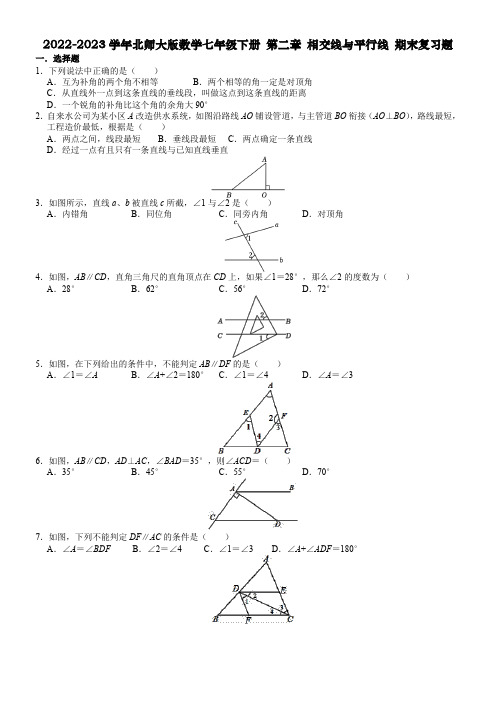
2022-2023学年北师大版数学七年级下册第二章相交线与平行线期末复习题一.选择题1.下列说法中正确的是()A.互为补角的两个角不相等B.两个相等的角一定是对顶角C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离D.一个锐角的补角比这个角的余角大90°2.自来水公司为某小区A改造供水系统,如图沿路线AO铺设管道,与主管道BO衔接(AO⊥BO),路线最短,工程造价最低,根据是()A.两点之间,线段最短B.垂线段最短C.两点确定一条直线D.经过一点有且只有一条直线与已知直线垂直3.如图所示,直线a、b被直线c所截,∠1与∠2是()A.内错角B.同位角C.同旁内角D.对顶角4.如图,AB∥CD,直角三角尺的直角顶点在CD上,如果∠1=28°,那么∠2的度数为()A.28°B.62°C.56°D.72°5.如图,在下列给出的条件中,不能判定AB∥DF的是()A.∠1=∠A B.∠A+∠2=180°C.∠1=∠4D.∠A=∠36.如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=()A.35°B.45°C.55°D.70°7.如图,下列不能判定DF∥AC的条件是()A.∠A=∠BDF B.∠2=∠4 C.∠1=∠3D.∠A+∠ADF=180°8.如图,在下列四组条件中,不能判断AD ∥BC 的是( )A .∠DAC =ACB B .∠ADB =∠DBC C .∠DAB +∠ABC =180°D .∠BAC =∠ACD9.如图,直线b ,c 被直线a 所截,则∠1与∠2是( ) A .对顶角 B .同位角 C .内错角D .同旁内角10.如图,在△ABC 中,∠BAC =40°,∠B =60°,AD ∥BC ,则∠DAC 大小为( ) A .20° B .40° C .60° D .80°11.下列图形中,由AB ∥CD ,能得到∠1=∠2的是( )A .B .C .D . 12.如图,已知AB ∥CD ,BC 平分∠ABE ,∠C =33°,则∠CEF 的度数是( ) A .66° B .49° C .33° D .16°13.如图,已知直线l 1∥l 2,直线l 与l 1,l 2分别相交于点A ,B ,把一块含30°角的直角三角尺按如图位置摆放,若∠1=130°,则∠ABD 的度数为( ) A .15° B .20° C .25° D .30°二.填空题(共7小题)11.若∠α=23°,则∠α的余角为 度,∠α的补角等于 . 12.一个角是它的补角的四分之一,则这个角的度数是 度.14.一个角比它的补角的13少40°,这个角等于 .15.如图,一艘轮船按箭头所示方向行驶,C 处有一灯塔,当轮船从A 点行驶到B 点时,∠ACB = °.16.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于.17.如图,一个弯形管道ABCD的拐角∠BCD=70°,管道所在直线AB∥CD,则∠ABC的度数是________;18.如图,点A,D,E三点在同一条直线上,在不添加辅助线的情况下,如果添加一个条件,使AB∥CD,则可以添加的条件为.(任意添加一个符合题意的条件即可)19.如图,C岛在A岛的北偏东52°方向,C岛在B岛的北偏西34°方向,则∠ACB=度.20.如图,AB∥CD,∠DCE=130°,则∠B的度数为度.21.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=40°,则∠2=度.22.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=68°,则∠ABO=,∠DCO=.三.解答题(共6小题)23.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.24.已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.25.如图,EF∥AD,∠1=∠2.则∠CGD与∠CAB相等吗?请说明理由.26.如图,已知AE∥BF,∠A=∠F,试说明:∠C=∠D.27.如图,EF∥AD,∠BAC=75°,若∠1=∠2,求∠AGD的度数.28.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.29.已知:如图∠BAC+∠GCA=180°,∠1=∠2.求证:∠E=∠F.30.(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(18)如图,如果AB∥EF,用含有α、 β、γ的式子表示X.
A B x
E
F
(14)如图, 已知AD∥BC, BO, CO分别 平分∠ABC,∠DCB. 若∠A+∠D=m, 则 ∠BOC= .
A O
D
B
C
(15)如图,点A、B、D共线,且BM∥AC, BN∥DE.若∠C=45°,∠EBC=60°, ∠E=30° ,求∠MBN的度数.
C
45o
NMLeabharlann E30oA
B
D
(16)如果∠A和∠B的两边分别平行, 那 么∠A和∠B的关系是 . (17)两平行直线被第三条直线所截,则 结论错误的是( ) A、内错角的平分线互相平行 B、同旁内角的平分线互相垂直 C、同位角的平分线平行 D、同位角的平分线不一定平行
3
A
C
三、两直线平行的判定: 同位角____________,两直线平行。 内错角____________,两直线平行。 同旁内角__________,两直线平行。
例:如图5,由∠1=∠3得___ //____( 由∠2=∠3得___ //____( ) 由∠3+∠4=180° 得___ // ____( ) 由∠2+∠4=180° 得___ // ____( ) )
例2:找出图中的同位角,内错角, 同旁内角: 同位角有__________ 内错角有__________
同旁内角有________
二、 同位角,内错角,同旁内角
如图,下列说法错误的是( ) A、∠A和∠B是同旁内角 B B、∠1和∠3是同位角 C、∠2和∠B是同位角 1 2 D、∠2和∠3是内错角
(11)如图,已知AD//BC,∠1=∠2, ∠A=112°,且BD⊥CD,则 ∠ABC=_____,∠C=_____.
(12)如图,CD⊥AB,EF⊥AB, ∠1=∠2,则∠AGD与∠ACB相等吗? 请说明理由。
A
D F 2 B E
1
G
C
(13)一艘轮船从A港出发沿 着北偏东65º 方向航行,行 驶至B处转向北偏西25º 方向 航行,到达C处需要把航向 恢复到出发时的航向,问应 如何调整航向?
(5)如图,已知四条直线AB,BC,AC,DE. 问: ③∠4=∠5是直线______和直线______ 被直线_____所截而成的____角. ④∠2=∠5是直线______和直线______ 被直线_____所截而成的____角.
(6)如图 ①∵∠1=∠2,∴_____∥_____, 理由是________________. ②∵AB∥DC,∴∠3=∠_______, 理由是_________________. ③∵AD∥______,∴∠5=∠ADC, 理由是__________________.
(7)如图,已知B、C、E在同一直线 上,且CD//AB,若∠A=55o,∠B=40o, 则∠ACE为_________.
(8)如图, a//b,,且∠2是∠1的2倍,
那么∠2等于————
(9) 如图, ∠1和∠2互补,∠3=130°,
那么∠4的度数是————
(10)如图, 若∠1+∠2+∠3+∠4=180°, 则_____________.
第二章 平行线与相交线
(期末复习)
本章知识结构图
第二章平行线与相交线
相交线
三线八角 两线四角
平行线
平 行 线 的 判 定 平 行 线 的 特 征
对 邻 顶 补 角 角
同 内 同 旁 错 位 内 角 角 角
用尺规作线段和角
作 一 线 段 等 于 已 知 线 段 作 一 个 角 等 于 已 知 角
知识回顾
四、平行线的特征: 两直线平行,同位角___________. 两直线平行,内错角____________. 两直线平行,同旁内角____________.
如右图,AB//CD,AD//BE,试说明∠ABE=∠D.
∵AB∥CD (已知) ∴∠ABE=______(两直线平行,内错角相等) ∵AD∥BE (已知) ∴∠D=______ ( ) ∴∠ABE=∠D ( 等量代换)
一、 余角、 补角、 对顶角 (对顶角相等)
1.例:如图, 互为余角的有_______
互为补角的有___________ 图中有对顶角吗?
答:_______
知识回顾
一、 余角、 补角、 对顶角 (对顶角相等)
2.如图: 对顶角有_______对. 它们分别是______.
二、 同位角,内错角,同旁内角
巩固练习
(1)∠A的余角是20°,那么 ∠A等于______度.
(2)∠A与∠B互补,如果 ∠ A=36° , 那 么 ∠ B 的 度 数 为 _________.
巩固练习
(3)如图所示,∠AOC=36, ∠DOE=90,则∠BOE=_______. (4)如图,有_________对对顶角.
(5)如图,已知四条直线AB,BC,AC,DE. 问: ①∠1=∠2 是 直 线 ______ 和 直 线 ______被 直线_____所截而成的____角. ②∠1=∠3是直线_____和直线_____ 被直线_____所截而成的____角.
