浙江省高三“五校联考”考试参考答案
浙江省2021-2023学年高三下学期五校联考语文试题及答案(逐题解析) 统编版高三总复习

浙江省2021-2023学年高三下学期五校联考语文试题及答案(逐题解析)统编版高三总复习2022学年第二学期五校联考试题高三年级语文学科命题:杭州学军中学一、语言文字运用1.下列各句中,没有错别字且加点字的注音全都正确的一项是()A.“燕京八景”中有“蓟门烟树”一景,意指北京前身蓟城的古城墙上树木蓊(wěng)郁,如雾如烟,古都残存的旧岁遗风,几近泯(mín)灭的明清趣味,在其身上都有。
B.一个农业产业能够发展起来,背后是创业者的筚路蓝缕、开拓者的不懈奋斗;能够成为知名品牌,凝结的是大众的心血(xuè),靠的是群众胼手胝(zhī)足,日夜付出。
C.近年来,网络谣言新伎俩(liǎng)不断涌现,网信办表示将建立溯源机制,加大对首发谣言信息平台和帐号的惩(chéng)处力度,这些举措无疑具有强大的震慑力。
D.当“碳水脑”“糖瘾症(zhèng)”等夺人眼球却又似是而非的概念纷至沓来时,戒瘾商品接踵(zhǒng)而至,这些半真半假的鼓躁反而容易使人们更加焦虑,无所适从。
【答案】B【解析】【详解】本题考查学生识记现代汉语常用字字音、字形能力。
A.“泯灭”的“泯”应读mǐn。
C.“帐号”的“帐”应为“账”。
D.“鼓躁”的“躁”应为“噪”。
故选B。
阅读下面的文字,完成下面小题。
香菜是一种有强烈气味的草本植物。
【甲】对香菜的爱憎,赤裸裸地写在食客的脸色上,外卖的留言中,火锅的蘸料里。
有人觉得,香菜是美食的“灵魂”,任何一盘平平无奇的凉拌菜只要撤上些许立刻就会惊艳无比;有人认为,香菜是料理的“黑手”,“不要香菜!不要香菜!不要香菜!”少说一遍都是对自己的不负责任。
或是如痴如醉,或是避犹不及,两派在美食江湖上可谓“势不两立”。
【乙】“无香不欢”还是“逢香寡欢”,这是每个人“舌尖上的选择”。
而当天壤之别的喜好遇到瞬息万变的市场,任何关注和猎奇的点都有可能转化为噱头和商机。
瞄准消费者味蕾的,有香菜薯片、香菜饼干、香菜冰淇淋;关乎消费者日常的,有香菜古龙水、香菜面膜、香菜沐浴露,【丙】“香菜星人”顶不住了,“买买买”就是对香菜最大的敬意;“反香菜星人”更顶不住,“一口入魂”是假,“一口惊魂”才是真!结果只有商家顶住了,收割了香菜爱好者的钱包,收获了香菜嫌恶者的关注,可谓两头赚!2.文段中的加点词语,运用不正确的一项是()A.势不两立B.天壤之别C.关乎D.结果3.文段中画线的甲、乙、丙句,标点误的一项是()A.甲B.乙C.丙【答案】2.B3.A【解析】【2题详解】本题考查学生正确运用词语的能力。
2021年10月浙江省五校(杭州高中杭州二中等)2021届高三毕业班上学期第一次联考数学试题及答案

绝密★启用前浙江省五校联考联盟(杭州高中 杭州二中 学军中学 绍兴一中 效实中学) 2022届高三毕业班上学期第一次联考质量检测数学试题2021年10月考生须知:1.本卷满分150分,考试时间120分钟;2.答题前,在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号;3.所有答案必须写在答题卷上,写在试卷上无效;4.考试结束后,只需上交答题卷。
参考公式:若事件A,B 互斥,则P(A +B)=P(A)+P(B)若事件A,B 相互独立,则P(AB)=P(A)P(B)若事件A 在一次试验中发生的概率是p,则n 次独立重复试验中事件A 恰好发生k 次的概率P n (k)=C n k p k (1-p)n -k (k =0,1,2,…,n)台体的体积公式:V =13(S 1+S 2)h 其中S 1、S 2分别表示台体的上、下底面积,h 表示台体的高柱体的体积公式:V =Sh其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式:V =13Sh 其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式:S =4πR 2球的体积公式:V =43πR 3 共中R 表示球的半径第I 卷(选择题部分,共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={x|0<x<2},B ={x|x 2+4x -5>0},则AI(∁R B)等于A.{x|0<x ≤1}B.{x|1≤x<2}C.{x|0<x<2}D.{x|-1≤x<2}2.已知点(1,1)在直线x +2y +b =0的下方,则实数b 的取值范围为A.b>-3B.b<-3C.-3<b<0D.b>0或b<-33.若a>b>0,m<0。
则下列不等式成立的是A.am 2<bm 2B.m b a ->1C.a m a b m b -<-D.22a m b m a b --> 4.已知sin(4π+α)=13,则cos(2π-2α)= A.-79 B.79C.-429D.429 5.函数f(x)=(1-x21e +)cosx(其中e 为自然对数的底数)的图象大致形状是6.有10台不同的电视机,其中甲型3台,乙型3台,丙型4台。
2021-2022学年浙江省五校(学军中学 杭二中等)高三上学期第一次联考 地理(解析版)
(1)莱茵兰-普法尔茨州的典型自然植被是____,分析当地旱涝灾害少的主要原因____。
(2)从地形角度,分析莱茵兰-普法尔茨州水灾严重的原因。
(3)简述荷兰打造人工渠道 必要性,并分析境内人工运河含沙量少的原因。
29.阅读图文材料,回答下列问题。
材料一:红芸豆是山西特产。岢岚县河流两岸的河谷平原是红芸豆的主产区。当地采用“豆类-谷物”轮作倒茬方式种植。4月-5月上旬播种;生长适宜温度为15~25℃,10℃以下低温或30℃以上高温会影响生长;光照弱时红芸豆容易落花落荚;要少浇勤浇,不可积水。
(3)指出“公司+合作社+农户(基地)”的农业产业化经营新模式的优越性。
2021学年第一学期五校联考试题
高三年级地理学科
一、选择题
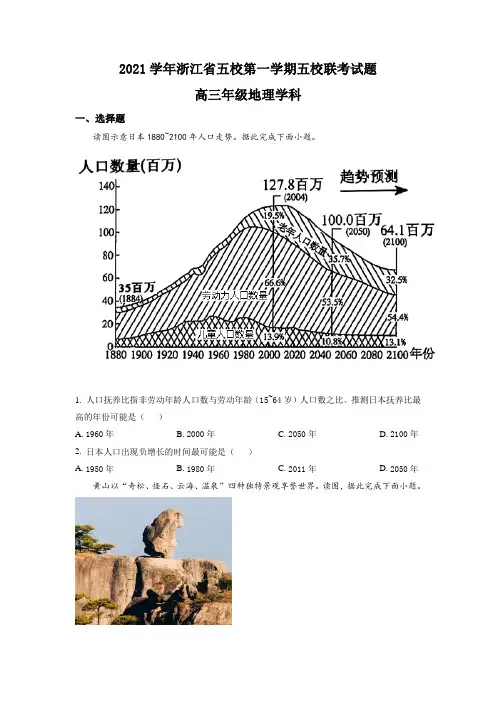
读图示意日本1880~2100年人口走势。据此完成下面小题。
1.人口抚养比指非劳动年龄人口数与劳动年龄(15~64岁)人口数之比。推测日本抚养比最高的年份可能是( )
A.1960年B.2000年C.2050年D.2100年
11. 形成北坡热带雨林带的因素有( )
A. 暖流信风B. 赤道低压信风C. 信风坡向D. 赤道低压暖洋流
12. 根据南北坡各自然带高度 差异,可推测( )
A. 北坡为阳坡,背风坡B. 南坡为阳坡,迎风坡
C. 北坡为阴坡,迎风坡D. 南坡为阴坡,迎风坡
下图示意为某城市的交通线路分布和土地利用方式的地理信息系统(GIS)图层,据此完成下面小题。
A.①②B.③④C.②④D.①③
【答案】3. B 4. D
【解析】
【3题详解】
花岗岩垂直节理发育较好,容易受到外力的风化、侵蚀作用,从而形成形态各异的岩石。因此黄山上由花岗岩形成的“怪石”是外力侵蚀作用的结果,地壳运动、变质作用、岩浆活动、重融再生属内力作用。故B正确,A、C、D错误。
2024届浙江省五校联盟高三下学期5月联考三模物理试题含答案

2024年浙江省高考物理模拟卷(答案在最后)本试题卷分选择题和非选择题两部分,共8页,满分100分,考试时间90分钟。
考生须知:1.本卷满分100分,考试时间90分钟;2.答题前,在答题卷指定区域填写班级、姓名、试场号、座位号及准考证号。
3.所有答案必须写在答题纸上,写在试卷上无效;4.考试结束后,只需上交答题纸。
5.可能用到的参数:重力加速度g取10m/s2。
选择题部分一、选择题I(本题共13小题,每小题3分,共39分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.下列物理量都是标量的是()A.位移路程B.电动势电势差C.速度加速度D.角速度线速度【答案】B【解析】【详解】线速度、位移、速度、加速度、角速度是矢量;路程、电动势、电势差是标量。
故选B。
2.2024年4月,杭州某中学举办春季运动会,图中师生正在进行“60米毛毛虫竞速赛”。
下列说法正确的是()A.正常完成比赛的队伍运动路程一定大于60米B.“毛毛虫”向前加速过程中,王老师对“毛毛虫”的力大于“毛毛虫”对王老师的力C.比赛中,可以把“毛毛虫”看作质点D.比赛开始前,“毛毛虫”静止时,所有人对“毛毛虫”的作用力倾斜向前方【答案】A【解析】【详解】A.路程为运动物体实际运动轨迹的长度,所以正常完成比赛的队伍运动路程一定大于60米,故A正确;B.“毛毛虫”向前加速过程中,根据牛顿第三定律可得,王老师对“毛毛虫”的力等于“毛毛虫”对王老师的力,故B错误;C.当物体的形状、大小对所研究的问题没有影响或者影响很小,可以忽略不计时,可以将物体看成质点,所以比赛中,不能把“毛毛虫”看作质点,故C错误;D.比赛开始前,“毛毛虫”静止时,所受重力与所有人对“毛毛虫”的作用力等大反向,所以所有人对“毛毛虫”的作用力竖直向上,故D错误。
故选A。
3.我国航天员在“天宫课堂”中演示了多种有趣的实验,提高了青少年科学探索的兴趣。
某同学设计了如下实验:细绳一端固定,另一端系一小球,给小球一初速度使其在竖直平面内做圆周运动。
浙江省五校联考2024届高三下学期联合考试化学试题含解析

2024年高考化学模拟试卷注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每题只有一个选项符合题意)1、关于下列各实验装置的叙述中正确的是A.装置①可用于吸收氯化氢气体B.装置②可用于制取氯气C.装置③可用于制取乙酸乙酯D.装置④可用于制取氨气2、我国对二氧化硫一空气质子交换膜燃料电池的研究处于世界前沿水平,该电池可实现硫酸生产、发电和环境保护三位一.体的结合。
其原理如图所示。
下列说法不正确的是()A.Pt1电极附近发生的反应为:SO2+2H2O-2e-=H2SO4+2H+B.相同条件下,放电过程中消耗的SO2和O2的体积比为2:1C.该电池工作时质子从Pt1电极经过内电路流到Pt2电极D.该电池实现了制硫酸、发电、环保三位一体的结合3、用N A表示阿伏加德罗常数的值。
下列叙述正确的是A.N A个Al(OH)3胶体粒子的质量为78gB.常温常压下,2.24L H2含氢原子数小于0.2N AD.0.1mol•L-1FeCl3溶液中含有的Fe3+数目一定小于0.1N A4、有以下六种饱和溶液①CaCl2;②Ca(OH)2;③Na2SiO3;④Na2CO3;⑤NaAlO2;⑥NH3和NaCl,分别持续通入CO2,最终不会得到沉淀或析出晶体的是A.①②B.③⑤C.①⑥D.④⑥5、下列指定反应的离子方程式正确的是()A.澄清石灰水与过量苏打溶液混合:Ca2++2OH-+2HCO3-=CaCO3↓+CO32-+2H2OB.少量SO2通入饱和的漂白粉溶液中:C1O-+SO2+H2O=SO42-+2H++Cl-C.向热的稀硫酸中加入铜粉并鼓入空气:2Cu+4H++O22Cu2++2H2OD.向酸性高锰酸钾溶液中滴加少量双氧水:7H2O2+2MnO4-+6H+=2Mn2++6O2↑+10H2O6、对二甲苯(PX)可发生如下反应生成对苯二甲酸(PTA)。
浙江省五校高三数学第一次联考试题 理 新人教A版

2013学年浙江省第一次五校联考数学(理科)试题卷本试题卷分选择题和非选择题两部分。
满分150分, 考试时间120分钟。
选择题部分(共50分) 参考公式:如果事件A , B 互斥, 那么棱柱的体积公式P (A +B )=P (A )+ P (B )V =Sh如果事件A , B 相互独立,那么 其中S 表示棱柱的底面积, h 表示棱柱的高P (A ·B )=P (A )· P (B ) 棱锥的体积公式如果事件A 在一次试验中发生的概率是p , 那么n V =31Sh次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积, h 表示棱锥的高P n (k )=C k n p k (1-p )n -k(k = 0,1,2,…, n ) 球的表面积公式 棱台的体积公式S = 4πR 2)2211(31S S S S h V ++=球的体积公式其中S 1, S 2分别表示棱台的上、下底面积, V =34πR 3h 表示棱台的高 其中R 表示球的半径一、选择题: 本大题共10小题, 每小题5分,共50分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
1. 已知集合{}21(),0,1(2),2x P y y x Q x y g x x ⎧⎫==>==-⎨⎬⎩⎭则()R C P Q 为( )A .[1,2)B .),1(+∞C .),2[+∞D .),1[+∞2. “2a <”是“对任意实数x ,11x x a ++-≥成立”的( )A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件3. 函数( )A .x π= D 4. 在ΔABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2Ab c 22ccos=+, 则ΔABC 的形状是( )A .正三角形B .直角三角形C .等腰三角形D .等腰直角三角形 5.设等差数列{}n a 的前n 项和为n S ,若15915a a a =,且15599111135a a a a a a ++=,则9S =( )A.27B.24C.21D.18 6. 用0,1,2,3,4这五个数字组成无重复数字的五位数,并且两个奇数数字之间恰有一个偶数数字,这样的五位数有( )A.12个B.28个C.36个D.48个7. 已知x ,y 满足⎪⎩⎪⎨⎧≤++≤+≥041c by ax y x x ,且2x y +的取值范围是[1,7],则=++a c b a ( ) A .1 B .2 C .-1 D . -2 8. 已知A B 、是单位圆上的两点,O 为圆心,且AOB ∠=0120,MN 是圆O 的一条直径,点C 在圆内,且满足(1)OC OA OB λλ=+-(01)λ<<,则CM CN ⋅的取值范围是( ) A .1[,1)-B .[1,1)-C .3[,0)4- D .[1,0)-9的两个极值点分别为12,x x ,且1201x x <<<,点(,)P m n 表示的平面区域内存在点00(,)x y 满足00log (4)a y x =+,则实数a 的取值范围是( ) A. 1(0,)(1,3)2 B. (0,1)(1,3) C. 1(,1)(1,3]2D. (0,1)[3,)+∞10. 对任意实数1x >,12y >,不等式222241(21)(1)x y a y ax +≥--恒成立,则实数a 的最大值为( )A.2B.4C.2D.非选择题部分 (共100分)二、 填空题: 本大题共7小题, 每小题4分, 共28分。
2024届浙江省五校联考高三冲刺模拟英语试题试卷含解析
2024届浙江省五校联考高三冲刺模拟英语试题试卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第一部分(共20小题,每小题1.5分,满分30分)1.____ up early in the morning to have a walk, I am sure, you are likely to feel active all day.A.Get B.Having got C.Getting D.To get2._______, the dancers practise hard to make their dreams come true.A.Instead of being disabled B.Being disabledC.Disabled as they are D.In case of being disabled3.Meizhou Island is such a beautiful place of interest______ everyone likes to visit.A.as B.that C.which D.where4.We’ll go early.,we may not get a seat.A.Otherwise B.Meanwhile C.However D.Besides5.Look! Here’ s a photo ______ in my classroom at primary school. Can you recognize me in it?A.taken B.takingC.to take D.being taken6.—I’m terribly sorry. I’m late because ….—That’s OK. You are here and that’s what _____.A.does B.works C.functions D.counts7.The majority of new businesses fail because, ________ they have a product or service that fills a gap in the market, they usually lack the skills in sales, marketing, and administration.A.now that B.even ifC.as long as D.as though8.It gives us great delight ______ Chinese science fictions are becoming increasingly popular.A.how B.whatC.that D.why9.—What happened to the young trees we planted last week?—The trees ________ well, but I didn’t water them.A.might grow B.needn’t have grownC.would have grown D.would grow10.Physically challenged as Jack was, he did not ________ himself to his fate.A.resist B.reserve C.resign D.rescue11.We ___have hurried all the way to the airport—the flight was called off because of the foggy weather. A.mustn’t B.couldn’t C.needn’t D.wouldn’t12.I really don’t know _________ she gets by on such a modest salary.A.what B.whyC.how D.that13.My son turned to bookstores and libraries seeking information about the book recommended by his professor, but ________ none.A.would find B.had foundC.found D.has been finding14.After the flooding, people were suffering in that area, ________ urgently needed clean water, medicine and shelter to survive.A.which B.whoC.where D.what15.—I am searching one online shopping site after another for a computer.—So __________I before I decided to buy a new camera.A.had B.have C.am D.would16.Andrew lives alone and enjoys the company of a pet cat _______ he’s grown so fond.A.which B.in whichC.of which D.when17.What I love most about reading novels is ______ the authors vividly describe the characters.A.what B.whyC.how D.whom18.__________him not to do so, he wouldn’t have made such a serious mistake.A.Did I persuade B.If I persuadeC.If I should persuade D.Had I persuaded19.What the country did _____ the international trade regulations, for which it was widely condemned. A.approved B.violated C.bothered D.interrupted20.—-What difference will it make _____we shall go to the concert on Tuesday or Saturday?—They offer a discount on weekdays.A.that B.whenC.if D.why第二部分阅读理解(满分40分)阅读下列短文,从每题所给的A、B、C、D四个选项中,选出最佳选项。
浙江省五校2020学年第一学期高三历史联考及答案
2020学年第一学期五校联考试题高三年级历史学科命题:杭州高级中学考生须知:1.本卷满分100分,考试时间90分钟;2.答题前,在答题卷指定区域填写学校.班级.姓名.试场号.座位号及准考证号。
3.所有答案必须写在答题卷上,写在试卷上无效;4.考试结束后,只需上交答题卷。
一.选择题(本大题共25小题,每小题2分,共50分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)。
1.西周大克鼎内壁铸有铭文,前半部分是克用华美的词语颂扬其祖父师毕父的功绩,后半部分是周天子重申对克职务的任命,克跪拜叩首,乃铸造大鼎以颂扬周天子,并祭祀祖父师毕父在天之灵。
其铸鼎的目的体现了A.王位传承B.宗法血缘 C.中央集权D.权利更替2.历史学家钱穆认为“中国历史上‘考试’与‘选举’两项制度,其用意是在政府和社会间打通一条路,好让社会在某种条件某种方式下来掌握政治,预闻政治和运用政治,这才是中国政治制度最根本问题之所在。
”以下说法符合题意的有①“考试”与“选举”分别为选官和监察②“打通一条路”有利于推动社会阶层流动③“考试”制度有利于重学风气形成④两项制度都具封闭性特征,民意无从体现A.①④B.①③ C.②③D.②④3.南北朝时期,在离城镇较远,交通便利的一些地方自然形成民间集市,经唐宋得到长足发展,下列属于宋代“民间集市”最大特点的是A.开始设草市尉进行严格管理 B.有比较完备的饮食服务设施C.突破原先城市坊市格局的限制D.商业活动不再受到官吏的监管4.王夫之是清初的一位思想巨人,他以“六经责我开生面”的气魄,对先秦至清初两千多年的文化遗产予以批判总结,下列属于他的主张的是A.天地之德不易,而天地之化日新 B.为天下之大害者,君而已矣C.君与臣,共曵木之人也 D.以天下之权,寄之天下之人5.2020年7月北京暴雨,故宫太和殿.中和殿.保和殿台基再现“龙吐水”景观。
这一景观充分体现出故宫的建筑A.布局严谨,井然有序 B.实用性与艺术性完美结合C.凸显皇权,树立权威 D.主次性与对称性巧妙融合6.1865年开始,阿古柏率军侵占新疆部分地区,左宗棠提出“重新疆者所以保蒙古,保蒙古者所以卫京师”,督办新疆军务,确定“先北后南,缓进急战”的策略,此策略制定的主要依据是A.阿古柏侵略路线B.清政府的命令C.英俄两国的干预D.新疆北可控南地形7.1873年8月创办的《昭文新报》,是中国人自办的最早的报纸之一,内容以“奇闻轶事居多,间有诗词杂作”,样式“仿香港上海之式而作”。
浙江省五校(学军中学 杭二中等)2021-2022学年高三上学期联考语文试题及参考答案解析(逐题解析
浙江省五校(学军中学杭二中等)2021-2022学年高三上学期联考语文试题及参考答案解析(逐题解析)浙江省五校(学军中学杭二中等)2021-2022学年高三上学期联考语文试题(逐题解析)2021 学年第一学期五校联考试题高三年级语文学科一、语言文字运用(20分)1. 下列各句中,没有错别字且加点字的注音全都正确的一项是()A. 阳关在我国西部边陲,因曾经是通往西域诸国的重要关隘而闻名遐迩,它与玉门关成掎(jǐ)角之势,宛如西域交通线上的一对雄狮,扼踞(jū)要地,虎视眈眈。
B. 突如其来的高温瞬间催熟了树叶,使它们变得枯槁,那些树儿似乎顷(qǐng)刻间就抖落了一身的叶子,为泥土铺上了黄澄(ch éng)澄的斗篷。
C. 远方层峦叠嶂,林场云雾氤氲(yūn),松涛阵阵,香樟叶上浓香的晨光,和那连绵的鸟鸣一起倾泄下来,刹(chà)那间将我们淹没。
D. 如果拷问雾霾成因,机动车尾气排放、焚烧秸(jiē)秆等等都是,其实,面对雾霾肆虐(nüè),每个人都责无旁贷,抱怨、责骂、急躁只会徒增烦恼,平添纷乱。
【答案】D【解析】【分析】【详解】本题考查学生识记现代汉语常用字字音、字形的能力。
A.“扼踞(jū) ”中的“踞”应读“jù”;B.“黄澄(chéng)澄”中“澄”应读“dēng”;C.“倾泄”中的“泄”应为“泻”。
故选D。
阅读下面的文字,完成各题。
《长恨歌》是白居易诗作中脍炙人口的名篇。
【甲】在这首长篇叙事诗里,诗人以精致的语言、优美的形象、浪漫的手法,叙述了这场安史之乱中的悲剧:唐明皇和杨贵妃用自己酿成的叛乱断送了爱情,只能没完没了地啃着这一精神的苦果。
诗人并不拘泥于历史,而是根据当时的传说和街坊的歌唱,从中蜕化出一个婉转动人的故事。
诗中的人物和情节都是艺术化的,是现实中人的复杂心理的再现,因而能在读者的心里漾起涟漪。
【乙】《长恨歌》就是歌“长恨”,“长恨”是诗歌的主题、故事的焦点,也是埋在诗里的一颗牵动人心的种子。
2024年浙江省五校(杭二、金一、绍一、衢二、温中)联盟高三3月联考试卷及答案
2024年浙江省五校联盟高三3月联考数学试题卷命题:浙江省杭州第二中学一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.若全集U ,集合,A B 及其关系如图所示,则图中阴影部分表示的集合是()A.()U A B ðB.()U A B ðC.()U BA ð D.()U A B ð2.已知(1,2)a =r,2b =r ,且a b ⊥r r ,则a b -r r 与a 的夹角的余弦值为()A.B.C.D.3.设,b c 表示两条直线,,αβ表示两个平面,则下列说法中正确的是()A.若,b c αα⊂∥,则b c ∥B.若,b c b α⊂∥,则c α∥C.若,c αβα⊥∥,则c β⊥ D.若,c c αβ⊥∥,则αβ⊥4.已知角α的终边过点(3,2cos )P α-,则cos α=()A.2B.2-C.2± D.12-5.设等比数列{}n a 的公比为q ,前n 项和为n S ,则“2q =”是“{}1n S a +为等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知实数,x y 满足3x >,且2312xy x y +-=,则x y +的最小值为()A.1+ B.8C. D.1+7.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,点A 为双曲线的左顶点,以12F F 为直径的圆交双曲线的一条渐近线于,P Q 两点,且23PAQ π∠=,则该双曲线的离心率为()A.B.C.213D.8.在等边三角形ABC 的三边上各取一点,,D E F ,满足3,90DE DF DEF ==∠=︒,则三角形ABC 的面积的最大值是()A. B. C.D.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.在学校组织的《青春如火,初心如炬》主题演讲比赛中,有8位评委对每位选手进行评分(评分互不相同),将选手的得分去掉一个最低评分和一个最高评分,则下列说法中正确的是()A.剩下评分的平均值变大B.剩下评分的极差变小C.剩下评分的方差变小D.剩下评分的中位数变大10.在三棱锥A BCD -中,已知3,2AB AC BD CD AD BC ======,点,M N 分别是,AD BC 的中点,则()A.MN AD⊥B.异面直线,AN CM 所成的角的余弦值是78C.三棱锥A BCD -的体积为3D.三棱锥A BCD -的外接球的表面积为11π11.已知函数()(sin cos )x f x e x x =⋅+,(浦江高中数学)则()A.()f x 的零点为,4x k k Z ππ=-∈B.()f x 的单调递增区间为32,2,22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C.当0,2x π⎡⎤∈⎢⎥⎣⎦时,若()f x kx ≥恒成立,则22k e ππ≤⋅D.当10031005,22x ππ⎡⎤∈-⎢⎥⎣⎦时,过点1,02π-⎛⎫⎪⎝⎭作()f x 的图象的所有切线,则所有切点的横坐标之和为502π三、填空题:本题共3小题,每小题5分,共15分.12.直线3430x y -+=的一个方向向量是________.13.甲、乙两人争夺一场羽毛球比赛的冠军,比赛为“三局两胜”制.如果每局比赛中甲获胜的概率为23,乙获胜的概率为13,则在甲获得冠军的情况下,比赛进行了三局的概率为________.14.已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x =',若(21),(2)f x g x --均为偶函数,且当[1,2]x ∈时,3()2f x mx x =-,则(2024)g =________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,斜三棱柱111ABC A B C -的底面是直角三角形,90ACB ∠=︒,点1B 在底面ABC 内的射影恰好是BC 的中点,且2BC CA ==.(1)求证:平面11ACC A ⊥平面11B C CB ;(2,求平面1ABB 与平面11AB C 夹角的余弦值.16.(本小题满分15分)已知函数()ln f x x ax =-,其中a R ∈.(1)若曲线()y f x =在1x =处的切线在两坐标轴上的截距相等,求a 的值;(2)是否存在实数a ,使得()f x 在(0,]x e ∈上的最大值是3-?若存在,求出a 的值;若不存在,说明理由.17.(本小题满分15分)记复数的一个构造:从数集中随机取出2个不同的数作为复数的实部和虚部.重复n 次这样的构造,可得到n 个复数,将它们的乘积记为n z .已知复数具有运算性质:()()()()a bi c di a bi c di +⋅+=+⋅+,其中,,,a b c d R ∈.(1)当2n =时,记2z 的取值为X ,求X 的分布列;(2)当3n =时,求满足32z ≤的概率;(3)求5n z <的概率n P .18.(本小题满分17分)在平面直角坐标系xOy 中,我们把点*(,),,x y x y N ∈称为自然点.按如图所示的规则,将每个自然点(,)x y 进行赋值记为(,)P x y ,例如(2,3)8P =,(4,2)14,(2,5)17P P ==.(1)求(,1)P x ;(2)求证:2(,)(1,)(,1)P x y P x y P x y =-++;(3)如果(,)P x y 满足方程(1,1)(,1)(1,)(1,1)2024P x y P x y P x y P x y +-+++++++=,求(,)P x y 的值.19.(本小题满分17分)在平面直角坐标系xOy 中,过点(1,0)F 的直线l 与抛物线2:4C y x =交于,M N 两点(M 在第一象限).(1)当||3||MF NF =时,求直线l 的方程;(2)若三角形OMN 的外接圆与曲线C 交于点D (浦江高中数学)(异于点,,O M N ),(i )证明:MND ∆的重心的纵坐标为定值,并求出此定值;(ii )求凸四边形OMDN 的面积的取值范围.参考答案一、选择题:本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合要求的.题号 1 2 3 4 5 6 7 8 答案CBDBCACA选对的得6分,部分选对的得部分分,有选错的得0分.题号 9 10 11 答案BCABDACD12. 3(1,)4 (答案不唯一) 13.2514. 6− 四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分13分)(第Ⅰ问,6分;第Ⅱ问,7分)解:(Ⅰ)取BC 中点为M ,连接1B M ,∵1B 在底面内的射影恰好是BC 中点, ∴1B M ⊥平面ABC ,又∵AC ⊂平面ABC ,∴1B M AC ⊥, 又∵90ACB ∠=,∴AC BC ⊥, ∵1,B M BC ⊂平面11B C CB ,1B MBC M =,∴AC ⊥平面11B C CB ,又∵AC ⊂平面11ACC A ,∴平面11ACC A ⊥平面11B C CB .(Ⅱ)以C 为坐标原点,建立如图所示空间直角坐标系,∵2BC CA ==, ∴11(2,0,0),(0,2,0),(0,1,0),(0,1,3),(0,1,3),A B M B C − 111(2,1,3),(2,2,0),(0,2,0)AB AB B C =−=−=−,设平面1BAB 的法向量为(,,)n x y z =,∴100n AB n AB ⎧⋅=⎪⎨⋅=⎪⎩则有230220x y z x y ⎧−++=⎪⎨−+=⎪⎩,令3,z =则3x y ==,∴(3,3,3)n =,设平面1BAB 的法向量为(,,)m a b c =,∴1110m AB m B C ⎧⋅=⎪⎨⋅=⎪⎩则有23020a b c b ⎧−++=⎪⎨−=⎪⎩,令3a =则0,2b c ==,∴(3,0,2)n =,∴||535|cos ,|||||7993304n m n m n m ⋅<>===++⨯++,平面1ABB 与平面11AB C 夹角的余弦值为57.16.(本小题满分15分)(第Ⅰ问,6分;第Ⅱ问,9分)∴f (x )的最大值是f (e)=1-a e =-3,解得a =4e >0,舍去;②当a >0时,由f ′(x )=1x -a =1-ax x =0,得x =1a,当0<1a <e ,即a >1e 时,∴x ∈⎝⎛⎭⎫0,1a 时,f ′(x )>0;x ∈⎝⎛⎭⎫1a ,e 时,f ′(x )<0, ∴f (x )的单调递增区间是⎝⎛⎭⎫0,1a ,单调递减区间是⎝⎛⎭⎫1a ,e , 又f(x )在(0,e]上的最大值为-3,∴f (x )max =f ⎝⎛⎭⎫1a =-1-ln a =-3,∴a =e 2; 当e≤1a ,即0<a ≤1e 时,f (x )在(0,e]上单调递增,∴f (x )max =f (e)=1-a e =-3,解得a =4e >1e,舍去.综上,存在a 符合题意,此时a =e 217.(本小题满分15分) (第Ⅰ问,6分;第Ⅱ问,4分;第Ⅲ问,5分) (Ⅰ)由题意可知,可构成的复数为{}11i +, 且1112i i ====+=+=.X 的可能取值为1234,,,()11221166119C C P X C C ⋅===⋅,(1142116629C C P X C C ⋅===⋅,()11421166229C C P X C C ⋅===⋅,()11221166139C C P X C C ⋅===⋅,(1142116629C C P X C C ⋅===⋅,()11221166149C C P X C C ⋅===⋅,所以分布列为:(Ⅱ)共有666216C C C ⋅⋅=种, 满足32z ≤的情况有:①3个复数的模长均为1,共有1112228C C C ⋅⋅=种;②3个复数中,2个模长均为1,12,共有2111322448C C C C ⋅⋅⋅=种; 所以()38487221627P z +≤==. (Ⅲ)当1n =或2时,显然都满足,此时1n P =; 当3n ≥时,满足5n z <共有三种情况: ①n 个复数的模长均为1,则共有()122nn C =;②1n −个复数的模长为1,剩余12,则共有()11111242n n n n C C C n −−+⋅⋅=⋅;③2n −个复数的模长为1,剩余2或者2,则共有()()22111124412n n n n C C C C n n −−+⋅⋅⋅=−⋅.故()()()()211216212*********n n n n n nnnn n n n n P z C ++++⋅+−⋅+<===,此时当12n ,=均成立.所以()21253n nn P z +<=.18. (本小题满分17分)(第Ⅰ问,4分;第Ⅱ问,7分;第Ⅲ问,6分) 解:(Ⅰ)根据图形可知()()1,11232x x P x x +=++++=, (Ⅱ)固定x ,则(),P x y 为一个高阶等差数列,且满足()(),1,1P x y P x y x y +−=+−,()()1,,P x y P x y x y +−=+,所以()()()()()1,1,112112y y P x y P x y y x y x ++−=++++−=+−,()()()()11,1122y y x x P x y y x +++=+−+,所以()()()()()11,1122x x y y P x y x y +−=++−−,()()()()()111,2122x x y y P x y x y −−−=++−−,所以()()()()()()()()()()221111,11,21122222322,x x y y y y x x P x y P x y x y y x x y xy y x P x y −−++++−=++−−++−+=++−−+=(Ⅲ)()()()()1,1,11,1,12024P x y P x y P x y P x y +−+++++++=,等价于()()()(),,11,1,12023P x y P x y P x y P x y +++++++=,等价于()(),131,2023P x y P x y +++=,即()()()()()()131211212202322x x y y x x x y y x +++−++++−+=⎡⎤⎡⎤⎣⎦⎣⎦,化简得()()2221010121010y xy x y x x y x y x ++−+=⇔+−++=,由于x y +增大,()()1x y x y +−+也增大,当31x y +=时,()()129921010x y x y x +−++<<,当33x y +=时,()()1210561010x y x y x +−++>>,故当32x y +=时,()()1210109,23x y x y x x y +−++=⇒==, 即()91023229,2382247422P ⨯⨯=++⨯=.19. (本小题满分17分)(第Ⅰ问,4分;第Ⅱ问,5分;第Ⅲ问,8分) 解:(Ⅰ)设直线MN :1x my =+,1122(,),(,)M x y N x y联立241x xy y m =+=⎧⎨⎩,消去x ,得2440y my −−=,所以12124,4y y m y y +=⋅=−,3MF NF =,则123y y =−∴122212224,34y y y m y y y +=−=⋅=−=−,则213m=,又由题意0,m >∴3m =,直线的方程是y =(Ⅱ)(ⅰ)方法1:设112233(,),(,),(,)M x y N x y D x y因为,,,O M D N 四点共圆,设该圆的方程为220x y dx ey +++=,联立22204x y dx ey y x⎧+++=⎨=⎩,消去x ,得()42416160y d y ey +++=,即()()3416160y y d y e +++=,所以123,,y y y 即为关于y 的方程()3416160y d y e +++=的3个根,则()()()()312341616y d y e y y y y y y +++=−−−,因为()()()()()32123123122313123y y y y y y y y y y y y y y y y y y y y y −−−=−+++++−,由2y 的系数对应相等得,1230y y y ++=,所以MND ∆的重心的纵坐标为0.方法2:设112233(,),(,),(,)M x y N x y D x y ,则1213234444,,,OM ON MD ND k k k k y y y y y y ====++, 因为,,,O M C N 四点共圆,所以MON MDN π∠+∠=,即tan tan 0MON MDN ∠+∠=,21124()tan 116OM ON OM ON k k y y MON k k y y −−∠==+⋅+,1213234()tan 1()()16ND MD ND MD k k y y MDN k k y y y y −−∠==+⋅+++,化简可得:312y y y =−−, 所以MND ∆的重心的纵坐标为0.(ⅱ)记,OMN MND △△的面积分别为12,S S ,由已知得直线MN 的斜率不为0 设直线MN :1x my =+,联立241x xy y m =+=⎧⎨⎩,消去x ,得2440ymy −−=,所以12124,4y y m y y +=⋅=−,所以1121122S OF y y =⋅⋅−==, 由(i )得,()3124y y y m =−+=−, 所以()22233114444x y m m ==⨯−=,即()24,4D m m −, 因为()212122444MN x x m y y m =++=++=+,点D 到直线MN的距离d =,所以()22211448122S MN d m m =⋅⋅=⋅+=−,所以)221281181S S S m m =+=+−=+− M 在第一象限,即120,0y y ><,340y m =−<,依次连接O ,M ,D ,N 构成凸四边形OMDN ,所以()3122y y y y =−+< ,即122y y −<,又因为124y y ⋅=−,2242y y <,即222y <,即20y <<,所以122244m y y y y =+=−>=,即4m >,即218m >,所以)218116S m m =+−=设t =4t >, 令()()2161f t t t =−,则()()()2221611614816f t t t t t '='=−+−−,因为4t >,所以()248160f t t −'=>,所以()f t在区间,4∞⎛⎫+ ⎪ ⎪⎝⎭上单调递增, 所以()42f t f ⎛⎫>= ⎪⎪⎝⎭, 所以S的取值范围为,2∞⎛⎫+ ⎪ ⎪⎝⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020学年第一学期浙江省高三“五校联考”考试参考答案
1-10.CBCADCDBBA
11.{|1}x x ≠,{|12}x x << 12.
43π,1
2
13.2y x =±,83
14.54e -,(27,12]
(11,)---+∞ 15.
43 16.1
2
17.335
[,]412
18.解:1cos 2()sin (sin )22-=+
=x f x x x x x 1sin(2)62π=-+x (3)
分
由
32222
6
2
π
π
π
ππ+≤-
≤
+k x k ,∈k Z 得
53
6
π
π
ππ+≤≤
+k x k ,∈k Z ∴()f x 的单调递减区间为5[
,
]3
6
k k k Z π
π
ππ++∈ ……………6分 (2)∵13()sin(2)6
22π
=-
+
=f A A ,则sin(2)16π
-=A , ∵0π<<A ,∴1126
6
6π
π
π-<-
<
A , 262ππ-=A ,解得3
π
=A . ……………8分 法一: ∵2=a ,3
π
=
A ,
由余弦定理得,
2222cos
3
a b c bc π
=+-,即224b c bc +-= ……10分
∴2
()43b c bc +-=,则2
2
()43(
)2
b c b c ++-≤ …………12分 又∵2b c +>,∴24b c <+≤ …………13分 ∴△ABC 周长的范围是(6,8] …………14分
法二:
由正弦定理得2sin sin sin a b c
R A B C
=
===
∴sin )b c B C +=
+ …………10分
∵23sin sin sin sin(
)sin )3226
B C B B B B B ππ+=+-=+=+ ………12分 又∵2(0,
)3
B π∈,∴1
sin()(,1]62B π+∈,∴(4,6]b c +∈ …………13分
∴△ABC 周长的范围是(6,8] …………14分 19.(1)
BC AB
AM PB PA ABCD BC PA BC PAB AM BC AM PBC BC ABCD AB PA A PB BC B AM PAB PC PBC ⊥⊥⎫⎫⎫
⎫⊥⎫⎪⎪⎪⎪
⇒⊥⇒⊥⇒⊥⇒⊥⎬⎬⎬⎬⎬
⊂⎭⎪⎪⎪⎪==⊂⊂⎭⎭⎭⎭面面面面面面 =PC AM
PC AN PC AMN AM AN A ⇒⊥⎫
⎪
⊥⇒⊥⎬⎪⎭
面 ………7分
(2)方法一:作DE AC E ⊥于,EF PC F ⊥于,连DF ,
PA ABCD ⊥面,
PAC ABCD ∴⊥面面,DE PAC ∴⊥面,
D
DE PC ∴⊥,EF PC ⊥,EF DE E =,PC DEF ∴⊥面,DF PC ∴⊥,
DFE ∴∠是二面角D PC A --的平面角,………11分
2PA AD ==
,AB =
AC ∴=,
30PCA ∴∠=
︒DE ∴=
,CE =,
EF =
tan DE DFE EF ∴∠== DFE ∴∠是二面角D PC A --
. ………15分
方法二:建立坐标系(以AD 为x 轴,以AB 为y 轴,以AP 为z 轴)
.
(0,0,0),(0,(2,(2,0,0),(0,0,2)A B C D P (0,22,0),(2,22,2),(0,0,2)DC PC AP ==-=
平面DPC 的法向量1(1,0,1)n =,平面APC 的法向量2(2,1,0)n =-
设二面角D PC A --的平面角为α,
12cos |
cos ,|n n α=<>=
tan α= 20. (1)证明:
1222a a +-=,23210a a +=,两式作差得112c =…………3分
对任意*n N ∈,21
21223
1n n n a a ---++=①,
2221231n n n a a ++=+② …………2分
②-①,得21212134n n n a a -+-⨯-=,即21
34n n c -⨯=,
于是1
4n n
c c +=.所以{}n c 是等比数列. …………7分 (2)证明当*n N ∈且2n ≥时,
2113153752123()()()()n n n a a a a a a a a a a =+-+-+-+⋅⋅⋅-+---
22131
(19)9292
2129n n --=+++++⋅⋅⋅=⋅+ …………10分
由(1)得11
2339321922n n n a --⋅++=-⋅+,所以2194n n a -= …………12分
1
2123(19)4n n n a a --+=-,得2391()48
n n S n -=- …………15分
21.解:(1
)由已知c e a =
=
,2b =,222a b c =+
得2b a ==,故椭圆C 的22
142
x y +=;……………………5分
(2)设()()()112200,,,,,A x y B x y M x y ,则
由2224x y y kx m
⎧+=⎨=+⎩得()222
214240k x mkx m +++-= 2121222424
,2121
mk m x x x x k k -⇒+=-=
++,点O 到直线l
的距离d =
1122S d AB =⋅⋅=
()2222422
21m k m k ++-=≤=
+S 22242m k m =+-即2221m k =+,① ……………10分
此时21200022221,221x x mk k k x y kx m m k m m m
+==-=-=+=-+=+,
法一:即00001,22x m m k x y y ==-=-代入①式整理得()22000102
x y y +=≠,
即点M 的轨迹为椭圆()2
21:102
x C y y +=≠ ………13分
且点N 恰为椭圆1C 的左焦点,则MN
的范围为)
1 ……………15分
法二:MN ==
由①得k
MN m
===- ………13分 设
k t m =代入2221m k =+得22221m m t =+,即22(12)1t m -=,22
1
012m t =>-
∴22t -
<<
,即22
k m -<<
∴)
1MN ∈
……………15分
22、解答:(Ⅰ)当2a =时,
()2sin sin 2f x x x =+,于是
()2cos 2cos22(1cos )(2cos 1)f x x x x x '=+=+- …………3分
于是
()0f x '>,解得(0,)3x π∈;()0f x '<,解得(,)3
x ππ∈
即(0,
)3x π
∈函数()f x 单调递增,(,)3
x π
π∈函数()f x 单调递减 …………6分
(Ⅱ)当1a =时,
()sin sin 2cos f x x x bx x =+≥对任意2(0,
)3
x π
∈恒成立
首先考察(0,
)2
x π
∈时,易得0b >
∵
()sin sin 2sin (12cos )cos f x x x x x bx x =+=+≥
∴2(
,)23
x ππ
∈时,()0cos f x bx x ≥≥,显然成立 …………9分
于是只考察
()sin sin 2cos f x x x bx x =+≥对任意(0,)2
x π
∈恒成立
由()14242
f b ππ=+≥⋅
,于是18b +≤
1
38
+>,所以3b ≤…11分 下证:
()sin sin 23cos f x x x x x =+≥对任意(0,)2
x π
∈恒成立
考察函数()tan 2sin 3g x x x x =+-,(0,
)2
x π
∈
322222
12cos 3cos 1(cos 1)(2cos 1)
()2cos 30cos cos cos x x x x g x x x x x
-+-+'=+-==> 于是()g x 在(0,
)2
x π
∈上单调递增,则()(0)0g x g >=
即tan 2sin 30x x x +->,则sin sin 23cos x x x x +≥ 综上可知,max 3b = ………15分。
