钢管订购优化
钢管订购与运输问题一的数学模型与求解

钢管订购与运输问题一的数学模型与求解
钢管订购与运输问题是一种组合优化问题,它涉及到钢管的订购和运输,旨在找到最佳的订购和运输方案,以最小的成本获得最大的收益。
这个问题通常可以用数学模型来表示。
设 n 个工地需要订购 m 根钢管,钢管订购和运输费用分别为
c1(订购费用)、c2(运输费用),订购钢管的最早时间 t0 为早订购时间,最迟时间为 t1 为晚订购时间,运输时间不计费用。
则钢管订购与运输问题的数学模型可以表示为:
minimize Σi=1~n c1(t1-t0) + Σj=i+1~n c2(t2-t1)
subject to:
t1≤t0
t2≥t1
t1+t2≤t0+30
x1=1, x2=1, ..., xnm=1
其中,x1、x2、...、xnm 是订购钢管的数量,1 表示订购,0 表示不订购。
通过这个数学模型,我们可以制定出钢管订购与运输问题的求解方法,以找到最佳的订购和运输方案。
在实际问题中,我们通常需要对求解结果进行评估和优化,以便找到更加优秀的方案。
因此,钢管订购与运输问题的数学模型和求解方法只是问题的第一步,实际应用中还需要进行进一步的分析和优化。
钢管“内六方”缺陷的产生原因及优化

钢管“内六方”缺陷的产生原因及优化孟庆飞(内蒙古包钢钢联股份有限公司,内蒙古包头014010)摘要:分析热轧无缝钢管生产中“内六方”问题产生的原因,并提出解决方案。
分析认为:在生产线设计投产后,由于受到机架备置量、产品范围要求的限制,通过修改总的减径量或者单机架的减径量,轻易无法改善“内六方”缺陷,因此并不是最好的优化措施;在一定的减径比和总减径比设计前提下,通过优化孔型椭圆度可以使“内六方”问题得到明显改善,椭圆度越大越容易出现“内六方”问题。
关键词:钢管;张力减径机;楠圆度;减径比;内六方中图分类号:TG335.71 文献标志码:B文章编号:1001-2311(2020)06-0045-04Causes for “Hexagonal Bore” Defect of Steel Pipeand Relevant Optimization MeasuresMENG Qingfei(Inner Mongolia Baotao Steel Union Co.,Ltd.,Baotou014010,China )Abstract: Analyzed here in the article are the causes for the**Hexagonal Bore'defect as encountered with during the production of the hot-rolled seamless steel pipe,and the solution for it.It is concluded as follows via the analysis. Since the start-up of the production line,as limited by the roll stand allocation and the product range requirement,etc., it has been not so easy to fix the said“Hexagonal Bore”defect problem just by correcting the general reduction amount or the individual stand reduction amount,which is not the best optimization way.Given the specific reduction ratio and the general reduction ratio are designed,optimizing the pass ovality will get the said defect obviously alleviated.The bigger the ovality,the higher possibility for the defect to occur.Key words:steel pipe;stretch reducing mill;ovality;reduction ratio;hexagonal bore内蒙古包钢钢联股份有限公司钢管公司中159 mm连轧管生产线,配套的24机架单独传动张力 减径机组[|-7],该机组生产小直径厚壁钢管时,一直受到“内六方”问题的困扰。
钢管的订购及运输优化方案

钢管的订购及运输优化方案钢管是一种常见的工业材料,主要用于建筑、桥梁、机器制造和能源开采等领域。
订购和运输钢管需要考虑多方面因素,如规格、数量、质量、运输距离、运输方式等。
本文将介绍一些钢管订购及运输的优化方案。
一、钢管订购方案1. 确定钢管规格和数量在订购钢管前,首先需要了解工程或项目的具体需求,确定钢管的规格和数量。
不同的工程或项目需要的钢管规格和数量可能会有所不同,选择合适的规格和数量可以避免浪费和损失。
2. 寻找可靠的供应商选择可靠的供应商可以确保钢管的质量和供应稳定性。
可以通过市场调研、参加行业展会或咨询同行业的项目经理、工程师等人员来寻找可靠的供应商。
3. 确定采购合同和交付方式在确定供应商后,需要签订采购合同并确定交付方式。
采购合同要明确规定钢管的规格、数量、价格和交付日期等具体条款,避免误解和纠纷。
交付方式可以选择集装箱运输、散装运输或其他方式,根据具体情况灵活选择。
4. 质量控制为确保钢管的质量,采购方可以要求供应商提供产品质量证明、实际样品或第三方检测报告。
在收到钢管后,可以进行抽检或全检,检查钢管的尺寸、表面状态、壁厚和材质等指标,避免存在不合格品质的钢管进入工程或项目。
二、钢管运输方案1. 选择合适的运输方式钢管的运输可以选择公路运输、铁路运输、水路运输或航空运输等方式。
具体选择哪种方式需要综合考虑运输距离、运输量、运输时间、运输成本及货物安全等各方面因素。
2. 管理运输过程在钢管运输过程中,需要对货车、火车、船舶或飞机等交通工具进行监控,确保运输过程中货物的安全。
可以使用GPS或其他定位技术实时掌握货物的位置和状态,及时处理运输中遇到的问题和风险。
3. 管理卸货和储存在将钢管卸货到工厂、工地或仓库后,需要将其储存到指定位置并标记钢管的规格、数量等信息。
可以采用RFID等智能化技术对钢管进行管理,便于日后的存储和使用。
4. 管理短途运输在项目工期中,可能需要短途运输钢管到具体施工位置。
第6讲 非线性规划

1 gi X
其中称r lng i X 或 r
i 1 i 1
m
m
1 为障碍项,r为障碍因子 gi X
X D
这样问题()就转化为求一系列极 1 值问题: k min I X , rk 得 X (rk) 0
10
内点法的迭代步骤
(1) 给定允许误差 0 ,取r1 0,0
k1
5) 判断精度: j 1,, n , 若 则点 X 为近似最优解;
k j
否则,令 k 1 k j 1,, n ,k=k+1,返回步骤(2). j j
14 返回
1、二次规划
标准型为: Min Z= 1 XTHX+cTX
2
s.t. AX<=b
m k
m
返回(3) .
11
近似规划法
近似规划法的基本思想:将问题(3)中的目标函数 f X
和约束条件 g i X 0 (i 1,..., m); h j X 0 ( j 1,, l )
近似为线性函数,并对变量的取值范围加以限制,从
而得到一个近似线性规划问题,再用单纯形法求解之,
i 1 j 1
(2)
将问题( )转化为无约束问题: minn T X , M 1
X E
(3)
其中T(X,M)称为罚函数,M称为罚因子,带M的项称为罚项,这 里的罚函数只对不满足约束条件的点实行惩罚:当 D 时,满 X 足各 i X 0, hi X 0 ,故罚项=0,不受惩罚.当 D 时, g X 必有 0或hi X 0 的约束条件,故罚项>0,要受惩罚. gi X
基于遗传模拟退火算法的钢管订购和运输优化问题求解

Vo . 9 N . 12 o 1 Ma . 0 7 r2 o
文 章 编 号 :06— 4 6 20 ) 1 0 9 0 10 0 5 (0 7 0 — 0 4— 5
基 于遗 传 模 拟退 火 算 法 的钢 管 订购 和 运 输 优 化 问题 求 解
王庆泉 , 武和 雷, 方梦飞
求解该 问题 的方法 , 并在此基础上提 出利用遗传算法与模 拟退火算法 相结合 的方 法对该 问题进 行求解. 实验结果 验证 了利用遗传模拟退 火算法 求解 该问题的可行性 与高效性 , 为求解该类问题提供 了一个有效的新途径. 关键词 : 钢管订购运输 ; 次规 划模 型 ; 二 遗传算法 ; 模拟退火 中图分 类号 :P 9 . ; 24 T 3 19 U 9 文献标识码 : A
g n t i l td a ቤተ መጻሕፍቲ ባይዱ ai g a p o c e ei smua e n e n p r a h,i e sb e a d e ce r f di h p i m r mee n t e c l sf a i l n f intf i ng t e o t i o n mu pa a tr i h Or rn de g i n n p r n fse lt b o i e o d wa o s l e t e qu sin. a d ta s o ig o te u e a d prv d sa g o y t ov h e to r t n
Th e Opt ia i n S l to n t d rn n a p ri g o i z to ou in i he Or e i g a d Tr ns o tn f m S e lTu n Ge tc S m u a e n ai g Alo ih te be o nei i l td An e ln g rt m
钢管下料优化方案
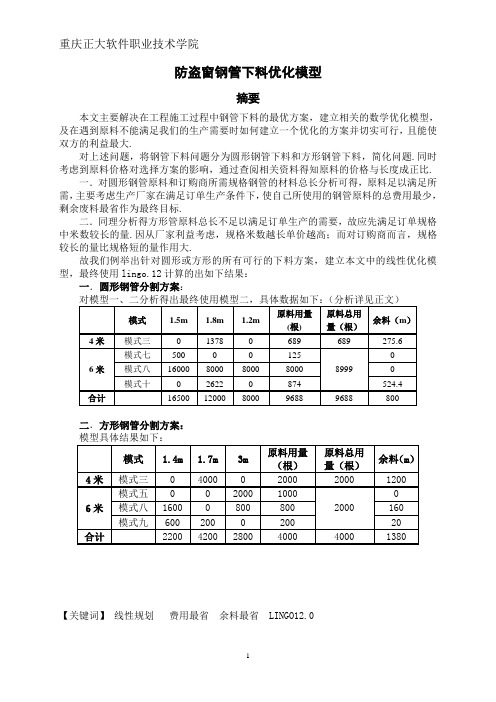
防盗窗钢管下料优化模型摘要本文主要解决在工程施工过程中钢管下料的最优方案,建立相关的数学优化模型,及在遇到原料不能满足我们的生产需要时如何建立一个优化的方案并切实可行,且能使双方的利益最大.对上述问题,将钢管下料问题分为圆形钢管下料和方形钢管下料,简化问题.同时考虑到原料价格对选择方案的影响,通过查阅相关资料得知原料的价格与长度成正比.一.对圆形钢管原料和订购商所需规格钢管的材料总长分析可得,原料足以满足所需,主要考虑生产厂家在满足订单生产条件下,使自己所使用的钢管原料的总费用最少,剩余废料最省作为最终目标.二.同理分析得方形管原料总长不足以满足订单生产的需要,故应先满足订单规格中米数较长的量.因从厂家利益考虑,规格米数越长单价越高;而对订购商而言,规格较长的量比规格短的量作用大.故我们例举出针对圆形或方形的所有可行的下料方案,建立本文中的线性优化模型,最终使用lingo.12计算的出如下结果:一.圆形钢管分割方案:对模型一、二分析得出最终使用模型二,具体数据如下:(分析详见正文)模式 1.5m 1.8m 1.2m 原料用量(根)原料总用量(根)余料(m)4米模式三0 1378 0 689 689 275.66米模式七500 0 0 12589990 模式八16000 8000 8000 8000 0 模式十0 2622 0 874 524.4合计16500 12000 8000 9688 9688 800二.方形钢管分割方案:模型具体结果如下:模式 1.4m 1.7m 3m 原料用量(根)原料总用量(根)余料(m)4米模式三0 4000 0 2000 2000 12006米模式五0 0 2000 100020000 模式八1600 0 800 800 160 模式九600 200 0 200 20合计2200 4200 2800 4000 4000 1380 【关键词】线性规划费用最省余料最省 LINGO12.0一.问题的提出某不锈钢装饰公司承接了一住宅小区的防盗窗安装工程,为此购进了一批型号为304的不锈钢钢管,分为方形管和圆形管两种,具体数据如下表:表1-1规格长4m 长6m方形管25×25×1.2(mm) 5000根9000根圆形管Φ19×1.2(mm) 2000根2000根根据小区的实际情况,需要截取钢管的规格与数量如下:表1-2圆形管规格 1.5m 1.8m 1.2m 方形管规格 1.4m 1.7m 3m 数量(根)16500 12000 8000数量(根)6000 4200 2800根据上述的实际情况建立数学模型,寻找经济效果最优的下料方案,使得厂家在满足订购商的订单需要的同时还能节约原料.二.问题的分析通过题目可知,要求我们在题目所给定的条件下,找寻最佳下料方案,使满足各种需要的前提下所使用的原材料的费用、所使用的量和所剩的余料最省.圆形钢管原材料的总长:()45000+69000=74000 m⨯⨯,订单产品的总长:()1.516500+1 .812000+1.28000=55950m⨯⨯⨯.方形钢管原材料的总长:()42000+ 62000=20000m⨯⨯,订单产品的总长:()1.46000+1.74200+32800=23940m⨯⨯⨯.通过计算,分析得出问题中的圆形钢管原料足够多,在使用时主要考虑所使用的原材料的费用、使用量和切割之后的余料最少;而方形管的原材料明显不能满足生产需要,此时应首先考虑切割不同长度的钢管的优先问题.通过查阅网络资料可得网络上对于304不锈钢钢管的单价是50元/公斤,而相应的不锈钢管重量公式:⨯⨯外径-壁厚)壁厚]0.0249每米的重量(千克/米)[(=又因为在我们的原材料中,规格都为Φ19×1.2(mm),所以可得每米的重量都是一定的,故我们可以得到每根钢管的单价与原材料的长度成正比,比例系数为k,即6米管的单价是6k,4米的单价是4k,所以6米管的单价是4米管的6k/4k=1.5倍.因此在处理这个问题时对于生产厂家而言,应考虑所生产的成品规格越长利益越大;对于订购商而言,规格长度越大材料的使用性越大.通过上诉分析可得,应该在原有材料使用完的情况下先满足规格为3米的钢管,其次是1.7米的钢管,再次生产1.4米的钢管.然而此类问题属于数学中最优解的求解问题,这是典型的线性优化,故该问题可以建立线性优化方程解决.三.模型假设1.假设钢管切割过程中无原料损耗或损坏;2.假设所生产的各种规格的钢管不能通过焊接产生;3.假设同种钢管采用的切割模式数量不限;4.假设每种钢管的单价相同且与长度成正比.四.符号说明x表示采用第i种模式下切割的钢管数id表示第i中模式下的第j种规格下的根数ijc表示第i种模式下的余料ia表示第j种规格的需求量jy表示使用4米的原料所以使用的根数1y表示使用6米的原料所以使用的根数2y表示生产规格为1.5米的钢管总数3y表示生产规格为1.8米的钢管总数4y表示生产规格为1.2米的钢管总数5y为满足生产需求产生的余料总和6k表示单位长度或者单位公斤数钢管原料的价格五.模型的建立与求解针对题目的要求我们将钢管下料方案分为圆形钢管和方形钢管两类,简化问题,并建立相关数学模型.首先根据题目已知条件可得要先给4米和6米不同规格的原材料进行分割,因此产生了不同的切割模式,选取最佳切割模式才是所要求的下料方案.其中切割所剩的余料必须小于所需切割的最小长度,在条件满足的不同组合的情况下,得知圆形管的切割方案有17种;方形钢管的切割方案有11种,具体切割方案如下:5.1 圆形钢管5.1.1圆形钢管的切割方案表5-1模式 1.5m 1.8m 1.2m 余料(m) 圆形`4 米 切 割 模 式模式一 0 0 3 0.4 模式二 2 0 0 1 模式三 0 2 0 0.4 模式四 0 1 1 1 模式五 1 0 2 0.1 模式六 1 1 0 0.7 6 米 切 割 模 式模式七 4 0 0 0 模式八 2 1 1 0 模式九0 0 5 0 模式十 0 3 0 0.6 模式十一 0 1 3 0.6 模式十二 1 0 3 0.9 模式十三 1 2 0 0.9 模式十四 0 2 2 0 模式十五 3 0 1 0.3 模式十六 2 0 2 0.6 模式十七1120.35.1.2圆形钢管的下料模型建立针对圆形管的切割方案,我们假设原材料采用模式i 切割的数量为x i (x i 必须为大于1的正整数),那么目标函数即为使生产厂家在完成订单需要的情况下所使用的原材料最少,同时所使用的原料的费用最少,且又因6米管的原料单价是4米管的1.5倍,所以目标函数是:min z (4)+1.5(6)k k =⨯⨯原料中米的总根数原料中米的总根数又由已知条件可得,所生产的量必须满足订购商的需要,即1.5m 圆管16500根,1.8m 圆管12000根,1.2m 圆管8000根,因此产生以下三个目标函数的约束条件:≤生产规格中所有的1.5米的总根数16500 ≤生产规格中所有的1.8米的总根数12000 8000≤生产规格中所有的1.2米的总根数因此可得如下数学模型:617176117717117311min k 1.550009000..0()i ii i i i i i i ii ij i j i j z x k x x x S T x x d x a ========+⎧≤⎪⎪⎪≤⎪⎪⎨⎪≥⎪⎪⎪≥⎪⎩∑∑∑∑∑∑∑为整数 利用lingo12.0编程运算得出最终结果如下表:(程序代码详见附录1)表5-2模式 1.5 1.8 1.2 原料用量 原料总用量 余料 4米模式三 0 1378 0 689 689275.6 6米模式七500 0 0 125 8999 0 模式八 16000 8000 8000 8000 0 模式十0 2622 0 874 524.4 合计1650012000800096889688 800且对于模型中钢管每米的单价k 进行不同程度改变,得知k 的值不会影响生产过程中我们对模式的选择,只会相应的改变原料成本,影响相应的利润.通过对上表的结果进行分析得,该模型已经满足生产不同规格钢管的需要,且没有多余的生产量,但该模型只考虑到所用的原料费用最省,不一定满足所要求的生产订单过后的余料最省,也就是不一定满足原料的使用率最大,故我们对模型进一步优化检验,把目标函数变为:min z 4(4)+6(6=⨯⨯⨯原料中米的总根数原料中米的总根数) -(订单中所有规格长)(订单中相应规格的根数)最终可得模型如下:617176117717117311min 465595050009000..0()i i i i i i i i i ii ij i j i j z x x x x s t x x d x a ========+-⎧≤⎪⎪⎪≤⎪⎪⎨⎪≥⎪⎪⎪≥⎪⎩∑∑∑∑∑∑∑为整数同样用lingo12.0编程运算得出结果如下:(程序代码详见附录2)表5-3模式 1.5m 1.8m 1.2m 原料用量(根) 原料总用量(根) 余料(m ) 4米模式三 0 1378 0 689 689275.6 6米模式七500 0 0 125 8999 0 模式八 16000 8000 8000 8000 0 模式十0 2622 0 874 524.4 合计1650012000800096889688 800从表一和表二相应结果可得,两张表结果一模一样.相应的证明了该切割方案是最优的切割方案,同时也满足最初的假设,即生产厂家在完成订购商的订单需要的情况下,原材料的使用最少,所产生的费用最少,并在生产过程种产生的废料最少,废料的总和才800米,同时也满足原料的使用率最大.故最佳的切割方案是使用用689根4米的原材料采用模式三进行切割,125根6米的原材料采用模式七进行切割,8000根6米的原材料采用模式八进行切割,874根6米的原材料采用模式十进行切割.5.2 方形钢管5.2.1方形钢管的切割方案表5-4模式 1.4m 1.7m 3m 余料(m)方形管4米切割模式模式一0 0 1 1模式二 2 0 0 1.2模式三0 2 0 0.6模式四 1 1 0 0.96米切割模式模式五0 0 2 0模式六 4 0 0 0.4模式七0 3 0 0.9模式八 2 0 1 0.2模式九 3 1 0 0.1模式十 1 2 0 1.2模式十一0 1 1 1.35.2.1方形钢管余料最少由于方型钢管所能提供的原材料远远不能满足生产所需,该情况下,如果还继续限制所用的材料,那么我们就无法满足生产方管的订单需要.根据问题分析中原材料的单价与它的长度成正比,并对于生产厂家而言,成品规格越长利益越大;对于订购商而言,规格长度越大材料的使用性越大.又因为:方管的总量为:42000+62000=20000m⨯⨯(),方管中的规格为1.7米和3米的钢管总长为:1.74200+32800=15540m⨯⨯().所以得出方管足以满足生产规格为3米和1.7米的钢管,即严格要求生产规格为3米和1.7米的钢管,对于规格为1.4米的钢管实在无法满足需要,只限制它的量必须大于0即可.故可得:3=2800生产出的规格为米的总根数1.7=4200生产出的规格为米的总根数1.4生产出的规格为米的总根数>0又因为总量本身不够生产,所以要求方管的所有材料必须用于生产,所以可得:=原料方管中所使用的4米的总根数2000综上分析可得关于余量最省的优化数学模型如下:()1114111511111312111111min 20002000..00i ii i i i i i i ij i j i j i i i x c x x S T x d x a d x a a ========⎧=⎪⎪⎪=⎪⎪⎪⎪≥⎨⎪⎪=⎪⎪⎪⎪≥=⎪⎩∑∑∑∑∑∑∑同样使用lingo12.0软件编程运算得出如下结果:(程序代码详见附录3) 表5-5模式 1.4m 1.7m 3m原料用量(根) 原料总用量(根) 余料(m )4米 模式三0 4000 0 2000 20001200 6米 模式五0 2000 1000 2000 0 模式八 16000 800 800 160 模式九600 200 0 200 20 合计22004200280040004000 1380对模型结果分析可得,该切割方案已是最优,没有成品钢管的浪费,又能满足生产厂家利润最大,同时还能满足订购商的长料利用率较大.并且在生产过程中总共产生1380米废弃材料.因此最优切割方案是用2000根4米的原材料采用模式三进行切割,1000根6米的原材料采用模式五进行切割,800根6米的原材料采用模式八进行切割,200根6米的原材料采用模式九进行切割.六.模型的分析与推广通过线性规划的应用,可以更好的求解一定约束条件下的最优值的求解问题,能够得出最佳合理的答案.同时线性规划对实际问题的分析与应用较为普遍,容易查找相关资料,同时可见其适于现实问题的求解,例如:对水管的下料,钢材的切割,电线的切割等,优化之后还能解决玻璃的切割问题等等.同时枚举法的运用是问题的求解思路更清晰的呈现,此为该模型的优点.但是切割模式较多,枚举法加大了运算量同时导致问题的解答相对繁杂,也是该模型的明显缺点.参考文献:[1] 颜文勇,数学建模,高等教育出版社,2011.6[2] 谢金星、薛毅,优化建模与LINDO/LINGO软件,北京,清华大学出版社,2009.12[3] /view/1266775.htm(钢管每米重量计算公式)附录附录1:MODEL:MIN=k*(X1+X2+X3+X4+X5+X6)+1.5*k*(X7+X8+X9+X10+X11+X12+X13+X14+X15+X16+X17);k=50;2*X2+X5+X6+4*X7+2*X8+X12+X13+X17>=16500;2*X3+X4+X6+X8+3*X10+X11+2*X13+2*X14+X17>=12000;X4+2*X5+X8+5*X9+3*X11+3*X12+X15+2*X16+2*X17>=8000; X1+X2+X3+X4+X5+X6<=5000;X7+X8+X9+X10+X11+X12+X13+X14+X15+X17<=9000;y1=x1+x2+x3+x4+x5+x6; !y1是使用4米长的原料所用的根数;y2=x7+x8+x9+x10+x11+x12+x13+x14+x15+x17; !y2是使用6米长的原料所用的根数;y3=2*x2+x5+x6+4*x7+2*x8+x12+x13+3*15+2*16+x17; !y3是切得规格为1.5米钢管的总数;y4=2*x3+x4+x6+x8+3*x10+x11+2*x13+2*x14+x17;!y4是切得规格为1.8米钢管的总数;y5=x4+2*x5+x8+5*x9+3*x12+3*x11+2*14+x15+2*x16+2*x17;!y5是切得规格为1.2米钢管的总数;y6=x1*0.4+x2+x3*0.4+x4+x5*0.1+x6*0.7+x7*0+x8*0+x9*0+x10*0.6+x11*0.6+x12*0.9+x13*0.9+x14*0+x15*0.3+x16*0.6+x17*0.3;!为满足生产需求产生的余料总和;@GIN( X1); @GIN( X2); @GIN( X3); @GIN( X4); @GIN( X5); @GIN( X6); @GIN( X7);@GIN( X8); @GIN( X9); @GIN( X10); @GIN( X11); @GIN( X12); @GIN( X13);@GIN( X14); @GIN( X15); @GIN( X16); @GIN( X17);END附录2:MODEL:MIN=4*X1+4*X2+4*X3+4*X4+4*X5+4*X6+6*X7+6*X8+6*X9+6*X10+6*X11+6*X12+6*X13+6*X14+6*X15+6*X16+6*X17-55950; 2*X2+X5+X6+4*X7+2*X8+X12+X13+X17>=16500;2*X3+X4+X6+X8+3*X10+X11+2*X13+2*X14+X17>=12000;X4+2*X5+X8+5*X9+3*X11+3*X12+X15+2*X16+2*X17>=8000; X1+X2+X3+X4+X5+X6<=5000;X7+X8+X9+X10+X11+X12+X13+X14+X15+X17<=9000;y1=x1+x2+x3+x4+x5+x6; !y1是使用4米长的原料所用的根数;y2=x7+x8+x9+x10+x11+x12+x13+x14+x15+x17; !y2是使用6米长的原料所用的根数;y3=2*x2+x5+x6+4*x7+2*x8+x12+x13+3*15+2*16+x17; !y3是切得规格为1.5米钢管的总数;y4=2*x3+x4+x6+x8+3*x10+x11+2*x13+2*x14+x17;!y4是切得规格为1.8米钢管的总数;y5=x4+2*x5+x8+5*x9+3*x12+3*x11+2*14+x15+2*x16+2*x17;!y5是切得规格为1.2米钢管的总数;y6=x1*0.4+x2+x3*0.4+x4+x5*0.1+x6*0.7+x7*0+x8*0+x9*0+x10*0.6+x11*0.6+x12*0.9+x13*0.9+x14*0+x15*0.3+x16*0.6+x17*0.3;!为满足生产需求产生的余料总和;@GIN( X1); @GIN( X2); @GIN( X3); @GIN( X4); @GIN( X5); @GIN( X6); @GIN( X7);重庆正大软件职业技术学院@GIN( X8); @GIN( X9); @GIN( X10); @GIN( X11); @GIN( X12); @GIN( X13);@GIN( X14); @GIN( X15); @GIN( X16); @GIN( X17);END附录3:MODEL:MIN=4*X1+4*X2+4*X3+4*X4+4*X5+4*X6+6*X7+6*X8+6*X9+6*X10+6*X11+6*X12+6*X13+6*X14+6*X15+6*X16+6*X17-55950; 2*X2+X5+X6+4*X7+2*X8+X12+X13+X17>=16500;2*X3+X4+X6+X8+3*X10+X11+2*X13+2*X14+X17>=12000;X4+2*X5+X8+5*X9+3*X11+3*X12+X15+2*X16+2*X17>=8000; X1+X2+X3+X4+X5+X6<=5000;X7+X8+X9+X10+X11+X12+X13+X14+X15+X17<=9000;y1=x1+x2+x3+x4+x5+x6; !y1是使用4米长的原料所用的根数;y2=x7+x8+x9+x10+x11+x12+x13+x14+x15+x17; !y2是使用6米长的原料所用的根数;y3=2*x2+x5+x6+4*x7+2*x8+x12+x13+3*15+2*16+x17; !y3是切得规格为1.5米钢管的总数;y4=2*x3+x4+x6+x8+3*x10+x11+2*x13+2*x14+x17;!y4是切得规格为1.8米钢管的总数;y5=x4+2*x5+x8+5*x9+3*x12+3*x11+2*14+x15+2*x16+2*x17;!y5是切得规格为1.2米钢管的总数;y6=x1*0.4+x2+x3*0.4+x4+x5*0.1+x6*0.7+x7*0+x8*0+x9*0+x10*0.6+x11*0.6+x12*0.9+x13*0.9+x14*0+x15*0.3+x16*0.6+x17*0.3;!为满足生产需求产生的余料总和;@GIN( X1); @GIN( X2); @GIN( X3); @GIN( X4); @GIN( X5); @GIN( X6); @GIN( X7);@GIN( X8); @GIN( X9); @GIN( X10); @GIN( X11); @GIN( X12); @GIN( X13);@GIN( X14); @GIN( X15); @GIN( X16); @GIN( X17);END11。
优化模型举例

一单位实物 行走时间(分钟) 捕获时间(分钟) 热量(焦耳)
X
2
2
25
Y
3
1
30
假设捕食者每天能得到 x 单位的食物 X 和
y 单位的食物 Y ,则每天获得的热量值为
max u 25x 30 y 2x 3y 120
s.t 2x y 80 x 0, y 0.
2020/7/1
2020/7/1
收点
发点
B1
B2
…. Bn
A1X11 X12….. X1na1
A2
X21 X22
…. X2n
a2
….. …..
Am
Xm1
Xm2 ….. Xmn
am
b1 b2
….
bn
2020/7/1
A1的总费用
A1 ~ B j
n
C11x11 C12 x12 ... C1n x1n C1 j x1 j j 1
2020/7/1
03年B题:“露天矿生产的车辆安排”,非线性 规划模型。 04年B题:“电力市场的输电阻塞管理”,双目
标线性规划模型。 05年B题:“DVD在现租赁”,0-1规划模型。 06年A题:“出版社的资源优化配置”,线性规 划模型。
2020/7/1
(一)优化模型的数学描述
将一个优化问题用数学式子来描述,即求函数
2.根据设计变量的性质 静态问题和动态问题。
3.根据目标函数和约束条件表达式的性质 线性规划,非线性规划,二次规划,多目标规划等。
2020/7/1
(1)非线性规划
目标函数和约束条件中,至少有一个非线性函数。
min u f (x) x
s. t. hi ( x) 0,i 1,2,..., m. gi ( x) 0(gi ( x) 0), i 1,2,..., p.
数学建模2000B题

i 1
m
ai
ji
n
bj
从发点A到收点B的距离(或单位运费)是已知的,设为
c ij ( i 1, 2 ,..., m , j 1, 2 ,..., n )
。
问题:寻求一个调运方案,使总运输费用达到最小。
一个调运方案主要由一组从发点
Ai
到收点 B j 的输
送量来描述。
发点
收点
B1
B2
290 S4 S3 S2 320 160 70 30 70 170 720 202 1100 20 12 195 1150 600 306 0 10 31 201 A8 480 680 A10 S1 70 42 10 520 88 462 S5 10 220 300 A11 S2 S6 110
30
70
A1
480
31
1150
A9 680
A10
300
A11
201
205 A7
A8
450
80 2 750 A4 606
图二
3
104 A1 301 A2
A3
问题
所属类型 做题 思路和关键点 结果 表示形式
优化模型
1、问题的分析
优化问题
1)优化模型的数学描述
求函数
u f (x)
x ( x 1 , x 2 , x 3 ,..., x n )
在约束条件 h i ( x ) 0 , i 1, 2 ,..., m . 和
g i ( x ) 0 ( g i ( x ) 0 ), i 1, 2 ,..., p .
下的最大值或最小值,其中 设计变量(决策变量) x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
学 号: 姓 名: 专业、班: 实验地点: 瑞樟6#307 指导教师:温倩 时 间 :2012-4-23
一、实验目的及要求
掌握用数学软件求解优化问题
二、实验设备(环境)及要求
计算机、MATLAB软件、LINGO 软件
三、实验内容与步骤
钢管订购和运输优化问题: 要铺设一条15
21
A A A →→→ 的输送天然气的主管道, 如图所示。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,如下表:
1521,,,A A A ,而是管道全线)。
钢厂到点的最小总费用(单位:万元)见附件. 问题:请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(1)模型假设
(2)符号说明
7
(3)模型建立
(4)模型求解
四、实验结果与数据处理
五、分析与讨论。
