传热例题
热传导和传热的容量练习题

热传导和传热的容量练习题传热是我们日常生活中一个非常重要的物理现象,它对于能量的传递和温度变化具有重要的影响。
而热传导则是传热过程中的一种重要方式。
本篇文章将通过几个练习题,帮助读者加深对热传导和传热容量的理解。
练习题一:问题:一根长度为1m,截面积为1cm²的金属棒,其中一端被加热,另一端保持常温。
已知棒的热导率为0.5 W/(m·K),散热面的温度为30℃,加热面的温度为100℃。
求金属棒上离加热面20cm处的温度。
解析:首先,我们可以利用热导率和传热面温差计算单位长度上的热流量。
在本题中,热流量Q可以通过以下公式计算:Q = λ * A * (ΔT/Δx)其中,λ代表热导率,A代表截面积,ΔT代表温度差,Δx代表长度差。
根据题目中的已知条件,热导率λ为0.5 W/(m·K),截面积A为1cm²,即0.0001 m²。
温度差ΔT为100℃-30℃,等于70K。
长度差Δx为20cm,等于0.2m。
将已知条件代入公式,可以计算出单位长度上的热流量Q:Q = 0.5 * 0.0001 * (70/0.2) = 0.175 W/m接下来,我们可以利用热流量和热导率计算出单位长度上的温度梯度。
单位长度上的温度梯度可以通过以下公式计算:ΔT/Δx = Q / (λ * A)将已知条件代入公式,可以计算出单位长度上的温度梯度:ΔT/Δx = 0.175 / (0.5 * 0.0001) = 3500 K/m最后,我们可以利用温度梯度和已知条件计算出离加热面20cm处的温度。
单位长度上的温度变化可以通过以下公式计算:ΔT = (ΔT/Δx) * Δx将已知条件代入公式,可以计算出离加热面20cm处的温度:ΔT = 3500 * 0.2 = 700 K由于加热面的温度为100℃,所以离加热面20cm处的温度为:100℃ + 700K = 800℃练习题二:问题:一块厚度为10cm,热导率为1 W/(m·K)的砖块,其上表面温度为800℃,下表面温度为20℃。
传热学计算例题

、室内一根水平放置的无限长的蒸汽管道,其保温层外径d=583 mm,外表面实测平均温度及空气温度分别为,此时空气与管道外表面间的自然对流换热的表面传热系数h=3.42 W /(m2 K),墙壁的温度近似取为室内空气的温度,保温层外表面的发射率问:(1)此管道外壁的换热必须考虑哪些热量传递方式;(2)计算每米长度管道外壁的总散热量。
(12分)解:(1)此管道外壁的换热有辐射换热和自然对流换热两种方式。
(2)把管道每米长度上的散热量记为qi当仅考虑自然对流时,单位长度上的自然对流散热q i,c =二d h t =二dh (j - t f )= 3.14 0.583 3.42 (48 - 23 )二156 .5(W / m)近似地取墙壁的温度为室内空气温度,于是每米长度管道外表面与室内物体及墙壁之间的辐射为:q i厂d (T; -T;)= 3.14 0.583 5.67 10》0.9 [(48 273)4-(23 273)4]= 274.7(W /m)总的散热量为q i = q i,c +q i,r = 156.5 +274.7 = 431.2(W/m)2、如图所示的墙壁,其导热系数为50W/(m- K),厚度为50mm在稳态情况下的墙壁内的一维温度分布为:t=200-2000x 2,式中t的单位为°C, x单位为m 试求:t(1) 墙壁两侧表面的热流密度;(2) 墙壁内单位体积的内热源生成的热量2t =200 —2000x解:(1)由傅立叶定律:①dtWq' (―4000x) = 4000二xAdx 所以墙壁两侧的热流密度:q x _. =4000 50 0.05 =10000(1)由导热微分方程 茫•生=0得:dx 扎3、一根直径为1mm 勺铜导线,每米的电阻为2.22 10 。
导线外包有厚度为0.5mm 导热系数为0.15W/(m • K)的绝缘层。
限定绝缘层的最高温度为 65°C,绝 缘层的外表面温度受环境影响,假设为40°C 。
传热例题
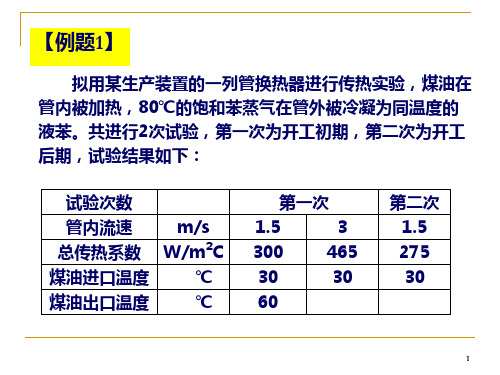
Re
0.05 0.643 880 7.245 104 3 0.39 10
湍流
1.86 103 0.39 103 Pr 5.41 0.134
cp
2 0.023
0.023
d2
Re0.8 Pr0.4
0.134 (7.254 104 ) 0.8 (5.41) 0.4 937W / m 2 0 C 0.05
(1)
(2)
(3)
K: 1、 2不变 Q: Q 排除法
K 不变
T2
假设Q不变,Δ tm不变,t2变大,Q增大, 矛盾 假设Q变小,Δ tm变小(1),T2增大(2) , t2增大 ,Q增大,矛盾
t1
t2
6
Q KAtm
(1)
Q ms 2cp 2 t2 t1
Q增大
Q ms1cp1 T1 T2
i 449.84W / m2 K 'i 783.21 W / m2 K
3
(2)
将 i 449.84W / m2 K
1 1 d o 1 d o K o o d m i di
代入(1)
解得 (3)
o
2029 .06W / m2 K
do 1 1 d o 1 Rsi '' d K o o d m i i (3)-(1) 1'' 1 Rsi d o K o Ko di
1.5m2cp 2 (t2 t1 ) K ' A1t 'm
t2 t1 1.5m2 c p 2 (t2 t1 ) K ' A1 T ' t1 ln ' T t2
传热学(第四版)例题

367.4W m2
例题1-4
对一台氟利昂冷凝器的传热过程作初步测 算得到以下数据:管内水的对流传热表面 传热系数 h1 8700W (m2 K ) ,管外氟利昂蒸 气凝结换热 表面传数 h2 1800W (m2 K ) , 换热管子壁厚 1.5mm 。 管子材料是导热 系数 383W (m k) 的铜。试计算三个环 节的热阻及冷凝器的总传热系数。欲增强 传热应从哪个环节入手?
发射率 = 0.9 。试求(1)此管道的散热必须
考虑哪些热量传递方式;(2)计算每米长度管 道的总散热量。
解:此管道的散热有辐射传热和自然对流传热两种方式。 把管道每米长度上的散热量记为 ql 。
单位长度上的自然对流散热量为
ql,c d ht dh(tw t f )
3.140.5833.42(48 23) 156.5 w m
(4)材料为硅藻土, 0.242W (mk)
解: 铜:
q tw1 tw2 375 300 100 1.50106W / m2
0.00 100 1.46105W / m2
0.05
鉻砖:
q tw1 tw2 2.32 300 100 9.28103W / m2
解:为求平均导热系数 ,先算出材料的平均温度
于是
500C 50C
t
275C
2
(0.0651 0.000105 275)W (m K )
(0.0651 0.0289)W (m K)
0.0940W (m K)
代入得每平方米炉墙的热损失为
q
(t1
t2 )
0.0940W (m 0.120m
单管是换热器传热例题

单管是换热器传热例题
换热器传热例题一般涉及以下几个方面:
1. 热传导:例如,“A型换热器两端温差为10°C,壁厚为5 mm,导热系数为10 W/(m·K),求热流量是多少?”
2. 强制对流传热:例如,“水流经B型换热器的流速为0.5 m/s,管道内径为0.03 m,求水的对流换热系数和热传递率是多少?”
3. 自然对流传热:例如,“一个垂直放置的C型换热器,外表面积为1 m^2,表面温度为60°C,环境温度为20°C,求自然对流传热系数和热传递率是多少?”
4. 辐射传热:例如,“高温辐射换热器的发射率为0.8,表面积为2 m^2,表面温度为700°C,求辐射热流量是多少?”
以上只是一些例题的简化描述,实际问题中还需考虑更多参数。
在实际计算中,可以根据不同类型的换热器选择相应的传热计算模型并运用换热理论来求解。
传热学-稳态导热例题

专题二 稳态热传导
【解】
专题二 稳态热传导
【名校真题解析】29 (北京科技大学2012) 【计算题】考察一管长6m, 内、外径分别为7.4cm、
8.0cm,导热系数为14W/(m·℃)的压缩空气管道。管的外表 面由总功率为300W的电阻带均匀加热,外包绝热层,通过 绝热层的散热损失为15%。管内空气的平均温度为−10℃ , 管道内表面的对流换热系数为30 W/(m2·℃)。试:
专题二 稳态热传导
温度场分布:
r=r2 处有最高温度:
t2
tf
q h
t2
150 ℃ 1.05105 3 500
q 2 (t1 t2 ) 2
t1
q 2 2
t2
186.30C
燃料层控制方程: 料层边界条件:
燃料层温度分布:
t
Φ
21
1
2
2
x2
t1
燃料层最高温度:
t0
t1
1 22
21
196.8℃
【计算题】一长为L的长圆柱内热源为 ,常物性,导 热系数为λ,左端面和侧面都绝热,右端与流体接触,温 度为tf,表面传热系数为 h,求
①写出微分方程和边界条件 ②温度分布 ③最大温度tmax
【解】 控制方程:
边界条件:
第一次积分:
第二次积分:
x L,
tL
Φ 2λ
L2
c2
tf
L ; h
c2 =t f
L h
Φ 2λ
L2
温度分布: 当x=0时,取得最大温度:
专题二 稳态热传导
【名校真题解析】 25(北京科技大学2011) 【计算题】考察一功率为800W的家用电熨斗
传热综合例题

例1.一列管换热器,管子规格为φ25×2.5mm ,管内流体的对流给热系数为100 W/(m ⋅K),管外流体的对流给热系数为2000 W/(m ⋅K),已知两流体均为湍流流动,管内外两侧污垢热阻均为0.0018 m ⋅℃/W 。
试求:①传热系数K 及各部分热阻的分配;②若管内流体流量提高一倍,传热系数有何变化?③若管外流体流量提高一倍,传热系数有何变化?解:①已知污垢热阻R i = R o = 0.00118 m 2⋅K/W , 钢管λ = 45 W/(m ⋅K)022502025002002...=+=+=o i m d d d m 0011802020100025002250450250002502000111......⨯+⨯+⨯⨯+=++++=o i ii o m o o o R R d d d d K αλδα = 0.01542 1/(W/m 2⋅K)K o = 64.84 W/(m 2⋅K)热阻分配:污垢: % (315153001542)000118021==⨯=+oi o K R R 管外: %..2430154202000111==ooK α 管内:% (181********)010002501=⨯=oi i oK d d α管壁:%.....4100154200220450250002501=⨯⨯=omoK d bd λ ②因为i i W W 2=', 所以 i i u u 2=' , i iαα802.=' ∴011R R ddd d K i ii o m o oo++'++='αλδα 00118020201002025002250450250002502000180.......⨯+⨯⨯+⨯⨯+== 0.01010 m 2⋅K/W9998.='o K W/( m 2⋅K)传热系数的增加的百分数:%.% (75210084)6484649998=⨯-=-'o o oK K K ③若o o W W 2=' , o o αα802.='∴ o i ii om o oo R R d d d d K ++++'='αλδα1100118020201000250022504502500025020002180.......⨯+⨯+⨯⨯+⨯== 0.01521 m 2⋅K/W7465.='o K W/( m 2⋅K)传热系数的增加的百分数:%.% (4110084)6484647465=⨯-=-'o o oK K K 可见,管内一侧的热阻远大于管外一侧的热阻,提高热阻大的一侧给热系数将有效地增加传热系数。
传热过程及换热器例题

传热过程与换热器1.一外直径为 20mm 的导线用橡胶做绝缘,橡胶绝缘层的厚度为 10mm ,导热系数为0.15 W/(m ・K),它与外部空气间的表面传热系数为 10 W/(m 2 .K)。
试分析此情况下的橡胶绝缘层是否妨碍导线的散热。
解 本题导线外直径d 1 =20mm ,绝缘层厚度:=10mm ,则绝缘层外直径 d 2 • 2" =20 • 2 10=40mm 。
临界绝缘直径 d c 为d c =2丄=2 015 =0.03m =30mm h 2 10显然,导线绝缘层外直径大于临界绝缘直径,即d 2 d c ,此时的热阻比临界绝缘直径时的热阻要大,使得导线的散热量减少。
因此从有利于导线的散热考虑,橡胶绝缘层厚度应取(d c -d 1)/2 =(30 -20)/2 =5mm 为宜。
2.已知热流体进口温度为 80C ,出口温度为 50C ,而冷流体进口温度为 10C ,出口 温度为30 C 。
试计算换热器为下列情况下的对数平均温压。
(1)纯顺流。
(2)纯逆流。
(3)1-2型壳管式。
解 根据题意,t ;=80 C,帚=50 C ; t 2 ^10 C, t ;=30 C,贝U(1)纯顺流时, t 二t ;-t 2 =80 -10 =70C ; t # -t 2 =50 -30 =20C,则丄ZT —A t " 70—20 :tm1 : 7039.9 Cln( ) In:t 20⑵ 纯逆流时, *—t2=80 —30=50 C ; f =t1—t 2 =50—10=40 C,则3 1-2型壳管式,因为不是纯顺流或纯逆流,因此需要先按纯逆流考虑,再进行修正即可。
■ * jU «1■« 1« it 2 -t 230 —10t 1 -t 230-10寸巾284,查得1-2型壳管式换热 m2•勺一•址 50—40=44.8 Cln(■ :t40即=f (R, P) =f (1.5,0.284) =0.95.■■:t m ^ _■ ■:t m 2 = 0.95 :• 44.8 = 42.6 C可见,换热器在相同的流体进、出口温度下,以纯逆流方式的对数平均温压最大,纯顺流 方式的对数平均温压最小,其他方式的对数平均温压介于纯逆流和纯顺流之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t m , 逆
950 Q m1 r 1099 290.0kW 3600
m2 17.37kg / s
第三部分 传热
氨 T=40℃,950kg/h, 1=7000kW/m2K
解一: LMTD 法
u2 m2
2 2 d 内
r=1099kJ/kg
t2=36℃
1 4
1 272 2 994 0.02 4 4 0.818m / s 994 0.818 0.02 Re 2 74.2 10 5 219162 104 .
Q m1 r m2 c p2 t 2 t1
化工原理专论
水 252.5mm,l=4m, N=272 根,m=4, D=700mm
T=40℃
四管程列管式
t 2 t 1 t 2 ln t 1 t1 t 2 5.77C T t2 ln T t1
11/14
解一: LMTD 法
A外 d外 1 1 1 Ra 2 Ra 2 K 2 A内 1 2 d内 1 0.025 1 0.0009 4043.5 0.02 7000
K 739.6W m 2 K
氨 T=40℃,950kg/h, 1=7000kW/m2K
0.910 216 2.0 L逆 1.56m Kd 外 3600
化工原理专论
第三部分 传热
8/14
解二: -NTU法
并流时:
1 e xp 1 C R NTU 1 CR
C Rh m h c ph mc c pc c ph c pc 2.0 0.478 4.187
Q A需 Kt m
290.0 103 68.0m 2 739.6 5.77
r=1099kJ/kg
t2=36℃ t1 =32℃ 水 252.5mm,l=4m, N=272 根,m=4, D=700mm T=40℃
A实 85.4m
2
A需 A实
化工原理专论
换热面积够用
化工原理专论 第三部分 传热
14/14
可对传热过程进行如下定性分析: 1.根据操作条件的改变情况,分析NTU、CR的变 化趋势; 2.利用图定出传热效率的变化趋势,随之确定出 口温度的变化趋势 3.根据热量衡算关系式去定Q和温度的变化趋势
化工原理专论
第三部分 传热
15/14
典型例题--------操作型问题分析
T1 m1 t2?
(4)
T2?
Q m 2 c p 2 t 2 t 1 (3) 1 1 b 1 Ra 1 Ra 2 KA 1 A1 Am 2 A2
套管式
假设 Q 变小,由式 1 得t m
T1 由式 2 得T2 ,由式 3 得t 2 ,
t m
热量衡算和传热速率
例3:无相变的冷、热流体在套管式换热器中进行换热,今 若热流体的质量流量增大,而其它操作参数不变,试定性分 析K、Q、t2、T2、tm的变化趋势。
t1 T1 m1 t2? T2?
套管式
化工原理专论 第三部分 传热
16/14
LMTD 法:
Q Kt m A
(1) (2)
Q m 1 c p1 T1 T2
t 2 53.4C
水 t1=20℃ 2=3.5kW/m2K cp=4.187 kJ/kgK LMTD 法 216kg/h 油 216kg/h T1=150℃ cp=2.0 kJ/kgK, t2 2 1=1.5 kW/m K
T2=80℃
K 0.894kW m 2 K (以外表面为基准)
kW m 2 K ,水侧的对流传热系数为 油侧对流传热系数为 1.5 kW m 2 K , 3.5 油的比热为 2.0kJ kg K , 试分别计算逆流和
并流操作所需要的管长。忽略污垢热阻及管壁导热热阻。
水 t2 2=3.5kW/m2K cp=4.187 kJ/kgK 216kg/h T2=80℃ t1=20℃
第三部分 传热
油 216kg/h T1=150℃ cp=2.0 kJ/kgK, 1=1.5 kW/m2K
化工原理专论
3/14
水 t2
解一: LMTD 法 逆流时:
Q m h c ph T1 T2 216 2.0 150 80 8.4 kJ s 3600
油 216kg/h T1=150℃ cp=2.0 kJ/kgK, 1=1.5 kW/m2K
专题三 传热
典型例题
化工原理专论
第三部分 传热
1/14
设计型 操作型
t1 T2
LMTD法:
对数平均温差法
Q Kt m A
Q m h c ph T1 T2 (2) Q m c c pc t 2 t 1 (3)
(1)
T1
-NTU 法
C Rc C Rh m c c pc m h c ph m h c ph m c c pc
t m,逆 t 2 t 1 T1 t 2 T2 t 1 76.9C t 2 T1 t 2 ln ln t 1 T2 t 1
t 2 53.4C
Q Kd 外 L逆 t m 逆
化工原理专论
L逆 1.56m
第三部分 传热
4/14
解一: 并流时: Q、t2、K与逆流时相同 Q 8.4 kJ s
1 1 NTU ln1 C R CR 1 CR 1
(1)
按冷、热流体当中的任一计算均可。以下以热流密度最小 的热流体为基准计算。
C Rh
m h c ph m c c pc
c ph
T1 T2 h T1 t 1
2.0 0.478 c pc 4.187 KA 代入式1得: NTU h 0.910 m h c ph
化工原理专论
其余情况: NTU f C R ,
第三部分 传热
1 e xp 1 C R NTU (并流时) 1 CR
2/14
KA m h c ph
典型例题
------设计型问题
例1 在套管式油冷却器里,热油在252.5mm 的金属管内流动, 冷却水在套管环隙内流动,油和水的质量流量皆为 216kg/h,油 的进、出口温度分别为 150℃和 80℃,水的进口温度为 20℃。
四管程列管式
13/14
第三部分 传热
传热定性分析方法 (1)平均推动力法 平均推动力法的核心是联合利用传热速率方程式和热 量衡算方程式来确定操作条件改变后传热效果(Q、 T2、t2)的变化情况。在分析时,由于三者之间的关 系是通过上述两式隐含地联系起来,且相互影响,通 常要用反证法,比较繁琐。 (2)传热效率-传热单元数法 由于传热单元数和传热效率以及CR的关系已知(若 传热单元数一定,则CR 增大对应的效率减小;若CR 一定,则传热单元数的增大将使传热效率增大。)
0.8
m1 2不变
K
假设 Q 不变,由式 1 得t m
由式 2 得T2 ,由式 3 得t 2 不变 ,2 t t m
T2
出现矛盾的结果,故假设不成立
0
化工原理专论 第三部分 传热
t1
17/14
A
t1
Q Kt m A
(1) (2)
Q m 1 c p1 T1 T2
化工原理专论 第三部分 传热
150 80 0.538 150 20
7/14
解二: -NTU法
前面已求得: A外 d外 1 1 1 0.025 1 K 1 A内 2 1d内 2 1.5 0.02 3.5
K 0.894kW m 2 K (以外表面为基准)
N m 17.37
t1 =32℃ 水 252.5mm,l=4m, N=272 根,m=4, D=700mm T=40℃
c p2 4.174 kJ kg K 2 0.6236W m K
Pr 2 4.97
四管程列管式 2 74.2 105 Pa s 2 994 kg m 3
1 1 b 1 Ra 1 Ra 2 KA 1 A1 Am 2 A2
t2
(4)
c
h
t 2 t1 T1 t 1
T1 T2 T1 t 1
NTUc
KA m c c pc
NTUh
1 1 NTU ln1 C R C R (逆流时) 1 CR 1
t 2 t 1 T1 t 1 T2 t 2 t m,并 65.1C t 2 T1 t 1 ln ln t 1 T2 t 2
Q L并 1.83m Kd 外 t m 并
化工原理专论 第三部分 传热
5/14
解一: LMTD 法
结论:在相同条件下,
T1 T2 150 80 h 0.538 T1 t 1 150 20
( 2)
代入式2得: NTU h
KA 1.07 m h c ph
1.07 216 2.0 L并 1.83m Kd 外 3600
化工原理专论 第三部分 传热
9/14
------操作型问题举例
Nu 0.023Re0.8 Pr 0.4 (0.7 Pr2 160)
2 0.023
2
d内
Re 2
0.8
Pr 2
0.4
0.6236 0.023 219162 0.8 4.970.4 . 0.02 4043 5W m 2 K .
第三部分 传热
化工原理专论
