2015年高考理科数学试题及答案-全国卷2
2015年高考全国新课标卷Ⅱ理科数学真题含答案解析(超完美版)

2015年高考全国新课标卷Ⅱ理科数学真题(青海;西藏;甘肃;贵州;内蒙古;新疆;宁夏;吉林;黑龙江;云南;辽宁;广西;海南)一、选择题1.已知集合A={-2,-1,0,1,2},B={X|(X-1)(X+2)<0},则AB=( ) A .{-1,0} B .{0,1} C .{-1,0,1} D .{0,1,2}2.若a 为实数,且(2+ai )(a-2i )= - 4i ,则a=( )A .-1B .0C .1D .23.根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化硫排放量的效果最显著B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫排放量呈减少趋势D .2006年以来我国二氧化硫排放量与年份正相关4.已知等比数列{a n } 满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7=( )A .21B .42C .63D .845.设函数f (x )=f (x )={1+log 2,(2−x ),x <12x−1,x ≥1则f (-2)+f (log 212)=( )A .3B .6C .9D .12 6.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A .18B .17C .16D .157.过三点A (1,3),B (4,2),C (1,-7)的圆交y 轴于M ,N 两点,则IMNI=( )A .2√6B .8C .4√6D .108.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图,若输入的a , b 分别为14 ,18,则输出的a=( )A .0B .2C .4D .149.已知A,B 是球O 的球面上两点,∠AOB=90o ,C 为该球上的动点,若三棱锥O-ABC 的体积最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π10.如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=,将动点P 到,A B 两点距离之和表示为x 的函数,则()y f x =的图像大致为( )A .B .C .D .11.已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为( )A B .2 C D 12.设函数f ’(x)是奇函数f(x)(x ∈R)的导函数,f(-1)=0,当x>0时,x f ’(x)- f(x)<0,则使得f(x)>0成立的x 的取值范围是( )A .(−∞,-1)∪(0,1)B .(−1,0)∪(1,+∞)C .(−∞,-1)∪(-1,0)D .(0,1)∪(1,+∞)二、填空题13.设向量a,b 不平行,向量λ a+b 与a+2b 平行,则实数 λ =14.若x ,y 满足约束条件,则z=x+y 的最大值为 15.4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a=16.设S n 是数列{a n }的前n 项和,且1111,n n n a a s s ++=-=,则S n =三、解答题17.△ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 面积是△ADC 面积的2倍(I )求Csin B sin ∠∠ (II )若AD=1,DC=22,求BD 和AC 的长18.某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机抽查了20个用户,得到用户对产品的满意度评分如下:A 地区:62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B 地区:73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:记事件C :“A 地区用户的满意等级高于B 地区用户的满意度等级”.假设两地区用户的评价结果互相独立。
2015全国卷2理科数学试题及答案解析

2014 年普通高等学校招生全国统一考试 理科(新课标卷二Ⅱ)第Ⅰ卷一. 选择题:本大题共 12小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题目要 求的 .1.设集合 M={0,1,2 },N= x|x 2 3x 2≤0 ,则 M N =( ) A. {1}B. {2}C. {0,1}D. { 1,2}【答案】 D 【解析】把 M={0,1,2} 中的数,代入不等式 x2-3x+2≤0, 经检验 x=1,2 满足。
所以选 D.2.设复数 z 1, z 2在复平面内的对应点关于虚轴对称, A. - 5B. 5C. - 4+【答案】 B 【解析】z 1= 2+i,z 1与z 2关于虚轴对称,∴z 2= -2+i, ∴ z 1z 2 = -1-4= -5,故选 B.3. 设向量 a,b 满足 | a+b |= 10 , | a-b |= 6 ,则 a b = ( )A. 1B. 2C. 3D. 5 【答案】 A【解析】2 2 2 2|a+b|= 10, | a - b |= 6,,∴ a +b + 2ab= 10,a +b -2ab= 6, 联立方程解得 ab = 1,故选 A.1, AB=1, BC= 2 ,则 AC=( )答案】 B 解】z 1 2 i ,则 z 1z 2 ( ) i D. - 4 - i4. 钝角三角形 ABC 的面积是 A. 5C. 2D. 111S ΔABC = acsin B = ? 2?1?sinB= ΔABC 2 2 ∴B= π,或3π.当B = π时,经计算ΔABC为等腰直角三角形,不 符合题意,舍去 4 4 4 ∴ B= 3π,使用余弦定理, b 2 = a 2 +c 2 - 2ac cosB,解得b= 5.故选B.4A. 17B.5C. 10D.1 279273【答案】 C 解析】加工前的零件半径为 3,高6,∴体积v 1 = 9π?6= 54π. 加工后的零件,左半部 为小圆柱,半径 2,高4,右半部为大圆柱,半 径为3,高为 2. ∴体积 v 2 = 4π ?4+ 9π?2= 34π.∴削掉部分的体积与原体 积之比 = 54π- 34π= 10.故选C. 54π 27【解析】sinB= 7 * 225. 某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75 ,连续两为优良的概率是6.如图,网格纸上正方形小格的边长为 1(表示 1cm ), 图中粗线画出的是某零件的三视图,该零件 由一个底面半径为 3cm ,高为 6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的 比值为( )x= 2,t= 2,变量变化情况如下:M S K1 3 12 5 2 273故选C.8. 设曲线 y=a x-ln(x+1) 在点 (0,0) 处的切线方程为 y=2x ,则 a =A. 0B. 1C. 2D. 3【答案】 D【解析】f(x)= ax - ln( x+ 1),∴f ′(x)= a- .x+1∴f(0)=0,且f ′(0)= 2.联立解得 a= 3.故选D.x y 7≤ 09. 设 x,y 满足约束条件x 3y 1≤0 ,则 z 2x y 的最大值为()3x y5≥0A. 10B. 8C. 3D. 2【答案】 B【解析】画出区域,可知区域为 三角形,经比较斜率, 可知目标函数 z= 2x- y 在两条直线 x-3y+1= 0与x+ y-7= 0的交点(5,2)处, 取得最大值 z= 8.故选 B.10.设 F 为抛物线 C: y 2 3x 的焦点,过F 且倾斜角为 30°的直线交 C 于 A,B 两点, O 为坐标原点,则△ OAB 的面积为( )A. 3 3B.9 3C.63D. 9 48 C.32 4【答案】 解析】D设点A 、B 分别在第一和第四象限 ,AF = 2m,BF = 2n ,则由抛物线的定义和 直角三角形知识可得, 2m= 2?3+ 3m,2n = 2?3- 3n ,解得m= 3(2+ 3),n= 3(2- 3),∴m+n= 6. ∴S ΔOAB =1?3?(m+n)= 9.故选D.Δ OAB2 4 42 2【答案】 C 【解析】如图,分别以 C 1B 1,C 1A 1,C 1C 为X,Y,Z 轴,建立坐标系。
2015年高考全国卷2理科数学试题解析
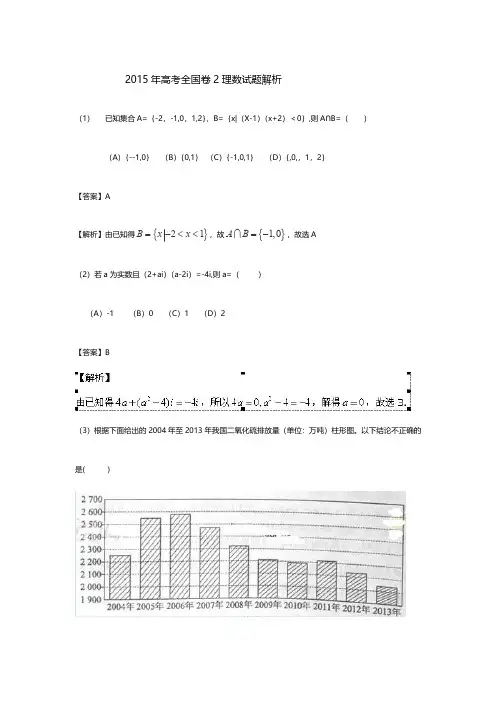
f (log2 12) 2log2121 2log2 6 6 ,故 f (2) f (log212) 9 .
(6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的 比值为
1
(A)
8
【答案】D
1
(B)
7
1
(C)
6
1
(D)
5
【解析】由三视图得,在正方体 ABCD A1B1C1D1 中,截去四面体 A A1B1D1 ,如图所示,,设正方
)
(A)21
(B)42
(C)63 (D)84
【答案】B
(5)设函数
f
(x)
12x1lo, xg2(12,
x), x
1,
,
f
(2)
f
(log 2 12)
(
)
(A)3 (B)6
(C)9 (D)12
【答案】C
【 解 析 】 由 已 知 得 f (2) 1 log 2 4 3 , 又 log2 12 1 , 所 以
1
【答案】
2
【解析】因为向量
a
b
与
a
2b
平行,所以
a
b
(k a
2b),则
k, 1 2k, 所以
1 2
.
x y 1 0, (14)若 x,y 满足约束条件 x 2 y 0, ,则 z x y 的最大值为____________.
(B)8
(C)4 6
(D)10
【答案】C
2015高考理科数学新课标全国2答案及解析

解析:������������+1=������������������������+1得到������������+1−������������=������������������������+1,同除������������������������+1,得到������������1+1-���1���������=-1
(11)D 解析:
(12)A
< ∠ABM=120,∆ABM 为等腰三角形 做 MC 垂直于 X 轴,交点为 C ∴∠MBA=30,∠MBA=60 AB=2a,所以 BM=2a,AM=2√3a OC=2a,MC=√3a M 点坐标(2a,√3a)代入双曲 线方程,为等轴双曲线,离心率 e=√2
解析:当 x>0 时,xf (́ x) − f(x) < 0可以构造可导函数 F(x)=������(������������)
V=13
×
1 2
������3=36
∴ R = 6,∴ S = 4π������2=144π
(10)B
解析:特殊点法,当点 P 与点 C 重合,x=���Байду номын сангаас���,此时 P 到 AB 两点距离之和=√5+1
当点 P 为 CD 中点,x=���2���,此时 P 到 AB 两点距离之和=2√2
当点 P 为 CD 中点,x=���2���时,P 到 AB 两点距离之和最小。
F
(́ x)=xf
(́ x)−f(x) ������2
<
0,所以
F(x)=������(������������),当
x>0
时为减函数
2015高考理科数学新课标全国2答案及解析

(5)C
解析:当 x=-2 时
f(x)=1+log2(2 − ������) = 1 + log2 4 = 1 + 2 = 3
当 x=log2 12 时 f(x)=2������−1=2log2 12−1=2log2 6=6
(6)D
f(-2)+ f(log2 12)=3+6=9
解析:
截去部分为三棱锥 B-AC������1 截去部分体积为正方体体积减去三棱锥体积
传播正能量 启迪大智慧 2015 高考理科数学新课标全国Ⅱ卷
选择题部分答案
一、选择题(每题 5 分,共 60 分)
(1)A
解析:B={x|(x -1)(x+2)<0}解得 B={x|-2<x<1}含有整数-1,0;
所以 A∩B={--1,0}
(2)B
解析:(2+ai)(a-2i)= 2a+(������2 − 4)i-2a������2=2a+(������2 − 4)i+2a=4a+(������2 − 4)i=-4i,
=
1 2
解析:λa+b=������(������
+
������������)则������
=
λ,2������
=
������,所以λ
=
1 2
(14)32
解析:三个交点为(-2,-1),(1,12),(0,1)最大值必在交点取得,代入32最大. (15)3
解析:a 与奇数项相乘 8a,x 与偶数项相乘系数为 8,8a+8=32,则 a=3
{ 1 }为首相为-1,公差为-1
������������
的等差数列 1
2015年高考理科数学全国卷(新课标II卷)含答案

1 2
3 . 2
y
B D
1 2 3 4
O
–1 –2 –3 –4
x
C
15. (a x)(1 x) 的展开式中 x 的奇数次幂项的系数之和为 32,则 a __________.
4
【答案】 3 【解析】 试题分析:由已知得 (1 x) 1 4 x 6 x 4 x x ,故 (a x)(1 x) 的展开式中 x 的奇数次幂项分别
x A O B
【答案】B 【解析】
考点:函数的图象和性质. 11.已知 A,B 为双曲线 E 的左,右顶点,点 M 在 E 上,∆ABM 为等腰三角形,且顶角为 120° ,则 E 的离 心率为( ) A. 5 【答案】D 【解析】 B. 2 C. 3 D. 2
x2 y 2 2 1(a 0, b 0) ,如图所示, AB BM ,ABM 1200 ,过点 M 2 a b 作 MN x 轴,垂足为 N ,在 RtBMN 中, BN a , MN 3a ,故点 M 的坐标为 M (2a, 3a ) ,
4 2 3 4
4
为 4ax , 4ax3 , x , 6 x 3 , x 5 ,其系数之和为 4a 4a 1+6+1=32 ,解得 a 3 . 考点:二项式定理. 16.设 S n 是数列 an 的前 n 项和,且 a1 1 , an1 Sn Sn1 ,则 Sn ________. 【答案】 【解析】 试题分析:由已知得 an1 Sn1 Sn Sn1 Sn ,两边同时除以 Sn 1 Sn ,得 是以 1 为首项, 1 为公差的等差数列,则
1 1 2 1 R R R3 36 , 故 R 6 , 则 球 O 的 表 面 积 为 3 2 6
2015年高考理科数学(全国二卷)真题
2015年普通高等学校招生全国统一考试理科数学(全国卷Ⅱ)(青海、西藏、甘肃、贵州、内蒙古、新疆、宁夏、吉林、黑龙江、云南、辽宁、广西、海南等)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页.2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4. 考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={-2,-1,0,1,2},B={X|(X-1)(X+2)<0},则A I B=()A.{-1,0}B.{0,1}C.{-1,0,1}D.{0,1,2} 2.若a为实数,且(2+ai)(a-2i)= - 4i,则a=()A.-1B.0C.1D.23.根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫排放量呈减少趋势D.2006年以来我国二氧化硫排放量与年份正相关4.已知等比数列{} 满足=3,+=21,则++=()A.21B.42C.63D.845.设函数f(x)=则f(-2)+f()=()A.3B.6C.9D.126.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.7.过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则IMNI=()A.2B.8C.4D.108.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图,若输入的a , b分别为14 ,18,则输出的a=()A.0B.2C.4D.149.已知A,B 是球O 的球面上两点,∠AOB=90o,C 为该球上的动点,若三棱锥O-ABC的体积最大值为36,则球O 的表面积为( ) A .36πB .64πC .144πD .256π10.如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=,将动点P 到,A B 两点距离之和表示为x 的函数,则()y f x =的图像大致为( )A .B .C .D .11.已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为( ) A .5B .2C .3D .212.设函数f’(x)是奇函数f(x)(x R)的导函数,f(-1)=0,当x>0时,x f’(x)- f(x)<0,则使得f(x)>0成立的x 的取值范围是( ) A .(,-1)∪(0,1)B .(,0)∪(1,+)C .(,-1)∪(-1,0)D .(,1)∪(1,+)二、填空题13.设向量a,b 不平行,向量λ a+b 与a+2b 平行,则实数 λ =14.若x ,y 满足约束条件,则z=x+y 的最大值为15.4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a=16.设S n 是数列{a n }的前n 项和,且1111,n n n a a s s ++=-=,则S n =三、解答题17.△ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 面积是△ADC 面积的2倍 (I )求Csin Bsin ∠∠ (II )若AD=1,DC=22,求BD 和AC 的长18.某公司为了了解用户对其产品的满意度,从A,B两地区分别随机抽查了20个用户,得到用户对产品的满意度评分如下:A地区:62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B地区:73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:记事件C:“A地区用户的满意等级高于B地区用户的满意度等级”.假设两地区用户的评价结果互相独立。
2015年普通高等学校招生全国统一考试 全国卷2 数学试卷含答案(理科)
2015年普通高等学校招生全国统一考试(课标全国卷Ⅱ)理 数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={-2,-1,0,1,2},B={x|(x-1)(x+2)<0},则A∩B=( ) A.{-1,0}B.{0,1}C.{-1,0,1}D.{0,1,2}2.若a 为实数,且(2+ai)(a-2i)=-4i,则a=( ) A.-1B.0C.1D.23.根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关4.已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7=( ) A.21B.42C.63D.845.设函数f(x)={1+log 2(2-x ), x <1,2x -1,x ≥1,则f(-2)+f(log 212)=( )A.3B.6C.9D.126.一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.157.过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=( )A.2√6B.8C.4√6D.108.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )A.0B.2C.4D.149.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )A.36πB.64πC.144πD.256π10.如图,长方形ABCD的边AB=2,BC=1,O是AB的中点.点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )11.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,且顶角为120°,则E的离心率为( )A.√5B.2C.√3D.√212.设函数f'(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf'(x)-f(x)<0,则使得f(x)>0成立的x 的取值范围是( ) A.(-∞,-1)∪(0,1)B.(-1,0)∪(1,+∞)C.(-∞,-1)∪(-1,0)D.(0,1)∪(1,+∞)第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.设向量a,b 不平行,向量λa+b 与a+2b 平行,则实数λ= . 14.若x,y 满足约束条件{x -y +1≥0,x -2y ≤0,x +2y -2≤0,则z=x+y 的最大值为 .15.(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a= . 16.设S n 是数列{a n }的前n 项和,且a 1=-1,a n+1=S n S n+1,则S n = .三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)△ABC 中,D 是BC 上的点,AD 平分∠BAC,△ABD 面积是△ADC 面积的2倍. (Ⅰ)求sin∠Bsin∠C; (Ⅱ)若AD=1,DC=√22,求BD 和AC 的长.18.(本小题满分12分)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:A地区:62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B地区: 73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);A地区B地区456789(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.19.(本小题满分12分)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说明画法和理由);(Ⅱ)求直线AF与平面α所成角的正弦值.20.(本小题满分12分)已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.(Ⅰ)证明:直线OM的斜率与l的斜率的乘积为定值;,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此(Ⅱ)若l过点(m3时l的斜率;若不能,说明理由.21.(本小题满分12分)设函数f(x)=e mx+x2-mx.(Ⅰ)证明:f(x)在(-∞,0)单调递减,在(0,+∞)单调递增;(Ⅱ)若对于任意x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤e-1,求m的取值范围.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4—1:几何证明选讲如图,O为等腰三角形ABC内一点,☉O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(Ⅰ)证明:EF∥BC;(Ⅱ)若AG等于☉O的半径,且AE=MN=2√3,求四边形EBCF的面积.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,曲线C 1:{x =tcosα,y =tsinα(t 为参数,t≠0),其中0≤α<π.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=2sinθ,C 3:ρ=2√3cosθ. (Ⅰ)求C 2与C 3交点的直角坐标;(Ⅱ)若C 1与C 2相交于点A,C 1与C 3相交于点B,求|AB|的最大值.24.(本小题满分10分)选修4—5:不等式选讲 设a,b,c,d 均为正数,且a+b=c+d,证明: (Ⅰ)若ab>cd,则√a +√b >√c +√d ;(Ⅱ)√a +√b >√c +√d 是|a-b|<|c-d|的充要条件.2015年普通高等学校招生全国统一考试(课标全国卷Ⅱ)一、选择题1.A 因为B={x|(x-1)(x+2)<0}={x|-2<x<1},A={-2,-1,0,1,2},故A ∩B={-1,0}.选A.2.B ∵(2+ai)(a -2i)=-4i ⇒4a+(a 2-4)i=-4i, ∴{4a =0,a 2-4=-4,解得a=0. 3.D 由柱形图可知:A 、B 、C 均正确,2006年以来我国二氧化硫年排放量在逐渐减少,所以排放量与年份负相关,∴D 不正确.4.B 设{a n }的公比为q,由a 1=3,a 1+a 3+a 5=21得1+q 2+q 4=7,解得q 2=2(负值舍去).∴a 3+a 5+a 7=a 1q 2+a 3q 2+a 5q 2=(a 1+a 3+a 5)q 2=21×2=42.5.C ∵-2<1,∴f(-2)=1+log 2[2-(-2)]=3;∵log 212>1, ∴f(log 212)=2log 212-1=2log 26=6.∴f(-2)+f(log 212)=9.6.D 如图,由已知条件可知,截去部分是以△ABC 为底面且三条侧棱两两垂直的正三棱锥D-ABC.设正方体的棱长为a,则截去部分的体积为16a 3,剩余部分的体积为a 3-16a 3=56a 3.它们的体积之比为15.故选D.评析 本题主要考查几何体的三视图和体积的计算,考查空间想象能力. 7.C 设圆心为P(a,b),由点A(1,3),C(1,-7)在圆上,知b=3-72=-2.再由|PA|=|PB|,得a=1.则P(1,-2),|PA|=√(1-1)2+(3+2)2=5,于是圆P 的方程为(x-1)2+(y+2)2=25.令x=0,得y=-2±2√6,则|MN|=|(-2+2√6)-(-2-2√6)|=4√6. 8.B 开始:a=14,b=18,第一次循环:a=14,b=4; 第二次循环:a=10,b=4; 第三次循环:a=6,b=4; 第四次循环:a=2,b=4; 第五次循环:a=2,b=2. 此时,a=b,退出循环,输出a=2.评析 熟悉“更相减损术”对理解框图所确定的算法有帮助. 9.C ∵S △OAB 是定值,且V O-ABC =V C-OAB ,∴当OC ⊥平面OAB 时,V C-OAB 最大,即V O-ABC 最大.设球O 的半径为R,则(V O-ABC )max =13×12R 2×R=16R 3=36,∴R=6,∴球O 的表面积S=4πR 2=4π×62=144π.评析 点C 是动点,如果以△ABC 为底面,则底面面积与高都是变量,因此转化成以△OAB 为底面(S △OAB 为定值),这样高越大,体积越大.10.B 当点P 与C 、D 重合时,易求得PA+PB=1+√5;当点P 为DC 的中点时,有OP ⊥AB,则x=π2,易求得PA+PB=2PA=2√2.显然1+√5>2√2,故当x=π2时, f(x)没有取到最大值,则C 、D 选项错误.当x ∈[0,π4)时, f(x)=tan x+√4+tan 2x ,不是一次函数,排除A,故选B.11.D 设双曲线E 的标准方程为x 2a 2-y 2b 2=1(a>0,b>0),则A(-a,0),B(a,0),不妨设点M 在第一象限内,则易得M(2a,√3a),又M 点在双曲线E 上,于是(2a)2a 2-(√3a)2b2=1,解得b 2=a 2,∴e=√1+b 2a 2=√2.12.A 令g(x)=f(x)x,则g'(x)=xf '(x)-f(x)x 2,由题意知,当x>0时,g'(x)<0,∴g(x)在(0,+∞)上是减函数.∵f(x)是奇函数, f(-1)=0,∴f(1)=-f(-1)=0, ∴g(1)=f(1)1=0,∴当x ∈(0,1)时,g(x)>0,从而f(x)>0; 当x ∈(1,+∞)时,g(x)<0,从而f(x)<0.又∵g(-x)=f(-x)-x=-f(x)-x=f(x)x=g(x),∴g(x)是偶函数,∴当x ∈(-∞,-1)时,g(x)<0,从而f(x)>0; 当x ∈(-1,0)时,g(x)>0,从而f(x)<0. 综上,所求x 的取值范围是(-∞,-1)∪(0,1).评析 出现xf '(x)+f(x)>0(<0)时,考虑构造函数F(x)=xf(x),出现xf '(x)-f(x)>0(<0)时,考虑构造函数g(x)=f(x)x.二、填空题 13.答案12解析 由于a,b 不平行,所以可以以a,b 作为一组基底,于是λa+b 与a +2b 平行等价于λ1=12,即λ=12.14.答案32解析 作出可行域,如图:由z=x+y 得y=-x+z,当直线y=-x+z 过点A (1,12)时,z 取得最大值,z max =1+12=32.15.答案 3解析 设f(x)=(a+x)(1+x)4,则其所有项的系数和为f(1)=(a+1)·(1+1)4=(a+1)×16,又奇数次幂项的系数和为12[f(1)-f(-1)],∴12×(a+1)×16=32,∴a=3.评析 二项展开式问题中,涉及系数和的问题,通常采用赋值法. 16.答案 -1n解析∵a n+1=S n+1-S n,∴S n+1-S n=S n+1S n,又由a1=-1,知S n≠0,∴1S n -1S n+1=1,∴{1S n}是等差数列,且公差为-1,而1S1=1a1=-1,∴1S n=-1+(n-1)×(-1)=-n,∴S n=-1n.三、解答题17.解析(Ⅰ)S△ABD=12AB·ADsin∠BAD,S△ADC=12AC·ADsin∠CAD.因为S△ABD=2S△ADC,∠BAD=∠CAD,所以AB=2AC.由正弦定理可得sin∠Bsin∠C =ACAB=12.(Ⅱ)因为S△ABD∶S△ADC=BD∶DC,所以BD=√2.在△ABD和△ADC中,由余弦定理知AB2=AD2+BD2-2AD·BDcos∠ADB,AC2=AD2+DC2-2AD·DCcos∠ADC.故AB2+2AC2=3AD2+BD2+2DC2=6.由(Ⅰ)知AB=2AC,所以AC=1.评析本题考查正弦定理,余弦定理的应用,以及三角形的面积公式.属常规题,中等偏易.18.解析(Ⅰ)两地区用户满意度评分的茎叶图如下:A地区B地区4 6 83 5 1 3 6 46 4 2 6 2 4 5 56 8 8 64 3 73 34 699 2 8 65 18 3 2 17 5 5 2 9 1 3通过茎叶图可以看出,A 地区用户满意度评分的平均值高于B 地区用户满意度评分的平均值;A 地区用户满意度评分比较集中,B 地区用户满意度评分比较分散.(Ⅱ)记C A1表示事件:“A 地区用户的满意度等级为满意或非常满意”;C A2表示事件:“A 地区用户的满意度等级为非常满意”;C B1表示事件:“B 地区用户的满意度等级为不满意”;C B2表示事件:“B 地区用户的满意度等级为满意”,则C A1与C B1独立,C A2与C B2独立,C B1与C B2互斥,C=C B1C A1∪C B2C A2.P(C)=P(C B1C A1∪C B2C A2)=P(C B1C A1)+P(C B2C A2)=P(C B1)P(C A1)+P(C B2)P(C A2).由所给数据得C A1,C A2,C B1,C B2发生的频率分别为1620,420,1020,820,故P(C A1)=1620,P(C A2)=420,P(C B1)=1020,P(C B2)=820,P(C)=1020×1620+820×420=0.48.19.解析 (Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作EM ⊥AB,垂足为M,则AM=A 1E=4,EM=AA 1=8.因为EHGF 为正方形,所以EH=EF=BC=10.于是MH=√EH 2-EM 2=6,所以AH=10.以D 为坐标原点,DA ⃗⃗⃗⃗⃗ 的方向为x 轴正方向,建立如图所示的空间直角坐标系D-xyz,则A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),FE ⃗⃗⃗⃗⃗ =(10,0,0),HE⃗⃗⃗⃗⃗⃗ =(0,-6,8). 设n =(x,y,z)是平面EHGF 的法向量,则{n ·FE ⃗⃗⃗⃗ =0,n ·HE⃗⃗⃗⃗⃗ =0,即{10x =0,-6y +8z =0, 所以可取n =(0,4,3).又AF ⃗⃗⃗⃗⃗ =(-10,4,8),故|cos<n ,AF ⃗⃗⃗⃗⃗ >|=|n ·AF ⃗⃗⃗⃗⃗||n||AF ⃗⃗⃗⃗⃗ |=4√515. 所以AF 与平面EHGF 所成角的正弦值为4√515. 评析 本题背景常规,设问新颖,鼓励动手试验、创新尝试、独立思考.对空间想象力有较高要求.20.解析 (Ⅰ)设直线l:y=kx+b(k ≠0,b ≠0),A(x 1,y 1),B(x 2,y 2),M(x M ,y M ).将y=kx+b 代入9x 2+y 2=m 2得(k 2+9)x 2+2kbx+b 2-m 2=0,故x M =x 1+x 22=-kb k 2+9,y M =kx M +b=9b k 2+9.于是直线OM 的斜率k OM =y M x M =-9k ,即k OM ·k=-9.所以直线OM 的斜率与l 的斜率的乘积为定值.(Ⅱ)四边形OAPB 能为平行四边形.因为直线l 过点(m 3,m),所以l 不过原点且与C 有两个交点的充要条件是k>0,k ≠3. 由(Ⅰ)得OM 的方程为y=-9k x.设点P 的横坐标为x P .由{y =-9k x,9x 2+y 2=m 2得x P 2=k 2m 29k 2+81,即x P =3√k 2+9. 将点(m 3,m)的坐标代入l 的方程得b=m(3-k)3,因此x M =k(k -3)m 3(k 2+9). 四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分,即x P =2x M .于是3√k 2+9=2×k(k -3)m3(k 2+9),解得k 1=4-√7,k 2=4+√7. 因为k i >0,k i ≠3,i=1,2,所以当l 的斜率为4-√7或4+√7时,四边形OAPB 为平行四边形.评析 本题考查直线与圆锥曲线的位置关系,设问常规,但对运算能力要求较高,考查学生的思维能力.21.解析 (Ⅰ)f '(x)=m(e mx -1)+2x.若m ≥0,则当x ∈(-∞,0)时,e mx -1≤0, f '(x)<0;当x ∈(0,+∞)时,e mx -1≥0, f '(x)>0.若m<0,则当x ∈(-∞,0)时,e mx -1>0, f '(x)<0;当x ∈(0,+∞)时,e mx -1<0, f '(x)>0.所以, f(x)在(-∞,0)单调递减,在(0,+∞)单调递增.(Ⅱ)由(Ⅰ)知,对任意的m, f(x)在[-1,0]单调递减,在[0,1]单调递增,故f(x)在x=0处取得最小值.所以对于任意x 1,x 2∈[-1,1],|f(x 1)-f(x 2)|≤e-1的充要条件是{f(1)-f(0)≤e -1,f(-1)-f(0)≤e -1,即{e m -m ≤e -1,e -m +m ≤e -1.① 设函数g(t)=e t -t-e+1,则g'(t)=e t -1.当t<0时,g'(t)<0;当t>0时,g'(t)>0.故g(t)在(-∞,0)单调递减,在(0,+∞)单调递增.又g(1)=0,g(-1)=e -1+2-e<0,故当t ∈[-1,1]时,g(t)≤0.当m ∈[-1,1]时,g(m)≤0,g(-m)≤0,即①式成立;当m>1时,由g(t)的单调性,g(m)>0,即e m -m>e-1;当m<-1时,g(-m)>0,即e -m +m>e-1.综上,m 的取值范围是[-1,1].22.解析 (Ⅰ)由于△ABC 是等腰三角形,AD ⊥BC,所以AD 是∠CAB 的平分线.又因为☉O 分别与AB,AC 相切于点E,F,所以AE=AF,故AD ⊥EF.从而EF ∥BC.(Ⅱ)由(Ⅰ)知,AE=AF,AD ⊥EF,故AD 是EF 的垂直平分线.又EF 为☉O 的弦,所以O 在AD 上. 连结OE,OM,则OE ⊥AE.由AG 等于☉O 的半径得AO=2OE,所以∠OAE=30°.因此△ABC 和△AEF 都是等边三角形.因为AE=2√3,所以AO=4,OE=2.因为OM=OE=2,DM=12MN=√3,所以OD=1.于是AD=5,AB=10√33.所以四边形EBCF 的面积为12×(10√33)2×√32-12×(2√3)2×√32=16√33.23.解析 (Ⅰ)曲线C 2的直角坐标方程为x 2+y 2-2y=0,曲线C 3的直角坐标方程为x 2+y 2-2√3x=0. 联立{x 2+y 2-2y =0,x 2+y 2-2√3x =0,解得{x =0,y =0,或{x =√32,y =32. 所以C 2与C 3交点的直角坐标为(0,0)和(√32,32). (Ⅱ)曲线C 1的极坐标方程为θ=α(ρ∈R ,ρ≠0),其中0≤α<π.因此A 的极坐标为(2sin α,α),B 的极坐标为(2√3cos α,α).所以|AB|=|2sin α-2√3cos α|=4|sin (α-π3)|.当α=5π6时,|AB|取得最大值,最大值为4.24.解析 (Ⅰ)因为(√a +√b )2=a+b+2√ab ,(√c +√d )2=c+d+2√cd ,由题设a+b=c+d,ab>cd得(√a+√b)2>(√c+√d)2. 因此√a+√b>√c+√d.(Ⅱ)(i)若|a-b|<|c-d|,则(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd.因为a+b=c+d,所以ab>cd.由(Ⅰ)得√a+√b>√c+√d.(ii)若√a+√b>√c+√d,则(√a+√b)2>(√c+√d)2,即a+b+2√ab>c+d+2√cd.因为a+b=c+d,所以ab>cd.于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.因此|a-b|<|c-d|.综上,√a+√b>√c+√d是|a-b|<|c-d|的充要条件.。
2015年高考理科数学全国卷2-答案
2015年普通高等学校招生全国统一考试(全国新课标卷2)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】由已知得{|21}B x x =-<<,故,}10{AB -=,故选A .【提示】解一元二次不等式,求出集合B ,然后进行交集的运算即可. 【考点】集合的交集运算和一元二次方程求根. 2.【答案】B【解析】由已知得24+(4)i 4i a -=-,所以40a =,244a -=-,解得0a =,故选B .【提示】首先将坐标展开,然后利用复数相等解之. 【考点】复数的四则运算. 3.【答案】D【解析】解:A .从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少,且减少的最多,故A 正确;B .2004~2006年二氧化硫排放量越来越多,从2007年开始二氧化硫排放量变少,故B 正确;C .从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C 正确;D .2006年以来我国二氧化硫年排放量越来越少,而不是与年份正相关,故D 错误. 故选:D【提示】A .从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多,故A 正确; B .从2007年开始二氧化硫排放量变少,故B 正确;C .从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C 正确;D .2006年以来我国二氧化硫年排放量越来越少,与年份负相关,故D 错误. 【考点】柱形图信息的获得. 4.【答案】B【解析】设等比数列公比为q ,则24111++21a a q a q =,又因为13a =,所以42+60q q -=,解得22q =,所以2357135++(++)42a a a a a a q ==,故选B .【提示】由已知,13a =,135++21a a a =,利用等比数列的通项公式可求q ,然后在代入等比数列通项公式53261)(0,1),故选())f x x=为减函数,,0)(0,+)∞上的偶函数,根据函数0等价于x g【解析】(Ⅰ)两地区用户满意度评分的茎叶图如下:122B A C C ,12212))+()B A A B C C P C 1,2A C ,C 108【解析】(Ⅰ)交线围成的正方形EHGF 如图:uuu r 即可求出法向量n,AF。
2015年高考理科数学全国卷2及答案
数学试卷 第1页(共21页)数学试卷 第2页(共21页)数学试卷 第3页(共21页)绝密★启用前2015年普通高等学校招生全国统一考试(全国新课标卷2)数学(理科)使用地区:海南、宁夏、黑龙江、吉林、辽宁、新疆、云南、内蒙古、青海、贵州、甘肃、广西、西藏本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共24题,共150分,共6页.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{2,1,0,1,2}A =--,{|(1)(2)0}B x x x =-+<,则AB =( )A .{1,0}A =-B .{0,1}C .{1,0,1}-D .{0,1,2} 2.若a 为实数,且(2i)(2i)4i a a +-=-,则a =( )A .1-B .0C .1D .23.根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化硫排放量的效果最显著B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫年排放量呈减少趋势D .2006年以来我国二氧化硫年排放量与年份正相关4.已知等比数列{}n a 满足13a =,135a a a ++=21,则357a a a ++=( )A .21B .42C .63D .845.设函数211log (2),1,()2, 1,x x x f x x -+-⎧=⎨⎩<≥则2(2)(log 12)f f -+=( )A .3B .6C .9D .126.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18B .17C .16D .157.过三点(1,3)A ,(4,2)B ,(1,7)C -的圆交y 轴于M ,N 两点,则||MN =( )A .26B .8C .46D .108.如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( )A .0B .2C .4D .149.已知A ,B 是球O 的球面上两点,∠AOB =90°, C 为该球面上的动点.若三棱锥O-ABC 体积的 最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π10.如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点.点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=.将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则()y f x =的图象大致为( )ABCD11.已知A ,B 为双曲线E 的左、右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为( )A .5B .2C .3D .2 12.设函数'()f x 是奇函数()()f x x ∈R 的导函数,(1)0f -=,当0x >时,'()()0xf x f x -<,则使得()0f x >成立的x 的取值范围( )A .(,1)(0,1)-∞-B .(1,0)(1,)-+∞C .(,1)(1,0)-∞--D .(0,1)(1,)+∞--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共21页)数学试卷 第5页(共21页)数学试卷 第6页(共21页)第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=________.14.若x ,y 满足约束条件10,20,220,x y x y x y -+⎧⎪-⎨⎪+-⎩≥≤≤则z x y =+的最大值为________.15.4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a =________. 16.设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________. 三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)ABC △中,D 是BC 上的点,AD 平分BAC ∠,ABD △面积是ADC △面积的2倍.(Ⅰ)求sin sin BC∠∠;(Ⅱ)若1AD =,22DC =,求BD 和AC 的长. 18.(本小题满分12分)某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:A 地区:62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89B 地区:73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79 (Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:满意度评分 低于70分 70分到89分 不低于90分 满意度等级 不满意 满意 非常满意记事件C :“A 地区用户的满意度等级高于B 地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C 的概率.19.(本小题满分12分)如图,长方体1111ABCD A B C D -中,=16AB ,=10BC ,18AA =,点E ,F 分别在11A B ,11D C 上,114A E D F ==.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说明画法和理由); (Ⅱ)求直线AF 与平面α所成角的正弦值.20.(本小题满分12分)已知椭圆222 9(0)C x y m m +=>:,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .(Ⅰ)证明:直线OM 的斜率与l 的斜率的乘积为定值; (Ⅱ)若l 过点(,)3mm ,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率;若不能,请说明理由.21.(本小题满分12分)设函数2()mx f x e x mx =+-.(Ⅰ)证明:()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增;(Ⅱ)若对于任意12,[1,1]x x ∈-,都有12()()1f x f x e --≤,求m 的取值范围.请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4—1:几何证明选讲如图,O 为等腰三角形ABC 内一点,⊙O 与ABC △的底边BC 交于M ,N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点. (Ⅰ)证明:EF BC ∥;(Ⅱ)若AG 等于⊙O 的半径,且23AE MN ==,求四边形EBCF 的面积.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩(t 为参数,0t ≠),其中0πα≤<.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线2:2sin C ρθ=,3:23cos C ρθ=. (Ⅰ)求2C 与3C 交点的直角坐标;(Ⅱ)若1C 与2C 相交于点A ,1C 与3C 相交于点B ,求||AB 最大值.24.(本小题满分10分)选修4—5:不等式选讲设a ,b ,c ,d 均为正数,且a b c d +=+,证明: (Ⅰ)若ab cd >,则a b c d +>+; (Ⅱ)a b c d +>+是||||a b c d -<-的充要条件.数学试卷 第7页(共21页)数学试卷 第8页(共21页)数学试卷 第9页(共21页)2015年普通高等学校招生全国统一考试(全国新课标卷2)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】由已知得{|21}B x x =-<<,故,}10{AB -=,故选A .【提示】解一元二次不等式,求出集合B ,然后进行交集的运算即可. 【考点】集合的交集运算和一元二次方程求根. 2.【答案】B【解析】由已知得24+(4)i 4i a -=-,所以40a =,244a -=-,解得0a =,故选B .【提示】首先将坐标展开,然后利用复数相等解之. 【考点】复数的四则运算. 3.【答案】D【解析】解:A .从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少,且减少的最多,故A 正确;B .2004~2006年二氧化硫排放量越来越多,从2007年开始二氧化硫排放量变少,故B 正确;C .从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C 正确;D .2006年以来我国二氧化硫年排放量越来越少,而不是与年份正相关,故D 错误. 故选:D【提示】A .从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多,故A 正确;B .从2007年开始二氧化硫排放量变少,故B 正确;C .从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C 正确;D .2006年以来我国二氧化硫年排放量越来越少,与年份负相关,故D 错误. 【考点】柱形图信息的获得. 4.【答案】B51AB CB k =-,所以径为5,所以面积为:4π144πS R ==,选C .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前2015年普通高等学校招生全国统一考试(全国卷2)理 科 数 学注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
答卷前,考生务必先将自己的姓名、准考证号码填写在答题卡上。
2.回答第I 卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第II 卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知集合A={-2,-1,0,1,2},B={x|(X-1)(x+2)<0},则A∩B=( )(A ){--1,0} (B ){0,1} (C ){-1,0,1} (D ){,0,,1,2}(2)若a 为实数且(2+ai )(a-2i )=-4i,则a=( )(A )-1 (B )0 (C )1 (D )2(3)根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图。
以下结论不正确的是( )(A ) 逐年比较,2008年减少二氧化硫排放量的效果最显著 (B ) 2007年我国治理二氧化硫排放显现(C ) 2006年以来我国二氧化硫年排放量呈减少趋势 (D ) 2006年以来我国二氧化硫年排放量与年份正相关(4)等比数列{a n }满足a 1=3,135a a a ++ =21,则357a a a ++= ( )(A )21 (B )42 (C )63 (D )84(5)设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )(A )3 (B )6 (C )9 (D )12(6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为(A )81 (B )71 (C )61 (D )51 (7)过三点A (1,3),B (4,2),C (1,-7)的圆交于y 轴于M 、N 两点,则MN =(A )26 (B )8 (C )46 (D )10(8)右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图,若输入a,b 分别为14,18,则输出的a=A.0B.2C.4D.14 (9)已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为A .36π B.64π C.144π D.256π10.如图,长方形ABCD 的边AB=2,BC=1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记∠BOP=x .将动点P 到A 、B 两点距离之和表示为x 的函数f (x ),则f (x )的图像大致为(11)已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,∆ABM 为等腰三角形,且顶角为120°,则E 的离心率为(A )5 (B )2 (C )3 (D )2(12)设函数f’(x)是奇函数()()f x x R ∈的导函数,f (-1)=0,当0x >时,'()()0xf x f x -<,则使得()0f x >成立的x 的取值范围是A .(,1)(0,1)-∞-B .(1,0)(1,)-+∞C .(,1)(1,0)-∞--D .(0,1)(1,)+∞二、填空题(13)设向量a ,b 不平行,向量a b λ+与2a b +平行,则实数λ=_________.(14)若x ,y 满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩,,则z x y =+的最大值为____________.(15)4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a =__________. (16)设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________. 三.解答题(17)∆ABC 中,D 是BC 上的点,AD 平分∠BAC ,∆ABD 是∆ADC 面积的2倍。
(Ⅰ)求CB∠∠sin sin ;(Ⅱ) 若AD =1,DC =22求BD 和AC 的长. (18)某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:A 地区:62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89B 地区:73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:记时间C :“A 地区用户的满意度等级高于B 地区用户的满意度等级”。
假设两地区用户的评价结果相互独立。
根据所给数据,以事件发生的频率作为相应事件发生的概率,求C 的概率19.(本小题满分12分)如图,长方体ABCD —A 1B 1C 1D 1中,AB = 16,BC = 10,AA 1 = 8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E = D 1F = 4,过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形。
(1)在图中画出这个正方形(不必说明画法和理由); (2)求直线AF 与平面α所成的角的正弦值。
20.(本小题满分12分)已知椭圆C :2229(0)x y m m +=>,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M 。
(1)证明:直线OM 的斜率与l 的斜率的乘积为定值;(2)若l 过点(,)3mm ,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率;若不能,说明理由。
21.(本小题满分12分)设函数2()mx f x e x mx =+-。
(1)证明:()f x 在(,0)-∞单调递减,在(0,)+∞单调递增;(2)若对于任意12,[1,1]x x ∈-,都有12|()()|1f x f x e -≤-,求m 的取值范围。
请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分。
作答时请写清题号 22.(本小题满分10分)选修4 - 1:几何证明选讲如图,O 为等腰三角形ABC 内一点,⊙O 与ΔABC 的底边BC 交于M ,N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点。
(1)证明:EF ∥BC ;(2)若AG 等于⊙O 的半径,且23AE MN ==,求四边形EBCF 的面积。
23.(本小题满分10分)GAEFONDB C M选修4 - 4:坐标系与参数方程在直角坐标系xOy 中,曲线C 1:cos sin x t y t αα=⎧⎨=⎩(t 为参数,t ≠ 0),其中0 ≤ α < π,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:2sin ρθ=,C 3:ρθ=。
(1)求C 2与C 3交点的直角坐标;(2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求||AB 的最大值。
24.(本小题满分10分)选修4 - 5:不等式选讲设a ,b ,c ,d 均为正数,且a + b = c + d ,证明:(1)若ab > cd ;(2||||a b c d -<-的充要条件。
参考答案一.选择题(1)A (2)B (3)D (4)B (5)C (6)D (7)C (8)B(9)C(10)B(11)D(12)A二.填空题(13)12(14)32(15)3(16)1n-三.解答题 (17)解: (Ⅰ)1sin 2ABDSAB AD BAD =∠ 1sin 2ADCSAC AD CAD =∠ 因为ABDADCS S=,BAD CAD ∠=∠,所以2AB AC =由正弦定理可得sin 1sin 2B AC C AB ∠==∠(Ⅱ)因为::ABDADCSSBD DC =,所以2BD =在ABD 和ADC 中,由余弦定理知2222cos AB AD BD AD BD ADB =+-∠, 2222cos AC AD DC AD DC ADC =+-∠故222222326AB AC AD BD DC +=++= 由(Ⅰ)知2AB AC =,所以1AC =(18)解:(Ⅰ)两地区用户满意度评分的茎叶图如下通过茎叶图可以看出,A 地区用户满意度评分的平均值高于B 地区用户满意度评分的平均值;A 地区用户满意度评分比较集中,B 地区用户满意度评分比较分散。
(Ⅱ)记1A C 表示事件:“A 地区用户的满意度等级为满意或非常满意”;2A C 表示事件:“A 地区用户的满意度等级为非常满意”; 1B C 表示事件:“B 地区用户的满意度等级为不满意”; 2B C 表示事件:“B 地区用户的满意度等级为满意”,则1A C 与1B C 独立,2A C 与2B C 独立,1B C 与2B C 互斥,1122B A B A C C C C C =,1122()()B A B A P C P C C C C =1122()()B A B A P C C P C C =+ 1122()()()()B A B A P C P C P C P C =+由所给数据得1212,,,A A B B C C C C 发生的频率分别为164108,,,20202020,故 1212164108(),(),(),()20202020A A B B P C P C P C P C ====164108()0.4820202020P C =⨯⨯⨯=(19)解:(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作EM AB ⊥,垂足为M ,则114,8AM A E EM AA ====因为EHGF 为正方形,所以10EH EF BC === 于是226MH EH EM =-=,所以10AH =以D 为坐标原点,DA 的方向为x 轴正方向,建立如图所以的空间直角坐标系D xyz -,则(10,0,0),(10,10,0),(10,4,8),(0,4,8),(10,0,0),(0,6,8)A H E F FE HE ==-设(,,)n x y z =是平面EHGF 的法向量,则0,0,n FE n HE ⎧=⎪⎨=⎪⎩即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n =又(10,4,8)AF =-,故||4|cos ,|15||||n AFn AF n AF <>== 所以AF 与平面EHGF 所成角的正弦值为15(20)解:(Ⅰ)设直线1122:(0,0),(,),(,),(,)M M l y kx b k b A x y B x y M x y =+≠≠将y kx b =+代入2229x y m +=得2222(9)20k x kbx b m +++-=,故12229,299M M M x x kb bx y kx b k k +-===+=++ 于是直线OM 的斜率9M OM M y k x k==-,即9OM k k =- 所以直线OM 的斜率与l 的斜率的乘积为定值(Ⅱ)四边形OAPB 能为平行四边形因为直线l 过点(,)3mm ,所以l 不过原点且与C 有两个交点的充要条件是0,3k k >≠ 由(Ⅰ)得OM 的方程为9y x k=-设点P 的横坐标为P x由2229,9,y x k x y m⎧=-⎪⎨⎪+=⎩得2222981P k m x k =+,即P x = 将点(,)3m m 的坐标代入l 的方程得(3)3m k b -=,因此2(3)3(9)M k k m x k -=+ 四变现OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分,即2P M x x =2(3)23(9)k k mk -=⨯+,解得1244k k ==因为0,3,1,2i i k k i >≠=,所以当l 的斜率为44+OAPB 为平行四边形(21)解:(Ⅰ)()(1)2mxf x m e x '=-+若0m ≥,则当(,0)x ∈-∞时,10,()0mxef x '-≤<;当(0,)x ∈+∞时,10mx e -≥,()0f x '>若0m <,则当(,0)x ∈-∞时,10,()0mxef x '-><;当(0,)x ∈+∞时,10mx e -<,()0f x '>所以,()f x 在(,0)-∞单调递减,在(0,)+∞单调递增(Ⅱ)由(Ⅰ)知,对任意的,()m f x 在[-1,0]单调递减,在[0,1]单调递增,故()f x 在0x =处取得最小值,所以对于任意1212,[1,1],|()()|1x x f x f x e ∈--≤-的充要条件是(1)(0)1,(1)(0)1,f f e f f e -≤-⎧⎨--≤-⎩即1,1,m me m e e m e -⎧-≤-⎪⎨+≤-⎪⎩ ① 设函数()1t g t e t e =--+,则()1tg t e '=-当0t <时,()0g t '<;当0t >时,()0g t '>,故()g t 在(,0)-∞单调递减,在(0,)+∞单调递增。
