C语言间接平差程序
误差理论与测量平差基础第七章 间接平差

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ X 1 X C , X 2 YC , X 3 X D , X 4 YD
ห้องสมุดไป่ตู้
第七章——间接平差
于是,误差方程为:
ˆ ˆ v1 ( X A X 3 ) 2 (Y A X 4 ) 2 L1 ˆ ˆ v 2 ( X B X 3 ) 2 (YB X 4 ) 2 L2 ˆ ˆ ˆ ˆ v3 ( X 1 X 3 ) 2 ( X 2 X 4 ) 2 L3 ˆ ˆ v 4 ( X A X 1 ) 2 (Y A X 2 ) 2 L4 ˆ ˆ v5 ( X B X 1 ) 2 (YB X 2 ) 2 L5
第七章——间接平差
1 A
ˆ ˆ v 2 AC AD v3 v4 v5 v6 v7 v8
ˆ ˆ X 2 YA X 4 YA arct an arct an L2 ˆ X ˆ X X X
3 A
ˆ ˆ YA X 4 YB X 4 ˆ ˆ DA DB arct an arct an L3 ˆ ˆ X A X3 XB X3 ˆ ˆ ˆ YB X 4 X2 X4 ˆ ˆ DB DC arct an arct an L4 ˆ ˆ X ˆ XB X3 X1 3 ˆ ˆ ˆ X4 X2 YA X 2 ˆ ˆ CD CA arct an arct an L5 ˆ X ˆ ˆ X3 X A X1 1 ˆ ˆ YA X 2 YB X 2 ˆ ˆ CA CB arct an arct an L6 ˆ ˆ X A X1 X B X1 ˆ ˆ X 4 YB X 2 YB ˆ ˆ BC BD arct an arct an L7 ˆ X ˆ X X3 X1 B B ˆ Y A YB X 4 YB ˆ BA BD arct an arct an L8 ˆ X XA XB X3 B
22间接平差--计算步骤

Lˆ L V
v1 1
v2
1
vv43
0
1
0
0 1.7
11012.7.7
7
0
2
2.7
(mm)
2.7
0.3
h1
A
P1
h2
B
h4
hhˆˆ12 hhˆˆ43
xˆ1
(h1
X
0 1
HA)
v2
xˆ1
xˆ 2
(h2
X
0 2
X
0 1
)
v3
xˆ 2
(h3
X
0 2
HC )
v4
xˆ1
(h4
X
0 1
HB)
v1 xˆ1 0 v2 xˆ1 xˆ2 (7) v3 xˆ2 0 v4 xˆ1 2
Xˆ Xˆ
1 2
X
0 1
X
0 2
xˆ1
xˆ2
1122..050131(m)
12.7.7(mm)
1122..05004873(m)
Xˆ X 0 xˆ
间接平差计算步骤
5.由误差方程计算V,求出观测量平差值 V Bxˆ l
令2公里观测高差为单位权观测值
2 0 0 0 P 0 1 0 0
0 0 1 0 0 0 0 2
间接平差程序设计
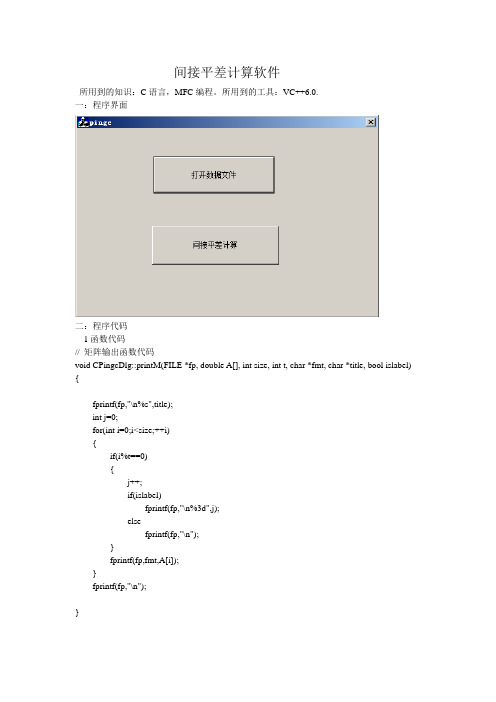
printM(fp,V,n,1,"%10.3lf","观测值的改正数(V)",true); //输出改正数v
printM(fp,X,r,1,"%10.3lf","参数x近似值",true); //输出参数x
{
FILE* fp=fopen(filename,"r");
if(fp==NULL)
{
MessageBox("数据文件打开失败!");
return;
}
int n,r;
fscanf(fp,"%d%d",&n,&r);
double *B=new double[n*r];
double* P=new double[n];
}
a[n*(n+1)/2-1]=1.0/a00;
}
delete []a0;
return计算函数代码
int CPingcDlg::ij(int i, int j)
{
return (i>=j)?i*(i+1)/2+j:j*(j+1)/2+i;
}
//间接平差计算函数代码
double CPingcDlg::jianjie(int n, int r, double B[], double P[],double L[], double V[], double X[])
N[ij(i,j)]=nij;
}
}
//矩阵W计算
double *W=new double[r];
水准网平差程序

AfxGetApp()->m_pMainWnd->MessageBox( "数据文件不存在或数据文件错!", "进程. . . . . .!!!",MB_OK|MB_ICONSTOP);
//重要说明:原始数据文件中,未知点的高程可以随意输入,也可以不输入空缺, 程序自动把待定点高程赋值为 0
} for(i=ne;i<nz;i++) {
fp.ReadString(buff,MAXLINE); sscanf(buff,"%d%s%lf",&dh,ch1,&gc); dm[i]=ch1;H[i]=0; } for(i=0;i<nn;i++) { fp.ReadString(buff,MAXLINE); sscanf(buff,"%d%d%lf%lf",
教师 评语
// Gckzwpc.cpp: implementation of the CGckzwpc class. // ////////////////////////////////////////////////////////////////////// #include "stdafx.h" #include "Survey.h" #include "Gckzwpc.h" #ifdef _DEBUG #undef THIS_FILE static char THIS_FILE[]=__FILE__; #define new DEBUG_NEW #endif ////////////////////////////////////////////////////////////////////// // Construction/Destruction ////////////////////////////////////////////////////////////////////// CGckzwpc::CGckzwpc() { } CGckzwpc::~CGckzwpc() { } bool CGckzwpc::ReadData(CString filename) {
测量程序设计_条件平差和间接平差

程序代码如下:
disp(‘-------水准网间接平差示例-------------’) disp(‘已知高程’) Ha = 5.015 % 已知点高程,单位m Hb = 6.016 % 已知点高程,单位m
A h2 D h1
C h6 E h7 B h4
h5
h3
disp(‘观测高差,单位m’)
L = [1.359; 2.009; 0.363; 1.012; 0.657; -0.357] disp(‘系数矩阵B’)
则: PV AT K
V P A K QA K
T
1 T
4、法方程: 将条件方程 AV+W=0代入到改正数方程V=QATK 中,则得到:
AQAT K W 0
r1 r1 r1
记作: 由于
N aa K W 0
rr
R( Naa ) R( AQAT ) R( A) r
Naa为满秩方阵, K Naa1W ( AQAT )1 ( AL A0 )
if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确') else disp(‘检核错误') end disp(‘平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
其中l=L-d.
ˆ 设误差Δ和参数X的估计值分别为V 和 X
则有
ˆ V AX l
X0 为了便于计算,通常给参数估计一个充分接近的近似值
ˆ ˆ X X0 x
则误差方程表示为
(完整)C语言间接平差程序

教材《误差理论与测量平差基础》第二版武汉大学出版社P108页的例7—1的运行结果:源程序:#define N 5 /*N是观测值个数*/#define T 3 /*T是必要观测数*/#include<stdio.h>#include<math。
h>float Nbb[T][T],Nb[T][T],W[T][1],x[T][1];main(){float D(float a[T][N],float b[N][N],float c[N][T]);float K(float a[T][N],float b[N][N],float c[N][1]);float G(float a[T][T]);float F(float ca[T-1][T—1]);float DM(float a[1][N],float b[N][N] ,float c[N][1]);int i,j,m,n;float B[N][T],BT[T][N],V[N][1],VT[1][N],P[N][N],C[N][1],Bx[N][1],f,g,h,x1; printf("请输入V的系数B[N][T]:\n”);for(i=0;i<N;i++)for(j=0;j〈T;j++)scanf(”%8f”,&B[i][j]);printf("请输入观测值的权阵P[N][N]:\n");for(i=0;i<N;i++)for(j=0;j<N;j++)scanf("%8f”,&P[i][j]);printf("请输入常数C[N][1]:\n”);for(i=0;i〈N;i++)for(j=0;j<1;j++)scanf(”%8f”,&C[i][j]);for(i=0;i〈N;i++)for(j=0;j<T;j++)BT[j][i]=B[i][j];g=D(BT, P, B);h=K(BT, P, C);f=G(Nbb);for(i=0;i〈T;i++)for(j=0;j〈1;j++){x[i][j]=Nb[i][0]*W[0][j];for(m=1;m〈T;m++)x[i][j]+=(Nb[i][m]*W[m][j]);}for(i=0;i〈T;i++)x[i][0]=x[i][0]/f;for(i=0;i〈N;i++)for(j=0;j〈1;j++){Bx[i][j]=B[i][0]*x[0][j];for(m=1;m〈T;m++)Bx[i][j]+=(B[i][m]*x[m][j]);}for(i=0;i〈N;i++)V[i][0]=(Bx[i][0]-C[i][0]);for(i=0;i<N;i++)for(j=0;j〈1;j++)VT[j][i]=V[i][j];x1=DM(VT,P,V);x1=x1/(N-T);printf("参数x[T][1]=\n");for(i=0;i〈T;i++)printf("%15f",x[i][0]);printf("\n");printf("改正数V[N][1]=\n”);for(i=0;i<N;i++)printf("%15f”,V[i][0]);printf("\n单位权中误差x1=%15f”,sqrt(x1)); printf("\n协因数阵Qxx[T][T]:\n");for(i=0;i<T;i++){for(j=0;j〈T;j++)printf(”%15f”,Nb[i][j]/f);printf(”\n");}}float G(float a[T][T]){int i,j,m,n;float c[T—1][T—1],y=0;for(i=0;i<T;i++)for(j=0;j<T;j++){for(m=0;m<T;m++)for(n=0;n〈T;n++){if(m〈i&&n<j)c[m][n]=a[m][n];if(m>i&&n〈j)c[m-1][n]=a[m][n];if(m<i&&n>j)c[m][n—1]=a[m][n];if(m>i&&n>j)c[m-1][n-1]=a[m][n];}if((i+j)%2==0)Nb[j][i]=F(c);elseNb[j][i]=(-1)*F(c);}for(m=0;m<T;m++)y+=(a[0][m]*Nb[m][0]);return (y);}float F(float ca[T—1][T—1]){int i,j,m,n,s,t,k=1;float f=1,c,x,sn;for (i=0,j=0;i<T—1&&j〈T—1;i++,j++){if (ca[i][j]==0){for (m=i;ca[m][j]==0;m++);if (m==T—1){sn=0;return (sn);}elsefor (n=j;n<T—1;n++){c=ca[i][n];ca[i][n]=ca[m][n];ca[m][n]=c;}k*=(-1);}for (s=T—2;s>i;s--){x=ca[s][j];for (t=j;t〈T-1;t++)ca[s][t]—=ca[i][t]*(x/ca[i][j]);}}for (i=0;i<T-1;i++)f*=ca[i][i];sn=k*f;return (sn);}float D(float a[T][N],float b[N][N] ,float c[N][T]){int i,j,m;float d[T][N];for(i=0;i<T;i++)for(j=0;j〈N;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m〈N;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i〈T;i++)for(j=0;j〈T;j++){Nbb[i][j]=d[i][0]*c[0][j];for(m=1;m〈N;m++)Nbb[i][j]+=(d[i][m]*c[m][j]);}return (Nbb[0][0]);}float K(float a[T][N],float b[N][N],float c[N][1]){int i,j,m;float d[T][N];for(i=0;i<T;i++)for(j=0;j<N;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m<N;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<T;i++)for(j=0;j〈1;j++){W[i][j]=d[i][0]*c[0][j];for(m=1;m〈N;m++)W[i][j]+=(d[i][m]*c[m][j]);}return (W[0][0]);}float DM(float a[1][N],float b[N][N] ,float c[N][1]){int i,j,m;float d[1][N],x;for(i=0;i〈1;i++)for(j=0;j<N;j++){d[i][j]=a[i][0]*b[0][j];for(m=1;m<N;m++)d[i][j]+=(a[i][m]*b[m][j]);}for(i=0;i<1;i++)for(j=0;j<1;j++){x=d[i][0]*c[0][j];for(m=1;m<N;m++)x+=(d[i][m]*c[m][j]);}return (x);}程序说明:1) 用该程序前,根据具体情况输入N和T;2)该程序中的(N-T)自由度(即多余观测数)必须大于等于2,不然程序运行时会出错,原因在于求行列式的逆时,有语句for (s=R-2;s>i;s—-),R=1时s=-1。
c+间接平差法

间接平差法是一种测量平差方法,通常用于解决线性系统中的超定方程问题,即有多余观测的情况。
这种方法通过解最小二乘问题来找到最佳的参数估计值。
在间接平差法中,待估参数和已知参数是通过最小二乘目标函数(通常是误差项的平方和)进行连接的。
具体步骤如下:
1. 列出误差方程:误差方程是观测值与计算出的观测值初值之间的差值。
2. 计算出V后与观测值求和,得到最终的平差值。
此外,间接平差法还可以用于解决GNSS SPP、摄影测量解算、光束法平差、控制网平差等测绘问题。
在解决这些问题时,通常会使用非线性最小二乘解法中的其他方法,如梯度下降法(最速下降法)来获得最佳的参数估计值。
总之,间接平差法是一种广泛应用的测量平差方法,通过最小化目标函数来求解线性系统中的超定方程问题。
它被广泛应用于各种测绘解算问题,为参数估计提供了有效的解决方案。
第4章间接平差原理

第一节 间接平差原理
ˆ 间接平差法(参数平差法)是通过选定 v1 = x1 − ( L1 − X 10 ) 间接平差法(参数平差法) t个独立未知量作为参数,将每个观 v2 = x2 − ( L2 − X 20 ) 个独立未知量作为参数, ˆ 测值分别表达成这t个参数的函数, 测值分别表达成这t个参数的函数, v3 = − x1 − x2 − ( L3 + X 10 + X 20 − 180) ˆ ˆ 建立函数模型,按最小二乘原理, 建立函数模型,按最小二乘原理, T 用求自由极值的方法解出参数的最 要求 V PV = min X1 或然值, 或然值,从而求得各观测值的平差 值。
− ˆ x = N bb1W
ˆ x = ( B T PB ) −1 B T Pl
5.求观测值改正数 5.求观测值改正数
ˆ ˆ X = X0 +x l = L − ( BX 0 + d )
ˆ V = Bx − l
6.求平差值 6.求平差值
L = L +V,
∧
ˆ V = Bx − l
3.组成法方程 3.组成法方程
3
第四章 间接平差
第一节
二、计算步骤 1.确定t,选 个独立量为参数X. 1.确定t,选t个独立量为参数X. 确定t, 2.列立误差方程 2.列立误差方程 ˆ L + V = BX + d 或
ˆ 或L + V = f ( X )
间接平差原理
4.解算法方程 4.解算法方程,求参数的改正数 解算法方程,
平差值
ˆ ˆ X = X0 + x ∧ L = L +V
∧ ∧
平差值方程为: 平差值方程为: 令:nL1 = [L1 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教材《误差理论与测量平差基础》第二版武汉大学出版社
P108页的例7-1的运行结果:
源程序:
#define N 5 /*N是观测值个数*/
#define T 3 /*T是必要观测数*/
#include<stdio.h>
#include<math.h>
float Nbb[T][T],Nb[T][T],W[T][1],x[T][1];
main()
{
float D(float a[T][N],float b[N][N],float c[N][T]);
float K(float a[T][N],float b[N][N],float c[N][1]);
float G(float a[T][T]);
float F(float ca[T-1][T-1]);
float DM(float a[1][N],float b[N][N] ,float c[N][1]);
int i,j,m,n;
float B[N][T],BT[T][N],V[N][1],VT[1][N],P[N][N],C[N][1],Bx[N][1],f,g,h,x1; printf("请输入V的系数B[N][T]:\n");
for(i=0;i<N;i++)
for(j=0;j<T;j++)
scanf("%8f",&B[i][j]);
printf("请输入观测值的权阵P[N][N]:\n");
for(i=0;i<N;i++)
for(j=0;j<N;j++)
scanf("%8f",&P[i][j]);
printf("请输入常数C[N][1]:\n");
for(i=0;i<N;i++)
for(j=0;j<1;j++)
scanf("%8f",&C[i][j]);
for(i=0;i<N;i++)
for(j=0;j<T;j++)
BT[j][i]=B[i][j];
g=D(BT, P, B);
h=K(BT, P, C);
f=G(Nbb);
for(i=0;i<T;i++)
for(j=0;j<1;j++)
{
x[i][j]=Nb[i][0]*W[0][j];
for(m=1;m<T;m++)
x[i][j]+=(Nb[i][m]*W[m][j]);
}
for(i=0;i<T;i++)
x[i][0]=x[i][0]/f;
for(i=0;i<N;i++)
for(j=0;j<1;j++)
{
Bx[i][j]=B[i][0]*x[0][j];
for(m=1;m<T;m++)
Bx[i][j]+=(B[i][m]*x[m][j]);
}
for(i=0;i<N;i++)
V[i][0]=(Bx[i][0]-C[i][0]);
for(i=0;i<N;i++)
for(j=0;j<1;j++)
VT[j][i]=V[i][j];
x1=DM(VT,P,V);
x1=x1/(N-T);
printf("参数x[T][1]=\n");
for(i=0;i<T;i++)
printf("%15f",x[i][0]);
printf("\n");
printf("改正数V[N][1]=\n");
for(i=0;i<N;i++)
printf("%15f",V[i][0]);
printf("\n单位权中误差x1=%15f",sqrt(x1));
printf("\n协因数阵Qxx[T][T]:\n");
for(i=0;i<T;i++)
{
for(j=0;j<T;j++)
printf("%15f",Nb[i][j]/f);
printf("\n");
}
}
float G(float a[T][T])
{
int i,j,m,n;
float c[T-1][T-1],y=0;
for(i=0;i<T;i++)
for(j=0;j<T;j++)
{
for(m=0;m<T;m++)
for(n=0;n<T;n++)
{
if(m<i&&n<j)
c[m][n]=a[m][n];
if(m>i&&n<j)
c[m-1][n]=a[m][n];
if(m<i&&n>j)
c[m][n-1]=a[m][n];
if(m>i&&n>j)
c[m-1][n-1]=a[m][n];
}
if((i+j)%2==0)
Nb[j][i]=F(c);
else
Nb[j][i]=(-1)*F(c);
}
for(m=0;m<T;m++)
y+=(a[0][m]*Nb[m][0]);
return (y);
}
float F(float ca[T-1][T-1])
{
int i,j,m,n,s,t,k=1;
float f=1,c,x,sn;
for (i=0,j=0;i<T-1&&j<T-1;i++,j++) {
if (ca[i][j]==0)
{
for (m=i;ca[m][j]==0;m++);
if (m==T-1)
{
sn=0;
return (sn);
}
else
for (n=j;n<T-1;n++)
{
c=ca[i][n];
ca[i][n]=ca[m][n];
ca[m][n]=c;
}
k*=(-1);
}
for (s=T-2;s>i;s--)
{
x=ca[s][j];
for (t=j;t<T-1;t++)
ca[s][t]-=ca[i][t]*(x/ca[i][j]);
}
}
for (i=0;i<T-1;i++)
f*=ca[i][i];
sn=k*f;
return (sn);
}
float D(float a[T][N],float b[N][N] ,float c[N][T]) {
int i,j,m;
float d[T][N];
for(i=0;i<T;i++)
for(j=0;j<N;j++)
{
d[i][j]=a[i][0]*b[0][j];
for(m=1;m<N;m++)
d[i][j]+=(a[i][m]*b[m][j]);
}
for(i=0;i<T;i++)
for(j=0;j<T;j++)
{
Nbb[i][j]=d[i][0]*c[0][j];
for(m=1;m<N;m++)
Nbb[i][j]+=(d[i][m]*c[m][j]);
}
return (Nbb[0][0]);
}
float K(float a[T][N],float b[N][N],float c[N][1]) {
int i,j,m;
float d[T][N];
for(i=0;i<T;i++)
for(j=0;j<N;j++)
{
d[i][j]=a[i][0]*b[0][j];
for(m=1;m<N;m++)
d[i][j]+=(a[i][m]*b[m][j]);
}
for(i=0;i<T;i++)
for(j=0;j<1;j++)
{
W[i][j]=d[i][0]*c[0][j];
for(m=1;m<N;m++)
W[i][j]+=(d[i][m]*c[m][j]);
}
return (W[0][0]);
}
float DM(float a[1][N],float b[N][N] ,float c[N][1]) {
int i,j,m;
float d[1][N],x;
for(i=0;i<1;i++)
for(j=0;j<N;j++)
{
d[i][j]=a[i][0]*b[0][j];
for(m=1;m<N;m++)
d[i][j]+=(a[i][m]*b[m][j]);
}
for(i=0;i<1;i++)
for(j=0;j<1;j++)
{
x=d[i][0]*c[0][j];
for(m=1;m<N;m++)
x+=(d[i][m]*c[m][j]);
}
return (x);
}
程序说明:
1) 用该程序前,根据具体情况输入N和T;
2) 该程序中的(N-T)自由度(即多余观测数)必须大于等于2,不然程序运行时会出错,原因在于求行列式的逆时,有语句for (s=R-2;s>i;s--),R=1时s=-1。
