导线网平差程序设计
导线网平差及精度评定程序设计平差

导线网平差及精度评定程序设计平差问题描述背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
使用 PA2005 软件进行导线精密平差
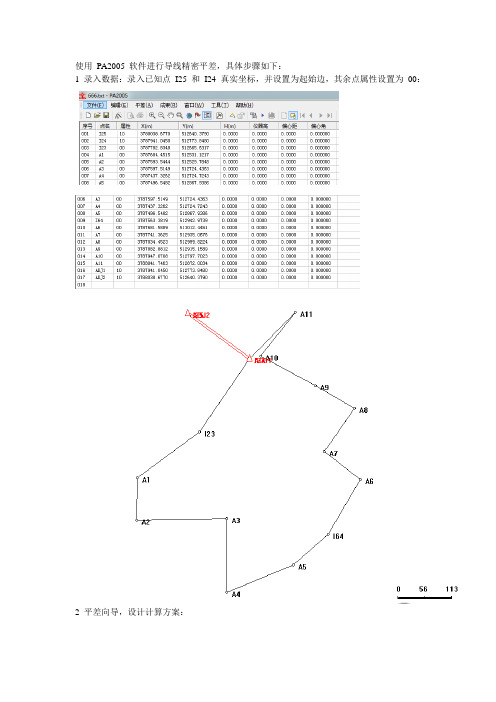
使用PA2005 软件进行导线精密平差,具体步骤如下:1 录入数据:录入已知点I25 和I24 真实坐标,并设置为起始边,其余点属性设置为00:2 平差向导,设计计算方案:3 平差计算:4 闭合差计算:5 控制网平差报告:控制网平差报告计算软件:南方平差易2005网名:计算日期:2015-11-5观测人:王宁宁记录人:王冬计算者:熊猛猛检查者:测量单位:备注:平面控制网等级:城市二级,验前单位权中误差:1.41(s)已知坐标点个数:4未知坐标点个数:13未知边数:14最大点位误差[A5] = 0.0425 (m)最小点位误差[A11] = 0.0206 (m)平均点位误差= 0.0344 (m)最大点间误差= 0.0312(m)最大边长比例误差= 4626平面网验后单位权中误差= 4.21 (s)[边长统计]总边长:1900.251(m),平均边长:135.732(m),最小边长:90.917(m),最大边长:194.692(m)[闭合差统计报告]序号:<1>:附合导线路径:[ADJ2-ADJ1-A11-A10-A9-A8-A7-A6-I64-A5-A4-A3-A2-A1-I23-I24-I25]角度闭合差=-44.00(s),限差=±10.92(s)fx=0.006(m),fy=0.068(m),fd=0.068(m)总边长[s]=1900.251(m),全长相对闭合差k=1/27966,平均边长=135.732(m)[方向观测成果表][平面点位误差表]5.3.7 坐标转换参数计算已知点录入:计算结果:可由DX、DY、R 和DK 值算得四参数为:a=DK*COSR=0.999868617;b=DK*sinR=-0.016392281;c=DX=3788038.6761196m ;d=DY=512640.380192 5588m。
导线平差计算方案设置-16页文档资料

导线平差计算方案设置一、导线类型:1.闭、附合导线(图1)2.无定向导线(图2)3.支导线(图3)4.特殊导线或网(见数据输入一节),该选项适用于所有的导线,但不计算闭合差。
而且该类型不需要填写未知点数目。
当点击表格最后一行时自动添加一行,计算时删除后面的空行。
5.坐标导线。
指使用全站仪直接观测坐标、高程的闭、附合导线。
6.单面单程水准测量记录计算。
指仅进行单面读数且仅进行往测而无返测的水准测量记录计算。
当数据中没有输入“中视”时可以用作五等、等外水准等的记录计算。
当输入了“中视”时可以用作中平测量等的记录计算。
说明:除“单面单程水准测量记录计算”仅用于低等级的水准测量记录计算外,其它类型选项都可以进行平面及高程的平差计算,输入了平面数据则进行平面的平差,输入了高程数据则进行高程的平差,同时输入则同时平差。
如果不需进行平面的平差,仅计算闭、附合高程路线,可以选择类型为“无定向导线”,或者选择类型为“闭附合导线”但表格中第一行及最后一行数据(均为定向点)不必输入,因为高程路线不需定向点。
二、概算1.对方向、边长进行投影改化及边长的高程归化。
2.应选择相应的坐标系统,以及Y坐标是否包含500KM。
选择了概算时,Y坐标不应包含带号。
三、平面计算设置(一)、等级:选择等级,以便根据《工程测量规范》自动进行限差等的设置。
不同的规范,或者相同的规范但不同的版本可能技术要求不同,请在软件进行自动设置后做必要的检查,如有不符,可以自行设置。
(二)、近似平差与严密平差的选择及近似平差的方位角、边长是否反算1.近似平差:程序先分配角度闭合差再分配坐标增量闭合差,即分别平差法。
2.严密平差:按最小二乘法原理平差。
3.《工程测量规范》规定:一级及以上平面控制网的计算,应采用严密平差法,二级及以下平面控制网,可根据需要采用严密或简化方法平差。
当采用简化方法平差时,应以平差后坐标反算的角度和边长作为成果。
《城市测量规范》规定:四等以下平面控制网可采用近似平差法和按近似方法评定其精度。
图根导线结点网平差软件设计及实现

Hale Waihona Puke 城市勘测
2 0 1 3年 1 2月
( 2 ) 闭合差 检核 功能 闭合 差 的检核 主要包 括 三个方 面 : 角度 闭合 差 、 坐
借助 M i c r o s o t f O f i f c e Wo r d 2 0 0 3的 O L E组 件实 现
制点测量的效率 , 相 比传统的三角测量、 G P S 静态测量
等 方式 更加 轻 松 、 迅 捷 。同 时 , 随 着城 市 的发 展 , 高 楼 大 厦越 来 越 多 , 卫 星信号 的遮挡也 影 响了 G P S — R T K 的测量 , 因此 “ R T K+ 全站仪” 的 测 量 模 式 很 好 地解 决
2 0 1 3年 1 2月 第 6期
城
市
勘
测
De c . 2 01 3
Ur b a n Ge o t e c h n i c a l I n v e s t i g a t i o n& S u r v e y i n g
No . 6
文章编号 : 1 6 7 2 — 8 2 6 2 ( 2 0 l 3 ) 0 6 — 1 4 3 — 0 4
了数字 化地 形 图测 量 中 图根 控 制 网 的测 绘 工作 , 采 用
读取 观测数据、 已知点 数据 、结点信息文件 搜索起算 点到结点、结点到结点的线路 检查观测数据 、 已知 点数据等
上 述测 量模 式测 设 的 导线 控 制 网灵 活 多 变 , 为 了对 图
根导线结点网的成果计算 , 编写 了一套 自动化高 的平
中图分类号 : P 2 0 9
文 献标 识码 : B
数据结构课程设计——导线网平差程序的设计与实现

数据结构课程设计——导线网平差程序的设计与实现设计二:导线网平差程序的设计与实现一、设计目的立足于《数据结构与测绘软件开发》这一课程的课堂教学及其实验课程设计,为着实提高学生基于计算机辅助的方式切实解决工程实际问题的动手能力,通过本实习,一方面,使学生深入了解课堂所学知识,另一方面,通过实践掌握测绘行业软件设计与开发的基本方法,深刻掌握矩阵运算、曲线/曲面拟合的数值解法,掌握不同类型的典型测绘软件设计方法,使得学生初步具备编写测绘软件常用算法的能力以及开发中小规模测绘专业软件的能力。
有导线网如图,观测了14条边长和16个转折角,已知测角精度10βδ''=,测边精度为1.0()()S S m mm δ=。
已知A 、B 、C 、D 、E 、F 点的坐标(无误差),如下表:表1 已知点数据点号 X(m) Y(m)A 5256.953 4520.068B 5163.752 4281.277C 3659.371 3621.210D 4119.879 3891.607E 4581.150 5345.292F 4851.5545316.953表2 角度观测值编号角度观测值(° ′ ″)编号角度观测值(° ′ ″)1 163 45 04 9 169 10 302 64 58 37 10 98 22 043 250 18 11 11 94 53 50 4 103 57 34 12 111 14 235 83 08 05 13 79 20 18三、关键问题描述3.1 未知点近似坐标计算平面控制网进行平差计算时需要计算未知点的近似坐标1.坐标计算公式1、2点的坐标已知,并观测了1-2、1-3的夹角,根据这些数据可以求出3号点坐标根据1、2两点的坐标,可以反算出1、2方向的方位角T12,3号点的坐标为++=++=)sin()cos(121313121313ααT S y y T S x x式子中S13为观测边长,α为观测角度 2.计算流程从读入的数据循环计算未知点的坐标,已计算出的坐标当做已知坐标的点处理参加下次计算,以此类推,逐步计算出未知点的坐标3.实现算法CMatrix CPlaneNetAdjust::XYJS() { CMatrix _XYJS(Pnumber,2); double T12; for(int i=0;i0&&xy[k2].Y>0) { T12=GetT12(k1,k2); } double s12=Gets12(k1,k2); double s13=Gets12(k1,k3); double T13=T12+guancejiao[i].Guancezhi; double dx=s13*cos(T13); double dy=s13*sin(T13); xy[k3].X=xy[k1].X+dx; xy[k3].Y=xy[k1].Y+dy; } for(int i=0;i<="" bdsfid="103" double="" p="" temp1="xy[i].X;" temp2="xy[i].Y;" {="">}return _XYJS;}3.2 误差方程列立1.理论分析平面控制网的误差方程都是非线性方程,必须引入参数近似值将误差方程线性化,取X的充分近似值 0X ,x ?是微小量,在按台劳公式展开时可以略去二次和二次以上的项,而只取至一次项,于是可对非线性平差值观测方程式线性化,于是有如下的式子对于观测角的改正数有对于边长观测值的改正数有2.实现算法如下:CMatrix CPlaneNetAdjust::B() { CMatrix _B1(Lnumber,Pnumber*2); double a; double b; double c; double d; double m; double n; double m1; double n1; for(int i=0;i<="">D A D A D B D B DA DB X X Y Y X X Y Y L ??arctan ??arctan 1-----=-=αα()()22??S AD A D Y Y X X -+-=kjkjk k jk jk j jk jkj jk jk jk y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200200200200"??+??-??-??+=ρρρραδh jhjh h jh jh j jh jh j jh jh jh y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200 200200200"??+??-??-??+=ρρρραδ)(?)("?)("?)("?)("?)("?)("?)(" )("00200200200200200200200200i jk jh h jh jhh jh jh j jh jh j jh jh k jk jkk jk jk j jk jk j jk jk i L y S X x S Y y S X x S Y y S X x S Y y S X xS Y v ---??+?-?-?-+?-?-?-=ααρρρρρρρρi k jkjkk jk jk j jk jk j jk jk i l y S Y x S X y S Y x S X v -?+?+?-?-=000000000jki i S L l -=2002000)()(j k j k jk Y Y X X S -+-=_B1.setValue(i,2*k1,0);_B1.setValue(i,2*k1+1,0);}else{_B1.setValue(i,2*k1,a);_B1.setValue(i,2*k1+1,b);}if(k2<knpnumber)< bdsfid="148" p=""></knpnumber)<> {_B1.setValue(i,2*k2,0);_B1.setValue(i,2*k2+1,0);}else{_B1.setValue(i,2*k2,-a);_B1.setValue(i,2*k2+1,-b);}}for(int i=0;i<tnumber;i++)< bdsfid="160" p=""></tnumber;i++)<>{const double p=206.265;int k1=cezhan[i];int k3=huoshi[i];int k2=qianshi[i];double dx12=xy[k2].X-xy[k1].X;double dy12=xy[k2].Y-xy[k1].Y;double dx13=xy[k3].X-xy[k1].X;double dy13=xy[k3].Y-xy[k1].Y;c=(p*dx13/Gets12(k1,k3)/Gets12(k1,k3)-p*dx12/Gets12(k1,k2)/Gets12(k1,k2));c=-c;d=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3)+p*dy12/Gets12(k1,k2)/Get s12(k1,k2);d=-d;m=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3);m=-m;n=p*dx13/Gets12(k1,k3)/Gets12(k1,k3);n=-n;m1=p*dy12/Gets12(k1,k2)/Gets12(k1,k2);m1=-m1;n1=-p*dx12/Gets12(k1,k2)/Gets12(k1,k2);n1=-n1;if(k1<knpnumber)< bdsfid="183" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k1,0);_B1.setValue(i+Snumber,2*k1+1,0);}else if(k1>=knPnumber){_B1.setValue(i+Snumber,2*k1,c);_B1.setValue(i+Snumber,2*k1+1,d);}if(k2<knpnumber)< bdsfid="194" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k2,0);_B1.setValue(i+Snumber,2*k2+1,0);}else if(k2>=knPnumber){ _B1.setValue(i+Snumber,2*k2,m1); _B1.setValue(i+Snumber,2*k2+1,n1); } if(k3=knPnumber) { _B1.setValue(i+Snumber,2*k3,m); _B1.setValue(i+Snumber,2*k3+1,n); } }CMatrix _B(Lnumber,2*(Pnumber-knPnumber)); for(int i=0;i<_B1.getRow();i++) { for(int j=2*knPnumber;j<2*Pnumber;j++) { double temp=_B1.getValue(i,j); _B.setValue(i,(j-2*knPnumber),temp); } } return _B;}3.3 法方程构建与解算1.理论分析误差方程系数构成法方程2.实现代码①计算LCMatrix CPlaneNetAdjust::L() { CMatrix _L(Lnumber,1); double l; double s; double s0; for(int i=0;i<="" bdsfid="209" const="" cout<<l<l x B V -=?0?=-Pl B x PB B TTmin =PV V T V L L +=?20σ20?σPV V T double A13; double A;int k1=cezhan[i]; int k2=huoshi[i]; int k3=qianshi[i];A12=GetT12(k1,k2); A13=GetT12(k1,k3); A=GetA(k1,k2,k3); l=A13-A12; if(l<0) { l=pi+l; }if(l>=pi) { l=l-pi; }l=l-A;//cout<<rad_dms(a12)<<" "<<rad_dms(a)<<"<="" "<<rad_dms(a13)<<"="" bdsfid="220" p=""></rad_dms(a12)<<">"<<rad_dms(l)<<endl;< bdsfid="222" p=""></rad_dms(l)<<endl;<>_L.setValue(i+Snumber,0,rad_dms(l));} return _L; }②计算权阵PCMatrix CPlaneNetAdjust::P() { CMatrix _P(Lnumber,Lnumber); for(int i=0;i<="" p="" {="">temp=temp=Cjwucha*Cjwucha/(1*sqrt(bianchang[i].Len))/( 1*sqrt(bianchang[i].Len)); _P.setValue(i,i,temp); } for(int i=Snumber;i<="">3.4 精度估计1.单位权中误差间接平差与条件平差虽采用了不同的函数模型,但它们是在相同的最小乘原理下进行的,所以两法的平差结果总是相等的,这是因为在满足条件下的V 是唯一确定的,故平差值不因方法不同而异。
闭合导线平差程序设计

角度闭合差垢龋邶理
角度闭合差(图根导线)的允许值:廊允=±,,、/i
fy=-fy+Y坐标增量 d=d+边长 endscan
thisform.1abel21.caption=dltrim(strOCx,7,3))
万方数据
32
·北京测绘·
2008年第3期
thisforrmlabel21.visible=.t. th厶form./abel22.caption---alhrim(str(fy,7,3)) th函form./abel22.visible=.t. 料计算导线全长闭合差 f=-round(sqrt弧2+:75,乞),3) x=int(d/s9 k=str(1,1)+’,/,’+alltrim(str(x)) thisform.1abel23.caption--alhrim(strOC,,7,3)) thisform./abel23.visible=.t. thisform.1abel24.caption=k thisform.1abel24.visible=.L -t计算坐标增量改正值 丘1=0 fyl=0 /f int(x)<2000
北京:科学出版社,2004
The Design of Procedure About Closed Traverse Adjustment
Abstract:This paper designs the traverse adjustment procedure on traverse approximate adjustment principle and Visual FoxPr06.0 developing platform.The procedure can accomplish the contmUed adjustment of level control and height control of closed traverse,and it gab also make result of adjustment into all kinds of file forms according to the different demands, meanwhile,it can draw the picture of the traverse. Key words:Closed Traverse;Adjustment:Procedure Design;Application
导线网平差及精度评定程序设计平差

导线网平差及精度评定程序设计平差引言导线网平差是测量领域中的一项重要工作,它对于保证测量结果的准确性和可靠性具有重要意义。
本文将介绍导线网平差的基本原理和流程,并且设计一个用于导线网平差及精度评定的程序。
程序设计平差流程数据预处理•导入原始测量数据:从测量仪器或文件中导入导线网的原始测量数据。
数据应包括导线长度、角度观测值以及观测仪器的精度等信息。
•数据格式检查:对导入的测量数据进行检查,确保数据的完整性和准确性。
•数据转换:将角度观测值转换为弧度制,便于后续计算。
•建立导线网模型:根据导线的连接关系,建立导线网的拓扑模型。
进行平差计算•确定已知点:根据实际情况,选取导线网中已知点,作为平差计算的基准点。
•建立平差方程:根据导线网模型和已知点的观测值,建立平差方程组。
•进行平差计算:使用最小二乘法或其他适当的方法,求解平差方程组,得到未知点的坐标和精度估计。
•检查计算结果:对平差结果进行检查,确保计算的准确性。
精度评定•计算精度指标:根据计算结果和观测数据的精度,计算导线网的精度指标,如相对误差、中误差等。
•统计分析:对计算结果进行统计分析,得出导线网的整体精度评定。
•生成报告:将计算结果和精度评定结果输出到报告中,方便用户阅读和使用。
程序设计考虑用户界面设计在程序设计过程中,为了方便用户使用,需要设计一个用户友好的界面。
该界面应允许用户导入原始测量数据、选择计算参数、查看计算结果和精度评定结果等。
可以使用图形界面或命令行界面来实现。
程序性能优化导线网平差是一项计算量较大的工作,特别是在处理大规模的导线网时。
为了提高程序的运行效率,可以采用一些优化技术,如矩阵运算优化、并行计算等。
同时,还可以合理选择数据结构和算法,减少计算和存储的开销。
错误处理和异常处理在程序设计中,要考虑到可能出现的数据错误和计算异常情况,为程序添加相应的错误处理和异常处理机制。
当程序发生错误或异常时,应给出合适的提示和错误信息,方便用户及时发现和解决问题。
【免费下载】导线网平差算例
闭合差计 算与检核
平差
平差报告的 生成和输出
实例 1 符合导线实例
这是一条符合导线的测量数据和简图,A、B、C 和 D 是已知坐标点,2、3 和 4 是
待测的控制点。
原始测量数据如下:
测站点 角度(°′″) 距离(米)
B
A
2
3
4
C
D
导线图如下:
85.30211
254.32322
.04333
272.20202
测站 3 的观测信息
以 4 号点为测站点,以 3 号点为定向点时,照准 C 点的数据输入如下图“测站 4 的观测信息”所示:
测站 4 的观测信息
说明:①数据为空或前面已输入过时可以不输入(对向观测例外) ②在电子表格中输入数据时,所有零值可以省略不输。
以上数据输入完后,点击菜单“文件\另存为”,将输入的数据保存为平差易数据 格式文件(格式内容详见附录 A): [STATION] (测站信息) B,10,8345.870900,5216.602100 A,10,7396.252000,5530.009000 C,10,4817.605000,9341.482000 D,10,4467.524300,8404.762400 2,00 3,00 4,00
导线网平差算例
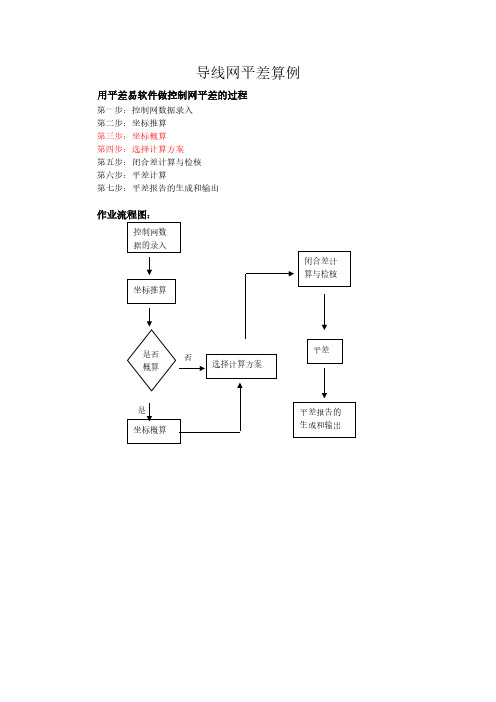
用平差易软件做控制网平差的过程
第一步:控制网数据录入 第二步:坐标推算 第三步:坐标概算 第四步:选择计算方案 第五步:闭合差计算与检核 第六步:平差计算 第七步:平差报告的生成和输出
作业流程图:
控制网数 据的录入
坐标推算
是否 概算
是 坐标概算
否 选择计算方案
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S EY cos(Y M iK )
照准归心与测站归心相同
概算--观测成果改化
• 野外观测是地球表面,而参考面是地球椭球面,计 算是在高斯平面上。方向改化和距离改化就是要将
椭球面上的观测值归化到高斯平面上。
方向改化: 距离改化:
iK
f ( X i X k ) (2 Yi Yk ) 3
E y -测站偏心距,
C Kj E y '' sin(M Ki Y ) / S Ki rKi ET '' sin(M ik T ) / S Ki
Y -测站偏心角,
M Ki -为测站上观测改正方向的方向观测值
ET -照准偏心距,
T -照准偏心角,
M iK -为照准点上观测改正方向的方向观测值
算、坐标转换、换带计算等。 对以上每项功能还需细化
数据描述
1.已知数据
已知边、已知方位角、已知点位坐标、测角先验精度信息、测边先验 精度信息,气象信息等
2.观测数据
观测方位,观测边长
3.网形数据
CAD草图或近似坐标及连接信息文件
4.平差成果数据
平差后的待定点点位坐标及其精度、误差椭圆参数、平差后的方位角 和边长及其精度等
概算--近似坐标解算方法
(1)整体解算法:设有n个待定点,则有2n未知
数,选取具有2n个独立未知数的观测值组成方程 组,进行整体解算。
(2)逐点解算法:选择已知点或已计算出坐标
的点作为起算点,根据具体的图形,逐个推算出 各点的坐标。
概算--观测成果归化到标石中心
方向观测值的归心: 测站归心和照准归心
V BX L
根据最小二乘原理: V T PV min ,求极值,
(V T PV ) 2V T P V 2V T PB 0
x
x
BT PV 0, BT P(BX L) 0, BT PBX BT PL 0 ,得:
法方程:
BT PBX BT PL 0
控制网平差软件需求分析
• 总体描述: 控制网平差程序对野外控制网观测数据
进行平差数据处理,其目的就是根据最小 二乘原理,消除网中的各种几何矛盾,求 出全网各待定元素(未知点的平面坐标或 三维坐标)。
功能需求
1.优化设计:根据控制网的观测精度与网形,全面评定网
的精度
2.数据输入:表格化输入、图形化输入、外部数据倒入
,即求条件极值法,利用拉格朗日不定乘数法:
V T PV 2K T ( AX W ) min
2V T P V 2K T A 2(BX L)T PB 2K T A 0
x
x
BT P(BX L) AT K BT PBX AT K BT PL 0
AX W 0
即: BT PB AT X BT PL
A
0
K
W
0
控制网间接平差的主要工作
• 平面控制网的计算通常包括:
• 概算:概算为平差前的准备工作,相当于
数据的预处理
• 平差:列出误差方程,根据最小二乘原理
进行解算
• 编制成果表:控制点成果 、观测成果等
ห้องสมุดไป่ตู้
法方程的解:
X (BT PB)1 BT PL
单位权中误差:
V T PV /(n t)
附有条件的间接平差原理:
设未知数个数为t,观测值个数为n,条件方程个数为m
误差方程:V BX L
条件方程: AX W 0
根据最小二乘原理:在条件 AX W 0下
V T PV min
平差计算--1误差方程式及条件方程式的列立
概算--计算近似坐标1
1 按方向观测值计算三角网中待定点的近似 坐标 (前方交会)
xk
xa ctgB xbctgA ya ctgA ctgB
yb
(1)
yk
ya ctgB ybctgA xa ctgA ctgB
xb
k
K
B
A
b
a
概算--计算近似坐标2
2.按边长观测值计算三边网中待定点的近似坐标 (边长交 会),先按公式(2)计算三角形的内角,再用公式(1)计 算待定点的坐标
3.概算:自动完成各方向的曲率改正及边长的高程归化与
投影改化,近似坐标的推算等。
4.平差计算:对观测数据进行精密平差计算,得到平差后
的点位坐标,方向观测值,边长观测值等,精度评定。
5.成果输出:控制网图形输出,平差结果报表及其输出,
绘制误差椭圆,打印输出等。
6.其它功能:粗差探测与剔除、方差分量估计、闭合差计
概算的主要工作
1.外业观测成果的整理、检查 2.绘制网的略图,编制观测数据表和已知数据表 3.计算近似坐标 4.观测成果归化到标石中心 5.观测成果改化(方向改化和距离改化) 6.根据平面控制网的几何条件检查观测成果的质量,
即各种闭合、附合条件的检验。 如:方位角闭 合(附合)差、坐标闭合(附合)差
S f SiK Ym2
式中:
Ym
Yi
Yk 2
;f
2 Rm2
Rm 本地区的地球平均半径
平差计算
1.列出误差方程及条件式 2.定权 3.组成法方程 4.解算法方程,求得dX=[dx1 dy1 dx2
dy2 …] 5. 平差后的坐标值计算X=X+dX。 6.精度评定,计算误差椭圆参数等
k
S1 K S2
a
A
B
S0
b
A
cos1
(
S
2 0
S12
S
2 2
)
2S0 S1
B
c
os1
(
S
2 0
S
2 2
S12
)
2S0 S 2
(2)
概算--计算近似坐标3
3按方向和边长观测值计算导线网中待定点的 近似坐标
b
tab A
t d
k
a
xk xa d cost xa d cos(tab A) yk ya d sin t ya d sin(tab A)
已 知 数 据
观测数据
平差模型
• 最小二乘平差模型
• 条件平差:条件方程式较少,占用内存小,但
条件方程与网形有关,很难编制通用的程序。
• 间接平差:一个观测值就是一个误差方程,占
用内存相对较大,但易于编程解算,容易编制通 用的程序
间接平差基本原理: 设:观测值为L,其权为P,相应的改正数为V,必要观测值个 数为t,选定未知数X,则有误差方程
