(整理)测边网.测角网.导线网典型计算
SL52-93水利水电工程施工测量规范

水利水电工程施工测量规范SL 52-93电力工业部部利水中华人民共和国关于颁发《水利水电工程施工测量规范》SL52-93的通知水建[1993]330号为推动水利水电工程施工测量技术的进步,保证施工测量的质量,水利部和原能源部委托水利水电长江葛洲坝工程局为主编单位,对原水利电力部水利水电建设总局局标准《水利水电工程施工测量规范》SDJS9-85进行了修订。
该规范的修订送审稿已通过两部审查,现批准为行业标准,编号为SL52-93,自1993年12月1日起执行,原局标准同时废止。
本规范由主编单位负责解释,水利电力出版社负责出版发行。
1993年6月25日1 总则1.0.1 本规范适用于水利水电工程施工阶段的测量工作。
其内容包括总则、控制测量、放样的准备与方法、开挖工程测量、立模与填筑放样、金属结构与机电设备安装测量、地下洞室测量、辅助工程测量、施工场地地形测量、疏浚及渠堤施工测量、施工期间的外部变形监测、竣工测量。
1.0.2 施工测量工作应包括下列内容。
(1)根据工程施工总布置图和有关测绘资料,布设施工控制网。
(2)针对施工各阶段的不同要求,进行建筑物轮廓点的放样及其检查工作。
(3)提供局部施工布置所需的测绘资料。
(4)按照设计图纸、文件要求,埋设建筑物外部变形观测设施,并负责施工期间的观测工作。
(5)进行收方测量及工程量计算。
(6)单项工程完工时,根据设计要求,对水工建筑物过流部位以及重要隐蔽工程的几何形体进行竣工测量。
1.0.3 本规范以中误差作为衡量精度的标准,以两倍中误差为极限误差。
1.0.4 施工测量主要精度指标应符合表1.0.4的规定。
表1.0.4 施工测量主要精度指标1.0.5 施工平面控制网坐标系统,宜与规划设计阶段的坐标系统一致,也可根据需要建立与规划设计阶段的坐标系统有换算关系的施工坐标系统。
施工高程系统,必须与规划设计阶段的高程系统相一致,并应根据需要就近与国家水准点进行联测,其联测精度不宜低于本工程首级高程控制的要求。
SL52-93水利水电工程施工测量规范

水利水电工程施工测量规范SL 52-93电力工业部部利水中华人民共和国关于颁发《水利水电工程施工测量规范》SL52-93的通知水建[1993]330号为推动水利水电工程施工测量技术的进步,保证施工测量的质量,水利部和原能源部委托水利水电长江葛洲坝工程局为主编单位,对原水利电力部水利水电建设总局局标准《水利水电工程施工测量规范》SDJS9-85进行了修订。
该规范的修订送审稿已通过两部审查,现批准为行业标准,编号为SL52-93,自1993年12月1日起执行,原局标准同时废止。
本规范由主编单位负责解释,水利电力出版社负责出版发行。
1993年6月25日1 总则1.0.1 本规范适用于水利水电工程施工阶段的测量工作。
其内容包括总则、控制测量、放样的准备与方法、开挖工程测量、立模与填筑放样、金属结构与机电设备安装测量、地下洞室测量、辅助工程测量、施工场地地形测量、疏浚及渠堤施工测量、施工期间的外部变形监测、竣工测量。
1.0.2 施工测量工作应包括下列内容。
(1)根据工程施工总布置图和有关测绘资料,布设施工控制网。
(2)针对施工各阶段的不同要求,进行建筑物轮廓点的放样及其检查工作。
(3)提供局部施工布置所需的测绘资料。
(4)按照设计图纸、文件要求,埋设建筑物外部变形观测设施,并负责施工期间的观测工作。
(5)进行收方测量及工程量计算。
(6)单项工程完工时,根据设计要求,对水工建筑物过流部位以及重要隐蔽工程的几何形体进行竣工测量。
1.0.3 本规范以中误差作为衡量精度的标准,以两倍中误差为极限误差。
1.0.4 施工测量主要精度指标应符合表1.0.4的规定。
表1.0.4 施工测量主要精度指标1.0.5 施工平面控制网坐标系统,宜与规划设计阶段的坐标系统一致,也可根据需要建立与规划设计阶段的坐标系统有换算关系的施工坐标系统。
施工高程系统,必须与规划设计阶段的高程系统相一致,并应根据需要就近与国家水准点进行联测,其联测精度不宜低于本工程首级高程控制的要求。
第五章 大地测量的基本技术与方法(1)

② 技术设计的内容和方法 [1] 搜集和分析资料 (1)测区内各种比例尺的地形图。 (2)已有的控制测量成果(包括全部有关技术文件、图表、手簿 等等)。 (3)有关测区的气象、地质等情况,以供建标、埋石、安排作业 时间等方面的参考。 (4)现场踏勘了解已有控制标志的保存完好情况。 (5)调查测区的行政区划、交通便利情况和物资供应情况。若在 少数民族地区,则应了解民族风俗、习惯。 对搜集到的上述资料进行分析,以确定网的布设形式,起始 数据如何获得,网的未来扩展等。 其次还应考虑网的坐标系投影带和投影面的选择。 此外还应考虑网的图形结构,旧有标志可否利用等问题。
上海港GPS扩展网网图
2 甚长基线干涉测量(VLBI) 甚长基线干涉测量系统是在甚长基线的两端(相距几千公里), 用射电望远镜,接收银河系或银河系以外的类星体发出的无线电辐 射信号,通过信号对比,根据干涉原理,直接确定基线长度和方向 的一种空间技术。长度的相对精度可优于10-6,对测定射电源的空 间位置,可达0.001”,由于其定位的精度高,可在研究地球的极移 、地球自转速率的短周期变化、地球固体潮、大地板块运动的相对 速率和方向中得到广泛的应用。
(3)从安全生产方面考虑 点位离公路、铁路和其他建筑物以及高压电线等应有一定的 距离。 图上设计的方法及主要步骤 图上设计宜在中比例尺地形图(根据测区大小,选用1:25 000~1 :100 000地形图)上进行,其方法和步骤如下: a 展绘已知点; b 按上述对点位的基本要求,从已知点开始扩展; c 判断和检查点间的通视; d 估算控制网中各推算元素的精度; e 据测区的情况调查和图上设计结果,写出文字说明,并拟定作业 计划。
2. 大地控制网应有足够的精度。 国家三角网的精度,应能满足大比例尺测图的要求。在测图中 ,要求首级图根点相对于起算三角点的点位误差,在图上应不 超过±0.1mm,相对于地面点的点位误差则不超过 ±0.1Nmm(N 为测图比例尺分母)。 为使国家三角点的误差对图点的影响可以忽略不计,应使相邻国 家三角点的点位误差小于(1/3) ×0.1Nmm。
控制测量方案
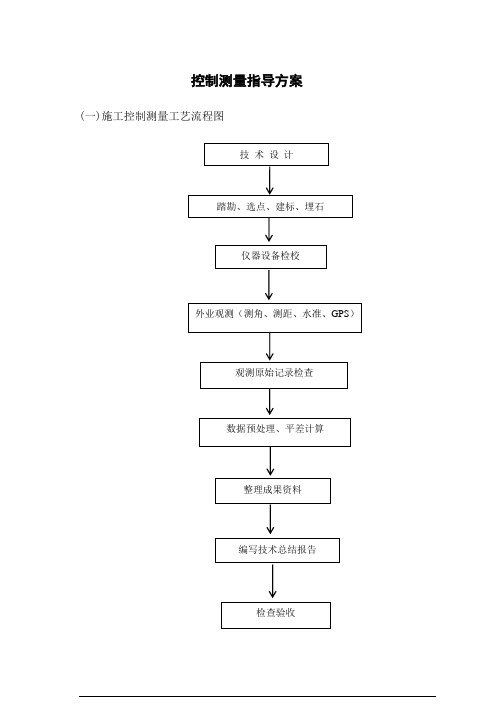
控制测量指导方案(一)施工控制测量工艺流程图(二)施工控制测量方法及要求本作业指导书是针对施工控制测量的特点和作业需要编写的,服务范围是二等以下施工平面控制网、平高控制网、高程控制网的建立和控制点加密。
使用本指导书进行测量作业,应遵守《国家三角测量规范》、《国家一、二等水准测量规范》、《国家三、四等水准测量规范》、《水利水电工程施工测量规范》等规程规范。
如业主有特殊要求的,按业主要求执行。
一、准备工作1.收集资料1.1广泛收集测区及其附近已有的控制测量成果和地形图资料。
(1)控制测量资料包括成果表、点之记、展点图、路线图、计算说明和技术总结等。
收集资料时要查明施测年代、作业单位、依据规范、平高系统、施测等级和成果的精度评定。
成果精度指三角网的高程、测角、点位、最弱边、相对点位中误差;水准路线中每公里偶然中误差和水准点的高程中误差等。
(2)收集的地形图资料包括测区范围内及周边地区各种比例尺地形图和专业用图,主要查明地图的比例尺、施测年代、作业单位、依据规范、坐标系统、高程系统和成图质量等。
(3)如果收集到的控制资料的坐标系统、高程系统不一致,则应收集、整理这些不同系统间的换算关系。
1.2收集合同文件、工程设计文件、业主(监理)文件中有关测量专业的技术要求和规定。
1.3准备相应的规范:《国家三角测量规范》、《国家一、二等水准测量规范》、《国家三、四等水准测量规范》、《GPS测量规范》、《水利水电工程施工测量规范》。
1.4了解测区的行政划分、社会治安、交通运输、物资供应、风俗习惯、气象、地质情况。
例如了解冻土深度,用以考虑埋石深度;最大风力,以考虑觇标的结构;雾季、雨季和风季的起止时间,封冻和解冻时间,以确定适宜的作业月份。
2.现场踏勘携带收集到的测区地形图、控制展点图、点之记等资料到现场踏勘。
踏勘主要了解以下内容:2.1原有的三角点、导线点、水准点、GPS点的位置,了解觇标、标石和标志的现状,其造标埋石的质量,以便决定有无利用价值。
[精品]高等(近代)测量平差复习资料.doc
![[精品]高等(近代)测量平差复习资料.doc](https://img.taocdn.com/s3/m/1c7811129b89680202d825d3.png)
第一章第一节绪论1、近代测量平差理论的主要内容⑴从独立观测值到相关观测值一相关平差⑵从函数模型和随机模型满秩到函数模型和随机模型奇异一秩亏自由网平差⑶从非随机参数到随机参数以及随机参数与非随机参数一并处理一最小二乘滤波、推估和配置⑷从先验定权到后验定权一随机模型的验后估计⑸从整体解算到分开解算——序贯平差⑹从处理静态数据到处理动态数据一动态测量平差⑺从线性模型的参数估计到非线性模型的参数估计一非线性平差⑻从确定性平差模型到不确定性平差模型一不确定性平差模型的处理⑼从偶然误差的处理到含有系统误差的处理一附加系统参数的平差(10) 从无偏估计到有偏估计(11) 从偶然误差的处理到含有粗差的处理——数据探测法与稳健估计第三节广义逆矩阵1、广义逆g逆:AGA=A解不唯一2、反射g逆:AGA=A, GAG=G解不唯一3、最小范数广义逆AGA=A, (GA T) =GA解不唯一「4、最小二乘广义逆AGA=A, (AG T) =AG解不唯一5、最小二乘最小范数广义逆AGA=A, GAG=G, (GA T) =GA, (AG T) =AG解唯一第二章秩亏自由网平差第一节概述1、平差时必要的起算个数称为基准2、基准数据:测角网d=4测边网、导线网、边角网d=3GPS 网d=5高程网d=l三维控制网d=73、没有足够起算数据的平差问题称为秩亏自由网平差4、秩亏自由网平差类型:普通秩亏自由网平差、拟稳平差、加权秩亏自由网平差例2-2-1课本19页例2-3-1课本27页例2-4-1课本30页第五节控制网附加阵G1 水准网:GT= (1 1 1 ........................ 1)2测边网、导线网、边角网GT=1010 ・・• (10)010 1 ・・• (01)-丫-Y2°X2°•••- -Y m°Xm°3二维测角网G T:第六节1、权逆阵奇异的原因⑴观测值向量中的一些分量是另一些分量的线性组合⑵观测值向量中的一些分量无误差2、权逆阵奇异的平差原则V T PV=V T P*V=V1T P1V1=min第三章最小二乘滤波推估和配置AA- -++-第一"P1、与观测值之间有函数关系的已测点参数称为滤波信号,求定滤波信号最佳估值的过程称为滤波2、与观测值之间没有函数关系的未测点参数称为推估信号,求定推估信号最佳估值的过程称为推估3、配置:最小二乘配置的函数模型L=BX+AY+A⑴当A=0或Y=0时模型变为L=BX+A,即高斯一马尔可夫模型⑵当B=0或X=0时模型变为L= AY+△即滤波和推估模型⑶当;=0时模型变为L=A1S + A即滤波模型第二节1、滤波的函数模型:L=AY+AL为观测向量,Y为随机参数A=[A1 0] Y=[ ]滤波的随机模型:E(A)=0, D(AJ=D A=P A-1,E(L)=U L D(L)=D LE(Y)= D(Y) =Cov(A, S)=D A,C OV(A, S,)=D A2、配置的函数模型:L=BX+AY+AL为观测向量,Y为随机参数A=[A1 0] Y=[ ]滤波的随机模型:E(A)=0, D(AJ=D A=P A-1,E(L)=U L D(L)=D LE(Y)= D(Y) =Cov(A, S)=D A,C OV(A, S,)=D A第五章1、卡尔曼滤波的基本思想:采用信号与噪声的状态空间模型,利用前一时刻的估计值和现时刻的观测值来更新状态变量的估计,求出现时刻的估计值。
测角网4个必要起算数据

测绘工程系
必要观测与多余观测
二、三角网(测角网、测边网、边角网)
3、边角网 3个必要起算数据:1个点的纵、横坐标,1条边的已知坐 标方位角 C S4 无已知点 假定必要起算数据:1个点的纵 、横坐标,1条边的已知坐标方 位角,无法确定大小,必须已知 A 1边,边长无误差,不参与平差 多余观测数r=n-2P+3
误差理论与测量平差
测绘工程系
必要观测与多余观测
一、水准网
1、水准网
水准网中,要确定各点的高程,需要一个高程基准。
B h1 h4 D 必要观测数=待定点个数 h5 A
有已知点 h3
h1
h2
即:t=P
B
C
无已知点
A
h6 h5 D h4
h2 h3
假定一个点高程已知
必要观测数=待定点个数-1
即t=p-1
C 误差理论与测量平差
思考:可否假定2个点高程已知?
测绘工程系
必要观测与多余观测
二、三角网(测角网、测边网、边角网)
1、测角网 4个必要起算数据: 1个点的纵、横坐标,1条边的已知坐标 方位角,1条已知边长
C
有两个及两个以上已知点 必要观测数=待定点个数P 的2倍,即t=2P 多余观测数r=n-2P
A
L3 L6
L5
误差理论与测量平差 测绘工程系
S1
L3 L6
L5
S3 B
D
L1
0 L2 L4
S2
必要观测数=待定点个数的2倍-4+1,即t=2P-3
必要观测与多余观测
三、单一附和导线
3个必要起算数据:1个点的纵、横坐标,1条边的已知坐 标方位角
大地测量学基础复习资料

大地测量学基础一、填空题:1、时间的计量包括时间原点和度量单位(尺度)两个元素。
坐标的计量包括坐标原点、坐标轴的指向和坐标的尺度三个元素。
2、测量外业工作的基准线是铅垂线,基准面是大地水准面。
在椭球面上进行大地测量计算的基准线是法线,基准面是椭球面。
3、经纬仪十字丝分划板上丝和下丝的作用是测量视距。
4、衡量精度的指标有中误差、极限误差、或然误差、平均误差、相对误差。
5、过椭球面上一点P 的垂线与赤道面的夹角称为大地纬度,椭球面上一点P 与椭球中心的连线与赤道面的夹角称为地心纬度,在过椭球面上一点P 的子午面上,以椭圆中心O 为圆心,以椭球长半径a 为半径做辅助圆,反向延长过P 点并与x 轴垂直的垂线,与辅助圆交于P 1点,则P 1与椭球中心的连线与赤道面的夹角称为归化纬度,符号q= BBN B M 0cos d 表示等量纬度。
6、某直线的方位角为123°20’,该直线的反方位角为303°20’。
已知P 1点坐标(-2,-2),P 2点坐标(-4,-4),则P 1P 2的方位角为225°,P 2P 1的方位角为45°。
【注释】在同一高斯平面直角坐标系内一条直线的正、反坐标方位角相差180°,即:α12=α21±180°。
(详见数字测图课本23页)7、水准路线按布设形式分为闭合水准路线、附合水准路线和支水准路线。
8、高斯投影属于横轴椭圆柱等角投影,保证了投影的角度不变性,图形的相似性,以及在某点方向上的长度比的同一性。
在高斯平面直角坐标系中,中央子午线的投影为坐标x 轴。
9、旋转椭球的形状和大小是由子午椭圆的5个基本几何参数来决定的,他们分别是长半轴a 、短半轴b 、扁率、第一偏心率、第二偏心率。
两个互相垂直的法截弧的曲率半径,在微分几何中统称为主曲率半径,它们是指子午圈曲率半径和卯酉圈曲率半径,椭球面上任意一点的平均曲率半径R 等于该点的子午圈曲率半径和卯酉圈曲率半径的几何平均值。
[整理]10控制网平差计算
![[整理]10控制网平差计算](https://img.taocdn.com/s3/m/e0263d420066f5335b812169.png)
§9.1 条件平差原理在条件观测平差中,以n 个观测值的平差值1ˆ⨯n L作为未知数,列出v 个未知数的条件式,在min =PV V T 情况下,用条件极值的方法求出一组v 值,进而求出平差值。
9.1.1基础方程和它的解设某平差问题,有n 个带有相互独立的正态随机误差的观测值 ,其相应的权阵为 , 它是对角阵,改正数为 ,平差值为 。
当有r 个多余观测时,则平差值 应满足r 个平差值条件方程为:⎪⎪⎭⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0ˆˆˆ221122112211οοοr L r L r L r b L b L b L b a L a L a L a n n n n n n (9-1) 式中i a 、i b 、…i r (i =1、2、…n )——为条件方程的系数;0a 、0b 、…0r ——为条件方程的常项数以ii i v L L +=ˆ(i =1、2、…n )代入(9-1)得条件方程(9-2)式中a w 、b w 、……r w 为条件方程的闭合差,或称为条件方程的不符值,即(9-3) 令⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n n n r r r r b b b a a a A212121⎪⎪⎭⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪⎭⎪⎪⎬⎫=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L ˆˆˆˆ211⎪⎪⎪⎪⎫ ⎛=⨯b a r w w W 1⎪⎪⎪⎪⎫ ⎛=⨯n v v V 211⎪⎪⎪⎫⎛=⨯οοb a A o r 11⨯n L nn P ⨯1⨯n V 1ˆ⨯n L 1ˆ⨯n L⎪⎪⎪⎫⎛=⨯n n p p P 000021则(9-1)及(9-2)上两式的矩阵表达式为0ˆ0=+A LA (9-4) 0=+W AV (9-5)上改正数条件方程式中V 的解不是唯一的解,根据最小二乘原理,在V 的无穷多组解中,取PV V T = 最小的一组解是唯一的,V 的这一组解,可用拉格朗日乘数法解出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录摘要0第1章测边网坐标平差 (1)1.1近似坐标计算 (2)1.2计算误差方程的系数及常数项 (3)1.3误差方程 (3)1.4计算观测值的权 (4)1.5组成法方程 (4)1.6平差值计算 (4)1.6.1 坐标平差值 (4)1.6.2 边长平差值计算 (5)1.7精度计算 (5)1.7.1 单位权中误差 (5)1.7.2 待定点坐标中误差 (5)第2章三角网坐标平差 (6)2.1测角网函数模型 (7)2.2坐标方位角计算 (8)2.2.1 近似坐标方位角计算 (8)2.2.2 坐标方位角计算 (8)2.3近似坐标增量、近似边长与误差方程系数 (8)2.4误差方程的组成 (9)2.5确定权和组成法方程 (10)2.6法方程系数阵的逆阵与参数改正数 (10)2.7平差值计算及精度评定 (10)2.7.1 待定点的最或然值 (10)2.7.2 观测值的改正数 (11)2.7.3 点位中误差 (11)2.7.4 观测值平差值 (11)第3 章导线网间接平差 (12)3.1计算各边坐标方位角改正数方程的系数 (14)3.2确定角和边的权 (15)3.3计算角度和边长误差方程系数和常数项 (17)3.4误差方程的组成和解 (17)3.5平差值计算 (23)3.6精度计算 (23)3.6.1 单位权中误差 (23)3.6.2 待定点点位中误差计算 (23)参考文献 (24)指导老师评语 (25)摘要本课程设计介绍了综合运用测量平差基础知识来解决测边网、三角网、导线网坐标平差及精度评定问题,先设定未知参数,根据空间几何关系找出相应的平差模型,按照间接平差的原理,列出观测值误差方程,求出法方程的各系数矩阵,解算未知参数、观测值的改正数,最后进行精度评定,完成课题要求。
通过这一课题,拓宽我们测量数据处理的知识面,启发我们处理实际生产问题的新思路,针对某一实际问题,用经典的误差理论和比较前沿的数据处理方法进行合理的求解,以巩固和加强我们对误差理论和现代测量数据处理方法的理解,增强我们用所学的理论方法解决实际问题的能力。
关键字:平差误差方程法方程平差值精度评定第1章 测边网坐标平差1.有测边网如下图所示。
网中A 、B 、C 及D 为已知点,P1、P2、P3及P4为待定点,现用某测距仪观测了13条边长,测距精度()S mm s 10613-⨯+=σ起算数据及观测边长见表7-17。
试按间接平差法求待定点坐标平差值及其中误差。
起算数据和观测数据解:由题意有n=13,t=8选待定点4321,,,P P P P 的坐标为参数,即)ˆ,ˆ(),ˆ,ˆ(),ˆ,ˆ(),ˆ,ˆ(444333222111Y X P Y X P Y X P Y X P ====1.1 近似坐标计算1P 的近似坐标由已知点A 、B 和观测边21,S S 交会计算得。
如下图中设h 为三角形1ABP 底边AB 上的高,S为S2在A 上的投影。
得 129.3500221222=-+=ABS AB S S m 526.3828222=-=S S h m所以待定点1P 的近似坐标为⎭⎬⎫=-++==-++=m h S Y Y m h S X X BA AB A BA AB A 505.60500)90sin(sin 270.48580)90cos(cos 0101αααα同理由A P 、1及S 3、S 4交会计算2P 点的近似坐标;由P 1、P 2及S 10、S 5交会计算P 3点的近似坐标;由P 1、P 3及S 12、S 9交会计算P 4点的近似坐标。
其近似坐标结果为:390.4868102=X 280.5501802=Y 224.4376703=X 596.5796803=Y218.4084304=X 877.6486704=Y1.2 计算误差方程的系数及常数项按公式:i k jkjkk jkjk j jkjkj jkjk i l ySY xSX ySY xSX v -∆+∆+∆-∆-=ˆˆˆˆ000000 0jk i i S S l -=计算误差方程的系数和常数项,由已知点坐标和待定点近似坐标计算系数及常数项结果见表1-1:根据表中的a 、b 系数及常数项l 可列出全网的误差方程,其系数和常数项结果列于表1-2中,共13个误差方程:表1-2 系数、常数项、改正数及边长平差值列表1.4 计算观测值的权将上表中的边长观测值代入测距精度公式:i S bS a i+=σ 220iiSS P σσ=,算的各边的测距精度i S σ,并设mm 100=σ,由此算得各条边的权,其结果均列于下表中。
Pl B xPB B T T =ˆ,Pl B T 及其解i x ˆ、i y ˆ列于下表中, 表1-4 坐标平差值求11)(--=PB B N TBB ,列于表中。
表1-5 参数的协因数1.6.1坐标平差值 按公式i ii x X X ˆˆ+=计算: 1011ˆˆx X X +==48580.268m 1011ˆˆy Y Y +==60500.500m 2022ˆˆx X X +==48681.382m 2022ˆˆy Y Y +==55018.290m 3033ˆˆx X X +==43767.189m 3033ˆˆy Y Y +==57968.610m4044ˆˆx X X +==40843.321m 4044ˆˆy Y Y +==64867.980m 1.6.2边长平差值计算 按公式V S S+=ˆ计算: 1011ˆˆv S S +==5760.711m 2022ˆˆv S S +==5187.344m 3033ˆˆv S S +==7838.878m 4044ˆˆv S S +==5483.143m 5055ˆˆv S S +==5731.813m 6066ˆˆv S S +==8719.088m 7077ˆˆv S S +==5598.642m 8088ˆˆv S S +==7494.959m 9099ˆˆv S S +==7493.356m 1001010ˆˆv S S +==5438.400m 1101111ˆˆv S S +==5486.903m 1201212ˆˆv S S +==8884.550m 1301313ˆˆv S S +==7228.488m 1.7 精度计算1.7.1单位权中误差:t n PV V T -=0ˆσ=813662.0-=0.36dm 1.7.2待定点坐标中误差:由参数的协因数阵(即1-BB N )取得参数的权倒数,计算待定点坐标点点位中误差:23.042.036.0ˆ1==X σdm 26.051.036.0ˆ1==Y σdm 35.026.023.0ˆˆˆ2222111=+=+=Y X P σσσdm29.067.036.0ˆ2==X σdm 31.074.036.0ˆ2==Y σdm 42.031.029.0ˆˆˆ2222222=+=+=Y X P σσσdm24.044.036.0ˆ3==X σdm 31.072.036.0ˆ3==Y σdm 39.031.024.0ˆˆˆ2222333=+=+=Y X P σσσdm26.053.036.0ˆ4==X σdm 34.091.036.0ˆ4==Y σdm 43.034.026.0ˆˆˆ2222444=+=+=Y X P σσσdm第2章 三角网坐标平差2.在下图所示的测角网中,A,B,C 为已知点,1P ,2P 为待定点,S1~S10为角度观测值,已知点坐标与待定点近似坐标为:同精度观测值为:(1) 误差方程及法方程;(2) 待定点最或是坐标及点位中误差; (3) 观测值改正值及平差值。
解:由题意有:t=4,设待定点1P ,2P 的坐标的平差值为参数,即)ˆ,ˆ(111Y X P =,)ˆ,ˆ(222Y X P =。
2.1 测角网函数模型:11ˆˆA AB L αα-= B A L 112ˆˆˆαα-= C B L 113ˆˆˆαα-= CB C L 114ˆˆˆαα-= 125ˆˆˆC C L αα-= C L 2216ˆˆˆαα-= 1217ˆˆˆαα-=C L A L 1128ˆˆˆαα-= 2129ˆˆˆαα-=A L 2110ˆˆˆA A L αα-= 其中i i i V L L +=ˆ,i i i x X X ˆˆ0+=,i i i y Y Y ˆˆ0+=,i j i j ij X X Y Y --=arctan α,ij i j ij X X Y Y ˆˆˆˆarctan ˆ--=α,00000arctaniji j ij XX Y Y --=α,0i i i L L l -=,将以上式子带入并线性化得:112011120111ˆ)(ˆ)(l yS X xS Y V A A A A -∆''-∆''=ρρ 212010120101120101201012ˆ))()((ˆ))()((l yS X S X xS Y S Y V BBAABBAA-∆''-∆''-∆''-∆''=ρρρρ 312010120101120101201013ˆ))()((ˆ))()((l yS X S X xS Y S Y V CCBBCCBB-∆''-∆''-∆''-∆''=ρρρρ 4120111201014ˆ)(ˆ)(l yS X xS Y V C C C C -∆''+∆''-=ρρ 522022220202120111201015ˆ)(ˆ)(ˆ)(ˆ)(l yS X xS Y yS X xS Y V C C C C C C C C -∆''+∆''-∆''-∆''=ρρρρ 6220202202121220202202121120212112021216ˆ))()((ˆ))()((ˆ)(ˆ)(l yS X S X xS Y S Y yS X xS Y V CCCC-∆''-∆''-∆''-∆''+∆''+∆''-=ρρρρρρ 72201201222012012120120122010*******12201017ˆ)(ˆ)(ˆ))()((ˆ))()((l yS X xS Y yS X S X xS Y S Y V C CC C-∆''-∆''+∆''-∆''-∆''-∆''=ρρρρρρ 822012012220120121201012012121201012012128ˆ)(ˆ)(ˆ))()((ˆ))()((l yS X xS Y yS X S X xS Y S Y V AAAA-∆''+∆''-∆''-∆''-∆''-∆''=ρρρρρρ 92202102120202220210212020*******21120210219ˆ))()((ˆ))()((ˆ)(ˆ)(l yS X S X xS Y S Y yS X xS Y V A A A A-∆''-∆''-∆''-∆''+∆''-∆''=ρρρρρρ 102202222022120111201110ˆ)(ˆ)(ˆ)(ˆ)(l yS X xS Y yS X xS Y V A A A A A A A A -∆''-∆''+∆''+∆''-=ρρρρ2.2 坐标方位角计算2.2.1 近似坐标方位角计算按公式00000arctaniji j ijXX Y Y --=α得:按公式ij i j ij X X Y Y --=arctanα得:8.5581205'''=AB a ,8.512095'''= BC α2.3 近似坐标增量、近似边长与误差方程系数按公式i i P j jp Y Y Y-=∆0,i i P j jp X X X-=∆0 ,2220)()()(i i i P j P j jp Y Y X X S -+-=,200)(ijij ij S Y a ∆''=ρ,200)(ij ij ij S X b ∆''-=ρ得:2.4 误差方程的组成按公式i h jh h jh k jk k jk j jh jk j jh jk i l y b x a y b x a y b b xa a V -++---+-=ˆˆˆˆˆ)(ˆ)( 000)(i i jh jk i i L L a a L l -=--=得:误差方程系数表和常数项因此误差方程为:8.0ˆ5660.14ˆ4623.8111++=y xV 9.3ˆ2296.20ˆ1745.1112---=y xV 8.0ˆ4653.1ˆ4603.13113+--=y xV 6.1ˆ1289.7ˆ1725.6114++=y xV 3.3ˆ5978.8ˆ4888.1ˆ1289.7ˆ1725.622115-+---=y x y xV 8.1ˆ9540.4ˆ4096.8ˆ6438.3ˆ8984.922116+---=y x y xV 1.2ˆ6438.3ˆ8984.9ˆ7727.10ˆ7259.322117--++-=y x y xV 0.5ˆ6438.3ˆ8984.9ˆ9222.10ˆ3607.1822118++-+=y x y xV 6.1ˆ9289.4ˆ6811.1ˆ6438.3ˆ8984.922119+-++-=y x y xV 1.5ˆ2851.1ˆ2173.8ˆ5660.14ˆ4623.8221110-++--=y x y xV2.5 确定权和组成法方程因为是等精度观测即:令E P = , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--==85921.257214.119854.229593.175Pl B W T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------==9644.1500007.413754.7928588.160007.412447.339791.73851.3783754.79791.73263.11992787.46628588.16851.3782787.466934.948PB B N T BB由0ˆ=-W xN BB 得法方程: ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------9644.1500007.413754.792859.160007.412447.3397910.738514.3783754.797910.732630.11992787.4662859.168514.3782787.4669340.948⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡2211ˆˆˆˆy xy x -⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--85921.257214.119854.229593.175=0 2.6 法方程系数阵的逆阵与参数改正数⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=-007173.0000999.0000530.0000015.0000999.0005854.0000588.0002609.0000530.0000588.0001147.0000807.0000015.0002609.0000807.0002492.01BBN ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡2211ˆˆˆˆyx y x =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----007173.0000999.0000530.0000015.0000999.0005854.0000588.0002609.0000530.0000588.0001147.0000807.0000015.0002609.0000807.0002492.0⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--85921.257214.119854.229593.175=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-18.040.018.006.0cm 2.7 平差值计算及精度评定 2.7.1 待定点的最或然值为:)(417.7770006.0416.777ˆˆ1011m x X X =+=+= )(645.3200018.0647.320ˆˆ1011m y Y Y =-=+= )(975.8440040.0971.844ˆˆ2022m x X X =+=+= )(162.5040018.0160.504ˆˆ2022m y Y Y =+=+= 即)645.320,417.777(1=P ,)162.504,975.844(2=P 。
