导线网条件平差
平差习题库

一、填空题:1、观测条件由观测仪器、____________和_____________三部分构成。
2、观测误差按其性质的不同可分为系统误差和偶然误差,其中____________误差在观测或计算过程中可以采用一定的措施消除或削弱,而___________误差在观测结果中必然存在。
3、测量平差的首要任务是经过数据处理,确定观测值的________________,而__________________________________________也是其必不可少的任务。
4、偶然误差的统计规律性是指:界限性、_______性、_______性和_______性。
5、在某相片上量得一距离长为200㎝,其相对中误差为1/3000,则该距离的绝对中误差为_____________________㎝。
6、测量平差是在______________的基础上利用_______________原理进行的。
7、单位权中误差mo、权Pi和中误差mi之间的关系为_______________________。
8、有一四边形导线环,同精度观测其各内角,共观测5组结果,计算出5个闭合差为﹣8″、9″、7″、﹣5″、-7″,则每组观测值之和中误差为____________,每个导线角观测值中误差___________。
(保留一位小数)9、设某角度观测值的协因数为3,则其观测值的权为_________。
10、观测成果的质量高低__________(能、否)反映观测条件的好坏。
11、理论上我们取3倍中误差为极限误差;而等级控制测量因为观测的精度要求比较高,往往规定______倍中误差为极限误差12、衡量精度常用的几种指标有中误差、___________误差和__________误差。
13、精度是指误差分布的________________程度。
14、由三角形闭合差ω计算测角中误差mβ的公式为______________________。
水准网条件平差程序设计毕业论文

本科生毕业设计说明书(毕业论文)题目:水准网条件平差程序设计学生姓名:房新明学号:1072143138专业:测绘工程班级:测绘10-1班指导教师:郭义水准网条件平差程序设计摘要近年来,随着我国经济的快速发展,国家大力于投资各种铁路建设和公路建设,测绘工程的运用也越来越突出。
以水准网布设的高程控制网在各类工程中随处可见。
但观测到的数据存在着各种各样的误差,这就需要我们通过简易平差或严密平差来对数据进行处理,从而使数据能够达到工程的预期精度。
本文主要研究如何解决绘图软件行业标准的网络数据处理问题。
从水准网的结构,平差基本原理、调整模型,基本方程及其解,并对法方程组成,求解,平差值的计算及其精度评定作了介绍。
和Visual studio6.0编程软件的利用,利用C语言是程序设计的相干事情。
在今后的测量工作中,可结合实际平差方案进行平差计算。
关键词:平差模型;精度评定;程序设计Leveling Network Adjustment Program DesignAbstractIn recent years, with China's rapid economic development, the state vigorously investment in all kinds of railway construction and road construction, the use of mapping project is also more and more prominent. In order to control the network level network in various engineering in everywhere. But the observed data exist various error, this needs us through simple adjustment or rigorous adjustment for data processing, so that data to achieve the desired precision engineering.This paper mainly studies how to solve the problem of mapping software industry standard network data processing. From the structure adjustment of leveling network, the basic principle, adjustment model, basic equation and its solution, and the composition of the solution of equations, adjustment calculation and precision evaluation, gross error elimination are introduced as well. And the use of Visual Studio6.0 programming software, using C programming language is related to program design. The measurement work in the future, can be combined with the actual adjustment adjustment calculation.Key words: adjustment model;the accuracy assessment;program design目录摘要 (I)Abstract .......................................................................................................................... I I 第一章绪论 (1)1.1研究背景及意义 (1)1.2国内外研究现状 (2)1.3本文研究的具体内容 (2)第二章条件平差数学模型 (3)2.1条件平差模型 (3)2.1.2测角网条件方程 (6)2.1.3测边网条件方程 (8)2.1.4以坐标为观测值的条件方程 (11)2.2精度评定 (13)2.3条件平差的计算步骤 (17)第三章水准网的设计 (18)3.1水准测量 (18)3.1.1水准网的基本概念 (18)3.2水准网的布设 (19)3.2.1国家水准网的布设 (19)3.2.2水准网的布设要求 (20)第四章C语言介绍 (21)4.1C语言的基本概念 (21)4.2C语言的介绍 (22)4.2.1C语言的特点 (22)第五章程序设计 (24)5.1水准网条件平差和测角网条件平差实例 (24)5.1.1水准网条件平差 (24)5.1.2测角网条件平差 (27)5.2程序代码 (32)参考文献 (57)附录A:外文文献 (58)附录B:中文译文 (70)致谢 (76)第一章绪论1.1研究背景及意义施工测量工作是非常基本的,重要环节。
导线网平差程序设计.ppt

分层数据流图(Data Flow Diagram, DFD)的画法-3
可用下述的方法来确定加工:
• 在数据流的组成或值发生变化的地方应画 一个加工,这个加工的功能就是实现这一 变化;
• 也可根据系统的功能确定加工。
分层数据流图(Data Flow Diagram, DFD)的画法-4
确定数据流的方法可以是:
– 不带反馈环:线性顺序进行开发 – 开发前提:
• 原型系统已经通过与用户交互而得到验证,从而得到正确的规格说明 文档。
• 开发人员通过建立原型系统已经知道该做什么不该做什么。
– 维护阶段:根据维护工作的种类可能需要返回到“需求分析”、 “规格说明”、“设计”或者“编码”等不同阶段。
3 增量模型
– 渐增模型--把软件产品作为一系列的增量构件来设 计、编码、集成和测试。
• 小型软件开发的基本过程
(参照软件工程,遵循软件开发的一般规律)
需求分析 设计 编码与单元测试 综合测试
需求分析
• 导线网平差软件 设计
编码
测试与维护
软件工程简介
• 软件工程是指导计算机软件开发和维护的工程学科。采用
工程的概念、原理、技术和方法来开发与维护软件。
1. 软件工程关注于大型程序的构造 2. 软件工程的中心课题是控制复杂性 3. 软件经常变化 4. 开发软件的效率非常重要 5. 和谐地合作是开发软件的关键 6. 软件必须有效地支持它的用户 7. 在软件工程领域中是由一种文化背景的人替另一文化
ijijijij4待定点点位误差yy5误差椭圆元素计算yyxxxyxyxxxyxx长半径方位角长半径短半径71数据流图导线网平差系统观测数据平差结果数据测量员测量员72平差数据处理系统观测数据平差结果数据数据输入系统73数据输入数据传输观测数据表格化输入观测数据图形化输入外部文件倒入全站仪电子手簿观测文件观测手簿系统标准格式的观测数据74数据预处理系统标准格式的观测数据已知数据先验精度数据气象数据观测数据改化近似坐标概算近似坐标数据改化后的观测数据75平差处理已知数据先验精度数据近似坐标数据改化后的观测数据组成误差方程法方程组成误差方程系数与常数项未知数改正数观测值改正数协因数精度评定坐标值计算精度评定参数未知点坐标76平差成果的报表与输出报表制作网图形绘制误差椭圆绘制所有成果数据控制点成果表观测数据表精度统计表控制网图形误差椭圆图形77导线网平差系统设计总体概要设计系统的总体框架导线网平差系统78导线网平差系统设计详细设计1
课内习题

第一部分习题一、野外测量的基准面、基准线是什么?测量计算的基准面和基准线是什么?为什么外业测量、内业计算要采用不同的基准面?二、名词解释1、大地水准面2、大地体3、总地球椭球4、参考椭球5、大地坐标系三、何为垂线偏差?造成地面各点垂线偏差不等的原因有哪些?四、水准面的不平行性是由什么原因引起的?这种现象对水准测量会产生什么影响?五、名词解释1、正常位水准面2、重力异常3、重力位水准面4、理论闭合差5、正高系统6、正常高系统7、似大地水准面六、既然地面上一点的正高相对于大地水准面有唯一确定的数值,为什么在实用时不用它来表示地面点的高程而要采用正常高系统?七、假设从郑州开始分别向北沿京汉线、向东沿陇海线布设两条长度和高差相等的水准路线。
试问哪条路线的水准面不平行的改正数大?八、国家等级水准网是用什么来衡量水准测量的观测精度?如何求出它们?第二部分习题1、为什么在作水平方向观测时,规定一个测回内不得重新调焦?2、何谓光学经纬仪度盘的长周期误差和短周期误差?作业时如何减弱其误差影响?3、采用“对径重合读数法”可消除什么误差影响?4、试例举出在“方向观测法”中有哪些操作(和规定要求)是为了消除或削弱哪些误差?5、什么叫“经纬仪的三轴误差”?如何消除或削弱它们对水平角观测的影响?6、L-R=2C,该式成立的条件是什么?在方向观测中计算2C的目的是什么?7、每期控制测量作业开始前应对精密光学经纬仪进行哪些项目的检验?检验的目的和作用是什么?8、当照准方向的垂直角超过±3º时,该方向如何进行2C互差比较,为什么?9、什么叫做“垂直角指标差”?在垂直角观测时如何消除它?观测中为何要计算它?10、如何消除测微器及微动螺旋的隙动误差?第三部分习题(平面控制)1、试论证大比例尺地形测图要求四等三角网中相邻点点位误差不超过5cm的必要性。
2、请写出三、四等平面工程控制网的主要技术要求。
3、什么是“测站归心改正”?什么是“照准点归心改正”?它们分别需要用哪些元素来计算?4、归心元素有哪些?它们惯用符号和严格定义是什么?5、三角测量概算的目的是什么?6、为什么导线推算边方位角中误差与转折角个数有关,而与导线形状无关?7、在导线测量中,什么情况下边长测量误差主要引起点的纵向误差,而测角误差则主要引起点的横向误差?8、为什么导线最弱点的横向误差往往比纵向误差大?如何控制横向误差的影响?9、为什么说某一等级导线,导线总长度一定时,导线的点位中误差主要取决于导线的平均边长?10、使用下式:式中 w---附合或闭合导线的方位角闭合差。
1-11单导线条件平差计算--附合导线坐标条件方程

平差值条件方程: ALˆ A0 0
改正数条件方程: AV W 0
STEP1
表达成角度和边
长平差值的形式
STEP2
表达成角度和边
长改正数的形式
附合导线坐标条件方程
1、纵坐标附合条件方程式
xˆN 1 xC 0
STEP1
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
3
N
SN-1
SN
D
TCD
βN+1
C (N+1)
纵坐标符合条件方程式就是:xˆN 1 xC 0 横坐标符合条件方程式就是:yˆ N 1 yC 0
B点坐标的已知值 (xB , yB ) 或 (x1, y1)
C点坐标已知值
(xC , yC ) 或 (xN 1, yN 1)
C点坐标观测值
A
D
β2
β4
βN
2
4
β1 S1 S2 β3 S3
N
SN-1
SN βN+1
3
B(1)
附合导线示例图
C(N+1)
附合导线坐标条件方程
补充:具体计算时的单位选取
如果x、y 以米为单位,w、vS 以厘米为单位、vβ 以秒为单位。
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
STEP2
表达成角度和边 长改正数的形式
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
非线性从这个式子着手!!
Tˆi TAB ˆ j
i
180
第三章条件平差
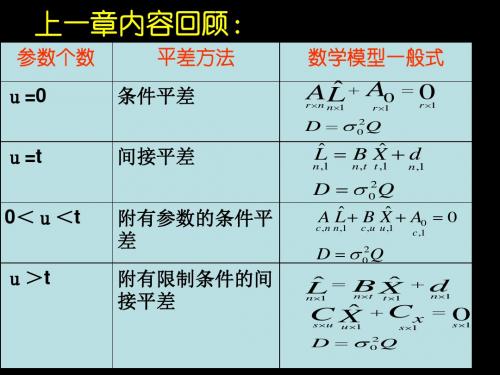
独立三角网
自由三角网
自由测角网
附合三角网(测角)
• 例:
∆ቤተ መጻሕፍቲ ባይዱ
α ∆
当n=35、n=22、n=35+22时,其条件式个数各为多 少?有哪些类型?
图形条件(内角和条件):
B
b1
a2
c1 D c2 a1 b3 c3 a3 b2 C
A
圆周条件(水平条件):
b1
a2
c1 a1 a3 c3
c2 b2 b3
5.1.06、 5.1.07
上节内容回顾:
改正数条件式 观测值的协方差阵 法方程
AV W 0
D P Q
2 0 1 2 0
r n n n
Naa K W 0 N aa AQ AT
r r n r
改正数方程
V P A K QA K
T
1 T
wr
T
• 则条件方程可写成:
ˆA 0 AL 0
• 以及改正数条件式:
W AL A0
AV W 0
这样一来,对于一个平差问题,我们能够得到 其数学模型:
AV W 0 D P Q
2 0 1 2 0
下面要解决的问题是: 由上述的数学模型来求改正数V。
不难发现,不能求得V的唯一解!!! 解决不唯一解的办法就是附加一个约束条件---“最小二乘估计” 即满足:
极条件(边长条件):
b1 a2
c1
a1 b3 c3
c2 b2 a3
极条件(边长条件)就是指由不同路线推算得到 的同一边长的长度应相等。
三角网的基本图形 1) 单三角形 2)大地四边形
3)中点多边形。
1-12单导线条件平差计算--单一闭合导线条件方程

A
三个条件方程:
1.多边形内角和闭合条件(1个)
N
SN-1
βN
SN βN+1 β1
N-1 βN-1
2.纵、横坐标增量闭合条件(2个)
β2
B(1)(N+1) S1 2
S2
β3 β4
3
S3
4
闭合导线示例图
单一闭合导线条件方程
1.多边形内角和闭合条件
由于导线网构成了多边形,其 N 个转折角的平差值应满足多边形内角和条件。
单一闭合导线条件方程
2.纵、横坐标增量闭合条件(2个)
如果x、y 以米为单位,w、vS 以厘米为单位、vβ 以秒为单位。
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
wx
0
[sin Ti
vSi ]1N
1
[(
x
N
1
xi )vi ]1N
wy
改正数条件方程式-纯量形式
A
[vi
]N 1 2
w
0
[cos Ti
vSi ]1N
1 2062.65
[(
y
N
1
yi )vi ]1N
wx
0
N
SN-1
βN
SN βN+1 β1
N-1 βN-1
[sin Ti
vSi ]1N
1 2062.65
[(
x
N
1
xi )vi ]1N
wy
0
第五章条件平差

二、法方程及改正数方程
将V T PV min的原则作用于条件方程 。
组成新函数:
V T PV-2k T AV W
式中
r 1
k k a , kb , k r 条件方程联系数
T
对新函数求导: T T 2V P 2A k ---改正数方程
dSCD ˆ f T dL SCD ˆ SCD T 2 T ˆ f D f f QL ˆL ˆ ˆL ˆ f 0 L S CD
得测边相对中误差为: 3、大地四边形测角网
2
ˆS
CD
SCD
=
ˆ 0 f T QL ˆL ˆ f
设
F ( f1 , f 2 , f m )
T T
G ( g1 , g 2 , g m ) 有
均为m维向量函数,且 f i、g i 均为x的函数, d F G dG F T dG T dF F G dx dx dx dx
注意:当N为满秩方阵时,才有 N 1唯一存在,法方程才有唯
测方向网
测角网
测角网
三角网
测边网
测边长
测边+测方向
边角网
(导线网) 测边+测角
三、三角网的布设--从高级到低级逐级布设 四、三角网平差的方法 1。严密平差 ----遵守VTPV=min原则 ; 2。近似平差
5.3 测角网条件平差
独立网(经典自由网)---只有必要起算数据d。
非独立网(附合网)---已知条件超过必要起算数据。
3 图形条件: n=12 t=2×2+4=8 r =4 1 极条件:
v2 v1 v6 v5 v11 v10 W1 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导线网条件平差计算导线网,包括单一附合导线、单一闭合导线和结点导线网,是目前较为常用的控制测量布设方式之一,其观测值有长度观测值和角度观测值。
在本节中我们主要讨论单一导线的平差计算,先讨论单一附合导线问题。
一.单一附合导线条件平差如图3-6所示,在这个导线中有四个已知点、n -1个未知点、n +1个水平角观测值和n 条边长观测值,总观测值数为2n +1。
从图中可以分析,要确定一个未知点的坐标,必须测一条导线边和一个水平角,即需要两个观测值;要确定全部n -1个未知点,则需观测n -1个导线边和n -1个水平角,即必要观测值数t = 2n -2;则多余观测个数r = (2n +1) – t = 3。
也就是说,在单一附合导线中,只有三个条件方程。
下面讨论其条件方程式及改正数条件方程式的写法。
设AB 边方位角已知值为T AB = T 0,CD 边方位角已知值为T CD 、计算值为T n+1,B 点坐标的已知值为(B x ,B y )或者(x 1, y 1),C 点坐标的已知值为(C x ,C y )、计算值为(x n +1, y n +1)。
三个条件中,有一个方位角附合条件、两个坐标附合条件。
方位角附合条件:从起始方位角推算至终边的方位角平差值应等于其已知值,即0ˆ1=-+CD n T T(3-3-1)纵横坐标附合条件:从起始点推算至终点所得到的坐标平差值应与终点的已知坐标值相等,即0ˆ1=-+C n x x(3-3-2) 0ˆ1=-+C n y y(3-3-3)1.方位角附合条件式180)1(][180)1(]ˆ[ˆ1101101⋅+±++=⋅+±+=+++n v T n T T n i n i n i βββ则(3-3-1)式可写为0180)1(][ˆ1101=-⋅+±++=-++CD n i CD n T n v T T T i ββ整理得0][11=-+T n w v i β (3-3-4)其中)180)1(][(110CD n i T T n T w -⋅+±+-=+ β2.纵坐标附合条件式 终点C 坐标平差值表示为n i B n x x x 11]ˆ[ˆ∆+=+(3-3-5)而第i 边的坐标增量为i i i T S x ˆcos ˆˆ=∆(3-3-6)式中i S i i v S S +=ˆii ij i i j i j i T v i T v i v T i T T j j j +=⋅±++=⋅±++=⋅±+=10111010][180][][180][180]ˆ[ˆββββββ其中T i 是第i 边的近似坐标方位角180][01⋅±+=i T T i j i β(3-3-7)则(3-3-6)式可表示为)]cos([)(ˆ1i i S i i T v v S x j i ++=∆β上式按泰勒级数展开,取至一次项,得ii S i i i j i v y v T x x1][cos ˆβρ''∆-⋅+∆=∆(3-3-8)其中i i i T S x cos =∆,为由观测值计算出的近似坐标增量。
(3-3-8)式代入(3-3-5)式,并按v β i 合并同类项得ni n n S i n ni i S i i B C i i j i v y y v T x v y v T x x x 11111])[(1][cos ][cos ˆββρρ-''-⋅+=⎥⎦⎤⎢⎣⎡''∆-⋅+∆+=+上式代入(3-3-2)式,整理得0])[(1][cos 111=-+-''-⋅+C n ni n nS i x x v y y v T i i βρ上式即为纵坐标条件方程式,也可写为统一形式:0])[(1][cos 111=--''-⋅+x ni n nS i w v y y v T i i βρ (3-3-9))(1C n x x x w --=+(3-3-10)3.横坐标附合条件式可以仿照纵坐标条件推导过程(请同学们自己具体推导一下),写出横坐标条件式0])[(1][sin 111=--''+⋅+y ni n nS i w v x x v T i i βρ(3-3-11) )(1C n y y y w --=+(3-3-12)为使计算方便,保证精度,在实际运算中,S 、x 、y 常以米为单位,w 、v S 、v β以厘米为单位,则(3-3-9)和(3-3-11)写为])[(65.20621][cos 111=---⋅+x ni n nS i w v y y v T i i β(3-3-13)])[(65.20621][sin 111=--+⋅+y ni n nS i w v x x v T i i β (3-3-14)综上所述,单一附合导线的平差计算的基本程序是:(1)计算各边近似方位角T i 和各点的近似坐标增量值Δx i 、Δy i ;(2)参照(3-3-4)写出方位角条件式,参照(3-3-9)、(3-3-10)、(3-3-11)、(3-3-12)或者(3-3-13)、(3-3-14)写出纵横坐标条件方程式;(3)按照条件平差计算的一般程序,计算最或是值并进行精度评定。
二.单一闭合导线条件平差单一闭合导线是单一附合导线的特殊情况,只要将图3-6中的B 和C 、A 和D 分别重合,就可得到图3-7所示的闭合导线。
图中有一个已知点和n -1个待定点,观测了n 个转折角和n +1条导线边。
为了定向,还观测了一个连接角β1。
不难分析,闭合导线中也只有三个多余观测值,产生三个条件式。
由于没有多余起算数据,因此没有附合条件,只有闭合条件,这一点是与单一附合导线不同的。
1.多边形内角和闭合条件由于导线网构成了多边形,其n +1个转折角的平差值应满足多边形内角和条件0180)2(]ˆ[12=⋅--+ n n i β (3-3-15)写成转折角改正数条件方程形式0][12=-+ββw v n i (3-3-16)其中180)2(][12⋅---=+n w n i ββ(3-3-17)2.坐标增量闭合条件从B 点开始,依次计算每一条边的纵横坐标增量的平差值,其总和应分别满足如下关系:0]ˆ[1=∆ni x (3-3-18) 0]ˆ[1=∆n i y(3-3-19)参照单一附合导线纵横坐标附合条件推导方法,可以得出坐标闭合条件的改正数条件方程式:0])[(1][cos 1111=--''-⋅++x ni i n n i S i w v y y v T βρ (3-3-20) 0])[(1][sin 1111=--''+⋅++y ni i n n i S i w v x x v T βρ(3-3-21) )(1B n x x x w --=+(3-3-22))(1B n y y y w --=+(3-3-23)如果S 、x 、y 以米为单位,w 、v S 、v β以厘米为单位,则(3-3-20)和(3-3-21)两式可写为:])[(65.20621][cos 111=---⋅+x ni n nS i w v y y v T i i β(3-3-24)])[(65.20621][sin 111=--+⋅+y ni n nS i w v x x v T i i β (3-3-25)三.边角权的确定及单位权中误差导线网中,既有角度又有边长,两者的量纲不同,观测精度一般情况下也不相等。
在依据最小二乘法进行平差时,应合理地确定边角权之间的关系。
为统一确定角度和边长观测值的权,可以采用以下方法。
取角度观测值的权及中误差为:p β、βσˆ;取边长观测值的权及中误差为:p S 、s σˆ;取常数0ˆσ,则角度及边长观测值的权为 220ˆˆββσσ=p , 220ˆˆS S p σσ=一般情况下,可以认为同一导线网中测角精度相等,但是由于导线边长变化较大使得测边精度不等。
可以取βσσˆˆ0=,则有1=βp , 22ˆˆS S p σσβ= (3-3-26)式中βσˆ以秒为单位,p β无量纲。
在实际计算边长的权时,为使边长观测值的权与角度观测值的权相差不至于过大,应合理选取测边中误差的单位,如果s σˆ的单位取为厘米,则p S 的量纲为秒2/厘米2;而在平差计算中,s σˆ的单位与改正数v S的单位要一致,均以厘米为单位。
按此方法确定的权,在平差之后还应进行统计假设检验。
检验通过后才能说明其合理性,否则,应作修正再进行平差和统计假设检验。
由于导线网中,既有角度又有边长,单位权中误差应按下式计算:r v v p v v p r pvv S S S ][][][ˆ0βββσ+±=±= (3-3-27)如前所述,由于在计算边角权时,通常取测角中误差作为单位权中误差(即m 0 = m β),所以在按(3-3-27)式算出的单位权中误差的同时,实际上也就计算出了测角中误差。
测边中误差可按下式计算:iiS S p 1ˆˆ0σσ= (3-3-28)四.例题如图3-8所示,为一四等附合导线,测角中误差βσˆ= ±2.5″,测边所用测距仪的标称精度公式s σˆ= 5mm+5ppm ·D k m 。
已知数据和观测值见表3-2。
试按条件平差法对此导线进行平差,并评定2号点的点位精度。
表3-2解:未知导线点个数n – 1 = 3,导线边数n = 4,观测角个数n + 1 = 5 近似计算导线边长、方位角和各导线点坐标,列于表3-2中表3-3(1)组成改正数条件方程及第3点平差后坐标函数式 改正数条件方程闭合差项:)(51CD T T w --== 3.9″ )(42C x x w --== -1.6 c m )(43C y y w --== 1.7 c m改正数条件方程0][151=-w v i β])[(65.20621][cos 241541=---⋅w v y y v T i i i S i β 0])[(65.20621][sin 341541=--+⋅w v x x v T i i i S i β即v β1 + v β2 + v β3 + v β4 + v β5 – 3.9 = 00.3868v S 1 - 0.7857v S 2 - 0.0499v S 3 – 0.9959v S 4 –1.8479v β1 –1.1887v β2- 0.7614v β3 + 0.0857v β4 + 1.6 = 00.9221v S 1 +0.6186v S 2 + 0.9988v S 3 - 0.0906v S 4 – 1.2502v β1 –1.5267v β2– 0.9840v β3 – 0.9417v β4 – 1.7 = 0⎪⎪⎪⎭⎫⎝⎛-----------=9417.09840.05267.12502.10906.09988.06186.09221.00857.07614.01887.18479.19959.00499.07857.03868.011111A W= [ 3.9 -1.6 1.7 ]T第3点平差后坐标函数式221112113ˆcos ˆˆcos ˆˆˆˆT s T s x x x x x ++=∆+∆+=221112113ˆsin ˆˆsin ˆˆˆˆT s T s y y y y y ++=∆+∆+=全微分得213213]ˆ)[(1]ˆˆ[cos ˆi i i i d y y s d T x d βρ-''+=213213]ˆ)[(1]ˆˆ[sin ˆi i i i d x x s d T y d βρ-''+=f x 3 = [ 0.3868 –0.7857 0 0 1.0865 0.4273 0 0 0 ]T f y 3 = [ 0.9221 0.6186 0 0 -0.2662 -0.5427 0 0 0 ]T(2)确定边角观测值的权设单位权中误差"5.2ˆˆ0±==χσσ;根据提供的标称精度公式D σˆ= 5 mm + 5ppm•D km 计算测边中误差 根据(3-3-26)式,测角观测值的权为 P β = 1;为不使测边观测值的权与测角观测值的权相差过大,在计算测边观测值权时,取测边中误差和边长改正值的单位均为厘米(cm )。
