苏科版2020年秋八年级上第十周周日培优练习(有答案)
2019—2020学年上苏科版初二数学第10周周练试卷

第9题图C A 0 B 初二数学第10周周练班级_____姓名________一、选择题(每小题3分,共30分)1.下列图形中,轴对称图形的个数为 ()A .1个B .2 个C .3个D .4个2.要使二次根式x -3有意义,则x 的取值范围是 ( ) A .x ≠3 B .x >3 C .x <3 D .x ≥3 3.在实数: 3.14159、364、1.010010001…… 、π、722中,无理数有 ( )A .1个B .2个C .3个D .4个4.下列各组数中,不能作为直角三角形三边长度的是( )A .2、3、4B .3、4、5C .6、8、10D .25、24、75.下列条件中,能判定两个直角三角形全等的是 ( )A .斜边相等B .面积相等C .两锐角对应相等D .两直角边对应相等 6.将23 700精确到千位并用科学记数法表示为 ( )A .2.37×104B .2.4×104C .23.7×103D .24×1037.如图,数轴上表示1,2的对应点分别为A 、B ,点B 关于点A 的对称点为C ,则点C 表示的实数为 ( ) A .2-1 B .1-2 C .2-2 D .2-2 8.化简A . D .( ) 9.如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿直线BE 折叠后得到△GBE ,延长BG 交CD 于点F .若AB =6,BC =46,则DF 的长为 () A .2 B .4 C .6D .3210.如图,∠MON =90°,已知△ABC 中,AC =BC =13,AB =10,△ABC 的顶点A 、B 分别在边OM 、ON 上,当点B 在边ON 上 运动时,A 随之在OM 上运动,△ABC 的形状始终保持不变, 在运动的过程中,点C 到点O 的最小距离为( ) A .5 B .6C .7 D .26二、填空题(本大题共8小题,每空2分,共24分.) 11. 的平方根是__________,-27的立方根是_________ 12.一个汽车牌照号码在水中的倒影为,则该车牌照号码为13.已知一个直角三角形的两条直角边分别为6和8,则它斜边上的中线的长为_______. 14.已知一个等腰三角形的顶角为100°,则它的底角为___________.15.等腰三角形的周长为16,其中一边为4,则另两边的长分别为______________ 16.计算:=_________,756=_______,21=_______,=________ 17.x x 44-=-成立的条件是_____________2731⨯ab a 1832⋅B CAOM N第10题图18.设2+3的整数部分用a 表示,小数部分用b 表示,4-3的整数部分用c 表示,小数部分用d 表示,则acdb +的值为____________ 三、解答题19.(每小题3分,共12分)(1)计算:9-(5-π)0+⎝⎛⎭⎫15-1(2)已知3x 2-12=0,求x 的值.(3)在实数范围内分解因式:①32242x x x -+;②2315a -.20.(5分)根据下面的运算程序,回答问题:①若输入x=-7,请计算输出的结果y 的值.②若输入一个正数x 时,输出y 的值是12,请问输入的x 的值是多少?21.(4分)如图,已知点B 、F 、C 、E 在一条直线上,BF =CE ,AB =DE ∠B =∠E .求证:AC//DF . D22.(6分)如图,在6×6的网格中(每个小正方形的边长为1), △ABC 的三个顶点都在格点上,且直线m 、n 互相垂直. (1)作△ABC 关于直线m 的对称图形△A ′B ′C ′; (2)在直线n 上存在一点P ,使△BCP 的周长最小, ①请在直线n 上作出点P ;②△BCP 的周长的最小值为__________.23.(4分)已知a 、b 为一个直角三角形的两条边长,并满足:b =2a -3+3-a +5,求这个三角形的周长.24.(4分)如图,长方体的底面是边长为1cm 的正方形,高为3cm . (1)如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B , 计算所用细线最短需要cm ?(2)如果从点A 开始经过4个侧面缠绕3圈到达点B ,那么所用细线最短需要 cm .(直接填空)25.(5分)如图,△ACB 与△ECD 都是等腰直角三角形,∠ACB =∠ECD =90º,点D 为AB 边上的一点, (1)求证:△ACE ≌△BCD ;(2分)(2)若AD =5,BD =12,求DE 的长.(3分) nmABC26.(6分)如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E(1)求证:DE∥BC;(2分)(2)若AE=6,AD=10,动点P以2cm/s的速度从B点出发沿BC向终点C运动,设运动时间为ts,是否存在这样的t值,使△DEP为等腰三角形,若存在,请求出所有t的值.若不存在,请说明理由。
苏科版八年级数学上册周末辅导练习.docx

姓名1、下列各式从左到右的变形不正确的是( ) A.y y 3232-=- B xy x y 66=-- C.y x y x 4343-=- D.y x y x 3535-=-- 2、下列各式中,正确的是:A .22b b a a =B .22a b a b a b+=++ C .22y y x y x y =++ D .11x y x y =--+- 3、当a 为任何实数时,下列分式中一定有意义的一个是( ) A.21a a + B.11+a C.112++a a D.112++a a 4、(2012贵州省毕节市)分式方程1412112-=+--x x x 的解是( ) A.0=x B.1-=x C.1±=x D.无解5、若分式方程231x x -=1m x -有增根,则m 的值为( ) A .1 B .-1 C .3 D .-36、、已知621153222-+-=-++x x x x B x A ,则A 、B 的值分别是( ) A. A=5,B=﹣11 B. A=3,B=﹣1 C. A=﹣1,B=3 D. A=﹣5,B=117、(2012四川内江)甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x 千米/小时,依题意列方程正确的是( )A .30x =4015x - B .3015x -=40x C .30x =4015x + D .3015x +=40x 8、为了绿化荒山,某村计划在荒山上种植1200棵树,原计划每天种x 棵,由于邻村的支援,每天比原计划多种了40棵,结果提前5天完成任务,则可以列出方程为( )A .401200+x -x 1200=5B .x 1200- 401200+x =5C .401200-x -x 1200 =5D .x 1200-401200-x =5 9已知关于x 的不等式组⎩⎨⎧≥01,25>---a x x 无解,则a 的取值范围是________. 10、若 a 2=b 3 ,则b b a +的值为 ; 若234z y x ==,则=+-xz y x 3_ ; 11、已知:m-m 1=3,则m 2+21m= , m+m 1= 。
苏科版物理八年级上册 全册全套试卷(培优篇)(Word版 含解析)
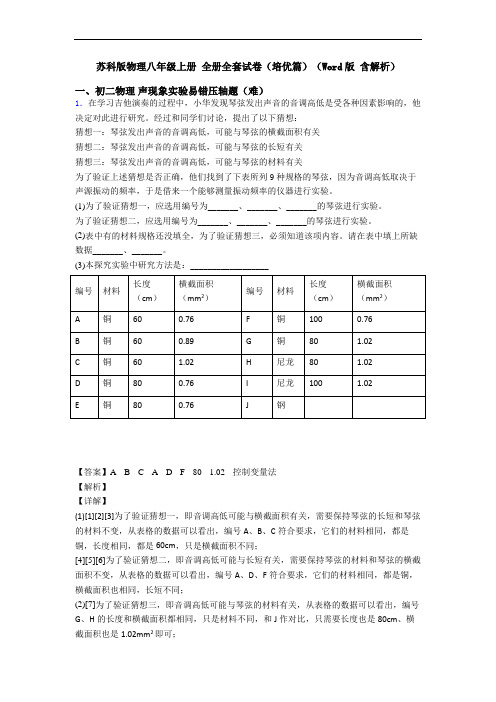
苏科版物理八年级上册全册全套试卷(培优篇)(Word版含解析)一、初二物理声现象实验易错压轴题(难)1.在学习吉他演奏的过程中,小华发现琴弦发出声音的音调高低是受各种因素影响的,他决定对此进行研究。
经过和同学们讨论,提出了以下猜想:猜想一:琴弦发出声音的音调高低,可能与琴弦的横截面积有关猜想二:琴弦发出声音的音调高低,可能与琴弦的长短有关猜想三:琴弦发出声音的音调高低,可能与琴弦的材料有关为了验证上述猜想是否正确,他们找到了下表所列9种规格的琴弦,因为音调高低取决于声源振动的频率,于是借来一个能够测量振动频率的仪器进行实验。
(1)为了验证猜想一,应选用编号为_______、_______、_______的琴弦进行实验。
为了验证猜想二,应选用编号为_______、_______、_______的琴弦进行实验。
(2)表中有的材料规格还没填全,为了验证猜想三,必须知道该项内容。
请在表中填上所缺数据_______、_______。
(3)本探究实验中研究方法是:__________________【答案】A B C A D F80 1.02控制变量法【解析】【详解】(1)[1][2][3]为了验证猜想一,即音调高低可能与横截面积有关,需要保持琴弦的长短和琴弦的材料不变,从表格的数据可以看出,编号A、B、C符合要求,它们的材料相同,都是铜,长度相同,都是60cm,只是横截面积不同;[4][5][6]为了验证猜想二,即音调高低可能与长短有关,需要保持琴弦的材料和琴弦的横截面积不变,从表格的数据可以看出,编号A、D、F符合要求,它们的材料相同,都是铜,横截面积也相同,长短不同;(2)[7]为了验证猜想三,即音调高低可能与琴弦的材料有关,从表格的数据可以看出,编号G、H的长度和横截面积都相同,只是材料不同,和J作对比,只需要长度也是80cm、横截面积也是1.02mm2即可;(3)[8]本探究实验过程中,三个变量,保持其中两个量不变,对比第三个量的变化与音调高低的关系,这是用到了控制变量法。
2019-2020年八年级数学上学期周练试题苏科版

2019-2020年八年级数学上学期周练试题苏科版一、选择题(每题2分,共16分)1、下列四组线段中,能组成直角三角形的是()A.a=1,b=2,c=3 B.a=2,b=3,c=4 C.a=2,b=4,c=5 D.a=3,b=4,c=5 2、如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则BE等于()A.2 B. C. D.3、如图,所有三角形都是直角三角形,所有四边形都是正方形,已知S1=4,S2=9,S3=8,S4=10,则S=()A.25 B.31 C.32 D.404、如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为()A.5 B.6 C.8 D.10第2题图第3题图第4题图5、已知x、y为正数,且|x2﹣4|+(y2﹣3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为()A.25 B.7 C.15 D.56、如图,每个小正方形的边长为1,若A,B,C是小正方形的顶点,则∠ABC的度数为 ( ) A.90° B.60° C.45° D.30°BA6cm3cm1cm第6题图第7题图第8题图7.如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC 能作出()A.2个B.3个C.4个D.6个8、如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是()A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定二、填空题(每空3分,共24分)9、一个直角三角形的两条直角边长分别为6cm、8cm,则斜边上的中线为 cm10、直角三角形两边长为3和5,则第三边的平方为11、一座垂直于两岸的桥长12米,一艘小船自桥北头出发,向正南方向驶去,因水流原因,到达南岸后,发现已偏离桥南头9米,则小船实际行驶了米.12、若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 cm2.13、如图,在高3米,坡面线段距离AB为5米的楼梯表面铺地毯,则地毯长度至少需米.14、如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于第13题图第14题图第15题图第16题图15、如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需__________cm.16、如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为.三、解答题(17-21每题6分,22-24每题10分)17、如图,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P.交AC 于点Q.试判断△APQ的形状,并证明你的结论.18、如图所示的一块地,AD=3m,CD=4m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.19、一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?20、小东拿着一根长竹竿进一个宽为3米的门,他先横着拿,进不去,又竖起来拿,结果竿比门高1米,当他把竿斜着时,两端刚好顶着门的对角,问:竿长多少米?21、如图,已知AB=12,AB⊥BC,垂足为点B,AB⊥AD,垂足为点A,AD=5,BC=10,点E是CD的中点,求AE的长.DCBAEFA B22、(4+6)折叠矩形ABCD 的一边AD,点D 落在BC 边上的点F 处,已知AB=8CM,BC=10CM, 求 :(1)求CF 的长 (2)求EC 的长23.(5+5)如图,在Rt △ABC 中,∠ACB=90°,E 为AC 上一点,且AE=BC , 过点A 作AD ⊥CA ,垂足为A ,且AD=AC ,AB 、DE 交于点F. (1)判断线段AB 与DE 的数量关系和位置关系,并说明理由;(2)连接BD 、BE ,若设BC=a ,AC=b ,AB=c ,请利用四边形ADBE 的面积证明勾股定理.24.(4+6)如图,在Rt △ABC 中,∠ACB=90°,BC=30cm ,AC=40cm ,点D 在线段AB 上从点B 出发,以2cm/s 的速度向终点A运动,设点D 的运动时间为t0.(1)AB= cm ,AB 边上的高为 cm ;(2)点D 在运动过程中,当△BCD 为等腰三角形时,求t 的值.。
苏科版物理八年级上册 全册全套试卷(培优篇)(Word版 含解析)

苏科版物理八年级上册全册全套试卷(培优篇)(Word版含解析)一、初二物理声现象实验易错压轴题(难)1.探究响度与什么因素有关器材:音叉,橡皮槌,铁架台,硬泡沫塑料小球,细线等.操作:(1)如图所示用细线栓在硬泡沫塑料小球,悬挂在铁架台上,小球的作用是_______________________;(2)用橡皮槌轻轻敲击音叉使它振动后,发出一个较小的声音.让音叉一臂的外侧靠近并接触小球(如图),可以看到小球被音叉弹开一个__________(填“较大”或“较小”)的角度;(3)以橡皮槌用力敲击音叉,可听到较响的声音,且让音叉一臂的外侧接触小球,可看到小球被音叉弹开一个________(填“较大”或“较小”)的角度.说明:声源发出声音的响度与_________有关.除此之外响度还与_________有关.(4)如果在真空中做这个实验,小球________(选“能”或“不能”)弹开.【答案】将微小的振动放大,便于观察较小较大振幅距离发声体的远近能【解析】【分析】【详解】(1)因为音叉的振动我们看不到,把小球悬挂在铁架台上是为了把音叉的振动传给小球,用小球可以放大音叉的振动,所以小球的作用是将微小的振动放大,便于观察;(2)当轻轻敲击音叉时因为音叉振动幅度小,所以发出较小的声音,振动的音叉接触小球会把小球弹起较小的角度;(3)当用力敲击音叉发出较响的声音,音叉振动剧烈,接触小球会把小球弹起更大的角度,这说明响度与振幅有关,响度的大小还与距离发声体的远近有关;(4)如果在真空中做这个实验,音叉能振动,小球也能被弹开,但听不到声音.2.某兴趣小组计划探究“铝棒的发声”。
同学们使用一根表面光滑的实心铝棒,一只手捏住铝棒的中间部位,另一只手的拇指和食指粘少许松香粉,在铝棒表面由手捏部位向外端摩擦,可以听见铝棒发出声音,而且发现在不同情况下铝棒发声的频率是不同的,为了探究铝棒发声频率的影响因素,该兴趣小组找到不同规格的铝棒、虚拟示波器等器材进行探究,实验前同学们提出了以下猜想:猜想A:铝棒发声的频率可能和铝棒的横截面积有关猜想B:铝棒发声的频率可能和铝棒的长度有关猜想C:铝棒发声的频率可能和手捏铝棒的部位有关为了验证猜想A,同学们选择4根铝棒,每次均捏住铝棒的中间部位,由手捏部位向外端摩擦,实验所得的数据记录于下面的表格中,在2%的误差允许范围内(频率相差在70Hz 以内)的测量值可以认为是相等的。
苏科版物理八年级上册初二上第10周周练.docx

初中物理学习材料唐玲出品 2014—2015学年度第一学期初二年级物理学科第十周周练命题范围:苏科版八年级上册第三章第一节-第五节命题人:丛扬 审核人:黄勇 分值: 100分;建议时间:45分钟班级: 姓名: 学号: 成绩:一.选择题(每空2分,共 40分)1.下列现象中不能说明光的直线传播的是 ( )A .日食B .小孔成像C .影子D .先闪电后打雷2.这本书是白纸上印有黑字,每个都看得特别清楚。
我们之所以能看清楚这些字的主要原因是 ( )A 、白纸和黑字分别发出了不同颜色的光进人眼睛B 、白光照到书上,白纸和黑字分别反射出白光和黑光进人眼睛C 、白光照到书上,白纸反射出白光进入眼睛,而黑字不反射光D 、黑字比白纸反射光的本领强3.下列说法不正确的是 ( )A 、太阳能汽车,将光能转化为动能B 、红外线具有热效应C 、紫外线最显著的性质是它能使荧光物质发光D 、紫外线易穿过臭氧层4.当太阳、水星、地球运行到一条直线上时,在地球上可以观察到太阳上有一个小黑斑在缓慢移动,这种现象称为“水星凌日”,是难得的天文奇观下列关于该现象的说法中正确的是 ( )A 、小黑斑是水星在太阳上形成的影子B 、小黑斑是由于水星挡住了太阳射向地球的一部分光而形成的C 、小黑斑是水星在太阳上形成的像D 、小黑斑是地球在太阳上形成的像5.关于小孔成像,正确的是 ( )A 、小孔成像实验中,小孔越大成像越清楚B 、小孔成像实验中,小孔越小像越亮C 、小孔成像实验中,小孔一定要是圆的D 、小孔成的像,一定是倒立的6.下列关于光现象的说法正确的是 ( )A 、光发生漫反射时,不遵守光的反射定律B 、光从空气射入水中,传播速度不变C 、月食是因为光的反射而形成的D 、平面镜可以成像,也可以改变光的传播路径7.如图所示,入射光线与平面镜成30°角,则: ( )A .入射角是30°B .反射光线与镜面的夹角是60°C .反射角是60°D .入射角增大50°,反射角增大10°8.生物学研究表明,绿色植物的生长需要光;而物理学研究表明,不透明物体的颜色是由它反射的色光决定的由此可以初步推测,不利于绿色植物生长的光是( ) 实际时间: 家长签字:A.红光B.黄光C.绿光D.紫光9.小明用如图所示的实验装置探究反射光线与入射光线是否在同一平面内,应进行的操作是A.沿ON向后转动板A B.沿ON向后转动板BC.改变入射光线与ON的夹角 D.改变反射光线与ON的夹角10.如图所示,在“探究平面镜成像特点”的试验中,下列说法正确得是()A.为了便于观察,该实验最好在较黑暗的环境中进行B.如果将蜡烛A向玻璃板靠近,像的大小会变大C.移去后面的蜡烛B,并在原位置上放一光屏,发现在光屏上能成正立的像D.保持A、B两支蜡烛的位置不变,多次改变玻璃板的位置,发现B始终能与A的像重合11.如从平面镜内看到的手表指针的位置。
苏科版八年级物理上册 全册全套试卷(培优篇)(Word版 含解析)
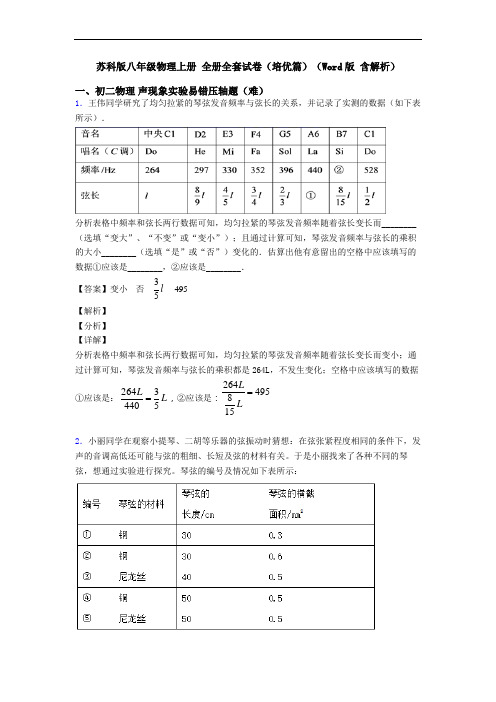
苏科版八年级物理上册全册全套试卷(培优篇)(Word版含解析)一、初二物理声现象实验易错压轴题(难)1.王伟同学研究了均匀拉紧的琴弦发音频率与弦长的关系,并记录了实测的数据(如下表所示).分析表格中频率和弦长两行数据可知,均匀拉紧的琴弦发音频率随着弦长变长而________(选填“变大”、“不变”或“变小”);且通过计算可知,琴弦发音频率与弦长的乘积的大小________(选填“是”或“否”)变化的.估算出他有意留出的空格中应该填写的数据①应该是________,②应该是________.【答案】变小否35l495【解析】【分析】【详解】分析表格中频率和弦长两行数据可知,均匀拉紧的琴弦发音频率随着弦长变长而变小;通过计算可知,琴弦发音频率与弦长的乘积都是264L,不发生变化;空格中应该填写的数据①应该是:26434405LL=,②应该是:264495815LL=2.小丽同学在观察小提琴、二胡等乐器的弦振动时猜想:在弦张紧程度相同的条件下,发声的音调高低还可能与弦的粗细、长短及弦的材料有关。
于是小丽找来了各种不同的琴弦,想通过实验进行探究。
琴弦的编号及情况如下表所示:(1)如果想探究发声时音调与弦的材料的关系,小丽应选择表中编号为________的琴弦。
(2)如果想探究发声时音调与弦的粗细的关系,小丽应选用表中编号为________的琴弦。
(3)通过查阅资料,小丽知道了琴弦的振动频率与琴弦长度的关系如图11所示。
如果小丽的实验无误,则可确定的是编号为________的琴弦一定比编号为________的琴弦振动时音调高。
【答案】④⑤①②③⑤【解析】【详解】(1)由表中数据可知,实验编号为④、⑤的琴弦材料,琴弦的粗细、长度相同而材料不同,因此可用来探究:琴弦发声的音调与弦的材料的关系。
(2)由表中数据可知,实验编号为①、②的琴弦材料,琴弦的材料、长度相同而横截面积不同,因此可用来探究:琴弦发声的音调与弦的粗细的关系。
苏科版2020年秋八年级上第十周周日培优练习(有答案)

2020八上苏科版第十周周日培优练习班级:___________姓名:___________得分:___________一、选择题1.在四边形ABCD中,AD//BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF//CD,AF⊥CE于F.连接DE交对角线AC于H.下列结论:①△ACD≌△ACE;②AC垂直平分ED;③CE=2BF;④CE平分∠ACB.其中结论正确的是()A. ①②B. ①③④C. ②③④D. ①②③④2.如图,在△ABC中,BD、BE分别是△ABC的高和角平分线,点F在CA的延长线上,FH⊥BE,分别交BD、BC于点G和点H。
下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC−∠C;④∠BGH=∠ABE+∠C,其中正确的结论有:()A. ①②③B. ①③④C. ①②④D. ①②③④3.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD交于点G.下列结论①DE=DF;②AE=AF;③∠EAF+∠EDF=180°;④AD垂直平分EF;⑤点G一定是△ABC的重心.其中结论正确的个数是A. 1 B. 2C. 3 D. 44.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A. 4B. 5C. 6D. 75.已知三角形三个内角的度数都是质数,则这三个内角中必定有一个内角等于()A. 2度B. 3度C. 5度D. 7度6.如图,在等腰直角△ABC中,∠ACB=90∘,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90∘,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有()A. ①④B. ②③C. ①②③D. ①②③④7.如图,▵ABC中,∠BAC=90∘,AD⊥BC,BE平分∠ABC交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有()A. 1个B. 2个C. 3个D. 4个8.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线CA2是∠A1CD的角平分线,BA3是A2BD∠的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为()A. α2013B. α22013C. α2012D. α22012二、填空题9.边长相等的等边三角形ABC和等边三角形DEF如图所示摆放,重叠部分的周长为6,等边三角形ABC的边长为______ .10.如图,正方形ABCD的边长为4,E为AB上一点,且AE=3,F为BC边上的一个动点,连接EF,以EF为边向左侧作等腰直角三角形FEG,EG=EF,∠GEF=90°,连接AG,则AG的最小值为____ ________.11.如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是______.12.在△ABC中,∠A=50°,∠B=30°,点D在边AB上,连接CD,若AC=AD,则∠BCD的大小是__________________.13.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为______s.14.等腰三角形周长为19cm,若有一边长为9cm,则等腰三角形其他两边长分别为______三、解答题15.(本题满分5分)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.(1)请画出平移后的△DEF.(2)若连接AD、CF,则这两条线段之间的关系是______.(3)画出△ABC的BC边上的高AM。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020八上苏科版第十周周日培优练习班级:___________姓名:___________得分:___________一、选择题1.在四边形ABCD中,AD//BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF//CD,AF⊥CE于F.连接DE交对角线AC于H.下列结论:①△ACD≌△ACE;②AC垂直平分ED;③CE=2BF;④CE平分∠ACB.其中结论正确的是()A. ①②B. ①③④C. ②③④D. ①②③④2.如图,在△ABC中,BD、BE分别是△ABC的高和角平分线,点F在CA的延长线上,FH⊥BE,分别交BD、BC于点G和点H。
下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC−∠C;④∠BGH=∠ABE+∠C,其中正确的结论有:()A. ①②③B. ①③④C. ①②④D. ①②③④3.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD交于点G.下列结论①DE=DF;②AE=AF;③∠EAF+∠EDF=180°;④AD垂直平分EF;⑤点G一定是△ABC的重心.其中结论正确的个数是A. 1 B. 2C. 3 D. 44.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A. 4B. 5C. 6D. 75.已知三角形三个内角的度数都是质数,则这三个内角中必定有一个内角等于()A. 2度B. 3度C. 5度D. 7度6.如图,在等腰直角△ABC中,∠ACB=90∘,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90∘,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有()A. ①④B. ②③C. ①②③D. ①②③④7.如图,▵ABC中,∠BAC=90∘,AD⊥BC,BE平分∠ABC交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有()A. 1个B. 2个C. 3个D. 4个8.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线CA2是∠A1CD的角平分线,BA3是A2BD∠的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2013为()A. α2013B. α22013C. α2012D. α22012二、填空题9.边长相等的等边三角形ABC和等边三角形DEF如图所示摆放,重叠部分的周长为6,等边三角形ABC的边长为______ .10.如图,正方形ABCD的边长为4,E为AB上一点,且AE=3,F为BC边上的一个动点,连接EF,以EF为边向左侧作等腰直角三角形FEG,EG=EF,∠GEF=90°,连接AG,则AG的最小值为____ ________.11.如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是______.12.在△ABC中,∠A=50°,∠B=30°,点D在边AB上,连接CD,若AC=AD,则∠BCD的大小是__________________.13.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为______s.14.等腰三角形周长为19cm,若有一边长为9cm,则等腰三角形其他两边长分别为______三、解答题15.(本题满分5分)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.(1)请画出平移后的△DEF.(2)若连接AD、CF,则这两条线段之间的关系是______.(3)画出△ABC的BC边上的高AM。
(4)满足三角形ACP的面积等于三角形ACB的面积的格点P有__________个(不和B重合)16.问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE≌△AFG,从而得出结论:_________.探索延伸:如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别∠BAD,上述结论是否仍然成立,并说明理由.是边BC,CD上的点,且∠EAF=12结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏东60°的A处,舰艇乙在指挥中心南偏西20°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正南方向以40海里/小时的速度前进,舰艇乙沿南偏东40°的方向以50海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.17.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=2S△ABP。
上述结论哪些正确并证明。
18.已知:四边形ABCD中,点E、F分别是CD、AB上的一点,将四边形BCEF沿EF折叠,得到四边形B′C′EF,使之与四边形ABCD在同一平面内(点B与点B′对应,点C与点C′对应),作∠FB′C′、∠EC′B′的平分线,交于点P.(1)如图,∠A+∠D=150°,若点B′、C′在四边形ABCD内,①求∠CEF+∠BFE的度数;②求∠P的度数;(2)探索∠P与∠DEC′、∠AFB′的数量关系,并说明理由.19.(1)已知如图1,在△ABC中,AB=BC,∠ABC=90°,点D在△ABC内部,点E在△ABC外部,满足BD⊥BE,且BD=BE.求证:△ABD≌△CBE.(2)已知如图2,在等边△ABC内有一点P,满足PA=5,PB=4,PC=3,求∠BPC的度数.答案和解析1.D解:∵AD//BC,∠ABC=90°,∴∠BAD=90°,∠BCA=∠CAD,∵AB=CB,,在△AEC与△ADC中,{AE=AD∠EAC=∠DACAC=AC,∴△AEC≌△ADC(SAS).∴①△ACD≌△ACE正确.∵△AEC≌△ADC,∴DC=CE.又∵AD=AE,∴AC是DE的垂直平分线.即AC垂直平分ED.∴②AC垂直平分ED正确.,∴F、A、B、C共圆,因为BC为弦,∠CFB=CAB=45°,FB//CD,所以∠FCD=45°,∠ACE=∠ACD=22.5°,又因为∠ACB=45°,所以∠FCB=22.5°=∠ACE,故④CE平分∠ACB正确;取EC的中点为O,∵∠ABC=90°,OE=OC,∴BO=CO=1CE,2∴∠OCB=∠OBC=22.5°.∵∠FOB=∠OCB+∠OBC=45°,∴∠CFB=∠FOB=45°,∴BF=OB,CE,∴BF=12即CE=2BF,故③正确.2.C解:①∵BD⊥FD,∴∠FGD+∠F=90°,∵FH⊥BE,∴∠BGH+∠DBE=90°,∵∠FGD=∠BGH,∴∠DBE=∠F,①正确;②∵BE平分∠ABC,∴∠ABE=∠CBE,∠BEF=∠CBE+∠C,∴2∠BEF=∠ABC+2∠C,∠BAF=∠ABC+∠C,∴2∠BEF=∠BAF+∠C,②正确;③∠ABD=90°−∠BAC,∠DBE=∠ABE−∠ABD=∠ABE−90°+∠BAC=∠CBD−∠DBE−90°+∠BAC,∵∠CBD=90°−∠C,∴∠DBE=∠BAC−∠C−∠DBE,由①得,∠DBE=∠F,∴2∠F=∠BAC−∠C,③错误;④∵∠AEB=∠EBC+∠C,∵∠ABE=∠CBE,∴∠AEB=∠ABE+∠C,∵BD⊥FC,FH⊥BE,∴∠FGD=∠FEB,∴∠BGH=∠ABE+∠C,④正确,正确答案为:①②④.3.D解:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,①正确,∠AED=∠AFD=90°,在△AED和△AFD中{AD=ADDE=DF,∴ΔAED≅ΔAFD,∴AE=AF,故②正确,∵DE=DF,∴AD垂直平分EF,故④正确,∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°,∴∠AED+∠AFD=180°,∴∠EAF+∠EDF=180°,故③正确,同理可得点G不一定是△ABC的重心,故⑤错误.4.B解:作出C关于直线AB的对称点C´,PC+PD=PC′+PD ≥C′D 如图则PC+PD的最小值为C′D=√C′B2+BD2=√32+(3+1)2=5,5.A解:∵三个内角的和是180°,是一个偶数,∴必有一个内角为偶数,又∵三角形三个内角的度数都是质数,∴既是偶数又是质数的只有2;∴这三个内角中必定有一个内角等于2°;6.D7.C解:∵∠BAC=90º,,∴∠C+∠ABC=90∘,∠BAD+∠ABC=90∘,∴∠BAD=∠C,故①正确;∵BE是∠ABC的平分线,∴∠ABE=∠CBE,∵∠ABE+∠AEF=90∘,∠CBE+∠BFD=90∘,∴∠AEF=∠BFD,又∵∠AFE=∠BFD(对顶角相等),∴∠AEF=∠AFE,故②正确;∵∠ABE=∠CBE,∴只有∠C=30∘时∠EBC=∠C,故③错误;∵∠AEF=∠AFE,∴AE=AF,∵AG平分∠DAC,∴AG⊥EF,故④正确.综上所述,正确的结论是①②④.8.D解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=1∠ABC,∠A1CD=1∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,∴12(∠A+∠ABC)=12∠ABC+∠A1,∴∠A1=12∠A,∵∠A1=α.同理理可得∠A2=12∠A1=12α则∠A2013=α22012.9.3解:∵△ABC和△DEF都是等边三角形,∴∠F=60°,FG=FH,FD=BC,∴△FHG是等边三角形,∴GH=FG.同理,IJ=ID,EL=KL,JK=KA,∴重叠部分的周长为:FD+BC=6,∴FD=BC=3,即等边△ABC的边长是3.10.1解:由题意可知,点F是主动点,点G是从动点,点F在线段BC上运动,点G也一定运动,将△AGE绕点E顺时针旋转90°,使EG与EF重合,得到△AGE≌△EMF,从而可知△AEM为等腰直角三角形,AE=EM=3,AG=MF,作MF⊥BC,则MF即为AG的最小值,此时,可知四边形MEBF为矩形,因为正方形ABCD的边长为4,且AE=3,所以BE=MF=1,即AG的最小值为1.11.5解:过点B作BE⊥l1于E,过点D作DF⊥l1于F,∵l1与l2的距离为1,l2与l3的距离为1,l1//l2//l3,∴DF=2,BE=1,∠DFA=∠AEB=90°,∴∠ADF+∠DAF=90°,∵四边形ABCD是正方形,∴AD=AB,∠DAB=90°,∴∠DAF+∠BAE=90°,∴∠ADF=∠BAE,在△ADF和△BAE中,{∠DFA=∠AEB ∠ADF=∠BAE AD=BA,∴△ADF≌△BAE(AAS)∴AE=DF=2,在Rt△ABE中,AB2=AE2+BE2=12+22=5,∴S正方形ABCD=5.12.35°解:∵∠A=50°,∠B=30°,∴∠ACB=180°−50°−30°=100°,∵AC=AD,∠A=50°,,∴∠BCD=∠ACB−∠ACD=100°−65°=35°,13.1或4解:∵AB=20cm,AE=6cm,BC=16cm,∴BE=14cm,BP=2tcm,PC=(16−2t)cm,当△BPE≌△CQP时,则有BE=PC,即14=16−2t,解得t=1,当△BPE≌△CPQ时,则有BP=PC,即2t=16−2t,解得t=4.14.9cm、1cm或5cm、5cm解:①当9cm为腰长时,则腰长为9cm,底边=19−9−9=1cm,因为9+1>9,所以能构成三角形;②当9cm为底边时,则腰长=(19−9)÷2=5cm,因为5+5>9,所以能构成三角形.则等腰三角形其他两边长分别为9cm、1cm或5cm、5cm.故答案为:9cm、1cm或5cm、5cm.15.解:(1)如图;(2)平行且相等;(3)如图;(4)4;解:(2)由平移的性质可得:AD与CF平行且相等,故答案为平行且相等;(4)满足三角形ACP的面积等于三角形ACB的面积的格点P有4 个,16.解:问题背景:EF=BE+FD;探索延伸:证明:如图2,将△ADF顺时针旋转得到△ABG,使得AD与AB重合,则△ADF≌△ABG,∴∠FAD=∠BAG,AF=AG,DF=GB,∵∠EAF=12∠BAD,∴∠EAF=∠EAG,在△EAG和△EAF中,{AG=AF∠GAE=∠FAEAE=AE,∴△EAG≌△EAF(SAS),∴GE=EF,∵GE=GB+BE=DF+BE,∴EF=BE+FD;结论应用:如图3,连接EF,∵∠AOB=30°+90°+20°=140°,∴∠FOE=70°=12∠AOB,又∵OA=OB,∠A+∠B=60°+120°=180°,符合探索延伸中的条件,∴结论EF=AE+FB成立.即,EF=AE+FB=2×40+2×50=180(海里).答:此时两舰艇之间的距离为180海里.解:问题背景:EF=BE+DF,证明如下:如图1,将△ABE绕点A逆时针旋转120°到△ADG的位置,易得G、D、F三点共线.∴△ABE≌△ADG,∴AE=AG,∠BAE=∠DAG,∵∠EAF=12∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD−∠EAF=∠EAF,∴∠EAF=∠GAF,在△AEF和△AGF中,{AE=AG∠EAF=∠GAF AF=AF,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF;故答案为EF=BE+DF;17.解:①②③④正确.证明:在△ABC中,∵∠ACB=90°,∴∠A+∠B=90°,又∵AD、BE分别平分∠BAC、∠ABC,∴∠BAD+∠ABE=12(∠A+∠B)=45°,∴∠APB=135°,故①正确.∴∠BPD=45°,又∵PF⊥AD,∴∠FPB=90°+45°=135°,∴∠APB=∠FPB,在△ABP和≌△FBP中,{∠APB=∠FPB BP=BP∠ABP=∠FBP,∴△ABP≌△FBP(ASA),∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.∵△ABP≌△FBP,∴∠BAP=∠BFP,PA=PF,又∵∠PAH=∠BAP,∴∠PAH=∠BFP在△APH和△FPD中,{∠APH=∠FPD=90°PA=PF∠PAH=∠BFP,∴△APH≌△FPD(ASA),∴AH=FD,又∵AB=FB,∴AB=FB=FD+BD=AH+BD.故③正确.连接HD,ED.∵△ABP≌△FBP,△APH≌△FPD,∴S△APB=S△FPB,S△APH=S△FPD,PH=PD,∵∠HPD=90°,∴∠HDP=∠DHP=45°=∠BPD,∴HD//EP,∴S△EPH=S△EPD,∵S=S△ABP+S△AEP+S△EPD+S△PBD四边形ABDE=S△ABP+(S△AEP+S△EPH)+S△PBD=S△ABP+S△APH+S△PBD=S△ABP+S△FPD+S△PBD=S△ABP+S△FBP=2S△ABP,故④正确.所以①②③④正确.18.解:(1)①根据四边形的内角和是360°,又因为∠A+∠D=150°,∴∠B+∠C=360°−150°=210°,∴∠CEF+∠BFE=360°−210°=150°;②根据翻折,可知∠EC′B′=∠C,∠FB′C′=∠B,∴∠EC′B′+∠FB′C′=∠C+∠B=210°.∵∠FB′C′、∠EC′B′的平分线,交于点P,∴∠PC′B′+∠PB′C′=1(∠EC′B′+∠FB′C′)=105°,2∴∠P=180°−105°=75°.(2)当B′,C′在AB,CD之间时,如图所示,∠DEC′=180°−∠CEF−∠C′EF=180°−2∠CEF,同理:∠AFB′=180°−2∠BFE,∴∠DEC′+∠AFB′=360°−2(∠CEF+∠BFE)=360°−2(∠EC′B′+∠FB′C′),∴∠EC′B′+∠FB′C ′=180°−12(∠DEC′+∠AFB′)∵∠P=180°−(∠PC′B′+∠PB′C′)=180°−12(∠EC′B′+∠FB′C′)=180∘−12[180∘−12(∠DEC′+∠AFB′)]=90∘+14(∠DEC′+∠AFB′),∴∠DEC′+∠AFB′=360°−4∠P;同理,当B′,C′不在AB,CD之间时,则得到:|∠DEC′−∠AFB′|=360°−4∠P.19.证明:∵∠ABC=90°,BD⊥BE,∴∠ABC=∠DBE=90°,即∠ABD+∠DBC=∠DBC+∠CBE,∴∠ABD=∠CBE,又∵AB=CB,BD=BE,∴△ABD≌△CBE(SAS);(2)证明:如图,把线段PC以点C为中心顺时针旋转60°到线段CQ处,连结AQ,由旋转知识可得:∠PCQ=60°,CP=CQ=3,∴△PCQ是等边三角形,∴CP=CQ=PQ=3.又∵△ABC是等边三角形,∴∠ACB=60°=∠PCQ,BC=AC,∴∠BCP+∠PCA=∠PCA+∠ACQ,即∠BCP=∠ACQ.在△BCP与△ACQ中{CP=CQ∠BCP=∠ACQ BC=AC∴△BCP≌△ACQ(SAS)∴BP=AQ=4,∠BPC=∠AQC.又∵PA=5,∴PB2+PC2=42+32=25=PA2.∴∠AQP=90°,又∵△PCQ是等边三角形,∴∠PQC=60°,∴∠BPC=∠AQC=∠AQP+∠PQC=90°+60°=150°,∴∠BPC=150°.。
