三角函数的定义导学案
职高第五章三角函数导学案

5.1.1任意角的概念教学目标:(1)引导学生用运动变化的观点了解角的概念的推广(2)明白“任意角”、“象限角”的概念教学重点:“任意角”、“象限角”的概念教学难点:“象限角”的判断预习案:一、复习:问题1:回忆初中我们是如何定义一个角的?______________________________________________________所学的角的范围是什么?______________________________________________________问题2:在体操、跳水中,有“转体0720”这样的动作名词,这里的“0720”,怎么刻画?______________________________________________________二、新知:1.角的概念角可以看成平面内一条______绕着它的_____从一个位置_____到另一个位置所形成的图形。
射线的端点称为角的________,射线旋转的开始位置和终止位置称为角的______和______。
2.角的分类按__________方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做_________。
如果一条射线没有作任何旋转,我们称它形成了一个_________,它的______和_______重合。
这样,我们就把角的概念推广到了_______,包括_______、________和________。
3、角的表示(1)常用字母A 、B 、C 等表示(2)用字母αβγϕθ、、、、等表示(3)当角作变量时可用字母x 表示4.象限角、轴线角(非象限角)的概念我们常在 直角坐标系 内讨论角。
为了讨论问题的方便,使角的________与__________重合,角的___________与_______________________重合。
那么,角的_________(除端点外)落在第几象限,我们就说这个角是__________________。
注重数形结合的“任意角的三角函数的定义”导学案

注重数形结合的“任意角的三角函数的定义”导学案【关键词】数形结合法三角函数定义导学案新课堂模式下,导学案的编写是非常重要的,它是学生学习新知识,形成独立思维的导航图,是课堂顺利、有效进行的方向标。
下面笔者结合具体案例,谈谈导学案的设计。
【导学目标】从数与形上理解任意角的三角函数概念,会利用定义及图形求三角函数值的问题。
【导学过程】问题引入:现实世界中有很多周期性的现象(比如钟表的指针),所形成的角不一定是锐角,那么我们又该怎样计算它们的三角函数值呢?如求sin180°=?一、独学1.初中锐角三角函数是如何定义的?请画图说明。
2.根据你所画的图形填空:sinα=________,cosα=________,tanα=________.二、群学活动1:初中学过锐角三角函数,是以为自变量,以为函数值的函数。
能否在直角坐标系中用角的终边上点的坐标来表示锐角三角函数?我们把锐角α的顶点与原点O重合,始边与轴非负半轴重合,那么角α的终边在第一象限,在α终边上任取一点P(x,y);tanα=________=________.【小组展示1】让点P在a角的终边上移动,与点O及点P不重合,得到P’(如图2),对于确定的角a,这三个比值不会随点P在α终边上位置的改变而改变。
活动2:根据小组展示1,取OP=1,即在单位圆中(如图3),可以用直角坐标系下角α终边与单位圆交点的坐标表示锐角三角函数,sinα=________=________;cosα=________=________;tanα=________=________.活动3:锐角三角函数可以用单位圆上点的坐标表示,画出钝角,同时,另外再画任意一个角,找出角的终边与单位圆的交点,能否用单位圆上点的坐标表示?你发现了什么规律?【小组展示2】角可以推广到实数表示的任意角,那么任意角是否也能像锐角一样定义三角函数,应如何设法定义?(如图4)把任意放在直角坐标系中,那么角α的终边与单位圆交于点P(x,y),那么siα=________=________;cosα=________=________;tanα=________=________.活动4:(1)让α角的终边旋转,当a=2k?仔+?仔(k∈Z)时,a的终边横坐标x=0,所以tana无意义,除此之外对任意角a,正弦、余弦、正切都是以角为,以单位圆上点坐标或坐标比值为的函数。
任意角的三角函数导学案

课题:3.2.1 任意角的三角函数(第一课时)1. 掌握任意角的正弦、余弦、正切的定义;2. 理解任意角的三角函数不同的定义方法;3. 已知角α终边上一点,会求角α的各三角函数值.二教学重难点:重点: 任意角的正弦、余弦、正切的定义。
难点: 任意角的三角函数不同的定义方法;已知角α终边上一点,会求角α的各三角函数值.三复习回顾:复习1:(1)坐标轴上;(2)第二、四象限.复习2:锐角的三角函数如何定义在初中,我们如果要求一个锐角的三角函数值,经常把这个角放到一个直角三角形中求其比值,从而得到锐角三角函数的值。
那么,你能用直角坐标系中角的终边上的点的坐标更方便的去求一个锐角的三角函数值吗我们可以采用以下方法:如图,设锐角α的顶点与原点O重合,始边与x轴的非负半轴重合,那么它的终边在第一象限.在α的终边上任取一点(,)P a b,它与原点的距离0r>. 过P作x轴的垂线,垂足为M,则线段OM的长度为a,线段MP的长度为b.可得:xsin MP b OP r α==;cos α= = ,tan MPOMα== .四、新课学习:知识点1:三角函数的定义认真阅读教材P 11-P 12,领会下面的内容:由相似三角形的知识,对于确定的角α,这三个比值不会 随点P 在α的终边上的位置的改变而改变,因此我们 可以将点P 取在使线段OP 的长为r=1的特殊位置上, 这样就可以得到用直角坐标系内的点的坐标 表示的锐角三角函数的值为:sin MP OP α==_____;cos OM OP α==_____;tan MPOMα==___ 问题:上述锐角α的三角函数值可以用终边上一点的坐标表示. 那么,角的概念推广以后,我们应该如何得到任意角的三角函数呢 显然,我们只需在角的终边上找到一个点,使这个点到原点的距离为1,然后就可以类似锐角三角函数求值的方法得到该角的三角函数值.注:单位圆:在直角坐标系中,我们称以原点O 为圆心,以单位长度为半径的圆为单位圆.上述的点P 就是α的终边与单位圆的交点,这样锐角三角函数就可以用单位圆上的点的坐标表示。
高一数学必修第一册2019(A版)_5.2.1_三角函数的概念_导学案(2)

【新教材】5.2.1 三角函数的概念(人教A版)1.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义.2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号.3.掌握公式一并会应用.1.数学抽象:理解任意角三角函数的定义;2.逻辑推理:利用诱导公式一求三角函数值;3.直观想象:任意角三角函数在各象限的符号;4.数学运算:诱导公式一的运用.重点:①借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义;②掌握任意角三角函数(正弦、余弦、正切)在各象限的符号.难点:理解任意角三角函数(正弦、余弦、正切)的定义.一、预习导入阅读课本177-180页,填写。
1.单位圆在直角坐标系中,我们称以原点O为圆心,以__________为半径的圆为单位圆.2.任意角的三角函数的定义(1)条件在平面直角坐标系中,设α是一个任意角,它的终边与__________交于点P(x,y),那么:图121(2)结论①y叫做α的__________,记作__________,即sin α=y;②x叫做α的__________,记作__________,即cos α=x;③yx叫做α的__________,记作__________,即tan α=yx(x≠0).(3)总结正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数.思考:若已知α的终边上任意一点P的坐标是(x,y),则其三角函数定义为?在平面直角坐标系中,设α的终边上任意一点P的坐标是(x,y),它与原点O的距离是r(r=x2+y2>0).三角函数定义名称sinα__________ 正弦cosα__________ 余弦tanα__________ 正切正弦函数、余弦函数、正切函数统称三角函数.3.正弦、余弦、正切函数在弧度制下的定义域三角函数定义域sin α__________cos α__________tan α__________4.正弦、余弦、正切函数值在各象限内的符号(1)图示:图122(2)口诀:“一全正,二__________,三__________,四__________”.5.诱导公式一1.若角α的终边经过点P (2,3),则有( )A .sin α=21313B .cos α=132C .sin α=31313D .tan α=232.已知sin α>0,cos α<0,则角α是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角3.sin 253π= .4.角α终边与单位圆相交于点M ⎝⎛⎭⎫32,12,则cos α+sin α的值为 .题型一 三角函数的定义及应用例1 在平面直角坐标系中,角α的终边在直线y =-2x 上,求sin α,cos α,tan α的值. 跟踪训练一1.已知角θ终边上一点P (x,3)(x ≠0),且cos θ=1010x ,求sin θ,tan θ. 题型二 三角函数值的符号例2 (1)若α是第四象限角,则点P (cos α,tan α)在第________象限.(2)判断下列各式的符号: ①sin 183°;②tan 7π4;③cos 5. 跟踪训练二1.确定下列式子的符号:(1) tan 108°·cos 305°;(2)cos 5π6·tan11π6sin2π3;(3)tan 120°·sin 269°.题型三 诱导公式一的应用例3 求值:(1)tan 405°-sin 450°+cos 750°;(2)sin 7π3cos ⎝⎛⎭⎫-23π6+tan ⎝⎛⎭⎫-15π4cos 13π3.跟踪训练三 1.化简下列各式:(1)a 2sin(-1 350°)+b 2tan 405°-2ab cos(-1 080°); (2)sin ⎝⎛⎭⎫-11π6+cos 125π·tan 4π.1.有下列说法:①终边相同的角的同名三角函数的值相等; ②sin α是“sin”与“α”的乘积;③若sin α>0,则α是第一、二象限的角;④若α是第二象限的角,且P (x ,y )是其终边上一点,则cos α=-. 其中正确的个数是( ) A .0 B .1 C .2 D .32.如果α的终边过点(2sin 30°,-2cos 30°),那么sin α=( )A. 12B .-12C. 32D .-323.若sin θ·cos θ>0,则θ在( )A .第一或第四象限B .第一或第三象限C .第一或第二象限D .第二或第四象限4.若cos α=-32,且角α的终边经过点P (x ,2),则P 点的横坐标x 是( )A .2B .±2C .-2D .-25.在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于x 轴对称,若sin α=51,则sin β= .6.求值:(1)sin 180°+cos 90°+tan 0°;(2)cos 25π3+tan15π4.答案小试牛刀 1.C 2.B 3.324.3+12. 自主探究例1 【答案】当α的终边在第二象限时,sin α=255,cos α=-55,tan α=-2.当α的终边在第四象限时, sin α=-255,cos α=55,tan α=-2.【解析】当α的终边在第二象限时,在α终边上取一点P (-1,2),则r =-12+22=5,所以sin α=25=255,cos α=-15=-55,tan α=2-1=-2.当α的终边在第四象限时, 在α终边上取一点P ′(1,-2), 则r =12+-22=5,所以sin α=-25=-255,cos α=15=55,tan α=-21=-2.跟踪训练一1.【答案】当x =1时,sin θ=31010,tan θ=3;当x =-1时,此时sin θ=31010,tan θ=-3.【解析】由题意知r =|OP |=x 2+9,由三角函数定义得cos θ=x r =xx 2+9.又∵cos θ=1010x ,∴x x 2+9=1010x .∵x ≠0,∴x =±1. 当x =1时,P (1,3),此时sin θ=312+32=31010,tan θ=31=3.当x =-1时,P (-1,3),此时sin θ=3-12+32=31010,tan θ=3-1=-3. 例2 【答案】(1)四; (2) ①sin 183°<0;②tan 7π4<0;③cos 5>0. 【解析】(1)∵α是第四象限角,∴cos α>0,tan α<0,∴点P (cos α,tan α)在第四象限. (2) ①∵180°<183°<270°,∴sin 183°<0; ②∵3π2<7π4<2π,∴tan 7π4<0;③∵3π2<5<2π,∴cos 5>0.跟踪训练二1.【答案】(1) tan 108°·cos 305°<0;(2) cos 5π6·tan11π6sin2π3>0;(3)tan 120°sin 269°>0.【解析】(1)∵108°是第二象限角,∴tan 108°<0.∵305°是第四象限角,∴cos 305°>0.从而tan 108°·cos 305°<0. (2)∵5π6是第二象限角,11π6是第四象限角,2π3是第二象限角,∴cos 5π6<0,tan 11π6<0,sin 2π3>0.从而cos 5π6·tan11π6sin2π3>0.(3)∵120°是第二象限角,∴tan 120°<0,∵269°是第三象限角,∴sin 269°<0.从而tan 120°sin 269°>0.例3 【答案】(1)32;(2)54. 【解析】 (1)原式=tan(360°+45°)-sin(360°+90°)+cos(2×360°+30°) =tan 45°-sin 90°+cos 30°=1-1+32=32. (2)原式=sin ⎝⎛⎭⎫2π+π3cos ⎝⎛⎭⎫-4π+π6+tan ⎝⎛⎭⎫-4π+π4·cos ⎝⎛⎭⎫4π+π3 =sin π3cos π6+tan π4cos π3=32×32+1×12=54.跟踪训练三1.【答案】(1)(a -b )2 ; (2)12.【解析】(1)原式=a 2sin(-4×360°+90°)+b 2tan(360°+45°)-2ab cos(-3×360°)=a 2sin 90°+b 2tan 45°-2ab cos 0° =a 2+b 2-2ab =(a -b )2. (2)sin ⎝⎛⎭⎫-116π+cos 125π·tan 4π =sin ⎝⎛⎭⎫-2π+π6+cos 125π·tan 0=sin π6+0=12. 当堂检测1-4. BDBD 5.−156.【答案】(1) 0;(2) 32 .【解析】 (1)sin 180°+cos 90°+tan 0°=0+0+0=0.(2) cos25π3+tan15π4=cos π3+tan π4=12+1=32.。
北师大版4.3.1三角函数的图像和性质导学案

单调
区间
奇偶性
周期性
对称性:对称区间和对称中心
2.图像变换问题--由函数 图象的基本步骤:
(1)平移变换:
(2)伸缩变换:
(3)振幅变换:
反过来, 怎样变换?
函数y=Asin(ωx+ )(A>0, )中A , 的物理意义:
【导学释疑】
1.函数 是()
A.最小正周期为 的奇函数B.最小正期为 的偶函数
3.理解正弦函数、余弦函数在[0,2π],正切函数在 上的性质(单调性、最大和最小值、图像与x轴的交点等);
4.了解函数 的实际意义,能用“五点法”画出函数的简图,知道参数A, 对函数图像变化的影响。
三、教学过程
【温故知新】
1.三角函数的两域四性:
1.函数
图象
大致
形态
x
y
O
-1
1
x
y
O
-1
1
y
x
O
定义域
C.最小正周期为 的奇函数D.最小正周期为 的偶函数
【检测反馈】
2.将函数 的图象向左平移 个单位,再向上平移1个单位,所得图象的函数解析式是( ).
A. B. C. D.
【学生小结】
谈谈学完本节课有什么收获?
教学反思
安边中学高三年级上学期数学学科导学稿执笔人:王广青总第27课时
备课组长签字:包级领导签字:学生:上课时间:2013.9
集体备课
个人空间
一、课题:4.3.1三角函数的图像和性质
二、学习目标
1.理解任意角三角函数(正弦、余弦、正切)的定义和周期,并能画出三角函数的图像;
2.了解任意角的三角函数线的含义;
初中中考总总结复习解直角三角形导学案

解直角三角形一、锐角三角函数的定义:B1. ∠ A 的正弦: sin AA 的对边________斜边 2.∠ A 的余弦:3.∠ A 的正切:cos AA 的邻边 ________斜边 sin AA 的对边 ________A 的邻边cabCA二、特别三角函数值和三角函数之间的关系1. 特其余三角函数值:30°45°60°sinA cosA tanA2. 简单三角函数之间的关系:⑴同角三角函数的关系 : ① sin 2 Acos 2 A 1② tan A sin Acos A⑵互为余角的三角函数之间的关系:① sin A cos 90A② cosA sin 90 A三、直角三角形的边角关系:1.直角三角形的边角关系⑴三边关系:勾股定理:.⑵三角关系:①∠ A+∠ B=∠ C ; ②∠ A+∠ B+∠ C=180°. ⑶边角关系:① sin Aa② cos Aba ; ; ③ tan Accb⑷面积关系: S ABC1ab1ch (h 为斜边 c 上的高)222 三角函数值的变换规律BcabCA⑴当 0 A 90 时, sin A , tan A 随角度增大而 ________. ⑵当 0A90 时, cos A 随角度增大而 ________.3. 解直角三角形的看法:.4.解直角三角形的方法与技巧⑴已知素来角边和一个锐角( a 和∠ A) .①∠ B=90° - ∠ A;② ca;③ ba也许b c 2 sin A tan B⑵已知斜边和一个锐角( c 和∠ A) .①∠ B=90° - ∠ A;② a c sin A ;③ b c cos A 也许b ⑶已知两直角边( a 和 b) .①c a 2b2;②tan A aA ;③∠B=90°-∠Ab ⑷已知斜边和一条直角边(c 和 a).①b c 2a2;②sin A aA ;③∠B=90° -∠Ac 四、解直角三角形的应用:仰角、俯角、坡度、坡角、方向角88a 2c 2a2BcabC A 解题指导【例 1】已知a3 , b a 【】b 4 b4B. 1 1 1A. C. D.33 4 4及时练习:1. 如图,乐器上的一根弦AB 80 cm,两个端点 A 、 B 固定在乐器板面上,支撑点 C 是凑近点 B 黄金切割点,支撑点 D 是凑近点 A 的黄金切割点,则 AC cm,DC cm.AD C B2.(2000?山西)请阅读下面资料,并回答所提出的问题.三角形内角均分线性质定理:三角形的内角均分线分对边所得的两条线段和这个角的两边对应成比率.已知:如图,△ABC中, AD是角均分线.求证:BD ABDC AC解析:要证BD AB BD、 DC与 AB、 AC或 BD、 AB与 DC、 AC所在三角形相似.DC,一般只要证AC现在 B、D、C在素来线上,△ ABD与△ ADC不相似,需要考虑用其余方法换比.在比率式BD ABDC AC 中, AC正是 BD、 DC、 AB 的第四比率项,所以考虑过C作 CE∥ AD,交 BA的延长线于E,从而得到BD、 DC、 AB 的第四比率项 AE,这样,证明证明:过 C 作 CE∥ DA,交 BA的延长线于 E.BD AB, 就可以转变为证AE=AC.DC AC1 ECE∥ DA? 2 3 E3 AC AE1 2CE ∥ DA BD BABA DCBDAEACAE AC DC(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)(2)在上述解析、证明过程中,主要用到了以下三种数学思想的哪一种?选出一个填在后边的括号内.[]①数形结合思想;②转变思想;③分类谈论思想.( 3)用三角形内角均分线性质定理解答问题:已知:如图,△ABC中, AD是角均分线, AB=5cm, AC=4cm,BC=7cm.求 BD的长.【例 2】以下四个三角形中,与左图中的三角形相似的是【】A.B.C.D.【例3】( 2010?衡阳)如图6,在ABCD中, AB=6,AD=9,∠ BAD的均分线交BC于点E,交DC的延长线于点F, BG⊥ AE,垂足为4 2,则CEF的周长为【】G, BG=例题 4【例4】如图,在正三角形ABC中, D, E, F 分别是BC, AC, AB上的点,DE⊥ AC,EF⊥ AB,FD⊥ BC,则△ DEF的面积与△ABC的面积之比等于.【例5】花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH= 5 米 . 若是小明的身高为 1.7 米,求路灯杆AB的高 ( 精确到0.1 米 )【例 6】如图,等腰梯形 ABCD中, AD∥ BC,AD=3, BC=7,∠ B=60°, P 为下底 BC上一点(不与 B、C 重合),过 P 点作 PE 交 DC于 E,使得∠ APE=∠ B.(1)求等腰梯形的腰长;(2)证明:△ ABP∽△ PCE;(3)在底边 BC上可否存在一点 P,使得 DE:EC=5:3?若是存在,求出 BP的长;若是不存在,请说明原由.【例 7】如图,在一个由4× 4 个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是()D A.3 : 4 ::C:2A B例题 7B CA ′【例 8】如图,△ABC与△A B C是位似图形,CA′且位似比是 1: 2,若AB=2cm,则 A B cm ,并在图中画出位似中心 O. B ′例题 8【例 9】如图 ( 十四 ) ,不等长的两对角线AC、 BD订交于O点,且将四边形ABCD分成甲、乙、丙、丁四个三角形。
三角函数线导学案

1.2.2三角函数线课前预习学案一、预习目标:了解三角函数线的基本做法.二、预习内容:1、 叫做有向线段。
2、当角的终边上一点(,)P x y 的坐标满足_______________时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。
设任意角α的顶点在原点O , 重合,终边与 相交与点P (,)x y 过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,它与角α的 交与点T .由四个图看出:当角α的终边不在坐标轴上时,有向线段,OM x MP y ==,于是有sin 1y y y MP r α====,_______ cos 1x xx OMr α====,________ tan y MP ATATx OM OAα====._________ 我们就分别称有向线段,,MP OM AT 为正弦线、余弦线、正切线。
课内探究学案一、学习目标(1)了解如何利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来;(2)掌握用单位圆中的线段表示三角函数值,从而使学生对三角函数的定义域、值域有更深的理解。
二、学习重难点重点: 三角函数线的正确应用 难点:三角函数线的正确理解.(Ⅳ)(Ⅲ)三、学习过程 (一)复习: 1.三角函数定义在直角坐标系中,设α是一个任意角,α终边上任意一点P (除了原点)的坐标为(,)x y ,它与原点的距离为(0)r r ==>,那么(1)比值_______叫做α的正弦,记作_______,即________ (2)比值_______叫做α的余弦,记作_______,即_________ (3)比值_______叫做α的正切,记作_______,即_________; 2.三角函数的定义域、值域3.三角函数的符号由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知: ①正弦值yr对于第一、二象限为_____(0,0y r >>),对于第三、四象限为____(0,0y r <>);②余弦值xr对于第一、四象限为_____(0,0x r >>),对于第二、三象限为____(0,0x r <>);③正切值yx对于第一、三象限为_______(,x y 同号),对于第二、四象限为______(,x y 异号).4.诱导公式由三角函数的定义,就可知道:__________________________即有:_________________________ _________________________ _________________________(二)例题例1、若π4 <θ < π2 ,则下列不等式中成立的是 ( )A .sin θ>cos θ>tan θB .cos θ>tan θ>sin θC . tan θ>sin θ>cos θD .sin θ>tan θ>cos θ例2..利用三角函数线比较下列各组数的大小:1. 32sin π与54sin π2. tan 32π与tan 54π当堂检测1.当2kπ-π4≤α≤2kπ+π4(k ∈Z )时,化简1-2sin αcos α+1+2sin αcos α的结果是________.2.已知sin αcos α=18且π4<α<π2,则cos α-sin α=______.3、若-2π3≤θ≤π6 ,利用三角函数线,可得sin θ的取值范围是 .4、若∣cos α∣<∣sin α∣,则∈α .5、试作出角α= 7π6正弦线、余弦线、正切线.课后练习与提高一、选择题1、角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异.那么α的值为( )A .π4B .3π4C .7π4D .3π4 或 7π42、若0<α<2π,且sin α<23 , cos α> 12 .利用三角函数线,得到α的取值范围是( )A .(-π3 ,π3 )B .(0,π3 )C .(5π3 ,2π)D .(0,π3 )∪(5π3 ,2π)3、依据三角函数线,作出如下四个判断: ①sinπ6 =sin 7π6 ;②cos (-π4 )=cos π4 ;③tan π8 >tan 3π8 ;④sin 3π5 >sin 4π5. 其中判断正确的有 ( )A .1个B .2个C .3个D .4个4、如果,42ππ<θ<那么下列各式中正确的是( ) A. cos tan sin θ<θ<θ B. sin cos tan θ<θ<θ C. tan sin cos θ<θ<θ D. cos sin tan θ<θ<θ5. 已知α的终边过(-a 39,2+a )且0cos ≤α,0sin >α,则α的取值范围是 。
锐角三角函数的定义 导学案
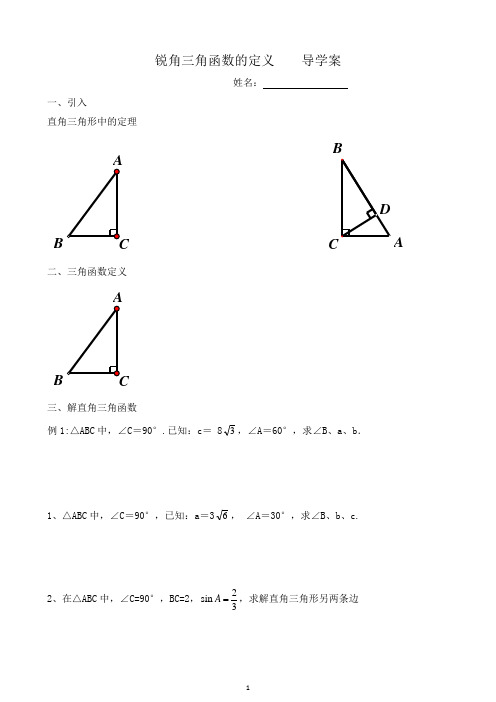
锐角三角函数的定义导学案姓名:一、引入直角三角形中的定理BD CBA二、三角函数定义B三、解直角三角函数例1:△ABC中,∠C=90°.已知:c= 83,∠A=60°,求∠B、a、b.1、△ABC中,∠C=90°,已知:a=36,∠A=30°,求∠B、b、c.2、在△ABC中,∠C=90°,BC=2,2sin3A ,求解直角三角形另两条边3、在△ABC 中,∠ACB =90°,cosA=33,AB =8cm ,则△ABC 的面积为4、由下列条件解直角三角形:在Rt △ABC 中,∠C=90°:(1)已知a=4,c=24, (2)已知b=10,∠B=60°.例2:在Rt △ABC 中,∠C =90°,a =2,b =3,则cosA = ,sinB = ,tanB = 。
1、直角三角形ABC 的面积为24cm 2,直角边AB 为6cm ,∠A 是锐角,则sinA = 。
2、如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sinB 的值是( )3、在△ABC 中,∠C=90°,AB=5,AC=4,则cosB = ,sinA = ,tanA = 。
cosA = ,sinB = ,tanB = 。
4、如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,tan ∠BCD=,AC=12,则BC= .5、在Rt△ABC 中,∠C=90°,AB=3,BC=1,则sinA="______," tanA=" _______," cosA=_______ SinB="______," tanB=" _______," cosB=_______6、如图,在菱形ABCD 中,DE ⊥AB , 垂足为E , DE =8cm , , 则菱形ABCD 的面积是__________.7、如图,正方形网格中,每一个小正方形的边长都是 , 四边形的四个顶点都在格点上,为边的中点,若把四边形绕着点顺时针旋转.【小题1】画出四边形旋转后的图形;【小题2】设点旋转后的对应点为 , 则;【小题3】求点在旋转过程中所经过的路径长.例3:已知tan α=125,α是锐角,则sin α= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5,则
b的值。
3的终边上,且|OP|=2,则点P的坐标?
2
,-3),,则定义:叫做角α的余弦,记作cosα,即cosα=;
α=-
5
2,则sin
α,tanα的值分别为(另外,角α的正割:secα=
1
cosαx
角α的余割:cscα=
1
sinαy
角α的余切:cotα=
1
2C-
3
A
1
高一数学学案
必修四第一章第3节三角函数的定义(1)
制作人:适用范围:高一使用日期:4.17
【教学目标】
1、三角函数定义;
2、利用定义求角的六个三角函数;
3、特殊角的三角函数值。
4、通过角定义的学习,进一步体会数形结合的思想方法
【教学重难点】
1、用定义求三角函数值;
2、特殊角三角函数值。
【教学内容】
1.任意角三角函数的定义
任意角三角函数的定义
如图所示,以任意角α的顶点O为坐标原点,以角α的始边的方向作为x轴的正方向,建立直
角坐标系.设P(x,y)是任意角α终边上不同于坐标原点的任意一点.
变式训练2:若角α的终边经过点P(-b,4)且cosα=-
3
例2、求下列各角的六个三角函数值:
(1)0;(2)π;(3)
3π
2
变式训练3:若点P在角
π
【课堂练习】
1、(1)已知角α终边经过点p(
1
cosα=______,sinα=______,tanα=______,
cotα=______,secα=______,cscα=______。
其中,r=OP=x2+y2>0.
x x
r r
y y
r叫做角α的正弦,记作sinα,即sinα=r;
2、设π
A、-1;不存在
B、1;不存在
C、-1;0
D、1;0
)。
y y
x叫做角α的正切,记作tanα,即tanα=x.
r
=;
r
=;
x
tanα=y.
例1、已知角α终边过点P(2,-3),求角α的六个三角函数值。
3、如果角α的终边过点(2sin30°,-2cos30°),则sinα的值等于()
13
2
B-
2
D
2
4、若角α的终边经过点M(0,m)(m≠0),则下列式子无意义的是()
A、sinα
B、cosα
C、tanα
D、cotα
15.已知角
α的终边上一点的坐标为(
3
,-
1
),则角α的最小正值为(
22)变式训练1:设角α的终边经过点P(3x,-4x)(x<0),则sinα-cosα的值?
A. 5π
6
3 3 6
A 、 - 7 C 、-7
B - 1
2
C - 2 - A . sin α = - 4
C . tan α = 4
3 A .1 或-1 B . 2 7.已知角 α 终边上一点 P(- 3,y),且 sin α= 3
5
D .-1 或 2
2.点 A(x ,y)是 300°角终边上异于原点的一点,则 的值为( )
A . 3
B .- 3
C . 3 3π⎫ ⎛
A .π
45.若角 α 的终边经过点 (-3λ,4 λ ),且 λ ≠ 0 ,则 sin α + cos α
2π 5π 11π B.
C.
D.
1 1
B 、
7
D 、7
62.若角 600︒ 的终边上有一点 (- 4, a ),则 a 的值是(
A . 4 3
B . - 4 3
C . ± 4 3
D . 3
)
56.已知角 α 的终边经过点 P(-8m ,-6 cos 60 o ) ,且 cos α = -
4
5
,则 m 的值是( )
73.已知角α 终边上一点 P (3a , 4a ),则下列关系中一定正确的是(
)
A
1
2
3 3
D 2
3
5 B . cos α = 5
3
3
D . cot α = - 4
二、解答题
6.若角 α 的终边过点 P(5,-12),求 sin α+cos α.
84.已知角α 的终边过点 P (- 4m ,m ), (m ≠ 0),则 2sin α + cos α 的值是(
)
5 或 - 2
5
4 y ,求 cos α 和 tan α 的值.
C .1 或 -
2
5
9、已知角 α 终边落在直线 y=2x 上,求 sin α,cos α,tan α 的值。
8.已知角 α 的终边上一点 P(-15a,8a) (a ∈R 且 a ≠0),求 α 的各三角函数值.
【课后作业】
一、选择题
1.若 α 的终边与 y 轴重合,则 α 的六种三角函数中,函数值不存在的是( A .sin α 与 cos α B .tan α 与 cot α C .tan α 与 sec α D .cot α 与 csc α
y
x
3
3 D .-
3
)
3π 3.已知点 P ⎝sin 4 ,cos 4 ⎭落在角 θ 的终边上,且 θ∈[0,2π),则 θ 的值为(
3π 5π 7π 4 B . 4 C . 4 D .
4
sin α - cos α 等于
)。
