结构力学综合复习资料(中国石油大学)
《结构力学》课程知识 复习 学习材料 试题与参考答案

《结构力学》课程知识复习学习材料试题与参考答案一、单选题1.力矩分配法是基于( A )原理推导出来的。
A.位移法B.力法 C.叠加法D.图乘法2.位移法中的形常数是( B )计算出来的。
A.用力矩分配法 B.力法C.叠加法D.图乘法3. ( A )不是力法的三要素。
A.基础连接方式 B. 力法方程C.基本结构 D. 基本未知量4.( B )可以作为结构A.瞬变体系B.几何不变体系C.有多余约束的可变体系D.自由度小于零的体系5.不属于画梁结构Q图的控制载面是( A )A.力偶作用面B.集中力作用面C.均布荷载的始截面D.均布荷载的末截面6.( A )不称为性线变形体系的互等定理A.功能互等定理B.功的互等定理C.位移互等定理D.反力互等定理7.超静定次数不可以用( D )方法求取A.求多余未知力个数 B.求结构自由度数C. 撤除多余约束D.分析外载形式8.(C )不是位移法的三要素A.基本未知量 B.基本体系 C.基本参数 D.基本方程9.载常数是利用(D )求出来的A.位移法 B.叠加法 C.图乘法 D.力法10.力矩分配法的主要步骤顺序是(C )A.分配与传递叠加求杆端弯矩求分配系数求固端弯矩B. 分配与传递叠加求杆端弯矩求固端弯矩求分配系数C. 求固端弯矩求固端弯矩分配与传递叠加求杆端弯矩D. 求固端弯矩求固端弯矩叠加求杆端弯矩分配与传递11.结构力学中主要研究的对象是( D )。
A.单个杆件B. 板壳C. 实体D. 杆系结构12.以下( D )不可以看成一个刚片。
A单个杆件 B.某一个几何不变的部分 C.地基 D. 某一几何可变的部分13.静定结构因支座移动,( B )A、会产生内力,但无位移B、会产生位移,但无内力C、内力和位移均不会产生D、内力和位移均会产生14. 结构的计算校核不包含有( B )。
A.计算过程的校核 B. 支座反力的校核C.平衡条件的校核 D. 位移条件的校核15. 零力杆是指( B )的杆件。
《结构力学》课程考试考前辅导资料

《结构力学》课程考试考前辅导资料一、考试题型介绍本次考试总共分为四个大题:(一)单项选择题,共10题,每题3分,共30分;(二)名词解释题,共5题,每题3分,共15分;(三)简答题,共4题,每题10分,共40分;(四)计算题,共1题,共15分;试卷中有注明本科和专科不同层次学生所做题目,请仔细阅读题目,不要盲目做题。
二、参考教材《结构力学Ⅰ》基本教程(第2版),龙驭球、包世华主编,高等教育出版社三、主要知识点及相关例题1.基本概念(1)自由度:是指体系远动时所具有的独立运动方式数目,也就是体系运动时可以独立变化的几何参数数目,或者说确定体系位置所需的独立坐标数目。
(2)刚片:在机动分析中,由于不考虑材料的变形,因此可以把一根杆件或已知是几何不变的部分看作是一个刚体,在平面体系中又将刚体称为刚片。
二维刚片有三个自由度。
(3)约束:限制运动的装置称为约束(或联系),体系的自由度可因加入约束而减少,能减少一个自由度的装置称为一个约束。
(4)虚铰:联结两个刚片的两根链杆的作用相当于在其交点处的一个单铰,不过这个铰的位置是随着链杆的转动而改变的,这种铰称为虚铰。
(5)几何不变体系:在不考虑杆件应变的假定下,体系的位置和形状是不会改变的体系叫做几何不变体系。
(6)几何可变体系:即使不考虑材料的变形,在很小的荷载作用下,也会发生机械运动而不能保持原有的几何形状和位置,这样的体系称为几何可变体系。
(7)瞬变体系:原为几何可变体系,经微小位移后即转化为几何不变的体系,称为瞬变体系。
(8)常变体系:经微小位移后仍能继续发生刚体运动的几何可变体系称为常变体系。
(9)结点法:为了求得桁架各杆的内力,可以截取桁架的一部分为隔离体,由隔离体的平衡件来计算所求的内力,若所取隔离体只包括一个节点,称为结点法。
(10)截面法:为了求得桁架各杆的内力,可以截取桁架的一部分为隔离体,由隔离体的平衡件来计算所求的内力,若所取隔离体不止包含一个结点,称为截面法(11)零杆:桁架中内力为零的杆件称为零杆。
结构力学期末复习提要

期末复习提要第一章绪论基本内容及要求:1.结构(1)理解结构的概念;(2)了解结构按其几何特征的三种分类。
2.结构力学的研究对象及任务(1)知道结构力学的研究对象;(2)了解结构力学的任务;(3)了解结构力学分析的三个基本条件。
3.结构计算简图及简化要点(1)了解结构计算简图的概念;(2)理解选择计算简图的原则;(3)掌握杆件结构计算简图的简化要点(共6点,关键是第3、4点)。
4.杆件结构的分类(1)掌握各种杆件结构的几何特点和力学特点。
5.荷载的分类(1)掌握荷载的概念(温度变化、基础沉降、材料收缩等因素广义上也称为荷载);(2)了解按荷载作用范围的分类及分布荷载、集中荷载的概念;(3)了解按荷载作用时间的分类及恒荷载、活荷载的概念;(4)了解按荷载作用性质的分类及静荷载、动荷载的概念及动荷载作用的基本特点。
第二章结构的几何构造分析(一)基本要求1.理解几何不变体系、几何可变体系、瞬变体系和刚片、约束、自由度等概念。
2.掌握无多余约束的几何不变体系的几何组成规则,体系的计算自由度的概念及计算及常见体系的几何组成分析。
3.了解结构的几何特性与静力特性的关系。
(二)基本内容1.几何构造分析的目的(1)了解几何构造分析的目的及意义。
2.几何构造分析的几个概念(1)掌握几何不变体系和几何可变体系的概念、特点;(2)掌握刚片、自由度、约束、多余约束的概念;(3)了解瞬变体系、瞬铰的概念和特点。
3.平面几何不变体系的组成规律(1)熟练掌握几何不变体系的三个组成规律及其应用;(2)能够利用几何不变体系的组成规律进行几何组成分析,并使分析过程简单化。
4.平面杆件体系的计算自由度(1)掌握计算自由度的概念;(2)掌握平面杆件体系的计算自由度的计算;(3)掌握根据计算自由度的数值,对体系的几何构造做定性的分析。
第三章静定结构的受力分析(一)基本要求1.掌握结构的支座反力的计算,结构的剪力和轴力计算的两种方法,内力图的形状特征和绘制内力图的叠加法。
结构力学复习资料(整理)

结构力学复习资料(整理)1. 引言本文整理了结构力学的重要概念和公式,以帮助读者复和掌握相关知识。
2. 静力学2.1 受力分析- 讲解了受力分析的基本原理和常用方法,如平衡方程和自由体图法。
- 提供了受力分析的步骤和实例,以加深理解。
2.2 结构的静力平衡- 介绍了结构的静力平衡条件,包括平衡方程和力矩平衡方程。
- 强调了结构的静力平衡在工程中的重要性。
2.3 支座反力计算- 讲解了支座反力计算的方法,包括自由体图法和平衡方程。
- 提供了支座反力计算的实例和注意事项。
3. 动力学3.1 动力学基本概念- 解释了动力学的基本概念,包括质点、力、加速度等。
- 提供了动力学相关公式和例题,以加强记忆。
3.2 牛顿第二定律- 介绍了牛顿第二定律的含义和应用,强调了力和加速度之间的关系。
- 提供了牛顿第二定律的公式和应用实例,帮助读者理解和运用该定律。
3.3 动量与冲量- 解释了动量与冲量的概念和计算方法。
- 强调了动量守恒定律和冲量定律的重要性。
- 提供了动量与冲量的公式和练题。
4. 应力与应变4.1 应力的概念- 介绍了应力的定义和常见类型,如拉应力、压应力和剪应力。
- 解释了应力的计算方法和单位,以及应力与受力的关系。
4.2 应变的概念- 讲解了应变的定义和类型,如线性应变和剪切应变。
- 强调了应变的计算方法和单位,以及应变与形变的关系。
4.3 应力-应变关系- 介绍了应力-应变关系的基本原理,包括胡克定律和弹性模量的概念。
- 提供了应力-应变关系的公式和实例,以帮助读者理解和运用该关系。
5. 结语本文整理了结构力学的复资料,包括静力学、动力学和应力与应变的重要概念和公式。
希望本文可以帮助读者复和巩固相关知识,提高结构力学的理解和应用能力。
以上为结构力学复习资料的简要整理,更详细的内容请参考相关教材和课堂讲义。
结构力学复习资料

一、简答题1. 简要说明图乘法的使用条件。
a )EI =常数;b )直杆;c )两个弯矩图至少有一个是直线。
2. 写出刚架和桁架的位移计算公式,并说明字母的含义?⎰∑=∆ds EIM M PEAlN N ds EA N N ds EA N N P P P ∑=∑=∑=∆⎰⎰3.请简述结构产生位移的主要缘故。
荷载作用;温度变化和材料胀缩;支座沉降和发明误差 4. 写出荷载作用下弹性位移的普通公式二、计算题1、作图示静定梁的弯矩图和剪力图。
[解](1)计算支座反力由0)(=∑F M C 得 F Ay =8kN (↑)由0)(=∑F M A 得 F Cy =20kN (↑)按照本例梁上荷载作用的情况,应分AB 、BC 两段作内力图。
(2)作F Q 图 (3)作M 图 )2 求超净定结构弯矩图,选作两题中的一题。
a 、使劲法计算图示结构,作弯矩图。
EI=常数。
10kN2m2m 4m解:(1) 一次超静定,基本体系和基本未知量,如图(a )所示。
(2) 列力法方程0X 11111=∆+=∆P δ(3) 作1M 图,见图(b ) 作P M 图,见图(c ) (4) 计算δ11、∆1P∑⎰∑⎰∑⎰++=∆s GAF F k s EA F F s EI M M d d d QP Q NP N P第 1 页/共 9 页EI EI EI EI M 325644413844211d s 2111=⨯⨯⨯+⨯⨯⨯⨯==∑⎰δEI EI EI d EI M M S P P 311604420131022021111-=⨯⨯⨯-⨯⨯⨯⨯-==∆∑⎰32145X 1=(kN )-X 110kNX 1=14m1M 10kN20PM 4mmkN⋅(a ) (b ) (c ) (5) 作M 图10kN290kN·m 60kN·mM (×1/32)b 、用位移法列出杆端方程及位移法基本方程。
(图中i AD =i CB= i DC =2i ,L AD =L BC =4m 、L DC =8m ,均布荷载为5kN/m )解:基本未知量为D θ∆、杆端方程:2141254412ADD M i i θ∆=--⨯⨯2181254412DA D M i iθ∆=-+⨯⨯ 6DC D M i θ= 64BC M i∆=- 0DAM=∑ 0DA DC M M +=20163043D i i θ∆-+= (1)212241044QDA D i F i θ∆=-+- 264QCB i F ∆=0QDA QCB F F += 127.5400D i i θ-+∆-= (1)因此位移方程为20163043127.5400DD i i i i θθ∆⎧-+=⎪⎨⎪-+∆-=⎩3、使劲矩分配法计算,并绘图示结构的M图。
《结构力学》考试题型串讲

14.内力影响线是表示单位移动荷载作用下结构各截面内力分 布规律的图形。 答:错误 内力影响线是表示单位移动荷载作用下结构截面 内力随荷载位置变化规律的图。
15.图2-15所示结构各杆端弯矩等于零
16.位移法方程的物理意义是结点位移的变形协调条件。 答:错误
21
17.图2-17所示两个三铰拱的高度和跨度相同,则两个三铰 拱的支座反力不相同。
35.平面杆件结构一般情况下的单元刚(劲)度矩阵为6×6矩阵,就 其性质而言,是 。 (A)非对称、奇异矩阵 (B)对称、奇异矩阵 (C)对称、非奇异矩阵 (D)非对称、非奇异矩阵 14
36.图1-36所示共有四种情况,不能使用力矩分配法求弯矩的 是 。
37.静定结构有温度变化时 。 (A)无变形、无位移、无内力 (B)有变形、有位移、有内力 (C)有变形、有位移、无内力 (D)无变形、有位移、无内力
16
5.图示结构几何对称,竖直方向对称荷载作用,且竖直方向 荷载自身平衡,则AB杆和ED杆上的弯矩为零
6.温度改变、支座移动和制造误差等因素在静定结构中引起内力。 答:错误 温度改变、支座移动和制造误差等因素在静定结构中不 引起内力。 7.虚功中的力状态和位移状态是彼此独立无关的,这两个状态中的任 意一个都可看作是虚设的。 答:正确 虚功中的力状态和位移状态是彼此独立无关的两个状态。 17
M A MC
M A MC
M A MC
不确定
8
19.用位移法计算图1-19所示的结构时,各杆的EI为常数, EA=∞,则基本未知量有 。
(A)4个 (C)6个 (B)5个 (D)3个
20.用位移法计算图1-20所示的结构时,各杆的EI为常数, EA=∞,则基本未知量有 。 (A)4个 (C)6个 (B)5个 (D)3个
结构力学笔记_复习题_考试题重点
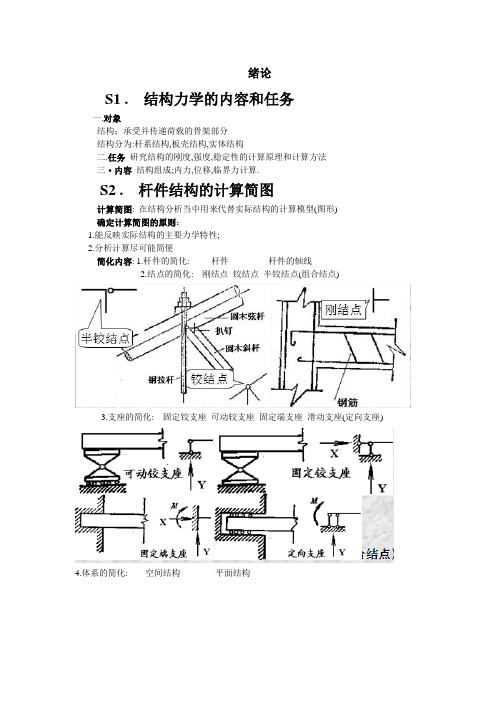
绪论S1 . 结构力学的内容和任务一.对象结构:承受并传递荷载的骨架部分结构分为:杆系结构,板壳结构,实体结构二.任务研究结构的刚度,强度,稳定性的计算原理和计算方法三·内容结构组成;内力,位移,临界力计算.S2 . 杆件结构的计算简图计算简图: 在结构分析当中用来代替实际结构的计算模型(图形)确定计算简图的原则:1.能反映实际结构的主要力学特性;2.分析计算尽可能简便简化内容: 1.杆件的简化: 杆件杆件的轴线2.结点的简化: 刚结点铰结点半铰结点(组合结点)3.支座的简化: 固定铰支座可动较支座固定端支座滑动支座(定向支座)4.体系的简化: 空间结构平面结构5.荷载的简化: 集中力、集中力偶、分布荷载S3 . 杆件结构的类型第一章杆件体系的几何组成分析本章假定:所有杆件均为刚体S1-1 基本概念一.几何不变体系几何可变体系几何可变体系不能作为建筑结构结构必须是几何不变体系本章目的:判定一个体系是否能作为结构结构是如何构造的S1. 几何组成分析S1-1 基本概念一.几何不变体系几何可变体系二.二. 刚片几何形状不能变化的平面物体三.自由度确定体系位置所需的独立坐标数几何不变体系的自由度一定等于零或者小于零几何可变体系的自由度一定大于零四.约束(联系) 能减少自由度的装置五.计算自由度六.多余约束必要约束计算自由度小于零一定不变吗?计算自由度小于零一定有多余约束S1-2 无多余约束的几何不变体系的组成规则一.三刚片规三刚片以不在一条直线上的三铰两两相联,构成无多余约束的几何不变体系.二.两刚片规则两刚片以一铰及不通过该铰的一个链杆相联,构成无多余约束的几何不变体系.两刚片以不相互平行,也不相交于一点的三个链杆相连,构成无多余约束的几何不变体系.三.二元体规则二元体:在一个体系上用两个不共线的链杆连接一个新结点的装置.在一个体系上加减二元体不影响原体系的机动性质.S1-3 几何组成分析举例例1: 对图示体系作几何组成分析解: 三刚片三铰相连,三铰不共线,所以该体系为无多余约束的几何不变体系.例2: 对图示体系作几何组成分析解:该体系为无多余约束的几何不变体系.方法1: 若基础与其它部分三杆相连,去掉基础只分析其它部分例3: 对图示体系作几何组成分析解: 该体系为无多余约束的几何不变体系.方法2: 利用规则将小刚片变成大刚片.例4: 对图示体系作几何组成分析解: 该体系为瞬变体系.方法3: 将只有两个铰与其它部分相连的刚片看成链杆. 例5: 对图示体系作几何组成分析解: 该体系为常变体系. 方法4: 去掉二元体.例6: 对图示体系作几何组成分析解: 该体系为无多余约束几何不变体系.方法5: 从基础部分(几何不变部分)依次添加. 例7: 对图示体系作几何组成分析解: 该体系为有一个多余约束几何不变体系.练习: 对图示体系作几何组成分析练习: 对图示体系作几何组成分析练习: 对图示体系作几何组成分析练习: 对图示体系作几何组成分析几何组成思考题几何组成分析的假定和目的是什麽?何谓自由度?系统自由度与几何可变性有何联系?不变体系有多余联系时,使其变成无多余联系几何不变体系是否唯一? 瞬变体系有何特点?可变体系时如何区分瞬变还是常变? 瞬铰和实际铰有何异同?无多余联系几何不变体系组成规则各有什麽限制条件?不满足条件时可变性如何? 按组成规则建立结构有哪些组装格式?组装格式和受力分析有无联系? 如何确定计算自由度?对体系进行组成分析的步骤如何? 作业:1-1 (b)试计算图示体系的计算自由度解:1-1 (c)试计算图示体系的计算自由度1-2 (a)试分析图示体系的几何组成1321138-=-⨯-⨯=W 由结果不能判定其是否能作为结构 或110222531-=-⨯-⨯+⨯=W 13240328=-⨯-⨯=W 或: 131216=-⨯=W 解由结果可判定其不能作为结构从上到下依次去掉二元体或从基础开始依次加二元体.几何不变无多余约束1-2 (d)试分析图示体系的几何组成依次去掉二元体. 几何常变体系 1-2 (f)试分析图示体系的几何组成有一个多余约束的几何不变体系1-2 (g)试分析图示体系的几何组成1-2 (k)试分析图示体系的几何组成有一个多余约束的几何不变体系三铰体系有无穷远铰的情况: 1. 有一个无穷远铰:三杆不平行不变 平行且等长常变 平行不等长瞬变常变体系 成2. 有两个无穷远铰:四杆不平行不变平行且各自等长常变 平行不等长瞬变3. 有三个无穷远铰:各自等长常变 否则瞬变1-2 (j)试分析图示体系的几何组成瞬变体系1-2 (L)试分析图示体系的几何组成几何不变无多余约束练习:试分析图示体系的几何组成几何不变无多余约束刚结点:一个单刚结点相当于三个约束. 单刚结点与其它约束的关系:复刚结点:连接N 刚片复刚结点相当于N-1个单刚结点.例: 试分析图示体系的几何组成 瞬变体系固定端支座:例: 计算图示体系的计算自由度并作几何组成分析有三个多余约束的几何不变体系 练习:试分析图示体系的几何组成无多余约束几何不变体系有两个多余约束的几何不变体系1-4 体系的几何组成与静力特征的关系 一. 无多余约束的几何不变体系是静定结构静定结构:由静力平衡方程可求出所有内力和约束力的体系.二. 有多余约束的几何不变体系是超静定结构超静定结构:由静力平衡方程不能求出所有内力和约束力的体系.333434-=-⨯-⨯=W 333333-=-⨯-⨯=W 错 0331=-⨯=W 333232-=-⨯-⨯=W q q三.瞬变体系不能作为结构瞬变体系的主要特性为:1.可发生微量位移,但不能继续运动2.在变形位置上会产生很大内力3.在原位置上,一般外力不能平衡4.在特定荷载下,可以平衡,会产生静不定力5.可产生初内力.四. 常变体系是机构第二章静定结构受力分析静定结构受力分析几何特性:无多余联系的几何不变体系静力特征:仅由静力平衡条件可求全部反力内力求解一般原则:从几何组成入手,按组成的相反顺序进行逐步分析即可本章内容:静定梁;静定刚架;三铰拱;静定桁架;静定组合结构;静定结构总论学习中应注意的问题:多思考,勤动手。
结构力学02结构的几何构造分析

图02—06a
19
瞬 铰
从瞬时微小运动来看,两根链杆所起的约束作用相当于在链杆 交点处的一个铰所起的约束作用。这个铰可称为瞬铰。用瞬铰 替换对应的两个链杆约束,这种约束的等效变换只适用于瞬时 微小运动。
图02—06a
20
瞬 铰
注意:图02—06c、图02—06d中O点为瞬铰,图02— 06e、图02—06f中A点不是瞬铰。
三个刚片之间的联结方式 规律:三个刚片用三个铰两两相连,且三个铰不在一直 线上,则组成几何不变的整体,并且没有多余约束。
图02—7c
26
平面几何不变体系的组成规律
图02—8a、图02—8b所示的体系不符合“三链杆不共点”的条 件,它们都是瞬变体系。在图02—8a中,三链杆相交于同一点 O ,刚片Ⅱ相对于基础Ⅰ可以绕O点作瞬时转动。 在图02—8b中,三链杆彼此平行(即相交于无限远的一点),刚 片Ⅱ相对于基础Ⅰ可以在垂直链杆的方向作瞬时移动(即绕无 限远的一点作瞬时转动)。
3
几何不变体系和几何可变体系
一个结构要能够承受各种可能的荷载,首先它的几何构造应当 合理,它本身应是几何稳固的,能够使其几何形状保持不变。 反之,如果一个杆件体系本身为几何不稳固,不能使其几何形 状保持不变,则它是不能承受任意荷载的。 因此,从几何构造的角度看,一个结构应是一个几何形状不变 的体系,简称几何不变体系。 进行结构的几何构造分析的一个目的,就是把杆件结构看成一 个杆件体系,检查它是不是一个几何不变体系。 为此,需要研究几何不变体系的组成规律。
图02—9b
图02—9a
31
平面几何不变体系的组成规律
装配的过程之一
图02—9c
32
平面几何不变体系的组成规律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《结构力学》综合复习资料
一、机动法作图示梁M K 的影响线,并利用影响线求出在图示荷载作用下M K 大小。
二、试利用余能驻值原理,求图始结构A 支座水平反力H A (线弹性材料,EI =常数)。
三、如图示结构,利用位移法求B 结点的转角和D 结点的位移(EI =常数)。
四、结构如图示,用位移法A 、B 结点的转角(各杆的线刚度相同)。
五、用直接刚度法的先处理法求出图示连续梁的结构刚度矩阵[K ] (EI =常数)。
六、如图示两自由度体系,求其频率(m 1=m 2=m ,EI =常数)
题一图
8
Pl M M BA AB -
=-= 题二图
q
题三图
题四图
题五图
B
A
2
12
1ql M M AB BA =
-=
参考答案一、
二、
三、
四、解:
Z 1
基本体系
列位移法方程 令l
EI i =
⎩⎨
⎧=++=++00
22221
211212111p p R Z Z R Z Z γγγγ Z 1
=1
4i
图
Z 2=1
图
2M
图
p M R 1
i i 1082211==γγ, i 22112==γγ 222112
1
121ql R ql R p p =-
=, 带入方程得
⎪⎩⎪⎨⎧
=++=-+0
121102012128221221ql iZ iZ ql iZ iZ 解得A 、B 结点转角⎪⎪⎩
⎪⎪⎨⎧-==i ql Z i
ql Z 456545662221 弯矩p M M Z M Z M ++=2211,弯矩图如
24
30M 图(2456
1
ql ⨯
) 五、
解:1.求柔度系数
图
a /2
图
2M
EI
a a a a EI f 3322113
11=⎥⎦⎤⎢⎣⎡⨯⨯⨯⨯= EI a a a a a a a EI f 4852322212432422113
22=
⎥⎦⎤⎢⎣⎡⨯⨯⨯⨯+⨯⨯⨯⨯⨯= EI
a a a a EI f f 63222113
2112=⎥⎦⎤⎢⎣⎡⨯⨯⨯⨯== 2.列振型方程
⎪⎪⎩⎪⎪⎨⎧=-+=+-0)1485(606)13(2231323
123A m EI a m A EI
a m A EI a A m EI a ωω 3.将
348ma EI 乘以上述各式,并令3
248a m EI
ωλ=可得
⎩⎨
⎧=-+=+-0
)5(80
8)16(2121A A A A λλ 4.令行列式
0)
5(88
)16(=--λλ,展开得016212=+-λλ,
即208.201=λ,792.02=λ 5.频率3
131541.148ma EI
ma EI ==
λω 3
232785.748ma EI
ma EI ==
λω。
