2019届人教A版(文科数学) 立体几何01 单元测试

合集下载

精选新版2019高中数学单元测试《立体几何初步》专题完整题(含答案)

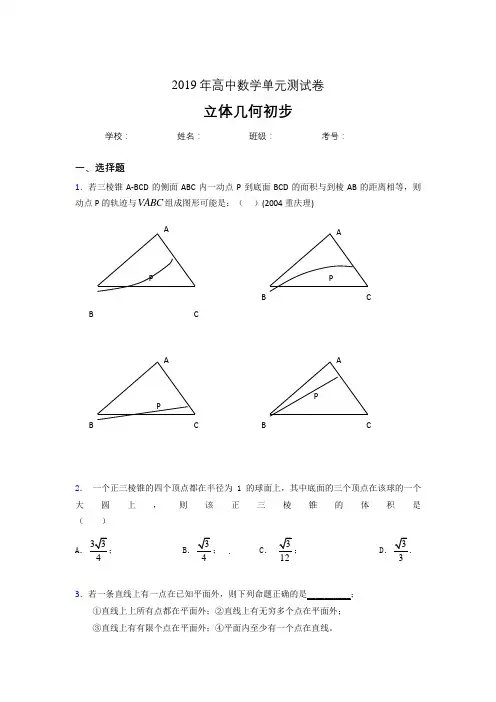
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．若三棱锥A-BCD 的侧面ABC 内一动点P 到底面BCD 的面积与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成图形可能是：（）(2004重庆理)2．一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（） A B C ． D .3．若一条直线上有一点在已知平面外，则下列命题正确的是__________；①直线上上所有点都在平面外；②直线上有无穷多个点在平面外； ③直线上有有限个点在平面外；④平面内至少有一个点在直线。

4．给出下列四个命题：①一个角是平面图形；②三条直线两两相交，它们必在同一平面内；③两个平面有三个公共点，它们必重合；④四边形是平面图形。

其中正确命题的个数是----------------------------------------------------------------------------------（） (A) 1 (B) 2 (C) 3 (D) 5．空间四边形ABCD 中，A B B CC D 、、的中点分别是P Q R 、、，且2,,3P Q Q P R ==，那么异面直线AC 和BD 所成的角是________________二、填空题6．已知圆柱的底面半径为1，母线长与底面的直径相等，则该圆柱的表面积为 ▲ ． 7．设平面α∥平面β，,A C α∈，,B D β∈，直线AB 与CD 交于点S ，且8AS =，9BS =，34CD =，SC =____ ．8．长方体1111ABCD A B C D -中，13,2AB BC AA ===，则四面体11A BC D 的体积为 9．如图，一个圆锥形容器的高为a ，内装有一定量的水，如果将容器倒置，这时所形成的圆锥的高恰为2a（如图2-②），则图2-①中的水面高度为 .2-①2-②10．用半径为2cm 的半圆形纸片卷成一个圆锥筒，则这个圆锥筒的高为． 11．若一个长方体的长、宽、高分别为3、2、1，则它的外接球的表面积是 ▲ .12．在空间中，①若四点不共面，则这四点中任何三点都不共线；②若两条直线没有公共点，则这两条直线是异面直线．以上两命题中，逆命题为真命题的是________(把符合要求的命题序号都填上)．解析：①的逆命题不正确，如平行四边形，②的逆命题显然是正确的，故逆命题是真命题的是②.13．已知a ，b 为异面直线，直线c ∥a ，则直线c 与b 的位置关系是．14．已知l 是一条直线，,αβ是两个不同的平面. 若从“①l α⊥；②//l β；③αβ⊥”中选取两个作为条件，另一个作为结论，试写出一个你认为正确的命题 ▲ .（请用代号表示）15．棱长都是1的三棱锥的表面积为_________▲_________。

2019届人教A版(文科数学) 立体几何初步单元测试

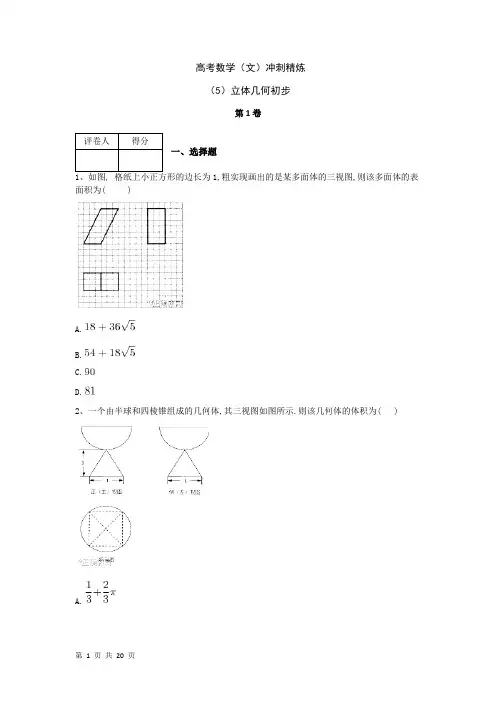
高考数学（文）冲刺精炼（5）立体几何初步第1卷一、选择题1、如图, 格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为( )A.B.C.D.2、一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )A.B.C.D.3、已知互相垂直的平面交于直线.若直线,满足,,则( ) A.B.C.D.4、如图,在正方体中,、分别为、的中点,则下列直线中与直线相交的是( )A.直线B.直线C.直线D.直线5、如图, 格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,该几何体有一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.B.C.D.6、某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.B.C.D.7、如图,在下列四个正方体中, ,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是( )A.B.C.D.8、某几何体挖去两个半球体后的三视图如图所示,若剩余几何体的体积为,则的值为( )A.B.C.二、填空题9、某四棱柱的三视图如图所示,则该四棱柱的体积为.10、已知某三菱锥的三视图如图所示,则该三菱锥的体积 .11、某几何体的三视图如图所示(单位:),则该几何体的表面积是,体积是.正视图侧视图俯视图12、由一个长方体和两个圆柱构成的几何体的三视图,如图,则该几何图的体积为 .13、已知三棱锥的所有顶点都在球的球面上,是球的直径,平面平面,,三棱锥的体积为,则球的表面积为.14、已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为,则这个球的15、如图,在四棱锥中,平面,,.1.求证:平面;2.求证:平面平面;3.设点为的中点,在棱上是否存在点,使得平面?说明理由.16、如图,在四棱锥中,.1.在平面内找一点,使得直线平面,并说明理由;2.证明:平面平面.17、由四棱柱截去三棱锥后得到的几何体如图所示,四边形为正方形,为与的交点,为的中点,平面1.证明:平面;2.设是的中点,证明:平面平面.18、如图,四棱锥中,侧面为等边三角形且垂直底面,,.1.证明:直线平面;2.若的面积为,求四棱锥的体积.19、如图,在四棱锥中,,且.1.证明:平面平面;2.若,,且四棱锥的体积为,求该四棱锥的侧面积.20、如图,在三棱锥中,,,,,为线段的中点,为线段上一点.1.求证:;2.求证:平面平面;3.当平面时,求三棱锥的体积.21、四棱台被过点的平面截去一部分后得到如图所示的几何体,其下底面四边形是边长为的菱形,,平面,1.求证:2.求点到平面的距离四、证明题22、在如图所示的几何体中,是的中点,.1.已知,.求证:;2.已知,分别是和的中点.求证:平面.参考答案一、选择题1.答案：B解析：由三视图该几何体是以侧视图为底面的斜四棱柱,所以该几何体的表面积,故选B.2.答案：C解析：由已知,半球的直径为,正四棱锥的底面边长为1,高为1,所以其体积为,选C.3.答案：C解析：由题意知,直线与以及直线与的位置关系不能确定,故A,B,D不正确;又且,则.故选C.4.答案：D解析：只有与在同一平面内,是相交的,其他A,B,C中直线与都是异面直线,故选D.考点:1.正方体的几何特征;2.直线与直线的位置关系.5.答案：B解析：由题意知该几何体是一个组合体,下半部分是一个底面半径为,高为的圆柱,其体积为,上半部分是一个底面半径为,高为的圆柱的一半,其体积为,改组合体体积为,选B.6.答案：C解析：该几何体是三棱锥,如图:图中红色线围成的几何体为所求几何体,该几何体的体积是,故选.7.答案：A解析：由B,,则直线平面;由C,,则直线平面;由D,,则直线平面.故A不满足,选A.8.答案：B二、填空题9.答案：解析：通过俯视图可知该四棱柱的底面为等腰梯形,则四棱柱的底面积,通过侧(左)视图可知四棱柱的高,所以该四棱柱的体积.10.答案：解析：由三视图可知该几何体是一个三棱锥,且底面积为,高为1,所以该几何体的体积为.11.答案：80; 40解析：由三视图知该组合体是一个长方体上面放置了一个小正方体,..考点:三视图.【方法点睛】解决由三视图求空间几何体的表面积与体积问题,一般是先根据三视图确定该几何体的结构特征,再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积.12.答案：解析：13.答案：36π解析：取的中点,连接,,因为,,所以,.因为平面平面所以平面.设.. 所以,所以球的表面积为.14.答案：解析：设正方体边长为,则,外接球直径为.三、解答题15.答案：1.【证明】因为平面,所以,又因为,,所以平面.2.【证明】因为,,所以,因为平面,所以,所以平面.所以平面平面.3.棱上存在点,使得平面.证明如下:取的中点,连接,,.因为为的中点,所以,又因为平面,所以平面.解析：考点:空间垂直判定与性质;空间想象能力,推理论证能力【名师点睛】平面与平面垂直的性质的应用:当两个平面垂直时,常作的辅助线是在其中一个面内作交线的垂线,把面面垂直转化为线面垂直,进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系),构造(寻找)二面角的平面角或得到点到面的距离等.16.答案：1.取棱的中点(平面),点即为所求的一个点.理由如下:因为,,所以, 且.所以四边形是平行四边形,从而.又因为平面,平面,所以平面.(说明:取棱的中点,则所找的点可以是直线上任意一点)2.【证明】由已知,,,因为,,所以直线与相交,所以平面.从而.因为,,所以,且.所以四边形是平行四边形.所以,所以.又因为,所以平面. 又因为平面,所以平面平面.17.答案：1.取中点,连接,. ∵为四棱柱∴∴为平行四边形∵又∵面∴面2.∵为中点,为中点,∴,∵为正方形,∴,,又∵面,∴,∴,∴面,又∵面,,∴面,面,∴平面平面.18.答案：1.在平面内,因为,所以.又面,面,故平面.2.取的中点,连接、.由及,得四边形为正方形,则.因为侧面为等边三角形且垂直于底面,平面平面,所以,底面.因为底面,所以.设,则,,,,取的中点,连接,则,所以.因为的面积为,所以,解得(舍去),.于是,,. 所以四棱锥的体积.19.答案：1.,∴,,∵,∴,∵,,,平面,平面,∴平面,又∵平面,∴平面平面.2.由1得平面,∴,∴四边形为矩形,设,∵,∴有,作于.,∵,,∴平面,∴为四棱柱的高,∴, ∴,∴,,,,,,∴为等边三角形,∴,∴四棱锥的侧面积为.20.答案：1.∵,,,平面,平面,∴平面,又∵平面,∴.2.∵,为的中点,∴,又∵,,平面,平面,∴平面,又∵平面,∴平面平面.3.∵平面,平面,平面平面,∴,又∵为的中点,,∴为的中位线,∴为的中点,且,由1得平面,,∴平面,∴为三棱锥的高,∴,,∴,∴三棱锥的体积为.21.答案：1.其底面四边形是边长为的菱形,则有,∵平面,∴,而∴平面,平面.∴2.利用等体积法,根据题目条件可求出,,,可知是直角三角形设点到平面的距离为,,,解得四、证明题22.答案：1.连接,因为,所以与确定平面.因为,为的中点,所以.同理可得,又因为,所以平面,因为平面,所以.2.设的中点为,连接,在中,因为是的中点,所以,又因为,所以.在中,因为是的中点,所以.又因为,, 所以平面平面.因为平面,所以平面.。

2021年人教A版(2019)选择性必修第一册数学第一章_空间向量与立体几何单元测试卷高中答案解析

2021年人教A 版（2019）选择性必修第一册数学第一章空间向量与立体几何单元测试卷（1）一、选择题1. 已知向量a →=(1,−2,2)，b →=(1,1,6)，则|a →−b →|=( ) A.25 B.17 C.√17 D.52. 已知向量a →=(λ, 6, 2)，b →=(−1, 3, 1)，满足a → // b →，则实数λ的值是( ) A.2 B.6 C.−2 D.−63. 在空间直角坐标系O −xyz 中，点A (−1,0,3)关于坐标原点的对称点为B ，则|AB|=( ) A.2 B.√10 C.2√10 D.104. 如图所示，在空间四边形OABC 中， OA →=a →，OB →=b →，OC →=C →，点N 在AB 上，且AN →=2NB →，M 为OC 中点，则MN →=( )A.12a →−23b →−12c →B.−23a →+12b →+12c →C.13a →+12b →−12c →D.13a →+23b →−12c →5. 设P (1,−2,5)是空间直角坐标系中的一点，则点P 关于坐标平面yOz 的对称点的坐标为( ) A.(1,2,−5) B.(−1,−2,5) C.(−1,−2,−5) D.(1,−2,−5)6. 已知平面α内有一点A (2,−1,2)，平面α 的一个法向量为n →=(12,16,13)，则下列四个点中在平面α内的是( ) A.P 1(1,−1,1) B.P 2(1,3,32)C.P 3(1,−3,32)D.P 4(−1,3,−32)7. 如图，在平行六面体ABCD −A 1B 1C 1D 1中，M 在AC 上，且AM =12MC ，N 在A 1D 上，且A 1N =2ND ，设AB →=a →，AD →=b →，AA 1→=c →，则MN →=( )A.−13a →+13b →+13c →B.a →+13b →−13c →C.13a →−13b →−23c →D.−13a →+b →+13c →8. 空间直角坐标系中A(1, 2, 3)，B(−1, 0, 5)，C(3, 0, 4)，D(4, 1, 3)，则直线AB 与CD 的位置关系是( ) A.平行 B.垂直 C.相交但不垂直 D.无法确定9. 已知A (0,0,2)，B (1,0,2)，C (0,2,0)，则点A 到直线BC 的距离为（） A.2√23B.1C.√2D.2√210. 如图，在正方体ABCD −A 1B 1C 1D 1中，点O 为线段BD 的中点．设点P 在线段B 1C 1上，直线OP 与平面A 1BD 所成的角为α，则sin α的取值范围是( )A.[√63，1] B.[√23，1] C.[√23，2√23] D.[√63，2√23]11. 《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.在如图所示的阳马P−ABCD中，侧棱PD⊥底面ABCD，且PD=CD=AD，点E是PC 的中点，则PD与BE所成角的余弦值是()A.√33B.√36C.√63D.√6612. 如图，直三棱柱ABC一A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90∘，D是A1B1的中点，F是棱BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为( )A.√510B.√1010C.12D.√105二、填空题13. 已知直线l的一个法向量是n→=(√3,−1)，则l的倾斜角的大小是________．14. 已知平面α的法向量为(2, −4, −2)，平面β的法向量为(k, 2, 1)，若α // β，则实数k的值为________.15. 给出下列命题：①直线l 的方向向量为a →=(1, −1, 2)，直线m 的方向向量b →=(2, 1, −12)，则l 与m 垂直； ②直线l 的方向向量a →=(0, 1, −1)，平面α的法向量n →=(1, −1, −1)，则l ⊥α； ③平面α，β的法向量分别为n 1→=(0, 1, 3)，n 2→=(1, 0, 2)，则α // β；④平面α经过三点A(1, 0, −1)，B(0, 1, 0)，C(−1, 2, 0)，向量n →=(1, u, t)是平面α的法向量，则u +t =1．其中真命题的是________.（把你认为正确命题的序号都填上）16. 如图所示的一块长方体木料中，已知AB =BC =2，AA 1=1，设F 为线段AD 上一点，则该长方体中经过点A 1，F ，C 的截面面积的最小值为________．三、解答题17. 已知向量b →=(−2,1,1)，点A(−3,−1,4)，B(−2,−2,2)，点E 在直线AB 上，使得OE →⊥b →，则点E 的坐标为多少.18. 如图，在空间直角坐标系中，正方体ABCD −A 1B 1C 1D 1棱长为2，E 为正方体的棱AA 1的中点，F 为棱AB 上的一点，若∠C 1EF =90∘，则点F 的坐标是多少.19.如图，正四棱柱ABCD −A 1B 1C 1D 1中，设AD =1，D 1D =λ(λ>0)，若棱C 1C 上存在唯一的一点P 满足A 1P ⊥PB ，求实数λ的值．20.在如图所示的几何体中，△FCB是等边三角形，四边形ABCD是等腰梯形，AB//CD，AB，平面FCB⊥平面ABCD.CB=CD=12(1)求证：AC⊥平面FCB；(2)求二面角F−BD−C的余弦值.21. 在直四棱柱ABCD−A1B1C1D1中，AD // BC，∠BAD=90∘，AB=√3，BC=1，AD=AA1=3．(1)证明：AC⊥B1D；(2)求直线B1C1与平面ACD1所成角的正弦值．22. 如图1，在矩形ABCD中，AB=2，BC=4，E为AD的中点，O为BE中点.将△ABE沿BE折起到A′BE，使得平面A′BE⊥平面BCDE（如图2）.(1)求证：A′O⊥CD；(2)求直线A′C与平面A′DE所成角的正弦值；(3)在线段A′C上是否存在点P，使得OP//平面A′DE？若存在，求出A′P的值；若不存在，A′C请说明理由.参考答案与试题解析2021年人教A 版（2019）选择性必修第一册数学第一章空间向量与立体几何单元测试卷（1）一、选择题 1.【答案】 D【考点】空间向量运算的坐标表示向量的模向量的减法及其几何意义【解析】先求出a →−b →=(0,−3,−4)，再利用模长公式求解即可. 【解答】解：∵ a →=(1,−2,2)，b →=(1,1,6)， ∴ a →−b →=(0,−3,−4)，∴ |a →−b →|=√02+(−3)2+(−4)2=5. 故选D . 2.【答案】 C【考点】共线向量与共面向量【解析】利用向量平行的性质直接求解．【解答】解：∵ 向量a →=(λ, 6, 2)，b →=(−1, 3, 1)，满足a → // b →， ∴ λ−1=63=21，解得λ=−2， ∴ 实数λ的值是−2. 故选C . 3.【答案】 C【考点】空间中的点的坐标空间两点间的距离公式求出B 点的坐标，再根据空间中两点间的距离公式即可得解. 【解答】解：设B (a,b,c )，由中点坐标公式可得：a−12=0，b+02=0，c+32=0，解得a =1，b =0，c =−3，所以B (1,0,−3)，所以点|AB |=√(−1−1)2+(0−0)2+(3+3)2=2√10. 故选C ． 4. 【答案】 D【考点】空间向量的加减法【解析】利用向量的加法，MN →=MO →+OB →+BN →，利用中点公式代入．【解答】解：MN → =MO → +OB → +BN →，MO → =−12OC →，BN → = 13BA → = 13(OA → −OB →)，所以MN →=−12OC → + 23OB → + 13OA →=−12c →+23b →+13a →. 故选D . 5. 【答案】 B【考点】空间直角坐标系【解析】根据空间点的对称性分别进行判断即可．【解答】解：因为点P(a, b, c)与点P ′关于坐标平面yOz 对称，则y ，z 不变，x 相反，所以对称点P ′(−a, b, c)，所以P (1,−2,5)关于坐标平面yOz 的对称点的坐标为(−1,−2,5). 故选B . 6.【答案】 B【考点】平面的法向量向量的减法及其几何意义若点P 在平面α内，则P 2A →⋅n →=0，经过验证即可判断出结论．【解答】解：由题意得P 1A →=(1,0,1)，P 1A →⋅n →=56≠0，排除选项A ．同理，可排除选项C ，D ．因为P 2A →=(1,−4,12)，所以P 2A →⋅n →=0．故选B ． 7.【答案】 A【考点】空间向量的基本定理及其意义向量的加法及其几何意义【解析】充分利用向量加法、减法的平行四边形、三角形法则以及数乘运算，将MN →表示出来，易知MN →=MA →+AA 1→+A 1N →，然后将三个向量分别用基底表示出来代入即可．【解答】解：因为M 在AC 上，且AM =12MC ，N 在A 1D 上，且A 1N =2ND ，所以AM →=13AC →，A 1N →=23A 1D →．又由已知平行六面体ABCD −A 1B 1C 1D 1，且AB →=a →，AD →=b →，AA 1→=c →得： AC →=a →+b →，A 1D →=b →−c →，所以MN →=MA →+AN →=−AM →+AA 1→+A 1N →=−13(a →+b →)+c →+23(b →−c →)．化简得MN →=−13a →+13b →+13c →．故选A ． 8. 【答案】 A【考点】共线向量与共面向量【解析】由已知得AB →=(−2, −2, 2)，CD →=(1, 1, −1)，AB →=−2CD →，从而得到直线AB 与CD 平行．【解答】解：在空间直角坐标系中，A(1, 2, 3)，B(−1, 0, 5)，C(3, 0, 4)，D(4, 1, 3)， ∴ AB →=(−2, −2, 2)，CD →=(1, 1, −1)， ∴ AB →=−2CD →， ∴ 直线AB 与CD 平行．故选A ． 9. 【答案】 A【考点】空间向量的夹角与距离求解公式【解析】求出|AB →|=(1,0,0)， |BC →|=(−1,2,−2)，根据空间向量的夹角与距离公式即可求解点A 到直线BC 的距离. 【解答】解：∵ A (0,0,2) ，B (1,0,2) ，C (0,2,0), ∴ AB →=(1,0,0)， BC →=(−1,2,−2)， ∴ 点A 到直线BC 的距离为： d =|AB →|√1−(cos <AB →，BC →>)2 =|AB →|√1−(AB →⋅BC→|AB →|⋅|BC →|)2=1×√1−(−11×3)2=2√23. 故选A . 10.【答案】 C【考点】用空间向量求直线与平面的夹角【解析】设正方体的棱长为2，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，利用向量法能求出sin α的取值范围．【解答】解：设正方体的棱长为2，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，则A 1(2, 0, 2)，B(2, 2, 0)，D(0, 0, 0)，O(1, 1, 0)，P(a, 2, 2)，0≤a ≤2，DA 1→=(2, 0, 2)，DB →=(2, 2, 0)，OP →=(a −1, 1, 2)，设平面A 1BD 的法向量n →=(x, y, z)，则{n →⋅BD →=2x +2y =0，n →⋅DA 1→=2x +2z =0，取x =1，得n →=(1, −1, −1)，∴ sin α=|cos <OP →,n →>|=|OP →⋅n →|OP →|⋅|n →|| =√(a−1)2+5⋅√3=√33⋅√(a−1)2+5， ∵ 0≤a ≤2，∴ a =2时，sin α取最小值 (sin α)min =√33√(2−1)2+5=√23， a =0时，sin α取最大值 (sin α)max =√33×√(0−1)2+5=2√23． ∴ sin α的取值范围是[√23,2√23]．故选C ．11. 【答案】D【考点】用空间向量求直线间的夹角、距离【解析】此题暂无解析【解答】解：建立空间直角坐标系如图所示，设PD =CD =AD =2，则E(0, 1, 1)，B(2, 2, 0)，P(0, 0, 2)，D(0, 0, 0)，∴ PD →=(0, 0, −2)，BE →=(−2, −1, 1)，设PD 与BE 的夹角为θ，则cos θ=|PD →⋅BE →||PD →|⋅|BE →| =22√6 =√66. 故选D .12.【答案】C【考点】点、线、面间的距离计算向量语言表述线面的垂直、平行关系【解析】以C 1为原点，C 1A 1为x 轴，C 1B 1为y 轴，C 1C 为z 轴，建立空间直角坐标系，利用向量法能求出线段B 1F 的长．【解答】解：以C 1为原点，C 1A 1为x 轴，C 1B 1为y 轴，C 1C 为z 轴，建立空间直角坐标系，由题意A 1(1, 0, 0)，B 1(0, 1, 0)，D(12,12, 0)，C 1(0, 0, 0)，A(1, 0, 2)，设F(0, 1, t)，0≤t ≤2，C 1D →=(12,12, 0)，AB 1→=(−1, 1, −2)，C 1F →=(0, 1, t)，因为AB 1⊥平面C 1DF ，{AB 1→⋅C 1D →=0，AB 1→⋅C 1F →=0，所以1−2t =0，解得t =12，所以B 1F →=(0,0,12)，所以线段B 1F 的长为12．故选C .二、填空题13.【答案】π3【考点】直线的方向向量直线的倾斜角【解析】设直线l 的倾斜角为θ，θ∈[0, π)．设直线的方向向量为u →=(x, y)，则u →∗n →=0，可得tan θ=y x ．【解答】解：设直线l 的倾斜角为θ，θ∈[0, π)．设直线的方向向量为u →=(x, y)，则u →⋅n →=√3x −y =0，∴ tan θ=y x =√3，解得θ=π3．故答案为：π3.14.【答案】−1【考点】向量语言表述面面的垂直、平行关系向量的数量积判断向量的共线与垂直【解析】设平面α的法向量为a →，平面β的法向量为b →．由于α // β，可得a → // b →，因此∃实数λ使得a →=λb →．再利用向量共线定理的坐标运算即可得出．【解答】解：∵ 平面α的法向量为(2, −4, −2)，平面β的法向量为(k, 2, 1)，且α // β， ∴ a → // b →，∴ 存在实数λ使得a →=λb →．∴ {2=kλ，−4=2λ，−2=λ，解得k =−1．故答案为：−1.15.【答案】①④【考点】平面的法向量共线向量与共面向量数量积判断两个平面向量的垂直关系用向量证明平行【解析】①根据直线l 、m 的方向向量a →与b →垂直，得出l ⊥m ；②根据直线l 的方向向量a →与平面α的法向量n →垂直，不能判断l ⊥α；③根据平面α、β的法向量n 1→与n 2→不共线，不能得出α // β；④求出向量AB →与BC →的坐标表示，再利用平面α的法向量n →，列出方程组求出u +t 的值．【解答】解：①，∵ a →=(1, −1, 2)，b →=(2, 1, −12)，∴ a →⋅b →=1×2−1×1+2×(−12)=0，∴ a →⊥b →，∴ 直线l 与m 垂直，故①正确；②，a →=(0, 1, −1)，平面法向量为n →=(1, −1, −1)，∴ a →⋅n →=0×1+1×(−1)+(−1)×(−1)=0，∴ a →⊥n →，∴ l // α或l ⊂α，故②错误；③，∵ n 1→=(0, 1, 3)，n 2→=(1, 0, 2)，∴ n 1→与n 2→不共线，∴ α // β不成立，故③错误；④，∵ 点A(1, 0, −1)，B(0, 1, 0)，C(−1, 2, 0)，∴ AB →=(−1, 1, 1)，BC →=(−1, 1, 0)，向量n →=(1, u, t)是平面α的法向量，∴ {n →⋅AB →=0,n →⋅BC →=0,即{−1+u +t =0,−1+u =0,∴ u +t =1，故④正确．综上，以上真命题的序号是①④.故答案为：①④.16.【答案】6√55【考点】空间向量的数乘运算空间直角坐标系棱柱的结构特征【解析】根据题意，建立建立空间直角坐标系O −xyz ，用坐标表示向量，通过向量计算截面面积，求出截面面积的最小值．【解答】解：如图所示，以DA 为x 轴，AB 为y 轴，AA 1为z 轴，建立空间直角坐标系A −xyz ，设截面与交B 1C 1点K ，F(−2λ, 0, 0)，则FC →=(−2+2λ, 2, 0)，FA 1→=(2λ, 0, 1)；∴ S =|FC →|⋅|FA 1→|sin θ，S 2=|FC →|2⋅|FA 1→|2−(FC →⋅FA 1→)2=[(−2+2λ)2+4](4λ2+1)−[(−2+2λ)⋅2λ]2=20λ2−8λ+8=20(λ−15)2+365，当λ=15时，S 2取最小值365，∴ S 的最小值为6√55．故答案为：6√55．三、解答题17.【答案】解：AB →=OB →−OA →=(1,−1,−2)，∵ 点E 在直线AB 上，∴ OE →=OA →+λAB →=(−3,−1,4)+λ(1,−1,−2)=(−3+λ,−1−λ,4−2λ)， ∴ OE →⋅b →=−2(−3+λ)+(−1−λ)+(4−2λ)=0,解得λ=95,∴ OE →=(−65,−145,25)， ∴ E 点坐标为(−65,−145,25). 【考点】空间向量运算的坐标表示共线向量与共面向量【解析】此题暂无解析【解答】解：AB →=OB →−OA →=(1,−1,−2)，∵ 点E 在直线AB 上，∴ OE →=OA →+λAB →=(−3,−1,4)+λ(1,−1,−2)=(−3+λ,−1−λ,4−2λ)， ∴ OE →⋅b →=−2(−3+λ)+(−1−λ)+(4−2λ)=0,解得λ=95,∴ OE →=(−65,−145,25)， ∴ E 点坐标为(−65,−145,25).18.【答案】解：由正方体的性质可得E(2,0,1)，C 1(0,2,2)，设F(2,y,0)，则EC 1→=(−2,2,1)，EF →=(0,y,−1)．因为∠C 1EF =90∘，所以EC 1→⋅EF →=2y −1=0，解得y =12，则点F 的坐标为(2,12,0)．【考点】空间向量的数量积运算空间中的点的坐标【解析】此题暂无解析【解答】解：由正方体的性质可得E(2,0,1)，C 1(0,2,2)，设F(2,y,0)，则EC 1→=(−2,2,1)，EF →=(0,y,−1)．因为∠C 1EF =90∘，所以EC 1→⋅EF →=2y −1=0，解得y =12，则点F 的坐标为(2,12,0)．19.【答案】解：如图，以点D 为原点O ，DA ，DC ，DD 1分别为x ，y ，z 轴建立空间直角坐标系O −xyz ，则D(0, 0, 0)，B(1, 1, 0)，A 1(1, 0, λ)，设P(0, 1, x)，其中x ∈[0, λ]，因为A 1P ⊥PB ，所以A 1P →⋅BP →=0，即(−1, 1, x −λ)⋅(−1, 0, x)=0，化简得x 2−λx +1=0，x ∈[0, λ]，由点P(0, 1, x)的唯一性知方程x 2−λx +1=0只有唯一解，所以，判别式Δ=λ2−4=0，且λ>0，解得λ=2．【考点】空间向量的数量积运算【解析】以点D 为原点O ，DA ，DC ，DD 1分别为x ，y ，z 轴建立空间直角坐标系O −xyz ，利用向量法能求出实数λ的值．【解答】解：如图，以点D 为原点O ，DA ，DC ，DD 1分别为x ，y ，z 轴建立空间直角坐标系O −xyz ，则D(0, 0, 0)，B(1, 1, 0)，A 1(1, 0, λ)，设P(0, 1, x)，其中x ∈[0, λ]，因为A 1P ⊥PB ，所以A 1P →⋅BP →=0，即(−1, 1, x −λ)⋅(−1, 0, x)=0，化简得x 2−λx +1=0，x ∈[0, λ]，由点P(0, 1, x)的唯一性知方程x 2−λx +1=0只有唯一解，所以，判别式Δ=λ2−4=0，且λ>0，解得λ=2．20.【答案】证明：(1)在等腰梯形ABCD 中，过点C 作CE ⊥AB 交AB 于点E ,设BC 长为1，则AB =2,BE =12,CE =√32,AC =√3，可得BC 2+AC 2=AB 2，即∠ACB =90∘，所以AC ⊥BC .因为面FCB 与面ABCD 交线为BC ，又AC ⊂面ABCD ,所以AC ⊥面FCB .（2）解：过点C 作CM ⊥平面BCD ，以点C 为原点，CA,CB,CM 所在的直线分别为x ，y ，z 轴建立如图所示的空间直角坐标系.则C(0,0,0),B(0,1,0),D (√32,−12,0),F (0,12,√32)，所以BD →=(√32,−32,0),BF→=(0,−12,√32)，设平面BDF 的法向量为m →=(x,y,z)，则{m →⋅BD →=0m →⋅BF →=0即{√32x −32y =0−12y +√32z =0，取z =1，则y =√3,x =3，得m →=(3,√3,1)，取平面BCD 的法向量为n →=(0,0,1) ，所以cos <m →,n →>=m →⋅n →|m →|⋅|n →|=1√9+3+1=√1313由图形知该二面角的平面角为锐角，所以二面角F −BD −C 的余弦值为√1313.【考点】用空间向量求平面间的夹角直线与平面垂直的判定【解析】此题暂无解析【解答】证明：(1)在等腰梯形ABCD 中，过点C 作CE ⊥AB 交AB 于点E ,设BC 长为1，则AB =2,BE =12,CE =√32,AC =√3，可得BC 2+AC 2=AB 2，即∠ACB =90∘，所以AC ⊥BC .因为面FCB 与面ABCD 交线为BC ，又AC ⊂面ABCD ,所以AC ⊥面FCB .（2）解：过点C 作CM ⊥平面BCD ，以点C 为原点，CA,CB,CM 所在的直线分别为x ，y ，z 轴建立如图所示的空间直角坐标系.则C(0,0,0),B(0,1,0),D (√32,−12,0),F (0,12,√32)，所以BD →=(√32,−32,0),BF→=(0,−12,√32)，设平面BDF 的法向量为m →=(x,y,z)，则{m →⋅BD →=0m →⋅BF →=0即{√32x −32y =0−12y +√32z =0，取z =1，则y =√3,x =3，得m →=(3,√3,1)，取平面BCD 的法向量为n →=(0,0,1) ，所以cos <m →,n →>=m →⋅n →|m →|⋅|n →|=1√9+3+1=√1313由图形知该二面角的平面角为锐角，所以二面角F −BD −C 的余弦值为√1313. 21.【答案】(1)证明：以AB →，AD →，AA 1→方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系．A(0,0,0)，C(√3,1,0)，B 1(√3,0,3),D(0,3,0)，C 1(√3,1,3)，D 1(0,3,3)，∴ AC →=(√3,1,0)，B 1D →=(−√3,3,−3)，∴ AC →⋅B 1D →=0，∴ AC ⊥B 1D .(2)解：设平面ACD 1的一个法向量为m →=(x,y,z)，AC →=(√3,1,0)，AD 1→=(0,3,3)，则{√3x +y =03y +3z =0， ∴ m →=(1,−√3,√3)设直线B 1C 1与平面ACD 1所成角为θ，∵ B 1C 1→=(0,1,0)，∴ sin θ=|B 1C 1→⋅m →||B 1C 1→||m →|=√217， ∴ 直线B 1C 1与平面ACD 1所成角的正弦值为√217. 【考点】用空间向量求直线与平面的夹角向量语言表述线线的垂直、平行关系两条直线垂直的判定【解析】(Ⅰ)以AB →,AD →,AA 1→方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系．求出相关点的坐标；通过计算AC →⋅B 1D →=0，证明AC ⊥B 1D ．(Ⅱ)求出平面ACD 1的法向量，设直线B 1C 1与平面ACD 1所成角为θ，求出B 1C 1→=(0,1,0)，利用向量的数量积求解直线B 1C 1与平面ACD 1所成角的正弦值．【解答】(1)证明：以AB →，AD →，AA 1→方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系．A(0,0,0)，C(√3,1,0)，B 1(√3,0,3),D(0,3,0)，C 1(√3,1,3)，D 1(0,3,3)，∴ AC →=(√3,1,0)，B 1D →=(−√3,3,−3)，∴ AC →⋅B 1D →=0，∴ AC ⊥B 1D .(2)解：设平面ACD 1的一个法向量为m →=(x,y,z)，AC →=(√3,1,0)，AD 1→=(0,3,3)，则{√3x +y =03y +3z =0， ∴ m →=(1,−√3,√3)设直线B 1C 1与平面ACD 1所成角为θ，∵ B 1C 1→=(0,1,0)，∴ sin θ=|B 1C 1→⋅m →||B 1C 1→||m →|=√217， ∴ 直线B 1C 1与平面ACD 1所成角的正弦值为√217. 22.【答案】(1)证明：由已知AB =AE =2，因为O 为BE 中点，所以A ′O ⊥BE .因为平面A ′BE ⊥平面BCDE ，且平面A ′BE ∩平面BCDE =BE ，A ′O ⊂平面A ′BE ，所以A ′O ⊥平面BCDE .又因为CD ⊂平面BCDE ，所以A ′O ⊥CD .(2)解：设F 为线段BC 上靠近B 点的四等分点，G 为CD 中点，由已知易得OF ⊥OG .由(1)可知，A ′O ⊥平面BCDE ，所以A ′O ⊥OF ，A ′O ⊥OG .以O 为原点，OF ，OG ，OA ′所在直线分别为x ，y ，z 轴建立空间直角坐标系（如图）.因为A ′B =2，BC =4，所以A ′(0,0,√2)，B(1,−1,0)，C(1,3,0)，D(−1,3,0)，E(−1,1,0). 设平面A ′DE 的一个法向量为m →=(x 1,y 1,z 1)，因为A ′D→=(−1,3,−√2)，DE →=(0,−2,0), 所以{m →⋅A ′D →=0，m →⋅DE →=0，即{−x 1+3y 1−√2z 1=0，−2y 1=0，取z 1=−1，得m =(√2,0,−1)，而A ′C →=(1,3,−√2)，所以直线A ′C 与平面A ′DE 所成角的正弦值sin θ=|2√22√3⋅√3|=√23. (3)解：在线段A ′C 上存在点P ，使得OP//平面A ′DE .设P (x 0,y 0,z 0)，且A ′PA ′C =λ(0≤λ≤1)，则A ′P →=λA ′C →，λ∈[0,1].因为A ′(0,0,√2)，C(1,3,0)，所以(x 0,y 0,z 0−√2)=(λ,3λ,−√2λ)，所以x 0=λ，y 0=3λ，z 0=√2−√2λ，所以P(λ,3λ,√2−√2λ)，OP →=(λ,3λ,√2−√2λ)，若OP//平面A ′DE ，则OP →⊥m →，即OP →⋅m →=0.由(2)可知，平面A ′DE 的一个法向量m →=(√2,0,−1)，即√2λ−√2+√2λ=0，解得λ=12∈[0,1]，所以当A ′P A ′C =12时，OP//平面A ′DE .【考点】用空间向量求直线与平面的夹角用向量证明平行直线与平面垂直的性质直线与平面垂直的判定【解析】此题暂无解析【解答】(1)证明：由已知AB =AE =2，因为O 为BE 中点，所以A ′O ⊥BE .因为平面A ′BE ⊥平面BCDE ，且平面A ′BE ∩平面BCDE =BE ，A ′O ⊂平面A ′BE ，所以A ′O ⊥平面BCDE .又因为CD ⊂平面BCDE ，所以A ′O ⊥CD .(2)解：设F 为线段BC 上靠近B 点的四等分点，G 为CD 中点，由已知易得OF ⊥OG .由(1)可知，A ′O ⊥平面BCDE ，所以A ′O ⊥OF ，A ′O ⊥OG .以O 为原点，OF ，OG ，OA ′所在直线分别为x ，y ，z 轴建立空间直角坐标系（如图）.因为A ′B =2，BC =4，所以A ′(0,0,√2)，B(1,−1,0)，C(1,3,0)，D(−1,3,0)，E(−1,1,0).设平面A ′DE 的一个法向量为m →=(x 1,y 1,z 1)，因为A ′D →=(−1,3,−√2)，DE →=(0,−2,0),所以{m →⋅A ′D →=0，m →⋅DE →=0，即{−x 1+3y 1−√2z 1=0，−2y 1=0，取z 1=−1，得m =(√2,0,−1)，而A ′C →=(1,3,−√2)，所以直线A ′C 与平面A ′DE 所成角的正弦值sin θ=|2√22√3⋅√3|=√23.(3)解：在线段A ′C 上存在点P ，使得OP//平面A ′DE . 设P (x 0,y 0,z 0)，且A ′P A ′C =λ(0≤λ≤1)，则A ′P →=λA ′C →，λ∈[0,1].因为A ′(0,0,√2)，C(1,3,0)，所以(x 0,y 0,z 0−√2)=(λ,3λ,−√2λ)，所以x 0=λ，y 0=3λ，z 0=√2−√2λ，所以P(λ,3λ,√2−√2λ)，OP →=(λ,3λ,√2−√2λ)，若OP//平面A ′DE ，则OP →⊥m →，即OP →⋅m →=0.由(2)可知，平面A ′DE 的一个法向量m →=(√2,0,−1)，即√2λ−√2+√2λ=0，解得λ=12∈[0,1]，所以当A ′P A ′C =12时，OP//平面A ′DE .。

精编新版2019高中数学单元测试《立体几何初步》专题完整考试题(含答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．已知平面α截一球面得圆M ，过圆心M 且与α成060，二面角的平面β截该球面得圆N ，若该球的半径为4，圆M 的面积为4π，则圆N 的面积为(A)7π (B)9π (c)11π (D)13π (2011年高考全国卷理科11)2．如图，四棱锥S-ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确．．．的是（）(2011年高考辽宁卷理科8)(A) AC ⊥SB (B) AB ∥平面SCD(C) SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 (D)AB 与SC 所成的角等于DC 与SA 所成的角3．下列说法中正确的是----------------------------------------------------------------------------------（） (A),a b αβ⊂⊂，则a 与b 是异面直线 (B)a 与b 异面，b 与c 异面，则a 与c 异面 (C)a b 、不同在平面α内，则a 与b 异面 (D)a b 、不同在任何一个平面内，则a 与b 异 4．1．下面给出四个命题中正确命题的个数是----------------------------------------------------------（）①若a b ∥，b c ∥，则a c ∥；②若a b ⊥，b c ⊥，则a c ⊥；③若a b 、相交，b c、相交，则a c 、也相交；④若a b 、是异面直线，b c 、是异面直线，则a c 、也是异面直线 (A) 1 (B) 2 (C) 3 (D) 二、填空题5．已知α，β是不重合的两个平面，则下列条件中，可推出α∥β的是_______(填序号) . ①,l m 是α内的两条直线且∥β，m ∥β； ②α内有不共线的三点到β的距离相等； ③α，β都与直线成等角； ④,l m 是异面直线且∥α，m ∥α，∥β，m ∥β.6．，则其外接球的表面积是 . 7．已知直线,m n 与平面,αβ，给出下列四个命题：①若//,//m n αα，则//m n ；②若//,m n αα⊥，则n m ⊥；③若n m m ⊥⊥,α，则α//n ；若,,//α⊥n n m 则α⊥m ，其中正确．．命题的个数．．是__________； 8．在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________（2013年高考上海卷（理））9．底为等边三角形的直棱柱的体积为V ，那么其表面积最小时，底面边长为。

2019届人教A版(文科数学) 立体几何单元测试

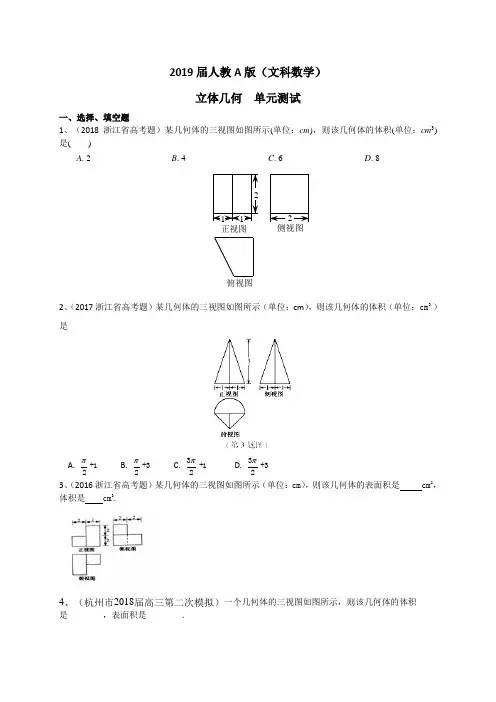
2019届人教A 版（文科数学）立体几何单元测试一、选择、填空题1、（2018浙江省高考题）某几何体的三视图如图所示(单位：cm )，则该几何体的体积(单位：cm 3)是( )A . 2B . 4C . 6D . 8侧视图俯视图正视图22112、（2017浙江省高考题）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是A.π+12B.π+32C.π3+12 D. π3+323、（2016浙江省高考题）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 cm 2，体积是 cm 3.4、（杭州市2018届高三第二次模拟）一个几何体的三视图如图所示，则该几何体的体积是，表面积是．5、（杭州市2018届高三上期期末）在三棱锥P ABC -中，PA ⊥平面ABC ，90BAC ∠=，,D E 分别是,BC AB 的中点，AB AC ≠，且AC AD >.设PC 与DE 所成角为α，PD 与平面ABC 所成角为β，二面角P BC A --为γ，则（）A.αβγ<<B.αγβ<<C.βαγ<<D.γβα<< 6、（湖州、衢州、丽水三地市2018届高三上期期末）设l 为直线，α，β是两个不同的平面，下列命题中正确的是A ．若αβ⊥，//l α，则l β⊥B ．若//l α，//l β，则//αβC ．若l α⊥，//l β，则//αβD ．若l α⊥，l β⊥，则//αβ7、（湖州市2018届高三5月适应性考试）一个棱锥的三视图如图（单位：cm ），则该棱锥的表面积是A ．426+2cm B ．462+2cmC ．432cm D ．226+2cm8、（暨阳联谊校2018届高三4月联考）某几何体的三视图如所示，则该几何体的表面积为，体积为 .9、（嘉兴市2018届高三4月模拟）某几何体的三视图如图（单位：m ），则该几何体的体积是A ．323mB ．343mC ．2 3mD ．4 3m10、（嘉兴市2018届高三上期期末）某几何体的三视图如图所示(单位：cm )，则该几何体的表面积(单位：2cm )是A ．22436+B ．51236+C ．22440+D ．51240+11、（金华十校2018届高三上期期末）已知正方体1111D C B A ABCD -边长为1，点O E ,分别在线段11D B 和BD 上，11154D B EB =，BO DO =，动点F 在线段1AA 上，且满足)210(1<<=λλAA AF ，分别记二面角E OB F --1，1B OE F --，O EB F --1的平面角为γβα,,，则（）A. βγα>>B. αβγ>>C. βαγ>>D. γαβ>>221正视图侧视图俯视图（第3题）（第6题）121俯视图12212正视图侧视图12、（金丽衢十二校2018届高三第二次联考）某四面体的三视图如图所示，正视图、左视图都是腰长为2的等腰直角三角形，俯视图是边长为2的正方形，则此四面体的最大面的面积是（） A ．2B ．C ．D ．413、（金丽衢十二校2018届高三第三次（5月）联考）正四面体ABCD ，E 为棱AD 的中点，过点A 作平面BCE 的平行平面，该平面与平面ABC 、平面ACD 的交线分别为l 1，l 2，则l 1，l 2所成角的正弦值为（）14、（宁波市2018届高三5月模拟）已知直线l 、m 与平面α、β，α⊂l ，β⊂m ，则下列命题中正确的是A ．若m l //，则必有βα//B ．若m l ⊥，则必有βα⊥C ．若β⊥l ，则必有βα⊥D ．若βα⊥，则必有α⊥m15、（宁波市2018届高三上期期末）圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若几何体的表面积为1620π+，则r =（） .1A .2B .4C .8D16、（绍兴市2018届高三第二次（5月）教质量调测）已知一个几何体的三视图如图所示，则该几何体的体积是A．83B．8C．203D．617、（浙江省2018届高三4月考目考试）如图，在正方体ABCD−A1B1C1D1中，直线A1C与平面ABCD所成角的余弦值是( )A. B.C. D.18、（台州市2018届高三上期期末质量评估）某四面体的三视图如图所示，则该四面体的体积为▲；表面积为▲.二、解答题1、（2018浙江省高考题）如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2（1）证明：AB 1⊥平面A 1B 1C 1（2）求直线AC 1与平面ABB 1所成的角的正弦值C 1B 1A 1CBA2、（2017浙江省高考题）如图，已知四棱锥P-ABCD ，△PAD 是以AD 为斜边的等腰直角三角形， BC ∥AD ，CD ⊥AD ，PC=AD=2DC=2CB,E 为PD 的中点. （I ）证明：CE ∥平面PAB ；（II ）求直线CE 与平面PBC 所成角的正弦值3、（2016浙江省高考题）如图,在三棱台ABC DEF -中,平面BCFE ⊥平面ABC ,=90ACB ∠,BE =EF =FC =1,BC =2,AC =3.(I)求证：EF ⊥平面ACFD ；(II)求二面角B -AD -F 的平面角的余弦值.4、（杭州市2018届高三第二次模拟）如图，在等腰三角形ABC 中，AB ＝AC ，∠A ＝120°，M 为线段BC 的中点，D 为线段BC 上一点，且BD ＝BA ，沿直线AD 将△ADC 翻折至△ADC ′，使AC ′⊥BD ．（Ⅰ）证明：平面AMC ′⊥平面ABD ；（Ⅱ）求直线C ′D 与平面ABD 所成的角的正弦值．5、（杭州市2018届高三上期期末）如图，在三棱锥A BCD -中，60BAC BAD DAC ∠=∠=∠=，2AC AD ==， 3.AB =（1）证明：AB CD ⊥；（2）求CD 与平面ABD 所成角的正弦值.6、（湖州、衢州、丽水三地市2018届高三上期期末）已知矩形ABCD 满足2AB =，2BC =，PAB ∆是正三角形，平面PAB ⊥平面ABCD ．（Ⅰ）求证：PC BD ⊥；（Ⅱ）设直线l 过点C 且l ⊥平面ABCD ，点F 是直线l 上的一个动点，且与点P 位于平面ABCD 的同侧．记直线PF 与平面PAB 所成的角为θ，若130+≤<CF ，求tan θ的取值范围．7、（湖州市2018届高三5月适应性考试）如图，三棱柱111ABC A B C -所有的棱长均为1，111A C B C ⊥．（Ⅰ）求证：1A B AC ⊥；（Ⅱ）若11A B =，求直线11AC 和平面11ABB A 所成角的余弦值．8、（暨阳联谊校2018届高三4月联考）如图，四边形ABEF 是正方形，1//,2AB CD AD AB BC CD ===.（1）若平面ABEF ⊥平面ABCD ，求证：BD ⊥平面EBC ；（2）若DF BC ⊥，求直线BD 与平面ADF 所成角的正弦值.9、（嘉兴市2018届高三4月模拟）如图，四棱锥ABCD P -中，底面ABCD 是边长为4的正方形，侧面PCD 为正三角形且二面角A CD P --为︒60．（Ⅰ）设侧面PAD 与PBC 的交线为m ，求证：BC m //；（Ⅱ）设底边AB 与侧面PBC 所成角的为θ，求θsin 的值．10、（嘉兴市2018届高三上期期末）如图，在矩形ABCD 中，点E 在线段CD 上，3=AB ，2==CE BC ，沿直线BE 将BCE ∆翻折成E BC '∆，使点'C 在平面ABED 上的射影F 落在直线BD 上.（Ⅰ）求证：直线⊥BE 平面'CFC ；（Ⅱ）求二面角D BE C --'的平面角的余弦值.11、（金华十校2018届高三上期期末）如图，四棱锥ABCD S -中，CD AB //，CD BC ⊥，2=AB ，1===SD CD BC ，侧面SAB 为等边三角形.（1）证明：SD AB ⊥；（2）求直线SC 与平面SAB 所成角的正弦值.12、（金丽衢十二校2018届高三第二次联考）四棱锥S ﹣ABCD 的底面是边长为1的正方形，则棱SB 垂直于底面．（Ⅰ）求证：平面SBD ⊥平面SAC ；（Ⅱ）若SA 与平面SCD 所成角为30°，求SB 的长．13、（金丽衢十二校2018届高三第三次（5月）联考）如图，直三棱柱ABC ﹣A 1B 1C 1中，∠ACB=90°，AC=BC=3，AA 1=2，以AB ，BC 为邻边作平行四边形ABCD ，连接DA 1和DC 1．（Ⅰ）求证：A 1D ∥平面BCC 1B 1；（Ⅱ）线段BC 上是否存在点F ，使平面DA 1C 1与平面A C 1F 垂直？若存在，求出BF的长；若不存在，说明理由．14、（宁波市2018届高三5月模拟）如图，四边形ABCD 为梯形，，∥︒=∠60,C CD AB 点E 在线段CD 上，满足BE CD ⊥,且124CE AB CD ===，现将ADE ∆沿AE 翻折到AME 位置，使得210MC =．（Ⅰ）证明：AE MB ⊥;（Ⅱ）求直线CM 与面AME 所成角的正弦值．15、（宁波市2018届高三上期期末）如图，在四棱锥P ABCD -中，侧面PCD ⊥底面ABCD ，底面ABCD 为矩形，E 为PA 的中点，2ABa =，BC a =，2PC PD a ==.（1）求证：//PC 面BDE ；（2）求直线AC 与平面PAD 所成角的正弦值.16、（绍兴市2018届高三第二次（5月）教质量调测）如图，在四棱锥A BCD -中，△ABD 、△BCD 均为正三角形，且二面角A BD C --为120.(Ⅰ) 求证：AC BD ⊥；(Ⅱ) 求二面角B AD C --的余弦值.17、（台州市2018届高三上期期末质量评估）如图，正方形ABCD的边长为4，点E，F分别为BA，BC的中点，将△ADE，△DCF，分别沿DE，DF折起，使A，C两点重合于点A'，连接A B'．（Ⅰ）求证:EF⊥平面A BD'；（Ⅱ）求A D'与平面BEDF所成角的正弦值．参考答案：一、选择、填空题1、C2、A3、72324、143π；6(613)++π5、A6、D7、A8、9、A 10、B11、D 12、C 13、A 14、C 15、B 16、A 17、D 18、323，16162+ 二、解答题1、（1）∵12AB B B ==，且1B B ⊥平面ABC ，∴1B B AB ⊥，∴122AB =. 同理，222211(23)113AC AC C C =+=+=.过点1C 作1B B 的垂线段交1B B 于点G ，则12C G BC ==且11B G =，∴115B C =. 在11AB C ∆中，2221111AB B C AC +=， ∴111AB B C ⊥，①过点1B 作1A A 的垂线段交1A A 于点H . 则12B H AB ==，12A H =，∴1122A B =. 在11A B A ∆中，2221111AA AB A B =+， ∴111AB A B ⊥，②综合①②，∵11111A B B C B ⋂=，11A B ⊂平面111A B C ，11B C ⊂平面111A B C ，∴1AB ⊥平面111A B C .（2）过点B 作AB 的垂线段交AC 于点I ，以B 为原点，以AB 所在直线为x 轴，以BI 所在直线为y 轴，以1B B 所在直线为z 轴，建立空间直角坐标系B xyz -.则(0,0,0)B ，(2,0,0)A -，1(0,0,2)B ，1(1,3,1)C ，设平面1ABB 的一个法向量(,,)n a b c =，则1020200n AB a c n BB ⎧⋅==⎧⎪⇒⎨⎨=⋅=⎩⎪⎩，令1b =，则(0,1,0)n =，又∵1(3,3,1)AC =，1339cos ,13113n AC <>==⨯. 由图形可知，直线1AC 与平面1ABB 所成角为锐角，设1AC 与平面1ABB 夹角为α. ∴39sin 13α=. 2、（Ⅰ）如图，设P A 中点为F ，连结EF ，FB .因为E ，F 分别为PD ，P A 中点，所以EF ∥AD 且，又因为BC ∥AD ，，所以EF∥BC且EF=BC，即四边形BCEF为平行四边形，所以CE∥BF，因此CE∥平面P AB.（Ⅱ）分别取BC，AD的中点为M，N.连结PN交EF于点Q，连结MQ.因为E，F，N分别是PD，P A，AD的中点，所以Q为EF中点，在平行四边形BCEF中，MQ∥CE.由△P AD为等腰直角三角形得PN⊥AD.由DC⊥AD，N是AD的中点得BN⊥AD.所以AD⊥平面PBN，由BC∥AD得BC⊥平面PBN，那么，平面PBC⊥平面PBN.过点Q作PB的垂线，垂足为H，连结MH.MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角.设CD=1.在△PCD中，由PC=2，CD=1，PD=得CE=，在△PBN中，由PN=BN=1，PB=得QH=，在Rt△MQH中，QH=，MQ=，所以sin∠QMH=，所以，直线CE与平面PBC所成角的正弦值是.3、（II）方法一：B．过点F作FQ⊥AK，连结Q因为F B ⊥平面C A K ，所以F B ⊥AK ，则AK ⊥平面QF B ，所以Q B ⊥AK ．所以，QF ∠B 是二面角D F B -A -的平面角．在Rt C ∆A K 中，C 3A =，C 2K =，得313FQ 13=．在Rt QF ∆B 中，313FQ 13=，F 3B =，得3cos QF 4∠B =．所以，二面角D F B -A -的平面角的余弦值为34．4、（Ⅰ）有题意知AM ⊥BD ，又因为 AC ′⊥BD ，所以 BD ⊥平面AMC ，因为BD ⊂平面ABD ，所以平面AMC ⊥平面AB D ． …………7分（Ⅱ）在平面AC ′M 中，过C ′作C ′F ⊥AM 交AM 于点F ，连接F D ．由（Ⅰ）知，C ′F ⊥平面ABD ，所以∠C ′DF 为直线C ′D 与平面ABD 所成的角．设AM ＝1，则AB ＝AC ＝2，BC ＝3，MD ＝2－3， DC ＝DC ′＝33－2，AD ＝6－2．在Rt △C ′MD 中， 22222(332)(23)MC C D MD ''=-=---＝9－43．设AF ＝x ，在Rt △C ′F A 中，AC ′2－AF 2＝MC ′2－MF 2，即 4－x 2＝(9－43)－(x －1)2，解得，x ＝23－2，即AF ＝23－2．所以 C ′F ＝2233-．故直线C D '与平面ABD 所成的角的正弦值等于C FAF '＝23331--． …………15分5、ABC′D M F （第19题）6、解：(Ⅰ) 取AB 的中点E ，连接PE ，EC ．-------2分由点E 是正PAB ∆边AB 的中点，PE AB ⊥，又平面PAB ⊥平面ABCD ，平面PAB平面=ABCD AB ,所以PE ⊥平面ABCD ，则PE BD ⊥．----------4分因为12,22BE BCBC CD ===90EBC BCD ∠=∠=︒，所以EBC BCD ∆∆∽．故ECB BDC ∠=∠，则CE BD ⊥，--------------------6分CEPE E =，故BD ⊥平面PEC ，又PC ⊂平面PEC因此PC BD ⊥．-------------------------------------------7分（Ⅱ）在平面PAB 内过点B 作直线//m FC ,过F 作FG m ⊥于G ，连接PG 。

精编新版2019高中数学单元测试《立体几何初步》专题完整考题(含参考答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD,正方体的六个面所+=在的平面与直线CE,EF相交的平面个数分别记为,m n,那么m n（）A．8 B．9 C．10 D．11（2013年高考江西卷（理））2．设四面体的六条棱的长分别为a,且长为a,则a的取值范围是（）A．B．C．D．（2012重庆理）3．梯形ABCD中AB//CD，AB⊂平面α，CD⊄平面α，则直线CD与平面α内的直线的位置关系只能是（）（A）平行（B）平行和异面（C）平行和相交（D）异面和相交4．已知m，n为异面直线，m∥平面α，n∥平面β，α∩β=l，则l（）（A）与m，n都相交（B）与m，n中至少一条相交（C）与m，n都不相交（D）与m，n中一条相交二、填空题5．若一个正三棱锥的高为5，底面边长为6，则这个正三棱锥的体积为．6．已知一圆柱的侧面展开图是一长和宽分别为π3和π的矩形，则该圆柱的体积是。

7．若圆锥的侧面展开图是圆心角为120°、半径为l 的扇形，则这个圆锥的表面积与侧面积的比是________．解析：设圆锥的底面半径为r ，则2π3l ＝2πr ，∴l ＝3r ，∴S 表S 侧＝πr 2＋πrl πrl ＝πr 2＋3πr 23πr 2＝43.8．已知直线a ，b ，平面α，则以下三个命题：①若a ∥b ，b ⊂α，则a ∥α；②若a ∥b ，a ∥α，则b ∥α；③若a ∥α，b ∥α，则a ∥b .其中真命题的个数是________．解析：对于命题①，若a ∥b ，b ⊂α ，则应有a ∥α或a ⊂α，所以①不正确；对于命题 ②，若a ∥b ，a ∥α，则应有b ∥α或b ⊂α，因此②也不正确；对于命题③，若a ∥α，b ∥α，则应有a ∥b 或a 与b 相交或a 与b 异面，因此③是错误的．综上，在空间中，以上三个命题都是错误的．9．，直线所成角的余弦值为 ▲ ．10．已知正六棱锥的底面边长是3，侧棱长为5，则该正六棱锥的体积是。

新版精选2019高中数学单元测试《立体几何初步》专题考试题(含答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设有直线m 、n 和平面α、β。

下列四个命题中，正确的是 A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β，m ⊂α,则m ⊥βD.若α⊥β，m ⊥β，m ⊄α,则m ∥α(2008湖南理)（D ）2．对于平面α和共面的直线m 、,n 下列命题中真命题是（A ）若,,m m n α⊥⊥则n α∥ （B ）若m αα∥,n ∥,则m ∥n（C ）若,m n αα⊂∥,则m ∥n （D ）若m 、n 与α所成的角相等，则m ∥n (2006福建理)3．不共面的四个定点到平面α的距离都相等，这样的平面α共有（）个 A.3 B.4 C.6 D.7(2005全国3理) 4．对于直线m 、n 和平面α，下面命题中的真命题是（）A ．如果m n m ,,αα⊄⊂、n 是异面直线，那么α//nB ．如果m n m ,,αα⊄⊂、n 是异面直线，那么α与n 相交C ．如果m n m ,//,αα⊂、n 共面，那么n m //D ．如果m n m ,//,//αα、n 共面，那么n m //（2004全国4理7）5．某玻璃制品公司需要生产棱长均为3cm 的玻璃三棱柱一批。

请问每个三棱柱需要用玻璃多少cm 3 ？A 272B 274 D 34276．过空间任一点和两条异面直线都平行的平面有-----------------------------------------------（）(A) 1个 (B) 无数个 (C)至多一个 (D)不存二、填空题7．已知m ，n 是不重合的两条直线，α，β是不重合的两个平面．下列命题： ①若α⊥β，m ⊥α，则m ∥β； ②若m ⊥α，m ⊥β，则α∥β； ③若m ∥α，m ⊥n ，则n ⊥α； ④若m ∥α，m ⊂β，则α∥β．其中所有真命题的序号是 ▲ ．答案: ②8．用长、宽分别是12与8的矩形硬纸卷成圆柱的侧面，则圆柱的体积为． 9．给出下列关于互不相同的直线,,m l n 和平面,αβ的四个命题： ①若,,m lA A m αα⊂=∉，则l 与m 不共面②若,m l 是异面直线， //,//,,,l m n l n m n ααα⊥⊥⊥且则 ③若//,//,//,//l m l m αβαβ则 ④若,,,//,//,l m lm A l m ααββαβ⊂⊂=则//其中为真命题的是10．已知直线⊥a 平面α，直线//b 平面α，则直线b a ,的位置关系是______________； 11．线n m ,和平面βα、，能得出βα⊥的一个条件是__________； A βα//n ,//m ,n m ⊥ B αβα⊆=⊥n ,m ,n m C αβ⊆⊥m n n m ,,// D βα⊥⊥n m n m ,,//12．若m 、n 为两条不重合的直线，α、β为两个不重合的平面，则下列命题中的真命题是． ①若m 、n 都平行于平面α，则m 、n 一定不是相交直线； ②若m 、n 都垂直于平面α，则m 、n 一定是平行直线；③已知α、β互相垂直，m 、n 互相垂直，若α⊥m ，则β⊥n ；④m 、n 在平面α内的射影互相垂直，则m 、n 互相垂直． 13．把半径为3cm ,中心角为π32的扇形卷成一个圆锥形容器，这个容器的容积为：__________．ABD1A 1B 1C 1D CEF 14．在正方体1111D C B A ABCD -中，与1AD 平行的表面的对角线有条15．如图，正方体1111D C B A ABCD -中，E 、F 分别是棱BC 与C C 1的中点，则直线EF 与直线C D 1所成角的大小是 ▲ ．16．如图，设平面α∩β＝EF ，AB ⊥α，CD ⊥α，垂足分别为B 、D . 若增加一个条件，就能推出BD ⊥EF ，现有：①AC ⊥β；②AC 与α，β所成的角相等；③AC 与CD 在β内的射影在同一条直线上；④AC ∥EF ，那么上述几个条件中能成为增加条件的是________． (填上你认为正确的序号)解析：对于①AC ⊥β，知AC ⊥EF ， ∴EF ⊥平面ABDC ，∴EF ⊥BD ，对于②④不能得到BD ⊥EF ；对于③知平面ABCD ⊥平面β，又平面ABCD ⊥α， ∴EF ⊥平面ABDC ， ∴EF ⊥BD ，填①③.17．下列命题中：①三点确定一个平面；②一点和一条直线确定一个平面；③垂直于同一平面的两条直线平行；④一条直线平行于一个平面，这条直线就和平面内任何直线不相交。

高中数学人教A版(2019)选择性必修一空间向量与立体几何单元测试

高中数学人教A 版（2019）选择性必修一空间向量与立体几何单元测试一、单选题(共8题；共16分)1．（2分）已知点 A(−3,1,−4) ， B(3,−5,10) ，则线段 AB 的中点 M 的坐标为（）A ．(0,−4,6)B ．(0,−2,3)C ．(0,2,3)D ．(0,−2,6)2．（2分）如果向量 a⃗ =(2,−1,3) ， b ⃗ =(−1,4,2) ， c ⃗ =(1,−1,m) 共面，则实数 m 的值是（） A ．-1 B ．1 C ．-5 D ．53．（2分）已知O ，A ，B ，C 为空间不共面的四点，且向量 a ⃗ = OA ⃗⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ ，向量 b ⃗ = OA ⃗⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗⃗ −OC ⃗⃗⃗⃗⃗ ，则不能与 a ⃗ ,b ⃗ 构成空间的一个基底的是（） A ．OA⃗⃗⃗⃗⃗⃗ B ．OB ⃗⃗⃗⃗⃗⃗ C ．OC ⃗⃗⃗⃗⃗D ．OA ⃗⃗⃗⃗⃗⃗ 或 OB⃗⃗⃗⃗⃗⃗ 4．（2分）已知向量 a ⃗ =(0，3，3) 和 b⃗ =(−1，1，0) 分别是直线 l 和 m 的方向向量，则直线 l 与 m 所成的角为( )A ．π6B ．π4C ．π3D ．π25．（2分）若向量 a ⃗ =(1，λ，1) ， b⃗ =(2，−1，−2)，且 a ⃗ 与 b ⃗ 的夹角余弦为 √26，则λ等于（） A ．−√2B ．√2C ．−√2 或 √2D ．26．（2分）如图，在空间直角坐标系中，正方体ABCD －A 1B 1C 1D 1的棱长为1，B 1E ＝ 14A 1B 1，则 BE → 等于( )A ．(0，14，−1)B ．(−14，0，1)C ．(0，−14，1)D ．(14，0，−1)7．（2分）设 x,y ∈R ，向量 a ⃗ =(x,1,1) ， b ⃗ =(1,y,1) ， c ⃗ =(2,−2,2) ，且 a ⃗ ⊥c ⃗ ， b ⃗ //c ⃗ ，则 |a+b⃗ |= （） A ．2√2 B ．3 C ．√5 D ．48．（2分）已知正四面体 D −ABC 的各棱长为1，点 E 是 AB 的中点，则 EC⇀⋅AD ⇀ 的值为（） A ．14B ．−14C ．√34D ．−√34二、多选题(共4题；共12分)9．（3分）已知M(-1，1，3)，N(-2，-1，4)，若M ，N ，O 三点共线，则O 点坐标可能为（）A ．(3，5，-2)B ．(-4，-5，6)C ．( −52， 12 ， −2 )D ．(0，3，2)10．（3分）空间直角坐标系中，下列说法正确的是（）A ．点 P(1,2,3) 关于坐标平面 xOy 的对称点的坐标为 (−1,2,−3)B ．点 Q(1,0,2) 在平面 xOz 面上C ．z =1 表示一个与坐标平面 xOy 平行的平面D ．2x +3y =6 表示一条直线11．（3分）在长方体 ABCD −A 1B 1C 1D 1 中， AB =AD =2 ， AA 1=3 ，以D 为原点， DA ⃗⃗⃗⃗⃗⃗ ， DC ⃗⃗⃗⃗⃗⃗ ， DD 1⃗⃗⃗⃗⃗⃗⃗⃗ 的方向分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，则下列说法正确的是（）A ．B 1 的坐标为(2，2，3)B ．BC 1⃗⃗⃗⃗⃗⃗⃗⃗ =(-2，0，3)C ．平面 A 1BC 1 的一个法向量为(-3，3，-2)D ．二面角 B −A 1C 1−B 1 的余弦值为 √221112．（3分）设动点 P 在正方体 ABCD −A 1B 1C 1D 1 的对角线 BD 1 上，记 D 1P ⃗⃗⃗⃗⃗⃗⃗⃗ =λD 1B ⃗⃗⃗⃗⃗⃗⃗⃗ 当 ∠APC 为钝角时，则实数可能的取值是（） A ．12B ．23C ．13D ．1三、填空题(共4题；共4分)13．（1分）如图所示，在正方体 ABCD −A 1B 1C 1D 1 中，点 E 为线段 AB 的中点，点 F 在线段 AD 上移动，异面直线 B 1C 与 EF 所成角最小时，其余弦值为 .14．（1分）如图,在三棱柱ABC−A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为.15．（1分）如图，二面角α−l−β为135°，A∈α，B∈β，过A，B分别作l的垂线，垂足分别为C，D，若AC=1，BD=√2，CD=2，则AB的长度为.16．（1分）四棱锥P−ABCD中，PD⊥底面ABCD，底面ABCD是正方形，且PD=1，AB=3，G是△ABC的重心，则PG与面P AB所成角θ的正弦值为.四、解答题(共6题；共65分)17．（10分）如图，在以A，B，C，D，E，F为顶点的多面体中，四边形ABCD是矩形，AB=2，AD=√6，EA⊥平面ABCD，FD//EA，EA=12FD=√2.（1）（5分）求证：BE//平面CDF；（2）（5分）求二面角C−EF−D的余弦值. 18．（10分）如图，在空间直角坐标系中有直三棱柱ABC−A1B1C1,底面是等腰直角三角形，AB=2，∠ACB=90°,侧棱BB1=2，D,E分别是CC1，A1B的中点.（1）（5分）求平面AED与平面AEC1的夹角的余弦.（2）（5分）求AC1与平面ADE所成角的余弦值.19．（10分）如图，在直三棱柱ABC−A1B1C1中，∠BAC=90°，AB=AC=AA1，E，F分别是AC和AB上动点，且AE=BF.（1）（5分）求证：B1E⊥C1F；（2）（5分）若AE=2EC，求二面角A1−EF−A的平面角的余弦值.20．（10分）如图，在四棱锥S−ABCD中，底面ABCD为矩形，SA⊥平面ABCD，AB=1,AD=AS=2，P是棱SD上一点，且SP=12PD.（1）（5分）求直线AB与CP所成角的余弦值；（2）（5分）求二面角A−PC−D的余弦值．21．（10分）如图，在直四棱柱ABCD−A1B1C1D1中，四边形ABCD为平行四边形，BC=BD=1,AB=√2，直线CC1与平面A1BD所成角的正弦值为√33.（1）（5分）求点C1到平面A1BD的距离；（2）（5分）求平面A1BD与平面C1BD的夹角的余弦值.22．（15分）如图，在四棱锥P−ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AB=AP，E 为棱PB的中点. （1）（5分）求直线PD与CE所成角的余弦值；（2）（5分）求直线CD与平面ACE所成角的正弦值；（3）（5分）求二面角E−AC−P的余弦值.答案解析部分1．【答案】B【解析】【解答】解：因为点 A(−3,1,−4) ， B(3,−5,10) ，线段 AB 的中点 M 的坐标为 (0,−2,3) ，故选B.【分析】利用中点坐标公式求解即可.2．【答案】B【解析】【解答】由于向量 a ⃗ =(2,−1,3) ， b ⃗ =(−1,4,2) ， c ⃗ =(1,−1,m) 共面，设 c ⃗ =xa ⃗ +yb ⃗ ，可得 {2x −y =1−x +4y =−13x +2y =m，解得 { x =37y =−17m =1. 故答案为：B.【分析】由向量的共线定理代入数值计算出结果即可。

精编新版2019高中数学单元测试《立体几何初步》专题考核题完整版(含参考答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图，正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，点P 在球面上，如果163P ABCD V -=，则球O 的表面积是（A ）4π （B ）8π （C ）12π （D ）16π(2006年高考四川文)2．设m 、n 是两条不同的直线，,,αβγ是三个不同的平面，给出下列四个命题： ①若，，则 ②若，，，则③若，，则 ④若αγ⊥，βγ⊥，则//αβ其中正确命题的序号是 A ①和② B ②和③ C ③和④D ①和④3．α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线, 给出四个论断：① m ⊥ n ②α⊥β ③ m ⊥β ④ n ⊥α以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：___________________.4．如图，四棱锥S-ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确．．．的是（）(2011年高考辽宁卷理科8)(A) AC ⊥SB (B) AB ∥平面SCD(C) SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 (D)AB 与SC 所成的角等于DC 与SA 所成的角 5．1．下列说法中正确的是----------------------------------------------------------------------------------（）(A)互相垂直的两条直线的直观图仍然是互相垂直的两条直线 (B)梯形的直观图可能是平行四边形 (C)矩形的直观图可能是梯形 (D)正方形的直观图可能是平行四边6．下列命题中，正确的是------------------------------------------------------------------------------（） (A)两条直线确定一个平面 (B)三条平行直线确定一个平面 (C)一条直线和一点确定一个平面 (D)两条相交直线确定一个平二、填空题7．三棱锥O ABC -的侧棱,,OA OB OC 两两垂直且长度分别为2cm ，3cm ，1cm ，则该三棱锥的体积是 ▲ cm 3．8．已知l 、m 、n 是直线，a 、b 、g 是平面，下列命题中为真命题是 ① 若//m l ，且m a ⊥，则l a ⊥； ② 若//m l ，且//m a ，则//l a ； ③ 若l a b =，m b g =，n g a =，则////l m n ；④ 若m a g =，l bg =，且//a b ，则//m l ．9．如图，在四棱锥O ABCD -中，底面A B C D 为菱形，3π=∠ABC ,OA ABCD ⊥底面, 2OA =,M 为OA 的中点，N 为BC 的中点。

精选最新版2019高中数学单元测试《立体几何初步》专题完整考题(含答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则（）A ．βα//,且α//lB ．βα⊥,且β⊥lC ．α与β相交,且交线垂直于lD ．α与β相交,且交线平行于l （2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））2．表面积为的正八面体的各个顶点都在同一个球面上，则此球的体积为（）A B ．13π C ．23π D (2006安徽理)3．把正方形ABCD 沿对角线AC 折起，当A 、B C 、D 四点为顶点的三棱锥体积最大时，直线BD 与平面ABC 所成的角的大小为（）A ．90°B ．60°C ．45°D ．30°(2004湖南理)4．设α、β 为两个不同的平面，l 、m 为两条不同的直线，且l ⊂α，m ⊂β，有如下的两个命题：①若α∥β，则l ∥m ；②若l ⊥m ，则α⊥β．那么（）(A) ①是真命题，②是假命题 (B) ①是假命题，②是真命题 (C) ①②都是真命题 (D) ①②都是假命题(2005浙江文)5．在正三棱柱111C B A ABC -中，若AB=2，11AA =则点A 到平面BC A 1的距离为（）A ．43 B ．23 C ．433 D ．3(2005江苏)6．线n m ,和平面βα、，能得出βα⊥的一个条件是A βα//n ,//m ,n m ⊥ Bαβα⊆=⊥n ,m ,n mC αβ⊆⊥m n n m ,,//D βα⊥⊥n m n m ,,//二、填空题7．已知,,αβγ是三个互不重合的平面， l 是一条直线，给出下列四个命题： ①若,l αββ⊥⊥，则//l α ②若,//l l αβ⊥，则αβ⊥③若l 上有两个点到α的距离相等，则//l α； ④若,//,αβαγ⊥则γβ⊥ 其中正确命题的序号是8．给出下列关于互不相同的直线,,m l n 和平面,αβ的四个命题： ①若,,m lA A m αα⊂=∉，则l 与m 不共面②若,m l 是异面直线， //,//,,,l m n l n m n ααα⊥⊥⊥且则 ③若//,//,//,//l m l m αβαβ则 ④若,,,//,//,l m lm A l m ααββαβ⊂⊂=则//其中为真命题的是9．线n m ,和平面βα、，能得出βα⊥的一个条件是__________； A βα//n ,//m ,n m ⊥ B αβα⊆=⊥n ,m ,n m C αβ⊆⊥m n n m ,,// D βα⊥⊥n m n m ,,//10．已知正四棱锥S ABCD -中，SA =，那么当该棱锥的体积最大时，它的高为．11．如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为__________.（2013年高考北京卷（理））12．已知直线b a ,和平面α，若αα⊥⊥b a ,，则a 与b 的位置关系是．13．设γβα,,为两两不重合的平面，n m l ,,为两两不重合的直线，给出下列四个命题：①若γα⊥，γβ⊥，则βα||；②若α⊂m ，α⊂n ，β||m ，β||n ，则βα||； ③若βα||，α⊂l ，则β||l ；④若l =βα ，m =γβ ，n =αγ ，γ||l ，则m ||其中真命题的个数是（）A ．1B ．2C ．3D ．4(2005江苏) 14．已知平面,,αβγ,直线,l m 满足：,,,αγγαγβ⊥==⊥m l l m ,那么①m β⊥； ②l α⊥； ③βγ⊥； ④αβ⊥.可由上述条件可推出的结论有 ▲ (请将你认为正确的结论的序号都填上). (江苏省盐城市2011届高三年级第一次调研) ②④15．已知两条直线m ，n ，两个平面βα,，给出下面四个命题： ①αα⊥⇒⊥n m n m ,//； ②n m n m //,,//⇒⊂⊂βαβα；③αα////,//n m n m ⇒；④./,//,//βαβα⊥⇒⊥n m n m其中真命题．．．的序号。

精选2019高中数学单元测试《立体几何初步》专题完整考题(含标准答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图，平面α⊥平面β，,,A B AB αβ∈∈与两平面α、β所成的角分别为4π和6π。

过A 、B 分别作两平面交线的垂线，垂足为'A 、',B 则:''AB A B =(A)A'B'A B βα（A ）2:1 （B ）3:1 （C ）3:2 （D ）4:3(2006全国2理)2．梯形ABCD 中AB//CD ，AB ⊂平面α，CD ⊄平面α，则直线CD 与平面α内的直线的位置关系只能是（）（A ）平行（B ）平行和异面（C ）平行和相交（D ）异面和相交3．下列说法中正确的是A 经过两条平行直线,有且只有一个平面直线B 如果两条直线同平行于同一个平面,那么这两条直线平行C 三点唯一确定一个平面D 不在同一平面内的两条直线相互垂直,则这两个平面也相互垂直二、填空题4．如图表示一个正方体表面的一种展开图,图中的四条线段AB 、CD 、EF 和GH 在原正方体中相互异面的有 ▲ 对5．如图，在ABC ∆中，90ACB ∠=，,AC b BC a ==，P 是ABC ∆所在平面外一点，PB AB ⊥，M 是PA 的中点，,AB MC MN PB ⊥⊥于N ，则异面直线MC 与PB 间的距离为________________6．已知球的一个截面的面积为9π，且此截面到球心的距离为4, 求此球的表面积为___________7．正方体的八个顶点中有四个恰好为正四面体的顶点，则正方体的全面积与正四面体的全面积之比为。

8．在正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为棱AA 1、CC 1的中点，则在空间中与三条直线A 1D 1、EF 、CD 都相交的直线有________条．解析：在A 1D 1上任取一点P .过点P 与直线EF 作一个平面α，因CD 与平面α不平行，所以它们相交，设α∩CD ＝Q ，连结PQ ，则PQ 与EF 必然相交，即PQ 为所求直线．由点P 的任意性，知有无数条直线与A 1D 1、EF 、CD 都相交．9．两个相交平面能把空间分成 ▲ 个部分10．已知棱长为3的正方体ABCD-A 1B 1C 1D 1中，P 、M 分别为线段BD 1，B 1C 1上的点，若112BP PD =则三棱锥M －PBC 的体积为 ▲11．设γβα,,为两两不重合的平面，m,n,l 为两两不重合的直线，给出下列命题： ①若βαγβγα//,,则⊥⊥； ②若βαββαα//,//,//,,则n m n m ⊂⊂； ③若βαβα//,//l l 则，⊂； ④若n m l n m l //,//,,,则γαγγββα=== ．其中真命题的个数是．12．已知某四面体的六条棱长分别为，，，则两条较长棱所在直线所成角的余弦值为 ▲ ．13．Rt ABC ∆在平面α内的射影是111A B C ∆，设直角边AB α，则111A B C ∆的形状是三角形．14．空间中可以确定一个平面的条件是 _．(填序号) ①两条直线； ②一点和一直线； ③一个三角形； ④三个点．15．已知三棱台111ABC A B C -中，三棱锥111B A B C -、1A ABC -的体积分别为2、18，则此三棱台的体积的值等于______________．16．正方体1111ABCD A B C D -中,异面直线AC 与1BC 所成的角为 _____17．如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号). （2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S18．已知正四棱柱1111ABCD A B C D -中，12AA AB =，E 为1AA 的中点，则异面直线BE 与1CD 所成角的正切值为．19．如图AB 为圆O 的直径，点C 在圆周上（异于B A ,点）直线PA 垂直于圆所在的平面，点M 为线段PB 的中点，有以下四个命题：(1)PA//平面MOB; (2)MO//平面PAC (3)OC ⊥平面PAB; （4）PC BC ⊥ 其中正确的命题是 ▲ .(第10题)20．如图，在底面是菱形的四棱锥P ABCD -中，060ABC ∠=，PA AC a ==，PB PD ==,点E 在PD 上，且21PE ED =.（1）证明：PA ⊥平面ABCD ；（2）在棱PC 上是否存在一点F ，使BF //平面AEC ？证明你的结论21．已知α、β是两个不同的平面，下列四个条件： ①存在一条直线a ，a α⊥，a β⊥； ②存在一个平面γ，,γαγβ⊥⊥；③存在两条平行直线a 、b ，,a b αβ⊂⊂，a ∥β，b ∥α； ④存在两条异面直线a 、b ，,a b αβ⊂⊂，a ∥β，b ∥α。

精选最新2019高中数学单元测试《立体几何初步》专题完整考试题(含标准答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设三棱柱ABC-A 1B 1C 1的体积是V ，P .Q 分别是侧棱AA 1上的点，且PA=QC 1，则四棱锥B-APQC 的体积为（）A.V 61 B.V 41 C.V 31 D.V 21 (2005全国3理)2．正三棱柱的侧面展开图是边长分别为6和4的矩形，则它的体积为 ( ) A.89 3 B ．4 3 C.29 3 D ．43或83 3 解析：分侧面矩形长、宽分别为6和4或4和6两种情况3．下列命题中正确的有---------------------------------------------------------------------------------（） ①三点确定一个平面；②两两相交的三条直线必在同一平面内；③任意三点都不共线的空间四点必共面；④空间三条相交于同一点的直线在同一平面内 (A) 1个 (B) 2个 (C) 3个 (D) 0 二、填空题4．已知,αβ是不重合的平面，,m n 是不重合的直线，下列命题正确的序号为 ▲ ①//,////m n n m αα⇒； ②,//m m αβαβ⊥⊥⇒ ③,//,////n m m m n αβαβ=⇒ ④,,m n m n αβαβ⊥⊥⊥⇒⊥5．如图，在正三棱锥A BCD -中，底面BCD ∆，点,E F 分别是CD 和AD 的中点，且EF BF ⊥，则正三棱锥A BCD -的外接球的表面积为 ▲ .第11题6．如图，有一圆柱形的开口容器（下表面密封），其轴截面是边长为2的正方形，P 是BC 中点，现有一只蚂蚁位于外壁A 处，内壁P 处有一米粒，则这只蚂蚁取得米粒所需经过的最短路程为．7．在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为 cm 3．8．已知三条不重合的直线两个不重合的平面，有下列命题：①若||,m n n α⊂，则||m α；②若,l m αβ⊥⊥，且||l m ，则||αβ；③若,,||,||m n m n ααββ⊂⊂则||αβ；④若,,,m n n m αβαββ⊥=⊂⊥，则n α⊥。

2019届人教A版(文科数学) 立体几何单元测试

立体几何一、选择、填空题1、（2018全国III 卷高考）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）2、（2017全国III 卷高考）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A ．πB ．3π4C ．π２D ．π43、（2016全国III 卷高考）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（A ）18365+ （B ）54185+ （C ）90 （D ）814、（成都市2018届高三第二次诊断）已知m ，是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，则下列命题正确的是（）A ．若m α⊂，则m β⊥B ．若m α⊂，n β⊂，则m n ⊥C ．若m α⊄，m β⊥，则//m αD ．若m αβ= ，n m ⊥，则n α⊥5、（成都市2018届高三第三次诊断）在正三棱柱111ABC A B C - (底面是正三角形,侧棱垂直于底面的棱柱)中，所有棱长之和为定值a .若正三棱柱111ABC A B C -的顶点都在球O 的表面上，则当正三棱柱侧面积取得最大值24时，该球的表面积为（） A ．43π B ．323π C ．12π D ．643π6、（达州市2017届高三第一次诊断）如图某几何体的三视图是直角边长为1的三个等腰直角三角形，则该几何体的外接球的表面积为（） A ．32π B ．3π C ．32π D ．3π7、（德阳市2018届高三二诊考试）如图所示的三视图表示的几何体的体积为323，则该几何体的外接球的表面积为（）A ．12πB ．24πC ．36πD ．48π8、（广元市2018届高三第一次高考适应性统考）设,m n 是两条不同的直线，,αβ是两个不同的平面，且,m n αβ⊂⊂，下列命题中正确的是（）A ．若αβ⊥，则m n ⊥B ．若//αβ，则//m nC ．若m n ⊥，则αβ⊥D ．若n α⊥，则αβ⊥ 9、（泸州市2018届高三第二次教学质量诊断）设a ，b 是两条不同的直线，α、β是不重合的两个平面，则下列命题中正确的是A ．若a b ⊥，a α⊥，则//b αB ．若//a α，αβ⊥，则//a βC ．若//a α，//a β，则//αβD ．若//a b ，a α⊥，b β⊥，则//αβ10、（南充市2018届高三第二次高考适应性考试）某三棱锥的三视图如图所示，则该三棱锥的表面积为( )A ．23472++B ．1072+ C. 710+ D ．3412+11、（仁寿县2018届高三上学期零诊）如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，E 为棱DD 1上的点，F 为AB 的中点，则三棱锥B 1﹣BFE 的体积为12、（遂宁市2018届高三三诊考试）在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示，则此机械部件的表面积为A ．π)27(-B ．π)27(+C ．π)26(+D ．π)37(-13、（雅安市2018届高三下学期三诊）某几何体的三视图如图所示，其中，正视图、俯视图都是矩形，侧视图是直角三角形，则该几何体的体积等于（）A ．1B ．2C ．3D ．414、（资阳市2018届高三4月模拟考试（三诊））如图，二面角BC αβ--的大小为6π，AB CD αβ⊂⊂，，且2AB =，243BC CD ABC BCD ππ==∠=∠=，，，则AD 与β所成角的大小为A ．π4B ．π3 C.π6D ．π1215、（成都市石室中学高2018届高三下期二诊模拟）一个底面为正方形的四棱锥，其三视图如图所示，若这个四棱锥的体积为2 ，则此四棱锥最长的侧棱长为 .23A.11B .13C .10D16、（成都市2018届高三第二次诊断）《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马，其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上，则该球的体积为（）A ．863π B ．86π C ．6π D ．24π 17、（2016全国III 卷高考）在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是（A ）4π （B ）92π（C ）6π （D ）323π二、解答题1、（2018全国III 卷高考）如图，边长为2的正方形ABCD 所在平面与半圆弧 CD所在平面垂直，M 是 CD上异于C ，D 的点． ⑴证明：平面AM D ⊥平面BMC ；⑵当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．2、（2017全国III 卷高考）如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形．ABD CBD ??，AB BD =．（1）证明：平面ACD ^平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分．求二面角D AE C --的余弦值．DABCE3、（2016全国III 卷高考）如图，四棱锥P ABC -中，PA ⊥地面A B C D ，AD BC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN 平面PAB ；（II ）求直线AN 与平面PMN 所成角的正弦值.4、（成都市2018届高三第二次诊断）如图，D 是AC 的中点，四边形BDEF 是菱形，平面BDEF ⊥平面ABC ，60FBD ∠=，AB BC ⊥，2AB BC ==.（1）若点M 是线段BF 的中点，证明：BF ⊥平面AMC ；（2）求平面AEF 与平面BCF 所成的锐二面角的余弦值.5、（成都市2018届高三第三次诊断）如图①,在等腰梯形ABCD 中，已知AB ∥CD ，60ABC ∠= ，2CD =，4AB =，点E 为AB 的中点；现将三角形BEC 沿线段EC 折起，形成直二面角P EC A --,如图②，连接,PA PD 得四棱锥P AECD -，如图③.（I ）求证：PD EC ⊥；（Ⅱ）求平面PEC 与平面PAD 所成的锐二面角的余弦值.6、（达州市2017届高三第一次诊断）如图在棱锥P ABCD -中，ABCD 为矩形，PD ⊥面ABCD ，2PB =，PB 与面PCD 成045角，PB 与面ABD 成030角.（1）在PB 上是否存在一点E ，使PC ⊥面ADE ，若存在确定E 点位置，若不存在，请说明理由；（2）当E 为PB 中点时，求二面角P AE D --的余弦值.7、（德阳市2018届高三二诊考试）如图，在四棱锥P ABCD -中，底面ABCD 为边长为2的菱形，60DAB ∠= ，90ADP ∠= ，面ADP ⊥面ABCD ，点F 为棱PD 的中点.（1）在棱AB 上是否存在一点E ，使得//AF 面PCE ，并说明理由；（2）当二面角D FC B --的余弦值为14时，求直线PB 与平面ABCD 所成的角. 8、（广元市2018届高三第一次高考适应性统考）如图，ABC ∆是以ABC ∠为直角的三角形，SA ⊥平面,2,4,,ABC SA BC AB M N ===分别是,SC AB 的中点. （1）求证：MN AB ⊥；（2）D 为线段BC 上的点，当二面角S ND A --的余弦值为66时，求三棱锥D SNC -的体积.9、（泸州市2018届高三第二次教学质量诊断）如图，三棱锥A BCD -的侧面ABD △是等腰直角三角形，90BAD ∠= ，BD DC =，120BDC ∠= ，且2AC AB =．（I ）求证：平面ABD ⊥平面BCD ；（II ）求二面角B AC D --的余弦值．DCBA10、（南充市2018届高三第二次高考适应性考试）如图，四棱锥ABCD P -中，底面ABCD 是边长为2的菱形，PB PA ABC ⊥︒=∠，660,2=PC . (Ⅰ)求证：平面⊥PAB 平面 ABCD ；(Ⅱ)若PB PA =,求二面角D PC A --的余弦值.11、（仁寿县2018届高三上学期零诊）如图，直角梯形ABCD 与等腰直角三角形ABE 所在的平面互相垂直，AB ∥CD ，AB ⊥BC ，AB=2CD=2BC ，EA ⊥EB （1）求证：EA ⊥平面EBC ；（2）求二面角C ﹣BE ﹣D 的余弦值．12、（遂宁市2018届高三三诊考试）如图所示的几何体中，111C B A ABC -为三棱柱，且⊥1AA 平面ABC ，四边形ABCD 为平行四边形，︒=∠=60,2ADC CD AD ．（1）若AC AA =1，求证：1AC ⊥平面CD B A 11；（2）若12,CD AA AC λ==，二面角11C A D C --的余弦值为24，求三棱锥11C ACD -的体积．13、（雅安市2018届高三下学期三诊）如图，在四棱锥S ABCD -中，SD ⊥底面ABCD ，M 为SD 的中点，底面ABCD 为直角梯形，AB AD ⊥，//AB CD ，且222CD AB AD ===.（1）求证：//AM 平面SBC ，平面SBC ⊥平面SDB ；（2）若SB 与平面SDC 所成角的正弦值为33，求二面角A SB C --的余弦值. 14、（资阳市2018届高三4月模拟考试（三诊））如图，三棱柱111ABC A B C -的各棱长均相等，1AA ⊥底面ABC ，E ，F 分别为棱1AA BC ，的中点．（1）过1FA 作平面α，使得直线BE //平面α，若平面α与直线1BB 交于点H ，指出点H 所在的位置，并说明理由；（2）求二面角1B FH A --的余弦值．15、（成都市石室中学高2018届高三下期二诊模拟）如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABC D 所在平面垂直，点M 为AE 的中点. （1）求证：BM //平面EFC（2）若DE AB =，求直线AE 与平面BDM 所成角的正弦值.参考答案：一、选择、填空题 1、A2、【答案】B【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径2213122r ⎛⎫=-= ⎪⎝⎭，则圆柱体体积23ππ4V r h ==，故选B.3、B4、C5、【答案】D【解析】设正三棱柱111ABC A B C -底面边长为x ，侧棱为y ，则63x y a +=，三棱柱111ABC A B C -侧面积3S xy =.所以2216336224x y a S xy +⎛⎫=≤= ⎪⎝⎭，当且仅当632a x y ==，即,126a a x y ==时，等号成立，所以24a =，2x =，4y =.所以正三棱柱111ABC A B C -的外接球的球心O 到顶点A 的距离为443434+=，所以该球的表面积为643π.故选D.6、D7、C8、D9、D 10、B 11、11212、B 13、B 14、C 15、C 16、C 17、【答案】B 【解析】试题分析：要使球的体积V 最大，必须球的半径R 最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径取得最大值32，此时球的体积为334439()3322R πππ==，故选B ．二、解答题1、解答：（1）∵正方形ABCD ⊥半圆面CMD ，∴AD ⊥半圆面CMD ，∴AD ⊥平面MCD .∵CM 在平面MCD 内，∴AD CM ⊥，又∵M 是半圆弧CD 上异于,C D 的点，∴CM MD ⊥.又∵AD DM D =I ，∴CM ⊥平面ADM ，∵CM 在平面BCM 内，∴平面BCM ⊥平面ADM .（2）如图建立坐标系： ∵ABC S ∆面积恒定，∴MO CD ⊥，M ABC V -最大.(0,0,1)M ，(2,1,0)A -，(2,1,0)B ，(0,1,0)C ，(0,1,0)D -,设面MAB 的法向量为111(,,)m x y z =u r ，设面MCD 的法向量为222(,,)n x y z =r， (2,1,1)MA =--，(2,1,1)MB =-，(0,1,1)MC =-，(0,1,1)MD =--，11111120(1,0,2)20x y z m x y z --=⎧⇒=⎨+-=⎩，同理(1,0,0)n =，，∴15cos 55θ==，∴ 25sin 5θ=.2、【解析】⑴取AC 中点为O ，连接BO ，DO ；ABC ∆ 为等边三角形 ∴BO AC ⊥ ∴AB BC =AB BC BD BDABD DBC =⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. ∴AD CD =,即ACD ∆为等腰直角三角形，ADC ∠ 为直角又O 为底边AC 中点 ∴DO AC ⊥令AB a =，则AB AC BC BD a ==== 易得：22OD a =，32OB a = ∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥OD AC OD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩ 平面平面OD ABC ∴⊥平面又∵OD ADC ⊂平面由面面垂直的判定定理可得ADC ABC ⊥平面平面 ⑵由题意可知V V D ACE B ACE --= 即B ,D 到平面ACE 的距离相等即E 为BD 中点以O 为原点，OA 为x 轴正方向，OB为y 轴正方向，OD为z 轴正方向，设AC a =，建立空间直角坐标系，则()0,0,0O ，,0,02a A ⎛⎫ ⎪⎝⎭，0,0,2a D ⎛⎫ ⎪⎝⎭，30,,02B a ⎛⎫ ⎪ ⎪⎝⎭，30,,44a E a ⎛⎫ ⎪ ⎪⎝⎭易得：3,,244a a AE a ⎛⎫=- ⎪ ⎪⎝⎭ ，,0,22a a AD ⎛⎫=- ⎪⎝⎭ ，,0,02a OA ⎛⎫= ⎪⎝⎭ 设平面AED 的法向量为1n ，平面AEC 的法向量为2n，则1100AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩ ，解得()13,1,3n = 2200AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩ ，解得()20,1,3n =- 若二面角D AE C --为θ，易知θ为锐角，则12127cos 7n n n n θ⋅==⋅3、DABCEODABCEyxOz设),,(z y x n =为平面PMN 的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=n ，于是2558|||||||,cos |=⋅=><AN n AN n AN n.4、解：（1）连接MD ，FD .∵四边形BDEF 为菱形，且60FBD ∠=， ∴DBF ∆为等边三角形.∵M 为BF 的中点，∴DM BF ⊥.∵AB BC ⊥，2AB BC ==，又D 是AC 的中点， ∴BD AC ⊥.∵平面BDEF 平面ABC BD =，平面ABC ⊥平面BDEF ，AC ⊂平面ABC ，∴AC ⊥平面BDEF .又BF ⊂平面BDEF ，∴AC BF ⊥.由DM BF ⊥，AC BF ⊥，DM AC D = ， ∴BF ⊥平面AMC.（2）设线段EF 的中点为N ，连接DN .易证DN ⊥平面ABC .以D 为坐标原点，DB ，DC ，DN 所在直线分别为轴，y 轴，轴建立如图所示的空间直角坐标系.则(0,1,0)A -，13(,0,)22E -，13(,0,)22F ，(1,0,0)B ，(0,1,0)C . ∴13(,1,)22AE =- ，(1,0,0)EF = ，13(,0,)22BF =- ，(1,1,0)BC =- .设平面AEF ，平面BCF 的法向量分别为111(,,)m x y z = ，222(,,)n x y z =. 由00AE m EF m ⎧⋅=⎪⎨⋅=⎪⎩111113022102x y z x ⎧-++=⎪⎪⇒⎨⎪=⎪⎩. 解得1132y z =-. 取12z =-，∴(0,3,2)m =-.又由00BC n BF n ⎧⋅=⎪⎨⋅=⎪⎩ 2222013022x y x z -+=⎧⎪⇒⎨-+=⎪⎩解得223y z =. 取21z =，∴(3,3,1)n =.∵cos ,m n <> m nm n⋅=11777==⋅.∴平面AEF 与平面BCF 所成的锐二面角的余弦值为17.5、【解析】6、1)法一：要证明PC ⊥面ADE ，易知AD ⊥面PDC ，即得AD ⊥PC ，故只需0DE PC ⋅=即可，所以由()00||1DP PE PC DP PC PE PC PE +⋅=⇒⋅+⋅=⇒=,即存在点E 为PC 中点 …6分法二：建立如图所示的空间直角坐标系D －XYZ ，由题意知PD ＝CD ＝1， 2CE =，设PE PB λ= ， (2,1,1)PE PB λλ∴==- ，(0,1,1)PC =-由()(0,1,1)(2,,1)0PC DE PC DP PE λλλ⋅=⋅+=-⋅-= ，得12λ=，即存在点E 为PC 中点。

精选最新2019高中数学单元测试《立体几何初步》专题完整题(含标准答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．已知正四棱锥S ABCD -的侧棱长与底面边长都相等，E 是SB 的中点，则AE SD ，所成的角的余弦值为（）A ．13B C D ．23(2008全国2理)2．已知m 、n 是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：①若βαβα//,,则⊥⊥m m ；②若βααβγα//,,则⊥⊥； ③若βαβα//,//,,则n m n m ⊂⊂；④若m 、n 是异面直线，βααββα//,//,,//,则n n m m ⊂⊂其中真命题是（） A ．①和②B ．①和③C ．③和④D ．①和④(2005辽宁)3．空间两直线平行是指它们--------------------------------------------------（）(A)无交点 (B)共面且无交点 (C)和同一直线垂直 (D)以上都不对 4．1．正方体1111ABCD A B C D -中，P Q R 、、分别是11AB AD B C 、、的中点，那么正方体的过P Q R 、、的截面图形是-----------------------------------------------------（）(A)三角形 (B)四边形 (C)五边形 (D)六边二、填空题5．如图，在四棱锥O ABCD-中，底面ABCD为菱形，3π=∠ABC,OA ABCD⊥底面, 2OA=,M为OA的中点，N为BC的中点（1）证明：BDOC⊥；（2）证明：ADAN⊥6．已知,a b是两条不重合的直线，,,αβγ是三个两两不重合的平面，给出下列四个命题：①若aα⊥，aβ⊥，则βα//②若βαγβγα//,,则⊥⊥③若baba//,,,//则βαβα⊂⊂④若baba//,,,//则=⋂=⋂γβγαβα其中正确命题的序号有____________。

精选2019高中数学单元测试《立体几何初步》专题完整考题(含答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．两个平面重合的条件是（）(A)有三个公共点 (B)有两条公共直线 (C)有无数多个公共点 (D)有一条公共直2．若干个棱长为2、3、5的长方体，依相同方向拼成棱长为90的正方体，则正方体的一条对角线贯穿的小长方体的个数是（） A ．64 B ．66C ．68D ．703．过正方体1111ABCD A B C D -的对角线1BD 的截面面积为S ，max S 和min S 分别为S 的最大值和最小值，则maxminS S 的值为（） A．2 B．2CD．3二、填空题4．在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为 cm 3．5．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个三棱柱的体积是，则这个球的体积是 .6．如图，在正方体ABCD -A 1B 1C 1D 1中，E ，F ，G 分别为棱AA 1，AB ，CC 1的中点，给出下列3对线段所在直线：①D 1E 与BG ；②D 1E 与C 1F ；③A 1C 与C 1F ．其中，是异面直线的对数共有 ▲ 对．BC DA 1 AB 1C 1D 1（第5题）EGF7．设,a b 是两条不同直线，,αβ是两个不同平面，给出下列四个命题：①若,,a b a α⊥⊥ b α⊄，则//b α；②若//,a ααβ⊥，则a β⊥；③若,a βαβ⊥⊥，则//a α或a α⊂；④若,,a b a b αβ⊥⊥⊥则αβ⊥．其中正确的命题是_____ ____（请把所有正确命题的序号都填上）．8．一个与球心距离为1的平面截球所得圆面面积为π，则球的体积为________.9．如图，直三棱柱ABC －A 1B 1C 1中，底面是等腰直角三角形， AB ＝BC ，BB 1＝3，D 为A 1C 1的中点，F 在线段AA 1上．（1）AF 为何值时，CF ⊥平面B 1DF ？（2）设AF =1，求平面B 1CF 与平面ABC 所成的锐二面角的余弦值. .10．已知命题：“若x ⊥y,y ∥z ，则x ⊥z ”成立，那么字母x,y,z 在空间所表示的几何图形有可能是：①都是直线；②都是平面；③x ，y 是直线，z 是平面； ④x ，z 是平面，y 是直线。

精编新版2019高中数学单元测试《立体几何初步》专题完整题(含标准答案)

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．关于直线m 、n 与平面α与β，有下列四个命题：（D ）①若//,//m n αβ且//αβ，则//m n ；②若,m n αβ⊥⊥且αβ⊥，则m n ⊥； ③若,//m n αβ⊥且//αβ，则m n ⊥；④若//,m n αβ⊥且αβ⊥，则//m n ；其中真命题的序号是A ．①②B ．③④C ．①④D ．②③(2006湖北文)2．已知空间三条直线.l m n 、、若l 与m 异面,且l 与n 异面,则（） A ．m 与n 异面. B ．m 与n 相交.C ．m 与n 平行.D ．m 与n 异面、相交、平行均有可能.（2012上海春）3．已知a b 、是异面直线，直线c 平行于直线a ，那么c 与b --------------------------------（）(A)一定是异面直线 (B)一定是相交直线 (C)不可能是平行直线 (D)不可能是相交直线二、填空题4．如图所示的“双塔”形立体建筑，已知P ABD -和Q CBD -是两个高相等的正三棱锥，四点,,,A B C D 在同一平面内．要使塔尖,P Q 之间的距离为50m ，则底边AB 的长为 m ．PQABD第6题图5．如图，用半径为2的半圆形铁皮卷成一个圆锥筒，那么这个圆锥筒的容积是 ▲ ____．6．已知直线m 、n 与平面α、β，给出下列三个命题：①若m ∥α，n ∥α，则m ∥n ；②若m ∥α，n ⊥α，则n ⊥m ；③若m ⊥α，m ∥β，则α⊥β.其中正确命题的个数是______________；7．将两个棱长为10cm 的正方体铜块熔化后铸成底面边长为5cm 的正四棱柱，则该四棱柱的高为________(不计损耗)．8．直角ABC ∆的三个顶点在半径为13的球面上，球心为O ，直角ABC ∆两直角边的长分别为6和8，则三棱锥O ABC -的体积为 .9．若M 、N 分别是△ABC 边AB 、AC 的中点，MN 与过直线BC 的平面β的位置关系是__________________10．下列四个命题：①若αα⊂b a ,//则b a //， ②若αα//,//b a 则b a // ③若α⊂b b a ,//则α//a ， ④若b a a //,//α则α//b 或α⊂b 其中为真命题的序号有 ☆ ．（填上所有真命题的序号）11．下列四个命题：①若αα⊂b a ,//，则b a //， ②若αα//,//b a ，则b a // ③若α⊂b b a ,//，则α//a ， ④若b a a //,//α，则α//b 或α⊂b 其中为真命题的序号有．（填上所有真命题的序号）12．给出下列命题：(1) 三条平行直线共面；(2) 在空间中，过直线外一点只能作一条直线与该直线平行；(3) 有三个公共点的两平面重合；(4) 若直线a b c 、、满足,a b a c ⊥⊥、则//b c . 其中正确命题的个数是．13．已知棱长为3的正方体ABCD-A 1B 1C 1D 1中，P 、M 分别为线段BD 1，B 1C 1上的点，若（第9题图）112BP PD =则三棱锥M －PBC 的体积为 ▲14．一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为h 1、h 2、h ，则h 1∶h 2∶h 等于________．解析：依题意，四棱锥为正四棱锥，三棱锥为正三棱锥，且棱长均相等，设为a ，h 2＝h ， h 1＝a 2－⎝⎛⎭⎫22a 2＝22a ，h 2＝a 2－⎝⎛⎭⎫33a 2＝63a ，故h 1∶h 2∶h ＝3∶2∶2.15．空间中，如果两个角的两条边分别对应平行，那么这两个角_____________________ 16．已知圆台上下底面半径之比是1:3，母线长10cm ，则截得该圆台的圆锥母线长__________17．若a b 、是异面直线，b c 、是异面直线，则a c 、的位置关系是____________________ 18．一个球与正四面体的六条棱都相切。

2019届人教A版(文科数学) 立体几何01 单元测试

精选新版2019高中数学单元测试《立体几何初步》专题完整题(含答案)

2019届人教A版(文科数学) 立体几何初步单元测试

2021年人教A版(2019)选择性必修第一册数学第一章_空间向量与立体几何单元测试卷高中答案解析

最新版精选2019高中数学单元测试《立体几何初步》专题完整版考核题(含答案)

精编新版2019高中数学单元测试《立体几何初步》专题完整考试题(含答案)

2019届人教A版(文科数学) 立体几何单元测试

精编新版2019高中数学单元测试《立体几何初步》专题完整考题(含参考答案)

新版精选2019高中数学单元测试《立体几何初步》专题考试题(含答案)

高中数学人教A版(2019)选择性必修一空间向量与立体几何单元测试

精编新版2019高中数学单元测试《立体几何初步》专题考核题完整版(含参考答案)

精选最新版2019高中数学单元测试《立体几何初步》专题完整考题(含答案)

精选2019高中数学单元测试《立体几何初步》专题完整考题(含标准答案)

精选最新2019高中数学单元测试《立体几何初步》专题完整考试题(含标准答案)

2019届人教A版(文科数学) 立体几何单元测试

精选最新2019高中数学单元测试《立体几何初步》专题完整题(含标准答案)

精选2019高中数学单元测试《立体几何初步》专题完整考题(含答案)

精编新版2019高中数学单元测试《立体几何初步》专题完整题(含标准答案)

最新精选2019高中数学单元测试《立体几何初步》专题完整考试题(含答案)

最新精选2019高中数学单元测试《立体几何初步》专题考试题(含答案)

2019届人教A版(文科数学) 立体几何01 单元测试

精选新版2019高中数学单元测试《立体几何初步》专题完整题(含答案)

2019届人教A版(文科数学) 立体几何初步 单元测试

2021年人教A版(2019)选择性必修第一册数学第一章_空间向量与立体几何单元测试卷高中答案解析

最新版精选2019高中数学单元测试《立体几何初步》专题完整版考核题(含答案)

精编新版2019高中数学单元测试《立体几何初步》专题完整考试题(含答案)

2019届人教A版(文科数学) 立体几何 单元测试

精编新版2019高中数学单元测试《立体几何初步》专题完整考题(含参考答案)

新版精选2019高中数学单元测试《立体几何初步》专题考试题(含答案)

高中数学人教A版(2019)选择性必修一空间向量与立体几何单元测试

精编新版2019高中数学单元测试《立体几何初步》专题考核题完整版(含参考答案)

精选最新版2019高中数学单元测试《立体几何初步》专题完整考题(含答案)

精选2019高中数学单元测试《立体几何初步》专题完整考题(含标准答案)

精选最新2019高中数学单元测试《立体几何初步》专题完整考试题(含标准答案)

2019届人教A版(文科数学) 立体几何 单元测试

精选最新2019高中数学单元测试《立体几何初步》专题完整题(含标准答案)

精选2019高中数学单元测试《立体几何初步》专题完整考题(含答案)

精编新版2019高中数学单元测试《立体几何初步》专题完整题(含标准答案)

最新精选2019高中数学单元测试《立体几何初步》专题完整考试题(含答案)

最新精选2019高中数学单元测试《立体几何初步》专题考试题(含答案)

2019届人教A版(文科数学) 立体几何初步单元测试

2019届人教A版(文科数学) 立体几何单元测试

2019届人教A版(文科数学) 立体几何单元测试