山东省临沂市2013-2014学年高一下学期期末质量抽测数学试题(扫描版)
2013-2014学年第一学期期末考试成绩册(登分版) (2)paiming (1)
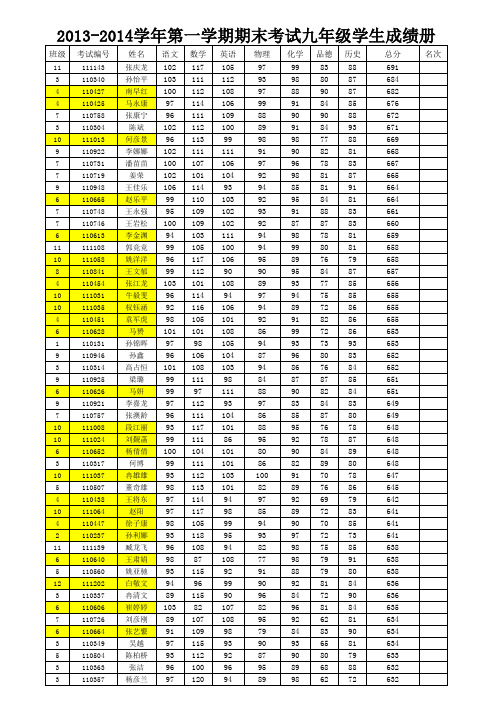
品德 83 80 90 84 90 84 77 82 78 81 81 84 88 87 78 80 76 84 77 75 72 82 72 73 80 76 87 82 84 87 76 78 84 89 70 76 69 72 70 72 75 79 79 81 72 81 62 83 65 80 68 62
名次
3 2 6 12 10 8 5 3 6 3 2 5 10 9 5 9 7 4 3 2 11 10 9 9 6 2 3 7 5 5 10 7 3 4 8 2 7 1 5 3 5 4 4 4 3 12 11 4 9 1 8 5 1 4 1
110305 110217 110615 111240 111042 110805 110562 110321 110605 110316 110241 110543 111057 110958 110565 110918 110754 110422 110320 110257 111147 111046 110963 110930 110617 110210 110350 110767 110546 110518 111019 110717 110356 110405 110802 110260 110713 110104 110550 110335 110508 110437 110444 110446 110327 111233 111115 110434 110957 110123 110814 110564 110143 110417 110146
88 88 90 88 92 98 90 90 82 91 91 76 85 82 90 96 89 88 87 93 87 77 67 90 89 94 92 86 87 75 94 94 89 84 89 94 89 91 79 94 88 90 83 88 92 84 89 82 82 88 91 77 91 83 84
山东省临沂市重点中学2013至2014高一下学期期中考试 数学

高中一年级期中质量调研考试试题数学2014.04本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟. 注意事项:1.答卷前,考生务必将自己的班级、姓名、准考证号、考试科目及试卷类型用中性笔和2B铅笔分别涂写在答题卡上;2.将所有试题答案及解答过程一律填写在答题卡上.试题不交,只交答题卡.参考公式: 回归直线方程abxy+=中:2121121)())((-=--==-=----=---=∑∑∑∑xnxyxnyxxxyyxxbniiniiiniiniii,---=xbya;第Ⅰ卷(选择题,共50分)3.对具有线性相关关系的变量x,y,有一组观测数据(ix,iy)(i=1,2,…,8),其回归直线方程是:16y x a=+,且1238...3x x x x++++=,1238(...)6y y y y++++=,则实数a的值是A.116B.18C.14D.11164.运行如图所示的程序框图,则输出的结果S为A.1007B.1008C .2013D .20145.天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数: 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,这三天中恰有两天下雨的概率近似为A .0.35B .0.25C .0.20D .0.156.某学校从高二甲、乙两个班中各选6名同学参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则y x +的值为 A.6 B. 7 C.8 D.97. 定义某种运算b a S ⊗=,运算原理如图所示,则式子1)31()35cos 4(25sin )45tan2(-⊗+⊗πππ的值为 A .4 B .8 C .11 D .138.已知圆C 的方程为012222=+-++y x y x ,当圆心C 到直线04=++y kx 的距离最大时,k 的值为 A .51-B .51C .5-D .59. 已知三棱锥S -ABC ,在三棱锥内任取一点P ,使得12P ABC S ABC V V --<的概率是 A.78 B.34 C.12D.1410. 已知两点(0,3),(4,0)A B -,若点P 是圆0222=-+y y x 上的动点,则ABP 面积的最小值为A .6 B.112 C .8 D.212高中一年级期中质量调研考试试题数 学 2014.04第Ⅱ卷 (非选择题,共100分)二、填空题:本大题共5个小题,每小题5分,共计25分.把正确答案填写在答题纸给定的横线上11. 已知(1,2,1),(2,2,2)A B -是空间两点,点P 在Z 轴上,且PA PB =,则点P 的坐标为 .12. 过点M (0,4)被圆4)1(22=+-y x 截得的线段长为32的直线方程为 .13.若1210,,,a a a ⋯这10个数据的样本平均数为x ,方差为0.33,则1210,,,a a a ⋯,x 这11个数据的方差为________.14. 在区间[]0,4内随机取两个数a 、b , 则使得函数22()f x x ax b =++有零点的概率为 .15.给出下列结论①扇形的圆心角为23π弧度,半径为2,则扇形的面积是43π;②某小礼堂有25排座位,每排20个,一次心理学讲座,礼堂中坐满了学生,会后为了了解有关情况,留下座位号是15的所有25名学生进行测试,这里运用的是系统抽样方法; ③一个人打靶时连续射击两次,则事件“至少有一次中靶”与事件“两次都不中靶”互为对立事件;④若数据:123n x ,x ,x ,,x 的方差为8,则数据12321212121n x ,x ,x ,,x ++++的方差为16;⑤相关系数r 越大,表示两个变量相关性越强.其中正确结论的序号为 . (把你认为正确结论的序号都填上). 三、解答题:本大题共6个小题.满分75分.解答应写出文字说明、证明过程或推演步骤16.(本小题满分12分)已知tan ααα=求:sin ,cos . 17.(本小题满分12分)假设关于某设备的使用年限x (年)和所支出的维修费用y (万元)有如下统计资料:(Ⅰ)回归直线方程;(Ⅱ)根据回归直线方程, 估计使用年限为10年时,当年维修费用约是多少?18.(本小题满分12分) 已知:10,sin cos .25x x x π-<<+= (Ⅰ)求sin cos x x -的值;(Ⅱ)求22cos()cos()tan()2sin ()sin ()2x x x x x πππππ---++-+的值.19.(本小题满分12分)有一个不透明的袋子,装有4个完全相同的小球,球上分别编有数字1,2,3,4.(Ⅰ)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;(Ⅱ)若先从袋中随机取一个球,该球的编号为a ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为b ,求直线10ax by ++=与圆22116x y +=有公共点的概率. 20.(本小题满分13分)已知圆C 的半径为3,圆心C 在直线20x y +=上,且在x 轴的下方,x 轴被圆C 截得的弦长为 (Ⅰ)求圆C 的方程;(Ⅱ)是否存在斜率为1的直线l ,使l 被圆C 截得的弦AB ,以AB 为直径的圆过原点?若存在求出直线l 的方程;若不存在,说明理由. 21.(本小题满分14分)从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人. (Ⅰ)求第七组的频率;(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm 以上 (含180cm )的人数;(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生, 记他们的身高分别为,x y , 事件=E {5x y -≤}, 事件F ={15->x y },求()P EF .高中一年级期中质量调研考试试题数学参考答案三、解答题:本大题共6个小题,满分75分. 16.(本小题满分12分) 解:sin tan 3cos ααα==-,sin 3αα∴=- 22sin cos 1αα+=,22(3)cos 1αα∴+=21cos 4α∴=.……………………………………………………………………4分 又tan 30α=-<,α∴只可能为第二象限角或第四象限角. ……………………………………6分(1)当α为第二象限角时,13cos ,sin 22αα=-=. (2)当α为第四象限角时,13cos ,sin 22αα==-. …………………12分 17.(本小题满分12分) 解:(Ⅰ)4,5XY ==.……………………………………………………2分52190ii X==∑,51112.3i ii X Y ==∑,…………………………………………………4分51522155i ii i i x y x yb x x==-=-∑∑=112.354512.31.23905410-⨯⨯==-⨯,…………………………6分5 1.2340.08a y bx =-=-⨯=,………………………………………………8分∴回归直线方程为1.230.08y x =+. ……………………………………10分 (Ⅱ)当x =10时,1.23100.0812.38y =⨯+=(元) …………………11分答: 使用年限为10年时,当年维修费用约是12.38万元 …………………12分 18. (本小题满分12分) 解:(Ⅰ)1sin cos 5x x +=,221(sin cos )()5x x ∴+=即:112sin cos ,25x x +=242sin cos .25x x ∴=- ……………………2分 249(sin cos )12sin cos 25x x x x ∴-=-=.……………………………4分 又0,sin 0,cos 0,2x x x π-<<∴<>sin cos 0.x x ∴-<7sin cos 5x x ∴-=-. ……………………………6分(Ⅱ)由已知条件:1sin cos 57sin cos 5x x x x ⎧+=⎪⎪⎨⎪-=-⎪⎩ ,解得3sin -54cos 5x x ⎧=⎪⎪⎨⎪=⎪⎩. ……………………………8分 22cos()cos()tan()2sin ()sin ()2x x x x x πππππ---+∴+-+22222sin cos .sin .sin cos cos sin cos sin x x x x x x x x x --==--…10分 22239()9525431697()()552525---===---- .………………………………………………12分 19.(本小题满分12分)解:(I )用(a ,b )(a 表示第一次取到球的编号,b 表示第二次取到球的编号)表示先后二次取球构成的基本事件,则基本事件有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12个.……………………………3分设“第一次取到球的编号为偶数且两个球的编号之和能被3整除”为事件A ,则事件A 包含的基本事件有:(2,1),(2,4),(4,2)共有3个,……………………5分 ∴31()124P A ==.………………………………………………………………………6分 (II)基本事件有(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,…………………………8分设“直线10ax by ++=与圆22116x y +=有公共的”为事件B14≤, 即2216a b +≥,则事件B 包含的基本事件有(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共8个, (11)分 ∴81()162P B ==.………………………………………………………………………12分 20.(本小题满分13分)解: (Ⅰ)设圆心为(,2)a a - 0a >由勾股定理可得2222MN r d ⎛⎫=+ ⎪⎝⎭(其中d 是弦心距,MN 是截得的弦长),即:29521a a =+-⇒=±.又a > 0,则a =1,圆心(1,-2).圆C 的标准方程是:22(1)(2)9x y -++=. ………………………………………4分 (Ⅱ)方法一:利用圆中的勾股定理(半径,半弦长,弦心距)解决问题.设以AB 为直径的圆M 的圆心为M (a ,b ), l 的斜率为1.在圆C 中有1MC k =-. 由C (1,-2)得211b a +=--即b =-a -1.(*) …………………………………………8分 以AB 为直径的圆过原点.OM =AM =BM由222AM MC AC +=得229a b += 把(*)式代入上式,得2230a a --=从而312a a =-=或,……………………11分 故312052a ab b ⎧=⎪=-⎧⎪⎨⎨=⎩⎪=-⎪⎩或 又(a ,b )在直线l :x -y +m =0上,故m =b -a 14m m ⇒==-或,∴直线l 的方程为10x y -+=或40x y --=.……………………………13分 方法二:利用韦达定理解决问题l 的斜率为1,可设:l y x b =+,交点A 1122(,),(,)x y B x y ,…………………5分圆C: 222440x y x y +-+-=故22()24()40x x b x x b ++-++-=22(22)440x b x b b ++++-=即2 ① ……………………………………7分韦达定理可得12212(1)442x x b b b x x +=-+⎧⎪⎨+-=⎪⎩ (★)…………………………………9分以AB 为直径的圆过原点.则12121y y x x =-,即 :12120x x y y += , …………10分 故21212()0x x b x x b +++=2, 把(★)式代入得2244(1)0b b b b b +--++=2340b b +-=即,∴1b = 或4b =-.……………………………………………12分经检验:14b b ==-当或时,均能使①式中的判别式大于0成立, 所以1b =或4b =-都是方程的解.∴直线l 的方程为 10x y -+=或40x y --=.………………………………13分所以身高在180cm 以上(含180cm )的人数为0.18800144⨯=人. ………………8分 (Ⅲ)第六组[180,185)的人数为4人,设为,,,a b c d ,第八组[190,195]的人数为2人, 设为,A B ,则有,,,,,,ab ac ad bc bd cd ,,,,,,,,aA bA cA dA aB bB cB dB AB 共15种情况,……………………………………………………………………………………………10分 因事件=E {5x y -≤}发生当且仅当随机抽取的两名男生在同一组,所以事件E 包含的基本事件为,,,,,,ab ac ad bc bd cd AB 共7种情况,故7()15P E =. ……………11分 由于max 19518015x y -=-=,所以事件F ={15->x y }是不可能事件,()0P F =.…………………………………………………………………………………12分由于事件E 和事件F 是互斥事件,所以7()()()15P EF P E P F =+=.………14分。
山东省临沂市2013-2014学年高一下学期期末考试 政治 扫描版含答案.pdf

2013—2014学年度下学期
临沂市高一教学质量抽测思想政治试题参考答案及评分标准
第Ⅰ卷(共50分)
1.C 2. D 3. A 4.?C 5.B 6.B 7. A 8.C 9. A. 10. D 11.B 12.A 13.C 14.A 15.A 16. B 17. D 18.C 19.B 20. D 21. C 22.D 23.D 24. B 25.C
第Ⅱ卷(共50分)
26、(9分)
(1)居委会是城市居民自我管理、自我教育、自我服务的基层群众性自治组织。
(2分)该居委会通过召开恳谈会、制定娱乐活动共约,在保证人民群众直接行使民主权利,维护居民合法权益,管理居民公共事务,调解居民纠纷等方面发挥了重要作用。
(3分)
(2)①坚持权利与义务相统一的原则②政府要加强公共文化设施建没,引导选择合适的场所和时间①中国共产党的领导核心②中国共产党的宗旨是全心全意为人民服务③中国共产党贯彻落实科学发展观,坚持科学执政。
山东省临沂市高一数学下学期期末试卷(含解析)

2014-2015学年山东省临沂市高一(下)期末数学试卷一、选择题(本题共10小题,每小题5分,共50分)1.sin600°的值是()A.B.C.D.2.已知cosα=,则sin2α+cos2α的值为()A.B.C.D.3.已知一扇形的圆心角的弧度数为2,其弧长也是2,则该扇形的面积为()A. 1 B. 2 C. sin1 D. 2sin14.若向量,满足||=||=1,且•(﹣)=,则向量与的夹角为()A.B.C.D.5.如图,在△ABC中,D为边BC的中点,则下列结论正确的是()A.+=B.﹣=C.+=D.﹣=6.在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1﹣30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为()A. 3 B. 4 C. 5 D. 67.根据如下样本数据:x 3 4 5 6 7 8y 10 9 7 6 4 3得到的回归方程为=x+,则()A.>0,>0 B.>0,<0 C.<0,>0 D.<0,<08.袋中有白球2个,红球3个,从中任取两个,则互斥且不对立的两个事件是()A.至少有一个白球;都是白球B.两个白球;至少有一个红球C.红球、白球各一个;都是白球D.红球、白球各一个;至少有一个白球9.在区间[0,π]上随机取一个x,sin(x+)≥的概率为()A.B.C.D.10.已知函数f(x)=sinx+λcosx的图象的一个对称中心是点(,0),则函数g(x)=λsinxcosx+sin2x的图象的一条对称轴是直线()A. x=B. x=C. x=D. x=﹣二、填空题(本题共5小题,每小题5分,共25分)11.某校有行政人员、教学人员和教辅人员共200人,其中教学人员与教辅人员的比为10:1,行政人员有24人,现采取分层抽样容量为50的样本,那么教学人员应抽取的人数.12.为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图,则这20名工人中一天生产该产品数量在[55,75)的人数是.13.执行如图所示的程序框图,则输出S的值为.14.i、j是两个不共线的向量,已知=i+2j,=i+λj,=﹣2i+j,若A,B,D三点共线,则实数λ的值为.15.关于函数f(x)=sin(2x+)+sin(2x﹣),则①y=f(x)的最大值为;②y=f(x)在区间[﹣,]上是增函数;③当x1﹣x2=π时,f(x1)=f(x2);④函数f(x)的图象关于点(,0)对称;⑤将函数y=cos2x的图象向右平移个单位后与函数f(x)的图象重合.其中正确结论的序号是.(填上所有正确结论的序号)三、解答题(本题共6小题,共75分)16.在平面直角坐标系xOy中,点A(﹣1,﹣2),B(2,3),C(﹣2,﹣1).(Ⅰ)求•;(Ⅱ)若实数t满足(﹣t)•=0,求t的值.17.某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下:甲10 30 47 28 46 14 26 11 43 46 乙37 21 31 29 19 32 23 25 20 33 (Ⅰ)求甲10场比赛得分的中位数;(Ⅱ)求乙10场比赛得分的方差.18.已知α,β为锐角,sinα=,cos(α+β)=.(Ⅰ)求sin(α+)的值;(Ⅱ)求cosβ的值.19.某品牌乒乓球按质量标准分为1,2,3,4四个等级,现从某工厂生产的一批乒乓球中随机抽取20个,对其等级进行统计分析,得到的频率分布表如下:等级 1 2 3 4频率m n 0.5 0.2(Ⅰ)在抽取的20个乒乓球中,等级为1的恰有2个,求m,n的值;(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.20.已知向量=(cosθ﹣2sinθ,2),=(sinθ,1).(Ⅰ)若∥,求tan2θ的值;(Ⅱ)f(θ)=(+)•,θ∈[0,],求f(θ)的值域.21.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,图象关于直线x=对称.(Ⅰ)求函数f(x)的解析式;(Ⅱ)求函数f(x)的单调增区间;(Ⅲ)在给定的坐标系中画出函数y=f(x)在区间[0,π]上的图象.2014-2015学年山东省临沂市高一(下)期末数学试卷参考答案与试题解析一、选择题(本题共10小题,每小题5分,共50分)1.sin600°的值是()A.B.C.D.考点:运用诱导公式化简求值.专题:计算题.分析:把原式的角度600°变形为2×360°﹣120°,然后利用诱导公式化简,再把120°变为180°﹣60°,利用诱导公式及特殊角的三角函数值即可求出值.解答:解:sin600°=sin(2×360°﹣120°)=﹣sin120°=﹣sin(180°﹣60°)=﹣sin60°=﹣.故选D点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键,同时注意角度的灵活变换.2.已知cosα=,则sin2α+cos2α的值为()A.B.C.D.考点:二倍角的余弦.专题:三角函数的求值.分析:由cosα的值,利用同角三角函数间的基本关系求出sin2α的值,原式变形后代入计算即可求出值.解答:解:∵cosα=,∴sin2α=1﹣cos2α=,则原式=sin2α+1﹣2sin2α=1﹣sin2α=,故选:A.点评:此题考查了二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.3.已知一扇形的圆心角的弧度数为2,其弧长也是2,则该扇形的面积为()A. 1 B. 2 C. sin1 D. 2sin1考点:扇形面积公式.专题:三角函数的求值.分析:利用扇形的面积计算公式、弧长公式即可得出.解答:解:由弧长公式可得2=2r,解得r=1.∴扇形的面积S=.故选:A点评:本题考查了扇形的面积计算公式、弧长公式,属于基础题.4.若向量,满足||=||=1,且•(﹣)=,则向量与的夹角为()A.B.C.D.考点:平面向量数量积的运算.专题:平面向量及应用.分析:首先由已知等式求出向量与的数量积,利用平面向量的数量积公式可得.解答:解:由已知||=||=1,且•(﹣)=,则,所以=,所以向量与的夹角的余弦值为,所以向量与的夹角为.故选B.点评:本题考查了屏幕录像的数量积公式的运用;属于基础题.5.如图,在△ABC中,D为边BC的中点,则下列结论正确的是()A.+=B.﹣=C.+=D.﹣=考点:向量的三角形法则.专题:平面向量及应用.分析:利用平面向量的三角形法则对选项分别分析选择.解答:解:由已知及图形得到,故A错误;;故B错误;;故C 正确;故D 错误;故选C.点评:本题考查了平面向量的三角形法则的运用;注意向量的起点与终点位置;属于基础题.6.在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1﹣30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为()A. 3 B. 4 C. 5 D. 6考点:茎叶图.专题:概率与统计.分析:根据茎叶图中的数据,结合系统抽样方法的特征,求出所要抽取的人数.解答:解:根据茎叶图得,成绩在区间[73,90]上的数据有15个,所以,用系统抽样的方法从所有的30人中抽取6人,成绩在区间[73,90]上的学生人数为6×=3.故选:A.点评:本题考查了系统抽样方法的应用问题,也考查了茎叶图的应用问题,是基础题目.7.根据如下样本数据:x 3 4 5 6 7 8y 10 9 7 6 4 3得到的回归方程为=x+,则()A.>0,>0 B.>0,<0 C.<0,>0 D.<0,<0考点:线性回归方程.专题:概率与统计.分析:已知中的数据,可得变量x与变量y之间存在负相关关系,且x=0时,>10>0,进而得到答案.解答:解:由已知中的数据,可得变量x与变量y之间存在负相关关系,故<0,当x=0时,>10>0,故>0,故选:B点评:本题考查的知识点是线性回归方程,正确理解回归系数的几何意义是解答的关键.8.袋中有白球2个,红球3个,从中任取两个,则互斥且不对立的两个事件是()A.至少有一个白球;都是白球B.两个白球;至少有一个红球C.红球、白球各一个;都是白球D.红球、白球各一个;至少有一个白球考点:互斥事件与对立事件.专题:概率与统计.分析:从装有3个红球和2个白球的红袋内任取两个球,所有的情况有3种:“2个白球”、“一个白球和一个红球”、“2个红球”.由于对立事件一定是互斥事件,且它们之中必然有一个发生而另一个不发生,结合所给的选项,逐一进行判断,从而得出结论.解答:解:从装有3个红球和2个白球的红袋内任取两个球,所有的情况有3种:“2个白球”、“一个白球和一个红球”、“2个红球”.由于对立事件一定是互斥事件,且它们之中必然有一个发生而另一个不发生,对于A,至少有1个白球;都是白球,不是互斥事件.故不符合.对于B两个白球;至少有一个红球,是互斥事件,但不是对立事件不是互斥事件,故符合.对于C红球、白球各一个;都是白球是互斥事件,但也是对立事件,故不符合.对于D红球、白球各一个;至少有一个白,不是互斥事件.故不符合.故选:B.点评:本题主要考查互斥事件与对立事件的定义,属于基础题.9.在区间[0,π]上随机取一个x,sin(x+)≥的概率为()A.B.C.D.考点:几何概型.专题:概率与统计.分析:由题意,本题是几何概型,而事件的集合是区间长度,利用几何概型公式求之.解答:解:区间[0,π]上随机取一个x,对应事件的集合为区间长度π,而在此条件下满足sin(x+)≥的范围是≤x+≤,即x∈[0,],区间长度为,由几何概型的公式得到在区间[0,π]上随机取一个x,sin(x+)≥的概率为:;故选D.点评:本题考查了几何概型的概率求法;关键是明确概率模型,利用区间长度为测度求概率.10.已知函数f(x)=sinx+λcosx的图象的一个对称中心是点(,0),则函数g(x)=λsinxcosx+sin2x的图象的一条对称轴是直线()A. x=B. x=C. x=D. x=﹣考点:两角和与差的正弦函数;正弦函数的对称性.专题:三角函数的求值.分析:由对称中心可得λ=﹣,代入g(x)由三角函数公式化简可得g(x)=﹣sin(2x+),令2x+=kπ+解x可得对称轴,对照选项可得.解答:解:∵f(x)=sinx+λco sx的图象的一个对称中心是点(,0),∴f()=sin+λcos=+λ=0,解得λ=﹣,∴g(x)=﹣sinxcosx+sin2x=sin2x+=﹣sin(2x+),令2x+=kπ+可得x=+,k∈Z,∴函数的对称轴为x=+,k∈Z,结合四个选项可知,当k=﹣1时x=﹣符合题意,故选:D点评:本题考查两角和与差的三角函数,涉及三角函数对称性,属中档题.二、填空题(本题共5小题,每小题5分,共25分)11.某校有行政人员、教学人员和教辅人员共200人,其中教学人员与教辅人员的比为10:1,行政人员有24人,现采取分层抽样容量为50的样本,那么教学人员应抽取的人数40 .考点:分层抽样方法.专题:计算题.分析:先求出每个个体被抽到的概率,再求出其中教学人员的数量,乘以每个个体被抽到的概率,即得教学人员应抽取的人数.解答:解:每个个体被抽到的概率等于样本容量除以个体的总数,即=,教学人员与教辅人员的和为 200﹣24=176,除行政人员外,教学人员所占的比列等于,故其中教学人员的数量为176×=160,160×=40.故答案为 40.点评:本题主要考查分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,求出教学人员的数量是解题的关键,属于基础题.12.为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图,则这20名工人中一天生产该产品数量在[55,75)的人数是13 .考点:频率分布直方图.专题:计算题.分析:根据直方图分析可知该产品数量在[55,75)的频率,又由频率与频数的关系计算可得生产该产品数量在[55,75)的人数.解答:解:由直方图可知:生产该产品数量在[55,75)的频率=0.065×10,∴生产该产品数量在[55,75)的人数=20×(0.065×10)=13,故答案为13.点评:本题是对频率、频数简单运用的考查,频率、频数的关系:频率=.13.执行如图所示的程序框图,则输出S的值为26 .考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的n,S的值,当n=31时不满足条件n<20,退出循环,输出S的值为26.解答:解:模拟执行程序框图,可得n=1,S=0满足条件n<20,S=1,n=3,满足条件n<20,S=4,n=7,满足条件n<20,S=11,n=15,满足条件n<20,S=26,n=31,不满足条件n<20,退出循环,输出S的值为26.故答案为:26.点评:本题主要考查了循环结构的程序框图,正确写出每次循环得到的n,S的值是解题的关键,属于基础题.14.i、j是两个不共线的向量,已知=i+2j,=i+λj,=﹣2i+j,若A,B,D三点共线,则实数λ的值为7 .考点:平行向量与共线向量.专题:平面向量及应用.分析:求出,利用A、B、D三点共线,列出方程组,求出实数λ的值即可.解答:解:=﹣=(﹣2i+j)﹣(i+λj)=﹣3i+(1﹣λ)j∵A、B、D三点共线,∴向量与共线,因此存在实数μ,使得=μ,即i+2j=μ[﹣3i+(1﹣λ)j]=﹣3μi+μ(1﹣λ)j∵i与j是两不共线向量,由基本定理得:,解得λ=7,故答案为:7.点评:本题重点考查了平面向量的共线条件的应用,属于基础题.15.关于函数f(x)=sin(2x+)+sin(2x﹣),则①y=f(x)的最大值为;②y=f(x)在区间[﹣,]上是增函数;③当x1﹣x2=π时,f(x1)=f(x2);④函数f(x)的图象关于点(,0)对称;⑤将函数y=cos2x的图象向右平移个单位后与函数f(x)的图象重合.其中正确结论的序号是①③④.(填上所有正确结论的序号)考点:三角函数中的恒等变换应用.专题:计算题;三角函数的图像与性质.分析:利用三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x﹣).利用正弦函数的图象和性质可判断①正确;由2kπ﹣≤2x﹣≤2kπ+,k∈Z可解得函数f(x)的单调递增区间,易证②错误;当x1﹣x2=π时,可求f(x1)=f(x2+π)=f(x2).可判断③正确;由2x﹣=kπ,k∈Z可解得函数对称点可判断④正确;根据三角函数图象的平移变换规律即可判断⑤错误.解答:解:f(x)=sin(2x+)+sin(2x﹣)=cos(2x﹣)+sin(2x﹣)=sin(2x﹣+)=sin(2x﹣).y=f(x)的最大值为,①正确;由2kπ﹣≤2x﹣≤2kπ+,k∈Z可解得函数f(x)的单调递增区间为:[kπ﹣,kπ+],k∈Z,易证②错误;当x1﹣x2=π时,f(x1)=f(x2+π)=sin[2(x2+π)﹣]=sin(2x2+2π﹣)=sin(2x2﹣)=f(x2).故③正确;由2x﹣=kπ,k∈Z可解得函数对称点为:(,0),k∈Z,当k=0时,④正确;将函数y=cos2x的图象向右平移个单位后得到函数解析式:y=cos[2(x﹣)]=cos(2x﹣)=sin(2x+),故⑤错误.故答案为:①③④.点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,属于基本知识的考查.三、解答题(本题共6小题,共75分)16.在平面直角坐标系xOy中,点A(﹣1,﹣2),B(2,3),C(﹣2,﹣1).(Ⅰ)求•;(Ⅱ)若实数t满足(﹣t)•=0,求t的值.考点:平面向量数量积的运算;平面向量的坐标运算.专题:平面向量及应用.分析:(I)利用点的坐标得出=(3,5),=(﹣1,1),根据向量的数量积运算公式求解即可.(Ⅱ)利用向量数乘、数量积的坐标表示,列出关于t的方程求即可.解答:解:(Ⅰ)∵点A(﹣1,﹣2),B(2,3),C(﹣2,﹣1).∴由题设知=(3,5),=(﹣1,1),∴=3×(﹣1)+5×1=2,(II)∵=(3,5),=(﹣2,﹣1),=(2,3),∴﹣t=(3+2t,5+t)∵实数t满足(﹣t)•=0,∴2×(3+2t)+3×(5+t)=0,∴t=﹣3点评:本题考查向量的坐标表示,向量数乘、数量积的坐标表示,属于基础题17.某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下:甲10 30 47 28 46 14 26 11 43 46 乙37 21 31 29 19 32 23 25 20 33 (Ⅰ)求甲10场比赛得分的中位数;(Ⅱ)求乙10场比赛得分的方差.考点:极差、方差与标准差;众数、中位数、平均数.专题:概率与统计.分析:(I)将甲10场比赛得分从小到大排列,中间两个的平均数求解即可.(II)乙10场比赛得分的平均数,运用方差的公式求解即可.解答:解:(I)将甲10场比赛得分从小到大排列:10,11,14,26,28,30,43,46,47故甲10场比赛得分的中位数:=29(II)乙10场比赛得分的平均数=(37+21+31+29+19+32+23+25+20+33)=27,故乙10场比赛得分的方差:S2=×[(37﹣27)2+(21﹣27)2+…+(33﹣27)2]=35点评:本题考察了统计数据的分析,中位数,方差平均数的求解,数字特征的判断分析,属于容易题.18.已知α,β为锐角,sinα=,cos(α+β)=.(Ⅰ)求sin(α+)的值;(Ⅱ)求cosβ的值.考点:两角和与差的正弦函数.专题:三角函数的求值.分析:(Ⅰ)由α的范围和平方关系求出sinα,再由两角和的正弦函数求出sin(α+)的值;(Ⅱ)由α,β为锐角得α+β∈(0,π),由平方关系求出sin(α+β),再由两角差的余弦函数求出cosβ=cos[(α+β)﹣α]的值.解答:解:(Ⅰ)∵α为锐角,sinα=,∴cosα==,∴sin(α+)=sinαcos+cosαsin)==;(Ⅱ)∵α,β为锐角,∴α+β∈(0,π),由cos(α+β)=得,sin(α+β)==,∴cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα==.点评:本题考查由两角和与差的正弦、余弦函数,以及平方关系的应用,注意角的范围和角之间的关系,属于中档题.19.某品牌乒乓球按质量标准分为1,2,3,4四个等级,现从某工厂生产的一批乒乓球中随机抽取20个,对其等级进行统计分析,得到的频率分布表如下:等级 1 2 3 4频率m n 0.5 0.2(Ⅰ)在抽取的20个乒乓球中,等级为1的恰有2个,求m,n的值;(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.考点:列举法计算基本事件数及事件发生的概率.专题:概率与统计.分析:(Ⅰ)通过频率分布表得推出m+n=0.3.利用等级系数为1的恰有2件,求出m,然后求出n.(Ⅱ)根据条件列出满足条件所有的基本事件总数,“从x1,x2,y1,y2,y3,y4这6件日用品中任取两件,等级系数相等”的事件数,求解即可.解答:解:(Ⅰ)由频率分布表得 m+n+0.5+0.2=1,即 m+n=0.3.…(2分)由抽取的20个零件中,等级为1的恰有2个,得 m==0.1.…(4分)所以n=0.3﹣0.1=0.2.…(5分)(Ⅱ):由(Ⅰ)得,等级为1的零件有2个,记作x1,x2,等级为2的零件有4个,记作y1,y2,y3,y4,从x1,x2,x3,y1,y2,y3,y4中任意抽取2个零件,所有可能的结果为:(x1,x2),(x1,y1),(x1,y2),(x1,y3),(x1,y4),(x2,y1),(x2,y2),(x2,y3),(x2,y4),(y1,y2),(y1,y3),(y1,y4),(y2,y3),(y2,y4),(y3,y4),共计15种.…(9分)记事件A为“从零件x1,x2,y1,y2,y3,y4中任取2件,其等级相等”.则A包含的基本事件为(x1,x2),(y1,y2),(y1,y3),(y1,y4),(y2,y3),(y2,y4),(y3,y4)共7个.…(11分)故所求概率为 P(A)=.…(12分)点评:本题考查概率、统计等基本知识,考查数据处理能力、运算能力、应用意识.20.已知向量=(cosθ﹣2sinθ,2),=(sinθ,1).(Ⅰ)若∥,求tan2θ的值;(Ⅱ)f(θ)=(+)•,θ∈[0,],求f(θ)的值域.考点:平面向量数量积的运算;平面向量共线(平行)的坐标表示.专题:平面向量及应用.分析:(Ⅰ)根据平行向量的坐标关系便可得到cosθ=4sinθ,从而tanθ=,根据正切的二倍角公式即可求出tan2θ=;(Ⅱ)先求出的坐标,再由两角和的正弦公式即可得到f(θ)=,而由θ的范围即可求出2θ的范围,从而结合正弦函数的图象即可得出sin(2θ+)的范围,从而得到f(θ)的值域.解答:解:(Ⅰ)∵∥;∴cosθ﹣2sinθ﹣2sinθ=0;∴cosθ=4sinθ;∴;∴;(Ⅱ);∴f(θ)===;∵;∴;∴;∴2≤f(θ)≤;∴f(θ)的值域为[2,].点评:考查平行向量的坐标的关系,切化弦公式,二倍角的正余弦、正切公式,向量加法的坐标运算,向量数量积的坐标运算,两角和的正弦公式,并熟悉正弦函数的图象.21.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,图象关于直线x=对称.(Ⅰ)求函数f(x)的解析式;(Ⅱ)求函数f(x)的单调增区间;(Ⅲ)在给定的坐标系中画出函数y=f(x)在区间[0,π]上的图象.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;复合三角函数的单调性.分析:(Ⅰ)由函数的周期求出ω的值,可得函数的解析式.(Ⅱ)由条件利用正弦函数的增区间求得函数f(x)的单调增区间.(Ⅲ)用五点法作出函数y=f(x)在区间[0,π]上的图象.解答:解:(Ⅰ)∵函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为=π,∴ω=2.再根据函数的图象关于直线x=对称,可得2×+φ=kπ+,k∈z,即φ=kπ﹣,∴φ=﹣,故f(x)=sin(2x﹣).(Ⅱ)令2kπ﹣≤2x﹣≤2kπ+,k∈z,求得kπ﹣≤x≤kπ+,可得函数的增区间为[kπ﹣,kπ+],k∈z.(Ⅲ)用五点法作函数y=f(x)在区间[0,π]上的图象:列表:2x﹣﹣ 0 πx 0 πy ﹣ 0 1 0 ﹣1 ﹣作图:点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的周期性、单调性,用五点法作出正弦函数在一个周期上的简图,属于中档题.。
山东省临沂市高一下学期期末数学试卷

山东省临沂市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019高二上·揭阳月考) 在中,已知,,,则的度数是()A . 或B .C .D .2. (2分)已知P是椭圆上的一点,F1,F2是该椭圆的两个焦点,若的内切圆半径为,则的值为()A .B .C .D . 03. (2分) (2016高一下·抚顺期末) 某小组有2名男生和2名女生,从中任选2名同学去参加演讲比赛.在下列选项中,互斥而不对立的两个事件是()A . “至少有1名女生”与“都是女生”B . “至少有1名女生”与“至多1名女生”C . “恰有1名女生”与“恰有2名女生”D . “至少有1名男生”与“都是女生”4. (2分) (2016高一下·抚顺期末) 已知角α,β均为锐角,且cosα= ,sinβ= ,则α﹣β的值为()A .B .C . -D .5. (2分) (2016高一下·抚顺期末) 如图,在△ABC中,点D是边BC的中点,点G在AD上,且是△ABC的重心,则用向量表示为()A .B .C .D .6. (2分) (2016高一下·抚顺期末) 已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是()A . =1.23x+4B . =1.23x﹣0.08C . =1.23x+0.8D . =1.23x+0.087. (2分) (2016高一下·抚顺期末) 已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,若其圆心到x 轴的距离恰好等于圆的半径,在y轴上截得的弦长为,则圆的方程为()A . (x+2)2+(y+3)2=9B . (x+3)2+(y+5)2=25C .D .8. (2分) (2016高一下·抚顺期末) 甲、乙两名同学8次数学测验成绩如茎叶图所示, 1 , 2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1 , s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有()A . 1> 2 , s1<s2B . 1= 2 , s1<s2C . 1= 2 , s1=s2D . 1< 2 , s1>s29. (2分) (2016高一下·抚顺期末) 如图所示的程序框图,它的输出结果是()A . ﹣1B . 0C . 1D . 1610. (2分) (2016高一下·抚顺期末) 已知函数f(x)=sin(ωx+ϕ)(ω>0)的部分图象如图所示,下面结论正确的个数是()①函数f(x)的最小正周期是2π②函数f(x)的图象可由函数g(x)=sin2x的图象向左平移个单位长度得到③函数f(x)的图象关于直线x= 对称④函数f(x)在区间[ ]上是增函数.A . 3B . 2C . 1D . 011. (2分) (2016高一下·抚顺期末) 已知k∈R, =(k,1), =(2,4),若| |<,则△ABC是钝角三角形的概率是()A .B .C .D .12. (2分) (2016高一下·抚顺期末) 如图,点P是圆C:x2+(y﹣2 )2=1上的一个动点,点Q是直线l:x﹣y=0上的一个动点,O为坐标原点,则向量在向量上的射影的数量的最大值是()A . 3B .C .D . 1二、填空题 (共4题;共4分)13. (1分)(2018·绵阳模拟) 的展开式中,的系数是________.14. (1分) (2016高一下·抚顺期末) 已知平面向量与满足| |=1,| ﹣ |= ,且< + ,﹣>= ,则| |=________.15. (1分) (2016高一下·抚顺期末) 若sin(x+ )= ,则sin(﹣x)+sin2(﹣x)+cos (2x+ )=________.16. (1分) (2016高一下·抚顺期末) 关于平面向量,有下列四个命题:①若.② =(1,1), =(2,x),若与平行,则x=2.③非零向量和满足| |=| |=| |,则与的夹角为60°.④点A(1,3),B(4,﹣1),与向量同方向的单位向量为().其中真命题的序号为________.(写出所有真命题的序号)三、解答题 (共6题;共45分)17. (10分)空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~250为重度污染;>300为严重污染.一环保人士记录2017年某地某月10天的AQI的茎叶图如下.(1)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共30天计算)(2)若从样本中的空气质量不佳(AQI>100)的这些天,随机地抽取两天深入分析各种污染指标,求这该两天的空气质量等级恰好不同的概率.18. (5分)(2017·抚顺模拟) 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:(Ⅰ)求图中的x的值;(Ⅱ)估计该校高一学生每周课外阅读的平均时间;(Ⅲ)为了进一步提高本校高一学生对课外阅读的兴趣,学校准备选拔2名学生参加全市阅读知识竞赛,现决定先在第三组、第四组、第五组中用分层抽样的放法,共随机抽取6名学生,再从这6名学生中随机抽取2名学生代表学校参加全市竞赛,在此条件下,求第三组学生被抽取的人数X的数学期望.19. (5分) (2018高三上·湖北月考) (某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示:(Ⅰ)试估计平均收益率;(Ⅱ)根据经验若每份保单的保费在元的基础上每增加元,对应的销量(万份)与(元)有较强线性相关关系,从历史销售记录中抽样得到如下组与的对应数据:(元)销量(万份)(ⅰ)根据数据计算出销量(万份)与(元)的回归方程为;(ⅱ)若把回归方程当作与的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.参考公示:20. (10分) (2018高一下·唐山期末) 某公司经营一种二手机械,对该型号机械的使用年数与再销售价格(单位:百万元/台)进行统计整理,得到如下关系:使用年数246810再销售价格16139.575附:参考公式:, .(1)求关于的回归直线方程;(2)该机械每台的收购价格为(百万元),根据(1)中所求的回归方程,预测为何值时,此公司销售一台该型号二手机械所获得的利润最大?21. (10分) (2018高一下·葫芦岛期末) 小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线和直线交于点.以为起点,再从曲线上任取两个点分别为终点得到两个向量,记这两个向量的数量积为.若去九寨沟;若去泰山;若去长白山;去武夷山.(1)若从这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;(2)按上述方案,小明在曲线上取点作为向量的终点,则小明决定去武夷山.点在曲线上运动,若点的坐标为,求的最大值.22. (5分) (2016高一下·抚顺期末) 在平面直角坐标系中,两点P1(x1 , y1),P2(x2 , y2)间的“L ﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤ .求:当|BC|取最大值时,边AB所在直线的斜率的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共45分)17-1、17-2、18-1、19-1、20-1、20-2、21-1、21-2、22-1、。
山东省临沂市高一下学期期末数学试卷

山东省临沂市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019高一下·丽水月考) 与角终边相同的角是()A .B .C .D .2. (2分)采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入间[451,750]的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为()A . 7B . 9C . 10D . 153. (2分)如图所示,图中有5组数据,去掉组数据后(填字母代号),剩下的4组数据的线性相关性最强()A . EB . CC . DD . A4. (2分) (2018高一下·北京期中) 甲、乙两人掷骰子,若甲掷出的点数记为a,乙掷出的点数记为b,则|a-b|≤1的概率为()A .B .C .D .5. (2分)下列赋值语句正确的是()A . a+b=5B . 5=aC . a+b=cD . a=a+16. (2分)下列式子中,不能化简为的是()A . ++B . ++-C . +-D . +-7. (2分) (2018高二下·重庆期中) 重庆一中为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的赛,两队各由4名选手组成,每局两队各派一名选手,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛队选手获胜的概率均为,且各局比赛结果相互独立,比赛结束时队的得分高于队的得分的概率为()A .B .C .D .8. (2分)要得到函数的图象,只需将函数的图象()A . 向上平移个单位B . 向下平移个单位C . 向上平移个单位D . 向下平移个单位9. (2分)在区间和内分别取一个数,记为a和b,则方程表示离心率小于的双曲线的概率为()A .B .C .D .10. (2分) (2020高一上·嘉兴期末) 为了得到函数的图象,可以将函数的图象()A . 向左平移个单位B . 向右平移个单位C . 向左移动个单位D . 向右平移个单位11. (2分)两相关变量满足如下关系:x1015202530Y 1 003 1 005 1 010 1 011 1 014两变量回归直线方程为()A . =0.56 +997.4B . =0.63 ﹣231.2C . =50.2 +501.4D . =60.4 +400.712. (2分) (2018高三上·泸州模拟) 已知函数的部分图象如图所示,将函数的图象上所有点的横坐标缩短为原来的,纵坐标不变,再将所得图象上所有点向右平移个单位长度,得到的函数图象关于直线对称,则的最小值为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高一下·郑州期末) 已知向量 =(2,3), =(﹣4,1),则向量在向量方向上的投影为________.14. (1分) (2019高一下·南海月考) 如图,茎叶图表示甲、乙两人在次测验中的数学分数,其中有一个被污损,若乙的中位数恰好等于甲的平均数,则·的值为________.15. (1分)(2020·宿迁模拟) 已知是第二象限角,且,则的值为________.16. (1分)(2020·南通模拟) 阅读如图所示的程序框,若输入的n是30,则输出的变量S的值是________.三、解答题 (共6题;共55分)17. (5分) (2016高一上·荆门期末) (I)化简求值:;(II)已知角α的终边上一点,求值:.18. (10分) (2016高一下·兰州期中) 某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i (i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.甲的频数统计表(部分)运行次数n 输出y的值为1的频数输出y的值为2的频数输出y的值为3的频数3014610…………21001027376697乙的频数统计表(部分)运行次数n 输出y的值为1的频数输出y的值为2的频数输出y的值为3的频数3012117…………21001051696353当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.19. (10分) (2017高一下·郑州期末) 为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):社团名称成员人数抽取人数话剧社50a创客社150b演讲社100c(1)求a,b,c的值;(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.20. (10分) (2017高一下·宜昌期中) 已知 =(4,5cosα), =(3,﹣4tanα)α∈(0,),⊥ .(1)求;(2)求.21. (10分) (2019高二下·延边月考) 为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.附: ,()(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?甲班乙班总计成绩优良成绩不优良总计(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.22. (10分) (2020高三上·嵊州期末) 已知函数.(1)求的最小正周期;(2)当时,求的值域.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、。
山东省临沂市高一下学期期末数学试题

山东省临沂市高一下学期期末数学试题姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)设集合A={x|﹣1≤x≤2,x∈N},集合B={2,3},则A∪B=()A . {1,2,3}B . {0,1,2,3}C . {2}D . {﹣1,0,1,2,3}2. (2分) (2016高二上·昌吉期中) 已知具有线性相关的两个变量x,y之间的一组数据如下:x01234y 2.2 4.3 4.5 4.8 6.7回归方程是 =bx+a,其中b=0.95,a= ﹣b .则当x=6时,y的预测值为()A . 8.1B . 8.2C . 8.3D . 8.43. (2分)有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为()A .B .C .D .4. (2分)已知等差数列{an}的前n项和为Sn ,且满足,则数列{an}的公差是()A .B . 1C . 2D . 35. (2分) (2018高一下·长春期末) 在中,内角所对的边分别为 ,且 ,若为锐角,则的最大值为()A .B .C .D .6. (2分) (2019高一上·琼海期中) 已知 ,按照从大到小排列正确的是()A .B .C .D .7. (2分)定义在[0,1]上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,,且当时,则等于()A .B .C .D .8. (2分) (2019高一上·成都期中) 方程的一根在区间内,另一根在区间内,则的取值范围是()A .B .C .D .9. (2分) (2017高二下·瓦房店期末) 若,则()A .B .C .D .10. (2分)(2016·浦城模拟) 已知函数f(x)=2x+log2x+b在区间(,4)上有零点,则实数b的取值范围是()A . (﹣10,0)B . (﹣8,1)C . (0,10)D . (1,12)11. (2分) (2019高三上·沈阳月考) 函数()A . 在单调递减B . 在单调递增C . 在单调递减D . 在单调递增12. (2分)设是等差数列,且,则其前15项和()A . 15B . 45C . 75D . 105二、多选题 (共1题;共3分)13. (3分) (2019高一下·化州期末) 若干个人站成排,其中不是互斥事件的是()A . “甲站排头”与“乙站排头”B . “甲站排头”与“乙不站排尾”C . “甲站排头”与“乙站排尾”D . “甲不站排头”与“乙不站排尾”三、填空题 (共4题;共8分)14. (1分)为了调查城市PM2.5的值,按地域把36个城市分成甲、乙、丙三组,对应的城市数分别为6,12,18.若用分层抽样的方法抽取18个城市,则乙组中应抽取的城市数为________.15. (5分)函数f(x)=1+logax(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,其中mn>0,则的最小值为________.16. (1分) (2016高三上·杭州期中) 将函数f(x)=sin(x+ )图象上各点的横坐标缩短到原来的倍(纵坐标不变),再把得到的图象向右平移个单位,得到的新图象的函数解析式为g(x)=________,g(x)的单调递减区间是________.17. (1分) (2017高二下·正定期末) 设的内角,,的对边分别为,,,已知的面积为,且,则 ________.四、解答题 (共6题;共75分)18. (10分)(2017·凉山模拟) 在△ABC中,角A,B,C所对边分别是a,b,c,若sin(A﹣B)= sinAcosB ﹣ sinBcosA.(1)求证:A=B;(2)若A= ,a= ,求△ABC的面积.19. (15分) (2019高二上·辽宁月考) 数列满足,().(1)求证:数列是等差数列;(2)若,求正整数的最小值.20. (10分)(2016·天津文) 某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:配A B C料原料甲483乙5510现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;(2)问分别生产甲、乙两种肥料,求出此最大利润.21. (10分) (2018高一下·南平期末) 已知为的三个内角的对边,向量,,且 .(1)求角的大小;(2)若,求的值及的面积.22. (15分) (2016高三上·沈阳期中) 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率分布直方图:附:临界值参考公式:,n=a+b+c+d.(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);(2)小明向班级同学发出倡议,为该小区居民损款,现从损失超过4000元的居民中随机抽出2户进行捐款援助,投抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,在表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?经济损失不超过4000元经济损失超过4000元合计捐款超过500元30损款不超过500元6合计P(K2≥k)0.150.100.050.0250.0100.0050.001 k 2.072 2.706 3.841 5.024 6.6357.87910.82823. (15分) (2019高一上·安达期中) 已知定义域为的单调减函数是奇函数,当时,.(Ⅰ)求的值;(Ⅱ)求的解析式;(Ⅲ)若对任意的,不等式恒成立,求实数的取值范围.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、多选题 (共1题;共3分)13-1、三、填空题 (共4题;共8分)14-1、15-1、16-1、17-1、四、解答题 (共6题;共75分) 18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、23-1、。
2013-2014山东省临沂市高一下学期期末考试数学试卷模拟5

2013-2014⼭东省临沂市⾼⼀下学期期末考试数学试卷模拟57 8 9 8 7 2 8 8 1 082 6 ⼄甲 2013—2014学年临沂市⾼⼀下学期期末考试⾼⼀数学试题(模拟五)第Ⅰ卷(选择题共50分)⼀、选择题:本⼤题共10个⼩题,每⼩题5分,共50分.在每⼩题给出的四个选项中,只有⼀个选项是符合题⽬要求的.1.甲⼄两位同学在⾼三的5次⽉考中数学成绩统计如茎叶图所⽰,若甲⼄两⼈的平均成绩分别是x x ⼄甲,,则下列正确的是()A. x x >⼄甲;⼄⽐甲成绩稳定B. x x >⼄甲;甲⽐⼄成绩稳定C. x x <⼄甲;⼄⽐甲成绩稳定D. x x <⼄甲;甲⽐⼄成绩稳定2.某班有学⽣52⼈,现⽤系统抽样的⽅法,抽取⼀个容量为4的样本,已知座位号为6号,32号,45号的同学都在样本中,那么样本中还有⼀位同学的座位号是A. 19B. 16C. 24D. 363. 若圆(x -3)2+(y +5)2=r 2上有且只有两个点到直线4x -3y =2的距离等于1,则半径r 的范围是( ) A .(4,6) B .[4,6] C .[4,6] D .(4,6]4、设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最⼩值等于 A 、13B 、3C 、6D 、9 5、如图所⽰算法程序框图运⾏时,输⼊a =tan315°,b =sin315°,c =cos 315°,则输出结果为( ) A.22B .-22C .-1D .16. 已知0a b ?=||2,||3a b ==且(32)()a b a b λ+⊥-则λ的值是()A.32B.32-C.32± D.1 7.若cos 2πsin 4αα=?-cos sin αα+的值为()A.2-B.12-C.12D.28.函数cos tan y x x =(0x π≤≤且2x π≠)的图象为()9.已知圆C 的半径为2,圆⼼在x 轴的正半轴上,直线0443=++y x 与圆C 相切,则圆C 的⽅程为 A. 03222=--+x y xB. 0422=++x y xC. 03222=-++x y xD. 0422=-+x y x10.定义在R 上的偶函数()f x ,满⾜(2)()f x f x +=,且()f x 在[]3,2--上是减函数,⼜,αβ是锐⾓三⾓形的两个内⾓, 则 ( ) A.(sin )(cos )f f αβ> B. (cos )(cos )f f αβ< C. (sin )(cos )f f αβ< D. (sin )(sin )f f αβ<第Ⅱ卷(⾮选择题共100分)⼆、填空题:本⼤题共5个⼩题,每⼩题5分;共25分.将答案填在题中横线上.11. 右图程序框图的运⾏结果是 12. ABCD 为长⽅形, AB =2,BC=1,O 为AB 的中点,在长⽅形ABCD 内随机取⼀点,取到的点到O 的距离⼤于1的概率为 13.已知下列命题14.已知⾓α的终边在2 (0)y x x =-<上,则sin 2()4πα+的值为____________.15..在下列结论中:①函数)sin(x k y -=π(k ∈Z )为奇函数;②函数)0,12()62tan(ππ的图象关于点+=x y 对称;③函数ππ32)32cos(-=+=x x y 的图象的⼀条对称轴为;④若.51cos ,2)tan(2==-x x 则π其中正确结论的序号为(把所有正确结论的序号都.填上). 三、解答题:本⼤题共6个⼩题,共75分.16、(本⼩题满分10分)某校从参加⾼⼀年级期中考试的学⽣中随机抽取60名学⽣,将其数学成绩(均为整数)分成六段[40, 50),[50, 60),…,[90, 100] 后得到如下部分频率分布直⽅图.观察图形的信息,回答下列问题:(I)求分数在 [70,80)内的频率,并补全这个频率分布直⽅图;(Ⅱ)统计⽅法中,同⼀组数据常⽤该组区间的中点值作为代表,据此估计本次考试的平均分;(Ⅲ) 根据频率分布直⽅图估计这次⾼⼀年级期中考试的学⽣成绩的中位数(保留整数)。
