2020年江苏省盱眙初级实验中学七年级上学期数学期末调研试卷(附答案)
江苏省2020学年七年级数学上学期期末教学质量调研测试

七年级数学上学期期末教学质量调研测试(试卷满分130分,考试时间120分钟)一、选择题(本大题共10小题,每小题3分,共30分.请将下列各题唯一正确的选项代号填涂在答题卡相应的位置上)1. 2-的值等于( )A. 2-B. 2C. 12-D.122.下列计算正确的是( )A.321a a -=B.2325a a a += C.325a b ab += D.32ab ba ab -= 3. 已知23x y =⎧⎨=⎩是关于x ,y 的方程431kx y -=-的一个解,则k 的值为( )A. 1B. 1-C. 2D.2- 4.如图,小军同学用剪刀沿虚线将一长方形剪掉一角, 发现剩下图形的周长比原长方形的周长要小,能正确解释这一现象的数学知识是( )A.垂线段最短B.经过一点有无数条直线C.两点确定一条直线D.两点之间,线段最短5.一张菱形纸片按如图1、图2依次对折后,再按如图3打出一个圆形小孔,则展开铺平后的图案是( )6.某测绘装置上一枚指针原来指向南偏西50°(如下 图),把这枚指针按逆时针方向旋转13周则结果指针的指向( )A.南偏东20°B.北偏西80°C.南偏东70°D.北偏西10°7.今年苹果的价格比去年便宜了20%,已知今年苹果的价格是每千克a 元,则去年的价格是每千克( )元.A. (120%)a +B. (120%)a -C.120%a - D. 120%a+8.若实数a ,b ,c 在数轴上对应点的位置如图所示,则下列不等式成立的是( )A.ac bc >B.ab cb >C.a c b c +>+D.a b c b +>+ 9.轮船沿江从P 港顺流行驶到Q 港,比从Q 港返回P 港少用3小时,若船速为26千米/时,水速为2千米/时,求P 港和Q 港相距多少千米.设P 港和Q 港相距x 千米.根据题意,可列出的方程是( )A.32824x x =- B. 32824x x =+ C.2232626x x +-=+ D.2232626x x -+=- 10. n 是小于100的正整数,且满足[][][]236n n nn ++=,其中[]x 表示不超过x 的最大正整数(如[1.25]1=,[2]2=,[2.8]2=),则这样的正整数n 有( )个. A. 2 B. 4 C. 12 D. 16 二、填空题(本大题共8小题,每小题3分,共24分)11.据最新统计,苏州市常住人口约为1062万人.数据10 620 000用科学记数法可表示为 .12.如图,A 、B 、C 三点在一条直线上,若CD CE ⊥,123∠=︒,则2∠的度数是 .13. 已知x ,y 满足24237x y x y +=⎧⎨+=⎩,则34x y += .14.若不等式(3)3a x a -≤-的解集在数轴上表示如图所示,则a 的取值范围是 . 15.己知多项式1A ay =-,351B ay y =--,且多项式2A B +中不含字母y ,则a 的值为 .16.把面值20元的纸币换成1元和5元的两种..纸币(两种纸币都要使用),则共有 种换法.17.如图,将一张长方形的纸片沿折痕E 、F 翻折,使点C 、D 分别落在点M 、N 的位置,且12BFM EFM ∠=∠,则BFM ∠的度数为 °.18.如图,某点从数轴上的A 点出发,第1次向右移动1个单位长度至B 点,第2次从B 点向左移动2个单位长度至C 点,第3次从C 点向右移动3个单位长度至D 点,第4次从D 点向左移动4个单位长度至E 点,…,依此类推,经过 次移动后该点到原点的距离为2018个单位长度.三、解答题(本大题共10小题,共76分,应写出必要的计算过程、推理步骤或文字说明) 19.(本题满分8分)计算: (1) 152()36269--⨯; (2) 201825(1)(5)0.813-÷-⨯+-20.(本题满分8分)解方程:(1) 7997x x -=- (2) 11(1)2(2)25x x -=-+21.(本题满分6分) 解不等式21531322x x -++≥,并把它的解集在数轴上表示出来.22.(本题满分5分)先化简,后求值:2211312()()4323x x y x y --+-+,其中22(2)0x y -++=.23. (本题满分6分)己知关于x ,y 的方程组3521x y m x y m +=⎧⎨+=-⎩的解满足22x y +=.(1)求m 的值;(2)若a m ≥,化简:12a a +--.24.(本题满分6分)在如图所示的55⨯的方格纸中,每个小正方形的边长为1,点A 、B 、C 均为格点(格点是指每个小正 方形的顶点). (1)按下列要求画图:①标出格点D ,使//CD AB ,并画出直线CD ; ②标出格点E ,使CE AB ⊥,并画出直线CE . (2)计算ABC ∆的面积.25.(本题满分7分)把边长为1厘米的6个相同正方体摆成如图的形式. (1)画出该几何体的主视图、左视图、俯视图;(2)直接写出该几何体的表面积为 cm 2;(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 小正方体.26.(本题满分9分)如图,直线AB 与CD 相交于O . OF 是BOD ∠的平分线,OE OF ⊥. (1)若BOE ∠比DOF ∠大38°,求DOF ∠和AOC ∠的度数; (2)试问COE ∠与BOE ∠之间有怎样的大小关系?请说明理由. (3)BOE ∠的余角是 ,BOE ∠的补角是 .27.(本题满分10分)某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:请解答下列问题:(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300 kg ,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少千克?28.(本题满分11分)如图,动点M 、N 同时从原点出发沿数轴做匀速运动,己知动点M 、N 的运动速度比是1:2(速度单位:1个单位长度/秒),设运动时间为t 秒.(1)若动点M 向数轴负方向运动,动点N 向数轴正方向运动,当2t =秒时,动点M 运动到A 点,动点N 运动到B 点,且12AB =(单位长度).①在直线l 上画出A 、B 两点的位置,并回答:点A 运动的速度是 (单位长度/秒);点B 运动的速度是 (单位长度/秒). ②若点P 为数轴上一点,且PA PB OP -=,求OPAB的值; (2)由(1)中A 、B 两点的位置开始,若M 、N 同时再次开始按原速运动,且在数轴上的运动方向不限,再经过几秒,4MN =(单位长度)?。
2019-2020学年江苏省淮安市盱眙县七年级(上)期末数学试卷(附详解)

2019-2020学年江苏省淮安市盱眙县七年级(上)期末数学试卷一、选择题(本大题共8小题,共32.0分)1.如果a与−2互为倒数,那么a是()A. −2B. −12C. 12D. 22.如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是()A. 85°B. 160°C. 125°D. 105°3.如图,AB、CD相交于点O,EO⊥AB,则∠1与∠2的关系是()A. 相等B. 互余C. 互补D. 对顶角4.数轴上三个点表示的数分别为P、R、S.若P−R=5,S−P=2,则S−R等于()A. 3B. −3C. 7D. −75.某商场举办“迎新春送大礼”的促销活动,全场商品一律打八折销售.赵老师买了一件商品,比标价少付了30元,那么他购买这件商品花了()A. 70元B. 120元C. 150元D. 300元6.两个角的大小之比是7:3,它们的差是72°,则这两个角的关系是()A. 相等B. 互余C. 互补D. 无法确定7.如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成这个几何体的小正方体的个数是()A. 5或6或7B. 6或7C. 7或8D. 6或7或88.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是103,则m 的值是()A. 9B. 10C. 11D. 12二、填空题(本大题共8小题,共24.0分)9.已知∠α=52°36′47″,则它的余角是______.10.将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为______.11.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,若∠DOC=28°,则∠AOB=______ °.12.如图,数轴上点A表示的数为a,化简:|a−3|−|a+1|=______.13.若4x+3y=5,则3(8y−x)−5(x+6y+2)的值等于______.14.建筑工人砌墙时,经常在两个墙角的位置分别插一根小桩,然后拉一条直的的参照线,可以这样做的数学道理是______.15.A、B两地相距10km,甲、乙两人分别从A、B两地沿AB方向同向而行,同时出发,甲的速度为4km/ℎ,乙的速度为1km/ℎ,则______小时后两人相距5km.16.在庆祝党的十九大召开期间,学校用了若干盆花摆成如图所示的三角形花阵(图中的数表示花盆的编号),如果我们把这个花阵看作是一个三角形数阵,则从左往右数第10行的第二盆花的编号是______.三、计算题(本大题共1小题,共6.0分)17.计算:(−2)2−|−8|+3−2×(−12).四、解答题(本大题共10小题,共88.0分)18.先化简,再求值:5(3a2b−ab2)−4(−ab2+3a2b),其中a=12,b=−4.19.解方程:(1)1−3(x−1)=2x+6;(2)2x−13−10x+16=2x+14−1.20.下列物体是由六个棱长为1cm的正方体组成如图的几何体.(1)该几何体的体积是______,表面积是______;(2)分别画出从正面、左面、上面看到的立体图形的形状.21.已知线段AB=20cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,试求AM的长度(提示:先画图)22.画图并计算:如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点).(1)找出格点D,画AB的平行线CD;(2)找出格点E,画AB的垂线AE;(3)计算格点△ABC的面积.23.一家商店因换季将某种服装打折销售,如果每件服装按标价的8折出售将赚40元,而按标价的4折出售将亏40元.问:(1)每件服装的标价、成本各多少元?(2)为保证不亏本,最多能打几折?24.如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.(1)图中除直角相等、平角相等外,还有其它相等的角,请写出三对:①______;②______;③______.(2)①如果∠AOD=140°.那么根据______,可得∠BOC=______°.∠AOD,求∠EOF的度数.②如果∠EOF=1525.根据国家发改委实施“阶梯电价“的有关文件要求,某市结合地方实际,决定从2019年9月1日起对居民生活用电实施“阶梯电价”收费,具体收费标准.见下表:一户居民一个月用电量的范围电费价格(单位:元/千瓦时)不超过150千瓦时的部分a超过150千瓦时,但不超过300千瓦时的b部分超过300千瓦时的部分a+0.32015年5月份,该市居民甲用电100千瓦时,交费60元;居民乙用电200千瓦时,交费122.5元.(1)求上表中a、b的值.(2)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月交费277.5元?26.如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体.(1)这个几何体由______个小正方体组成.(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有______个正方体只有一个面是黄色,有______个正方体只有两个面是黄色,有______个正方体只有三个面是黄色.(3)这个几何体喷漆的面积为______cm2.27.几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.【回忆】如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.【探索】(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.答案和解析1.【答案】B【解析】解:∵a与−2互为倒数,∴a是−1.2故选:B.根据乘积是1的两个数叫做互为倒数解答.本题考查了倒数的定义,倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.是基础题,熟记概念是解题的关键.2.【答案】C【解析】解:AB于正东方向的夹角的度数是:90°−70°=20°,则∠BAC=20°+90°+15°=125°.故选:C.首先求得AB与正东方向的夹角的度数,即可求解.本题考查了方向角,正确理解方向角的定义是关键.3.【答案】B【解析】解:∵EO⊥AB,∴∠EOB=90°,∵∠1+∠BOE+∠2=180°,∴∠1+∠2=90°,即∠1和∠2互余.故选B.根据EO⊥AB,可知∠EOB=90°,然后根据平角为180°,可求得∠1+∠2=90°,即可得出∠1和∠2的关系.本题考查了余角的知识,解答本题的关键是掌握互余两角之和为90°.4.【答案】C【解析】解:∵P −R =5,S −P =2,∴P −R +S −P =S −R =5+2=7,则S −R =7.故选:C .直接利用已知结合整式的加减运算法则计算,即可得出答案.此题主要考查了整式的加减,正确合并同类项是解题关键.5.【答案】B【解析】解:设商品的标价是x 元,x −80%x =30,x =150,150×80%=120.他花了120元.故选:B .设商品的标价是x 元,根据全场商品一律打八折,比标价少付了30元,可列方程求解. 本题考查理解题意的能力,关键是设出标价,根据少花的钱数列出方程求解,最后求出花了多少钱.6.【答案】C【解析】解:设这两个角分别是x°,y°,根据题意得:{x:y =7:3x −y =72, 解得:{x =126y =54, 则这两个角互补.故选:C .本题需先根据题意设出未知数列出方程组,求出这两个角的度数,即可得出这两个角的关系.本题主要考查了二元一次方程组的应用,在解题时要能根据题意列出二元一次方程组是本题的关键.7.【答案】D【解析】解:根据几何体的左视图,可得这个几何体共有3层,从俯视图可以可以看出最底层的个数是4个,(1)当第一层有1个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数是:1+1+4=6(个);(2)当第一层有1个小正方体,第二层有2个小正方体时,或当第一层有2个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数是:1+2+4=7(个);(3)当第一层有2个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数是:2+2+4=8(个).综上,可得组成这个几何体的小正方体的个数是6或7或8.故选:D.首先根据几何体的左视图,可得这个几何体共有3层;然后从俯视图中可以看出最底层小正方体的个数及形状;最后从左视图判断出第二层、第三层的个数,进而求出组成这个几何体的小正方体的个数是多少即可.此题主要考查了由三视图判断几何体,考查了空间想象能力,要熟练掌握,解答此题的关键是要明确:由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.8.【答案】B【解析】【分析】本题题是数字规律应用的考查,重点考查分析问题和解决问题以及计算方面的能力,确定每一个“拆分数”中第一个数构成的数列的规律是关键.观察可知,分裂成的奇数的个数与底数相同,然后求出到m3的所有奇数的个数的表达式,再求出奇数103的是从3开始的第52个数,然后确定出52所在的范围即可得解.【解答】解:∵底数是2的分裂成2个奇数,底数为3的分裂成3个奇数,底数为4的分裂成4个奇数,∴m3有m个奇数,∵2n+1=103,n=51,∴奇数103是从3开始的第52个奇数,∵(9−1)(9+2)2=44,(10+2)(10−1)2=54,∴第52个奇数是底数为10的数的立方分裂的奇数的其中一个,即m=10.故选:B.9.【答案】37°23′13″【解析】解:∵若两个角的和为90°,则这两个角互余,∴∠a的余角=90°−∠a=90°−52°36′47″=37°23′13″.故答案为:37°23′13″.若两个角的和为90°,则这两个角互余,哟此解答即可.此题主要考查了角的关系,余角和补角的理解和掌握.要求学生正确理解余角的定义.10.【答案】90°【解析】解:∵一张长方形纸片沿BC、BD折叠,∴∠ABC=∠A′BC,∠EBD=∠E′BD,而∠ABC+∠A′BC+∠EBD+∠E′BD=180°,∴∠A′BC+∠E′BD=180°×12=90°,即∠CBD=90°.故答案为:90°.根据折叠的性质得到∠ABC=∠A′BC,∠EBD=∠E′BD,再根据平角的定义有∠ABC+∠A′BC+∠EBD+∠E′BD=180°,易得A′BC+∠E′BD=180°×12=90°,则∠CBD=90°.本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应相等相等.也考查了平角的定义.11.【答案】152【解析】解:∵三角形AOC和三角形DOB为直角三角形,∠DOC=28°,∴∠AOD+∠DOC=90°,∠DOC+∠COB=90°,∴∠AOD=∠BOC=62°,∴∠AOB=∠AOD+∠DOB=90°+62°=152°.故答案是:152.本题主要考查了余角和补角,角度的计算,正确得出∠AOD+∠DOC=90°,∠DOC+∠COB=90°,∠AOD=∠BOC=62°是解题关键.12.【答案】2−2a【解析】解:由题意可知0<a<3,所以a−3<0,a+1>0,所以|a−3|−|a+1|=−(a−3)−(a+1)=2−2a,故答案为:2−2a.由点A在数轴上的位置可知,0<a<3,则a−3<0,a+1>0,由绝对值的性质可知|a−3|=−(a−3),|a+1|=a+1,去掉绝对值符号再合并同类项即可.此题考查数轴、绝对值、整式的加减等知识,解题的关键是根据点A在数轴上对应的数a 的大小确定a−3及a+1的正负号,再根据绝对值的性质去掉绝对值符号.13.【答案】−20【解析】解:∵4x+3y=5,∴3(8y−x)−5(x+6y+2)=24y−3x−5x−30y−10=−8x−6y−10=−2(4x+3y)−10=−2×5−10=−20.故答案为:−20由于4x+3y=5,可将原式化简变形,得出含有4x+3y的形式,整体代入即可求解.此题考查的是整式的加减,通过观察可知已知与所求的式子的关系,然后将变形的式子代入即可求出答案.14.【答案】两点确定一条直线【解析】解:建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是:两点确定一条直线.故答案为:两点确定一条直线.由直线公理可直接得出答案.此题主要考查了直线的性质,要想确定一条直线,至少要知道两点.15.【答案】1或3【解析】解:设经过x小时,相遇前两人相距10千米,依题意得:(4+1)x+5=10,解得:x=1,或(4+1)x−5=10,解得:x=3,综上所述,经过1或3小时,两人相距5千米.故答案是:1或3.需要分类讨论:相遇前两人相距5千米、相遇后两人相距5千米.此题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.16.【答案】99【解析】解:由题意得:第奇数行的最后一个数为n2,第偶数行的第一个数为n2,当n=10时,则第10行第一个数为:102=100,∴从左往右数第10行的第二盆花的编号是:99.故答案为:99.由表格得出第奇数行的最后一个数为n2,从左往右增大;第偶数行的第一个数为n2,从左往右减小,据此可得.本题主要考查数字的变化规律,解答的关键是由所给的数字总结出存在的规律.17.【答案】解:原式=4−8+3+1=0.【解析】原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.18.【答案】解:原式=15a2b−5ab2+4ab2−12a2b=3a2b−ab2,当a=12,b=−4时,原式=−3−8=−11.【解析】此题考查了整式的加减−化简求值,熟练掌握运算法则是解本题的关键.原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.19.【答案】解:(1)1−3(x−1)=2x+6,去括号,得1−3x+3=2x+6,移项,得−3x−2x=6−3−1,合并同类项,得−5x=2,系数化为1,得x=−25;(2)2x−13−10x+16=2x+14−1,去分母,得4(2x−1)−2(10x+1)=3(2x+1)−12,去括号,得8x−4−20x−2=6x+3−12,移项,得8x−20x−6x=3+4+2−12,合并同类项,得−18x=−3,系数化为1,得x=16.【解析】(1)方程去括号,移项,合并同类项,系数化为1即可;(2)方程去分母,去括号,移项,合并同类项,系数化为1即可.本题考查了解一元一次方程,掌握解一元一次方程的基本步骤是解答本题的关键.20.【答案】(1)6cm3;24cm2;(2)如图所示:【解析】【分析】本题考查组合几何体的计算和三视图的画法;用到的知识点为:主视图、左视图、俯视图分别是从物体的正面、左面、上面看到的平面图形.(1)根据几何体的形状得出立方体的体积和表面积即可;(2)主视图有3列,从左往右每一列小正方形的数量为2,2,1;左视图有2列,小正方形的个数为2,1;俯视图有3列,从左往右小正方形的个数为1,2,1.【解答】解:(1)几何体的体积:1×1×1×6=6(cm3),表面积:5+5+3+3+4+4=24(cm2);故答案为:6cm3,24cm2;(2)见答案.21.【答案】解:当C在线段AB上时,如图1:由线段的和差,得AC=AB−BC=20−6=14.由M是线段AC的中点,得AM=12AC=12×14=7cm;当C在线段AB的延长线上时,如图2:由线段的和差,得AC=AB+BC=20+6=26.由M是线段AC的中点,得AM=12AC=12×26=13cm.综上所述:AM的长为7cm或13cm.【解析】分类讨论:C在线段AB上,C在线段AB的延长线上,根据线段的和差,可得AC 的长,根据线段中点的性质,可得答案.本题考查了两点间的距离,利用线段的和差得出AC的长是解题关键,要分类讨论,以防遗漏.22.【答案】解:(1)如图,线段CD即为所求;(2)如图,线段AE即为所求;(3)S△ABC=3×4−12×3×3−12×1×2−12×1×4=4.5.【解析】(1)利用网格特征以及数形结合的思想画出图形即可;(2)利用网格特征以及数形结合的思想画出图形即可;(3)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.本题考查作图−应用与设计作图,平行线的判定和性质,三角形的面积等知识,解题的关键是学会利用数形结合的思想解决问题,学会由分割法求三角形面积,属于中考常考题型23.【答案】解:(1)设每件服装的标价是x元,根据题意得:0.4x+40=0.8x−40,解得:x=200.∵x=200,∴0.4x+40=0.4×200+40=120.答:每件服装的标价是200元,每件服装的成本是120元;(32设可以打y折,−120≥0,根据题意得:200× y10解得:y≥6.答:为了保证不亏损,最多可以打6折.【解析】(1)设每件服装的标价是x元,根据服装的成本价不变,即可得出关于x的一元一次方程,解之即可得出结论,将x=200代入0.4x+40中,即可求出结论;(2)设可以打y折,根据售价−进价=利润结合不亏损,即可得出关于y的一元一次不等式,解之取其中的最小值即可得出结论.本题考查了一元一次方程的应用、代数式求值以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;代入x=200求出结论;(2)根据各数量之间的关系,正确列出一元一次不等式.24.【答案】∠FOE=∠DOB∠FOE=∠AOC∠AOF=∠EOD对顶角相等140【解析】解:(1)图中除直角相等外,还有相等的角,请写出三对:①∠FOE=∠DOB;②∠FOE=∠AOC;③∠AOF=∠EOD;故答案为:∠FOE=∠DOB;∠FOE=∠AOC;∠AOF=∠EOD;(2)①如果∠AOD=140°.那么根据对顶角相等,可得∠BOC=140°;故答案为:对顶角相等,140;②设∠EOF=α,则∠AOD=5α,∵OE⊥AB,OF⊥CD,∴∠DOF=∠BOE=90°,∴∠EOF+∠DOE=∠DOE+∠BOD=90°,∴∠EOF=∠BOD,∵∠AOD+∠BOD=180°,∴5α+α=180°,∴α=30°,∴∠EOF=30°.(1)利用余角的性质,对顶角相等、垂直的定义,即可找到相等的角;(2)①根据对顶角性质即可得到答案;②30°.此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂直定义,所求角与已知角的关系转化求解.25.【答案】解:(1)a=60÷100=0.6,150×0.6+50b=122.5,解得b=0.65.(2)若用电300千瓦时,0.6×150+0.65×150=187.5<277.5,所以用电超过300千瓦时.设该户居民月用电x千瓦时,则0.6×150+0.65×150+0.9(x−300)=277.5,解得x=400,∴该户居民月用电400千瓦时.【解析】(1)利用居民甲用电100千瓦时,交电费60元,可以求出a的值,进而利用居民乙用电200千瓦时,交电费122.5元,求出b的值即可;(2)首先判断出用电是否超过300千瓦时,再根据收费方式可得等量关系:前150千瓦时的部分的费用+超过150千瓦时,但不超过300千瓦时的部分的费用+超过300千瓦时的部分的费用=交费277.5元,根据等量关系列出方程,再解即可.本题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.26.【答案】(1)10;(2)1,2,3;(3)3200.【解析】解:(1)这个几何体由10个小正方体组成;(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有1个正方体只有一个面是黄色,有2个正方体只有两个面是黄色,有3个正方体只有三个面是黄色;(3)露出表面的面一共有32个,则这个几何体喷漆的面积为3200cm2,故答案为:(1)10;(2)1,2,3;(3)3200.【分析】(1)根据几何体的形状,可得左列三排,第一排一层,第二排两层,后排三层,中间列两排,每排一层,右列一排,共一层,可得答案;(2)根据几何体的形状,可得小正方体露出表面的个数;(3)根据露出的小正方体的面数,可得几何体的表面积.本题考查了几何体的表面积,小正方体露出面的面积和,露出4个面的有两个正方形,露出5个面的有两个正方形.27.【答案】解:【回忆】如图所示:理由:两点之间线段最短;【探索】(1)如图所示:理由:点到直线的距离垂线段最短;(2)如图所示:理由:两点之间线段最短(到OA、OC最短在AC上;到OB、OD最短在BD上).【解析】【回忆】根据两点之间线段最短即可确定;【探索】(1)根据垂线段最短即可解答;(2)根据两点之间线段最短即可解答.本题考查了应用、作图设计,正确理解两点之间,线段最短是解决本题的关键.。
2020年江苏省七年级上学期数学期末检测试卷(附答案)

江苏省七年级上学期数学期末检测试卷一、选择题(本大题共6小题,每小题2分,共12分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号直接填写在试卷相应位置上)1.下列各数是无理数的是 【 】 A .-2 B .227C .0.010010001D . π 2.下列四个数中,在-2到0之间的数是 【 】 A .-1 B . 1 C .-3 D . 33.下面四个立体图形,从正面、左面、上面观察都不可能...看到长方形的是 【 】4.下列计算正确的是 【 】 A .3a +4b =7ab B .7a -3a =4 C .3a +a =3a 2 D .3a 2b -4a 2b =-a 2b5.如图,直线AB 、CD 被直线EF 所截,AB ∥CD ,∠1=105°,则∠2等于 【 】 A . 65°B . 70°C . 75°D .80°6.下列说法正确的有 【 】(1)两条直线相交,有且只有一个交点;(2)在同一平面内,过一点有且只有一条直线与已知直线垂直; (3)过一点有且只有一条直线与已知直线平行;(4)若两条直线相交所成直角,则这两条直线互相垂直.A .4个B .3个C .2个D .1个二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在试卷相.应位置...上) 7.十八大报告指出:在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国 际社会广泛赞誉.将1 460 000 000用科学记数法表示为 .8.绝对值大于23且不大于3的所有负整数的和为: . 9.若∠α的补角为76°28′,则∠α= .10.如果代数式x 2-3x 的值为3,那么代数式-2x 2+6x +6的值是 .11.服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元, 则这款服装每件的标价比进价多 元.12.如图,∠AOB 中,OD 是∠BOC 的平分线,OE 是∠AOC 的平分线,若∠AOB=140o,则 ∠EOD=___________度.13.如图,已知a ∥b ,小亮把三角板的直角顶点放在直线b 上.若∠1=35°,则∠2的度数为 度.14.用边长为1的正方形,做了一套七巧板,拼成如图①所示的图形,则图②中阴影部分 的面积为 .15.已知0121232=⎪⎭⎫⎝⎛++-n m ,则2m-n = ___________.16.圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把 这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始, 沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种 走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长, 即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后 从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移 位”后,他到达编号为 的点. 三、解答题(本大题共9小题,共68分.请在试卷指定区域内作答,解答时应写出必要的文字说明、证......明过程或演算步骤.........) 17.(本题8分)计算:⑴ 18(14)(18)13-+---- ⑵()4211(1)33(3)2---÷⨯--18.(本题8分)解下列方程:⑴5(2)1x x --=; ⑵ 1615312=--+x x .第16题图5432119.(本题6分)已知A=3x 2+3y 2-5xy ,B=2xy-3y 2+4x 2, 求:⑴2A-B ; ⑵当x=3,y=31时,2A-B 的值.20.(本题6分)粗蜡烛和细蜡烛的长短一样,粗蜡烛可以点5小时,细蜡烛可以点4小时,如果同时点燃这两支蜡烛,过了一段时间后,剩余的粗蜡烛长度是细蜡烛长度的2倍,问这两支蜡烛已点燃了多少时间?21.(本题满分8分)利用直尺..画图: ⑴利用图1中的网格,过P 点画直线AB 的平行线和垂线.⑵把图⑵网格中的三条线段通过平移使三条线段AB 、CD 、EF 首尾顺次相接组成一个三角形. ⑶ 如果每个方格的边长是单位1,那么图⑵中组成的三角形的面积等于 .22.(本题满分6分)已知:关于x 的方程332-=-bx x a 的解是x=2,其中0≠a 且0≠b , 求代数式abb a -的值. .23.(本题满分6分)如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求x+y+z 的值.24.(本题满分9分)如下图, AD ∥EF, ∠1+∠2=180o ,⑴求证:DG ∥AB,在下列橫线上填写; 证明:∵AD ∥EF(已知)∴ ( )又∵∠1+∠2=180o (已知),∴ ( )∴DG ∥AB ( )⑵若DG 是∠ADC 的角平分线,∠1=30o ,求∠B 的度数.25.(本题满分11分)如图,射线OM 上有三点A 、B 、C ,满足OA=20cm ,AB=60cm ,BC=10cm, 点P 从点O 出发,沿OM 方向以1cm/秒的速度匀速运动,点Q 从点C 出发在线段CO 上向 点O 匀速运动(点Q 运动到点O 时停止运动),两点同时出发.⑴当P 在线段AB 上且PA=2PB 时,点Q 运动到的位置恰好是线段AB 的三等分点,求点Q 的运动速度;⑵若点Q 运动速度为3cm/秒,经过多长时间P 、Q 两点相距70cm ? ⑶当点P 运动到线段AB 上时,分别取OP 和AB 的中点E 、F ,求EFAPOB 的值.参考答案22.解:∵关于x的方程与323a x bx--=的解是x=2,∴22323a b--=………………………2分∴3a=4b.………………………4分∵a≠0且b≠0,∴43437,,343412a b a bb a b a==∴-=-=…………………………6分23.解:由于正方体的平面展开图共有六个面,其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对,则z+3=5,y+(-2)=5,x+10=5,…………………………3分解得z=2,y=7,x=-5.故x+y+z=4. …………………………6分。
江苏省2020学年七年级数学上学期期末教学质量调研卷 (2)

七年级数学上学期期末教学质量调研卷本试卷由填空题、选择题和解答题三大题组成,共28小题,满分130分,考试时间120分钟. 注意事项:1.答题前,考生务必将自己的学校、班级、姓名、考试号、考场号、座位号,用0.5毫米黑色墨水签字笔填写在答题卷相对应的位置上,并认真核对;2.答题必须用0. 5毫米黑色墨水签字笔写在答题卷指定的位置上,不在答题区域内的答案一律无效,不得用其它笔答题;3.考生答题必须答在答题卷上,保持纸面清洁,不要折叠,不要弄破,答在试卷和草稿纸上一律无效.一、选择题(本大题共10小题,每小题3分,共30分).在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母代号坡写在答题卷相应的位置上.1.13-的相反数是 A.13 B.3 C.3- D.13-2.下列计算正确的是A.325a b ab +=B.22523a a -=C. 277a a a +=D.222242a b a b a b -=- 3.若773x y a b +和2427y x a b --是同类项,则x 、y 的值为 A.3x =-,2y = B.2x =,3y =- C.2x =-,3y = D.3x =,2y =- 4.下列关于多项式221a b ab +-的说法中,正确的是A.次数是5B.二次项系数是0C.最高次项是22a bD.常数项是1 5.下列图形中,线段AD 的长表示点A 到直线BC 距离的是6.若二元一次方程37x y -=,231x y +=,9y kx =-有公共解,则k 的值为 A. 3 B.3- C. 4- D. 47.实数a 、b 在数轴上的位置如图,则化简a b +的结果为A. a b -B. a b +C. a b -+D.a b -- 8.如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是9.下列说法中正确的是A.过一点有且仅有一条直线与已知直线平行B.若AC BC =,则点C 是线段AB 的中点C.相等的角是对顶角D.两点之间的所有连线中,线段最短10.如图,正方形ABCD 的边长为1,电子蚂蚁P 从点A 分别以1个单位/秒的速度顺时针沿正方形运动,电子蚂蚁Q 从点A 以3个单位/秒的速度逆时针沿正方形运动,则第2019次相遇在A.点AB.点BC.点CD.点D二、填空题(本大题共8小题,每小题3分,共24分).把答案直接填在答题卷相应的位置上。
2023年江苏省盱眙初级实验中学七年级上学期数学期末调研试卷(附答案)
江苏省盱眙初级实验中学七年级上学期数学期末调研试卷(满分:120分;考试时间:120分钟)温馨提示:请在答题卡上相应题目的答题区域内作答,否则不得分。
一、选择题(单项选择,每小题3分,共21分)在答题卡上相应题目的答题区域内作答. 1.-3的绝对值为( ).A. 3B. -3C.13-D.132.下列合并同类项的结果正确的是( )A .a +3a=3aB . 3a -a=2C .3a +b=3abD . a -3a=-2a 3. 用一副三角板不可以拼出的角是( ).A .105°B .75°C .85°D .15° 4.下列6个数中,负数出现的频率是( ) -6.1,1||2--,-(-1),(-2)2,(-2)3,-[-(-3)]A .83.3%B . 66.7%C .50%D .33.3%5.用边长为1的正方形做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积为原正方形面积的( ). A .31 B. 21 C.32D.不能确定6.如图OA ⊥OB ,∠BOC =30°,OD 平分∠AOC ,则∠BOD的度数是( )度。
A .40B . 60C .20D .30 7. 如图,把左边的图形折起来,它会变成右边的正方体( ).二、填空题(每小题3分,共30分)在答题卡上相应题目的答题区域内作答. 8.-2的相反数是_________.9.温度升高1C 记做+1C ,气温下降5°c 记做________.10.人的大脑每天能记录大约86000000条信息,数据86000000用科学计数法表示为 . 11.表示“x 与的和的3倍”的代数式为_____________.第5题图DCOBA第6题图第7题图 ○12.已知线段AB=7cm ,在直线AB 上画线段2BC cm =,那么线段AC 的长是________ cm 或_____ cm.. 13.把多项式1532432-+-+x x x x 按字母x 降幂排列是__________________. 14.一个多项式减去223x x -+-得到12-x,这个多项式是 .15.如图,已知∠AOB 是直角,COD 是一条直线,∠AOC=300,则∠BOD= 度.16.如图,已知EF GH ,与AB CD ,都相交,162=∠,2118=∠,374=∠, 则4∠= 度。
2020年苏科教版七年级上册数学期末调研试卷(附答案)

苏科教版七年级上册数学期末调研试卷总分:100分 时间: 100分钟一、精心选一选(3分×8=24分)1.在-2.3和0.6 之间的整数个数为( )个.A .1个B .2个C . 3个D .4个 2.一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的是 ( ) A .25.30千克 B .24.70千克 C .25.51千克 D .24.80千克 3.下列方程变形正确的是 ( ) A . 方程3x ﹣2=2x ﹣1移项,得3x ﹣2x=﹣1﹣2B . 方程3﹣x=2﹣5(x ﹣1)去括号,得3﹣x=2﹣5x ﹣1C . 方程可化为3x=6D .方程系数化为1,得x=﹣14.如图,是将正方体切去一块后的几何体,则它的俯视图是( ).A .B .C .D .5.如图,∠AOC 和∠BOD 都是直角,如果∠AOB = 150º,那么∠COD 等于 ( )A .30ºB .40ºC .50°D .60°6.点C 在线段AB 上,不能判断点C 是线段AB 中点的式子是( ) A. AB=2AC B. AC+BC=AB C.AB BC 21= D.AC=BC 7.若m 是有理数,则m m -一定是 ( )A .零B .非负数C .正数D .非正数8.下列说法:①有理数的绝对值一定是正数 ②两点之间的所有连线中,线段最短;③相等的角是对顶角; ④过一点有且仅有一条直线与已知直线垂直; ⑤不相交的两条直线叫做平行线 其中正确的有 ( )A. 1个B. 2个C. 3个D. 4个 二.细心填一填(2分×12=24分)9. -2的倒数是 ,单项式的次数是 .10.截止5月初,受H7N9禽流感的影响,家禽养殖业遭受了巨大的冲击,最新数据显示,损失已超过4.1亿元,用科学记数法表示为 元. 11.一个角的度数为78º45′,则它的余角为 . 12.代数式12+a 与a 21+互为相反数,则=a . 13.关于x 的方程||2(26)10m m x--+=是一元一次方程,则m = .14.若m n 1-=-,则()2m n 2m 2n --+= .15.用边长为10cm 的正方形,做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积是 cm 2.16.一块正方形铁皮,4个角截去4个一样的小正方形,折成底面边长是cm 40的无盖长方体盒子,其容积是324000cm .则原正方形铁皮的边长是 cm .17.线段PQ 被分成3:4:5三部分,若第一和第二两部分的中点间的距离是2.1cm ,则线段PQ 的长是 cm.18.一家商店将某种服装按成本提高40%标价,又以8折优惠卖出,结果每件服装仍可获利15元,则这种服装每件的成本价是 元.19.正整数按如图所示的规律排列.则第10行,第11列的数字是 .三、做一做(共52分)20.计算:(4分×2=8分)(1(221.解方程(4分×2=8分)22.(6分)化简后再求值:()()2224232y x x y x ---+,其中23.(4分)如图,已知射线OX ,当OX 绕端点O 按逆时针方向旋转30°到OA 时,如果线段OA 的长是2cm ,那么点A 用记号A (2,30°)表示.画出两点B (1,40°),C (3,120°)的位置.24.(9分)如图,已知直线 AB 与CD 相交于点O ,OE 、OF 分别是∠BOD 、∠AOD 的平分线.(1)∠DOE 的补角有 ; (2)若∠BOD =62°,求∠AOE 和∠DOF 的度数;(3)判断射线OE 与OF 之间有怎样的位置关系?并说明理由.25.(8分)小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日6:00)A DFBCEOX分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图2),同时将前4个月的用电量和相应电费制成表格(如表1)根据上述信息,解答下列问题:(1)计算5月份的用电量和相应电费,将所得结果填入表1中; (2)小明家这5个月的月平均用电量为 度;(3)小明家这5个月的月平均用电量呈 趋势(选择“上升”或“下降”);这5个月每月电费呈 趋势(选择“上升”或“下降”);(4)小明预计7月份家中用电量很大,估计7月份用电量可达500度,相应电费将达243元,请你表126.(9分)已知数轴上两点A 、B 对应的数分别为-1、3,点P 为数轴上一动点,其对应的数为x . (1)若点P 到点A 、点B 的距离相等,则点P 对应的数是 ;(2)数轴上是否存在点P ,使点P 到点A 、点B 的距离之和为8?若存在,请直接写...出.x 的值;若不存在,说明理由; (3)现在点A 、点B 分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P 以6 个单位长度/秒的速度同时从O 点向左运动.当点A 与点B 之间的距离为3个单位长度时,求点P 所对应的数是多少?48.55参考答案一、选择题:(3分×8=24分)1、C2、D3、C4、C5、A6、B7、B8、B 二、填空题:(2分×12=24分)9、21-,4; 10、元8101.4⨯; 11、⋅1511 ; 12、-0.5; 13、m=—3; 14、3; 15、50cm 2; 16、70cm ; 17、7.2cm; 18、125元 19、110. 三、解答题:(共52分)20、(1)原式=1441552+---…………………(2分) =525-……………………(2分)(2)原式=63211⨯÷--…………………(2分)=—2……………………(2分) 21、(1)解:5x+6-3x=8…………………(1分) 5x-3x=8-6………………(1分) 2x=2……………………(1分) x=1……………………(1分) (2) 解:3(2x-1)=12-4(x+2)…………………(1分) 6x-3=12-4x-8………………(1分) 10x=7……………………(1分) x=107……………………(1分) 22、(6分)解得x=2 ……… (1分) ,y=-1 ……… (1分) 化解得 21011y x +- ………(2分) 代入值为 -12 ………(2分) 23、图略 一个点2分24、(1)∠AOE (1分),∠COE (1分)(2)OE 是BOD ∠的角平分线,62=∠BOD…………………(1分) 149180=∠-=∠∴BOE AOE …………………(1分)118=∠∴AOD ∴∠DOF=⨯21118°=59°…………………(2分) (3)位置关系是OE OF ⊥ …………………(1分)理由如下:OF OE , 分别是,,BOD AOD ∠∠的平分线180=∠+∠AOD DOB90EOF DOE DOF ∴∠=∠+∠=OF OE ∴⊥ …………………(2分)25、(1)110 46.95 …………………(2分)(2)99 …………………(1分)(3)上升 下降 …………………(2分) (4)解:设平时段用电x 度,则谷时段用电(500-x )度 243)500(3.061.0=-+x x ………………(2分)解得 x=300 500-x=200答:平时段用电300度,则谷时段用电200度 …………………(1分) 26、(1) 1 ……………(1分) (2)x=-3或x=5 ……………(4分)则点P 对应的数为436-=⨯- ……………(2分) 个单位时,此时需要的时间为3+0.5t 则点P 对应的数为2836-=⨯- ……………(2分) 综上可得当点A 与点B 之间的距离为3个单位长度时,求点P 所对应的数是-4或-28.。
2020年江苏省七年级上册期末数学调研试卷

江苏省七年级上册期末数学调研试卷一.选择题(本题共8小题,每小题2分,共16分)1.-2的相反数是 ( )A .12B .2C .-12D .-2 2.在中国共产党第十八次全国代表大会期间,新民网发起了有关调查,截至2012年11月15日13时30分,共吸引了约262900人次参与.请将262900用科学记数法表示为( )A. 0.2629×106B. 2.629×106C. 2.629×105D. 26.29×1043.下列各式计算正确的是( )A .6a +a =6a 2B .3ab 2-5b 2a =-2ab 2C .4m 2n -2mn 2=2mnD .-2a +5b =3ab4.如图是一个正方体的平面展开图,原正方体中“祝”的对面是 ( )A .羊B .年C .吉D .大5.起源于宋朝的古典智力玩具“七巧板”是由七块基本图形组成.下列图形中,不属于...七巧板中的是( )6.如图,直线AB 、CD 相交于点O ,OD 平分∠BOE ,OF 平分∠AOE ,则∠AOF 的余角的个数为 ( )A.1个B.2个C.3个D.4个第3题 第6题 第8题 7.下列说法正确的有 ( )① 两点之间的所有连线中,线段最短;② 相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;⑥在同一平面内的两直线位置关系只有两种:平行或相交A .1个B .2个C .3个D .4个8.如图,直线l 1与l 2相交于点O ,OM ⊥l 1,若∠α=44°,则∠β等于( )A .46°B .44° C.45° D .56°二.填空题:(本大题共10小题,每小题2分,共20分) 9.已知x=3是方程32-=-x ax 的解,则a=10.若代数式-2x a y b +2与3x 5y 2-b 是同类项,则代数式3a -b =____________.11.26°15′的补角为 ____________12.已知代数式x 2+x +3的值是8,那么10+2x 2+2x 的值是13.如图,将一刻度尺放在数轴上(数轴的单位长度是1cm ),刻度尺上“1cm ”和“9cm ”分别对应数轴上的-3和x ,那么x 的值为 .14.课本上有这样两个问题:如图,从甲地到乙地有3条路,走哪条路较近?从甲地到乙A .B .C .D .地能否修一条最短的路?这些问题均与关于线段的一个基本事实....相关,这个基本事实是 .第13题 第14题15.如图,直线AB、CD 、EF 相交于点O ,则∠1=∠3=30°,则∠2的度数是______16.已知一个多项式与3x 2+9x+2的和等于3x 2+4x -3,则此多项式是17.如图,线段AB =10cm ,C 是线段AB 上任意一点,M ,N 分别是AC ,BC 的中点,AM=4cm ,BN 的长为_____cm .18.将一个边长为10cm 正方形,沿粗黑实线剪下4个边长为 cm 的小正方形,拼成一个大正方形作为直四棱柱的一个底面;余下部分按虚线折叠成一个无盖直四棱柱;最后把两部分拼在一起,组成一个完整的直四棱柱,它的表面积等于原正方形的面积。
江苏省2020学年七年级数学上学期期末教学质量调研卷

七年级数学上学期期末教学质量调研卷本试卷由填空题、选择题和解答题三大题组成,共28题,满分130分.考试用时120分钟. 注意事项:1.答题前,考生务必将学校、姓名、考场号、座位号、考试号填写在答题卡相应的位置上.2.答题必须用0.5mm 黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答 案一律无效,不得用其他笔答题.3.考生答题必须在答题卡上,答在试卷和草稿纸上一律无效.一、选择题(本大题共有10小题,每小题3分,共30分.以下各题都有四个选项,其中只有 一个是正确的,选出正确答案,并在答题卡上将该项涂黑.) 1. 2019的相反数是A. 2019B.-2019C.12019D. 12019-2.计算2223a b a b -的正确结果是A. 2abB. 2ab -C. 2a bD. 2a b - 3.下列平面图形中能围成三棱柱的是4. 2018年12月8日2时23分,我国的探月卫星“嫦娥四号”由长征三号乙运载火箭在西 昌卫星发射中心成功发射,并成功飞向距地球约384400000m 的月球,384400000用科学 记数法可表示为A. 38.44× 108B. 3.844× 108C. 3.844× 109D. 3.8× 1095.下列各数..43.14,,0.57,,0.10100100013π--…(相邻两个1之间0的个数逐次加1).其中无 理数A. 4个B. 3个C. 2个D. 1个 6.如图,点,,,A B C D 都在直线MN 上,点P 在直线MN 外,若160,290∠=︒∠=︒,3120,4150∠=︒∠=︒,则点P 到直线MN 的距离是A. P ,A 两点之间的距离B. P ,B 两点之间的距离C. P ,C 两点之间的距离D. P ,D 两点之间的距离7.今年苹果的价格比去年便宜了20%,己知去年苹果的价格是每千克a 元,则今年苹果每千克的价格是 A.20%a B. 120%a - C. 20%a D. (120%)a - 8.圆柱是由长方形绕着它的一边所在直线旋转1周得到的. 那么下列绕直线旋转1周后能得到如图所示图形的是9.如图,己知AOB BOC COD ∠=∠=∠,下列结论中错误的是 A. ,OB OC 分别平分,AOC BOD ∠∠ B. AOD AOB AOC ∠=∠+∠C. 12BOC AOD AOB ∠=∠-∠ D. 1()2COD AOD BOC ∠=∠-∠10.一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动,设该机器人每秒钟前进或后退1步,并且每步的距离为1个单位长,n x 表示第n 秒时机器人在数轴上的位置所对应的数.给出下列结论(1) 33x =, (2) 51x =,(3) 7677x x >, (4) 103104x x <, (5) 20182019x x >其中,正确结论的个数是A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共8 小题,每小题3分,共24分,把答案直接填在答题卡相应的位置上.)11.单项式25a b-的系数为 .12.如果213n ab -与1n ab +是同类项,则n 是 .13.若α∠与β∠是对顶角,α∠的补角是100°,则β∠的余角的度为 . 14.如图,甲从O 点向北偏东30°走200m 到达A 处,乙从O 点向南偏东30°东走200m 到达B 处,则A 在B 的 方向.15.如右图,线段10AB =,点C 在线段AB 上,且:3:2AC BC =,点M 是线段AC 的中点,则BM = .16.有一数值转换器,原理如图所示,若输入的x 值是1,则输出的结果y 是6,若输入的x 值是2,则输出的结果y 是1,若输出的结果y 是2018,则输入的x 值是 . 17.若关于x 的一元一次不等式组0122x a x x ->⎧⎨->-⎩无解,则a 的取值范围是 .18.如图,直线AB 、CD 相交于点O ,OE 平分BOD ∠,OF 平分COE ∠,45AOC COB ∠=∠,则BOF ∠= °. 三、解答题(本大题共10小题,共76分,解答时应写出必要的计算过程、推演步骤或文字说明.)19.(每题4分;共8分)计算:(1)12(12)33+-÷⨯ (2)232018549[(2)](1)3---⨯-+⨯-20.(每题4分;共12分)解方程、解不等式: (1)3(2)186x x -=+ (2) 32190.20.5x x -+-= (3)31212x x --≥21.(本题6分)先化简,再求值:22225(3)4(3)a b ab ab a b +--+,其中12a =,13b =-.22.(本题6分) 求不等式组2151132513(1)x x x x -+⎧-≤⎪⎨⎪-<+⎩的整数解.23.(本题6分) 如图,在66⨯ 的正方形网格中,每个小 正方形的边长为1,点A 、B 、C 、D 、E 、F 、M 、N 、P 均为格点(格点是指每个小正方形的顶点). (1)利用图①中的网格,过点P 画直线MN 的平行线和垂线.(2)把图②网格中的三条线段通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形) .(3)第(2)小题中线段AB 、CD 、EF ,首尾顺次相接组成一个三角形的面积是 . 24.(本题7分)如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目:(1)正面图中有 块小正方体;(2)请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影); (3)用小正方体搭一个几何体,使得它的左视图和俯视图与你在(2)中所画的图一致,则这样的几何体最多要 块小正方体.25.(本题6分)甲骑电瓶车,乙骑自行车从相距17km 的两地相向而行.(1)甲、乙同时出发经过0.5h 相遇,且甲每小时行程是乙每小时行程的3倍少6km.求乙骑自行车的速度.(2)若甲、乙骑行速度保持与(1)中的速度相同,乙先出发0.5h ,甲才出发,问甲出发几小时后两人相遇? 26.(本题7分)己知代数式:①222a ab b -+;②2()a b -.(1)当a 、b 满足2(5)150a ab -+-=时,分别求代数式①和②的值;(2)观察(1)中所求的两个代数式的值,探索代数式222a ab b -+和2()a b -有何数量关系,并把探索的结果写出来;(3)利用你探索出的规律,求22128.52128.528.528.5-⨯⨯+的值.27.(本题8分)如图,己知,A 、O 、B 在同一条直线上,AOE COD ∠=∠,30EOD ∠=︒. (1)若8830'AOE ∠=︒,求BOC ∠的度数; (2)若射线OC 平分EOB ∠,求BOC ∠的度数.28.(本题10分)为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240 m3/月、200 m3/月,经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.(1) A、B两种型号的设备每台的价格是多少?(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?(3)若每月需处理的污水约2040 m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省盱眙初级实验中学七年级上学期数学期末调研试卷
(满分:120分;考试时间:120分钟)
温馨提示:请在答题卡上相应题目的答题区域内作答,否则不得分。
一、选择题(单项选择,每小题3分,共21分)在答题卡上相应题目的答题区域内作答. 1.-3的绝对值为( ).
A. 3
B. -3
C.13-
D.
13
2.下列合并同类项的结果正确的是( )
A .a +3a=3a
B . 3a -a=2
C .3a +b=3ab
D . a -3a=-2a 3. 用一副三角板不可以拼出的角是( ).
A .105°
B .75°
C .85°
D .15° 4.下列6个数中,负数出现的频率是( ) -6.1,1||2
--,-(-1),(-2)2
,(-2)3
,-[-(-3)]
A .83.3%
B . 66.7%
C .50%
D .33.3%
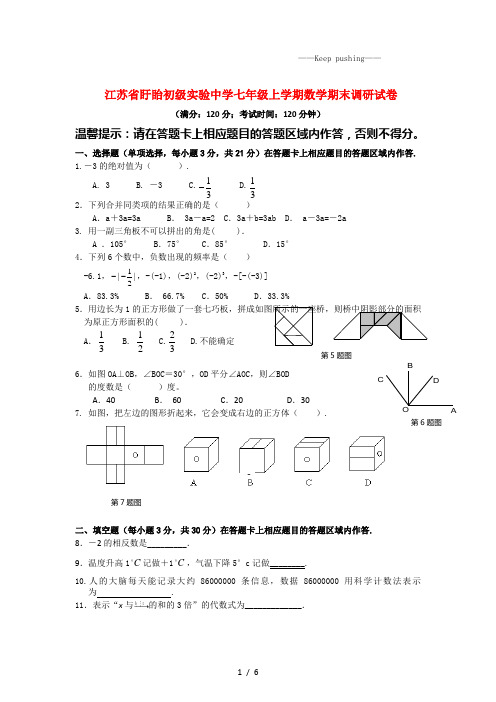
5.用边长为1的正方形做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积为原正方形面积的( ). A .
31 B. 21 C.3
2
D.不能确定
6.如图OA ⊥OB ,∠BOC =30°,OD 平分∠AOC ,则∠BOD
的度数是( )度。
A .40
B . 60
C .20
D .30 7. 如图,把左边的图形折起来,它会变成右边的正方体( ).
二、填空题(每小题3分,共30分)在答题卡上相应题目的答题区域内作答. 8.-2的相反数是_________.
9.温度升高1C 记做+1C ,气温下降5°c 记做________.
10.人的大脑每天能记录大约86000000条信息,数据86000000用科学计数法表示为 . 11.表示“x 与的和的3倍”的代数式为_____________.
第5题图
D
C
O
B
A
第6题图
第7题图 ○
12.已知线段AB=7cm ,在直线AB 上画线段2BC cm =,那么线段AC 的长是________ cm 或_____ cm.. 13.把多项式1532432-+-+x x x x 按字母x 降幂排列是__________________. 14.一个多项式减去2
23x x -+-得到12
-x
,这个多项式是 .
15.如图,已知∠AOB 是直角,COD 是一条直线,∠AOC=300,则∠BOD= 度.
16.如图,已知EF GH ,与AB CD ,都相交,162=∠,2118=∠,374=∠, 则4∠= 度。
17.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第n 个图案中白色正方形的个数为___________.
三、解答题(共59分)在答题卡上相应题目的答题区域内作答. 18.计算题(第(1)小题5分,第(2)小题5分,计10分) (1))413181()24(+-
⨯-; (2))2(16
1)32()2()2(42-⨯-+-÷-+- 19.(第(1)小题5分,第(2)小题6分,计11分) (1)化简:(
)(
)
x x x x 7251232
2
--++-
(2)先化简,再求值: )3
2
(36922x y x y -++-其中1,2-==y x
20. (6分)画图题:在方格纸上画出图形,并用适当的方式表示这些图形.
(1) 画一个45º的角;(2分)
(2) 画两条互相平行的线段(要求所画线段不能和方格线重合或平行);(2分) (3) 画两条互相垂直的线段(要求所画线段不能和方格线重合或平行).(2分)
(1)
(2)
第一个 第二个 第三个 …… 第n 个
第16题图
(3)
21.(6分)随着科技的发展,计算机行业近年来飞速发展,电脑的每台零售价也以每年平均20%的速度降价,如果去年一台电脑零售价为a万元,(1)那么现在的电脑的零售价为多少钱呢?(2)如果去年一台电脑零售价为0.6万元,也以每年平均20%的速度降价,且元旦打8.8折,那么一台电脑的零售价是多少钱呢?
22.(8分)某市出租车收费标准是:起步价6元,2千米后每千米1.6元,且每趟另加燃油附加费1元.某乘客乘坐了x千米(x>3)
(1)请用含x的代数式表示出他应该支付的车费;
(2)若该乘客乘坐了7千米,那他应该支付多少钱?
(3)如果他一趟支付了33元,你能算出他最多乘坐的里程吗?
23.(8分)“十一”黄金周期间,某博物馆在七天假期中每天旅游的人数变化如下表(正
(1)填空:若9月30日的游客人数记为a万人,则10月1日的游客人数为万人,10月2日的游客人数为万人;
(2)若以9月30日的游客人数为0点,则用折线统计图表示这7天的游客人数变化情况;
(3)根据统计图,请判断七天内游客人数最多的是哪天?最少的是哪天?
24.(10分)看图填空,并在括号内注明说理依据。
如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?下面是解答过程,请你将它补充完整。
解:∵∠1=35°,∠2=35°( 已知)
∴∠1=∠2
∴ ∥ ( ) 又∵AC ⊥AE(已知)
∴∠EAC =90°( )
∴∠EAB =∠EAC +∠1=125° ( 等式的性质 ) 同理可得,∠FBD +∠2= °
FBH EAB ∠=∠
∴ ∥ ( ) 25.(10分)如图所示,A 、B 、C 是一条公路上的三个村庄,A 、B 间的路程为100km ,A 、C 间的路程为40km ,现在A 、B 之间设一个车站P ,设P 、C 之间的路程为x km 。
(1)用含x 的代数式表示车站到三个村庄的的路程之和;(4分) (2)若路程之和为102km
(34
分)
H
参考答案及评分标准
一、1.A ; 2.D ; 3.C ; 4.B ; 5.B ; 6.D ;7.C
二、8.2; 9.-5o ; 10.8.6×107
; 11.3(x -4);
12.5、9; 13. 1235234--++x x x x ;14.42-+-x x ; 15.120; 16.74;17.5n+3. 三、18.解:(1)原式=-3+8-6 …………4分
=-1 …………6分 (2)原式=4+2×32 +161
⨯(-16)………………4分
=4+3-1 ………………6分
=6 ………………8分 19(1)原式=x x x x 72512322--++-…………4分 =692+-x x …………6分
(2))3
2
(36922x y x y -++-=-6y+4x 2 (5分)
当1,2-==y x ,上式=22 (8分)
20.图略,每图2分,每空1分,(1) 如∠1=45度, (2)如AB ∥CD (3) 如AB ⊥ CD 21.解:(1)(1-20%)a ………………4分
(2) (1-20%)×6000×0.88=4224(元)………………8分
22.解:(1)1.6x+3.8………3分
(2) 15元. ………6分
(3) 1.6x+3.8=33………8分,
x=20(千米) ………10分
23.解:(1)a+1.6 ,a+2.4;………2分
(2)图略,画图要求清晰正确………8分
(3)七天内游客人数最多的是10月3日,最少的是10月7日………10分
24. AC ∥ BD …2分( 同位角 相等,两直线平行) …4分
(垂直的定义) …6分, 125o
………8分
AE ∥ BF …10分( 同位角 相等,两直线平行) ………12分
25.如图所示,A 、B 、C 是一条公路上的三个村庄,A 、B 间的路程为100km ,A 、C 间的路程
为40km ,现在A 、B 之间设一个车站P ,设P 、C 之间的路程为x km 。
解:(1)车站到三个村庄的的路程之和为40+x+x +60-x =100+x (4分) (2)100+x =102,x =2,则车站应设在CB 间离C 村庄2km 的地方。
(4分)
(3)若要使车站到三个村庄的路程总和最小,问车站应设在C 处,最小值是100(4分)。
