2011年普通高等学校招生全国统一考试模拟试题(一)数学理科

合集下载

2011年高考全国数学试卷(新课标)-理科(含详解答案)

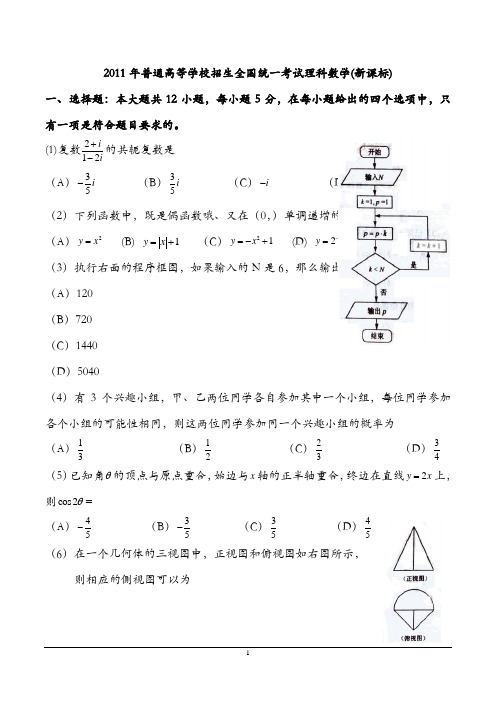
2011年普通高等学校招生全国统一考试理科数学第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)复数212ii+-的共轭复数是（A ）35i -（B ）35i （C ）i - （D ）i 解析：212i i+-=(2)(12),5i i i ++=共轭复数为C （2）下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（A ）3y x = (B) 1y x =+ （C ）21y x =-+ (D) 2xy -=解析:由图像知选B（3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是（A ）120 （B ）720 （C ）1440 （D ）5040解析：框图表示1n n a n a -=⋅，且11a =所求6a =720 选B（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（A ）13 （B ）12 （C ）23 （D ）34解析;每个同学参加的情形都有3种，故两个同学参加一组的情形有9种，而参加同一组的情形只有3种，所求的概率为p=3193=选A （5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=解析：由题知tan 2θ=,222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++选B （A ）45- （B ）35- （C ）35 （D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为解析：条件对应的几何体是由底面棱长为r 的正四棱锥沿底面对角线截出的部分与底面为半径为r 的圆锥沿对称轴截出的部分构成的。

故选D（7）设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（A （B （C ）2 （D ）3解析：通径|AB|=222b a a=得2222222b a a c a =⇒-=，选B （8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（A ）-40 （B ）-20 （C ）20 （D ）40解析 1.令x=1得a=1.故原式=511()(2)x x x x +-。

2011新课标全国卷数学(理科)(含答案)

2011年普通高等学校招生全国统一考试理科数学(新课标)一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)复数212ii+-的共轭复数是（A ）35i - （B ）35i （C ）i - （D ）i （2）下列函数中，既是偶函数哦、又在（0，）单调递增的函数是（A ）2y x = (B) 1y x =+ （C ）21y x =-+ (D) 2x y -= （3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是（A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（A ）13（B ）12（C ）23（D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=（A ）45- （B ）35- （C ）35（D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（7）设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于 A,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（A（B （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（A ）-40 （B ）-20 （C ）20 （D ）40 （9）由曲线y =2y x =-及y 轴所围成的图形的面积为（A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P（11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（A ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减（B ）()f x 在3,44ππ⎛⎫ ⎪⎝⎭单调递减（C ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有焦点的横坐标之和等于（A ）2 (B) 4 (C) 6 (D)8 二、填空题：本大题共4小题，每小题5分。

2011年高考全国新课标理科数学试卷及答案

(1)复数212ii+-的共轭复数是（A ）35i - （B ）35i （C ）i - （D ）i（2）下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（A ）3y x = (B) 1y x =+ （C ）21y x =-+ (D) 2xy -=（3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是（A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（A ）13 （B ）12 （C ）23 （D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（A ）45-（B ）35- （C ）35 （D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（7）设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（A （B （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（A ）-40 （B ）-20 （C ）20 （D ）40（9）由曲线y =2y x =-及y 轴所围成的图形的面积为（A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P （11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（A ）()f x 在0,2π⎛⎫⎪⎝⎭单调递减（B ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减（C ）()f x 在0,2π⎛⎫⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于（A ）2 (B) 4 (C) 6 (D)8第Ⅱ卷二、填空题：本大题共4小题，每小题5分。

2011年高考理科数学试卷(及答案)_全国卷(word版)[1]1

2011年普通高等学校招生全国统一考试(全国卷)数学（理工农医类）本试卷共4页，三大题21小题。

满分150分，考试时间120分钟。

★祝考试顺利★注意事项：1. 答题前，考生务必将自己的姓名、准考证号填在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上指定位置。

2. 选择题每小题选出答案后，用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答在试题卷上无效。

3. 填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内，答在试题卷上无效。

4. 考试结束，请将本试题卷和答题卡一并上交。

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是满足题目要求的。

1.复数1z i =+，z 为z 的共轭复数，则1z z z --= (A) -2i (B) -i (C) i (D) 2i2. 函数()20y x x =≥的反函数为(A)()24xy x R =∈ (B)()204xy x =≥(C)()24y xx R =∈ (D)()240y xx =≥3.下面四个条件中，使a b >成立的充分而不必要的条件是 (A) 1a b >+ (B) 1a b >- (C)22a b > (D) 33a b >4.设n S 为等差数列{}n a 的前n 项和，若11a =，公差22,24k k d S S +=-=，则k= (A) 8 (B) 7 (C) 6 (D) 55.设函数()()cos 0f x x ωω=>，将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，则ω的最小值等于 (A)13(B) 3 (C) 6 (D) 96.已知直二面角l αβ--，点,,A AC l C α∈⊥为垂足，,,B BD l D β∈⊥为垂足，若2,1A B A C B D ===，则D 到平面ABC 的距离等于(A)22(B)33(C)63(D) 17.某同学有同样的画册2本，同样的集邮册3本，从中取出4本赠送给4为朋友，每位朋友1本，则不同的赠送方法共有(A) 4种 (B) 10种 (C) 18种 (D) 20种8.曲线21x y e =+在点()0,2处的切线与直线0y =和y x =围成的三角形的面积为 (A)13(B)12(C)23(D) 19.设()f x 是周期为2的奇函数，当01x ≤≤时，()()21f x x x =-，则52f ⎛⎫-= ⎪⎝⎭(A) 12-(B) 14-(C)14(D)1210.已知抛物线C ：24y x =的焦点为F ，直线24y x =-与C 交于A 、B 两点，则cos A F B ∠= (A)45(B)35(C) 35-(D) 45-11.已知平面α截一球面得圆M ，过圆心M 且与α成60 二面角的平面β截该球面得圆N ，若该球面的半径为4.圆M 的面积为4π，则圆N 的面积为 (A) 7π (B) 9π (C) 11π (D) 13π12. 设向量,,a b c 满足11,,,602a b a b a c b c ===---=，则c 的最大值等于(A) 2 (B) 3 (C) 2 (D) 1二、填空题：本大题共4小题，每小题5分，共20分.请将答案填在答题卡对应题号的位置上,一题两空的题,其答案按先后次序填写. 13. ()201x-的二项展开式中，x 的系数与9x 的系数之差为 .14. 已知,2παπ⎛⎫∈⎪⎝⎭，5sin 5α=，则tan 2α= . 15. 已知12F F 、分别为双曲线22:1927xyC -=的左、右焦点，点A C ∈，点M 的坐标为()2,0，AM 为12F A F ∠的角平分线，则 2AF = .16. 已知点E 、F 分别在正方体1111ABC D A B C D - 的棱11BB C C 、上，且12B E E B =,12C F FC =,则面AEF 与面ABC 所成的二面角的正切值等于 .三、解答题：本大题共6小题，共70分。

2011年高考理科数学试题及答案-全国卷1

2011年高考理科数学试题及答案-全国卷12011年普通高等学校招生全国统一考试（全国卷1）理科数学第I卷一、选择题：本大题共12小题，每小题5分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1) 复数 $2+i$ 的共轭复数是（）A) $-i$ (B) $i$ (C) $-1+2i$ (D) $1-2i$2) 下列函数中，既是偶函数又是单调递增的函数是（）A) $y=x^3$ (B) $y=x+1$ (C) $y=-x^2+1$ (D) $y=2|x|$3) 执行右面的程序框图，如果输入的 $N$ 是 $6$，那么输出的 $p$ 是（）A) $120$ (B) $720$ (C) $1440$ (D) $5040$4) 有 $3$ 个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（）A) $\frac{1}{2}$ (B) $\frac{1}{3}$ (C) $\frac{1}{4}$ (D) $\frac{2}{3}$5) 已知角 $\theta$ 的顶点与原点重合，始边与 $x$ 轴的正半轴重合，终边在直线 $y=2x$ 上，则 $\cos2\theta$ =（）A) $-\frac{3}{4}$ (B) $-\frac{1}{4}$ (C) $\frac{3}{4}$ (D) $\frac{1}{4}$6) 在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（）此处应该有图片，但无法显示]7) 设直线 $L$ 过双曲线 $C$ 的一个焦点，且与 $C$ 的一条对称轴垂直，$L$ 与 $C$ 交于 $A,B$ 两点，$AB$ 为 $C$ 的实轴长的 $2$ 倍，则 $C$ 的离心率为（）A) $2$ (B) $3$ (C) $4$ (D) $6$8) 已知 $\frac{x+2}{x-2}$ 的展开式中各项系数的和为 $2$，则该展开式中常数项为（）A) $-40$ (B) $-20$ (C) $20$ (D) $40$9) 由曲线 $y=x$，直线 $y=x-2$ 及 $y$ 轴所围成的图形的面积为（）A) $\frac{10}{16}$ (B) $4$ (C) $\frac{3}{16}$ (D)$\frac{3}{32}$10) 已知 $a$ 与 $b$ 均为单位向量，其夹角为 $\theta$，有下列四个命题text{P}_1$:$a+b>1$ $\Leftrightarrow$ $\theta\in\left(0,\frac{2\pi}{3}\right)$text{P}_2$:$a+b>1$ $\Leftrightarrow$ $\theta\in\left(\frac{\pi}{3},\pi\right)$text{P}_3$: $a-b>1$ $\Leftrightarrow$ $\theta\in\left(0,\frac{\pi}{3}\right)\cup\le ft(\frac{2\pi}{3},\pi\right)$text{P}_4$: $a-b>1$ $\Leftrightarrow$ $\theta\in\left(\frac{\pi}{3},\frac{2\pi}{3} \right)$其中的真命题是（）A) $\text{P}_1,\text{P}_4$ (B) $\text{P}_1,\text{P}_3$ (C) $\text{P}_2,\text{P}_3$ (D) $\text{P}_2,\text{P}_4$11) 设函数 $f(x)=\sin(\omega x+\theta)+\cos(\omegax+\theta)$（$\omega>0,\theta<\frac{\pi}{2}$）的最小正周期为$\pi$，且 $f(-x)=f(x)$，则（）A) $f(x)$ 在 $\left(0,\frac{\pi}{2}\right)$ 单调递减 (B)$f(x)$ 在$\left(0,\frac{\pi}{4}\right)\cup\left(\frac{3\pi}{4},\pi\right)$ 单调递减C) $f(x)$ 在 $\left(\frac{\pi}{4},\frac{3\pi}{4}\right)$ 单调递减 (D) $f(x)$ 在$\left(0,\frac{\pi}{4}\right)\cup\left(\frac{\pi}{2},\frac{3\pi}{4}\ri ght)$ 单调递减P(X=-2)=0.04.P(X=2)=0.54.P(X=4)=0.42，因此X的分布列为：2: 0.042: 0.544: 0.42根据配方A，生产的产品中有22/100的次品率，根据配方B，生产的产品中有8/1000的次品率。

2011年普通高等学校招生全国统一考试(全国新课标卷)数学试题 (理科)(解析版)

2011年普通高等学校招生全国统一考试（全国新）数学（理）试题解析第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）(2011全国新课标卷理)复数212i i+-的共轭复数是 ( ) （A ）35i - （B ）35i （C ）i - （D ）i 解析：212i i +-=(2)(12),5i i i ++=共轭复数为C（2）(2011全国新课标卷理)下列函数中，既是偶函数又在+∞（0，）单调递增的函数是( )（A ）3y x = （B ） 1y x =+ （C ）21y x =-+ （D ） 2x y -=解析:由图像知选B（3）(2011全国新课标卷理)执行右面的程序框图，如果输入的N 是6，那么输出的p 是( )（A ）120 （B ）720（C ）1440 （D ）5040解析：框图表示1n n a n a -=⋅，且11a =所求6a =720选B（4）(2011全国新课标卷理)有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为( )（A ）13 （B ）12 （C ）23 （D ）34解析;每个同学参加的情形都有3种，故两个同学参加一组的情形有9种，而参加同一组的情形只有3种，所求的概率为p=3193=选A（5）(2011全国新课标卷理)已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ= ( )（A ）45-（B ）35- （C ）35 （D ）45解析：由题知tan 2θ=,222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++选B（6）(2011全国新课标卷理)在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为( )解析：条件对应的几何体是由底面棱长为r 的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。

数学_2011年某校高考数学模拟试卷(理科)(含答案)

2011年某校高考数学模拟试卷（理科）一、选择题：本大题有10小题，每小题5分，共50分.1. 复数z =(1+mi)2（i 为虚数单位）为纯虚数，则实数m =( ) A ±1 B −1 C 1 D 02. 已知集合P ={x||x −2|≤1, x ∈R}，Q ={x|x ∈N}，则P ∩Q 等于（） A [1, 3] B {1, 2} C {2, 3} D {1, 2, 3}3. 已知定义在R 上的函数f(x)满足f(x +1)=−f(x)，且x ∈(−1, 1]时f(x)={1,(−1<x ≤0)−1,(0<x ≤1)，则f(3)=( ) A −1 B 0 C 1 D 1或04. 在△ABC 中，若B 、C 的对边边长分别为b 、c ，B =45∘，c =2√2，b =4√33，则C 等于（）A 30∘B 60∘C 120∘D 60∘或120∘5. a →，b →为非零向量，“函数f(x)=(a →x +b →)2为偶函数”是“a →⊥b →”的（）A 充分但不必要条件B 必要但不充分条件C 充要条件D 既不充分也不必要条件 6. 已知A 、B 是两个不同的点，m 、n 是两条不重合的直线，α、β是两个不重合的平面，则①m ⊂α，A ∈m ⇒A ∈α；②m ∩n =A ，A ∈α，B ∈m ⇒B ∈α；③m ⊂α，m ⊥β⇒α⊥β；④m ⊂α，n ⊂β，m // n ⇒α // β．其中真命题为（） A ①③ B ①④ C ②③ D ②④7. 连掷两次骰子得到的点数分别为m 和n ，记向量a →=(m,n)与向量b →=(1,−1)的夹角为θ，则θ∈(0,π2]的概率是（） A 512B 12C 712D 568. 在函数y =|x|(x ∈[−1, 1])的图象上有一点P(t, |t|)，此函数与x 轴、直线x =−1及x =t 围成图形（如图阴影部分）的面积为S ，则S 与t 的函数关系图可表示为( )A B C D9. 己知双曲线的方程为x 2−y 23=1，直线m 的方程为x =12，过双曲线的右焦点F 的直线l 与双曲线的右支相交于P 、Q ，以PQ 为直径的圆与直线m 相交于M 、N ，记劣弧MN ̂的长度为n ，则n|PQ|的值为（） A π6B π4C π3D π210. 若在曲线f(x, y)=0（或y =f(x)）上两个不同点处的切线重合，则称这条切线为曲线线f(x, y)=0（或y =f(x)）的自公切线，下列方程的曲线：①x 2−y 2=1；②y =3sinx +4cosx ；③y =x 2−|x|；④|x|+1=√4−y 2，存在自公切线的是（） A ①③ B ①④ C ②③ D ②④二、填空题：本大题有5小题，每小题4分，共20分. 11. 在二项式(√x +2)6的展开式中，x 2的系数是________．12. 若等比数列{a n }的首项为23，且a 4=∫(411+2x)dx ，则公比q 等于________．13. 运行如图的程序框图，当输入m =−4时的输出结果为n ，若变量x ，y 满足{x +y ≤3x −y ≥−1y ≥n，则目标函数z =2x +y 的最大值为________．14. 若函数f(x)=13x 3−x 在(a,10−a 2)上有最小值，则a 的取值范围为________．15. 如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横纵坐标分别对应数列{a n }(n ∈N ∗)的前12项，如下表所示：按如此规律下去，则a 200920102011三、解答题：本大题有6小题，共80分.16. 设函数f(x)=cos2x +2√3sinxcosx(x ∈R)的最大值为M ，最小正周期为T ．（1）求M 、T ；（2）若有10个互不相等的正数x i 满足f(x i )=M ，且x i <10π(i =1, 2,…,10)，求x 1+x 2+...+x 10的值．17. 在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD // EF，EF // BC，BC=2AD=4，EF=3，AE=BE=2，G是BC的中点．（1）求证：AB // 平面DEG；（2）求证：BD⊥EG；（3）求二面角C−DF−E的余弦值．18. 投掷四枚不同的金属硬币A、B、C、D，假定A、B两枚正面向上的概率均为12，另两枚C、D为非均匀硬币，正面向上的概率均为a(0<a<1)，把这四枚硬币各投掷一次，设ξ表示正面向上的枚数．（1）若A、B出现一正一反与C、D出现两正的概率相等，求a的值；（2）求ξ的分布列及数学期望（用a表示）；（3）若出现2枚硬币正面向上的概率最大，试求a的取值范围．19. 一个截面为抛物线形的旧河道（如图1），河口宽AB=4米，河深2米，现要将其截面改造为等腰梯形（如图2），要求河道深度不变，而且施工时只能挖土，不准向河道填土．（1）建立恰当的直角坐标系并求出抛物线弧AB的标准方程；（2）试求当截面梯形的下底（较长的底边）长为多少米时，才能使挖出的土最少？20. 已知函数f(x)＝lnx，g(x)=12ax2+bx(a≠0)(Ⅰ)若a＝−2时，函数ℎ(x)＝f(x)−g(x)在其定义域内是增函数，求b的取值范围；(Ⅱ)在(Ⅰ)的结论下，设φ(x)＝e2x+be x，x∈[0, ln2]，求函数φ(x)的最小值；(Ⅲ)设函数f(x)的图象C1与函数g(x)的图象C2交于点P、Q，过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N，问是否存在点R，使C1在M处的切线与C2在N处的切线平行？若存在，求出R的横坐标；若不存在，请说明理由．21. 本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多作，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将选题号填入括号中．（1）选修4一2：矩阵与变换设矩阵M所对应的变换是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸缩变换．（I）求矩阵M的特征值及相应的特征向量；（II）求逆矩阵M−1以及椭圆x24+y29=1在M−1的作用下的新曲线的方程．（2）选修4一4：坐标系与参数方程已知直线C 1：{x =1+tcosαy =tsinα（t 为参数），C 2：{x =cosθy =sinθ（θ为参数）．(I)当α=π3时，求C 1与C 2的交点坐标；(II)过坐标原点O 做C 1的垂线，垂足为A ，P 为OA 中点，当α变化时，求P 点的轨迹的参数方程．（3）选修4一5：不等式选讲已知a ，b ，c 均为正实数，且a +b +c =1．求√4a +1+√4b +1+√4c +1的最大值．2011年某校高考数学模拟试卷（理科）答案1. A2. D3. A4. D5. C6. A7. C8. B9. C 10. C 11. 60 12. 3 13. 514. [−2, 1) 15. 100516. 解：∵ f(x)=√3sin2x +cos2x =2sin(2x +π6)(I)∵ M =2∴ T =2π2=π（2）∵ f(x i )=2，即2sin(2x i +π6)=2 ∴ 2x i +π6=2kπ+π2， ∴ x i =kπ+π6(k ∈Z)又0<x i <10π，∴ k =0，1，…，9∴ x 1+x 2+⋯+x 10=(1+2+⋯+9)π+10×π6=1403π17. 解：（1）证明：∵ AD // EF ，EF // BC ，∴ AD // BC ．又∵ BC =2AD ，G 是BC 的中点，∴ AD = // BG ，∴ 四边形ADGB 是平行四边形，∴ AB // DG ．∵ AB ⊄平面DEG ，DG ⊂平面DEG ，∴ AB // 平面DEG ．（2）证明：∵ EF ⊥平面AEB ，AE ⊂平面AEB ，∴ EF ⊥AE ，又AE ⊥EB ，EB ∩EF =E ，EB ，EF ⊂平面BCFE ，∴ AE ⊥平面BCFE ．过D 作DH // AE 交EF 于H ，则DH ⊥平面BCFE ．∵ EG ⊂平面BCFE ，∴ DH ⊥EG ．∵ AD // EF ，DH // AE ，∴ 四边形AEHD 平行四边形，∴ EH =AD =2，∴ EH =BG =2，又EH // BG ，EH ⊥BE ，∴ 四边形BGHE 为正方形，∴ BH ⊥EG ．又BH ∩DH =H ，BH ⊂平面BHD ，DH ⊂平面BHD ，∴ EG ⊥平面BHD ．∵ BD ⊂平面BHD ，∴ BD ⊥EG ．（3）分别以EB 、EF 、EA 为x 轴、y 轴、z 轴，建立空间坐标系，由已知得EB →=(2,0,0) 是平面EFDA 的法向量．设平面DCF 的法向量为n =(x, y, z)，∵ FD →=(0,−1,2)，FC →=(2,1,0)，∴ {FC →⋅n →=0˙，即{−y +2z =02x +y =0，令z =1，得n =(−1, 2, 1)．设二面角C −DF −E 的大小为θ，则cosθ=cos <n,EB →>=−22√6=−√66，∴ 二面角C −DF −E 的余弦值为−√66．18. 解：（1）由题意得：2×12×(1−12)=a 2 ∴ a =√22（2）ξ=0，1，2，3，4P(ξ=0)=C 20(1−12)2C 20(1−a)2=14(1−a)2，P(ξ=1)=C 2112(1−12)C 20(1−a)2+C 20(1−12)2C 21a(1−a)=12(1−a)P(ξ=2)=C 22122C 20(1−a)2+C 2112(1−12)C 21a(1−a)+C 20(1−12)2C 22a 2=14(1+2a −2a 2) P(ξ=3)=C 22122C 21a(1−a)+C 2112(1−12)C 22a 2=a2P(ξ=4)=C 22(12)2C 22a 2=14a 2，得ξ得分布列为：∴ Eξ=1×12(1−a)+2×14(1+2a −2a 2)+3×a2+4×14a 2=2a +1 （3）∵ 0<a <1，显然14(1−a)2<12(1−a)，即P(ξ=0)<P(ξ=1)∵ a 2>14a 2，即P(ξ=3)>P(ξ=4)由P(ξ=2)−P(ξ=1)=14(1+2a −2a 2)−12(1−a)=−14(2a 2−4a +1)≥0且P(ξ=2)−P(ξ=3)=14(1+2a −2a 2)−a 2=−14(2a 2−1)≥0得{2a 2−4a +1≤02a 2−1≤0解得2−√22≤a ≤√22 即a 三问取值范围是：[2−√22,√22] 19. 当梯形的下底边长等于3√2米时，挖出的土最少．20. （I ）依题意：ℎ(x)＝lnx +x 2−bx ． ∵ ℎ(x)在(0, +∞)上是增函数，∴ ℎ(x)=1x +2x −b ≥0对x ∈(0, +∞)恒成立， ∴ b ≤1x+2x ，∵ x >0，则1x+2x ≥2√2．∴ b 的取值范围是(−∞,2√2]．(II)设t ＝e x ，则函数化为y ＝t 2+bt ，t ∈[1, 2]． ∵ y =(t +b 2)2−b 24．∴ 当−b2≤1，即−2≤b ≤2√2时，函数y 在[1, 2]上为增函数，当t ＝1时，y min ＝b +1；当1<−b2<2，即−4<b <−2时，当t =−b2时，y min =−b 24； −b2≥2，即b ≤−4时，函数y 在[1, 2]上是减函数，当t ＝2时，y min ＝4+2b ．综上所述：φ(x)={b +1−2≤b ≤2√2−b 24−4<b <−24+2b b ≤−4(III)设点P 、Q 的坐标是(x 1, y 1)，(x 2, y 2)，且0<x 1<x 2．则点M 、N 的横坐标为x =x 1+x 22．C 1在点M 处的切线斜率为k 1=1x |x=x 1+x 22=2x1+x 2．C 2在点N 处的切线斜率为k 2=ax +b|x=x 1+x 22=a(x 1+x 2)2+b ．假设C 1在点M 处的切线与C 2在点N 处的切线平行，则k 1＝k 2．即2x 1+x 2=a(x 1+x 2)2+b ．则2(x 2−x 1)x 1+x 2=a(x 22−x 12)2+b(x 2−x 1)=(a 2x 22+bx 2)−(a2x 12+bx 1)=y 2−y 1=lnx 2−lnx 1=ln x2x 1，∴ ln x 2x 1=2(x 2−x 1)x 1+x 2=2(x 2x 1−1)1+x 2x 1设u =x 2x 1>1，则lnu =2(u−1)1+u,u >1，（1）令r(u)=lnu −2(u−1)1+u,u >1，则r ′(u)=1u −4(u+1)2=(u−1)2u(u+1)2，∵ u >1，∴ r′(u)>0，所以r(u)在[1, +∞)上单调递增，故r(u)>r(1)＝0，则lnu >2(u−1)u+1，与（1）矛盾！21. 解：(I)由条件得矩阵M =[2003]，它的特征值为2和3，对应的特征向量为[10]及[01]；(II)M−1=[1213]，椭圆x 24+y 29=1在M −1的作用下的新曲线的方程为x 2+y 2=1．(2)(I)当α=π3时，C 1的普通方程为y =√3(x −1)， C 2的普通方程为x 2+y 2=1．联立方程组{y =√3(x −1)x 2+y 2=1，解得C 1与C 2的交点为(1, 0)，(12，−√32)． (II)C 1的普通方程为xsinα−ycosα−sinα=0．A 点坐标为(sin 2α, −cosαsinα)，故当α变化时，P 点轨迹的参数方程为：{x =12sin 2αy =−12sinαcosα（α为参数）（3）由柯西不等式得(1⋅√4a +1+1⋅√4b +1+1⋅√4c +1)≤(12+12+12)⋅(4a +1+4b +1+4c +1) =3[4(a +b +c)+3]=2 当且仅当a =b =c =13时等号成立故√4a +1+√4b +1+√4c +1的最大值为√21．。

2011年高考理科数学试题及答案全国卷1

2011年一般高等学校招生全国统一考试（全国卷1）理科数学第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)复数212ii+-的共轭复数是（）（A ）35i - （B ）35i （C ）i - （D ）i （2）下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（）（A ）3y x = (B) 1y x =+ （C ）21y x =-+ (D) 2x y -= （3）执行右面的程序框图，假如输入的N 是6，那么输出的p 是（）（A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个爱好小组，甲、乙两位同学各自参与其中一个小组，每位同学参与各个小组的可能性一样，则这两位同学参与同一个爱好小组的概率为（）（A ）13（B ）12（C ）23（D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=（）（A ）45- （B ）35- （C ）35（D ）45（6）在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为（）（7）设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（）（A （B （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的绽开式中各项系数的与为2，则该绽开式中常数项为（）（A ）-40 （B ）-20 （C ）20 （D ）40 （9）由曲线y =直线2y x =-及y 轴所围成的图形的面积为（）（A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题（）其中的真命题是（）（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P （11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（）（A ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减（B ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减（C ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增(12)函数11-y x=的图像与函数2sin (24)y x x π=-≤≤的图像全部交点的横坐标之与等于（）（A ）2 (B) 4 (C) 6 (D)8第Ⅱ卷本卷包括必考题与选考题两局部。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

绝密★启用前2011年普通高等学校招生全国统一考试模拟试题（一）理科数学(必修+选修II)第I 卷注意事项：1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

3．本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A B 、互斥，那么球的表面积公式()()()P A B P A P B +=+ 24S R π=如果事件A B 、相互独立，那么其中R 表示球的半径 ()()()P A B P A P B=球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 343V R π=n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(0,1,2,)kkn kn n P k C p p k n -=-=…一．选择题 (1)．复数213i i-+的虚部是（）A ．15B ．15-C ．15iD ．15i -(2)．函数()f x 的图象与函数ln(1)(2)y x x =->的图象关于直线y x =对称，则()f x 为（）A ．1()(0)x f x ex +=>B ．1()(1)x f x ex -=>C ．()1()xf x e x R =+∈D ．()1(0)xf x e x =+>(3)．已知βα,是三次函数bx axx x f 22131)(23++=的两个极值点，且)2,1(),1,0(∈∈βα,则12--a b 的取值范围是（）A )1,41(B )1,21( C )41,21(- D )21,21(-（4）.在各项均为正数的等比数列{a n }中，若a 5·a 6＝27，则log 3a 1＋log 3a 2＋…＋log 3a 10等于（） A ．12 B ．10 C ．15 D ．27log 35（5）.不等式22x x xx--> 的解集是（）A. (02)，B. (0)-∞，C. (2)+∞，D. (0)∞⋃+∞（-，0），（6）.在7名运动员中，选4名运动员组成接力队，参加4×100米接力赛，那么甲、乙两人都不跑中间棒的安排方法共有种。

（）A ．120B ．240C ．400D ．420(7)．已知函数f （x ）＝A sin （x ωϕ+）（A ＞0，ω＞0，0＜ϕ＜π＝，其导函数()f x '的部分图象如图所示，则函数f （x ）的解析式为（） A ．f （x ）＝4sin （1324x π+）B ．f （x ）＝4sin （124x π+） C ．f （x ）＝4sin （134x π+）D ．f （x ）＝4sin （234x π+）(8)．设O 是△ABC 内部的一点，且220OA OB OC ++=，则△ABC 和△BOC 的面积之比为（）A ．3：2B ．5：2C ．4：D ．5：1（9）.正三棱柱ABC —A 1B 1C 1的各棱长都相等，E 是AB 的中点，则C 1E 与侧面ABB 1A 1所成角的余弦为（）A7B．7C7D7（10），ay x ），（xx y 垂直处的切线与直线在点0133sin cos 2).10(=++-=π为则a（）A ． 0B ． 83-C ．83 D ． 38-（11）.若三棱柱的一个侧面是边长为2的正方形，另外两个侧面都是有一个内角为060的菱形，则该棱柱的体积等于（）A． B．C． D．(12)．已知双曲线22221 ()cos sin 2xyπθπθθ-=<<的右焦点为F ，P 是右支上任意一点，以P 为圆心，PF长为半径的圆在右准线上截得的弦长恰好等于P F ，则θ的值为（） A ．6πB ．34π C ．56π D ．23π第Ⅱ卷注意事项：1．用0.5毫米的黑色字迹签字笔在答题卡上作答。

2．本卷共10小题，共90分。

二．填空题：本大题共4小题，每小题5分，共20分. （13）°°°°°°tan 18tan 42+tan 120tan 18tan 42tan 60＋＝_____________（14）若291()ax x-的展开式中常数项为672，则a = 。

（15）已知点F 是双曲线)0,0(12222>>=-b a by ax 的左焦点，点E 是该双曲线的右顶点，过F 且垂直于x 轴的直线与双曲线交于A B 、两点，若ABE ∆是锐角三角形，则该双曲线的离心率e 的取值范围是____________．（16）已知一个球的表面积为96π，球面上有两点P 、Q ，过P 、Q 作球的截面O 1，若11O P O Q ⊥，且球心O 到截面PQO 1的距离为4，那么球心O 到PQ 的距离为。

三．解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．（17）（本小题满分10分）设锐角△ABC 的三内角A ，B ，C 的对边分别为 a ，b ，c ，向量m(1,sin )A A =+ ，n 3(sin ,)2A = ，已知m 与n 共线。

（Ⅰ）求角A 的大小；（Ⅱ）若2a =，c B =，且△ABCB 的取值范围。

（18）（本小题满分12分）已知等比数列{}n a 中，*143,81().a a n N ==∈（1）若{}n b 为等差数列，且满足2152,b a b a ==，求数列{}n b 的通项公式；（2）若1n n c a =-，数列1{}n n n a c c +的前n 项和为n T ，求lim .n x T →∞（19）（本小题满分12分）如图，四棱锥P—ABCD中，PA⊥底面ABCD，AB//CD，AD=CD=1，120,90.∠=︒∠=︒BAD ACB （1）求证：B C⊥平面PAC，，求点A到平面PBC的距离。

（2）若二面角D—PC—A5（20）（本小题满分12分）某工厂2010年第三季度生产的A、B、C、D四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取50件样品参加四月份的一个展销会：（1）问A、B、C、D型号的产品各抽取多少件？（2）从50件样品随机的抽取2件，求这2件产品恰好是不同型号产品的概率；（3）从A、C型号的样品中随机地抽取3件，用ξ表示抽取A种型号的产品件数，求ξ的分布列和数学期望。

（21）（本小题满分12分）已知A O B ∆的顶点A 在射线1:(0)l y x =>上，A ，B 两点关于x 轴对称，O 为坐标原点，且线段AB 上有一点M 满足||||3AM MB ⋅=，当点A 在1l 上移动时，记点M 的轨迹为W 。

（1）求轨迹W 的方程；（2）设N （2，0），是否存在过N 的直线l 与W 相交于P 、Q 两点，使得1O P O Q ⋅=，若存在，求出直线l ，若不存在，说明理由。

（22）（本小题满分12分）已知函数x ax x f ln )(=图像上点))(,(e f e 处的切线与直线x y 2=平行（其中 71828.2=e ），.2)(2--=tx x x g（I ）求函数)(x f 的解析式；（II ）求函数)0](2,[)(>+n n n x f 在上的最小值；（III ）对一切(]0,,3()()x e f x g x ∈ ≥恒成立，求实数t 的取值范围。

2011年普通高等学校招生全国统一考试理科数学(必修+选修II)参考答案第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中。

只有一项是符合题目要求的）13．--114．215．()1,216．25三、解答题（本题共6小题，总分70分．解答应写出文字说明，证明过程或演算步骤）17．【解】（Ⅰ）因为m ∥n，则3sin (sin)2A A A+=，即23sincos 2A A A +=.……（2分）所以1cos 232222AA -+=，即1sin 2cos 2122A A -=，即sin(2)16A π-=. ……… （5分）A 是锐角，则262A ππ-=，所以3A π=. ……………………（6分）（Ⅱ）因为2a =，c B =，则1sin 2A B C S ac B =2122B =⨯⨯2B =1cos 22B-=2B =. ……………………（9分）由已知，2B <，即1cos 22B >. …………………… （11分）因为B 是锐角，所以023B π<<，即06B π<<，故角B 的取值范围是(0,)6π. …………（13分）22、解：（I ）由点))(,(e f e 处的切线方程与直线02=-y x 平行，得该切线斜率为2，即.2)('=e f又,1,2)1(ln ),1(ln )('==++=a e a x a x f 令所以.ln )(x x x f = …………4分（II ）由（I ）知1ln )('+=x x f ，显然10)('-==ex x f 时当,0)(')1,0(<∈x f ex 时所以函数)1,0()(ex f 在上单调递减.当),1(+∞∈ex 时0)('>x f ，所以函数),1()(+∞ex f 在上单调递增，①m in 111(,2],()();n n f x f e e e ∈+==-时 ②21+<≤n n e时，函数]2,[)(+n n x f 在上单调递增，因此m in ()()ln ;f x f n n n ==…………7分所以m in11,(0),()1ln ,().n e e f x n n n e ⎧-<<⎪⎪=⎨⎪≥⎪⎩…………10分（III ）对一切(])()(3,,0x g x f e x ≥∈恒成立，又,2ln 3,2)(22--≥∴--=tx x x x tx x x g即.2ln 3xx x t --≥设(],,0,2ln 3)(e x xx x x h ∈--=则,)2)(1(23231)('2222xx x xx x xx x h --=+-=+-=由,210)('===x x x h 或得)(,0)('),1,0(x h x h x >∈∴单调递增， (1,2),'()0,()x h x h x ∈<单调递减， (2,),'()0,()x e h x h x ∈>单调递增，,123)(,1)1()(1-<--=-==∴-ee e h h x h 且极大值所以.1)1()(max -==h x h因为对一切(])()(3,,0x g x f e x ≥∈恒成立，.1)(max -=≥∴x h t故实数t 的取值范围为[).,1+∞- …………14分。