对数频率特性(精选)
2第二节对数频率特性

1-Apr-21
1
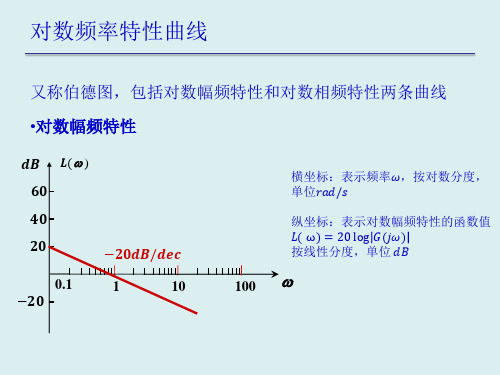
一、对数频率特性曲线(波德图,Bode图)
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率,纵坐标是幅值和相角)的分度:
横坐标(称为频率轴)分度:它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值,因此对w 而言是 非线性刻度。w 每变化十倍,横坐标变化一个单位长度,称为 十倍频程(或十倍频),用dec表示。类似地,频率w 的数值变化
w L(w )
2 20 log
A(w )
20 log
K
w
40
K 10
20log K 20log w,
20
w 当K 1时,w 1, L(w) 0;
20 40
j (w)
1 10 100 K 1 w
当w 10时,L(w) 20 可见斜率为-20/dec 当K 1时,w 1, L(w) 20log K;
0.3
-120° 0.5
-150° 0.7
1.0
-180°
1
1
10T 5T
1
1
2
2T
T
T
对数幅频特性和对数相频特性
图。上图是不同阻尼系数情况
下的对数幅频特性实际曲线与
渐近线之间的误差曲线。
5 T
10 T
当0.3<<0.8,误差约为±4.5dB
1-Apr-21
16
振荡环节的波德图
相频特性:j
1-Apr-21
6
比例环节的bode图
二、典型环节的波德图 ⒈ 比例环节: G(s) K ;
G( jw) K
幅频特性:A(w) K;相频特性:j(w) 0
频率响应法示例之二_对数频率特性

频率响应示例之二――对数频率特性一、绘制下列传递函数的对数幅频渐近特性曲线)110)(1(200)(2++=s s s s G 解:开环系统由以下典型环节组成:2200,11+s , 1101+s 1101+s 的转折频率为ω11+s 的转折频率为ω2因为2=m ,K =200>1,L a )(0ω绘制频段1ωω> k ,1,11.0221=≤==<≤=ωωωωω2003年4.(10分/150分)已知单位反馈系统的开环传递函数为)164)(12()1.0(16)(22+++++=s s s s s s s G ,试绘制对数幅频特性渐近线 解: dBk s s s s s s s s s s s s s G n n 201.0lg 20lg 2011,4,1,1.0)116416)(12()110(1.0)164)(12()1.0(16)(323212222−========+++++=+++++=时,转折频率为:ωζζωωω2000年4.(10分/70分)系统的对数幅频特性如图所示,据此写出该系统相应的传递函数。
解:图中兰色是解题时作的辅助线及环节示意将对数幅频特性曲线进行分解,从左依次向右可得到系统所包含的开环环节为: K ,111+s T ,12+s T ,113+s T ;其中:2.011=T ;112=T ;1013=T 故:51=T ;12=T ;1.03=T ;又因 20lgK =20,故K =10所以,系统的传递函数:)11.0)(15()1(10)(+++=s s s s Gw (1/sec ) db 20lg|G|1996年三、2.(10分/60分)系统的对数幅值曲线如图所示。
试推导:系统的传递函数。
解:图中兰色是解题时作的辅助线及环节示意将对数幅频特性曲线进行分解,从左依次向右可得到如图辅助所示的环节⋅sT 11⋅+12s T ⋅+13s T ⋅+114s T ⋅+115s T 116+s T 其中:811=T ;212=T ;413=T ;814=T ;2415=T ;3616=T 故:125.01=T ;5.02=T ;25.03=T ;125.04=T ;04.05=T ;03.06=T 所以,系统的传递函数:)103.0)(104.0)(1125.0()125.0)(15.0(8)(+++++=s s s s s s s G由已知的Bode 图求对象的传递函数小结:1. 根据给出的渐近线,先找出基本的环节与各转折频率――求出时间常数,若有二阶环节,还需要求出ζ值。
开环对数频率特性和时域指标.

5-6 开环对数频率特性和时域指标根据系统开环对数频率特性对系统性能的不同影响,将系统开环对数频率特性分为三个频段。
即低频段、中频段和高频段。
一、 低频段低频段通常是指开环对数幅频特性的渐近曲线在第一个交接频率以前的频段,这一频段完全由开环传递函数中的积分环节和放大环节所决定。
低频段的对数幅频为ωωωωlg 20lg 20lg 20)()(lg 20⨯-==v K Kj H j G v (5-32)式中v 为开环传递函数中的积分环节数。
根据式(5-32)及积分环节数,就可作出开环对数幅频特性曲线的低频段,如图5-39所示。
若已知低频段的开环对数幅频特性曲线,则很容易得到K 值和积分环节数v ,故低频段的频率特性决定了系统的稳态性能。
二、中频段中频段是指开环对数幅频特性曲线截止频率c ω附近的频段。
这决定系统的稳定程度,即决定系统的动态性能。
设有二个系统,均为最小相位系统,它们的开环对数幅频特性曲线除中频段的斜率不同(即一个为20-dB/dec,另一个为40-dB/dec) 之外, 其余低频、 高频段均相同。
并且中频段相当长,如图5-40 所示。
显然,系统(a)有将近90°的相裕量,而系统(b)则相裕量很小。
假定另有二个系统, 均为最小相位系统, 开环对数幅频特性曲线除中频段 (斜率为 -20 dB/dec ) 线段的长度不同外, 其余部分完全相同, 如图 5-41 所示。
显然, 中频段线段较长的系统 (a) 的相裕量将大于中频段线短的系统(b)。
可见,开环对数幅频特性中频段斜率最好为20-dB/dec ,而且希望其长度尽可能长些,以确保系统有足够的相角裕量。
如果中频段的斜率为40-dB/dec 时,中频段占据的频率范围不宜过长,否则相裕量会很小;若中频段斜率更小(如60-dB/dec),系统就难以稳定。
另外,截止频率c ω越高,系统复现信号能力越强,系统快速性也就越好。
三、 高频段高频段是指开环对数幅频特性曲线在中频段以后的频段(一般c ωω10>的频段)。
对数频率特性讲解

? 关系
deg -100
-120
-140
-160
-180
-1
10
Phase of 2-order factor
? ? 0.1
0
1
10
10
0
-20
-40
-60
相频特性与 -80
? 关系
deg -100
-120
?
20log ? ?
2
2 n
?
?40log ? ?n
dB
高频时的对数幅频特性曲线是一条斜率为-40分贝/十倍频程的直线
由于在
? ??n
时
? 40 log ? ? ?40 log1 ? 0 dB ?n
所以高频渐近线与低频渐近线在
? ? ? n 处相交。这个频率就是上述二阶因子的转角频率。
20
10
0
幅频特性与
请看下页
Asymptote 渐近线
0
Corner frequency
Bode Diagram of G(jw )=1/(jw T+1) T=0.1
-5
(dB) agnitude
-10 -15
M
-20
精确曲线 Exact curve
-25 0
Asymptote 渐近线
(deg) Phase
-45
精确曲线 Exact curve
? (? ) ? arctg (? T )
0
0
1
2
10
10
10
Frequency (rad/sec)
图: 一阶因子的对数频率特性曲线
L(? ) ? 20 log [1 ? (? T )2] ? 20 log ? T (dB)
典型环节伯德图

精选完整ppt课件
10
惯性环节的相频特性为:
对应的相频特性曲线如图5-14所 示。它是一条由 至 范围内变化 的反正切函数曲线,且以 和 的交点为斜对称.
精选完整ppt课件
11
四一阶微分环节 一阶微分环节频率特性为: 其对数幅频特性是:
一阶微分环节的对数幅频特性如图5-16所示,渐
近线的转折频率为 ,转折频率处渐近特性与精确特
的误差愈大。 等于转折频率
时,误差最大,最大误差为:
精选完整ppt课件
9
时的误差是:
时的误差是:
误差曲线对称于转折频率 ,如 图5-15所示。由图5-15可知,惯 性环节渐近线特性与精确特性的误 差主要在交接频率 上下十倍频
程范围内。转折频率十倍频以上的 误差极小,可忽略。经过修正后的 精确对数幅频特性如图5-14所示 。
,与零分贝线重合; 是一条斜率为
-20(dB/dec.)的直线。
两条直线在 处相交, 称为转折频率,由这两条直
线构成的折线称为对数幅频特性的渐近线。如图5-14所 示。
精选完整ppt课件
8
很明显,距离转折频率 愈
远
, 愈能满足近似条
件,用渐近线表示对数幅频
特性的精度就愈高;反之,
距离转折频率愈近,渐近线
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示,它是一条与角频率ω无 关且与ω轴重合的直线。
精选完整ppt课件
4
二积分环节 积分环节的频率特性是: 其幅频特性为:
对数幅频特性是:
精选完整ppt课件
5
设
,则有:
可见,其对数幅频特性是一条在 ω=1(弧度/秒)处穿过零分贝线 (ω轴),且以每增加十倍频率降 低20分贝的速度(-20dB/dec) 变化的直线。
自动控制原理第五章第二部分
当L(w=0时:
L(w
)
20
lg
K
w
0K
wv
I型系统
斜率为-20db/dec的低频段渐近线或其延长线与横轴的 交点的频率值与开环放大系数K相等。
II型系统
斜率为-40db/dec的低频段渐近线或其延长线与横轴的 交点的频率值的平方与开环放大系数K相等。
例1:已知某最小相位系统由频率响应实验获得的对数幅 频曲线如图所示,试确定其传递函数。
3.开环对数幅频特性:
L(w)
60
40dB / dec
40
转折频率 w1 1
w2 2
w3 20
环节 惯性 一阶微分
振荡
20
60dB / dec
0
0.1
12
10 20
100 w
20
40dB / dec
40
80dB / dec
传递函数的频域实验确定
1.频率响应实验
Asinwt
L(w )
20dB / dec
0dB / dec
20
20dB / dec
0
0.1
1
20
w
40dB / dec
解: (1)确定系统积分环节的个数
低频段的渐近线为-20dB/dec 1
(2)确定系统传递函数
K ( 1 s 1)
G(s)
0.1 s(s 1)( 1
s 1)
20
L(w )
一阶微分环节 二阶微分环节
一点+一斜率确定初始段渐近线
(4)从低频渐近线开始,沿w 增大的方向,每遇到一个
转折频率改变一次渐近线斜率,直到绘出转折频率最高 的环节为止;
5.3 对数频率特性(Bode图)

ωn
ωn
ωn
L(ω) ≈ −20 lg1 = 0dB
表明 L(ω ) 的低频段渐近线是一条 0dB 的水平线。 当 ω >> 1 时,略去式(5-55)中 L(ω ) 的 ωn
1 和 2ξ ω 项,有 ωn
L(ω ) = −20 lg( ω )2 = −40 lg ω
ωn
ωn
表明 L(ω ) 的高频段渐近线是一条斜率为 − 40dB 的直线。
(1)将开环传递函数写成尾 1 标准形式:
∏∏ ∏∏ G(s)
=
p
K
i =1 q
sv (
j =1
(s zi
(m− p)
+ 1)
h =1
2
[(
s
)2
ωzh
+ 2ξzh
s ωzh
+ 1]
s pj
(n−q−v)
+ 1)
k =1
2
[(
s
ω pk
)2
+ 2ξ pk
s ω pk
+ 1]
确定系统开环增益 K 和型别 v ,把各典型环节的转折频率由小到大依次标在频率轴上。
在 ω3 = 8 处,振荡环节使渐近线斜率由 −20 dB/dec 改变为 −20(n − m) = −60 dB/dec 。由
图 5-30 例 5-6 图
此绘制出渐近对数幅频特性曲线 L(ω) 。
(4)若有必要,可利用误差曲线对 L(ω) 进行修正。 (5)绘制对数相频特性曲线ϕ (ω) 。比例环节相角恒为零,积分环节相角恒为 − 90o ,惯
174
⎧L(ω) = 20 lg A(ω) = 20 lg[ A1(ω) A2 (ω)L Al (ω)]
5.2-对数坐标图

这一点斜对称。
1 T
90
180
振荡环节具有相位滞后的作用,输出滞后于输入的范围为0º→-
180º;同时的取值对曲线形状的影响较大。
2021/5/23
27
不同ζ情况下二阶系统的对数相频特 性曲线。
2021/5/23
28
微分环节的频率特性
6 微分环节的频率特性:
微分环节有三种:纯微分、一阶微分和二阶微分。传递函 数分别为:
2021/5/23
22
低频渐 近线
T [40]
高频渐 近线
T=1/T为低频渐近线与高频渐近线交点处的 横坐标,称为转折频率,也就是环节的无阻尼自
然振荡频率n。
2021/5/23
23
40dB/Dec
o
1 T
G(j)s2
10 0.6s1
K10,T1 ,0.3
由图可见:对数幅频特性曲线有峰值。
2021/5/23
一倍频程
30 40 50 60 80 100 一倍频程
十倍频程 十倍频程
十倍频程
一倍频程 十倍频程
lg
0
1
2
ω 1 2 3 4 5 6 7 8 9 10 lgω 0.000 0.301 0.477 0.602 0.699 0.778 0.845 0.903 0.954 1.000
2021/5/23
4
20dB/Dec
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
2021/5/23
18
2)对数相频特性
精确相频特性为: ()atctgT
T 0.01 0.02 0.05 0.1 0.2 0.3 0.5 0.7 1.0 -0.6 -1.1 -2.9 -5.7 -11.3 -16.7 -26.6 -35 -45 T 2.0 3.0 4.0 5.0 7.0 10 20 50 100 -63.4 -71.5 -76 -78.7 -81.9 -84.3 -87.1 -88.9 -89.4
