流量频率分析计算
超声流量计的测量原理以及计算方程

超声流量计的测量原理以及计算方程1.基本工作原理超声波流量计的测量原理是以物理学中的多普勒效应为基础的。
依赖声学多普勒效应,当声源和观察者之间有互相运动时,观察者所感受到的声频率将不同于声源所发出的频率。
这个因相对运动而产生的频率变化与两物体的相对速度成正比.在超声波多普勒流量测量方法中,超声波发射器为一固定声源,随流体一起运动的固体颗粒起了与声源有相对运动的“观察者”的作用,当然它仅仅是把入射到固体颗粒上的超声波反射回接收据.发射声波与接收声波之间的频率差,就是由于流体中固体颗粒运动而产少的声波多普勒频移.由于这个频率差正比于流体流速,所以测量频差可以求得流速.进而可以得到流体的流量.因此,超声波多普勒流量测量的一个必要的条件是:被测流体介质应是含有一定数量能反射声波的固体粒子或气泡等的两相介质.这个工作条件实际上也是它的一大优点,即这种流量测量方法适宜于对两相流的测量,这是其它明渠流量计难以解决的问题.因此,作为一种极有前途的两相流测量方法和电磁流量计,超声波多普勒流量测量方法目前正日益得到应用.2.流量方程假设,超声波波束与流体运动速度的夹角为,超声波传播速度为c,流体中悬浮粒子运动速度与流体流速相同,均为u.现以超声波束在一颗固体粒子上的反射为例,导出声波多普勒频差与流速的关系式.当超声波束在管轴线上遇到一粒固体颗粒,该粒子以速度u沿营轴线运动.对超声波发射器而言,该粒子以u cos a的速度离去,所以粒子收到的超声波频率f2应低于发射的超声波频率f1,降低的数值为f2-f1=- f1 (3-73)即粒子收到的超声波频率为f2=f1- f1 (3-74)式中f1――发射超声波的频率;a――超声波束与管轴线夹角;c――流体中声速。
固体粒子又将超声波束散射给接收器,由于它以u cos a 的速度离开接收器,所以接收器收到的超声波频率f3又一次降低,类似于f2的计算,f3可表示为f3=f2- f2 (3-75)将f2的表达式代入上式,可得:f3=f1(1- )2 =f1(1-2 +)(3-76)由于声速c远大于流体速度u,故上式中平方项可以略去,由此可得:f3=f1(1-2 )(3-77)接收器收到的超声波频率与发射超声波频率之差,即多普勒频移 f1,可由下式计算:f=f1-f3=f1-f1(1-2 )=f1 (3-78)由上式可得流体速度为u= f (3-79)体积流量qv可以写成:qv=uA= f (3-80)式中,A为被测管道流通截面积.出以上流量方程可知,当流量计、管道条件及被测介质确定以后,多普勒频移与体积流量成正比,测量频移 f就可以得到流体流量qv。
水文频率计算

《水文频率计算》根据某水文现象的统计特性,利用现有水文资料,分析水文变量设计值与出现频率(或重现期)之间的定量关系的工作过程称为水文频率计算。
自然界的现象按发生情况可分成:必然事件,即在一定条件下必然会发生的事情,如降雨以后就要涨水是必然发生的;不可能事件,即在各条件实现之下永远不会发生的事情,如只在重力作用下的水由低处向高处流是不可能的;随机事件(也称偶然事件),即在一定条件下可能发生也可能不发生的事件,如每条河流每年出现一个流量的年最大值是必然的,但这个最大值可能是这个值也可能是那个值,它在数量上的出现是一种随机事件。
频率计算中是以1来表示必然事件出现的可能性(即百分之百出现),以0表示不可能事件出现的可能性,随机事件出现的可能性介于0与1之间。
水文要素。
如降雨、流量等在量的出现方面都有随机性的特点,水文变量如年雨量、年最大洪峰流量、枯季最小流量等都属于随机事件,均可用频率分析方法来分析计算。
水文频率分析主要包括:利用现有水文资料组成样本系列,选择合适的频率曲线线型和估计它的统计参数,根据所绘制的频率曲线推求相应于各种频率(或重现期)的水文设计值。
样本系列。
无限个成因相同、相互独立的同类水文变量的集合称为该水文变量的总体。
这个总体是未知的,现有水文资料只是过去发生过的和今后可能发生的整个总体中的一个样本。
把现有水文资料的水文变量按大小次序排列组成一个系列,称为样本系列,其中所含水文变量的项数(系列长度)叫做样本容量。
系列愈长,样本容量愈大。
水文频率分析就是通过样本系列的统计特征来估计其总体的统计特征,如各种统计参数、某水文变量的频率等。
因此,样本系列是水文频率分析的基础。
用样本系列去推估容量很大或无限的总体的情况,会产生因抽样而引起的误差,这就是抽样误差。
水文统计分析中所估计出的各种数值(如频率、分析中的各个参数、相关系数等)都有抽样误差。
样本的容量越大误差越小,否则误差越大。
抽样误差分析方法有两种:①解析法。
暴雨流量计算方法和步骤

暴雨流量计算方法和步骤引言:暴雨流量是指暴雨期间单位时间内过一定涵容量的断面的径流量,是城市洪水灾害预测和防治中的重要参数。
暴雨流量计算是根据大气环流、降水形态、降水量、地表特征等因素,通过数学模型计算得出的。
本文将介绍暴雨流量计算的常用方法和步骤。
一、暴雨流量计算方法:1.单位线法:即根据不同暴雨频率及其历时,通过单位线方法揭示暴雨过程的时空分布规律和径流量的关系,然后通过设计频率的单位线乘以实际暴雨过程历时,即可计算出暴雨流量。
2.单位面积法:即根据暴雨产流过程的特点,将流域划分为一系列面积大小相等的单元,利用每个单元上的降雨量与径流量的关系,计算得到整个流域的暴雨流量。
3.经验公式法:通过历史洪水事件的统计数据和实测数据,寻找暴雨降雨量与洪水流量之间的经验公式,根据给定的暴雨降雨量,通过经验公式计算得出暴雨流量。
4.数学模型法:利用物理方程或统计模型等,通过观测数据拟合出洪水流量与降雨量之间的关系。
这种方法通常需要大量的观测数据和计算资源。
二、暴雨流量计算步骤:根据上述方法,暴雨流量计算通常包括以下步骤:1.收集数据:收集相关的气象数据、地形数据和水文数据等。
包括年降水量、暴雨频率、区域降水特征,流域面积、地形起伏以及土壤类型等信息。
2.预处理数据:对收集到的数据进行预处理和分析。
包括数据清洗、数据间的关系分析和处理,排除异常数据等。
3.选择计算方法:根据实际情况和相关要求,选择合适的计算方法。
比如单位线法适用于较大流域和流域面积分布均匀的情况,而单位面积法适用于小流域和流域面积分布不均匀的情况。
4.暴雨径流计算:根据选择的计算方法,进行暴雨径流计算。
如单位线法中,计算每个历时区间的单位线,再与实际降雨过程相乘得出单位线过程的流量,再将不同历时的单位线流量相加得到总的暴雨流量。
5.结果分析:对计算得到的暴雨流量进行分析和评估。
包括计算结果的合理性检验、灵敏性分析、计算误差的评估等。
6.结果应用:根据分析结果,对洪水防治、规划设计等工程提出建议和措施。
安徽省部分山丘区中小河流水文分析与频率计算

《河南水利与南水北调》2024年第2期水文水资源安徽省部分山丘区中小河流水文分析与频率计算施文天(安徽省水文局宣城水文站,安徽芜湖241200)摘要:通过外业调查洪水宣城市11个乡镇3条河流共11调查点和内业数据分析,安徽省宣城市小河主要存在治理不完善,堤防达标率不高,防洪设施薄弱、标准低;山洪灾害防御能力不足。
山区众多山溪性小支流,水土流失、河床淤积严重,且极不稳定等诸多问题,建议推进防洪治理工程,加强防洪安全教育,以提高防洪水平。
关键词:宣城;小河流;水文;频率中图分类号:TV211.1文献标识码:A文章编号:1673-8853(2024)02-0032-02Hydrological Analysis and Frequency Calculation of Small and Medium-sized Rivers inSome Hilly Areas of Anhui ProvinceSHI Wentian(Xuancheng Hydrological Station of Anhui Hydrology Bureau,Wuhu241200,China)Abstract:Through field investigation and analysis of11survey points and internal data from11townships and3rivers in Xuancheng City,Anhui Province,it was found that the main problems with small rivers in Xuancheng City have such problems as incomplete governance,low embankment compliance rate,weak flood control facilities,low standards and insufficient ability to defend against flash floods.There are numerous small tributaries of mountain streams in mountainous areas,with serious soil erosion,riverbed siltation,and extreme instability.It is suggested to advance the flood control project and strengthen the education of flood control safety so as to improve flood control level.Key words:Xuancheng;small rivers;hydrology;frequency1研究区概况宣城市位于安徽省东南部,地势南高北低,土地总面积12340km2。
风机变频流量计算

这有一台变频风机,想知道其在不同频率下的风量,理论值即可不知这样计算可否,因变频电机转速时n=60*频率/电极对数,通过公式可知不同频率下的转速;再因风机流量与转速成正比关系即流量Q1/Q2=n1/n2,Q为流量n为转速。
这样就可求得不同频率下风机的风量。
1、电机转速730r/min,属于6极。
频率在28Hz时转速为n1=60×28÷6=280r/minQ1/Q2=n1/n2Q1=n1/n2*Q2=280÷730×120000=46027m3/h.变频器的变频调速是通过调节频率实现的,工频情况下的频率是50Hz,如果使用的频率是40Hz,也就是频率下降至0.8,则电机转速下降至原额定转速的0.8,下降的幅度与频率下降的幅度成一次方程式关系,也就是所谓的线性关系,而且风机的风量下降也为额定风量的0.8。
但风机的风压下降比例则变化大了,成二次方比例下降,即风压下降为0.8x0.8=0.64,风压会变为额定风压的0.64,下降了0.36。
至于输出功率,则成三次方比例关系,即0.8x0.8x0.8=0.512,下降了0.488.。
2、电机转速730r/min,属于6极。
频率在28Hz时转速为n1=28÷50×730=409r/minQ1/Q2=n1/n2Q1=n1/n2*Q2=409÷730×124820=69933m3/h2、电机转速730r/min,属于6极。
频率在49Hz时转速为n1=49÷50×730=715r/minQ1/Q2=n1/n2Q1=n1/n2*Q2=715÷730×124820=122255m3/h。
洪峰流量频率计算
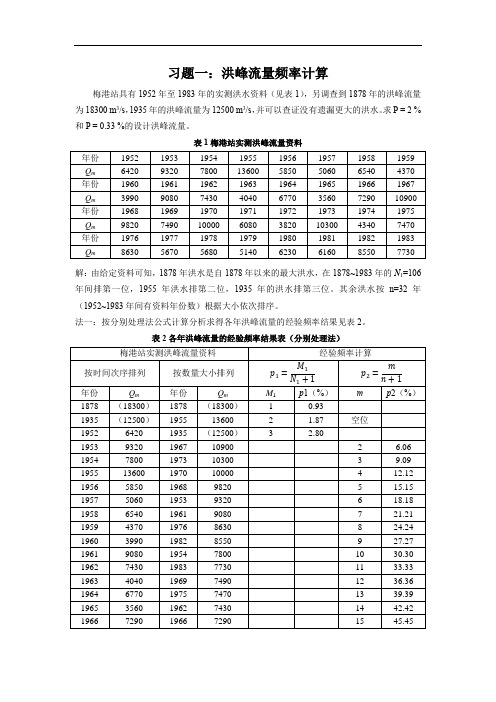
习题一:洪峰流量频率计算梅港站具有1952年至1983年的实测洪水资料(见表1),另调查到1878年的洪峰流量为18300 m3/s,1935年的洪峰流量为12500 m3/s,并可以查证没有遗漏更大的洪水。
求P = 2 %和P = 0.33 %的设计洪峰流量。
表1梅港站实测洪峰流量资料解:由给定资料可知,1878年洪水是自1878年以来的最大洪水,在1878~1983年的N1=106年间排第一位,1955年洪水排第二位,1935年的洪水排第三位。
其余洪水按n=32年(1952~1983年间有资料年份数)根据大小依次排序。
法一:按分别处理法公式计算分析求得各年洪峰流量的经验频率结果见表2。
表2各年洪峰流量的经验频率结果表(分别处理法)根据表2中的流量数据和计算的经验频率,点绘经验点据,如图1中圆形点据所示。
图1分别处理法求得的频率曲线经过调整,参数最终选用Q̅=7146.25 m3/s, C v=0.38,C s=1.32 ,拟合度达96.79%。
经检验,当P = 2 %时的设计洪峰流量为14408.97 m3/s>13900 m3/s,故成果合理。
据此组参数求得P = 2 %和P = 0.33 %的设计洪峰流量分别为14408.97 m3/s和18227.16 m3/s。
法二:按统一处理法公式计算分析求得各年洪峰流量的经验频率结果见表3。
表3各年洪峰流量的经验频率结果表(统一处理法)根据表3中的流量数据和计算的经验频率,点绘经验点据,如图2中圆形点据所示。
图2统一处理法绘制的频率曲线经过调整,参数最终选用Q̅=7080.47 m3/s, C v=0.38,C s=1.33 ,拟合度达96.70%。
经检验,当P = 2 %时的设计洪峰流量为14286.92 m3/s>13900 m3/s,故成果合理。
据此组参数求得P = 2 %和P = 0.33 %的设计洪峰流量分别为14286.92 m3/s和18085.61 m3/s。
流量频率分析计算

附件1流量频率分析计算根据业主提供的1966年至2010年共计45年的流量统计,其中1980年、1988年、2002年、2003年这4年10月中旬没有流量记录,进行频率分析计算如下。
各设计频率下的洪水流量采用矩法进行计算: 1. 计算经验频率:计算公式为%1+=n m P式中 P-----经验频率;m-----洪水资料从大到小排列序号;n-----洪水资料全部项数,此处取n=41。
列表计算10月中旬平均流量经验频率:见表一 2.统计参数的初步计算:平均流量 83.2214105.9095===∑n Q Q变差系数C v偏态系数C s以上三式中 Q i -----系列变量,共计41个;Q -----系列变量均值;n -----系列项数;n=41;C v -----变差系数; C s -----偏态系数。
76.1082.383.221)141(83.2214135.8084508)1(22222==-⨯-=--=∑Qn Q n Q C V 64.4)3()(333=--=∑Vi S C Q n Q Q C表一:10月中旬平均流量频率决算表年份10月中旬平均流量3序号按流量排序Qi(m3/s)Qi2经验频率Pm(%)1966 99.28 12341.345481873.0 2.4 1967 180.40 2902.19813946.80 4.8 1968 86.94 3896.9804429.61 7.1 1969 49.82 4413.43170924.36 9.5 1970 131.61 5343.64118088.45 11.9 1971 75.64 6319.3101952.49 14.3 1972 37.32 730693636.00 16.7 1973 176.67 8230.953314.81 19.0 1974 107.16 9213.7445684.79 21.4 1975 191.44 10193.2737353.29 23.8 1976 43.22 11191.44 36649.45 26.2 1977 47.34 12180.932724.81 28.6 1978 119.29 13180.40 32543.44 31.0 1979 58.48 14176.67 31213.63 33.3 1981 153.63 15165.2327300.95 35.7 1982 144.32 16153.7423635.99 38.1 1983 60.07 17153.63 23603.33 40.5 1984 17.49 18144.32 20826.97 42.9 1985 96.30 19131.61 17320.64 45.2 1986 97.07 20119.29 14230.10 47.6 1987 92.99 21109.3211950.86 50.0 1989 62.41 22107.16 11482.52 52.4 1990 57.35 2399.28 9857.04 54.8 1991 65.322497.07 9423.52 57.1 1992 319.32596.30 9272.85 59.5 1993 3062692.99 8646.85 61.9 1994 165.232786.94 7559.31 64.3 1995 180.92875.64 5720.72 66.7 1996 343.642965.324266.70 69.0 1997 230.93062.41 3894.63 71.4 1998 902.193160.07 3608.70 73.8 1999 2341.343258.48 3419.85 76.2 2000 896.93357.35 3288.83 78.6 2001 213.743449.82 2482.03 81.0 2004 413.433547.34 2240.94 83.3 2005 10.743646.962205.24 85.7 2006 15.93743.22 1867.91 88.1 2007 193.273837.32 1392.99 90.5 2008 153.743917.49 305.78 92.9 2009 46.964015.9252.81 95.2 2010 109.324110.74115.35 97.6 ∑9095.05 9095.05 8084508.3平均值221.83 221.833.频率计算:假定不同的C s 值,用公式)1(V p p C Q Q φ+=计算各频率的洪水数值。
数据分析中的频数与频率计算

数据分析中的频数与频率计算一、引言数据分析是现代社会中非常重要的一个领域,通过对数据的处理和分析,可以帮助我们揭示事物之间的关联和规律。
而在数据分析中,频数(frequency)和频率(frequency rate)的计算是非常基础和重要的操作。
本文将介绍频数与频率的概念、计算方法以及其在数据分析中的应用。
二、频数的概念与计算方法1. 频数的概念频数是指某个特定数值或范围内的观测值出现的次数。
在数据分析中,我们常常要对样本或总体的某个特征进行计数,这时就需要用到频数。
2. 频数的计算方法频数的计算方法相对简单,可以根据数据的类型和表现形式进行不同的计算。
以下以两种常见的数据类型为例:a.分类数据的频数计算分类数据是指在预先定义好的几个类别中,将观测值进行分类的数据类型。
计算分类数据的频数时,我们可以通过统计每个类别中的观测值个数来得到。
b.连续数据的频数计算连续数据是指可以在某个区间内取得无限个数值的数据类型。
对于连续数据的频数计算,我们可以先将数据进行分组,然后统计每个组内的观测值个数。
三、频率的概念与计算方法1. 频率的概念频率是指某个特定数值或范围内的观测值出现的相对次数,通常以百分比或比例的形式表示。
频率相比频数更能反映数据的分布情况,能够更好地进行数据比较和分析。
2. 频率的计算方法频率的计算方法与频数相似,只是在计算过程中需要将频数除以总样本量或总观测次数,然后将结果乘以100或百分比符号进行表示。
四、频数与频率的应用频数与频率的计算在数据分析中具有广泛的应用,以下列举几个常见的应用场景:1. 数据清洗与预处理在数据分析的初步阶段,我们常常需要对数据进行清洗和预处理,例如查找数据中的缺失值、异常值等。
通过计算频数和频率,可以帮助我们定位和处理这些问题。
2. 数据分布分析频数和频率的计算可以帮助我们了解数据的分布情况,例如数据的集中趋势和离散程度。
通过绘制直方图、柱状图等图表,可以更直观地展示数据的分布情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附件1
流量频率分析计算
根据业主提供的1966年至2010年共计45年的流量统计,其中1980年、1988年、2002年、2003年这4年10月中旬没有流量记录,进行频率分析计算如下。
各设计频率下的洪水流量采用矩法进行计算: 1. 计算经验频率:
计算公式为
%1
+=n m P
式中 P-----经验频率;
m-----洪水资料从大到小排列序号;
n-----洪水资料全部项数,此处取n=41。
列表计算10月中旬平均流量经验频率:见表一 2.统计参数的初步计算:
平均流量 83.22141
05.9095===
∑n
Q Q
变差系数C v
偏态系数C s
以上三式中 Q i -----系列变量,共计41个;
Q -----系列变量均值; n -----系列项数;n=41;
C v -----变差系数; C s -----偏态系数。
76.1082.383.221)141(83.2214135.8084508)1(2
2222==-⨯-=--=∑Q
n Q n Q C V 64.4)3()(3
33=--=∑V
i S C Q n Q Q C
3.频率计算:
假定不同的C s 值,用公式)1(V p p C Q Q φ+=计算各频率的洪水数值。
上式中 Q p -----各频率洪水数值; φp -----离均系数,可查表; 则可得:
即在10月中旬10年一遇平均流量为565.40m ³/s ,5年一遇平均流量为268.68m ³/s 。
40.565)76.188.01(83.221)1(%10%10=⨯+=+=V C Q Q φ68
.268)76.112.01(83.221)1(%20%20=⨯+=+=V C Q Q φ。
