模糊控制与PID控制性能比较
模糊控制算法PID算法比较分析
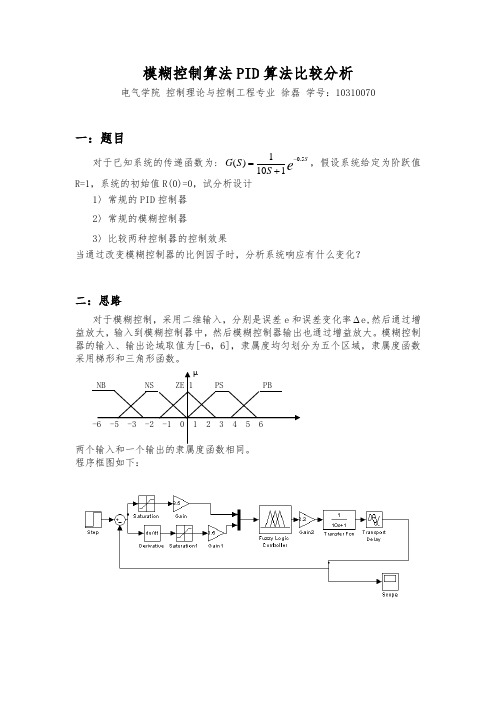
模糊控制算法PID 算法比较分析电气学院 控制理论与控制工程专业 徐磊 学号:10310070一:题目对于已知系统的传递函数为: e S S S G 5.01101)(-+=,假设系统给定为阶跃值R=1,系统的初始值R(0)=0,试分析设计 1〉常规的PID 控制器2〉常规的模糊控制器3〉比较两种控制器的控制效果当通过改变模糊控制器的比例因子时,分析系统响应有什么变化?二:思路对于模糊控制,采用二维输入,分别是误差e 和误差变化率∆e,然后通过增益放大,输入到模糊控制器中,然后模糊控制器输出也通过增益放大。
模糊控制器的输入、输出论域取值为[-6,6],隶属度均匀划分为五个区域,隶属度函数采用梯形和三角形函数。
µNB NS ZE 1 PS PB-6 -5 -3 -2 -1 0 1 2 3 4 5 6程序框图如下:三:程序clear;num=1;den=[10,1];[a1,b,c,d]=tf2ss(num,den);x=[0]; %状态变量初始T=0.01; %采样周期h=T;N=10000; %采样次数td=0.5; %延时时间Nd=50; %延时周期R=1*ones(1,N); % 输入信号e=0;de=0;ie=0; %误差,误差导数,积分kp=12.5;ki=0.8;kd=0.01;for k=1:Nuu(1,k)=-(kp*e+ki*de+kd*ie); %PID输出序列if k<=Ndu=0;elseu=uu(1,k-Nd);end%龙格库塔法仿真k0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6;y=c*x+d*u;e1=e;e=y(1,1)-R(1,k);de=(e1-e)/T;ie=ie+e*T;yy1(1,k)=y;end%设计模糊控制器a=newfis('Simple');a=addvar(a,'input','e',[-6,6]);a=addmf(a,'input',1,'NB','trapmf',[-6 -6 -5 -3]); a=addmf(a,'input',1,'NS','trapmf',[-5 -3 -2 0]); a=addmf(a,'input',1,'ZR','trimf',[-2 0 2]);a=addmf(a,'input',1,'PS','trapmf',[0 2 3 5]);a=addmf(a,'input',1,'PB','trapmf',[3 5 6 6]);a=addvar(a,'input','de',[-6 6]);a=addmf(a,'input',2,'NB','trapmf',[-6 -6 -5 -3]); a=addmf(a,'input',2,'NS','trapmf',[-5 -3 -2 0]); a=addmf(a,'input',2,'ZR','trimf',[-2 0 2]);a=addmf(a,'input',2,'PS','trapmf',[0 2 3 5]);a=addmf(a,'input',2,'PB','trapmf',[3 5 6 6]);a=addvar(a,'output','u',[-6 6]);a=addmf(a,'output',1,'NB','trapmf',[-6 -6 -5 -3]); a=addmf(a,'output',1,'NS','trapmf',[-5 -3 -2 0]); a=addmf(a,'output',1,'ZR','trimf',[-2 0 2]);a=addmf(a,'output',1,'PS','trapmf',[0 2 3 5]);a=addmf(a,'output',1,'PB','trapmf',[3 5 6 6]);%规则表rr=[5 5 4 4 35 4 4 3 34 4 3 3 24 3 3 2 23 3 2 2 1];r1=zeros(prod(size(rr)),3);%初始化%r1赋值k=1;for i=1:size(rr,1)for j=1:size(rr,2)r1(k,:)=[i,j,rr(i,j)];k=k+1;endendr2=ones(25,2);rulelist=[r1,r2];%得到规则表a=addrule(a,rulelist);e=0;de=0;ie=0;x=[0];ke=8.5;kd=0.5;ku=2.2;%增益,比例因子ki=0.01;for k=1:Ne1=ke*e;de1=kd*de;if e1>=6e1=6;elseif e1<=-6e1=-6;endif de1>=6de1=6;elseif de1<=-6de1=-6;endin=[e1 de1];uu(1,k)=ku*evalfis(in,a)-ie*ki;if k<=Ndu=0;elseu=uu(1,k-Nd);endk0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6;y=c*x+d*u;yy(1,k)=y;e1=e;e=y-R(1,k);de=(e-e1)/T;end%画图kk=[1:N]*T;figure(1);plot(kk,R,'k',kk,yy,'r',kk,yy1,'b'); xlabel('time');ylabel('output');四:结论运行后,如图,红色的为模糊控制输出,蓝色的为PID控制器输出。
几种控制方法比较
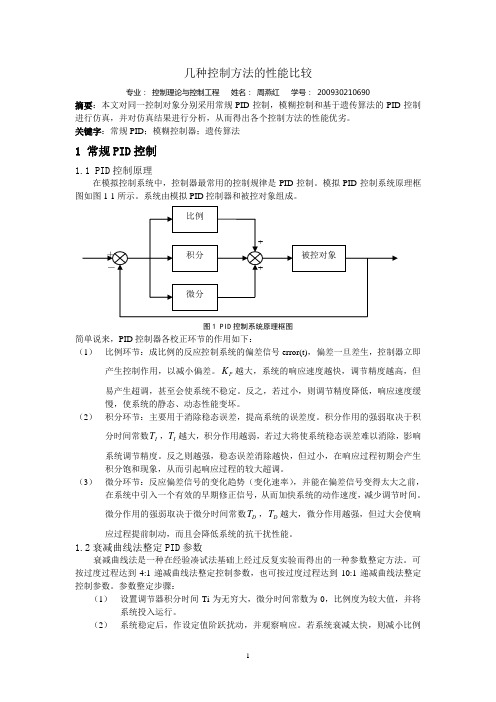
几种控制方法的性能比较专业: 控制理论与控制工程 姓名: 周燕红 学号: 200930210690摘要:本文对同一控制对象分别采用常规PID 控制,模糊控制和基于遗传算法的PID 控制进行仿真,并对仿真结果进行分析,从而得出各个控制方法的性能优劣。
关键字:常规PID ;模糊控制器;遗传算法1 常规PID 控制1.1 PID 控制原理在模拟控制系统中,控制器最常用的控制规律是PID 控制。
模拟PID 控制系统原理框图如图1-1所示。
系统由模拟PID 控制器和被控对象组成。
图1 PID 控制系统原理框图简单说来,PID 控制器各校正环节的作用如下:(1) 比例环节:成比例的反应控制系统的偏差信号error(t),偏差一旦差生,控制器立即产生控制作用,以减小偏差。
P K 越大,系统的响应速度越快,调节精度越高,但易产生超调,甚至会使系统不稳定。
反之,若过小,则调节精度降低,响应速度缓慢,使系统的静态、动态性能变坏。
(2) 积分环节:主要用于消除稳态误差,提高系统的误差度。
积分作用的强弱取决于积分时间常数I T ,I T 越大,积分作用越弱,若过大将使系统稳态误差难以消除,影响系统调节精度。
反之则越强,稳态误差消除越快,但过小,在响应过程初期会产生积分饱和现象,从而引起响应过程的较大超调。
(3) 微分环节:反应偏差信号的变化趋势(变化速率),并能在偏差信号变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间。
微分作用的强弱取决于微分时间常数D T ,D T 越大,微分作用越强,但过大会使响应过程提前制动,而且会降低系统的抗干扰性能。
1.2衰减曲线法整定PID 参数衰减曲线法是一种在经验凑试法基础上经过反复实验而得出的一种参数整定方法。
可按过度过程达到4:1递减曲线法整定控制参数,也可按过度过程达到10:1递减曲线法整定控制参数。
参数整定步骤:(1) 设置调节器积分时间Ti 为无穷大,微分时间常数为0,比例度为较大值,并将系统投入运行。
模糊控制与PID控制的对比及其复合控制

Co a io n mp st f u z nrl n nr l mp r na dCo o i o z yCo t dPI Co t s e F oa D o
YANG h ・ o Байду номын сангаасU u - n S iy ng, G ol i
( . c o l f mp trYa ti i es yYa ti 6 0 5C ia 1 S h o Co ue, na v ri , na 4 0 hn ; o Un t 2 2 De at n lcr a gn eig Y na o ain olg , a ti 6 0 0Chn . pr me t f et c l ie r , a ti ct a C l e Y na 2 4 0 ia) oE i En n V ol e
o e s o t n h re e u aig t e e s , h I c n r le c st e v tt ro . t o i e h rt o h v rh o d s o tnr g lt i , le t eP D o to lra t or mo esai er r I c mb n steme is fte a n m c t o to to s a d i y t ei u lt sa eb t rt a ec m mo D o to n h a i u z o to . e woc n r l meh d , n ss n h t q aii r et h n t o t c e e h nPI c nr la dt eb scf z yc n r 1 Th
短、 优势互补 , 了一种模糊 PD复合 型控 制器 。 设计 I 该复合控制器根据偏差范围的大小 , 通过模糊控制与 PD 制的 自 I控 动切换
模糊控制与PID控制的比较

模糊控制与PID控制的比较自20世纪60年代中期起,模糊控制逐渐崭露头角,其优越性也引起了人们的关注。
除了模糊控制,当今热门的控制算法之一是PID控制。
那么,模糊控制与PID控制之间的区别是什么呢?它们各自的优缺点是什么?在特定的应用场合下,哪种控制算法更适用?一、模糊控制概述模糊控制是一种无需准确模型或参数即可执行复杂控制系统的方法,它仅使用模糊逻辑来描述输入和输出之间的关系。
模糊控制系统的输入和输出都是模糊变量。
与其他控制方法相比,模糊控制系统可以更好地处理不确定性和模糊性,具有更强的容错能力和适应性。
模糊控制系统由四个主要组成部分组成:模糊化、模糊推理、解模糊化和规则库。
模糊化部分将传感器输出信号转换为模糊变量,模糊推理部分使用模糊逻辑基于模糊规则将模糊变量转换为控制信号,解模糊化部分将控制信号转换为精确的控制信号,规则库存储了模糊规则及其权重。
二、PID控制概述比例积分微分(PID)控制是一种经典的控制算法,其控制草图由三个部分组成。
比例项(P)根据当前误差大小进行输出,积分项(I)可以消除稳态误差,微分项(D)可以提高系统的稳定性并抑制系统的震荡。
PID控制器的设计基于系统的数学模型,在许多应用中,这个模型是已知的。
在这些情况下,PID控制器可以通过调整不同部分的增益以进行优化。
三、模糊控制与PID控制的对比1. 精度PID控制器可以实现非常高的精度,特别是在恒定环境下,模糊控制器具有更高的容错能力和适应性,而且围绕控制正常的范围内快速做出反应。
2. 调节PID调节通常是更容易实现的PLC控制器中自动化开发环境的系统。
Fuzzy可能更多地需要手动调整和对规则进行逐步精细的训练,但它也可以被训练自动化。
3. 适应性模糊控制器的好处是可以轻松地处理不确定性和模糊性,因此可以应对复杂环境。
PID控制器则对不确定性和模糊性更加敏感,而且会因不确定性的变化而导致过度响应或不足响应的问题。
4. 实际应用PID控制器广泛应用于许多领域,如化工、制造和机械工程。
经典PID与模糊PID控制29695培训资料

经典P I D与模糊P I D 控制29695)4)(3)(1(2)(+++=s s s ss G 经典PID 与模糊PID 控制一、PID 控制规律控制输出由三部分组成:比例环节——根据偏差量成比例的调节系统控制量,以此产生控制作用,减少偏差。
比例系数的作用是加快系统的响应速度,比例系数越大,系统响应速度越快,系统的调节精度越高,但容易产生超调,甚至会导致系统的不稳定;比例系数过小,会降低系统调节精度,系统响应速度变慢,调节时间变长,系统动态、静态特性变坏。
比例控制是最简单的控制结构,然而,它也能使系统满足某一方面的特性要求,如GM 、PM 、稳态误差等。
积分环节——用于消除静差,提高系统的无差度。
积分作用的强弱取决于积分时间常数TI 的大小, TI 越小,积分作用越强。
需要注意的是积分作用过强,可能引起系统的不稳定。
微分环节——根据偏差量的变化趋势调节系统控制量,在偏差信号发生较大的变化以前,提前引入一个早期的校正注意的是微分作用过强,可能引起系统的振荡。
已知被控对象的数学模型:二、经典PID 设计由于在设计PID 控制器中要调整3个参数,根轨迹与波特图设计方法通常不被直接采用。
Ziegler 与Nichols 发展了PID 调节器设计方法。
该方法基于简单的稳定性分析方法。
首先,置0==I D K K ,然后增加比例系数直至系统开始振荡(即闭环系统极点在jw 轴上)。
再将该比例系数乘0.6,其他参数按下式计算:m P K K 6.0= m P D w Pi K K 4= Pi w K K m P I =式中,m K 为系统开始振荡时的K 值;m w 为振荡频率。
然而,该设计方法在设计过程中没有考虑任何特性要求。
但是Ziegler 与Nichols 发现这种设计方法给予过程控制器提供了好的工作性能。
工程师们的多年实践经验证明,这种设计方法的确是一种好的方法。
根据给定传递函数用SIMULINK 搭建结构图如下:起振时m K =391,如图:根据公式计算Kp 、I K 、D K 分别为234.6、276、49.8525 此时对于常数3的响应曲线如图:可见,此时系统振荡,不稳定,继续等比例调节参数得新参数65、77、14,得响应曲线:可见此时系统响应时间过长,而且存在比较大的静态误差,为了减小响应K,同时调节过程中会因参数变动时间应增大Kp,为了减小静态误差应增大I产生超调量,综合以上几点性能决定确定参数为120、300、14。
经典PID与模糊PID控制

)4)(3)(1(2)(+++=s s s ss G 经典PID 与模糊PID 控制一、PID 控制规律控制输出由三部分组成:比例环节——根据偏差量成比例的调节系统控制量,以此产生控制作用,减少偏差。
比例系数的作用是加快系统的响应速度,比例系数越大,系统响应速度越快,系统的调节精度越高,但容易产生超调,甚至会导致系统的不稳定;比例系数过小,会降低系统调节精度,系统响应速度变慢,调节时间变长,系统动态、静态特性变坏。
比例控制是最简单的控制结构,然而,它也能使系统满足某一方面的特性要求,如GM 、PM 、稳态误差等。
积分环节——用于消除静差,提高系统的无差度。
积分作用的强弱取决于积分时间常数TI 的大小, TI 越小,积分作用越强。
需要注意的是积分作用过强,可能引起系统的不稳定。
微分环节——根据偏差量的变化趋势调节系统控制量,在偏差信号发生较大的变化以前,提前引入一个早期的校正注意的是微分作用过强,可能引起系统的振荡。
已知被控对象的数学模型:二、经典PID 设计由于在设计PID 控制器中要调整3个参数,根轨迹与波特图设计方法通常不被直接采用。
Ziegler 与Nichols 发展了PID 调节器设计方法。
该方法基于简单的稳定性分析方法。
首先,置0==I D K K ,然后增加比例系数直至系统开始振荡(即闭环系统极点在jw 轴上)。
再将该比例系数乘0.6,其他参数按下式计算:m P K K 6.0= m P D w Pi K K 4= Pi w K K m P I =式中,m K 为系统开始振荡时的K 值;m w 为振荡频率。
然而,该设计方法在设计过程中没有考虑任何特性要求。
但是Ziegler 与Nichols 发现这种设计方法给予过程控制器提供了好的工作性能。
工程师们的多年实践经验证明,这种设计方法的确是一种好的方法。
根据给定传递函数用SIMULINK 搭建结构图如下:起振时m K =391,如图:根据公式计算Kp 、I K 、D K 分别为234.6、276、49.8525 此时对于常数3的响应曲线如图:可见,此时系统振荡,不稳定,继续等比例调节参数得新参数65、77、14,得响应曲线:可见此时系统响应时间过长,而且存在比较大的静态误差,为了减小响应时K,同时调节过程中会因参数变动产生间应增大Kp,为了减小静态误差应增大I超调量,综合以上几点性能决定确定参数为120、300、14。
DC/DC变换器模糊控制和PID控制比较研究

特 定 工作 点 Q , R) 控制 到输 出 电压 的 ( D, 处
ma c s u i g t e e t o c n r l r ae c mp e a e n h x e me t e u s p ro e y r tt p f a n e sn h s w o tol s r o a d b s d o t e e p r n a r s h ef r d b a p o oy e o e r i l m
摘要 : 糊控 制器 因 具有控 制鲁 棒性 强 , 模 设计 不 依赖 于被控 对 象精 确模 型等 优 点而 逐渐 应用 在 电力 电子变 换 器 中。以 B ot 换器 为例 , os变 从设计 方法 、 具体 工程 实现和 实验 结果三方 面对传 统线性 比例积 分微 分 (i ) ro 控制 器和模 糊控 制器进 行 了对 比分析 。详细 阐述 了 PD控制 器和 模糊控 制器 的设 计方 法 , I 对其 设计 的侧 重 点进行 了对 比。 过实验 对 比 了线性 PD控 制器 与模糊控 制器 的控制 性能 。 通 I 实验结 果表 明 , 糊控 制技 术相对 于线性 模
一
个 比例 环 节 , : 即
H( ) 1G , G () 1 s= / : / () 4
I
(I ) 厂
.
1V ] hS
调节器
一 V c} D =
&J -
: ;
I
PID控制与模糊控制比较

PID控制与模糊控制的比较专业:控制理论与控制工程班级:级班姓名:X X X学号:xxxxxxxxxxxxxx摘要:介绍了PID控制系统和模糊控制系统的工作原理。
PID控制器结构简单,实现简单,控制效果良好,已经得到了广泛的应用。
而模糊控制器相对复杂,但在许多的智能化家用电器中也得到了大量应用。
但对于一个简单的系统来讲,哪一种控制方法更好,是不是越智能的控制就能得到越好的效果。
关键词:PID控制,模糊控制,比较Abstract: Introduced the working principle of PID control system and fuzzy control system. PID controller structure is simple, implementation is simple, the control effect is good, has been widely used. And fuzzy controller is relatively complicated, but in a lot of intelligent household appliances also received a large number of applications. But for a simple system, which kind of control method is better, is weather the intelligent control can obtain the good effect.Key words: PID control, fuzzy control, compare目录一、问题的提出 (1)二、PID控制器的设计 (2)1.PID控制原理图: (2)2.PID控制器传递函数的一般表达式 (2)三、模糊控制器的设计 (3)1.模糊控制原理图 (3)2.模糊控制器传递函数一般表达形式 (4)四、系统仿真 (4)五、总结 (14)参考文献: (15)一、问题的提出当今的自动控制技术都是基于反馈的概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本程序选自楼顺天,胡昌华,张伟编著《基于MATLAB 的系统分析与设计:模糊系统》,西安电子科技大学出版社,2001年5月第一版,ISBN7-5606-1011-0,定价:14元第77-87页例3.8中源程序。
程序运行输出图形如下:
00.51 1.52 2.53
3.54
4.5
0.2
0.4
0.6
0.8
1
1.21.4
1.6
1.8
时间(0.01秒)输出程序运行后在输出图形时需要用鼠标左键分别先后在红色曲线和蓝色曲线上方点一下,输出提示文本,否则若在图形区域外直接点击鼠标左键,会输出错误提示。
源程序清单如下: %Example 3.8
%-------------------------
%典型二阶系统的模糊控制与传统PID 控制的性能比较
%------------------------
num=20;
den=[1.6,4.4,1];
[a1,b,c,d]=tf2ss(num,den);
x=[0;0];
T=0.01;h=T;
umin=0.07;umax=0.7;
td=0.02;Nd=td/T;
N=500;R=1.5*ones(1,N);
%--------------------
%传统PID 控制
%--------------------
e=0;de=0;ie=0;
kp=5;ki=0.1;kd=0.001;
for k=1:N
uu1(1,k)=-(kp*e+ki*de+kd*ie);
%延迟环节
if k<=Nd
u=0;
else
u=uu1(1,k-Nd);
end
%死区和饱和环节
if abs(u)<=umin
u=0;
elseif abs(u)>umax
u=sign(u)*umax;
end
%利用龙格-库塔法进行系统仿真
k0=a1*x+b*u;
k1=a1*(x+h*k0/2)+b*u;
k2=a1*(x+h*k1/2)+b*u;
k3=a1*(x+h*k2)+b*u;
x=x+(k0+2*k1+2*k2+k3)*h/6;
y=c*x+d*u;
%计算误差、微分和积分
e1=e;
e=y(1,1)-R(1,k);
de=(e-e1)/T;
ie=e*T+ie;
yy1(1,k)=y;
end
%-----------------
%模糊控制
%-----------------
%定义输入和输出变量及其隶属度函数
a=newfis('Simple');
a=addvar(a,'input','e',[-6,6])
a=addmf(a,'input',1,'NB','trapmf',[-6,-6,-5,-3]); a=addmf(a,'input',1,'NS','trapmf',[-5,-3,-2,0]); a=addmf(a,'input',1,'ZR','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trapmf',[0,2,3,5]);
a=addmf(a,'input',1,'PB','trapmf',[3,5,6,6]);
a=addvar(a,'input','de',[-6,6]);
a=addmf(a,'input',2,'NB','trapmf',[-6,-6,-5,-3]); a=addmf(a,'input',2,'NS','trapmf',[-5,-3,-2,0]); a=addmf(a,'input',2,'ZR','trimf',[-2,0,2]);
a=addmf(a,'input',2,'PS','trapmf',[0,2,3,5]);
a=addmf(a,'input',2,'PB','trapmf',[3,5,6,6]);
a=addvar(a,'output','u',[-3,3]);
a=addmf(a,'output',1,'NB','trapmf',[-3,-3,-2,-1]); a=addmf(a,'output',1,'NS','trimf',[-2,-1,0]);
a=addmf(a,'output',1,'ZR','trimf',[-1,0,1]);
a=addmf(a,'output',1,'PS','trimf',[0,1,2]);
a=addmf(a,'output',1,'PB','trapmf',[1,2,3,3]);
%模糊规则矩阵
rr=[5 5 4 4 3
5 4 4 3 3
4 4 3 3 2
4 3 3 2 2
3 3 2 2 1];
r1=zeros(prod(size(rr)),3);k=1;
for i=1:size(rr,1)
for j=1:size(rr,2)
r1(k,:)=[i,j,rr(i,j)];
k=k+1;
end
end
[r,s]=size(r1);
r2=ones(r,2);
rulelist=[r1,r2];
a=addrule(a,rulelist);
%模糊控制系统仿真
e=0;de=0;ie=0;
x=[0;0];
ke=60;kd=2.5;ki=0.01;ku=.8;
for k=1:N
e1=ke*e;
de1=kd*de;
if e1>=6
e1=6;
elseif e1<=-6
e1=-6;
end
if de1>=6
de1=6;
elseif de1<=-6
de1=-6;
end
in=[e1 de1];
uu(1,k)=ku*evalfis(in,a)-ki*ie;
if k<=Nd
u=0;
else
u=uu(1,k-Nd);
end
if abs(u)<=umin
u=0;
elseif abs(u)>umax
u=sign(u)*umax;
end
k0=a1*x+b*u;
k1=a1*(x+h*k0/2)+b*u;
k2=a1*(x+h*k1/2)+b*u;
k3=a1*(x+h*k2)+b*u;
x=x+(k0+2*k1+2*k2+k3)*h/6;
y=c*x+d*u;
e1=e;
e=y-R(1,k);
de=(e-e1)/T;
ie=ie+e*T;
yy(1,k)=y;
end
%绘制结果曲线
kk=[1:N]*T;
figure(1);
plot(kk,R,'k',kk,yy,'r',kk,yy1,'b'); xlabel('时间(0.01秒)');
ylabel('输出');
gtext('模糊控制');gtext('PID控制');。
