2021八年级暑假作业数学参考答案北师大版
2021-2022学年北师大版八年级下期数学暑假作业——第3次(附答案)
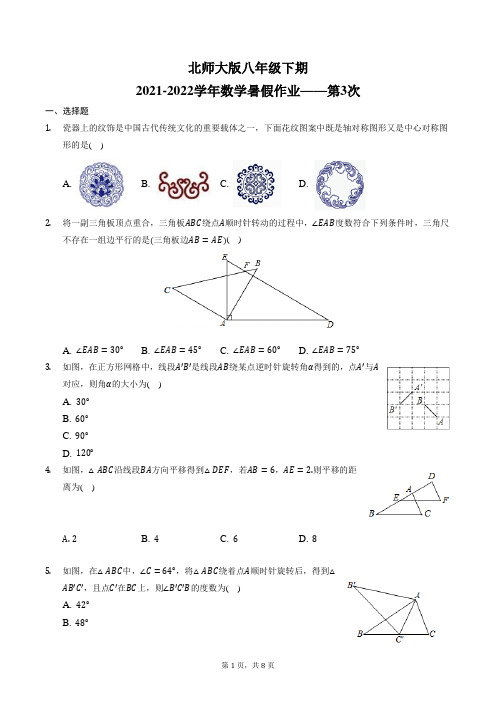
北师大版八年级下期2021-2022学年数学暑假作业——第3次一、选择题1.瓷器上的纹饰是中国古代传统文化的重要载体之一,下面花纹图案中既是轴对称图形又是中心对称图形的是( )A. B. C. D.2.将一副三角板顶点重合,三角板ABC绕点A顺时针转动的过程中,∠EAB度数符合下列条件时,三角尺不存在一组边平行的是(三角板边AB=AE)( )A. ∠EAB=30°B. ∠EAB=45°C. ∠EAB=60°D. ∠EAB=75°3.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )A. 30°B. 60°C. 90°D. 120°4.如图,△ABC沿线段BA方向平移得到△DEF,若AB=6,AE=2.则平移的距离为( )A.2B. 4C. 6D. 85.如图,在△ABC中,∠C=64°,将△ABC绕着点A顺时针旋转后,得到△AB′C′,且点C′在BC上,则∠B′C′B的度数为( )A. 42°B. 48°C. 52°D. 58°6.如图,在三角形ABC中,∠ABC=90°,将三角形ABC沿AB方向平移AD的长度得到三角形DEF,已知EF=8,BE=3,CG=3,则图中阴影部分的面积是( )A. 12.5B. 19.5C. 32D. 45.57.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于( )A. 3√2B. 2√3C. 4√2D. 3√38.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90∘后得到△A′B′C′,则其旋转中心的坐标是( )A. (1.5,1.5)B. (1,0)C. (1,−1)D. (1.5,−0.5)二、填空题9.如图所示的图案,可以看作是一个四边形(阴影部分)按顺时针方向通过5次旋转得到的,每次旋转的角度是______.10.将点P(−3,y)向下平移3个单位,再向左平移2个单位后得到点Q(x,−1),则x+y=.11.如图,将..........∠B的度数....B,.C,.D恰好在同一直线上,则.......△ABC绕点..A逆时针旋转.....150°,得到...△ADE,这时点为...12.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是______.13.如图,将三角形ABC绕点A顺时针旋转角100°,得到三角形ADE,若点E恰好在CB的延长线上,则∠BED=______°.14.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2cm.把△ABC沿AB方向平移1cm,得到△A′B′C′,连结CC′,则四边形AB′C′C的周长为______cm.三、解答题15.如图,在△ABC中,∠ABC=60°,AC沿AB方向平移BC长,得DE,连接BE.(1)求∠CBE的度数;(2)在BC取一点F,且BF=BD,连接AF,求证:AF=DE.16.在如图所示的直角坐标系中,解答下列问题:(1)分别写出A、B两点的坐标;(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1.17.如图所示,将△AOB绕着点O旋转180度得到△DOC,过点O的一条直线分别交BA、CD的延长线于点E、F,求证:AE=DF.18.如图,在直角三角形ABC中,∠ABC=90°,将△ABC沿射线BC方向平移得到△DEF,A,B,C的对应点分别是D,E,F.(1)若∠DAC=56°,求∠F的度数.(2)若BC=6cm,当AD=2EC时,则AD=______.19.已知在△ABC中,O为BC边的中点,连接AO,将△AOC绕点O顺时针方向旋转(旋转角为钝角),得到△EOF,连接AE,CF.(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是______;(2)如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.20.如图,在△ABC中,∠BAC=90°,AB=AC=1,P是△ABC内一点,求PA+PB+PC的最小值.参考答案1.C2.C3.C4.B5.C6.B7.A8.C9.60°10.−311.15°12.20cm13.8014.8+2√315.(1)解:连接CE,如图,∵AC沿AB方向平移BC长,得DE,∴AD=CE=BC,AD//CE,∴∠BCE=∠ABC=60°,∴△BCE为等边三角形,∴∠CBE=60°;(2)证明:∵∠DBF=60°,BD=BF,∴△BDF为等边三角形,∴DF=BD,∠BDF=60°,∵∠ADF=180°−∠BDF=120°,∠EBD=∠CBE+∠DBF=120°,∴∠ADF=∠EBD,∵△BCE为等边三角形,∴BE=BC=AD,在△ADF和△EBD中,{AD=EB∠ADF=∠EBD DF=BD,∴△ADF≌△EBD(SAS),∴AF=DE.16.解:(1)由点A、B在坐标系中的位置可知:A(2,0),B(−1,−4);(2)如图所示:17.证明:∵△AOB绕着点O旋转180度得到△DOC,∴OB=OC,AB=CD,∠B=∠C,在△OBE和△OCF中{∠B=∠COB=OC∠BOE=∠COF,∴△OBE≌△OCF,∴BE=CF,∴BE−AB=CF−CD,即AE=DF.18.4cm.19.AE=CF20.解:如图所示,以点C为旋转中心,将△CPB顺时针旋转60°得到△CMN,连接BN,连接PM,交BC于点Q由旋转可得,△CMN≌△CPB,∴MN=BP,PC=CM,∠PCM=60°=∠BCN,BC=CN,∴△PCM、△BCN都是等边三角形,∴PC=PM,∴PA+PB+PC=PM+MN+PA,∴点A、P、M、N四点共线时,PA+PB+PC有最小值,∵∠BAC=90°,AB=AC=1,∴BC=2√2,当A、P、M、N四点共线时,由CA=AB,NC=NB,∴AN垂直平分CB,∴AQ=12CB=√22=CQ,NQ=√62,此时AN=AP+PM+MN=PA+PB+PC=√22+√62,PA+PB+PC的最小值为√22+√62.。
mjt6-图形的平移与旋转——全等三角形证明旋转专练 2021年暑假作业北师大版数学八年级下册
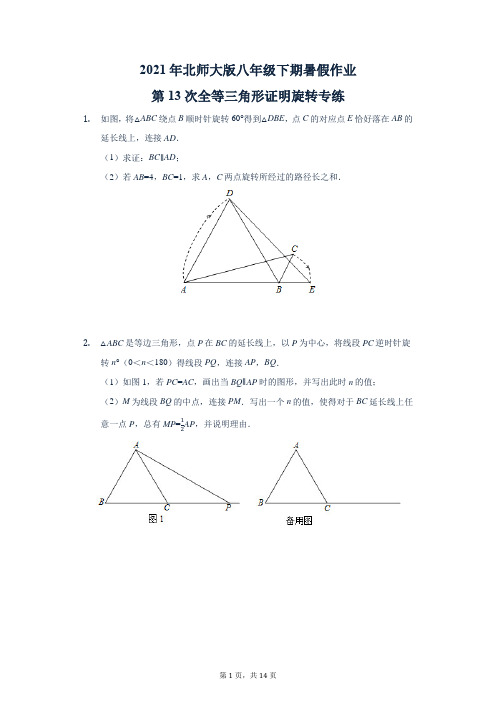
2021年北师大版八年级下期暑假作业第13次全等三角形证明旋转专练1.如图,将△ABC绕点B顺时针旋转60°得到△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.(1)求证:BC∥AD;(2)若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.2.△ABC是等边三角形,点P在BC的延长线上,以P为中心,将线段PC逆时针旋转n°(0<n<180)得线段PQ,连接AP,BQ.(1)如图1,若PC=AC,画出当BQ∥AP时的图形,并写出此时n的值;(2)M为线段BQ的中点,连接PM.写出一个n的值,使得对于BC延长线上任AP,并说明理由.意一点P,总有MP=123.如图,点P是等边△ABC内一点,将△APC绕点C顺时针旋转60°得到△BDC,连接PD.(1)求证:△DPC是等边三角形;(2)当∠APC=150°时,试判断△DPB的形状,并说明理由;(3)当∠APB=100°且△DPB是等腰三角形,求∠APC的度数.4.如图,在等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.(1)当AC=4,AP:PC=1:3时,PQ的长为_____;(2)当点P在线段AC上运动时(P不与A,C重合),请写出一个反映PA,PB,PC之间关系的等式,并加以证明.5.在△ABC中,∠ABC=120°,线段AC绕点A逆时针旋转60°得到线段AD,连接CD,得到等边三角形ACD,BD交AC于P.(1)若∠BAC=α,求∠BCD的度数(用含α的代数式表示);(2)求AB,BC,BD之间的数量关系;6.在△ABC中,AB=AC,∠BAC=100°.将线段CA绕着点C逆时针旋转得到线段CD,设∠ACD=α,且0°<α<360°,连接AD、BD.(1)如图1,当α=60°时,求∠CBD的大小.(2)如图2,当α=20°时,求∠CBD的大小.7.一副三角板如图1摆放,∠C=∠DFE=90°,∠B=30°,∠E=45°,点F在BC上,点A在DF上,且AF平分∠CAB,现将三角板DFE绕点F以每秒5°的速度顺时针旋转(当点D落在射线FB上时停止旋转),设旋转时间为t秒.(1)当t=______秒时,DE∥AB;当t=______秒时,DE⊥AB;(2)在旋转过程中,DF与AB的交点记为P,如图2,若△AFP有两个内角相等,求t的值;(3)当边DE与边AB、BC分别交于点M、N时,如图3,连接AE,设∠BAE=x°,∠AED=y°,∠DFB=z°,试问x+y+z是否为定值?若是,请求出定值;若不是,请说明理由.8.在等腰△ABC中,已知AB=AC=2,∠BAC=45∘.将△ABC绕点A逆时针旋转α度(0 ∘<α<180 ∘)得到△ADE,B、C两点的对应点分别为点D、E,BD、CE所在直线交于点F.(1)当△ABC旋转到图1位置时,∠CAD=_____________(用含α的代数式表示),∠BFC的度数为__________∘;(2)当α=45 ∘时,在图2中画出△ADE,并求此时点A到直线BE的距离.9.如图,△ABC为等边三角形,△AP′B旋转后能与△APC重合,那么:(1)指出旋转中心;(2)求旋转角的度数;(3)求∠PAP′的度数.10.如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.(1)求证:BD=CE,BD⊥CE;(2)如图2,连接AF,DC,已知∠BDC=135°,判断AF与DC的位置关系,并说明理由.11.如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.(1)请求出旋转角的度数;(2)请判断AE与BD的位置关系,并说明理由;(3)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.12.如图,点O是等边△ABC内一点,将CO绕点C顺时针旋转60°得到CD,连接OD,AO,AD,(1)求证:△BCO≌△ACD.(2)若∠BOC=150°,OB=8,OC=6,求△AOD的面积.13.如图,在四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.(1)求证:AE⊥BD;(2)若AD=1,CD=2,试求四边形ABCD的对角线BD的长.14.如图,点O是等边△ABC内一点,∠AOB=110∘,∠BOC=α,将△BOC绕点C按顺时针方向旋转60∘得到△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当α=150∘时,试判断△AOD的形状,并说明理由;(3)当α为多少度时,△AOD是等腰三角形?15.如图,在△ABC中,点D是BC上一点,且BD=DA=AC.把边AB绕着点A顺时针旋转一定角度得到∠BAE,连接DE,交AB于点F.(1)若∠B=α,请用含α的式子表示∠C;(2)若∠CAD=∠BAE,求证:DA平分∠CDE.16.如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.(1)求∠DAD′的度数.(2)当∠DAE=45°时,求证:DE=D′E;17.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.(1)求证:△BAP≌△CAQ.(2)若PA=3,PB=4,∠APB=150°,求PC的长度.18.(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:①旋转角是______度;②线段OD的长为______;③求∠BDC的度数.(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,∠AOB=135︒,OA=1,OB=2,求OC的长.小明同学借用了图1的方法,将△BAO绕点B顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.19.如图,在△ABC中,∠B+∠ACB=30∘,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点.(1)指出旋转中心,并求出旋转角的度数;(2)求出∠BAE的度数和AE的长.20.如图,△ABC为等边三角形,AD为△ABC的中线,点E为线段AD上一点,连接BE,将线段BE绕着点B逆时针旋转60°得到线段BF,连接CE,AF.(1)求证:△AFB≌△CEB;(2)若BF⊥BC,BF=2,求BC的长.21.如图,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△PˈAB.求:(1)PPˈ的长度;(2)∠APB的度数.22.如图①,P为正三角形内一点,且PC=3,PB=4,PA=5,求∠BPC的度数.解题思路:将△ABP绕点B按顺时针方向旋转60°,得△CBP1,它的位置如图②.易得△BPP1为等边三角形,△CPP1为直角三角形,所以∠BPC=60°+90°=150°.根据以上的解题思路解决下列问题:如图③,在等腰直角△ABC中,∠BAC=90°,P是△ABC内一点,PA=1,PB=3,PC=√7.求∠CPA的度数.23.已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.(1)探究:把△ADE绕顶点A旋转,使点D在BC的延长线上(如上图),连接CE.①求证:BD=CE;②求∠ BCE的度数;(2)拓展:已知AD=13,BC=10,在△ADE绕点A的旋转过程中,当点B,C,D在同一直线上时,求BD的长.24.如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.(1)三角尺旋转了多少度?(2)连接CD,试判断△CBD的形状.(3)求∠BDC的度数.25.如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系是______,位置关系是______.(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.。
2021-2022学年北师大版八年级下期数学暑假作业——第6次(附答案)

北师大版八年级下期2021-2022学年数学暑假作业——第6次一、选择题1.如图,在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( )A. 26cmB. 24cmC. 20cmD. 18cm2.顺次联结对角线相等的四边形各边中点所得到的四边形是( )A. 平行四边形B. 矩形C. 正方形D. 菱形3.已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )A. 6B. 7C. 8D. 94.已知▱ABCD的周长为32cm,AB=4cm,则BC的长为A. 4cmB. 12cmC. 16cmD. 24cm5.如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作BCDE,则∠E的度数为( )A. 40°B. 50°C. 60°D. 70°6.如图,在▱ABCD中,AC与BD相交于点O,则下列结论中不一定成立的是( )A. AB=CDB. AO=COC. AC=BDD. BO=DO7.小红同学周末在家做家务,不慎把家里的一块平行四边形玻璃打碎成如图所示的四块,为了能从玻璃店配到一块与原来相同的玻璃,他应该带其中两块去玻璃店.( )A. ①②B. ②④C. ②③D. ①③8.如图,▱ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若▱ABCD的周长为28,则△ABE的周长为( )A. 28B. 24C. 21D. 14二、填空题9.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A′处,若∠1=∠2=50∘,则∠A′=.10.如图,在四边形ABCD中,AD//BC,AD=BC,E为AD上一点,CF⊥BE,垂足为F.如果四边形ABCD的面积为48,BE=7,那么CF=.11.如图,五边形ABCDE是正五边形,若l1//l2,则∠1−∠2=________.12.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是.13.如图,▱ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD、BC于点M、N.若△CON的面积为2,△DOM的面积为4,则△AOB的面积为_________.14.如图,点P是▱ABCD内的一点,连结AP、BP、CP、DP,再连结对角线AC,若S△PAB=27,S△PAD=15,那么S△PAC=______.三、解答题15.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,求这个多边形的内角和.16.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.CE;(1)求证:DM=12(2)若AD=6,BD=8,DM=2,求AC的长.17.如图,E,F是▱ABCD的对角线AC上的两点,AF=CE.求证:BE//DF.18.如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.四边形EGFH是平行四边形吗?请证明你的结论.19.如图,在平行四边形ABCD中,点E,F分别是AB,CD上的点,CF=BE.(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AD=2,AB=4,求BD的长.20.如图,在▱ABCD中,对角线AC,BD相交于点O,AB=AD.(1)求证:AC⊥BD;(2)若点E,F分别为AD,AO的中点,连接EF,EF=3,AO=2,求BD的长及四边形ABCD的周长.2参考答案1.D2.D3.D4.B5.D6.C7.B8.D9.105∘10.48711.72°12.313.614.1215.解:设多边形的一个外角为α,则与其相邻的内角等于3α+20°,由题意得,(3α+20)+α=180°,解得α=40°.即多边形的每个外角为40°.又∵多边形的外角和为360°,∴多边形的外角个数为360°÷40=9.∴多边形的边数为9,∴这个多边形的内角和为(9−2)⋅180°=1260°.16.(1)证明:在△ADB和△ADE中,{∠BAD=∠EADAD=AD∠ADB=∠ADE=90°,∴△ADB≌△ADE(ASA)∴AE=AB,BD=DE,∵BD=DE,BM=MC,∴DM=12CE;(2)解:在Rt△ADB中,AB=√BD2+AD2=10,∴AE=10,由(1)得,CE=2DM=4,∴AC=CE+AE=14.17.证明:如图,连接BD,交AC于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.又∵AF=CE,∴AE=CF.∴OE=OF.在△BOE与△DOF中,{OE=OF∠BOE=∠DOFOB=OD ∴△BOE≌△DOF(SAS).∴∠EBO=∠FDO.∴BE//DF.18.解:四边形EGFH是平行四边形.理由如下:∵点E、G分别是线段AB、AC的中点,∴EG//BC,同理HF//BC,GF//AD,EH//AD,∴GE//HF,GF//EH,∴四边形EGFH是平行四边形.19.(1)证明:∵四边形ABCD是平行四边形,∴AB//CD,AB=CD,∵CF=BE,∴CD−CF=AB−BE,即DF=AE,又∵DF//AE,∴四边形AEFD是平行四边形;(2)解:如图,过B作BG⊥AD于G,∵∠A=60°,∴∠ABG=90°−60°=30°,∴AG=12AB=2,∵AD=2,∴AG=AD,∴G与D重合,∴BD⊥AD,∴BD=√AB2−AD2=√42−22=2√3.20.(1)证明:∵四边形ABCD是平行四边形,AB=AD,∴▱ABCD是菱形,∴AC⊥BD;(2)解:∵点E,F分别为AD,AO的中点,∴EF是△AOD的中位线,∴OD=2EF=3,由(1)可知,四边形ABCD是菱形,∴AB=BC=CD=AD,AC⊥BD,BD=2OD=6,在Rt△AOD中,由勾股定理得:AD=√AO2+OD2=√22+32=√13,∴菱形ABCD的周长=4AD=4√13.。
2021年八年级数学下册暑期练习(北师大版有答案)题型归纳

2021年八年级数学下册暑期练习(北师大版有答案)题型归纳最让我快乐的是什么?是假期,接下来看看为大家推荐的____年八年级数学下册暑期练习,即使在家里也能快乐的学习呀!一、选择题(每小题3分,共24分)1. 若a0,则下列不等式不成立的是( )A. a+52.下列从左到右的变形是因式分解的是( )A.(_+1)(_-1)=_2-1B.(a-b)(m-n)=(b-a)(n-m)C.ab-a-b+1=(a-1)(b-1)D.m2-2m-3=m(m-2- )3.方程的解为( )A.2B.1C. 2D. 14.不等式3(2_+5) 2(4_+3)的解集为( )A._4.5B._4.5C._=4.5D._9一5.下面的图形是天气预报的图标,其中既是轴对称图形又是中心对称图形的是( )6.在△ABC中,C=90,AC=BC,AD平分CAB,交BC于点D,DEAB于点E,且AB=10,则△EDB的周长是( )A.4B.6C.8D.107.在△ABC中,ACB=90 ,点O为△ABC的三条角平分线的交点,ODBC,OEAC,OFAB,点D,E,F分别为垂足,且AB=10,BC=8,则点O到三边AB,AC,BC的距离分别是( )A.2,2,2B.3,3,3C.4,4,4D.2,3,58.如图,平行四边形ABCD的对角线相交于点O,且ABAD,过O作OEBD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )A.10B.15C.25D.30二.填空题(每题3分,共24分)9.分解因式: _2y-y3= .10.当时,分式值为0.11.如图,已知函数y = 3_ + b和y = a_ - 3的图象交于点P( -2,-5) ,则根据图象可得不等式3_ + b a_ - 3的解集是 .12.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是______cm2.13. 已知两个分式: .其中_2且_-2,则A与B的关系是 .14.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要时间与原计划生产450台机器所需时间相同,现在平均每天生产台机器.15. 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则⊿DOE的周长为 .16. 如图,Rt△ABC中,ABC=90,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为 .三、解答题(本大题7个小题,共72分)17.(12分)分解因式:(1)-4a2_+12a_-9_ (2) (2_+y)2 (_+2y)218.(9分)解不等式组,并写出该不等式组的最大整数解.19.(9分)先化简,然后给a选择一个你喜欢的数代入求值.20.(9分)解方程21.(10分)如图,OC是AOB的平分线,点P为OC上一点,若POD+PEO=180,试判断PD和PE的大小关系,并说明理由.22.(11分)我国沪深股市交易中,如果买、卖一次股票均需要付交易金额的0.5%作费用.张先生以每股5元的价格买入陕西电力股票1000股,若他期望获利不低于1000元,问至少要等到该股涨到每股多少元时才能卖出?(精确到0.01元)23.(12分)将两块全等的三角板如图①摆放,其中A1CB1=ACB=90,A1=A=30.(1)将图①中的△A1B1C顺时针旋转45得图②,点P1是A1C与AB的交点,点Q 是A1B1与BC的交点,求证:CP1=CQ;(2)在图②中,若AP1=2,则CQ等于多少?为大家推荐的____年八年级数学下册暑期练习,还满意吗?相信大家都会仔细阅读,加油哦!。
2021-2022学年北师大版八年级下期数学暑假作业——第7次(附答案)

北师大版八年级下期2021-2022学年数学暑假作业——第7次1. 解不等式:x−22≤7−x 3.2. 解不等式6−4x ≥3x −8,并写出其正整数解.3. 解不等式x−52+1>x −3.4. 解不等式:x 3>1−x−22.5. 解不等式:x−12≤4−x .6. 解不等式组{5x −1>3(x +1)12x −1≤7−32x .7. 解不等式组:{3(x −1)<2x +1x−12≤x +2.8. 解不等式组{x −2>03(x −2)≤x +2.9. 解不等式组:{5x −2>3(x +1)①12x −1⩾7−32x②.10. 解不等式组:{5x +2≥4x −1x+14>x−32+1.11. 把下列各式因式分解:(1) −x 2+6xy −9y 2.(2)a 3+9ab 2−6a 2b.12. 把下列各式因式分解:(1)3x 3+6x 4. (2)4a 3b 2−10ab 3c.13. 把下列各式因式分解:(1)28x 4−21x 3+7xy .(2)−10m 4n 2+8m 4n −2m 3n.14.把下列各式因式分解:(1)16m3−mn2;(2)a2(a−b)−4(a−b).15.把下列各式因式分解:(1)x2(y−2)−x(2−y)(2)(a2+b2)2−4a2b216.化简:(3a−2−1a+2)⋅(a2−4).17.计算:(1)2aa−b −2ba−b;(2)a2a2−6a+9÷aa−3.18.计算:m2−2m+1m2−1÷(m−1−m−1m+1).19.计算(1)a2−b2a+b ⋅2a+2b a2−ab;(2)xx2−4−12x−4+1x+2.20.化简:(2a−1a2−a −aa−1)÷a2−1a.21.解方程:1−x2−x −3=1x−222.解方程:xx−1−1=3x2−1.23.解分式方程:x−2x+2−1=16x2−4.24.解分式方程:(1)3x −2x−2=0(2)34−x +2=1−xx−4.25.解方程:2xx−2−x−3x2−2x=2.参考答案1.解:去分母得:3(x−2)≤2(7−x),去括号得:3x−6≤14−2x,移项合并得:5x≤20,解得:x≤4.2.解:移项得:−4x−3x≥−6−8,合并同类项得:−7x≥−14,系数化为1得:x≤2,∴正整数解为1,2.3.解:将不等式x−52+1>x−3两边同乘以2得,x−5+2>2x−6,解得x<3.4.解:x>125.5.解:x−12≤4−xx−1≤8−2xx+2x≤8+13x⩽9x⩽3 6.解:解不等式5x−1>3(x+1),得:x>2,解不等式12x−1≤7−32x,得:x≤4,则不等式组的解集为2<x≤4.7.解:{3(x−1)<2x+1①x−12≤x+2②,解不等式①,得:x<4,解不等式②,得:x≥−5,故原不等式组的解集是−5≤x<4.8.解:{x−2>0①3(x−2)≤x+2②,由不等式①,得x>2,由不等式②,得x≤4,故原不等式组的解集是2<x≤4.9.解:解不等式①,得x>52.解不等式②,得x⩾4.在同一条数轴上表示不等式①②的解集,如图.所以,原不等式组的解集是x⩾4.10.解:{5x+2≥4x−1①x+14>x−32+1②,解不等式①得:x≥−3,解不等式②得:x<3.∴不等式组的解集为−3≤x<3.11.解:(1)原式=−(x−3y)2.(2)原式=a(a−3b)2.12.解:(1)原式=3x3(1+2x).(2)原式=2ab2(2a2−5bc).13.解:(1)原式=7x(4x3−3x2+y).(2)原式=−2m3n(5mn−4m+1).14.解:(1)原式=m(4m+n)(4m−n).(2)原式=(a−b)(a+2)(a−2).15.解:(1)原式=x2(y−2)+x(y−2)=x(y−2)(x+1);(2)原式=(a2+b2)2−(2ab)2=(a2+b2+2ab)(a2+b2+2ab)=(a+b)2(a−b)2.16.解:(3a−2−1a+2)⋅(a2−4)=3(a+2)−(a−2)(a+2)(a−2)⋅(a+2)(a−2)=3a+6−a+2=2a+8.17.解:(1)原式=2a−2ba−b=2(a−b)a−b=2;(2)原式=a2(a−3)2⋅a−3a=aa−3.18.解:原式=(m−1)2(m+1)(m−1)÷m2−1−m+1m+1=m−1m+1⋅m+1m(m−1)=1m.19.解:(1)原式=(a+b)(a−b)a+b ⋅2(a+b) a(a−b)=2(a+b)a=2a+2ba;(2)原式=x(x+2)(x−2)−12(x−2)+1x+2=2x2(x+2)(x−2)−x+22(x+2)(x−2)+2(x−2)2(x+2)(x−2)=2x−x−2+2x−4 2(x+2)(x−2)=3(x−2)2(x+2)(x−2)=32x+4.20.解:原式=[2a−1a(a−1)−a2a(a−1)]÷(a+1)(a−1)a=2a−1−a2a(a−1)⋅a(a+1)(a−1)=−(a−1)2a(a−1)⋅a(a+1)(a−1)=−1a+1.21.解:原方程可化为1−x2−x −3=−12−x,方程的两边同乘(2−x),得:1−x−3(2−x)=−1,解得:x=2.检验:把x=2代入(2−x)=0,x=2是增根,故原分式方程无解.22.解:方程两边都乘以(x+1)(x−1),去分母得x(x+1)−(x2−1)=3,即x2+x−x2+1=3,解得x=2,检验:当x=2时,(x+1)(x−1)=(2+1)(2−1)=3≠0,∴x=2是原方程的解,故原分式方程的解是x=2.23.解:x−2x+2−1=16x2−4(x−2)2−(x+2)(x−2)=16x2−4x+4−x2+4=16x2−4x−x2=16−4−4−4x=8x=−2,检验:当x=−2时,(x+2)(x−2)=0,∴x=−2是原方程的增根,原方程无解.24.解:(1)去分母得3(x−2)−2x=0,解得x=6,经检验x=6是原方程的根,则原分式方程的根为x=6;(2)去分母得3+2(4−x)=x−1,解得x=4,经检验x=4是原方程的增根,则原分式方程无解.25.解:去分母,得2x2−(x−3)=2x(x−2),去括号,得2x2−x+3=2x2−4x,移项、合并同类项,得3x=−3,系数化为1,得x=−1,检验:当x=−1时,x(x−2)≠0,∴原方程的解为x=−1.。
北京师范大学版八年级暑期生活指导答案2021

北京师范大学版八年级暑期生活指导答案2021自己整理的北京师范大学版八年级暑期生活指导答案2021相关文档,希望能对大家有所帮助,谢谢阅读![基本通行证]一、选择题1。
A2.D3.A4.D5.C6.A7.A8.B9.B10,d11.B12.A13.C二、非选择题14.(1)侵犯生命健康权的,王阿姨应当赔礼道歉,赔偿经济和精神损失。
人身自由权被侵犯,要求超市道歉。
如果协商不成,超市可以报警或者打官司,依法追究。
(3)侵犯了隐私权,要求偷信人道歉。
15.(1)儿童的父母侵犯了儿童的生命权和健康权。
(2)要依法维护自己的合法权益,同时加强自己的学习。
16.我们有权珍爱生命,保持健康,积极运动,增进健康,让自己拥有强健的体魄和向上的精神;患病有权及时治疗,恢复健康,增强体质;当自己的生命健康受到他人非法侵害时,有权依法为自己辩护,请求法律保护。
17.(1)我国中小学生安全仍然存在诸多隐患。
(2)答案能联系实际,合理。
【能力提升】一、单项选择题13.d B2 . a3 . C4 . b5 . B6 . a7 . c8 . a9 . C10 . b 11 . a 12.13 . d省略二、非选择题14.(1)举办本期墙报,有利于保护未成年人的生命健康权。
侵犯未成年人生命权和健康权的行为包括校园暴力、招募童工、体罚学生等。
(2)要不断掌握安全自救的知识和方法,提高安全意识和自救能力,勇于打击危害校园安全的行为。
15.(1)同学A的行为对他人的生命健康漠不关心,不是违法,而是被道德谴责;同学B的行为见义勇为,受到法律和道德的奖励。
但是对于未成年人来说,首先要保护好自己,然后聪明理智地救人;同学C 和D的做法值得学习和提倡。
他们勇敢而足智多谋,珍惜自己的生命和健康,表现出对他人生命和健康的关心。
(2)小技巧:1。
学会在危机时刻保护自己,千方百计拯救他人;2.珍惜自己的生命安全和健康,关心他人的生命安全和健康。
16.(1)生命权和健康权(或人格权)(2)有权依法为自己辩护并请求法律保护(3)省略17.(1)生命权和健康权(2)生命宝贵,永远不要放弃生命的希望;肯定生命的价值,尊重自己和他人的生命;我们应该珍惜生命等等。
2021年北师大版八年级数学暑假作业11

2021年北师大版八年级数学暑假作业11----21b47828-6ea2-11ec-93c2-7cb59b590d7d初中八年级数学(北师大版)暑假作业(十一)一、填写基础培训的空格:乐洋洋给我们送来了一组题目,(总共是30枚会标)赶快去收集吧。
1.如果两个相似三角形的相似比为2:3,则其周长比为2:3,面积比为4:9。
已知的△ 基础知识≓△ A.BCab:a?b?=1: 4. 如果△ 那么ABC是10△ A.BC面积为。
3.一个多边形面积扩大为原来的9倍,形状不变,则周长扩大为原来的__3___倍.4.在1:100设计图上设计一个三角形图案。
如果图案的面积为100cm2,则实际面积为1×106 u5、两正方形的边长比是1:2,它们的周长比与面积比分别是1:2和1:4。
虽然标题很简单!严肃点!二.基础训练之选择题:同学们,我是阿祥。
乐洋洋问题的答案是什么?我有个问题。
老师给了我我出了一些更难的题,我没达到老师的要求,没能收集到会标,全靠你们了(总共是30枚会标)。
网】1.以下几组数字可能不相似:(b)A.每个角是60?两个等腰三角形B,每个都有45度角?两个等腰三角形C,每个角为105?两个等腰三角形D.两个等腰直角三角形2.在△abc与△a?b?c?中,已知加成条件为(c)abbc,若使△abc∽△a?b?c?,还应增?a?b?b?c?a、 ac=a?CB∠a=∠A.C∠b=∠BD∠c=∠C3.在△abc中,d是ab上的一点,在ac上取一点e,要使△ade与△abc相似,则满足这样条件的e点共有(c)a.0个b.1个c.2个d.无数个4.在RT中△ 美国广播公司,∠ ACB=90?,CD是斜面上的高度。
如果ad=4,BD=9,则CD=(a)ada.6b.5c.43d.42E5。
如图所示,e是正方形ABCD一侧Cd的中点,F是BC一侧的点。
补充以下条件之一:① ∠ AED=∠ CFE② AE⊥ Fe③ BF:FC=3:1④ AE:EF=2:1。
初中八年级暑假数学作业答案(北师大版)题型归纳

初中八年级暑假数学作业答案(北师大版)题型归纳放暑假了,同学们应该怎样度过这个暑假呢?初中阶段是我们一生中学习的“黄金时期”。
暑假这一个月的时间对同学们尤其重要。
下文为大家准备了八年级暑假数学作业参考答案。
《暑假乐园》(一)答案:1-8、DABDDDCA;9、1,2,3;10、a≤b;11、a-1;13、7;14、(1)_(2)_15、a≤ ;16、1;17、18厘米;18、2121、18题;22、(1)a=0.6 ,b=0.4;(2)35%到50%之间(不含35%和50%)。
暑假乐园(2)答案:1:D 2:A 3:A 4::A 5:C 6:C7:-2 8:1,9:_=2,10:_.≥0且_≠1, 11、略,12、略,13、2-a,14、a-3、1,15、(1)_=4,(2)_=-2/3,16、B,17、C,18、2,19、-1,20、k=1、4、7,21、互为相反数,22、47,23、375,24、略,《暑假乐园》三答案1,-1 2,y=2/_ 3,B 4,D 5,B 6,C 7,B 8,1/2 9,2∏ 10, B 11,(1)y=4-_(2)略 12,(1)_ =1 m=1(2)与_轴交点(-1,0),与y轴交点(0,1) 13,_ 0)(2)3000(3)6000《暑假乐园》四答案(四)1、B;2、B ;3、B;4、A;5、B;6、B;7、D;8、D;9、≠5;=—1;10、t≤—1;11、—6;12、减小;13、a—3;14、3和4;15、19;16、3或4/3;17、_≥1;18、_19、_—3,原式=- ;20、略;21、_=4;22、y=-_+2,6;23、略,BD=6《暑假乐园》五答案(五)1.4:3 2.6 3.3858 4.18 5.1:9 6.18 7.①④ 8.∠A=∠D9.(-2,-3) 10.2 11.B 12.D 13.C 14.A 15.A 16.C 17.略 18.14.4cm19. 略 20.5.2 21. 或 22.5 23.6.4《暑假乐园》六答案1-8: CCCBBABC 9:1.6,26;10:8.75;11:∠A=∠A,∠AFE=∠B, ∠AEF=∠C, 12:7;13:6.4;14: 8:5;15: 48;16: 6, 4.8, 8.64;17: 9:4; 18: 1:3 ;19: 4 20: 13, ;21: 8.3《暑假乐园》七答案1、C2、A3、D4、C5、B6、B7、B8、D9、如果在一个三角形中有两个角相等,那么这个三角形是直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021八年级暑假作业数学参考答案北师大版16.1分式基础能力题一、选择题(每小题3分,共18分)1.代数式-中是分式的有( )A.1个B.2个C.3个D.4个2.使分式有意义的是( )A. B. C. D. 或3. 下列各式中,可能取值为零的是( )A. B. C. D.4. 分式,,,中是最简分式的有( )A.1个B.2个C.3个D.4个5. 分式中,当x=-a时,下列结论正确的是( )A.分式的值为零;B.分式无意义C.若a≠-时,分式的值为零;D.若a≠时,分式的值为零6.如果把分式中的都扩大2倍,则分式的值( )A.扩大2倍B.缩小2倍C.是原来的D.不变二、填空题(每小题3分,共18分)7. 分式,当x 时,分式有意义.8.当x 时,分式的值为0.9.在下列各式中,分式有 .10. 不改变分式的值,使分式的各项系数化为整数,分子、分母应乘以11. 计算= . 12..三、解答题(每大题8分,共24分)13. 约分:(1); (2).14. 通分:(1),; (2),.15.若求的值.拓展创新题一、选择题(每小题2分,共8分)1.如果把分式中的字母扩大为原来的2倍,而缩小原来的一半,则分式的值( )A.不变B.是原来的2倍C.是原来的4倍D.是原来的一半2. 不改变分式的值,使分子、分母次项的系数为正数,正确的是(• )A. B. C. D.3.一项工程,甲单独干,完成需要天,乙单独干,完成需要天,若甲、乙合作,完成这项工程所需的天数是( )A. B. C. D.4.如果那么的值是( )A.7B.8C.9D.10二、填空题(每小题2分,共8分)5. 李丽从家到学校的路程为s,无风时她以平均a米/•秒的速度骑车,便能按时到达,当风速为b米/秒时,她若顶风按时到校,请用代数式表示她必须提前出发.6. 当m= 时,分式的值为零.7.已知2+若10+为正整数)则, .8. 若一个分式含有字母,且当时,它的值为12,则这个分式可以是 . (写出一个即可)三、解答题(每大题8分,共24分)9. 已知-=3,求的值.10.先能明白(1)小题的解答过程,再解答第(2)小题,(1)已知求的值,解,由知∴;(2)已知:求的值.11. 已知a2-4a+9b2+6b+5=0,求-的值.16.2分式的运算(1)基础能力题1.计算下列各题:(1)×=______;(2)÷=_______;(3)3a·16ab=________;(4)(a+b)·4ab2=________;(5)(2a+3b)(a-b)=_________.2.把下列各式化为最简分式:(1)=_________; (2)=_________.3.分数的乘法法则为_____________________________________________________;分数的除法法则为_____________________________________________________.4.分式的乘法法则为____________________________________________________;分式的除法法则为____________________________________________________. 题型1:分式的乘法运算5.·(-)等于( ) A.6xyz B.- C.-6xyz D.6x2yz6.计算:·.题型2:分式的除法运算7.(技能题)÷等于( )A. B.b2x C.- D.-8.(技能题)计算:÷.9.(-)÷6ab的结果是( )A.-8a2B.-C.-D.-10.-3xy÷的值等于( )A.-B.-2y2C.-D.-2x2y211.若x等于它的倒数,则÷的值是( )A.-3B.-2C.-1D.012.计算:(xy-x2)·=________.13.将分式化简得,则x应满足的条件是________.14.下列公式中是最简分式的是( )A. B. C. D.15.计算·5(a+1)2的结果是( )A.5a2-1B.5a2-5C.5a2+10a+5D.a2+2a+116.计算÷.17.已知+=,则+等于( )A.1B.-1C.0D.2拓展创新题18.(巧解题)已知x2-5x-1 997=0,则代数式的值是( )A.1 999B.2 000C.2 001D.2 00219.(学科综合题)使代数式÷有意义的x的值是( )A.x≠3且x≠-2B.x≠3且x≠4C.x≠3且x≠-3D.x≠-2且x≠3且x≠420.(数学与生活)王强到超市买了a千克香蕉,用了m元钱,又买了b千克鲜橙,•也用了m元钱,若他要买3千克香蕉2千克鲜橙,共需多少钱?(列代数式表示).16.2分式的运算(2)基础能力题1.计算下列各题:(1)·; (2)÷; (3)÷; (4)·.2.55=____×____×_____×_____×5=_______;an=_______.()2=____×______= ____;()3=_____·______·_____=.3.分数的乘除混合运算法则是____ ____.题型1:分式的乘除混合运算4.计算:·÷.5.计算:÷·.题型2:分式的乘方运算6.计算:(-)3.7.(-)2n的值是( )A. B.- C. D.-题型3:分式的乘方、乘除混合运算8.计算:()2÷()·(-)3.9.计算()2·()3÷(-)4得( )A.x5B.x5yC.y5D.x1510.计算()·()÷(-)的结果是( )A. B.- C. D.-11.(-)2n+1的值是( )A. B.- C. D.-12.化简:()2·()·()3等于( )A. B.xy4z2 C.xy4z4 D.y5z13.计算:(1)÷(x+3)·; (2)÷·.拓展创新题14.如果()2÷()2=3,那么a8b4等于( )A.6B.9C.12D.8115.已知│3a-b+1│+(3a-b)2=0.求÷[()·()]的值.16.先化简,再求值:÷(·).其中x=-.17.一箱苹果a千克,售价b元;一箱梨子b千克,售价a元,•试问苹果的单价是梨子单价的多少倍?(用a、b的代数式表示)18.有这样一道题:“计算÷-x的值,其中x=2 004”甲同学把“x=2 004”错抄成“x=2 040”,但他的计算结果也正确,你说这是怎么回事?6.3分式方程基础能力题一、选择题(每小题3分,共18分)1.在下列方程中,关于的分式方程的个数有( )① ②. ③. ④. ⑤ ⑥.A.2个B.3个C.4个D.5个2. 关于x的方程的根为x=1,则a应取值( )A.1B.3C.-1D.-33.方程的根是( )A.=1B.=-1C.=D.=24.那么的值是( )A.2B.1C.-2D.-15.下列分式方程去分母后所得结果正确的是( )A. 去分母得,;B.,去分母得,;C.,去分母得,;D. 去分母得,2;6. .赵强同学借了一本书,共280页,要在两周借期内读完.当他读了一半时,发现平均每天要多读21页才能在借期内读完.他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读x页,则下面所列方程中,正确的是( )A.=14B. =14C.=14D. =1二、填空题(每小题3分,共18分)7. 满足方程:的x的值是________.8. 当x=________时,分式的值等于.9.分式方程的增根是 .10. 一汽车从甲地开往乙地,每小时行驶v1千米,t小时可到达,如果每小时多行驶v2千米,那么可提前到达________小时.11. 农机厂职工到距工厂15千米的某地检修农机,一部分人骑自行车先走40分钟后,其余人乘汽车出发,结果他们同时到达,已知汽车速度为自行车速度的3倍,若设自行车的速度为x千米/时,则所列方程为 .12.已知则 .三、解答题(每题8分,共24分)13. .解下列方程(1) (2)14. 有一项工程,若甲队单独做,恰好在规定日期完成,若乙队单独做要超过规定日期3天完成;现在先由甲、乙两队合做2天后,剩下的工程再由乙队单独做,也刚好在规定日期完成,问规定日期多少天?15.在一次军事演习中,红方装甲部队按原计划从A处向距离150的B地的蓝方一支部队直接发起进攻,但为了迷惑蓝方,红方先向蓝方另一支部队所在的C 地前进,当蓝方在B 地的部队向 C地增援后,红方在到达D地后突然转向B地进发。
一举拿下了B地,这样红方比原计划多行进90,而且实际进度每小时比原计划增加10,正好比原计划晚1小时达到B地,试求红方装甲部队的实际行进速度.(由于实际地形条件的限制,速度不能超过每小时50)16.3分式方程拓展创新题一、选择题(每小题2分,共8分)1.若关于的方程,有增根,则的值是( )A.3B.2C.1D.-12.若方程那么A、B的值为( )A.2,1B.1,2C.1,1D.-1,-13.如果那么( )A.1-B.C.D.4.使分式与的值相等的等于( )A.-4B.-3C.1D.10二、填空题(每小题2分,共8分)5. 时,关于的方程的解为零.6.飞机从A到B的速度是,返回的速度是,往返一次的平均速度是 .7.当时,关于的方程有增根.8. 某市在旧城改造过程中,需要整修一段全长2400m的道路.为了尽量减少施工对城市交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8小时完成任务.求原计划每小时修路的长度.若设原计划每小时修路x m,则根据题意可得方程 .三、解答题(每题8分,共24分)9. 解方程.10. 在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.(1)甲、乙两队单独完成建校工程各需多少天?(2)在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?11.关于的方程:的解为:(可变形为)的解为:的解为:的解为:…(1)请你根据上述方程与解的特征,比较关于的方程(与它们的关于,猜想它的解是什么?(2)请总结上面的结论,并求出方程的解.17.1反比例函数基础能力题一、选择题1.下列表达式中,表示是的反比例函数的是( )① ②. ③ ④是常数,A.①②④B.①③④C.②③D.①③2.下列函数关系中是反比例函数的是( )A.等边三角形面积S与边长的关系B.直角三角形两锐角A与B的关系C.长方形面积一定时,长与宽的关系D.等腰三角形顶角A与底角B的关系3.若反比例函数的图象经过点,其中,则此反比例函数的图象在( )A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限4.函数的图象经过点(-4,6),则下列个点中在图象上的是( )A.(3,8 )B.(-3,8)C.(-8,-3)D.(-4,-6)5. 在下图中,反比例函数的图象大致是( )D6. 已知反比例函数的图象在第二、第四象限内,函数图象上有两点A(,y1)、B(5,y2),则y1与y2的大小关系为( )。
