《应用时间序列分析》考试方案
人大版应用时间序列分析(第5版)习题答案
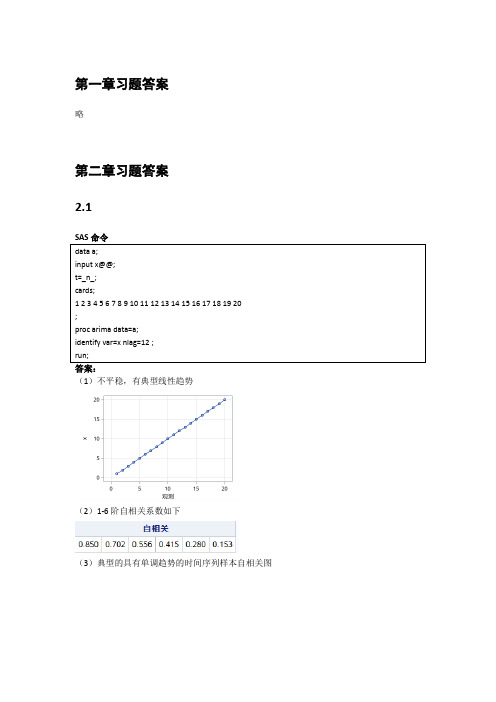
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
应用时间序列分析考试重点

且
1 1 , 2 1
,可以导出
2 12
<1,
1 2 = 12 1 2
模型的可逆性:
=
1 (1 1 )(1 2 ) <1, 1 2 = 12 1 2 = 1 (1 1 )(1 2 ) <1, 即 为 平 稳 域 。 3 、 MA
1、时间序列:按时间顺序排列的一组随机变量。2、平稳性:序列所有的统计性质都不随着时间的推移而变化时,叫严平稳; 当一个时间序列满足均值为常数,且自协方差函数只与时间长度有关时,叫弱平稳。3、随机过程:是一连串随机事件动态关系 的定量描述。4、白噪声序列:也叫纯随机序列,各项之间没有任何相关关系,且存在方差齐性,服从正态分布,最简单的平稳 序列。5、随机游走:是非平稳的,未来的发展趋势无法预测。6、单整与协整:单整是指时间序列显著平稳,不存在单位根, 则称序列为零阶单整序列;协整是指几个时间序列本身是非平稳的,但具有长期均衡关系,以它们建立的回归模型的残差序列 是平稳的,称这几个时间序列存在协整关系。二、方法、重要模型与公式 1、AR 模型的平稳性检验:a、特征根判别或特征系数判别:所
模 型 model:
,
2 2
2
2 1 12 22
Ex t
,
k 0, k 3 (3)ARMA
0
,自协方差函数:
xt 0 1 xt 1 ... p xt p t 1 t 1 2 t 2 .... q t q
,
可逆 4、ARMA 模型(1) AR 模型:model: xt 0 1 xt 1 2 xt 2 .... p xt p t 性质:均值
中 心 化 后 为 0 方 差 : AR(p) :
《应用时间序列分析》期末上机实践报告

得分《应用时间序列分析》期末上机实践报告课程名称:应用时间序列分析《应用时间序列分析》期末课程上机报告要求六、(30分)实践题(另交3-10页的题目、程序和答案纸)要求:系统复习各章上机指导的相关内容,从问题出发,解决三个具体时间序列数据的分析处理全过程(包含:1、数据的背景和拟用到的处理方法,提供可以独立运行的SAS程序,程序的主要运行结果和结果的解读;2、每个学生都必做ARIMA过程的较完整运用,包括数据的输入、输出,时序图、自相关图、偏相关图,并建立成功的拟合模型;3、自由选择其它两个数据和用到自己熟悉的时间序列分析程序过程的处理方法(如趋势拟合、X11、GARCH模型等),但尽量不要三题都用同一个方法)。
、ARIMA模型数据来源:《应用时间序列分析》第5章习题5已知1867-1938年英国(英格兰及威尔士)绵羊的数量如表1所示(行数据),运用时间序列模型预测未来三年英国的绵羊数量。
2203236022542165202420782214229222072119 2119213721321955178517471818190919581892 19191853186819912111 21191991185918561924 1892191619681928189818501841182418231843 188019682029199619331805171317261752 1795 1717164815121338138313441384148415971686 17071640161116321775185018091653164816651627 1791(1)确定该序列的平稳性。
(2)选择适当模型,拟合该序列的发展。
(3)利用拟合模型预测1939-1945年英国绵羊的数量(1)平稳性检验建立临时数据集IhfOl data IhfOl;in put x@@; difx=dif(x);y=log(x); t=_n_; cards;220323602254216520242078 221422922207211921192137 213219551785174718181909 195818921919185318681991211121191991185918561924 189219161968192818981850184118241823184318801968 202919961933180517131726 175217951717164815121338 138313441384148415971686 170716401611163217751850 180916531648166516271791proc gplot data=lhf01;plot x*t difx*t y*t;symbol c=red i=joi n v=star; run;proc arima;iden tify var=x;run;输出时序图显示这是一个典型的非平稳序列。
应用时间序列分析第4章答案
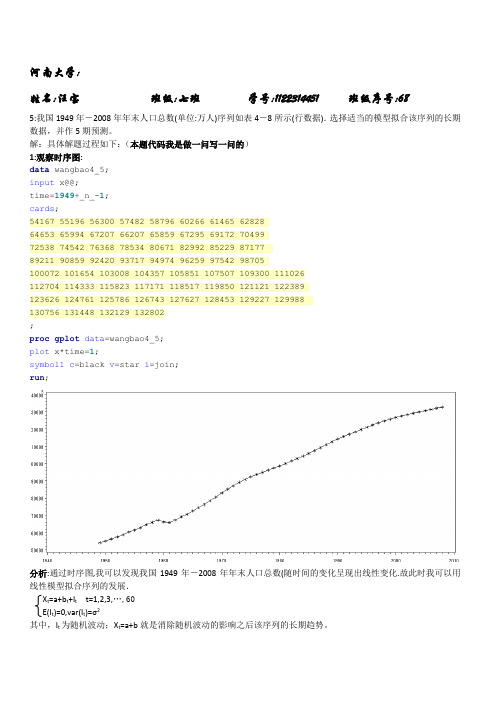
河南大学:姓名:汪宝班级:七班学号:1122314451 班级序号:685:我国1949年-2008年年末人口总数(单位:万人)序列如表4-8所示(行数据).选择适当的模型拟合该序列的长期数据,并作5期预测。
解:具体解题过程如下:(本题代码我是做一问写一问的)1:观察时序图:data wangbao4_5;input x@@;time=1949+_n_-1;cards;54167 55196 56300 57482 58796 60266 61465 6282864653 65994 67207 66207 65859 67295 69172 7049972538 74542 76368 78534 80671 82992 85229 8717789211 90859 92420 93717 94974 96259 97542 98705100072 101654 103008 104357 105851 107507 109300 111026112704 114333 115823 117171 118517 119850 121121 122389123626 124761 125786 126743 127627 128453 129227 129988130756 131448 132129 132802;proc gplot data=wangbao4_5;plot x*time=1;symbol1c=black v=star i=join;run;分析:通过时序图,我可以发现我国1949年-2008年年末人口总数(随时间的变化呈现出线性变化.故此时我可以用线性模型拟合序列的发展.X t=a+b t+I t t=1,2,3,…,60E(I t)=0,var(I t)=σ2其中,I t为随机波动;X t=a+b就是消除随机波动的影响之后该序列的长期趋势。
2:进行线性模型拟合:proc autoreg data=wangbao4_5;model x=time;output out=out p=wangbao4_5_cup;run;proc gplot data=out;plot x*time=1 wangbao4_5_cup*time=2/overlay ;symbol2c=red v=none i=join w=2l=3;run;分析:由上面输出结果可知:两个参数的p值明显小于0.05,即这两个参数都是具有显著非零,4:模型检验又因为Regress R-square=total R-square=0.9931,即拟合度达到99.31%所以用这个模型拟合的非常好。
《应用时间序列分析》教学大纲

《应用时间序列分析》课程教学大纲课程代码:090541040课程英文名称:Applied Time Series Analysis课程总学时:32 讲课:32 实验:0 上机:0适用专业:应用统计学专业大纲编写时间: 2017.6一、大纲使用说明(一)课程的地位及教学目标本课程是应用统计学专业的一门专业必修课。
时间序列分析是应用统计学业的一个重要分支,是利用随机方法分析随机时间变化的随机数据序列的统计规律性,其内容包括构建模型,参数估计及最佳预测与控制等。
时间序列分析在经济学、社会科学领域以及自然科学领域均得到了十分广泛的和。
课程是为使学生掌握时间序列分析的基本知识和基本方法,培养学生运用时间序列分析的知识和方法来分析、拟合及预报时间序列的基本能力,并为实际问题的解决提供有效的方法。
学好时间序列分析已成为对统计学专业本科生的基本要求,同时也将为学生后续的学习与实践打下重要的基础。
(二)知识、能力及技能方面的基本要求1.基本知识:掌握时间序列分析的基本原理,基本模型。
2.基本方法:利用时间序列的基本原理和模型,分析的基本方法。
3.基本技能:要求学生能在真实案例中了解时间序列分析的常用软件。
(三)实施说明1.教学方法:为了从统计学的整体上更好地认识和把握时间序列分析的基本原理、主要方法、应用技术和重要意义,教学中应注意思想方法的解释和学生基础情况的把握,处理好抽象与具体,收集与整理、描述与数据分析,理论与实践的关系。
采用启发式教学,培养学生思考问题、分析问题和解决问题的能力;引导和鼓励学生通过自学获取知识,培养学生的自学能力;增加讨论课,调动学生学习的主观能动性,培养学生的创新能力。
2.教学手段:本课程从技术与应用出发,在教学中采用CAI课件及多媒体教学系统等先进教学手段,以确保在有限的学时内,全面、高质量地完成课程教学任务。
(四)对先修课的要求本课的先修课程:概率论与数理统计。
要求学生取得概率论与数理统计课程学分。
应用时间序列分析习题答案解析

第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 解:1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221 +++=-=-229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解:对于AR (2)模型:⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得:⎩⎨⎧==15/115/721φφ3.3 解:根据该AR(2)0)(=t x E3.4 解:原模型可变形为:由此可知c即当-1<c<0时,该AR(2)模型平稳。
应用时间序列分析课程设计.

课程设计报告课程:应用时间序列分析学号:姓名:班级:教师:《应用时间序列分析》课程设计指导书一、课程设计的目的随着社会经济的不断发展,越来越多的集体甚至个人都参与到股票的投资当中,希望在保值的前提下使得财富增值。
但因股票的波动性和风险性,因而股市中股票价格的形成机制是个很具吸引力的研究课题。
时间序列分析是预测股票价格走势的方法之一,应用数理统计方法加以处理,以预测股价未来的走势。
课程设计运用专业课程《应用时间序列分析》的知识,对青岛海尔股票在2012年1月4日至2013年12月16日收盘情况运用minitab统计软件对数据进行分析,时序图和自相关图的平稳性检验,对原序列进行差分运算,再对差分序列进行平稳性检验,然后对平稳厚的差分序列进行白噪声检验,对平稳非白噪声差分序列的ARIMA模型拟合,模型检验,以及模型预测。
二、设计名称:青岛海尔股票收盘价的分析与预测三、设计要求对青岛海尔股票在2012年1月4日至2013年12月16日的共456个数据,建立模型模型,并对其后五日收盘价格进行预测。
四、设计过程1、画出时间序列的时序图,根据所画的时序图粗略判别序列是否平稳;2、根据序列的自相关图判别序列是否平稳;3、利用单位根检验方法,判别序列的平稳性;4、模型识别。
根据自相关系数和偏自相关系数的性质和特点,判别模型属于哪种类型;5、参数估计。
根据选定的模型类别进行模型的参数估计;6、进行相应的检验。
包括模型的稳定性、可逆性的判定;参数的显著性检验;残差的白噪声检验等;7、模型优化。
对所建立的多个模型,根据AIC准则等进行优化选择;9、预测。
应用所建立的模型,进行未来5期的预测;10、模型的评价。
应用相关的评价准则,对所选择的模型进行评价。
11、撰写设计报告。
报告一律要求用Word文档纂写,内容及要求见指导书。
五、设计细则六、说明课程设计任务书姓名学号班级课程名称应用时间序列分析课程性质专业必修设计时间2013年12月8 日——2013 年12 月20日设计名称青岛海尔股票收盘价的分析与预测设计要求对青岛海尔股票在2012年1月4日至2013年12月16日的共456个数据,建立模型模型,并对其后五日收盘价格进行预测。
应用时间序列分析实验手册

应用时间序列分析实验手册时间序列分析是分析和预测时间序列数据的一种重要方法。
它可以用来研究时间序列数据中的趋势、季节性、周期性和随机性等特征,并通过建立适当的时间序列模型来对未来的数据进行预测。
为了进行时间序列分析,需要按照一定的步骤进行实验。
下面是一个应用时间序列分析的实验手册,它包括了以下几个步骤:1. 收集数据:首先需要收集时间序列数据。
时间序列可以是连续的,比如每天、每周或每月的数据,也可以是离散的,比如每小时或每分钟的数据。
数据可以来自不同的来源,如统计局、公司、网站等。
2. 数据预处理:在进行时间序列分析之前,需要对数据进行预处理。
预处理的目的是去除异常值、平滑数据、填补缺失值等。
常用的预处理方法包括平滑法、插值法、滤波法等。
3. 数据可视化:在进行时间序列分析之前,需要对数据进行可视化。
可以使用折线图、柱状图、散点图等方法展示时间序列数据的趋势和季节性。
4. 应用时间序列模型:时间序列模型是用来描述时间序列数据的数学模型。
常用的时间序列模型包括平稳ARMA模型、非平稳ARIMA模型、指数平滑模型等。
根据数据的不同特点选择合适的模型。
5. 模型诊断:在应用时间序列模型后,需要对模型进行诊断。
诊断的目的是检查模型的拟合程度和预测能力。
常用的诊断方法包括残差分析、模型的稳定性检验等。
6. 模型预测:基于已建立的时间序列模型,可以对未来的数据进行预测。
预测的方法包括单步预测、多步预测、滚动预测等。
7. 模型评估:在进行时间序列预测之后,需要对预测结果进行评估。
常用的评估指标包括均方误差、平均绝对误差、相对误差等。
评估结果可以用来评估模型的预测准确性和稳定性。
总结:时间序列分析是一种重要的数据分析方法,可以用来研究和预测时间序列数据的趋势、季节性、周期性和随机性等特征。
通过按照上述步骤进行实验,可以有效地应用时间序列分析方法,提高对时间序列数据的理解和预测能力。
8. 趋势分析:在时间序列分析中,趋势是指数据中的长期变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《应用时间序列分析》课程考试大纲
课程性质:专业限选课
总学时: 56
总学分: 3
开课学期:第5学期
适用专业:应用统计学专业
一、课程描述
《应用时间序列分析》作为统计学专业十分重要的专业限选课,在专业培养上有其特殊的地位,因为它是处理大量特殊结构数据的非常有效的一种统计方法,具有非常广泛的应用领域,通过这门课的学习,不仅要把前期的课程内容应用于其中,而且还要为后续的毕业实习、毕业论文打下坚实的理论和技术基础,提升统计学专业学生毕业后的就业能力。
二、考试内容及要求
第一章时间序列分析简介
1.了解时间序列的定义。
2.识记时间序列的基本性质。
3.了解时间序列的基本分析方法。
4.了解时间序列的应用软件介绍。
第二章时间序列的预处理
1.识记时间序列平稳性检验的定义和方法。
2.识记时间序列纯随机性检验的定义和方法。
3.熟练应用Eviews完成基本上机操作。
第三章平稳时间序列分析
1.了解平稳时间序列分析的方法性工具。
2.识记ARMA模型的性质。
3.熟练应用平稳序列完成建模过程。
4.熟练应用平稳序列进行预测。
5.熟练应用Eviews完成平稳序列建模的上机操作。
第四章非平稳序列的确定性分析
1.了解时间序列的分解方法。
2.了解确定性因素分解方法。
3.应用趋势分析的方法。
4.应用季节效应分析的方法。
5.应用综合分析的方法。
6.熟练应用Eviews完成非平稳序列建模的上机操作。
第五章非平稳序列的随机分析
1.识记差分运算方法。
2.应用ARIMA模型的方法。
3.应用残差自回归模型。
4.识记异方差的性质。
5.熟练应用Eviews完成非平稳序列的随机分析建模。
三、考试形式及要求
1.考试方式:考试类型分为小论文、笔试、出勤及课堂表现。
2.考试次数:期末总评成绩由平时考核成绩、阶段考核成绩和结课考核成绩三部分组成。
阶段考核方式为小论文,结课考核为开卷考试,平时作业5次,课堂出勤及课堂表现每节课统计。
3.记分方式:采用百分制计分方式。
4.课程总评成绩构成:平时考核占总成绩的25%、阶段考核占总成绩的25%、结课考核占总成绩的50%。
平时考核和阶段考核重点考核单元知识的重点和难点,强调对学生平时课下学习、自学能力、创新意识和学习态度的考核。
结课考核的内容涵盖教学大纲中的全部教学内容,并加强对学生应用软件解决实际问题能力的考核。
四、教材及主要参考书
1.选用教材:王燕编著,《应用时间序列分析(第二版)》,中国人民大学出版社,2011年.
2.参考书:易丹辉主编,《时间序列分析:方法与应用》,中国人民大学出版社,2011年.
3.必读书:马慧慧,《Eviews统计分析与应用》,电子工业出版社,2016年版.。
