概率论与数理统计期末复习资料(学生)
概率论与数理统计期末考试复习资料
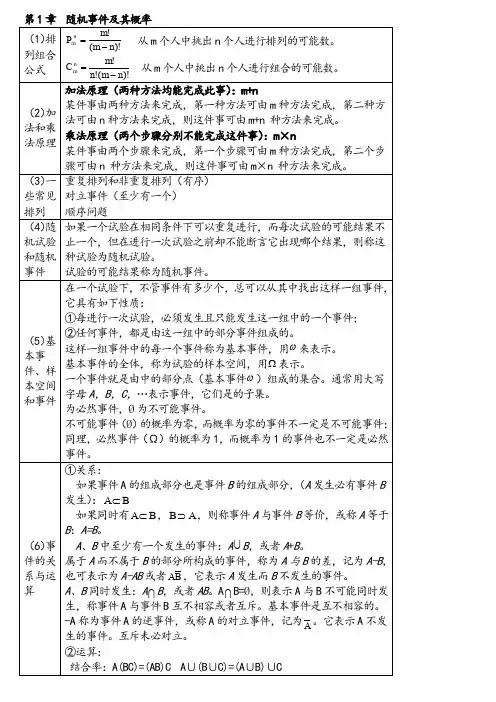
F (x) x f (x)dx ，
则称 X 为连续型随机变量。f (x) 称为 X 的概率密度函数或密度函 数，简称概率密度。 密度函数具有下面 4 个性质： 1° f (x) 0 。
2° f (x)dx 1。
X
| x1, x2,, xk, 。
P( X xk) p1, p2,, pk,
显然分布律应满足下列条件：
（2）连 续型随 机变量 的分布 密度
（3）离 散与连 续型随 机变量 的关系 （4）分 布函数
（5）八 大分布
（1） pk 0 ，k 1,2,， （2） pk 1。 k 1
ba
f
(x)
b
1
a
,
0,
a≤x≤b
其他，
则称随机变量 X 在[a，b]上服从均匀分布，记为 X~U(a，b)。
分布函数为
0，
xa, ba
x<a， a≤x≤b
x
F (x) f (x)dx
1，
x>b。
当 a≤x1<x2≤b 时，X 落在区间（x1, x2 ）内的概率为
P( A)
条件概
下，事件 B 发生的条件概率，记为P(B / A) P(AB) 。
P( A)
率
条件概率是概率的一种，所有概率的性质都适合于条件概率。
例如 P(Ω/B)=1P( B /A)=1-P(B/A)
（13） 乘法公式：P(AB) P(A)P(B / A)
乘法公 更一般地，对事件 A1，A2，…An，若 P(A1A2…An-1)>0，则有
大学概率论和数理统计复习资料全
第一章 随机事件及其概率知识点：概率的性质 事件运算 古典概率事件的独立性 条件概率 全概率与贝叶斯公式常用公式)()()()()()2(加法定理AB P B P A P B A P -+= ),,()()(2111有限可加性两两互斥设n ni i ni i A A A A P A P ∑===),(0)()()()()(互不相容时独立时与B A AB P B A B P A P AB P ==)()()()()5(AB P A P B A P B A P -==-)()()()()(时当A B B P A P B A P B A P ⊂-==-))0(,,()()/()()()6(211>Ω=∑=i n ni i i A P A A A A B P A P B P 且的一个划分为其中全概率公式 ),,()](1[1)(2111相互独立时n ni i n i i A A A A P A P ∏==--=)/()()/()()()4(B A P B P A B P A P AB P ==)(/)()/()3(A P AB P A B P =)()/()()/()()/()7(1逆概率公式∑==ni iii i i A B P A P A B P A P B A P )(/)()(/)()1(S L A L AP nr A P ==应用举例1、已知事件,A B 满足)()(B A P AB P =，且6.0)(=A P ，则=)(B P （ ）。
2、已知事件,A B 相互独立，,)(k A P =6.0)(,2.0)(==B A P B P ，则=k （ ）。
3、已知事件,A B 互不相容，,3.0)(=A P ==)(,5.0)(B A P B P 则（ ）。
4、若,3.0)(=A P ===)(,5.0)(,4.0)(B A B P B A P B P （ ）。
5、,,A B C 是三个随机事件，C B ⊂，事件()A C B -与A 的关系是（ ）。
概率论与数理统计期末考试试卷复习资料
数理统计练习 一、填空题1、设A 、B 为随机事件，且P (A)=0.5，P (B)=0.6，P (B A)=0.8，则P () 0.7 。
2、某射手对目标独立射击四次，至少命中一次的概率为8180，则此射手的命中率3、设随机变量X 服从[0，2]上均匀分布，则=2)]([)(X E X D 1/3 。
4、设随机变量X 服从参数为λ的泊松（）分布，且已知)]2)(1[(--X X E ＝1， 则=λ1。
5、一次试验的成功率为p ，进行100次独立重复试验，当=p 1/2时 ， 成功次数的方差的值最大，最大值为 25 。
6、（X ，Y ）服从二维正态分布),,,,(222121ρσσμμN ，则X 的边缘分布为 ),(211σμN7、已知随机向量（X ，Y ）的联合密度函数⎪⎩⎪⎨⎧≤≤≤≤=其他,010,20,23),(2y x xy y x f ，则E (X )=8、随机变量X 的数学期望μ=EX ，方差2σ=DX ，k 、b 为常数，则有)(b kX E += k μ+)(b kX D +=22k σ。
9、若随机变量X ～N (－2，4)，Y ～N (3，9)，且X 与Y 相互独立。
设Z ＝2－Y ＋5，则Z ～ N(-2, 25) 。
10、θθθ是常数21ˆ ,ˆ的两个 无偏 估计量，若)ˆ()ˆ(21θθD D <，则称1ˆθ比2ˆθ有效。
1、设A 、B 为随机事件，且P (A )=0.4, P (B )=0.3, P (A ∪B )=0.6，则P (B A )0.3。
2、设X B (2)，Y B (3)，且P {X ≥ 1}=95，则P {Y ≥ 1}=2719。
3、设随机变量X 服从参数为2的泊松分布，且Y =3X -2, 则E (Y )=4 。
4、设随机变量X 服从[0,2]上的均匀分布，21，则D (Y )= 4/3 。
5、设随机变量X 的概率密度是：⎩⎨⎧<<=其他103)(2x x x f ，且{}784.0=≥αX P ，则α=0.6 。
概率论与数理统计复习资料要点总结--学生
《概率论与数理统计》复习资料一、复习提纲注：以下是考试的参考内容，不作为实际考试范围，仅作为复习参考之用。
考试内容以教学大纲和实施计划为准；注明“了解”的内容一般不考。
1、 会事件关系的运算，了解概率的古典定义2、 能较熟练地求解古典概率；了解概率的公理化定义3、 掌握概率的基本性质和应用这些性质进行概率计算；理解条件概率的概念；掌握加法公式与乘法公式4、 能准确地选择和运用全概率公式与贝叶斯公式解题；掌握事件独立性的概念及性质。
5、 理解随机变量的概念，掌握离散性随机变量分布率的性质及求法,掌握(0—1)分布、二项分布、泊松分布的分布律。
6、 理解分布函数的概念及性质，理解并掌握连续型随机变量的概率密度及性质。
7、 掌握指数分布(参数λ)、均匀分布、正态分布8、 会求特殊的一维随机变量函数分布的分布律或概率密度。
9、 会求分布中的待定参数。
会求区间的概率.10、 会求边缘分布律、边缘密度函数，会判别随机变量的独立性。
11、 掌握二维连续型随机变量未知参数的计算,落在区域概率的计算。
12、 理解二维随机变量的概念，理解二维随机变量的联合分布函数及其性质，掌握二维离散型随机变量的联合分布律及其性质，掌握二维连续型随机变量的联合概率密度及其性质，并会用它们计算有关事件的概率。
13、 会求二维离散型随机变量函数的分布率.14、 掌握数学期望和方差的定义及性质,会熟练地求随机变量及其函数的数学期望和方差。
会熟练地默写出几种重要随机变量的数学期望及方差。
15、 较熟练地求协方差与相关系数.16、 会用独立正态随机变量线性组合性质解题。
17、 理解总体、样本、简单随机样本、统计量及抽样分布概念，样本均值与样本方差及样本矩概念，掌握χ2分布(及性质)、t 分布、F 分布及其分位点概念。
18、 理解正态总体样本均值与样本方差的抽样分布定理；会用矩估计方法来估计未知参数。
19、 掌握极大似然估计法，无偏性与有效性的判断方法。
大学概率论与数理统计复习资料
知识点：概率的性质事件运算古典概率常用公式(2)P(A BP P(A) P(B)- P(AB)(加法定理)nnP(U A) Y p(A)i d innP(U A)=l-n [1-P(A)]i di d(3) P(B/A)二 P(AB)/P(A) (4)P(AB)二 P(A)P(B/A)二P(B)P(A/B) P(AB)二 P(A)P(B) (A 与B 独立时)P(AB)二0(A,B 互不相容时)(5) P (A- Bp P(ABp P(A)- P(AB)P(A- B)二 P(AB)二 P(A) - P(B)(当B A 时)n(6) P (B)八 P(A i )P(B/A i )(全概率公式)i=1(其中A ,,A 2 A n 为"的一个划分,且P(A i 0)) (7) P (A /B) = nP(A)P(B/A)(逆概率公式)迟 P(A i )P(B/A)事件的独立性条件概率全概率与贝叶斯公式(1)P(Ap r/nP(AP L(A)/L(S)（设A,4…A 两两互斥,有限可加性）（A ，4, A 相互独立时）i =1应用举例1、已知事件A, B 满足P(AB) = P(AB),且P(A) = 0.6 ,贝卩P(B)=()。
2、已知事件A,B 相互独立，P(A) =k, P(B) =0.2, P(0 B)=0.6，贝k - ()。
3、已知事件A,B 互不相容，P(A) =0.3, P(B) = 0.5,则 P(A B)=()。
4、若P(A) =0.3, P(B)=0.4 ,P(AB) = 0.5, P(BA B)=( )。
5、A, B,C是三个随机事件，C B，事件AUC - B与A的关系是6、5张数字卡片上分别写着1, 2, 3, 4, 5,从中任取3张，某日他抛一枚硬币决定乘地铁还是乘汽车。
(1 )试求他在5:40〜5:50到家的概率；(2)结果他是5:47到家的。
试求他是乘地铁回家的概率。
概率论与数理统计期末考试复习资料汇编
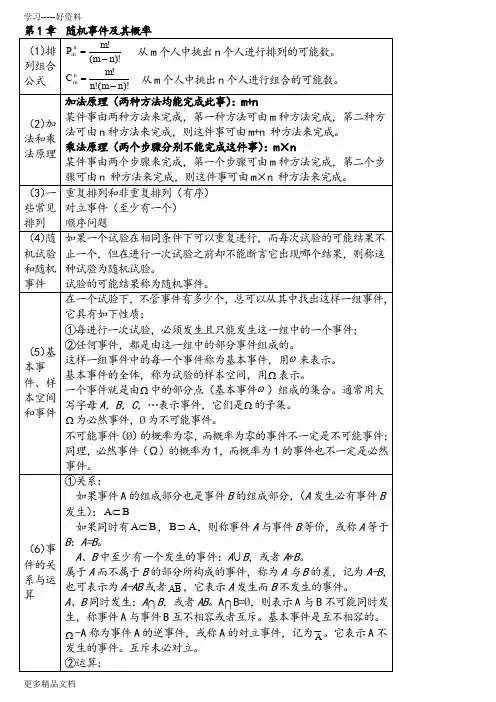
式
P( A1A2 … An) P( A1)P( A2 | A1)P( A3 | A1A2) ……P( An | A1A2 … An 1) 。
①两个事件的独立性
（14） 设事件 A 、B 满足P(AB) P(A)P(B) ，则称事件 A 、B 是相互独立 独立性 的。
若事件 A 、B 相互独立，且P(A) 0 ，则有
学习-----好资料
第 1 章 随机事件及其概率
（1）排 列组合 公式
Pmn
m! (m n)!
C
n m
m! n!(m n)!
从 m 个人中挑出 n 个人进行排列的可能数。 从 m 个人中挑出 n 个人进行组合的可能数。
加法原理（两种方法均能完成此事）：m+n
（2）加 法和乘 法原理
某件事由两种方法来完成，第一种方法可由 m 种方法完成，第二种方 法可由 n 种方法来完成，则这件事可由 m+n 种方法来完成。 乘法原理（两个步骤分别不能完成这件事）：m×n 某件事由两个步骤来完成，第一个步骤可由 m 种方法完成，第二个步
（6）事 件的关 系与运 算
B：A=B。 A、B 中至少有一个发生的事件：A B，或者 A+B。
属于 A 而不属于 B 的部分所构成的事件，称为 A 与 B 的差，记为 A-B， 也可表示为 A-AB 或者 AB ，它表示 A 发生而 B 不发生的事件。 A、B 同时发生：A B，或者 AB。A B=Ø，则表示 A 与 B 不可能同时发
德摩根率：
Ai
Ai
AB AB，AB AB
i1
i 1
设 为样本空间，A 为事件，对每一个事件 A 都有一个实数 P(A)，
概率论与数理统计期末必备复习资料
全概率公式
划分：设S为试验E的样本空间，B1, B2,L , Bn 为E的一 组事件，若
① Bi Bj ,i j,i, j 1, 2,L , n ② B1 U B2 UL U Bn S 则称 B1, B2,L , Bn 为样本空间S的一个划分.
例 E：掷骰子观察点数
S {1，2，3，4，5，6}
条件概率小结
缩减样本空间
条件概率 乘法公式
定义式
全概率公式
贝叶斯公式
浙江师范大学 14
独立性
独立事件：两事件A、B，A发生对B发生没有影响， B发生也对A没有影响，则称两事件相互独立.即 P(A|B)=P(A)且P(B|A)=P(B)，则 P(AB)=P(A)P(B|A)=P(A)P(B)
例 抛甲，乙两枚硬币，A={甲出现正面H}，B={乙 出现正面H}，问A，B同时发生的概率.
注：全概率公式给出我们一个用来计算在众多原 因 B1, B2,L , Bn 的作用下事件A发生概率的方法. （由因得果）
浙江师范大学 12
贝叶斯公式（由果溯因）
设E的样本空间为S，A为E的事件. B1, B2 ,L , Bn 为S的一个划分，且 P(A)>0,P(Bi ) 0.(i 1, 2,L , n) ，
即在f (x)的连续点
x1 x2
f (x) F '(x) lim F(x x) F(x) lim P{x X x x}
k
均有：P Ai1 Ai2 L Aik P Aij j 1
则称A1, A2,L , An相互独立
浙江师范大学 16
定义 随机试验的结果可以用一个实值变量表示， 这个变量的取值是随机的，但又服从一定的统计规 律性，这种变量称为随机变量，通常用X，Y，Z表 示。
非常全面的《概率论与数理统计》复习材料
《概率论与数理统计》复习大纲第一章随机事件与概率事件与集合论的对应关系表古典概型古典概型的前提是Ω={ω1, ω2,ω3,…, ωn,}, n为有限正整数，且每个样本点ωi出现的可能性相等。
例1设3个球任意投到四个杯中去，问杯中球的个数最多为1个的事件A1，最多为2个的事件A2的概率。
[解]：每个球有4种放入法，3个球共有43种放入法，所以|Ω|=43=64。
(1)当杯中球的个数最多为1个时，相当于四个杯中取3个杯子，每个杯子恰有一个球，所以|A1|= C433！=24；则P(A1)=24/64 =3/8. (2) 当杯中球的个数最多为2个时，相当于四个杯中有1个杯子恰有2个球(C41C32)，另有一个杯子恰有1个球(C31C11)，所以|A2|= C41C32C31C11=36；则P(A2)=36/64 =9/16例2从1,2,…,9，这九个数中任取三个数，求：(1)三数之和为10的概率p1；(2)三数之积为21的倍数的概率p2。
[解]：p1=4C93=121, p2=C31C51+C32C93=314P(A)=A包含样本总个数样本点总数=|A||Ω|几何概型前提是如果在某一区域Ω任取一点，而所取的点落在Ω中任意两个度量相等的子区域的可能性是一样的。
若A⊂Ω，则P(A)=A的度量Ω的度量例1把长度为a的棒任意折成三段，求它们可以构成一个三角形的概率。
[解]：设折得的三段长度分别为x,y和a-x-y，那么，样本空间，S={(x,y)|0≤x≤a,0≤y≤a,0≤a-x-y≤a}。
而随机事件A：”三段构成三角形”相应的区域G应满足两边之和大于第三边的原则，得到联立方程组，⎩⎪⎨⎪⎧a-x-y<x+yx<a-x-y+yy<a-x-y+x解得0<x<a2, 0<y<a2,a2<x+y<a 。
即G={(x,y)| 0<x<a2, 0<y<a2,a2<x+y<a }由图中计算面积之比，可得到相应的几何概率P(A)=1/4。
非常全面的《概率论与数理统计》复习材料
非常全面的《概率论与数理统计》复习材料概率论与数理统计是一门研究随机现象及其统计规律的学科，它在自然科学、社会科学、工程技术、经济管理等众多领域都有着广泛的应用。
对于学习这门课程的同学来说，掌握好相关的知识和方法是非常重要的。
下面就为大家提供一份非常全面的《概率论与数理统计》复习材料。
一、概率论的基本概念1、随机事件随机事件是指在一定条件下，可能出现也可能不出现的事件。
比如掷骰子出现的点数，就是一个随机事件。
2、样本空间样本空间是指随机试验中所有可能结果组成的集合。
3、事件的关系与运算包括事件的包含、相等、和、积、差、互斥、对立等关系及相应的运算。
4、概率的定义与性质概率是对随机事件发生可能性大小的度量。
概率具有非负性、规范性和可加性等性质。
5、古典概型与几何概型古典概型是指试验结果有限且等可能的概率模型；几何概型则是与几何图形的长度、面积、体积等有关的概率模型。
二、随机变量及其分布1、随机变量随机变量是用来表示随机现象结果的变量。
2、离散型随机变量常见的离散型随机变量有二项分布、泊松分布等。
3、连续型随机变量常见的连续型随机变量有正态分布、均匀分布、指数分布等。
4、随机变量的分布函数分布函数能够完整地描述随机变量的概率分布特征。
5、随机变量的数字特征包括期望、方差、协方差、相关系数等。
期望反映了随机变量取值的平均水平，方差反映了随机变量取值的离散程度。
三、多维随机变量及其分布1、二维随机变量研究两个随机变量之间的关系。
2、边缘分布通过二维随机变量的联合分布可以得到其边缘分布。
3、条件分布给定一个随机变量的取值，另一个随机变量的分布就是条件分布。
4、相互独立的随机变量如果两个随机变量的联合分布等于它们各自边缘分布的乘积，则称它们相互独立。
四、大数定律与中心极限定理1、大数定律阐述了在大量重复试验中，随机变量的平均值具有稳定性。
2、中心极限定理表明在一定条件下，大量独立随机变量的和近似服从正态分布。
概率论与数理统计期末复习资料
《概率统计》、《概率论与数理统计》、《随机数学》课程期末复习资料注：以下是考试的参考内容，不作为实际考试范围，考试内容以教学大纲和实施计划为准；注明“了解”的内容一般不考。
1、能很好地掌握写样本空间与事件方法，会事件关系的运算，了解概率的古典定义2、能较熟练地求解古典概率；了解概率的公理化定义3、掌握概率的基本性质和应用这些性质进行概率计算；理解条件概率的概念；掌握加法公式与乘法公式4、能准确地选择和运用全概率公式与贝叶斯公式解题；掌握事件独立性的概念及性质。
5、理解随机变量的概念，能熟练写出(0—1)分布、二项分布、泊松分布的分布律。
6、理解分布函数的概念及性质，理解连续型随机变量的概率密度及性质。
7、掌握指数分布(参数λ)、均匀分布、正态分布，特别是正态分布概率计算8、会求一维随机变量函数分布的一般方法，求一维随机变量的分布律或概率密度。
9、会求分布中的待定参数。
10、会求边缘分布函数、边缘分布律、条件分布律、边缘密度函数、条件密度函数，会判别随机变量的独立性。
11、掌握连续型随机变量的条件概率密度的概念及计算。
12、理解二维随机变量的概念，理解二维随机变量的联合分布函数及其性质，理解二维离散型随机变量的联合分布律及其性质，理解二维连续型随机变量的联合概率密度及其性质，并会用它们计算有关事件的概率。
13、了解求二维随机变量函数的分布的一般方法。
14、会熟练地求随机变量及其函数的数学期望和方差。
会熟练地默写出几种重要随机变量的数学期望及方差。
15、较熟练地求协方差与相关系数.16、了解矩与协方差矩阵概念。
会用独立正态随机变量线性组合性质解题。
17、了解大数定理结论，会用中心极限定理解题。
18、掌握总体、样本、简单随机样本、统计量及抽样分布概念，掌握样本均值与样本方差及样本矩概念，掌握χ2分布(及性质)、t分布、F分布及其分位点概念。
19、理解正态总体样本均值与样本方差的抽样分布定理；会用矩估计方法来估计未知参数。
概率论与数理统计第一章期末复习
概率论与数理统计第一章期末复习(一)随机事件1.随机现象定义1在一定的条件下，并不总是出现相同结果的现象称为随机现象．定义2只有一个结果的现象称为确定性现象．2.样本空间定义3一个试验如果满足下述条件：(1)试验可以在相同的情形下重复进行；(2)试验的所有可能结果是明确可知的，并且不止一个；(3)每次试验总是恰好出现这些可能结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果．就称这样的试验是一个随机试验，记作E．定义4随机试验E的所有可能结果组成的集合称为E的样本空间，记作Ω．样本空间的元素，即E的每个结果，称为样本点，记作ω．3.随机事件定义5随机试验的某些样本点的集合称为随机事件，简称事件，常用大写英文字母A，B，C，…表示．定义6由样本空间Ω中的单个元素组成的子集称为基本事件．而样本空间Ω的最大子集(即Ω本身)称为必然事件，样本空间Ω的最小子集(即空集∅)称为不可能事件．4.事件的关系与运算下面的讨论总是假设在同一个样本空间Ω中进行．1)包含关系⊂如果属于A的样本点必属于B，则称A包含于B或称B包含A，记作A B ⊃．用概率的语言说：事件A发生必然导致事件B发生．或B A对任一事件A，必有∅Ω⊂A．⊂2)相等关系如果属于A的样本点必属于B，且属于B的样本点必属于A，即BA⊂且=．AB⊂，则称事件A与B相等，记作A B3)互不相容(互斥)如果A 与B 没有相同的样本点，则称A 与B 互不相容(互斥)．即事件A 与事件B 不可能同时发生．4)两事件的和事件“事件A 与B 中至少有一个发生”，这样的一个事件称作事件A 与B 的和(或并)，记作B A ．5)两事件的积事件“事件A 与B 同时发生”，这样的一个事件称作事件A 与B 的积(或交)，记作B A (或AB )．6)两事件的差事件“事件A 发生而B 不发生”，这样的事件称为事件A 对B 的差，记作A B -．7)对立事件或逆事件若=AB ∅且Ω=B A ，则称A 与B 为对立事件或互为逆事件，事件A 的对立事件记作A ．【例1】设A 、B 、C 是Ω中的随机事件，则(1)事件{A 发生且B 与C 至少有一个发生}可表示为：)(C B A ；(2)事件{A 与B 发生而C 不发生}可表示为：C AB ；(3)事件{A 、B 、C 中至少有两个发生}可表示为：BC AC AB ；(4)事件{A 、B 、C 中至多有两个发生}可表示为：ABC ；(5)事件{A 、B 、C 中不多于一个发生}可表示为：AB BC AC ；(6)事件{A 、B 、C 中恰有一个发生}可表示为：ABC ABC ABC ．【例2】关系()成立，则事件A 与B 为对立事件．A ．=AB ∅B ．Ω=B AC ．=AB ∅，Ω=B AD ．=AB ∅，Ω≠B A 【解析】由对立事件的概念可知选项C 正确．【例3】甲、乙两人谈判，设事件A ，B 分别表示甲、乙无诚意，则B A 表示()A ．两人都无诚意B ．两人都有诚意C ．两人至少有一人无诚意D ．两人至少有一人有诚意【解析】由题可知A 与B 分别表示甲、乙有诚意，则B A 表示甲、乙两人至少有一人有诚意，故选项D 正确．5.事件的运算性质(1)交换律：A B B A =，BA AB =；(2)结合律：C B A C B A )()(=，)()(BC A C AB =；(3)分配律：()()()A B C AB AC = ，()()()A B C A C B C = ；(4)对偶律：B A B A = ，B A AB =．一些有用的等式：A A A = ，A Ω=Ω ，A A ∅= AA A =，A A Ω=，A ∅=∅A B A AB AB -=-=，A B A B A =【例4】化简下列各式：(1)))((B A B A ；(2)))((C B B A ；(3)))((B A B A B A ．【解】(1) A B B A B A B A ==)())((ØA =；(2)AC B C A B C B B A ==)())((；(3)))(())((B A B B A B A B A B A =AB AB A A B A A === )(．(二)随机事件的概率1.概率的公理化定义定义1设E 是随机试验，Ω是它的样本空间．对于E 的每一事件A 赋予一个实数，记为)(A P ，称为事件A 的概率，如果集合函数)(⋅P 满足下列条件：(1)非负性0)(≥A P ，对Ω∈A ；(2)规范性()1P Ω=；(3)可列可加性若=j i A A ∅，j i ≠， ,2,1,=j i ，有∑+∞=+∞==11)()(i i i i A P A P ．2.概率的性质性质1不可能事件的概率为0，即()0P ∅=．性质2概率具有有限可加性，即若=j i A A ∅(n j i ≤<≤1)，则∑===ni i n i i A P A P 11)()( ．性质3对任一随机事件A ，有()1()P A P A =-．性质4若A B ⊂，则)()()(B P A P B A P -=-．推论若A B ⊂，则)()(B P A P ≥．性质5对任意的两个事件A ，B ，有)()()(AB P A P B A P -=-．性质6对任意的两个事件A ，B ，有()()()()P A B P A P B P AB =+- ．对任意三个事件A ，B ，C ，有)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++= ．推论对任意的两个事件A ，B ，有)()()(B P A P B A P +≤ ．【例1】设A 与B 互不相容，且0)(>A P ，0)(>B P ，则下列结论正确的是()A ．A 与B 为对立事件B ．A 与B 互不相容C ．)()()(B P A P B A P -=-D ．)()(A P B A P =-【解析】因为A 与B 互不相容，所以AB =∅，0)(=AB P ，故选项A ：互不相容不一定对立，故选项A 错误；选项B ：互不相容不一定对立，故B A 不一定等于Ω，所以B A B A =不一定等于∅，即A 与B 不一定互不相容，故选项B 错误；选项C ：)()()()(A P AB P A P B A P =-=-，故选项C 错误，进而选项D 正确．【例2】已知B A ⊂，3.0)(=A P ，5.0)(=B P ，求(A P ，)(AB P ，)(B A P 和)(B A P ．【解】(1)7.0)(1)(=-=A P A P ；(2)∵B A ⊂，∴A AB =，则3.0)()(==A P AB P ；(3)2.0)()()()(=-=-=AB P B P A B P B A P ；(4))(1()(B A P B A P B A P -==5.0)]()()([1=-+-=AB P B P A P ．【注】事件的概率的计算常常需要结合对偶律，应用性质3．【例3】已知事件A ，B ，B A 的概率分别是0.4，0.3，0.6，求(B A P ．【解】)()()()(AB P B P A P B A P -+= )(3.04.06.0AB P -+=所以1.0)(=AB P ，则3.0)()()((=-=-=AB P A P B A P B A P ．【例4】已知41)()()(===C P B P A P ，0)(=AB P ，161)()(==BC P AC P ．求：(1)A ，B ，C 中至少发生一个的概率；(2)A ，B ，C 都不发生的概率．【解】(1)因为0)(=AB P ，且AB ABC ⊂，所以由概率的单调性知0)(=ABC P ；再由加法公式，得A ，B ，C 中至少发生一个的概率为)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++= 8516243=-=．(2)因为{A ，B ，C 都不发生}的对立事件为{A ，B ，C 中至少发生一个}，所以A ，B ，C 都不发生的概率为83851(=-=C B A P ．3.古典概型定义2若随机试验E 具有下述特征：(1)样本空间的元素(即样本点)只有有限个，不妨设为n 个，并记它们为12,,,n ωωω ．(2)每个样本点出现的可能性相等(等可能性)，即有12()()()n P P P ωωω=== ．则称这种等可能性的概率模型为古典概型．对任意一个随机事件Ω∈A ，有nk A A P =Ω=中所有样本点的个数所含有样本点的个数事件)(．【例5】袋中有大小相同的4个白球，3个黑球，从中任取3个至少有2个白球的概率为．【解析】袋中共有7个球，从中任取3个，共有37C 中取法，即样本空间Ω中共有37C 个样本点．取出的3个球中至少有2个白球，分为2个白球1个黑球和3个白球两种情况．当取出的3个球中有2个白球1个黑球时，共有1324C C 中取法；当取出的3个球中有3个白球时，共有0334C C 中取法．记=A {从中任取3个至少有2个白球}，则事件A 中共有03341324C C C C +个样本点．因此3522)(3703341324=+=C C C C C A P ．(三)条件概率1.条件概率定义1设A 与B 是样本空间Ω中的两个事件，若0)(>B P ，则称)()()(B P AB P B A P =为“在事件B 发生条件下事件A 发生的条件概率”，简称条件概率．【例1】已知31)()(==B P A P ，61)(=B A P ，求(B A P ．【解】∵61)()()(==B P AB P B A P ，∴181)(=AB P ，)(1)()()()(B P B A P B P B A P B A P -== )(1)]()()([1B P AB P B P A P --+-=127=．【注】条件概率的计算通常与概率的性质结合使用．【技巧】在计算过程中，只要有概率的性质可以用，就一直用概率的性质计算，直到没有概率的性质可用时，对得到的式子进行化简整理，代入已知数据计算．2.乘法公式定理1(乘法公式)(1)若0)(>B P ，则)()()(B A P B P AB P =．(2)若0)(121>-n A A A P ，则)()()()()(12121312121-=n n n A A A A P A A A P A A P A P A A A P ．【例2】一批零件共100个，次品率为10%，每次从其中任取一个零件，取出的零件不再放回，求第三次才取得合格品的概率．【解】设=i A {第i 次取得合格品}，3,2,1=i ．由题意知，所求概率为)(321A A A P ，易知10010)(1=A P ，999)(12=A A P ，9890)(213=A A A P ．由此得)()()()(213121321A A A P A A P A P A A A P =0083.0989099910010≈⋅⋅=．3.全概率公式定义2设Ω为试验E 的样本空间，1B ，2B ，…，n B 为E 的一组事件．如果=j i B B ∅，j i ≠，n j i ,,2,1, =且Ω=n B B B 21，则称1B ，2B ，…，n B 为样本空间Ω的一个划分．定理2(全概率公式)设1B ，2B ，…，n B 为样本空间Ω的一个划分，若0)(>i B P ，n i ,,2,1 =，则对任一事件A 有)()()(1i ni i B A P B P A P ∑==．4.贝叶斯公式定理3(贝叶斯公式)设1B ，2B ，…，n B 为样本空间Ω的一个划分，若0)(>A P ，0)(>i B P ，n i ,,2,1 =，则∑==n i j j i i i B A P B P B A P B P A B P 1)()()()()(，n i ,,2,1 =．【例3】一批同型号的零件由编号为Ⅰ、Ⅱ、Ⅲ的三台机器共同生产，各台机器生产的零件占这批零件的比例分别为35%、40%和25%，各台机器生产的零件的次品率分别为3%、2%和1%．(1)求该批零件的次品率；(2)现从该批零件中抽到一颗次品，试问这颗零件由Ⅰ号机器生产的概率是多少？【解】设=A {零件是次品}，=1B {零件由Ⅰ号机器生产}，=2B {零件由Ⅱ号机器生产}，=3B {零件由Ⅲ号机器生产}，则由题设知35.0)(1=B P ，4.0)(2=B P ，25.0)(3=B P ，03.0)(1=B A P ，02.0)(2=B A P ，01.0)(3=B A P ．(1)题目要求的是)(A P ，由全概率公式，得∑==31)()()(i i i B A P B P A P 021.0=．(2)题目要求的是)(1A B P ，由贝叶斯公式，得21)|()()|()()(31111==∑=i i i B A P B P B A P B P A B P ．【例4】有甲、乙、丙三厂同时生产某种产品．甲、乙、丙三厂的产量之比为1：1：3，次品率分别为4%，3%，2%．(1)若从一批产品中随机抽出一件，求这件产品为次品的概率．(2)若产品的售后部门接到一名顾客投诉，说其购买的产品为次品，请问哪个厂最该为此事负责，为什么？【解】设=A {产品为次品}，=1B {产品由甲厂生产}，=2B {产品由乙厂生产}，=3B {产品由丙厂生产}，则由题设知，2.0)(1=B P ，2.0)(2=B P ，6.0)(3=B P ，04.0)(1=B A P ，03.0)(2=B A P ，02.0)(3=B A P ．(1)题目要求的是)(A P ，由全概率公式，得∑==31)()()(i i i B A P B P A P 026.0=．(2)由贝叶斯公式，得134)|()()|()()(31111==∑=i i i B A P B P B A P B P A B P ，133)|()()|()()(31222==∑=i i i B A P B P B A P B P A B P ，136)|()()|()()(31333==∑=i i i B A P B P B A P B P A B P ．所以在产品为次品的情况下，产品来自丙厂的可能性最大，丙厂最该负责．【注】全概率公式与贝叶斯公式通常一起考试．(四)独立性1.两个事件的独立性定义1若)()()(B P A P AB P =成立，则称事件A 与事件B 相互独立，简称A 与B 独立．否则称A 与B 不独立或相依．定理1若事件A 与B 独立，则A 与B 独立；A 与B 独立；A 与B 独立．【例1】甲、乙两人彼此独立的向同一个目标射击，甲击中目标的概率为0.9，乙击中目标的概率为0.8，求目标被击中的概率．【解】设=A {甲击中目标}，=B {乙击中目标}，则=B A {目标被击中}．则)()()()(AB P B P A P B A P -+= )()()()(B P A P B P A P -+=98.0=．【例2】若事件A 与B 相互独立，8.0)(=A P ，6.0)(=B P ，求：)(B A P 和)|(B A A P ．【解】∵A 与B 相互独立，∴)()()()(AB P B P A P B A P -+= )()()()(B P A P B P A P -+=92.0=．)())(()|(B A P B A A P B A A P =)()()()()(B A P B P A P B A P B A P ==13.0=．【例3】设)()(B A P B A P =，证明：A 与B 相互独立．【证】因为)()(B A P B A P =，所以有)(1)()()(1)()()()()(B P AB P A P B P B A P B P B A P B P AB P --=--==，即有)]()()[()](1)[(AB P A P B P B P AB P -=-，整理得)()()(B P A P AB P =，所以A 与B 相互独立．2.多个事件的相互独立性定义2设A ，B ，C 是三个事件，若有⎪⎩⎪⎨⎧===)()()()()()()()()(C P B P BC P C P A P AC P B P A P AB P (1)第11页共11页则称A ，B ，C 两两独立．若还有)()()()(C P B P A P ABC P =，(2)则称A ，B ，C 相互独立．注意：只有(1)式与(2)式同时成立，事件A ，B ，C 才相互独立．(1)式成立不能保证(2)式成立；反过来，(2)式成立也不能保证(1)式成立．定义3设有n 个事件1A ，2A ，…，n A ，对任意的n k j i ≤<<<≤ 1，若以下等式均成立⎪⎪⎩⎪⎪⎨⎧===)()()()()()()()()()()(2121n n k j i k j i j i j i A P A P A P A A A P A P A P A P A A A P A P A P A A P 则称此n 个事件1A ，2A ，…，n A 相互独立．定理2如果n (2≥n )个事件1A ，2A ，…，n A 相互独立，则其中任何m (n m ≤≤1)个事件换成相应的对立事件，形成的n 个新的事件仍相互独立．【例4】三人独立地去破译一份密码，已知各人能译出的概率分别为51，31，41，问三人中至少有一人能将此密码译出的概率是多少？【解】设A ，B ，C 分别表示三人独立译出密码，则51)(=A P ，31)(=B P ，41)(=C P ，且A ，B ，C 相互独立，有方法1：)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++= )()()()()()()()()()()()(C P B P A P C P B P C P A P B P A P C P B P A P +---++=6.0=．方法2：)(1)(C B A P C B A P -=(1C B A P -=()()(1C P B P A P -=53411)(311)(511(1=----=．。
《概率论与数理统计》总复习资料
《概率论与数理统计》总复习资料概率论部分1．古典概型中计算概率用到的基本的计数方法。
例1：袋中有4个白球，5个黑球，6个红球，从中任意取出9个球，求取出的9个球中有1个白球、3个黑球、5个红球的概率.解：设B ＝｛取出的9个球中有1个白球、3个黑球、5个红球｝样本空间的样本点总数：915C n ==5005事件B 包含的样本点：563514C C C r ==240，则P (B )=240/5005=0.048例2：在0～9十个整数中任取四个，能排成一个四位偶数的概率是多少？解：考虑次序.基本事件总数为：410A =5040，设B ={能排成一个四位偶数}。
若允许千位数为0，此时个位数可在0、2、4、6、8这五个数字中任选其一，共有5种选法；其余三位数则在余下的九个数字中任选，有39A 种选法；从而共有539A =2520个。
其中，千位数为0的“四位偶数”有多少个？此时个位数只能在2、4、6、8这四个数字中任选其一，有4种选法；十位数与百位数在余下的八个数字中任选两个，有28A 种选法；从而共有428A =224个。
因此410283945)(A A A B P -==2296/5040=0.4562．概率的基本性质、条件概率、加法、乘法公式的应用；掌握事件独立性的概念及性质。
例1：事件A 与B 相互独立，且P (A )=0.5，P (B )=0.6，求：P (AB )，P (A －B )，P (A B )解：P (AB )=P (A )P (B )=0.3，P (A －B )=P (A )－P (AB )=0.2，P (A B )=P (A )＋P (B )－P (AB )=0.8例2：若P (A )=0.4，P (B )=0.7，P (AB )=0.3，求：P (A －B )，P (A B )，)|(B A P ，)|(B A P ，)|(B A P 解：P (A －B )=0.1，P (A B )=0.8，)|(B A P =)()(B P AB P =3/7，)|(B A P =)()()()()(B P AB P B P B P B A P -==4/7，|(B A P =)(1)()()(B P B A P B P B A P -==2/33．准确地选择和运用全概率公式与贝叶斯公式。
概率论与数理统计期末总复习
1 (样本 X1, X2,…, Xn的r 阶矩为 Ar X ir ，r 1, 2, , k ) n i 1 得未知参数 1, ,k 的矩估计量: ˆ ˆ 1 1 ( A1 , A2 , , Ak ) ˆ ˆ k k ( A1 , A2 , , Ak )
上页
下页
返回
结束
第七章
1.点估计的方法
(1)矩估计法步骤：
(1) 求出总体的各 阶原点矩,
E ( X ) i x f ( x;1 , 2 ,, k )dx
i
i
或
E ( X i ) i x j i p( x j ;1 , 2 , , k )
j
(i 1, 2 k )
3. 正态总体均值与方差的区间估计 (P28 13 P29－30 14、 15、16 、17)
上页
下页
返回
结束
上页 下页 返回 结束
n
(2)极大似然估计的步骤： 1. 写出似然函数
L(1 , 2 , k ) f ( xi , 1 , 2 , k )
i 1
n
2. 似然函数 L(1 , 2 , k ) 取对数函数
ln L(1 , 2 , k ) ln f ( xi , 1 , 2 , k )
2
n
LXY
n 1 n ( xi x )( yi y ) x i y i x i y i n i 1 i 1 i 1 i 1
n
上页
下页
返回
结束
2.求一元线性回归方程 (P35 3(2)) (1) 根据样本观察值求回归系数
非常全面的《概率论与数理统计》复习材料
非常全面的《概率论与数理统计》复习材料一、基本概念1、随机事件随机事件是指在一定条件下，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件。
例如，掷一枚骰子，出现点数为 6就是一个随机事件。
2、样本空间样本空间是指随机试验的所有可能结果组成的集合。
例如，掷一枚骰子的样本空间就是｛1, 2, 3, 4, 5, 6}。
3、概率概率是用来衡量随机事件发生可能性大小的数值。
概率的取值范围在 0 到 1 之间，0 表示不可能事件，1 表示必然事件。
4、条件概率条件概率是指在已知某一事件发生的条件下，另一事件发生的概率。
二、随机变量1、离散型随机变量离散型随机变量是指其取值可以一一列举的随机变量。
例如，掷一枚骰子出现的点数就是一个离散型随机变量。
2、连续型随机变量连续型随机变量是指其取值充满某个区间的随机变量。
例如，某地区一天的气温就是一个连续型随机变量。
3、随机变量的分布函数分布函数是描述随机变量取值概率分布的函数。
4、常见的离散型分布（1）二项分布：描述 n 次独立重复试验中成功的次数。
（2）泊松分布：常用于描述在一定时间或空间内稀有事件发生的次数。
5、常见的连续型分布（1）正态分布：在自然界和社会现象中广泛存在，具有重要的地位。
（2）均匀分布：在某个区间内取值的概率相等。
三、数字特征1、数学期望数学期望反映了随机变量取值的平均水平。
2、方差方差衡量了随机变量取值的离散程度。
3、协方差和相关系数用于描述两个随机变量之间的线性关系程度。
四、大数定律和中心极限定理1、大数定律表明随着试验次数的增加，样本均值趋近于总体均值。
2、中心极限定理指出大量独立随机变量的和近似服从正态分布。
五、抽样分布1、样本均值和样本方差的分布了解样本均值和样本方差在不同条件下的分布规律。
2、 t 分布、F 分布和χ²分布这三种分布在假设检验和参数估计中经常用到。
六、参数估计1、点估计通过样本数据估计总体参数的值。
概率论与数理统计期末复习知识点
fZ(z)
f (z y, y)dy
f (x, z x)dx
当X 和Y 相互独立:卷积公式
fZ (z) f X ( x) fY (z x)dx
f X (z y) fY ( y)dy
(2) 当X 和Y 相互独立时:
M = max(X,Y ) 的分布函数
Fmax(z) P{M z} FX (z)FY (z)
E(Y ) E[g( X )] g( xk )pk k 1
(1-3)设( X,Y ) 离散型随机变量. 分布律为：
P{X xi , Y y j } pij i, j 1,2,
若 Z=g(X,Y)（g为二元连续函数）
则 E(Z ) E[g( X ,Y )]
g( xi , y j )pij
(2) 连续型随机变量的分布函数的定义
x
F ( x) f (t)dt
f(x)的性质
1. f (x) 0
2. f ( x)dx 1
3. P{x1 X x2}
x2 f ( x)dx
x1
4. F( x) f ( x)，在f ( x)的连续点.
⁂ 三种重要的连续型随机变量
(一)均匀分布
pi1
p•1
pi2
p•2
pij pi•
p• j 1
性质：
1 0 pij 1
2
pij 1.
j 1 i1
2.边缘分布律
3. 独立性
pij pi• p• j , ( i, j 1,2, )
4.分布函数 ( x, y) R2
F ( x, y) pij xi x yjy
n
n
则
Ai Ai
Ai Ai
i 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
概率论与数理统计期末复习资料一 填空1．设A ，B 为两个随机事件，若A 发生必然导致B 发生，且P (A )=0.6，则P (AB ) =______． 2．设随机事件A 与B 相互独立，且P (A )=0.7，P (A -B )=0.3，则P (B ) = ______．3．己知10件产品中有2件次品，从该产品中任意取3件，则恰好取到一件次品的概率等于______．4．已知某地区的人群吸烟的概率是0.2，不吸烟的概率是0.8，若吸烟使人患某种疾病的概率为0.008，不吸烟使人患该种疾病的概率是0.001，则该人群患这种疾病的概率等于______．5．设连续型随机变量X 的概率密度为⎩⎨⎧≤≤=,,0;10,1)(其他x x f 则当10≤≤x 时，X 的分布函数F (x )= ______．6．设随机变量X ～N (1，32)，则P{-2≤ X ≤4}=______．(附：)1(Φ=0.8413) 7．设二维随机变量(X ，Y )的分布律为则P {X <1,Y 2≤}=______．8．设随机变量X 的期望E (X )=2，方差D (X )=4，随机变量Y 的期望E (Y )=4，方差D (Y )=9，又E (XY )=10，则X ，Y 的相关系数ρ= ______．9．设随机变量X 服从二项分布)31,3(B ，则E (X 2)= ______．10．中心极限定理证明了在很一般条件下，无论随机变量Xi 服从什么分布，当n →∞时，∑=ni iX1的极限分布是_________________11．设总体X ～N (1，4)，x 1，x 2，…，x 10为来自该总体的样本，∑==101101i ixx ，则)(x D = ______.·12．设总体X ～N (0，1)，x 1，x 2，…，x 5为来自该总体的样本，则∑=512i ix服从自由度为______的2χ分布．15．对假设检验问题H 0：μ=μ0，H 1：μ≠μ0，若给定显著水平0.05，则该检验犯第一类错误的概率为______． 16．设A ，B 为两个随机事件，且A 与B 相互独立，P （A ）=0.3，P （B ）=0.4，则P （A B ）=__________.17．盒中有4个棋子，其中2个白子，2个黑子，今有1人随机地从盒中取出2个棋子，则这2个棋子颜色相同的概率为_________.18．设随机变量X 的概率密度⎪⎩⎪⎨⎧≤≤=,,0;10,A )(2其他x x x f 则常数A=_________.,22．设二维随机变量（X ，Y ）的概率密度为⎪⎩⎪⎨⎧≤≤-≤≤-=,,0;11,11,41),(其他y x y x f 则P{0≤X ≤1,0≤Y ≤1}=___________.23．设二维随机变量（X ，Y ）的分布律为Y X 1231 261 121 81 81 41 41 则P{Y=2}=___________.24．设随机变量X ~ B ⎪⎭⎫⎝⎛31,18，则D （X ）=_________.25．设随机变量X 的概率密度为⎩⎨⎧≤≤=,,0;10,2)(其他x x x f 则E （X ）=________.27．中心极限定理证明了在很一般条件下，无论随机变量Xi 服从什么分布，当n →∞时，∑=ni iX1的极限分布是_________________28．设总体X 的概率密度为⎪⎩⎪⎨⎧<=.,0;1||,23)(2其他x x x f x 1 , x 2 , … , x n 为来自总体X 的一个样本，x 为样本均值，则E （x ）=____________.29．设x 1 , x 2 , … , x 25来自总体X 的一个样本，X ~ N （25,μ），则μ的置信度为0.90的置信区间长度为____________.（附：u 0.05=1.645）30．设总体X 服从参数为λ（λ>0）的泊松分布，x 1 , x 2 , … , x n 为X 的一个样本，其样本均值2=x ，则λ的矩估计值λˆ=__________. 31. 100件产品中有10件次品，不放回地从中接连取两次，每次取一个产品，则第二次取到次品的概率为________ 32. 设A ，B 为随机事件，且()0.8P A =，()0.4P B =，(|A)0.25P B =，则(A|B)P =_______ 34. 设连续型随机变量X 的分布 函数为()F x = 31xe-- x>0 ， 则{1}P X ≤=________0 x 035. 设随机变量~()X P λ，且1{0}P X e -==，则{}(1,2,)P X k k ==…=_________ 36. 设随机变量X 的分布律为P 2C 0.4 C记2Y X =，则{4}P Y ≥=_________38. 设二维随机变量(,)X Y 服从区域G ：02x ≤≤，02y ≤≤上的均匀分布，则{1,1}P X Y ≤≤=________ 39. 设二维随机变量(,)X Y 的概率密度为(,)f x y = (2)2x y e -+ x>0，y>0 ， 则(,)X Y0 其他的分布函数为________则()E XY =________41. 设随机变量X 的数学期望()E X 与方差()D X 都存在，且有()10E X =，2()109E X =，试由切比雪夫不等式估计{|10|6}P X -≥≤_________42. 设随机变量~(0,1)X N ，2~()Y x n ，且X ，Y 相互独立，则~Z =________ 43. 由来自正态总体~(,0.09)N N μ、容量为15的简单随机样本，得样本均值为2.88，则μ的置信度0.95的置信区间是__________0.0250.05( 1.96, 1.645)μμ==44. 设α，β分别是假设检验中犯第一、二类错误的概率，0H ，1H 分别为原假设和备择假设，则00{H |H }P 拒绝不真=_________45. 已知一元线性回归方程为)º04y x β=+，且3x =，6y =，则º0β=________二 选择1．设A ，B 为两个互不相容事件，则下列各式错误．．的是（ ） A ．P （AB ）=0B ．P （A ∪B ）=P （A ）+P （B ）C ．P （AB ）=P （A ）P （B ）D ．P （B-A ）=P （B ）2．设事件A ，B 相互独立，且P （A ）=31，P （B ）>0，则P （A|B ）=（ ）A ．151 B ．51 C ．154 D ．31 3．设随机变量X 在[-1，2]上服从均匀分布，则随机变量X 的概率密度f （x ）为（ ）A ．⎪⎩⎪⎨⎧≤≤-=.,0;21,31)(其他x x f B ．⎩⎨⎧≤≤-=.,0;21,3)(其他x x fC ．⎩⎨⎧≤≤-=.,0;21,1)(其他x x fD ． ⎪⎩⎪⎨⎧≤≤--=.,0;21,31)(其他x x f4．设随机变量X ~ B ⎪⎭⎫⎝⎛31,3，则P{X ≥1}=（ ）A ．271 B ．278 C ．2719 D ．2726 5．设二维随机变量（X ，Y ）的分布律为则P{XY=2}=（ ） A ．51 B ．103 C ．21 D ．53 6．设二维随机变量（X ，Y ）的概率密度为⎩⎨⎧≤≤≤≤=,,0;10,10,4),(其他y x xy y x f则当0≤y ≤1时，（X ，Y ）关于Y 的边缘概率密度为f Y （ y ）= （ ） A ．x 21B ．2xC ．y21D ．2y7．设二维随机变量（X ，Y ）的分布律为则E （XY ）=（ ） A ．91- B ．0C ．91 D ．31 9．设x 1, x 2, …, x 100为来自总体X ~ N （0，42）的一个样本，以x 表示样本均值，则x ~（ ） A ．N （0，16） B ．N （0，0.16） C ．N （0，0.04） D ．N （0，1.6）10．要检验变量y 和x 之间的线性关系是否显著，即考察由一组观测数据（x i ，y i ），i =1，2，…，n ，得到的回归方程x y 10ˆˆˆββ+=是否有实际意义，需要检验假设（ ） A ．0∶,00100≠=ββH H ∶ B ．0∶,0∶1110≠=ββH H C ．0ˆ∶,0ˆ∶0100≠=ββH H D ．0ˆ∶,0ˆ∶1110≠=ββH H 11．设A 与B 是任意两个互不相容事件，则下列结论中正确的是（ ） A ．P (A )=1-P (B ) B ．P (A -B )=P (B ) C ．P (AB )=P (A )P (B )D ．P (A -B )=P (A )12．设A ，B 为两个随机事件，且0)(,>⊂B P A B ，则P (A |B )=（ ） A ．1 B ．P (A ) C ．P (B )D ．P (AB )13．下列函数中可作为随机变量分布函数的是（ ） A ．⎩⎨⎧≤≤=.,0;10,1)(1其他x x F 1B ．⎪⎩⎪⎨⎧≥<≤<-=.1,1;10,;0,1)(2x x x x x FC ．⎪⎩⎪⎨⎧≥<≤<=.1,1;10,;0,0)(3x x x x x FD ．⎪⎩⎪⎨⎧≥<≤<=.1,2;10,;00,0)(4x x x x F15．设二维随机变量(X ，Y)的分布律为且X 与Y 相互独立，则下列结论正确的是（ ） A ．a =0.2，b =0.6 B ．a =-0.1，b =0.9 C ．a =0.4，b =0.4D ．a =0.6，b =0.216．设二维随机变量(X ，Y )的概率密度为f (x ，y )=⎪⎩⎪⎨⎧<<<<,,0;20,20,41其他y x则P{0<X <1，0<Y <1}=（ ）A ．41B ．21 C ．43 D ．117．设随机变量X 服从参数为21的指数分布，则E (X )=（ ） A ．41 B ．21 C ．2 D ．418．设随机变量X 与Y 相互独立，且X ～N (0，9)，Y ～N (0，1)，令Z =X -2Y ，则D (Z )=（ ） A ．5 B ．7 C ．11D ．1319．设(X ，Y )为二维随机变量，且D (X )>0，D (Y )>0，则下列等式成立的是（ ） A ．)()()(Y E X E XY E ⋅= B ．)()(Cov Y D X D (X,Y)XY ⋅⋅=ρ C ．)()()(Y D X D Y X D +=+D ．),(Cov 2)2,2(Cov Y X Y X =20．设总体X 服从正态分布N(2,σμ)，其中2σ未知．x 1，x 2，…，x n 为来自该总体的样本，x 为样本均值，s 为样本标准差，欲检验假设H 0：μ=μ0，H 1：μ≠μ0，则检验统计量为（ ） A ．σμ0-x n B ．sx nμ- C ．)(10μ--x n D ．)(0μ-x n21.设A 、B 为随机事件，且A B ⊂，则AB =（ ）A ．AB. BC. A B ⋃D. AB22. 对于任意两事件A ，B ，()P A B -=（ ）A ． ()()P A PB -B. ()()()P A P B P AB -+C. ()()P A P AB -D. ()()()P A P A P AB --23. 设随机变量X 的分布律为1{}()2n P X n a ==，(1,2,)n =…则a=（ ） A ．1B.12C. 2D. 324. 设随机变量2~(1,2)X N ，(1)Φ=0.8413，则{13}P X ≤≤=（ ） A ．0.1385B. 0.2413C. 0.2934D. 0.341325. 设二维随机变量()X Y 、的联合分布律为 XY 0120 14 14 112 1 112 16 0 2112112则{0}P X ==（ ） A ．14B.13C.512D.71226. 设二位随机变量()X Y 、的概率密度为()f x y =、 x y + 0x 1，0y 1 ， 0 其他 则{}P X Y <=（ ） A ．13B.23C.12D.1427．设随机变量~(0,1)X N ，~(0,1)Y N ，令Z X Y =+，则有（ ） A ．()0E Z =B. ()2E Z =C. ()0D Z =D. ()2D Z =28. 设总体~(0,1)X N ，1,2,(1)X X Xn n >…来自X 的一个样本，X ，S 分别是样本均值与样本方差，则有（ ）A ．~(0,1)X N B. ~(0,1)nX N C.221~()ni i X x n =∑ D.~(1)Xt n S- 29．设1X ，2X 来自任意总体X 的一个容量为2的样本，则在下列()E X 的无偏估计量中，最有效的估计量是（ ）A ．211233X X + B. 131244X X + C. 231255X X + D. 111222X X + 30. 对非正态总体X ，当样本容量50n ≥时，对总体均值进行假设检验就可采用（ ）A ．u 检验 B. t 检验 C. 2x 检验 D. F 检验三、综合应用 1、设变量y 与x 的观测数据在某条直线的附近已知∑∑∑∑==========1012101101101.8250,88700,350101,25,101i i i i i i i i i x y x y y x x试用最小二乘法建立y 对x 的线性回归方程．2．设一批产品中有85％的合格品，且在合格品中一等品的占有率为65％． 求：(1)从该批产品中任取1件，其为一等品的概率；(2)在取出的1件产品不是一等品的条件下，其为不合格品的概率．3．某气象站天气预报的准确率为0.9，且各次预报之间相互独立.试求： （1）6次预报全部准确的概率p 1； （2）6次预报中至少有1次准确的概率p 2.已知E （X ）=0.2，试求：4．设离散型随机变量X 的分布律为 ,且（1）p 1和p 2; （2）D （6X-3）.5．设某厂生产的零件长度X ～N (2,σμ)(单位：mm)，现从生产出的一批零件中随机抽取了10件，经测量并算得零件长度的平均值x =2000，标准差s =150，如果2σ未知，在显著水平05.0=α下，是否可以认为该厂生产的零件的平均长度是2015mm? （t 0.025(15)=2.131）。