静电场二
10真空中的静电场二解答
2 0 sin q cos q i sin q j d q E d E y 4 R 0 0 Rdq 2 sin q cos q d q 0 , sin d q 2 R q
q
0
q q q q
指向缺口
R
o
d
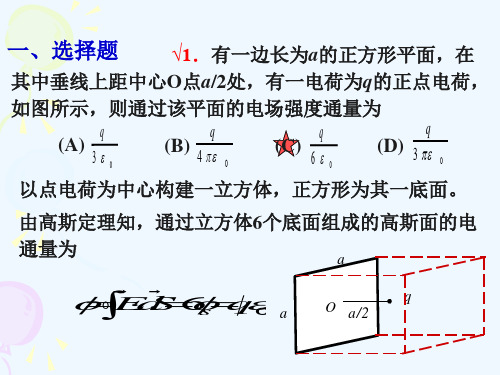
2.一均匀带电直线长为d,电荷线密度为+,以导线 中点O为球心,R为半径(R>d)作一球面,P为带电直 线延长线与球面交点,如图所示.则通过该球面的电场 强度通量为 .P点电场强度的大小为 ; 方向为 . q d i E dS R e 0 0 S E O d2
dx E i 2 4 R x d2 0
P
d
1 1 d i i 2 2 d d 4 R d 0 04 R R 2 2
x
3.地球表面上晴空时,地球表面以上10km范围内的 电场强度都约为100V/m。此电场的能量密度为 ; 在该范围内电场所储存的能量共有 kw· h。
3 1 (C) 4 0l 3 q
(B)
1 5 4 0l 5 q
D l C l l -q B l
E F
5 1 (D) 4 0l 5 q
A +q
题图 q q q 1-1 q A q CF CF C F 4 l 4 l 4 5 l 0 0 0
1.如图,一半径为R的带有一缺口的细圆环,缺口长 度为d(d<<R).环上均匀带正电,总电量为q.则圆 心O处的场强大小E= .场强方向为 .
d q d qd E 4 R2 R d 4 R8 R
大学物理第10章 电荷和静电场-2
例如 孤立的导体球的电容
Q
Q C V
地球
Q Q 4π 0 R
4π 0 R
6
R
4
RE 6.4 10 m, CE 7 10 F
二 电容器
导体组合,使之不受周 围导体的影响 ——电容器
电容器的电容:
当电容器的两极板分
别带有等值异号电荷Q时 ,电量Q与两极板间相应 的电势差VA-VB的比值。
详细说明如下
二、导体表面的电荷和电场 导体表面电荷的分布与导体本身的形状以及附近 带电体的状况等多种因素有关。
孤立导体的电荷面密度与其表面的曲率有关,曲率越大 电荷面密度越大。 表面突出尖锐部分曲率大, 电荷面密度大;
表面比较平坦部分曲率小, 电荷面密度小; 表面凹进部分曲率为负, 电荷面密度最小。
S
–q'
说明空腔内表面所带总电量与空腔内带电体的电量 相等、符号相反。导体空腔是等势体,腔内场强不 为零,不是等电势区间。
四、导体静电平衡性质的应用
1. 静电屏蔽 (electrostatic shielding)
+q +q +q
-q
-q
利用导体静电平衡的性质,使导体空腔内部空 间不受腔外电荷和电场的影响,或者将导体空腔 接地,使腔外空间免受腔内电荷和电场影响,这 类操作都称为静电屏蔽。无线电技术中有广泛应 用,例如,常把测量仪器或整个实验室用金属壳 或金属网罩起来,使测量免受外部电场的影响。
Cn
VB
等效
VA
C
VB
令 U VA VB
q1 C1U
q2 C2U
•导导体表面外附近的场强 E 0
★ 注意:
E 仅由 S 处电荷产生而与其它电荷无关吗?为什么?
用模拟法测绘静电场(2)

矢量E, 根据U
,可以通过标量电势的分布,求得电强度的分
布。对于较复杂的电场需要通过实验来测量电势的分布。因此,等势
线的描绘是研究电场的基础。
然而真正的静电场不能用电表直接测量。因此考虑把带电体放 在导电介质,维持带电体间的电势差不变。理论和实验都证明,导电 介质里由恒定电流产生的电场与静电场的规律完全相似。因此可以用 稳恒电流场来模拟静电场,这叫模拟法。
总电阻为(半径a到b之间圆柱片的电阻)
R ra rb
2 t
ln
rb ra
设Ub=0,则两圆柱面间所加电压为Ua,径向电流为
距轴线r处的电势为
I U a 2 tU a Rrarb ln rb ra
ln rb
U r
IRrrb
Ua
r ln rb
ra
由以上分析可见,Ur与Ur,Er与Er的分布函数完全相同。即长直同轴
大学物理实验
实验四
用模 拟 法 测 绘 静 电 场
内容
实验意义 实验目的 实验原理
实验仪器 实验操作 实验报告
一、实验意义
在带电物体周围存在着电场,带电体通过场相互作用。
知道场的分布,就可以计算出带电体之间相互作用力的大小,并根据
一定的初始条件求得带电体的运动规律或者形变的大小。因此,测量
电场有重要的物理意义。电场强度是用来描述电场分布大小和方向的
U (r)
r
b
a
U (a)
b
根据模拟原理,讨论稳恒电流场的分布(如图3-3)。取厚度
为t的圆柱形同轴不良导体片为研究对象。设材料电阻率为,则任意半
径r到r+dr的圆周间的电阻是 dR
dr
dr
dr
静电场2
8
3)求积分 3)求积分
E = Exi
y
dq Q
E x = ∫ dE x
R
r
o
θ
p
x
dEy
dEx dE
x
dEx = dE cos θ cos θ =
Ex = ∫ dEx =
z
2
x x +R
2
,
xλ
dE =
l 3
1
1
λ dl
2 2
4πε 0 x + R
0 2
1
4πε 0 ( x 2 + R 2 )
2
P
E
dS⊥
dN ∝ EdS⊥
静电场中电场线的性质: 静电场中电场线的性质: 中电场线的性质 有头(源)有尾, 由+(或∞)指向(或∞) 有头( 有尾, +(或 指向 无电荷处不中断 不闭合, 不相交 不闭合,
dN → E∝ dS⊥
18
线分布: 几种电荷的 E 线分布:
带正电的点电荷
电偶极子
均匀带电的直线段
一个点电荷所产生的电场, 一个点电荷所产生的电场,在以点电荷为 中心的任意球面的电通量等于 q
ε0
25
点电荷q被 点电荷 被 任意曲面 曲面包围 任意曲面包围
q dS ' q r dS q dΦE = = = d 2 2 4πε 0 r 4πε 0 r 4πε 0
对整个闭合面S有 对整个闭合面 有
p
dE x E
α
x
θ1
dE y
dE
λ Ex = 2πε 0 a
Ey = 0
θ2 → π , θ1 → 0 , 有
17
10 静电场2高考真题分项详解(解析板)

十年高考分类汇编专题10静电场2(2011—2020)目录题型一、带电粒子在复合场中的运动 ................................................................................................ 1 题型二、带电粒子在纯电场、复合场中运动的综合类问题 (5)题型一、带电粒子在复合场中的运动1.(2019天津)如图所示,在水平向右的匀强电场中,质量为m 的带电小球,以初速度v 从M 点竖直向上运动,通过N 点时,速度大小为2v ,方向与电场方向相反,则小球从M 运动到N 的过程( )A .动能增加212mvB .机械能增加22mv C .重力势能增加232mv D .电势能增加22mv【考点】:功能关系、动能定理、运动的独立性、电场力做功【答案】:C【解析】:小球的动能增加量为2222321)2(21mv mv v m E E KM KN =-=-;故A 错误;除重力外其它力对小球做功的大小为小球机械能的增加量,在本题中电场力对小球做功的大小为小球机械能的增加量,在水平方向上研究小球可知电场力对其做正功,电势能减小,可求得电场力对小球做功大小为小球水平方向动能的增量2221)(v m ;即小球的机械能增加了22mv ;电势能减小了22mv ;故B 对,D 错;从M 点到N 点对小球应用动能定理得:2221)2(21mv v m W W G D -=-;又22mv W D =;可求得221mv W G =故C 错;2.(2016江苏)如图所示,水平金属板A 、B 分别与电源两极相连,带电油滴处于静止状态.现将B 板右端向下移动一小段距离,两金属板表面仍均为等势面,则该油滴( )A. 仍然保持静止B. 竖直向下运动C. 向左下方运动D. 向右下方运动【考点】带电粒子在复合场中的运动、受力分析【答案】D【解析】两极板平行时带电粒子处于平衡状态,则重力等于电场力,当下极板旋转时,板间距离增大场强减小,电场力小于重力;由于电场线垂直于金属板表面,所以电荷处的电场线如图所示,所以重力与电场力的合力偏向右下方,故粒子向右下方运动,选项D正确.3.(2013广东)喷墨打印机的简化模型如图所示.重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )A.向负极板偏转B.电势能逐渐增大C.运动轨迹是抛物线D.运动轨迹与带电量无关【考点】带电粒子在复合场中的运动、受力分析、类平抛运动【答案:C】【解析】选C.带电微滴垂直进入电场后,在电场中做类平抛运动,根据平抛运动的分解——水平方向做匀速直线运动和竖直方向做匀加速直线运动.带负电的微滴进入电场后受到向上的静电力,故带电微滴向正极板偏转,选项A错误;带电微滴垂直进入电场受竖直方向的静电力作用,静电力做正功,故墨汁微滴的电势能减小,选项B错误;根据x=v0t,y =12at 2及a =qE m ,得带电微滴的轨迹方程为y =qEx22mv 20,即运动轨迹是抛物线,与带电量有关,选项C 正确,D 错误.4.(2016全国1) 如图,一带负电荷的油滴在匀强电场中运动,其轨迹在竖直面(纸面)内,且相对于过轨迹最低点P 的竖直线对称。
大学物理静电场2电势

各电势的零点应是同一点)
用“点电荷电势叠加的方法”:
对点电荷系:
对有限的 连续电荷分布:
qi
4 π ori
(选
0)
d q
q 4πor
(选 0)
例. 求半径为 R、带电量为 q 的细圆环 轴线上任意点的电势。
【解】 这是连续带电体, 任取一电荷元dq,
用“点电荷电势叠加法”
dq
R 0
r R2 x2 取轴线上任一点 P,电势:
x
x
P
d q
(q)4 π0r
所以
4π 0
q R2 x2
1/ 2
1
dq
4 π0r (q)
思考: 环上电荷均匀或不均匀结果一样吗?
等势面:
电场中电势相等的点组成的面称为等势面。 等势面是形象描述电场的一种表示方法。 画法:相邻等势面的电势差为常数。
例1. 正点电荷电场的等势面。
等势面有如下特点:
2π0 r
r > r0 的点,电势为负,
r = r0 的点,电势为零,
r < r0 的点,电势为正。
r
可以看到,若选无限远为 电势零点,
会使积分发散。
8.4.5 电势叠加原理
由
po
E
d
l
及
E
p
Ei
得 ( po p
Ei ) d l
po p
i Ei
d
l
i
i
i
i
(注意:用电势叠加原理时,
静电势能是属于电荷 q0 和场源所共有的 (正如重力势能是属于物体和地球),
也叫电荷之间的相互作用能。
例 1. 氢原子中的电子在原子核电场中的 静电势能为
静电场二

S
r r dφe = EdS⊥ = E(dS cosθ ) = E ⋅ dS
r dS
θ
dS
1) 通过面元的电通量: 通过面元的电通量:
r E
r r dφe = EdS⊥ = E(dS cosθ ) = E ⋅ dS
θ < θ > θ = π π π
2 2 2 dφe > 0 dφe < 0 dφe = 0
只有S 只有S内电荷有贡献
关于高斯定理的讨论: 关于高斯定理的讨论:
r r 1 ∫ E⋅ dS = ∑q内
s
ε0
2. 揭示了静电场中“场”和“源”的关系 揭示了静电场中“ 电场线有头有尾
+ q : 发出 q ε 0 条电场线,是电场线的“头” 条电场线,是电场线的“ − q : 吸收 q ε 0 条电场线,是电场线的“尾” 条电场线,是电场线的“
高斯面: 高斯面: 的同轴圆柱面,加上底、 取长 L 的同轴圆柱面,加上底、下底构成高斯面 S
λ
dq o dq'
∫∫
S r '
s
r r r r r r r r E ⋅ dS = ∫ E ⋅ dS + ∫ E ⋅ dS + ∫ E ⋅ dS
上 下 侧
L
r
P
dE
r dE
r r' dE+dE
= ∫ E cos dS + ∫ E cos dS + ∫ E cos 0o dS 2 2 上 下 侧 = E ⋅ 2πrL
即其疏密与场强的大小成正比。 即其疏密与场强的大小成正比。
实例: 实例:
+ -
⊕
均匀带电直导线 的 电 场 线
备战2021新高考物理-基础专题-静电场(二)(含解析)

备战2021新高考物理-基础专题-静电场(二)一、单选题1.如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带电粒子,运动轨迹如图中虚线所示.则()A.a一定带正电,b一定带负电B.a的速度将减小,b的速度将增加C.a的加速度将减小,b的加速度将增加D.两个粒子的电势能一个增加一个减小2.均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心初产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R.已知M点的场强大小为E,则N点的场强大小为()A.﹣EB.C.﹣ED.+E3.如图所示,平行板电容器的两个极板为A、B,B板接地,A板带有电荷量+Q,B板带有电荷量﹣Q,板间电场中有一个固定的点P,以下说法正确的是()A.若将B板固定,A板下移时,P点的电场强度不变,P点的电势降低B.若将B板固定,A板下移时,P点的电场强度增大,P点的电势升高C.若将A板固定,B板上移时,P点的电场强度不变,P点的电势降低D.如果A板固定,B板上移时,P点的电场强度增大,P点的电势升高4.如图所示,一个带电粒子从粒子源飘入(初速度很小,可忽略不计)电压为U1的加速电场,经加速后从小孔S沿平行金属板A、B的中线射入,A、B板长为L,相距为d,电压为U2.则带电粒子能从A、B板间飞出应该满足的条件是()A. B. C. D.5.一带负电的微粒只在电场力作用下沿x轴正方向运动,其电势能随位移x变化的关系如图所示,其中0~x1段是曲线,x1~x2段是平行于x轴的直线,x2~x3段是倾斜直线,则下列说法正确的是()A.0~x1段电势逐渐升高B.0~x1段微粒的加速度逐渐减小C.x2~x3段电场强度减小D.x2处的电势比x3处的电势高6.两块大小、形状完全相同的金属平板平行放置,构成一平行板电容器,与它相连接的电路如图所示,接通开关S ,电源即给电容器充电()A.保持S接通,减小两极板间的距离,则两极板间电场的电场强度减小B.保持S接通,减小两极板的正对面积,则极板上的电荷量增大C.充电后断开S ,减小两极板间的距离,则两极板间的电势差增大D.充电后断开S ,减小两极板的正对面积,则两极板间的电势差增大7.如图所示,一个绝缘圆环,当它的均匀带电且电荷量为+q时,圆心O处的电场强度大小为E,现使半圆ABC均匀带电+2q,而另一半圆ADC均匀带电–2q,则圆心O处电场强度的大小和方向为()A.2 E,方向由O指向DB.4E,方向由O指向DC.2 E,方向由O指向BD.08.将一正点电荷从无穷远处移向M点,电场力做功为7.0×10﹣9J,若将一个等量的负电荷从电场中N点移向无穷远处,电场力做功6.0×10﹣9J,设无穷远处电势为零,则M,N两点的电势φM,φN有下列关系()A.φM<φN<0B.φN<φM<0C.φM>φN>0D.φN>φM>09.真空中,两个相距L的固定点电荷P、Q所带的电荷量的绝对值分别为和,在它们共同形成的电场中,有一条电场线如图中实线所示,实线上的箭头表示电场线的方向,电场线上标出了M、N两点,其中过N点的切线与P、Q连线平行,且,则()A.P带负电,Q带正电B.点电荷P、Q所带电荷量的关系为C.在M点由静止释放一带正电的检验电荷,该电荷仅在电场力的作用下有可能沿电场线运动到N点D.带负电的检验电荷在M点的电势能大于在N点的电势能10.空间有一匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标为(0,a,0),,N点的坐标为(a,0,0),P点的坐标为(a,,),已知电场方向平行直线MN,M点电势为0,N点电势为1V,则P点的电势为()A. B. C. D.二、多选题11.如图所示,图中MN是由负点电荷产生的电场中的一条电场线.一带电粒子+q飞入电场后,只在电场力作用下沿图中虚线运动,a、b是该曲线上的两点,则下列说法正确是()A.a点的电场强度小于b点的电场强度B.B.a点的电势低于b点的电势C.粒子在a点的动能小于在b点的动能C.D.粒子在a点的电势能小于在b点的电势能12.汤姆孙利用真空玻璃管测得了电子的电量与质量的比值,叫电子的比荷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q内 ∝ r
2
1 E∝ 2 r
总效果 E 大小为恒量 内
例3. 在半径R1 ,体电荷密度ρ 的均匀带电球体内挖去 在半径 一个半径R 的球形空腔。空腔中心o 与带电球体中心o 一个半径 2的球形空腔。空腔中心 2与带电球体中心 1 相距为a 相距为 [(R2+ a )< R1], r r 求空腔内任一点电场 。 R E 1 E1 2 r P 思考: 选用何种方法求解? 思考:(1) 选用何种方法求解? r r 1 ρ o r r22 o 1a R 失去球对称性, 挖去空腔 —— 失去球对称性 2 能否恢复对称性?补偿法! 能否恢复对称性?补偿法!
S
r r dφe = EdS⊥ = E(dS cosθ ) = E ⋅ dS
r dS
θ
dS
1) 通过面元的电通量: 通过面元的电通量:
r E
r r dφe = EdS⊥ = E(dS cosθ ) = E ⋅ dS
θ < θ > θ = π π π
2 2 2 dφe > 0 dφe < 0 dφe = 0
r r r 才能找到恰当的高斯面,使 E ⋅ d S 中的 E 能够 才能找到恰当的高斯面, ∫
s
r 以标量形式提到积分号外, 分布。 以标量形式提到积分号外,从而简便地求出 E 分布。
球对称性
常见类型: 常见类型: 场源电荷分布
轴对称性 面对称性
[例一] 求均匀带电球体(q、R )的电场分布 例一] 求均匀带电球体( 对称性分析
S
r r 2) 通过曲面 S 的电通量 φ e = ∫sdφ e = ∫s E ⋅ dS r r 3) 通过封闭曲面的电通量 φ e = ∫ E ⋅ d S
s
r n
通过封闭曲面的电通量 r nr r r E φ e = ∫ E ⋅ dS
s
规定:封闭曲面外法向为正 规定:
r n
S
穿入的电场线 穿出的电场线
E内 =
qr 4πε 0 R
3
即:
r E=
r qr ( r ≤ R) 3 4πε 0 R r qr ( r ≥ R) 3 4πε 0 r
球体内区域
E∝r
球体外区域 ~ 电量 集中于球心的点电荷
E
q 4πε 0 R 2
∝r
R
1 ∝ 2 r
r
o
[例2] 求半径 ,电荷体密度 例 求半径R
ρ =k r
R2
R1
计算带电球层( 1 计算带电球层( R , R2, ρ
)
o
ρ
0
的电场分布
E =
ρ R 13 (r − 2 ) ( R1 ≤ r ≤ R 2 ) 3ε 0 r ρ ( R 23 − R 13 ) q = (r ≥ R2 ) 2 2 3ε 0 r 4 πε 0 r
( r ≤ R1 )
R1 R2
φe < 0 φe > 0
练习1 空间有点电荷 练习1:空间有点电荷q ,求下列情况下穿过曲面的电通量 1) 曲面为以电荷为中心的球面 2) 曲面为包围电荷的任意封闭曲面 3) 曲面为不包围电荷的任意封闭曲面
1) 曲面为以电荷为中心的球面
r E
r E
q>0
q > 0 : φe > 0
q<0
r
S
r
S
q < 0 : φe < 0
r r φe = ∫ E ⋅ dS =
∫
r q r0 ⋅ d S q q = dS = 2 2 ∫ 4πε 0 r 4πε 0 r ε0
与 r 无关
单个点电荷场中, 单个点电荷场中,由 +q 发出的电场线延伸到 ∞ , 终止。在无电荷处, 由 ∞ 而来的电场线到 -q 终止。在无电荷处,电场线 不中断、不增加。 不中断、不增加。
r r
R
R
dr ′
S
r
r′ o
ρ
R
<4> 电场强度的大小,方向 ? 电场强度的大小, r r 1 由高斯定理: 由高斯定理: ∫ E ⋅ dS = ∑q 内
s
ε0
E ⋅ 4πr =
2
1
ε0
∑q
内
得:
κ κR2 E = ; E外 = 内 2ε0 2ε0r2
沿径向
〈5〉对结果的定性理解: 〉对结果的定性理解:
r r r r E = E1 + E2 + L + En
S
所有电荷的贡献。 包括 S 内、S 外,所有电荷的贡献。 的电通量: 穿过 S 的电通量:
r r r r r r r r φe = ∫ E ⋅ dS = ∫ E1 ⋅ dS + ∫ E2 ⋅ dS + L + ∫ En ⋅ dS
s
= φe1 + φe 2 + L + φen =
c b 厚度 a 较大
厚度 较小
厚度 为零 球面
E
a b c
E
区 区 区
o R1 R2
E
r
o R R2 1
o R 1= R2
[例4]
无限长均匀带电直线( 无限长均匀带电直线(
λ)的电场
λ
dq
对称性分析: 对称性分析:
S r '
r P点处合场强 E
L
o dq '
r
P
dE
r dE
r r' dE + dE
s
(3) ∑q内 = ?
∑q
内
= ρ ⋅V = ⋅ π r r 3
╳
κ 4
dr ′
3
S
对否 ?
r
r′ o
ρ
R
k dq = ρdV = ⋅ 4πr′2dr′ r′
r > R:
r < R:
k q内 = ∫ ρdV = ∫ ⋅ 4πr′2dr′ = 2πkR2 ∑ r′ 0 0
k ′2dr′ = 2πkr2 ∑q内 = ∫ ρdV = ∫ r′ ⋅ 4πr 0 0
只有S 只有S内电荷有贡献
关于高斯定理的讨论: 关于高斯定理的讨论:
r r 1 ∫ E ⋅ dS = ∑q内
s
ε0
2. 揭示了静电场中“场”和“源”的关系 揭示了静电场中“ 电场线有头有尾
+ q : 发出 q ε 0 条电场线,是电场线的“头” 条电场线,是电场线的“ − q : 吸收 q ε 0 条电场线,是电场线的“尾” 条电场线,是电场线的“
§4.4 静电场的高斯定理
一.电场线
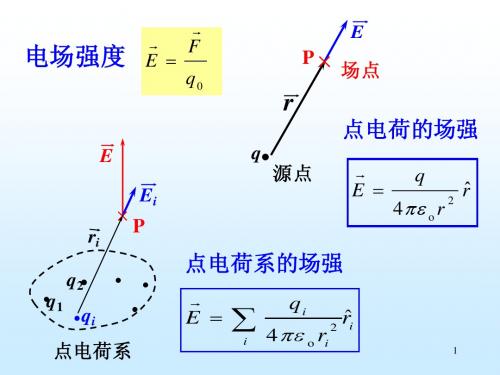
r 定量研究电场: 定量研究电场:对给定场源电荷求出其分布函数 E (r )
定性描述电场整体分布: 定性描述电场整体分布:电场线方法 电 场 线
r 空间矢量函数 E :空间矢量函数
r 其上每点切向: 其上每点切向: 该点 E 方向 r 的单位面积的条数等于场强的大小, 通过垂直 E 的单位面积的条数等于场强的大小,
r' dE
S q
R
dq
o
P
dq′
r r' r dE + dE
dE
为中心, 以 O 为中心,r 为半径的球面 S 上各点彼此等价
r 大小相等 E r E 方向沿径向
确定高斯面 以半径 r 的同心球 面 S 为高斯面
S q
R
dq
r' dE
o
P
dq′
r r' r dE + d E
dE
r r o 2 通过S的电通量 的电通量: 通过S的电通量: ∫ E ⋅ dS = ∫ E cos 0 dS = E ⋅ 4πr
“头”、 “尾” “源”
静电场是有源场 静电场的重要性质 —— 静电场是有源场
关于高斯定理的讨论: 关于高斯定理的讨论:
r r 1 ∫ E ⋅ dS = ∑q内
s
ε0
3. 反映了库仑定律的平方反比关系 4. 利用高斯定理可方便求解具有某些对称分布的静电场 成立条件:静电场 成立条件: 求解条件:电场分布具有某些对称性 求解条件:
即其疏密与场强的大小成正比。 即其疏密与场强的大小成正比。
实例: 实例:线
电偶极子的电场线
r 线分布的实验现象: 几种电荷的 E 线分布的实验现象:
单个点 电 极 极 单个点 电
正负点电极
两个同号的点电极
单个带电平板电极
分别带正负电的平行平板电极
带异号电荷的点电极和平板电极
“怒发冲冠”
二. 电通量 通过电场中某一给定面的电场线的总条数叫做通过 该面的电通量。 该面的电通量。
r dS
θ
dS
r E
r r 面积元矢量: 面积元矢量: dS = dS n
r 面积元范围内 E 视为均匀
微元分析法:以平代曲; 微元分析法:以平代曲; 以不变代变。 以不变代变。 1) 通过面元的电通量: 通过面元的电通量:
1
ε0
∑q
内
的电通量有贡献。 只有 S 内的电荷对穿过 S 的电通量有贡献。
练习3:请总结穿过静电场中任意封闭曲面的电通量 练习 :请总结穿过静电场中任意封闭曲面的电通量 空间电荷分布的关系。 与空间电荷分布的关系。 三 .高斯定理 静电场中,通过任意封闭曲面(高斯面)的电通量 静电场中,通过任意封闭曲面(高斯面) 等于该封闭曲面所包围的电量代数和的 1 ε 0 倍:
( k 为常数 , r ≤ R )带电球体内外的场强 。
ρ
o
R
用高斯定理求解方便 . 选高斯面
S
s
ρ = k r 未破坏电场分布的球对称性。 未破坏电场分布的球对称性。
