江西专用2018中考数学总复习基础知识梳理第7单元圆7.2与圆有关的位置关系课件
中考数学一轮复习 第七章 与圆有关的知识 7.2 与圆有关的位置关系及有关计算(试卷部分)优质课件

则PQ=5k=12.5,∴PH=10,HQ=7.5. 在Rt△POH中,OH= =P2O42. PH 2 ①当点P在O右上方时,如图, x=OQ=OH+HQ=31.5.
6
②当点P在O左上方时,如图, -x=OQ=OH-HQ=16.5,∴x=-16.5.
③当点P在O左下方时,如图, -x=OQ=OH+HQ=31.5,∴x=-31.5.
2
2.(2014河北,19,3分)如图,将长为8 cm的铁丝AB首尾相接围成半径为2 cm的扇形,则S扇形= cm2.
答案 4
解析
由题意可知扇形的周长为8 cm.因为半径r=2 cm,所以弧长l=8-2×2=4(cm),所以S扇形=
1l·r
2
= 1 ×4×2=4(cm2).
2
3
3.(2018河北,25,10分)如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧 A,︵B
中考数学 (河北专用)
§ 7.2 与圆有关的位置关系及有关计算
1
五年中考 A组 2014-2018年河北中考题组
1.(2018河北,15,2分)如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重 合,则图中阴影部分的周长为 ( )
A.4.5 B.4 C.3 D.2 答案 B 如图,连接AI,BI,∵点I为△ABC的内心,∴AI平分∠BAC,BI平分∠ABC,∵AC∥IE,∴ ∠CAI=∠AIE,∴∠EAI=∠AIE,∴AE=EI.同理,BF=FI,∴阴影部分的周长=EI+FI+EF=AE+BF+ EF=AB,∵AB=4,∴阴影部分的周长为4,故选B.
3
情形:点P在O的右上方、左上方、左下方求出x的值.
2018年中考数学必考知识点圆-文档资料

2018中考数学必考知识点-圆2018中考数学必考知识点-圆1圆的重要性质;2直线与圆、圆与圆的位置关系;③3与圆有关的角的定理;4与圆有关的比例线段定理。
一、圆的基本性质1.圆的定义(两种)2.有关概念:弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。
3.“三点定圆”定理4.垂径定理及其推论5.“等对等”定理及其推论5.与圆有关的角:⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理,与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.三种位置及判定与性质:2.切线的性质(重点)3.切线的判定定理(重点)。
圆的切线的判定有⑴…⑵…4.切线长定理三、圆换圆的位置关系1.五种位置关系及判定与性质:(重点:相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线:⑴定义⑵性质四、与圆有关的比例线段1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及计算中心角:内角的一半: (右图)(解Rt△OAM可求出相关元素,、等)六、一组计算公式1.圆周长公式2.圆面积公式3.扇形面积公式4.弧长公式5.弓形面积的计算方法6.圆柱、圆锥的侧面展开图及相关计算七、点的轨迹六条基本轨迹八、有关作图1.作三角形的外接圆、内切圆2.平分已知弧3.作已知两线段的比例中项4.等分圆周:4、8;6、3等分九、基本图形十、重要辅助线1.作半径2.见弦往往作弦心距3.见直径往往作直径上的圆周角4.切点圆心莫忘连5.两圆相切公切线(连心线)6.两圆相交公共弦。
中考数学总复习 第七单元 圆 第29课时 与圆有关的位置关系数学课件

清单
(2)若△ ABC 的三边长分别为 a,b,c,☉I 的半径为 r,则有 S△ ABC= r(a+b+c);
2
1
2
+-
(3)(选学)在△ ABC 中,若∠ACB=90°,AC=b,BC=a, AB=c,则内切圆半径 r=
2
课前双基巩固
对点演练
题组一
[答案] C
必会题
1.如图 29-1,∠O=30°,C 为 OB 上一点,且 OC=6,以点 C 为圆
点 E 在 OD 上,∠DCE=∠B.
(1)求证:CE 是半圆的切线;
2
(2)若 CD=10,tanB= ,求半圆的半径.
3
图 29-12
高频考向探究
解:(1)证明:如图,连接 OC.∵AB 是半圆的直径,AC 是半圆的弦,∴∠ACB=90°.
∵点 D 在弦 AC 的延长线上,∴∠DCB=180°-∠ACB=90°.∴∠DCE+∠BCE=90°.
(1)求∠P 的度数;
(2)连接 PB,若☉O 的半径为 a,写出求△ PBC 面积的思路.
图 29-9
高频考向探究
解:(1)∵PA 切☉O 于点 A,∴PA⊥AB.∴∠P+∠1=90°.∵∠1=∠B+∠2,∴∠P+∠B+∠2=90°.
∵OB=OC,∴∠B=∠2.又∵∠P=∠B,∴∠P=∠B=∠2.∴∠P=30°.
解:(1)证明:如图①,∵DC⊥OA,∴∠1+∠3=90°,
∵BD 为切线,∴OB⊥BD,∴∠2+∠5=90°,∵OA=OB,∴∠1=∠2,
又∵∠3=∠4,∴∠4=∠5,∴DE=DB.
1
(2)如图②,作 DF⊥AB 于 F,连接 OE,∵DB=DE,∴EF= BE=3,
中考数学总复习 第一部分 基础篇 第七章 圆 考点30 与圆有关的位置关系课件.pptx

4
考点三 切线的性质与判定
5
考点四 三角形的外接圆和内切圆
6
真题探源
7
8
9
10
11
12
第一部分 基 础 篇
第七章 圆
30 与圆有关的位置关系
1
目标方向
点和圆、直线和圆都是用量的关系来确定图形 的位置关系,这部分内容的重点在于对切线的判定 和性质的理解应用.点与圆的位置关系多以客观题的 形式考查,而直线与圆的位置关系则是中考热点, 在考查推理论证、操作计算、开放探索以及综合应 用代数与几何各方面知识的能力方面可谓常考常新.
中考数学复习之与圆有关的位置关系,考点过关与基础练习题
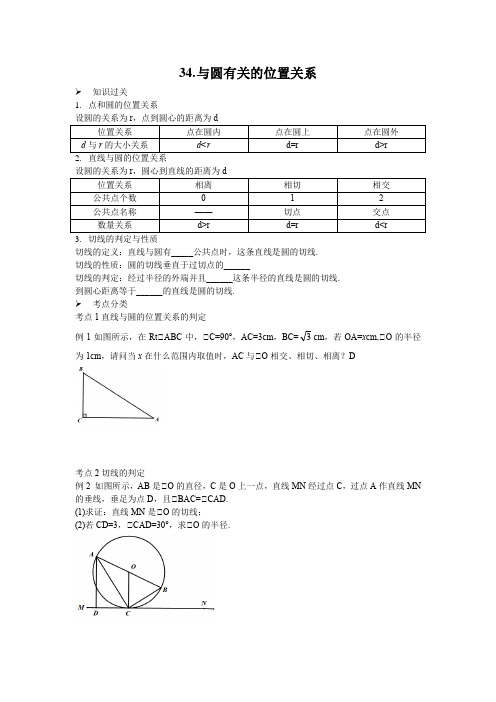
34.与圆有关的位置关系➢知识过关1.点和圆的位置关系2.直线与圆的位置关系3.切线的判定与性质切线的定义:直线与圆有_____公共点时,这条直线是圆的切线.切线的性质:圆的切线垂直于过切点的______切线的判定:经过半径的外端并且______这条半径的直线是圆的切线.到圆心距离等于______的直线是圆的切线.➢考点分类考点1直线与圆的位置关系的判定例1如图所示,在Rt△ABC中,△C=90°,AC=3cm,BC=3cm,若OA=x cm,△O的半径为1cm,请问当x在什么范围内取值时,AC与△O相交、相切、相离?D考点2切线的判定例2 如图所示,AB是△O的直径,C是O上一点,直线MN经过点C,过点A作直线MN 的垂线,垂足为点D,且△BAC=△CAD.(1)求证:直线MN是△O的切线;(2)若CD=3,△CAD=30°,求△O的半径.考点3 切线的性质 例3 如图所示,在△O 中,点C 是直径AB 延长线上一点,过点C 作△O 的切线,切点为D ,连接BD.(1)求证:△A=△BDC(2)若CM 平分△ACD ,且分别交AD 、BD 于点M 、N ,当DM=1时,求MN 的长.➢ 真题演练1.如图,A 、P 、B 、C 是⊙O 上的四点,∠APC =∠BPC =60°,P A =2,PC =4,则△ABC 的面积为( )A .43√3B .32√3C .2√3D .3√32.如图,四边形ABCD 是⊙O 的内接四边形,∠B =90°,∠BCD =120°,AB =4,BC =2,则AD 的长为( )A .2√3B .4−√3C .√3+1D .2+√33.如图,P A 、PB 、CE 分别与⊙O 相切于点A 、B 、D 点,若圆O 的半径为6,OP =10,则△PCE 的周长为( )A .10B .12C .16D .204.如图所示,点P 是⊙O 的半径OC 延长线上的一点,过点P 作⊙O 的切线,切点为A ,AB 是⊙O 的弦,连接AC ,BC ,若∠P AB =70°,则∠ACB 的大小为( )A .70°B .110°C .120°D .140°5.如图,在△ABC 中,∠A =60°,BC =12,若⊙O 与△ABC 的三边分别相切于点D ,E ,F ,且△ABC 的周长为32,则DF 的长为( )A .2B .3C .4D .66.如图,已知DC 是⊙O 的直径,点B 为CD 延长线上一点,AB 是⊙O 的切线,点A 为切点,且∠BAD =35°,则∠ADC =( )A .75°B .65°C .55°D .50°7.如图,PC 、PB 是⊙O 的切线,AB 是⊙O 的直径,延长PC ,与BA 的延长线交于点E ,过C 点作弦CD ,且CD ∥AB ,连接DO 并延长与圆交于点F ,连接CF ,若AE =2,CE =4,则CD 的长度为( )A .3B .4C .185D .2458.如图,四边形ABCD 内接于⊙O ,AE ⊥CB ,交CB 的延长线于点E .若BA 平分∠DBE ,AD =7,CE =√13,则AE 的长度为 .9.如图,四边形ABCD 内接于⊙O ,AB 为直径,AD =CD ,过点D 作DE ⊥AB 于点E ,连接AC 交DE 于点F .若sin ∠CAB =35,DF =5,则AB 的长为 .10.如图,P A、PB分别与⊙O相切于A、B两点,C为⊙O上一点连接AC、BC,若∠C=55°,则∠P的度数是°.11.如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.(1)求CD的长度.(2)求EG的长度.(3)求FB的长度.12.如图,P A、PB、CD是⊙O的切线,点A、B、E为切点.(1)如果△PCD的周长为10,求P A的长;(2)如果∠P=40°,①求∠COD;②连AE,BE,求∠AEB.13.如图,P A、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.(1)求证:∠POA=2∠PCB;(2)若OA=3,P A=4,求tan∠PCB的值.➢ 课后练习1.如图,P A ,PB 是⊙O 的两条切线,A ,B 是切点,过半径OB 的中点C 作CD ⊥OB 交P A 于点D ,若PD =3,AD =5,则⊙O 的半径长为( )A .2√7B .4√2C .3√3D .2√52.如图,等边三角形ABC 的边长为4,⊙C 的半径为√3,P 为AB 边上一动点,过点P 作⊙C 的切线PQ ,切点为Q ,则PQ 的最小值为( )A .12B .√3C .2√3D .33.如图,点O 是矩形ABCD 对角线BD 上的一点,⊙O 经过点C ,且与AB 边相切于点E ,若AB =4,BC =5,则⊙O 的半径长为( )A .165B .258C .5√419D .44.如图,在△ABC 中,∠ACB =90°,AC =BC =√2,点D 是AB 边上一个动点,以点D 为圆心r 为半径作⊙D ,直线BC 与⊙D 切于点E ,若点E 关于CD 的对称点F 恰好落在AB 边上,则r 的值是( )A .√2−1B .1C .√2D .√2+15.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,如果∠D=30°,AB=4,那么线段CD的长是.6.如图,△ABD内接于⊙O,AD为直径,CD为⊙O的切线,连接BC,若CD=AD,AB =2,BC=2√13,则BD=.7.已知菱形ABCD的边长为4,∠BAD=60°,M是线段AD的中点,点P是对角线AC 上的动点,连接PM,以P为圆心,PM长为半径作⊙P,当⊙P与菱形ABCD的边相切时,AP的长为.8.如图,已知△ABC,以AB为直径的⊙O交AC于点E,交BC于点D,且BD=CD,DF ⊥AC于点F.给出以下四个结论:̂=DÊ;④∠A=2∠FDC.①DF是⊙O的切线;②CF=EF;③AE其中正确结论的序号是.9.如图,在Rt△ABC中,AC=BC=6,点O为边BC上一动点,连接OA.以O为圆心,OB为半径作圆,交OA于D,过D作⊙O的切线,交AC于点E.当⊙O与边AC相切时,CE的长为.10.如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=12∠DOQ.若AQ=AC,AD=4时,写出BP的长为.11.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆交于点D.(1)如图1,连接DB,求证:DB=DE;(2)如图2,若∠BAC=60°,求证:AB+AC=√3AD.12.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F.(1)若∠ABC=50°,∠ACB=75°,求∠BOC的度数;(2)若AB=13,BC=11,AC=10,求AF的长.➢冲击A+。
中考数学总复习 基础知识梳理 第7单元 圆 7.2 与圆有关的位置关系课件

12/9/2021
知识体系图
点与圆的位置关系
要点梳理
与圆有关的 位置关系
直线与圆的位置关系
相交 相切 相离
切线的性质、判定 切线长及性质
12/9/2021
7.2.1 点与圆的位置关系
要点梳理
如果圆的半径是r,点到圆心的距离为d,那么:
(1)点在圆外 d>r; (2)点在圆上 d=r; (3)点在圆内 d<r.
经典考题
【解析】设小正方形的边长为1.由点在图形中的位置和勾股定理可 知,OG=1,OE=OF=2,OA=12+22=5,OH= 22 22=2 2 , ∴OG<OE=OF<OA<OH,∴需要被移除的树是E、F、G. 【答案】A
12/9/2021
经典考题
【例2】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径, 过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接 DB,DF. (1)求∠CDE的度数; (2)求证:DF是⊙O的切线; (3)若AC= 2 5 DE,求tan∠ABD的值.
第七单元 圆
第28课时 与圆有关的位置关系
12/9/2021
考纲考点
考情分析
(1)了解点与圆、直线与圆的位置关系; (2)掌握切线的概念,理解切线与过切点的半径之间的关系;能 判定一条直线是否为圆的切线,会过圆上一点画圆的切线,了解切 线长定理.
江西中考每年都考查了一道“圆的切线的性质与判定”解答题,预 测2018年江西中考仍会考查一道解答题——有关圆的切线的性质与 判定的综合题.
12/9/2021
7.2.2 直线与圆的位置关系
要点梳理
(1)定义:如果直线和圆没有公共点,直线和圆相离;直线和圆 只有一个公共点ห้องสมุดไป่ตู้直线和圆相切;直线和圆有两个公共点,直线和
中考数学基础过关复习 第七章 圆 第2课时 与圆有关的位置关系数学课件

12/9/2021
第三页,共四十九页。
(1)证明(zhèngmíng):连接OD. ∵BD为∠ABC平分线,∴∠1=∠2. ∵OB=OD,∴∠1=∠3. ∴∠2=∠3,∴OD∥BC. ∵∠C=90°,∴∠ODA=90°, ∴OD⊥AC, ∴AC为⊙O的切线.
12/9/2021
第四页,共四十九页。
12/9/2021
12/9/2021
第二十三页,共四十九页。
12/9/2021
第二十四页,共四十九页。
[解答](1)证明:连接(liánjiē)OD,则 ∠ABC=∠OBD=∠ODB. ∵OA⊥l,∴∠PCD+∠ABC=90°,∴∠PCD+∠ODB=90°. ∵∠PCD=∠PDC, ∴∠PDC+∠ODB=90°,即∠ODP=90°, ∴PD是⊙O的切线.
3.解决与切线有关的求角度或线段问题的方法:
(1)构造直角三角形,然后利用勾股定理或相关的三角函数知识计算 线段长度;
(2)通过寻找三角形相似的条件或全等的条件计算长度 (3)在求角度时,往往利用圆周角定理及其推论(tuīlùn),三角 形内角和、内外角关系等知识求解.
12/9/2021
第三十五页,共四十九页。
12/9/2021
第四十页,共四十九页。
(1)证明:∵AB为⊙O的直径(zhíjìng), ∴∠ADB=90°, ∴∠ADO+∠BDO=90°. ∵AC为⊙O的切线,∴OA⊥AC, ∴∠OAD+∠CAD=90°. ∵OA=OD,∴∠OAD=∠ODA. ∵∠1=∠BDO,∴∠1=∠CAD.
12/9/2021
12/9/2021
第三十三页,共四十九页。
2.证明直线是圆的切线有两种方法: (1)已知直线与圆的交点在圆上,只需连接圆心(yuánxīn)和这一
2018届中考数学总复习 第一部分 基础篇 第七章 圆 考点30 与圆有关的位置关系

考点聚焦
考点一 点与圆的位置关系
考点二 直线与圆的位置关系
考点三 切线的性质与判定
考点四 三角形的外接圆和内切圆
真题探源
第一部分 基 础 篇第七章 圆来自30 与圆有关的位置关系
目标方向
点和圆、直线和圆都是用量的关系来确定图形 的位置关系,这部分内容的重点在于对切线的判定 和性质的理解应用.点与圆的位置关系多以客观题的 形式考查,而直线与圆的位置关系则是中考热点, 在考查推理论证、操作计算、开放探索以及综合应 用代数与几何各方面知识的能力方面可谓常考常新.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2.3 圆的切线
(1)切线的判定方法:①用定义判断;②用等价条件判断;③用 定理判断:经过半径的外端且垂直于这条半径的直线是圆的切线. (2)切线的性质: 定理:圆的切线垂直于过切点的半径; 推论:①经过圆心且垂直于切线的直线必经过切点; ②经过切点且垂直于切线的直线必经过圆心. (3)切线长定理:从圆外一点可以引圆的两条切线,它们的切线 长相等.这一点和圆心的连线平分这两条切线的夹角.
第七单元 圆
第28课时 与圆有关的位置关系
考纲考点
(1)了解点与圆、直线与圆的位置关系; (2)掌握切线的概念,理解切线与过切点的半径之间的关系;能 判定一条直线是否为圆的切线,会过圆上一点画圆的切线,了解切 线长定理. 江西中考每年都考查了一道“圆的切线的性质与判定”解答题,预 测2018年江西中考仍会考查一道解答题——有关圆的切线的性质与 判定的综合题.
【例2】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径, 过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接 DB,DF. (1)求∠CDE的度数; (2)求证:DF是⊙O的切线; (3)若AC= 2 5 DE,求tan∠ABD的值.
【解】(1)∵对角线AC为⊙O的直径, ∴∠ADC=90°, ∴∠EDC=90°; (2)证明:连接DO, ∵∠EDC=90°,F是EC的中点, ∴DF=FC, ∴∠FDC=∠FCD, ∵OD=OC, ∴∠OCD=∠ODC, ∵∠OCF=90°, ∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°, ∴DF是⊙O的切线.
知识体系图
点与圆的位置关系
与圆有关的 位置关系 直线与圆的位置关系
相交 相切 相离 切线的性质、判定 切线长及性质
7.2.1 点与圆的位置关系
如果圆的半径是r,点到圆心的距离为d,那么: (1)点在圆外 d>r; (2)点在圆上 d=r; (3)点在圆内 d<r.
7.2.2 直线与圆的位置关系
【例1】在公园的O处附近有E、F、G、H四棵树,位置如图所示 (图中小正方形的边长均相等),现计划修建一座以为圆心,OA为 半径的圆形水池,要求池中不留树木,则E、F、G、H 四棵树中需 要被移除的为 ( ) A.E、F、G B.F、G、H C.G、H、E D.H、E、F
【解析】设小正方形的边长为1.由点在图形中的位置和勾股定理可 知,OG=1,OE=OF=2,OA=12+22=5=OF<OA<OH,∴需要被移除的树是E、F、G. 【答案】A
