复习共点力平衡条件的应用
高一物理共点力平衡条件的应用(2019年10月整理)

4.运用平衡条件,选择合适的方法列出平衡方程 解题
若物体受力较多时,一般可选用力的正交分 解法,即建立直角坐标系.将各力分解到两相互 垂直的坐标轴上,然后列等式解题.
对有些问题,我们也可采用根据力的作用效 果分解后根据平衡条件解题,对三力平衡的问题, 常采用三力组成封闭三角形的特征,利用三角形 方面的数学知识来求解.
2.由于滑动摩擦力F=FN,要特别注意题目中正
压力FN的大小的分析和计算,防止出现错误.
例1:A、B、C三个物体质量分别为M、m和m0,作如下图所
示的连结,绳子不可伸长,且绳子质量、滑轮的摩擦均不 计,若B随A一起沿水平桌面做匀速运动,则可以断定:
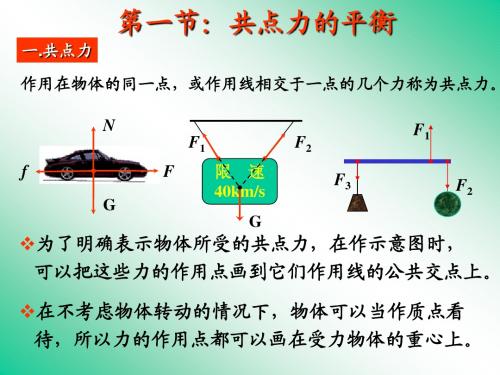
二、共点力平衡条件的应用
一、应用共点力平衡条件解题的 一般方法和步骤
1.确定研究对象 合理选择研究对象是解决平衡问题的关键,它
关系到能否做出解答或能否顺利地解答. 研究对象的选取可以是一个物体,一个结点,
或一个系统(相互作用物体的全体).通常在分 析外力对系统的作用时,用整体法,在分析系统 内务物体间相互作用力时,用隔离法.
5.视问题的要求,对结果做出说明或讨论.
二、跟摩擦力有关的平衡问题
• 这类问题是指平衡的物体受到了包括摩擦力在内共 点力的作用. 做这类题目时要注意两点: 1.由于静摩擦力的大小和方向都要随运动趋势的 改变而改变,因此维持物体静止状态所需的外力允 许有一定范围;又由于存在着最大静摩擦力,所以 使物体起动所需要的力应大于某一最小的力.总之, 包含摩擦力在内的平衡问题,物体维持静止或起动 需要的动力的大小是允许在一定范围内的,只有当 维持匀速运动时,外力才需确定的数值.
; 搞笑gif 搞笑gif
;
改为卢龙县 汉中阳县 又以废昌州蒲县来属 隋改永宁为盛山 六年 八年 汉魏郡城 武德
《共点力平衡条件的应用》 讲义

《共点力平衡条件的应用》讲义一、共点力平衡的概念当物体受到几个力的作用,如果这几个力都作用在物体的同一点,或者它们的作用线相交于一点,这几个力就叫做共点力。
当物体在共点力的作用下处于静止或者匀速直线运动状态时,我们就说物体处于共点力平衡状态。
二、共点力平衡条件共点力平衡的条件是合力为零。
也就是说,如果物体受到多个共点力的作用而处于平衡状态,那么这些力的合力必定为零。
可以用数学表达式表示为:\(F_{合}=0\)如果将力进行正交分解,分别在 x 轴和 y 轴上投影,则有:\(F_{x合}=0\)\(F_{y合}=0\)三、共点力平衡条件的应用1、静态平衡问题(1)物体在水平面上的平衡例如,一个静止在水平地面上的物体,受到重力\(G\)、地面的支持力\(N\)和水平方向可能存在的摩擦力\(f\)。
由于物体处于静止状态,合力为零。
在竖直方向上,重力和支持力大小相等、方向相反,即\(G = N\);在水平方向上,如果没有外力作用,摩擦力\(f = 0\)。
(2)物体在斜面上的平衡当一个物体静止在斜面上时,它受到重力\(G\)、斜面的支持力\(N\)和斜面的摩擦力\(f\)。
将重力沿斜面和垂直斜面方向分解,分别为\(G_{1}\)和\(G_{2}\)。
在垂直斜面方向上,支持力\(N\)与\(G_{2}\)大小相等、方向相反,即\(N= G_{2}\);在沿斜面方向上,如果物体静止,摩擦力\(f\)与\(G_{1}\)大小相等、方向相反,即\(f = G_{1}\)。
2、动态平衡问题(1)缓慢移动问题在一些情况下,物体的位置在缓慢变化,但始终处于平衡状态。
比如,一个用绳子悬挂的物体,缓慢地从一个位置移动到另一个位置。
在这个过程中,因为移动缓慢,可以认为每个时刻物体都处于平衡状态,仍然满足合力为零的条件。
(2)多力动态平衡有些物体受到多个力的作用,且这些力的大小和方向在不断变化,但物体仍保持平衡。
例如,一个用三根绳子悬挂的重物,通过改变三根绳子的长度来改变拉力的大小和方向,使重物始终处于平衡状态。
(必修1)共点力平衡条件的应用
F 0 F 0 F 0
x y
X轴 : Fx1 Fx 2 Fx 3 0 Y轴 : Fy1 Fy 2 Fy 2 0
F1
F
y N
f
F2
x
G
正交分解法
6.如图所示,质量为 m的物体放在倾角为 θ的斜面上, 它与斜面的滑动摩擦因数为μ,在水平推力的作用下, 物体沿斜面向上匀速滑动,则物体所受的摩擦力为: A.μmgcosθ B.μ(mgcosθ+Fsinθ) C.μ(mgcosθ-Fsinθ) D. Fcosθ-mgsinθ
例3: 如图示半径为r,表面光滑的半球体被固定在水平地 面上,跨过无摩擦的定滑轮,用一根轻绳下挂一个质量为m 的小球,将小球置于半球体光滑的表面上,并使定滑轮位于 半球体的正上方,现用力F斜左向下拉绳的自由端,使小球 沿光滑半球面缓慢向上滑动。在此过程中,半球体对小球的 支持力FN 和绳子的拉力F的变此情况。
②利用分解法,特别是正交分解法分析平衡问题 时,其平衡方程为Fx=0,Fy=0.
5、数学方法求解 建立平衡方物体放在倾角为θ的斜面 上,它与斜面的滑动摩擦因数为 μ,在水平推力的作 用下,物体沿斜面向上匀速滑动,则物体所受的摩擦 力为: A.μmgcosθ B.μ(mgcosθ+Fsinθ) C.μ(mgcosθ-Fsinθ) D. Fcosθ-mgsinθ
F 0 F 0 F 0
x y
⑤解方程(组),必要时验证结论。
实验1
1N
1200
1200
1200
1N 1N
2.5N
1N 实验2
1.5N 2N 1200 900 1500
2.5N
第五节 共点力的平衡条件 三.学以致用
共点力的平衡条件和应用复习

1共点力的平衡条件和应用3.静态平衡问题的解题“五步骤”1.受力分析的一般顺序: (1)画出已知力。
(2)分析场力(重力、电场力、磁场力) (3)分析弹力。
(4)分析摩擦力。
2.平衡中的研究对象选取 (1)单个物体;(2)能看成一个物体的系统; (3)一个结点。
例题:如图所示,倾角θ的光滑斜面体固定在水平面上,一个质量为m 的可视为质点的小物块在水平推力的作用下沿斜面匀速上滑,求推理F 及物块受到的支持力F N 。
1.(多选)下列各组提供的三个力可能平衡的是A. 3N、4N、8NB. 8N、7N、4NC. 7N、9N、16ND. 6N、10N、2N2.如图,一个人站在水平地面上的长木板上用力F向右推箱子,木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g,则()A. 箱子受到的摩擦力方向向右B. 地面对木板的摩擦力方向向左C. 木板对地面的压力大小为3mgD. 若人用斜向下的力推箱子,则木板对地面的压力会大于3mg3.如图所示,质量为m的物块放在水平面上,物块与水平面间的动摩擦因数为0.25,在两个大小相等的力F(其中一个方向为水平向左,另一个与水平方向成37°角向下)作用下沿水平面做匀速直线运动,(重力加速度大小为g,sin37°=0.6,cos37°=0.8)则以下判断正确的是()A.B.C.D.4.如图所示,人握住竖直旗杆匀速向下滑,则下列说法正确的是( )A. 人受到的摩擦力的方向是竖直向下的B. 人受到的摩擦力的方向是竖直向上的C. 手握旗杆的力越大,人受到的摩擦力越大D. 手握旗杆的力增加,人受到的摩擦力可能减小5.一根钢管,一端支在水平地面上,另一端被竖直绳悬吊着,如图所示,有关钢管的叙述正确的是()A.钢管的重心一定在几何中心B.绳对钢管的拉力等于钢管的重力C.钢管对地面压力方向垂直钢管向下D.地面与钢管之间不存在静摩擦力36. 用手施加水平向左的力F 把物体a 、b 压在竖直墙上,如图所示,a 、b 处于静止状态,关于a 、b两物体的受力情况,下列说法正确的是( )A. a 受到墙壁摩擦力的大小随F 的增大而增大B. a 共受到五个力的作用C. b 共受到三个力的作用D. 物体b 对物体a 的弹力是由手的形变产生的7. 如图所示,倾角θ=37°的粗糙斜面体固定在水平面上,一个可视为质点的小物块在平行斜面向上的推力F 1作用下沿斜面匀速上滑,现将力突然改为水平向右的推力F 2=2F 1,物体仍沿斜面匀速上滑,已知sin37°=0.6,则物块与斜面间的动摩擦因数μ为( ) A. B. C. D.8. 图中所有的球都是相同的,且形状规则质量分布均匀。
第1节共点力平衡条件的应用

F2 = G tan300 = 40×√3/3N=23.1N F1=COGS300 =40÷√3/2N=46.2N
例题2 物体A在水平力F1= 400 N 的作用下,沿倾角θ=600 的斜面 匀速下滑。 物体A受的重力G = 400N,求斜面对物体A的支持力 和A与斜面间的动摩擦因数μ。
学以致用
质量为 4kg的物体在五个共点力的作用下 向东做匀速直线运动,撤去其中大小为 8N, 方向向东的力F1,而保 持其余四个力不变, 则物体( ) D A. 继续保持向东做匀速直线运动. B. 向东做匀加速直线运动. C. 向西做匀加速直线运动. D. 向东做匀减速直线运动.
N F
f G1
300
F = mg sin300 +μ mgcos300 = 50×9.8×(0. 5 +0. 3×0. 87)N
= 37 2. 9 N
θ a
b F1
F2 θ G
练习四 如图所示, 用一根绳子a 把物体 挂起来, 再用另一根水平的绳子b 把物体 拉向一旁固定起来. 物体的重量是40N, 绳 子a 与竖直方向的夹角θ=300,绳子a 和b对 物体的拉力分别是多大?
共点力作者做匀 速直线运动,我们就说这个 物体处于平衡状态
二、 平衡条件:
共点力作用下物体的平衡条 件是合力为零
A 例题 1 沿光滑的墙壁用网兜把一个足球
α
挂在A点(如图), 足球的质量为m, 网兜的 质量不计. 足球与墙壁的接触点为B, 悬
G G2
练习3 一个质量为50Kg的物体,在平行 于斜面的拉力F作用下,沿倾角为300的斜 面匀速运动(如图),已知斜面的动摩擦 因数为0.3。求拉力F为多大?
高中物理课件 共点力的平衡条件及其应用

【拓展例题】考查内容:利用相似三角形法求解力 【典例】如图所示,一个重为G的小球套在竖直放置的半径为R的光滑圆环上,一 个劲度系数为k,自然长度为L(L<2R)的轻质弹簧,一端与小球相连,另一端固定在 圆环的最高点,求小球处于静止状态时,弹簧与竖直方向的夹角φ。
【生活情境】 如图是手机静止吸附在支架上。这款手机支架其表面采用了纳米微吸材料,用 手触碰无粘感,接触到平整光滑的硬性物体时,会牢牢吸附在物体上。
(3)沿光滑斜面下滑的物体处于平衡状态。
(×)
(4)物体所受合力为零时,就一定处于平衡状态。 (√ )
要点透析
知识点一 物体的静态平衡问题来自1.平衡条件的表达式:
(1)F合=0。
(2)
Fx合 0
Fy合
0
其中Fx合和Fy合分别是将所受的力进行正交分解后,物体在x轴和y轴方向上所受
的合力。
2.由平衡条件得出的三个结论:
根据三角函数、 勾股定理、等 边三角形、相 似三角形等计 算合力(或分力)
根据平衡条件 确定与合力 (或分力)平衡 的力
受力个数≤3 已知力个数=2
受力个数≤3 已知力个数=1
提醒:“静态平衡”是指物体在共点力作用下处于静止状态。
【问题探究】 情境:图甲物体静止于斜面上;图乙物体沿斜面匀速下滑;图丙物体到达光滑斜 面的最高点;图丁物体与斜面一起向左加速运动。 讨论:说明物体所处的状态。
探究:若撑竿对涂料滚的推力为F1,墙壁对涂料滚的支持力为F2,粉刷工人站在离 墙壁某一距离处缓缓上推涂料滚的过程中,F1、F2如何变化?
谢谢观赏
3.静态平衡问题的常见研究方法:
正交 分解 法
合 成 法
分 解 法
第一步:作图
《共点力平衡条件的应用》 讲义

《共点力平衡条件的应用》讲义一、共点力平衡的概念在物理学中,共点力是指作用在物体上的力,它们的作用线或者延长线相交于同一点。
当一个物体受到的共点力的合力为零时,我们就说这个物体处于共点力平衡状态。
处于共点力平衡状态的物体,其运动状态保持不变,即保持静止或者做匀速直线运动。
二、共点力平衡条件共点力平衡的条件是物体所受合外力为零。
这个条件可以用以下两种方式来表达:1、物体在两个力作用下平衡时,这两个力大小相等、方向相反,且作用在同一条直线上。
2、物体在多个力作用下平衡时,其中任意一个力与其余力的合力大小相等、方向相反,且作用在同一条直线上。
三、共点力平衡条件的应用实例(一)静态平衡问题1、悬挂物体的平衡例如,一个质量为 m 的物体被一根绳子悬挂在天花板上。
此时,物体受到重力 G = mg 和绳子的拉力 T。
由于物体处于静止状态,所以重力和拉力大小相等、方向相反,且作用在同一条直线上。
即T =G,方向竖直向上。
我们可以通过受力分析,利用共点力平衡条件来计算绳子的拉力大小。
2、放在水平面上的物体的平衡一个质量为 M 的物体静止放在水平地面上,它受到重力 Mg、地面的支持力 N 和可能存在的水平方向的摩擦力 f。
如果物体没有受到水平方向的力,那么支持力N 大小等于重力Mg,方向竖直向上;如果物体受到水平方向的拉力或推力,且物体仍保持静止,那么水平方向的拉力或推力与摩擦力大小相等、方向相反。
(二)动态平衡问题1、缓慢移动的物体比如,一个质量为 m 的小球通过一根轻绳悬挂在一个光滑的斜面上,缓慢移动小球。
在这个过程中,小球始终处于平衡状态。
我们对小球进行受力分析,它受到重力 G、绳子的拉力 T 和斜面的支持力 N。
随着小球位置的改变,拉力和支持力的大小和方向都会发生变化,但它们的合力始终为零。
2、用绳子牵引物体匀速上升或下降一个物体用绳子牵引,匀速上升或下降时,物体受到重力、绳子的拉力以及可能存在的空气阻力。
共点力平衡条件的应用“轻绳”、“轻杆”与“轻弹簧” “活结”与“死结” “活动杆”与“固定杆

模型3:轻弹簧 轻弹簧的质量可忽略不计,可以被压缩或拉伸。 其弹力的主要特征是: ①轻弹簧能产生沿弹簧轴线伸缩方向的压力或拉力; ②轻弹簧各处受力大小相等,且与弹簧形变的方向相反; ③轻弹簧产生的弹力是连续变化的,不能发生突变,只能 渐变(除弹簧被剪断外); ④在弹性限度内,弹力的大小与弹簧的形变量成正比,即 F=kΔx,其中k为弹簧的劲度系数,Δx为弹簧的伸长量或缩 短量。
由于杆AB不可转动(即是“固 定杆”),所以杆所受弹力的方向 不一定沿杆AB方向.由于B点处是 滑轮,它只是改变绳中力的方向, 并未改变力的大小,滑轮两侧绳 上的拉力大小均是100 N,夹角为 120°,故滑轮受绳子作用力即是 两拉力的合力。
总结: 1.什么是活结,什么是死结? 2.什么是活动杆,什么是固定杆? 2.它们各有什么特点?
②绳上任何一个横截面两边相互作用的拉力叫做“张 力”,因此轻绳只有两端受力时,任何一个横截面上的张力 大小都等于绳的任意一端所受拉力的大小,即同一轻绳张力 处处相等,且与运动状态无关.
③轻绳的弹力大小可发生突变.
模型2:轻杆 轻杆的质量可忽略不计,轻杆是硬的,它的劲度系数 非常大,可认为在受外力作用时形变极微小,看作不可伸 长或压缩. 其弹力的主要特征是: ①轻杆既可产生压力、也可产生拉力,且能产生侧向 力(力的方向不一定沿着杆的方向); ②轻杆各处受力大小相等,且与运动状态无关; ③轻杆的弹力可发生突变.
分析:
TC mg 50N
TB cos mg
TA A
mg 50
TB cos
62.5N 0.8
TA TB sin 62.5 0.6 37.5N
B TB θ θ O
mg
例2.轻绳AB一段固定于A点,另一端自由。在绳中某处O点 打结系另一轻绳OC,下挂一质量为m的物体。现保持O点的 位置不变,在OB段由水平方向缓慢转到竖直方向的过程中, 拉力F和绳OA的张力变化?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共点力平衡条件的应用
教学目标:
一、知识目标
1:能用共点力的平衡条件,解决有关力的平衡问题;
2:进一步学习受力分析,正交分解等方法。
二、能力目标:
学会使用共点力平衡条件解决共点力作用下物体平衡的思路和方法,培养学生灵活分析和解决问题的能力。
三、德育目标:
培养学生明确具体问题具体分析:
教学重点:
共点力平衡条件的应用
教学难点:
受力分析、正交分解、共点力平衡条件的综合应用。
教学方法:
讲练法、归纳法
教学用具:
投影仪、ppt
教学步骤:
一、导入新课(ppt)
1:复习题:
(1)如果一个物体能够保持或,我们就说物体处于平衡状态。
(2)当物体处于平衡状态时:
a:物体所受各个力的合力等于,这就是物体在共点力作用下的平衡条件。
b:它所受的某一个力与它所受的其余外力的合力关系是。
2:学生回答问题后,教师进行评价和纠正。
3:引入:本节课我们来运用共点力的平衡条件求解一些实际问题
二:新课教学
1:共点力作用下物体的平衡条件的应用举例:
(1)用投影片出示例题1:
如图所示:细线的一端固定于A点,线的中点挂一质量为m的物体,另一端B用手拉住,当AO与竖直方向成 角,OB沿水平方向时,AO及BO对O点的拉力分别是多大?
(2)教师解析本题:
先以物体m为研究对象,它受到两个力,即重力和悬线的拉力,因为物体处于平衡状态,所以悬线中的拉力大小为F=mg。
再取O 点为研究对像,该点受三个力的作用,即AO 对O 点的拉力F 1,BO 对O 点
的拉力F 2,悬线对O 点的拉力F ,如图所示:
a :用力的分解法求解:
将F =mg 沿F 1和F 2的反方向分解,得到 ,cos /;///θθmg F mgtg F ==
得到
θθmgtag ;F mg F ==21cos /
b :用正交分解合成法求解
建立平面直角坐标系
由F x 合=0;及F y 合=0得到: ⎩⎨⎧==-2
11sin 0cos F F mg F θθ 解得: θθtan ;cos /21mg F mg F ==
2:结合例题总结求解共点力作用下平衡问题的解题步骤:
(1)确定研究对象
(2)对研究对象进行受力分析,并画受力图;
(3)据物体的受力和已知条件,采用力的合成、分解、图解、正交分解法,确定解
题方法;
(4)解方程,进行讨论和计算。
3:学生用上述方法求解课本上例1,并抽查部分同学的答案在投影仪上进行评析。
4:讲解有关斜面问题的处理方法:
(1)学生阅读课本例题,并审题;
(2)分析本题;
a :定物体A 为研究对于;
b :对物体A 进行受力分析。
解题过程(略)
5:巩固训练:
如图所示:重为G =10N 的小球在竖直挡板作用下静止在倾角为θ=30o 的光滑斜面上,已知挡板也是光滑的,求:
(1)挡板对小球弹力的大小;
(2)斜面对小球弹力的大小。
三、小结
本节课我们主要学习了以下几点:
1:应用共点力平衡条件解题时常用的方法--力的合成法、力的分解法、正交分解法 2:解共点力作用下物体平衡问题的一般步骤:
(1)定研究对象;
(2)对所选研究对象进行受力分析,并画出受力示意图
(3)分析研究对象是否处于平衡状态;
(4)运用平衡条件,选用适当方法, 列出平衡方程求解。
四、作业,
练习册P27 。
1、2、3、4题
五、板书设计: ⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧==列出平衡方程求解当方法,运用平衡条件,选择适平衡状态
分析研究对象是否处于画出受力示意图析,并
对研究对象进行受力分结点)确定研究对象(物体或解题的一般步骤正交分解法相似三角形法力的分解法
力的合成法常用的方法共点力平衡条件的应用合合00y x F F。
