高中物理理想气体物态方程与内能
理想气体的内能、热容和焓

4
(2)由图可以看出:
PaVa = PcVc ∴Ta = Tc ⇒ ΔU = 0
P (atm )
a 3
2
b
1
c
o 1 2 3 V(10−3m3)
(3)由热力学第一定律得:
Q = ΔU + A = 405.2J
5
二、理想气体的热容
1. 热容、比热容、摩尔热容
设系统温度升高 dT ,所吸收的热量为dQ
在等压过程中,dp=0,故 pdVm = RdT 将其代入 Cp,mdT = CV ,mdT + pdVm 得:
Cp,mdT = CV ,mdT + RdT 等式两边约去dT得:
迈耶公式 C p,m = Cv,m + R
表明:理想气体定压摩尔热容等于定体摩尔热容与普适
气体常量R之和。
C p,m > CV ,m
质量之比。
c
=
C m
=
1 m
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠
M:摩尔质量
摩尔热容Cm:物质的量为v的该物质的热容C与v之比。
Cm
=
C
ν
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠
=
cm
ν
=
Mc
或: c = Cm
M
单位: J·mol-1·K-1
(1)定体摩尔热容CV, m:
CV ,m
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠V
(2)定压摩尔热容Cp, m:
热容:
C = lim ΔQ = dQ ΔT →0 ΔT dT
单位:J/K
(1)定体热容:
CV
ch.1-7 理想气体的内能
dH Cp dT
(1.7.6)
H
C dT H p 0
此即理想气体焓的积分表达式。
3.理想气体的迈尔公式
由式(1.7.4)、(1.7.2)和(1.7.7)可得
C p C V nR
(1.7.7)
上式称为迈尔公式,它给出了理想气体的定压热容 量与定容热容量之差。当年迈尔正是由这个关系最先得 到了热功当量。引入γ表示定压热容量与定容热容量的 比值:
§1.7
理想气体的内能
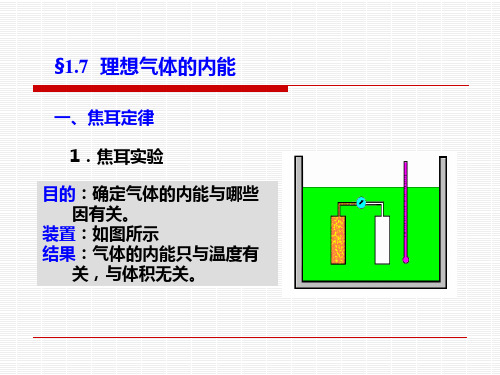
一、焦耳定律 1.焦耳实验 目的:确定气体的内能与哪些 因有关。 装置:如图所示 结果:气体的内能只与温度有 关,与体积无关。
2.焦耳定律
1845年,焦耳用自由膨胀实验研究了气体的内能,得 出气体内能仅仅是温度的函数而与体积无关这一重要结论。 这条结论称为焦耳定律,可表示为
U U U (T )或 0 V T
(1.7.3)
2.理想气体的焓 根据焓的定义(1.6.6)式和理想气体物态方程,可得理 想气体的焓为 H= U + pV = U + nRT (1.7.4)
可以看出, H也仅是T的函数,因此,对于理想气体, 式(1.6.7)的偏导数也可写成
dH Cp dT
(1.7.5)
(1.6.7)的偏导数也可写成 将上式积分,得
后来,人们发现焦耳实验的结果不够可靠。
(1.7.1)
于是,焦耳和汤姆逊在1852年用节流方法重新做了实 验,并发现实际气体的内能不仅是温度的函数而且还是体 积的函数。不过,焦耳定律在实际气体压强趋于零的极限 情形下是正确的,所以可认为它是理想气体所遵守的定律。 即,理想气体的内能只是温度的函数而与体积无关。 可表达为 U=U(T)
平衡态理想气体物态方程热力学第零定律

目录
• 理想气体物态方程 • 平衡态理想气体 • 热力学第零定律 • 平衡态理想气体物态方程与热力
学第零定律的关系
01
理想气体物态方程
理想气体定义
理想气体是一种理想化的气体模型, 它忽略了气体分子间的相互作用和分 子本身的体积,只考虑分子间的碰撞 和热运动。
02
平衡态理想气体
平衡态的定义
平衡态
当一个系统与外界没有能量和物质的交换时,系统内 部各部分之间达到相对平衡的状态。
动态平衡
系统内部各部分之间虽然达到相对平衡,但仍然在不 断进行着微观运动和相互作用。
热平衡
系统内部各部分之间达到相同的温度,不再发生热交 换。
平衡态理想气体的特性
分子间无相互作用力
01 02 03 04
理想气体物态方程在热力学、化学和工程领域中有着广泛的应用。
通过理想气体物态方程,可以计算气体的压力、体积和温度之间的关 系,了解气体的性质和行为。
在化学反应中,理想气体物态方程可以帮助我们了解反应前后气体的 状态变化,从而推导反应热力学参数。
在工程领域中,理想气体物态方程可以用于计算气体的流量、换热器 效率以及各种气体的热力学性能参数。
平衡态理想气体物态方程和热力学第零定律的应用可以帮助我们更好地理解气体系统的性质和行为, 为相关领域的研究提供理论支持和实践指导。
感谢您的观看
THANKS
在研究和设计热力系统时,该定律也是必不可少的, 因为它为确定不同部分之间的热平衡提供了基础。
在气象学、化学工程、航天工程等领域中,热力学第 零定律也是重要的理论基础之一。
04
平衡态理想气体物态方程与 热力学第零定律的关系
物质的内能与状态变化

物质的内能与状态变化一、内能的概念1.内能是指物体内部所有分子由于热运动而具有的动能及分子间势能的总和。
2.内能与物体的温度、质量和物质种类有关。
3.内能是状态量,用符号U表示。
二、内能的改变1.做功:对物体做功(如克服摩擦力、压缩气体等),物体的内能增加;物体对外做功,内能减少。
2.热传递:物体与外界之间发生热传递,内能也会发生改变。
3.内能的改变可以通过做功和热传递实现,这两种方式在效果上是等效的。
三、物态变化与内能1.熔化:固体吸热熔化成为液体,内能增加。
2.凝固:液体放热凝固成为固体,内能减少。
3.汽化:液体吸热汽化成为气体,内能增加。
4.液化:气体放热液化成为液体,内能减少。
5.升华:固体吸热升华成为气体,内能增加。
6.凝华:气体放热凝华成为固体,内能减少。
四、热量与内能的关系1.热量是指在热传递过程中,能量的转移量,用符号Q表示。
2.热量总是从高温物体传递到低温物体,或者从物体的高温部分传递到低温部分。
3.热量是一个过程量,只有在热传递过程中才有意义。
五、热力学第一定律1.热力学第一定律指出:一个封闭系统的总内能保持不变,即ΔU=Q+W(其中ΔU表示内能的变化,Q表示热量,W表示做功)。
2.该定律说明,在一个封闭系统中,内能的改变可以通过热传递和做功来实现,且内能的改变量等于热量和做功的代数和。
六、热力学第二定律1.热力学第二定律指出:在一个热力学过程中,热量总是自发地从高温物体传递到低温物体,不可能自发地从低温物体传递到高温物体。
2.该定律说明了热传递的方向性,即热量的传递总是从高温物体向低温物体进行。
综上所述,物质的内能与状态变化涉及内能的概念、内能的改变、物态变化与内能的关系、热量与内能的关系、热力学第一定律和热力学第二定律等内容。
掌握这些知识点有助于深入理解物质在不同状态变化过程中的能量变化规律。
习题及方法:1.习题:一个质量为2kg的铁块,温度为300K,放入一个温度为100K的环境中,求铁块的内能变化量。
高中物理竞赛第三阶段 第二讲 理想气体的内能(无答案)

1. 理想气体的压强,温度的微观解释2. 理想气体的内能3. 热力学第一定律知识点拨一.理想气体的微观模型先来作个估算:在标准状态下,1mol 气体体积1330104.22--⨯=moI m V ,分子数1231002.6-⨯=moI N A ,若分子直径m d 10100.2-⨯=,则分子间的平均间距m N V L A 93/101034.3)/(-⨯==,相邻分子间的平均间距与分子直径相比17/≈d L 。
由此可知:气体分子间的距离比较大,在处理某些问题时,可以把气体分子视为没有大小的质点;同时可以认为气体分子除了相互碰撞或者跟器壁碰撞之外,分子力也忽略不计,分子在空间自由移动,也没有分子势能。
因此理想气体是指分子间没有相互作用和分子可以看作质点的气体。
这一微观模型与气体愈稀薄愈接近于理想气体的宏观概念是一致的。
1.理想气体的压强宏观上测量的气体施给容器壁的压强,是大量气体分子对器壁不断碰撞的结果。
在通常情况下,气体每秒碰撞21cm 的器壁的分子数可达2310。
在数值上,气体的压强等于单位时间内大量分子施给单位面积器壁的平均冲量。
可以用动量定理推导,其表达式为K n P ε32=设气体分子都以平均速率运动,因沿上下、左右、前后各向运动的机会均等,所以各占总数的.若分子的数密度(即单位体积内气体的分子数)为,则单位时间内碰撞单位面积器壁的分子数应为.每个分子每次与器壁碰撞时将施于器壁的冲量,所以压强,假设每个分子的速率相同.每个分子的平均平动动v 16n 1(1)6n v ×2mv 211(1)263p n v mv nmv ==××知识体系介绍第二讲 理想气体的内能能,所以.,式中n 是单位体积内分子个数,221υεm K=是分子的平均平动动能,n 和K ε增大,意味着单位时间内碰撞单位面积器壁的分子数增多,分子碰撞器壁一次给予器壁的平均冲量增大,因而气体的压强增加。
物态方程与理想气体

物态方程与理想气体气体是一种无定形物质,具有高度可压缩性和自由扩散性。
在研究气体性质时,物态方程是一种重要的工具。
而理想气体则是对气体行为进行简化和理论化的概念模型。
本文将探讨物态方程的基本原理和应用,并介绍理想气体的特性和其对物态方程的适用性。
物态方程是描述气体状态的数学表达式。
根据气体的状态方程,物态方程可以分为多种形式,如理想气体状态方程、范德瓦尔斯方程等。
其中,理想气体状态方程是最简化的形式,也是最广泛使用的物态方程。
根据理想气体状态方程,气体的体积、压力和温度之间存在一定关系。
理想气体的特性可以通过一系列实验观测得出,并用数学模型进行描述。
首先,理想气体分子是无相互作用的点状物体,它们之间没有体积、力量和势能等之间的相互作用。
其次,理想气体分子的碰撞是完全弹性的,即能量和动量在碰撞过程中完全守恒。
最后,理想气体的分子运动是混乱和无序的,并且具有高度的自由度。
根据理想气体的特性,我们可以得到理想气体状态方程。
根据理想气体状态方程,气体的压力和体积成反比,与温度成正比。
这可以用以下数学关系式表示:PV = nRT其中,P表示气体的压力,V表示气体的体积,n表示气体的物质量,R表示气体常数,T表示气体的绝对温度。
上述关系式可以进一步推导出其他重要的物态方程,如分压定律和道尔顿混合定律。
理想气体状态方程的应用非常广泛。
首先,它可以用于计算气体的物态变化,如气体在不同条件下的压强、体积和温度的变化。
这对于科学研究、实验设计和工程计算都有重要意义。
其次,理想气体状态方程可以帮助我们理解气体在不同条件下的行为规律,如气体的扩散和溶解等现象。
这对于环境保护和工艺控制等领域具有实际应用价值。
然而,理想气体状态方程也存在一定的局限性。
首先,理想气体假设忽略了气体分子之间的相互作用和体积,因此在高压和低温条件下不太适用。
其次,理想气体假设也无法描述气体的相变行为,如液体-气体和固体-气体的转变。
因此,在研究和应用时需要考虑其他修正因素,如修正气体状态方程和实际气体模型等。
理想气体物态方程

目录
• 理想气体定义 • 理想气体物态方程的应用 • 理想气体物态方程的特性 • 理想气体物态方程与其他物理量的关系 • 理想气体物态方程的实验验证
01
理想气体定义
理想气体假设
气体分子无体积、无相互作用, 且分子运动速度远大于分子间的
平均距离。
气体分子在容器内自由移动,不 受容器壁的限制,且不与容器壁
利用统计物理学和热力学的原理,通过数学推导得到理想气体物态方程的 表达式。
通过实验验证理想气体物态方程的正确性和适用范围,并不断修正和完善 方程的形式和参数。
02
理想气体物态方程的应 用
计算气体体积
总结词
理想气体物态方程可以用于计算气体 的体积。
详细描述
根据理想气体物态方程,气体的体积 V可以通过气体的物质的量n、气体常 数R和气体的热力学温度T计算得出。 公式为:V = nRT/P,其中P表示气体 的压力。
发生碰撞。
气体分子之间以及气体分子与容 器壁之间的碰撞可以忽略不计。
理想气体状态方程
• 理想气体状态方程是描述理想气体状态变 量之间关系的方程,即PV=nRT,其中P表 示压强,V表示体积,n表示摩尔数,R表 示气体常数,T表示温度。
理想气体物态方程的推导
从理想气体假设出发,通过分析气体分子运动和相互作用的微观过程,推 导出理想气体物态方程。
数据分析
对实验数据进行统计分析,计算误差范围和置信区间。
结果对比
将实验结果与理论值进行对比,分析误差来源和影响因子。
结果可靠性
评估实验结果的可靠性和稳定性,确保实验结论的可信度。
实验结论
01
理想气体物态方程的实验验证 表明,在一定条件下,理想气 体物态方程能够准确描述气体 的状态变化。
中考物理辅导--理想气体的内能及其变化

中考物理辅导--理想气体的内能及其变化
验结果又表明此过程中气体的温度并没改变,这就说明气体的内能只跟温度有关而跟体积无关,因此得到结论:理想气体的内能只与温度有关,与体积无关,这一结论称为焦耳定律。
从气体分子动理论的观点来看,气体的内能是气体中所有分子热运动的动能和分子间相互作用的势能的总和,而分子热运动的动能与气体的温度有关,分子间相互作用的势能与气体的体积有关,所以气体的内能是温度和体积的函数,而理想气体,是指分子间没有相互作用和分子可以看作没有大小的质点的气体,因而理想气体内能中就不存在分子间相互作用的势能,所以,理想气体的内能只是所有分子热运动的动能的总和,而分子热运动的动能只与温度有关,故理想气体的内能只与温度有关,与体积无关。
二、理想气体内能的变化
下面我们来分析理想气体在一些简单过程中内能的变化。
1、等容过程
一定质量的理想气体在体积不变的情况下,由初态A(p1,V,T1)变到末态B(p2,V,T2),其过程如图2、图3所示,因为气体体积不变,所以W=0,根据热力学第一定律,有△U=Q,可见理想气体在等容过程中,内能的变化完全是由外界对气体传递的热量决定的:若理想气体等容吸热(图2),Q>0,则T2>T1,p2>p1,△U>0,即理想气体在等容吸热过程中,
温度升高,压强增大,理想气体从外界吸收热量,吸收的热量全部用来增加自身的内能;若理想气体等容放热(图3),Q <0,则T2<T1,p2<p1,△U<0,即理想气体在等容放热过程中,温度降低,压强减小,理想气体等容放热过程是靠减少自身的内能来向外界释放热量的,或者说理想气体在等容放热过程中是以传热的方式把内能传给了外界。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想气体宏观定义:遵守三个实验定律的气体 .
玻意耳(Boyle)定律
T不变时 pV c
查理(Charles)定律
V不变时 p / T c
盖—吕萨克(Gay-Lussac)定律
p不变时 V / T c
记忆方法
B C G
T V p
物态方程:描述物质存在的物理状态所需的参量之间的函数关系。如理想气体平衡 态宏观参量间的函数关系
研究热现象的规律。
v
等,来
单个分子 的运动是无序的,具有偶然性,遵循力学规律。但整体(大量分子)服从 统计规律 。
微观量
统计平均
宏观量
热力学 (宏观研究方法)与气体; 2)知其然而不知其所以然; 3)应用宏观参量 。
微观研究方法 1)揭示宏观现象的本质;2)有局限性,与实际有偏差,不可任意推广 .
V2 V1 V2 V1
W 0 W 0
气体对外界不作功
外界对气体作正功,气体对外界 作负功
注意
气体对外界作功 外界对气体作功
W 0 W 0
七 热量(heat)(过程量)
通过传热方式传递能量的量度,系统和外界之间存在温差而发生的能量传 递.
功与热量的异同
1)过程量:与过程有关; 2)等效性:改变系统热运动状态作用相同;
作正功,同时气体又吸收热量,根据能量守恒定律,气体的能量必然增加。
从宏观上看,气体增加的能量表现在哪里呢? 气体变热了,温度升高了!
从微观上看,气体增加的能量又表现在哪里呢? 气体分子运动的机械能!
气体分子运动的动能与分子之间的势能、分子内部原子振动的动能与原子间的 势能,总称为气体的内能(internal energy) 。
2 体积(Volume)V:气体所能达到的最大空间(几何描述)。
单位: 1m3 103 L 103 dm3
3 温度(Temperature)T:气体冷热程度的量度(热学描述)。
热力学温标(temperature scale) 单位:开尔文(Kelvin)K
T 273.15 t
三 理想气体(ideal gas)物态方程(equation of state)
一 热力学(thermodynamics)的研究对象与研究方法 物态(state of matter):物质存在的物理状态
物质主要存在三种基本物理状态:固态、液态和气态
热学是研究一切物态的热现象的学科,我们这里主要研究气态,但有时也会牵涉 到固态和液态。
从宏观上看,热学研究物体的宏观热现象:与温度有关的物态的物理性质的变化。 由观察和实验来总结热现象的规律,得出热现象的宏观理论,这部分称为热力学。
一个热力学系统的平衡态一般需要几何参量、力学参量、化学参量、电磁参量 和热学参量来描述。对理想气体,需要:
p 1 气体压强(Pressure) :作用于容器壁上单位面积的正压力(力学描述)。
标准大气压:
国际单位:
1Pa 1N m2
45 纬度海平面处,
0 C 时的大气压.
1atm 1.013105 Pa
T f p,V
对于理想气体
一定质量的同种气 体
理想气体物态方程
p1V1 p2V2
T1
T2
pV m RT RT
M
摩尔(mole)气体常量
R 8.31J mol 1 K1
1 mol气体的分子数为 Avogadro 常数
N A 6.022 1023 ( 个分子/mol )
气体
o V1 V2 V
六 功(work)(过程量)
宏观运动能量
热运动能量
功是能量传递和转换的量度,它引起系统热运动状 态的变化 .
准静态过程功的计算
dW Fdl pSdl dW pdV
W V2 pdV V1
注意:作功与过程有关 .
V2 V1
W V2 pdV V1 W 0 气体对外界作功
热力学利用宏观上可观测的物理量,如:
p,V ,T 来研究热现象的规律。
从微观上看,热学主要研究宏观热现象的本质,即宏观热现象的微观解释:构成宏观 物体的大量微观粒子的永不休止的无规运动的统计规律,这部分称为气体动理论,也 称为统计物理学。
气体动理论利用不可直接测量的、描述个别分子运动状态的微观量,如
标准状态: 1atm 1.013105 Pa T 273.15K
1 mol气体的体积
(0 oC )
V 22.4L 2.24 102 m3
pV RT
R 如何计算?
pV pVmol psVsmol R
T
T
Ts
R
psVsmol
1.013105 22.4 103
Ts
273.15
8.307 8.31(J mol1 K1)
五 准静态过程(quasi-static process)(理想化的过程)
准静态过程:从一个平衡态到另一平衡态所经过的每一中间状态均可近似当作 平衡态的过程 .
p
砂子
p1 1 ( p1,V1,T1)
活塞
p2
2 ( p2 ,V2 ,T2 )
两种方法的关系
热力学
相辅相成
气体动理论
二 气体的宏观物态参量
用什么物理量来描述一个热力学系统? 一个热力学系统,如果没有外界因素的影响,当这个系统经过足够长的时间
以后,将会达到一个稳定的、宏观性质不随时间变化的状态,这一状态称为平衡 态 .(理想状态)
从微观上看,组成气体的分子的运动状态时刻都在变化,所以,热力学系统 的平衡态是一种动态平衡。
以后我们可以证明:
理想气体的内能仅是温度的函数。
E E(T )
系统内能为表征系统状态的单值函数,它的增量只与系统起始和终了状态有 关,与系统所经历的过程无关。
由能量守恒定律:系统吸收的热量
Q
实验证明系统从 A 状态变化到 B 状态,可以采用做功和传热的方法,不管经过 什么过程,只要始末状态确定,外界做功和传给系统的热量之和保持不变 .
T1 T2
T1 Q T2
1卡(calorie) = 4.18 J , 1 J = 0.24 卡
3)功与热量的物理本质不同 .
功 宏观运动
热量 分子热运动
分子热运动 分子热运动
规定
吸热 Q 0 放热 Q 0
作机械功改变系统 状态的焦耳实验
作电功改变系统 状态的实验
A V
八 热力学第一定律 我们可以通过作功、传热等方式,把外界的能量传给气体。如果外界对气体
