2007年慈溪中学保送生招生考试数学试题
2007年高中阶段学校招生考试数学试卷

2007年高中阶段学校招生考试数学试卷(考试时间:120分钟全卷满分120分)题号基础卷拓展卷总分总分人-一--二二三合计四五1~89~121314151617~2021222324得分注意事项:1. 答题前,必须把考号和姓名写在密封线内;2. 直接在试卷上作答,不得将答案写到密封线内I基础卷(全体考生必做,共3个大题,共72分)一、选择题:(本大题8个小题,每小题3分,共24分)以下每个小题均给出了代号为A、B、C、D的四个答案,其中只有一个答案是正确的,请将正确答案的代号直接填在题后的括号中•1.25的算术平方根是()A. 5B. 5 C .-5 D .土512.在函数y = x~2中,自变量x的取值范围是()A. x 工0B. x > 2C. x 工2D. x < -23 .某市在今年4月份突遇大风、冰雹灾害性天气,造成直接经济损失5000万元.5000万元用科学记数法表示为()A. 5000万元B . 5 102万元C. 5 103万元 D . 5 104万元4•实数a、b在数轴上的位置如图所示,则化简代数式|a+b|-a的结果是()_____ I I Ia 0bA. 2a+bB. 2a(第4题图)C. aD. b5.已知:如图,四边形ABCD是O O的内接正方形,点P是劣弧CD上不同于点C的任意一点,则/ BPC的P 度数是()A. 45 °B. 60 °6•下面是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中既是轴称图形又是中心对称图形的是()若设该班男生人数为x,女生人数为y,则下列方程组中,能正确计算出C. 75D. 90°7.某班共有学生49人.一天,该班某男生因事请假, 当天的男生人数恰为女生人数的一半A.x -y= 49y=2(x+i)x+y= 49y=2(x+1)C.x -y= 49y=2(x-)lx+y= 49y=2(x-1)& 2006年的夏天,某地旱情严重.该地10号、15号的人日均用水量的变化情况如图所示•若该地10号、15号的人均用水量分别为18千克和15千克,并一直按此趋势直线下降当人日均用水量低于10千克时,政府将向当地居民送水•那么政府应开始送水的号数为()A. 23B. 24C. 25D. 26二、填空题:(本大题4个小题,每小题3分,共12分)在每小题中,请将答案直接填在题中的横线上•9 .因式分解:10.如图,在△(第10题图)以确定△ ABC是等腰三角形•你添加的条件是____________ . ________11. 一组数据1 , 6, x , 5, 9的平均数是5,那么这组数据的中位数是___________ .12.不等式组七第的解是_______________________x、y的是()三、解答题:(本大题4个小题,共36分)解答时每小题都必须给出必要的演算过程或推理步骤•13.(本题共3个小题,每小题x——1,其中x =5x5分,共15分)(2)计算:-2+ ,8+( 37 -2007)0 -4sin45(3)甲、乙两同学设计了这样一个游戏:把三个完全一样的小球分别标上数字1、2、3后, 放在一个不透明的口袋里,甲同学先随意摸出一个球,记住球上标注的数字,然后让乙同学抛掷一个质地均匀的、各面分别标有数字1、2、3、4、5、6的正方体骰子,又得到另一个数字,再把两个数字相加•若两人的数字之和小于7,则甲获胜;否则,乙获胜•①请你用画树状图或列表法把两人所得的数字之和的所有结果都列举出来;②这个游戏公平吗?如果公平,请说明理由;如果不公平,请你加以改进,使游戏变得今年4月18日,是全国铁路第六次大提速的第一天,小明的爸爸因要出 差,于是去火车站查询列车的开行时间 •下面是小明的爸爸从火车站带回始发点 发车时间 终点站 到站时间 A 站上午8 : 20B 站次日12 : 20小明的爸爸找出以前同一车次的时刻表如下:公平.14.(本小题满分7分)如图,将△ BOD 绕点0旋转180°后得到△ AOC ,再过点0任意画一条与 AC 、BD 都相交的直线 MN ,交点分别为 M 和N.试问:线段 OM = ON 成 立吗?若成立,请进行证明;若不成立,请说明理由C(第14题图)15 .本小题满分7分) 家的最新时刻表:始发点发车时间终点站到站时间A站下午14 : 30B站第三日8 : 30比较了两张时刻表后,小明的爸爸提出了如下两个问题,请你帮小明解答:(1 )现在该次列车的运行时间比以前缩短了多少小时?(2)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果精确到个位)H 拓展卷(升学考生必做,共2个大题,共48分)四、填空题:(本大题4个小题,每小题3分,共12分)在每小题中,请将答案直接填在题中的横线上•17.数学家发明了一个魔术盒,当任意实数对(a, b)进入其中时,会得到一个新的实数:a2+b+1.例如把(3,- 2)放入其中,就会得到32+(乞)+仁8.现将实数对(2 3)放入其中得到实数m,再将实数对(m, 1)放入其中后,得到的实数是____________ .16.(本小题满分7分)18•如图,是几个相同的小正方体搭成的几何体的三种视图, 则搭成这个几何体的小正方体19.已知:如图,△ ABC 中,过 AB 的中点F 作DE 丄BC , 垂足为E ,交CA 的延长线于点 D.若EF =3, BE =4,/ C = 45 ° 贝U DF : FE 的值为 _________________ . 20•如图,二次函数 y=ax 2+bx+c (aM )).图象的顶点为 D , 其图象与x 轴的交点A 、B 的横坐标分别为 -、3,与y 轴负半轴交于点 C.下面四个结论:①2a+b=0;1②a+b+c>0 :③只有当a= 3时,△ ABD 是等腰直角三角形;④使△ ACB 为等腰三角形的a 的值可以有三个. 那么,其中正确的结论是 (只填你认为正确结论的序号)2(注:二次函数 y=ax +bx+c (a 和)图象的顶点坐 24ac_b_4a ))五、解答题:(本大题4个小题,共36分)解答时每小题都必须给出必要的演算过程或推理21 .(本小题满分8分)某商场将某种商品的售价从原来的每件 40元经两次调价后调至每件 元.(1 )若该商店两次两次调价的降价率相同,求这个降价率;(2)经调查,该商品每降价 0.2元,即可多销售10件.若该商品原来每月可销售 500件,那么两次调价后,每月可销售该商品多少件?\0 /\ r的个数是标为(-暑, 32.4主视图(第20题图)22. (本小题满分8分)已知;如图,在△ ABC中,AB =AC,/ ABC=90°.F为AB延长线上一点,点E在BC上,BE = CF,连接AE、EF和CF.(1)求证:AE=CF ;(2)若/ CAE=30,求/ EFC 的度数.23. (本小题满分8分)已知:如图,在半径为4的O O中,圆心角/ AOB=90°,以半径0A、OB的中点C、F为顶点作矩形CDEF,顶点D、E在O 0的劣弧A B上,0M丄DE于点M.试求图中阴影部分的面积.(结果保留n )(第22题图)(第23题图)24. (本小题满分12分)已知:如图,二次函数y=/+(2k-)x+k+1的图象与x轴相交于0、A两点.(1)求这个二次函数的解析式;(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角厶A0B的面积等于3.求点B的坐标;(3)对于⑵中的点B,在抛物线上是否存在点P,使/ POB=90°若存在,求出点P的坐标,并求出厶P0B的面积;若不存在,请说明理由.(第24题图)。
最新慈溪中学保送生模拟考试试题
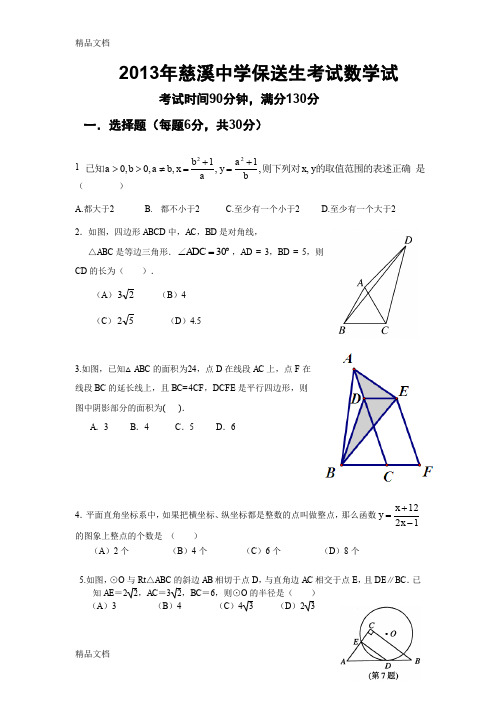
2013年慈溪中学保送生考试数学试考试时间90分钟,满分130分 一.选择题(每题6分,共30分)1 ( )A.都大于2B.都不小于2C.至少有一个小于2D.至少有一个大于2 2.如图,四边形ABCD 中,AC ,BD 是对角线,△ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5,则CD 的长为( ).(A )23 (B )4 (C )52 (D )4.53.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC=4CF ,DCFE 是平行四边形,则图中阴影部分的面积为( ).A .3B .4C .5D .64.平面直角坐标系中,如果把横坐标、纵坐标都是整数的点叫做整点,那么函数1212-+=x x y 的图象上整点的个数是 ( )(A )2个 (B )4个 (C )6个 (D )8个5.如图,⊙O 与Rt △ABC 的斜边AB 相切于点D ,与直角边AC 相交于点E ,且DE ∥BC .已知AE =22,AC =32,BC =6,则⊙O 的半径是( ) (A )3 (B )4 (C )4 3 (D )2 3是的取值范围的表述正确则下列对已知y x ba y ab x b a b a ,,1,1,,0,022+=+=≠>>二.填空题(每题6分,共36分)6.函数1422-+=x x y 的最小值是 .7、 已知正整数a 、b 、c 满足a +b 2-2c -2=0,3a 2-8b +c=0,则abc 的最大值为 . 8、 实数a 、b 、c 、d 满足:一元二次方程x 2+cx +d=0的两根为a 、b ,一元二次方程x 2+ax +b=0的两根为c 、d ,则所有满足条件的数组(a 、b 、c 、d )为 . 9.如图,四边形ABCD 内接于⊙O ,AB 是直径,AD = DC . 分别延长BA ,CD , 交点为E . 作BF ⊥EC ,并与EC 的延长线 交于点F . 若AE = AO ,BC = 6,则CF 的 长为 .10.如图,正方形ABCD 的边长为215, E ,F 分别是AB ,BC 的中点,AF 与DE ,DB 分别交于点M ,N ,则△DMN 的面积是 .11.如图,已知AB 是⊙O 的直径,弦CD 与AB 交于点E ,过点A 作圆的切线与CD 的延长线交于点F ,如果CE DE 43=,58=AC ,D 为EF 的中点,则AB = .DFBOACE三.解答题(每题16分,共64分)12.在直角坐标系xOy中,一次函数y=kx+b+2(k≠0)的图象与x轴、y轴的正半轴分别交于A,B两点,且使得△OAB的面积值等于|OA|+|OB|+3.(1)用b表示k;(2)求△OAB面积的最小值.13.如图,M、N、P分别为△ABC三边AB、BC、CA的中点,BP与MN、AN分别交于E、F,(1)求证:BF=2FP;(2)设△ABC的面积为S,求△NEF的面积.BAC MNPEF14.如图,在菱形ABCD 中, E, F, G, H,分别在AB ,BC ,CD ,DA 上,且AE=AH=BF=DG ,已知EH=EF=5,FG=11,求tanB 的值以及AB 的长。
练习卷2教学文档

慈溪中学保送生数学练习卷21、如图,已知图中每个小方格的边长为1,则点C 到AB 所在直线的距离等于_______________.2、已知一个梯形的上下底分别为2006和2008,两腰长恰为方程x 2-4x+m=0的两实根,则m 的取值范围为 。
3、将一个边长为1的正方形,绕其一个顶点旋转60°后得到一个新的正方形,则两正方形重叠部分的面积为 。
4、若 x ≠0,则的最大值为 。
5、如图,ABCDEF 内接于圆,且AB=CD=DE=2,BC=EF=FA=1,则六边形的面积为 。
6、7、在Rt △ABC 中,∠C=90°,BC=2,AC=3,∠A 和∠B 的内角平分线交于P ,又PE ⊥AB 与E ,则AE ×BE= 。
8、过P (0,2)的直线交抛物线y= x 2+1,与A 、B 则以AB 为直径的圆与x 轴位置关系( )A 、相交B 、相离C 、相切D 、与AB 的位置有关9、已知四边形1S 的两条对角线相等,但不垂直,顺次连结1S 各边中点得四边形2S ,顺次连结2S 各边中点得四边形3S ,以此类推,则2006S 为( )A .是矩形但不是菱形B. 是菱形但不是矩形C. 既是菱形又是矩形D. 既非矩形又非菱形 10、过点P(-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( )A . 4条B . 3条C . 2条D . 1条11、点P 是半径为5的圆内的一点,且P 到圆心的距离为3,在过P 点的所有弦中,长度为整数的弦共 条。
12、水池装有编号为①②③④⑤的五个水管,其中有进水管,也有出水管,如果同时开放两个水管,注满水池所需时间如下表:试确定那些是进水管,那些是出水管。
13、开放水管号 ①② ②③ ③④ ④⑤ ①⑤ 所需时间(小时) 15 6 3 10 214、设直线与两坐标轴所围成的图形面积为S k ,求S 1+S 2+S 3+…+S 2006 的值。
2007年普通高等学校招生全国统一考试数学卷(浙江.文)含答案

2007年普通高等学校招生全国统一考试(浙江卷)数学(文科)第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{13568}U =,,,,,{16}A =,,{568}B ,,,则()UA B =( )A .{6}B .{58},C .{68},D .{3568},,,2.已知π3cos 22ϕ⎛⎫+=⎪⎝⎭,且π||2ϕ<,则tan ϕ=( ) A .33-B .33C .3-D .33.“1x >”是“2x x >”的( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.直线210x y -+=关于直线1x =对称的直线方程是( ) A.210x y +-= B.210x y +-= C.230x y +-=D.230x y +-=5.要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是( ) A.6 B.5 C.4 D.36.91x x ⎛⎫- ⎪⎝⎭展开式中的常数项是( )A .36-B .36C .84-D .847.若P 是两条异面直线l m ,外的任意一点,则( ) A .过点P 有且仅有一条直线与l m ,都平行 B .过点P 有且仅有一条直线与l m ,都垂直 C .过点P 有且仅有一条直线与l m ,都相交 D .过点P 有且仅有一条直线与l m ,都异面8.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜,根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是( )第5题A .0.216B .0.36C .0.432D .0.6489.若非零向量,a b 满足-=a b b ,则( ) A.22>-b a b B.22<-b a b C.2>-a 2a bD. 2<-a 2a b10.已知双曲线22221(00)x y a b a b-=>>,的左、右焦点分别为1F ,2F ,P 是准线上一点,且12PF PF ⊥,124PF PF ab =,则双曲线的离心率是( ) A.2B.3C.2D.3第II 卷(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.函数221x y x =+(x ∈R )的值域是 .12.若1sin cos 5θθ+=,则sin 2θ的值是 . 13.某校有学生2000人,其中高三学生500人,为了解学生的身体素质情况,彩用按年级分层抽样的方法,从该校学生中抽取一个200人的样本,则样本中高三学生的人数为 .14.2z x y =+中的x y ,满足约束条件250300x y x x y -+=⎧⎪-⎨⎪+⎩,≥,≥,则z 的最小值是 .15.曲线32242y x x x =--+在点(13)-,处的切线方程是 .16.某书店有11种杂志,2元1本的8种,1元1本的3种.小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答). 17.已知点O 在二面角AB αβ--的棱上,点P 在α内,且45POB ∠=.若对于β内异于O 的任意一点Q ,都有45POQ ∠≥,则二面角AB αβ--的大小是.三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤. 18.(本题14分)已知ABC △的周长为21+,且sin sin 2sin A B C +=.(I )求边AB 的长; (II )若ABC △的面积为1sin 6C ,求角C 的度数. 19.(本题14分)已知数列{}n a 中的相邻两项212k k a a -,是关于x 的方程2(32)320k k x k x k -++=的两个根,且212(123)k k a a k -=≤,,,.(I )求1a ,3a ,5a ,7a 及2n a (4n ≥)(不必证明); (II )求数列{}n a 的前2n 项和2n S .20.(本题14分)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点.(I )求证:CM EM ⊥;(II )求DE 与平面EMC 所成的角的正切值.21.(本题15分)如图,直线y kx b =+与椭圆2214x y +=交于A B ,两点,记AOB △的面积为S .(I )求在0k =,01b <<的条件下,S 的最大值;(II )当2AB =,1S =时,求直线AB 的方程.22.(本题15分)已知22()|1|f x x x kx =-++. (I )若2k =,求方程()0f x =的解;(II )若关于x 的方程()0f x =在(02),上有两个解12x x ,,求k 的取值范围,并证明12114x x +<.EDCMA(第20题)BAyxO B(第21题)2007年普通高等学校招生全国统一考试(浙江卷)数学(文科)试题参考答案一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分. 1.B 2.C 3.A 4.D 5.C 6.C7.B 8.D 9.A 10.B二、填空题:本题考查基本知识和基本运算.每小题4分,满分28分. 11.[01),12.2425-13.5014.53-15.520x y +-=16.26617.90三、解答题18.本题主要考查利用正弦定理、余弦定理来确定三角形边、角关系等基础知识和基本运算能力.满分14分.解:(I )由题意及正弦定理,得21AB BC AC ++=+,2BC AC AB +=,两式相减,得1AB =. (II )由ABC △的面积11sin sin 26BC AC C C =,得13BC AC =, 由余弦定理,得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--==, 所以60C =.19.本题主要考查等差、等比数列的基本知识,考查运算及推理能力.满分14分.(I )解:方程2(32)320k kx k x k -++=的两个根为13x k =,22k x =.当1k =时,13x =,22x =, 所以12a =;当2k =时,16x =,24x =, 所以34a =;当3k =时,19x =,28x =, 所以58a =;当4k =时,112x =,216x =, 所以712a =.因为当4n ≥时,23nn >,所以22(4)nn a n =≥.(II )解:2122k n S a a a =+++2(363)(222)n n =+++++++2133222n n n ++=+-.20.本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.满分14分. 方法一: (I )证明:因为AC BC =,M 是AB 的中点,所以CM AB ⊥.又因为EA ⊥平面ABC , 所以CM EM ⊥.(II )解:连结MD ,设AE a =,则2BD BC AC a ===, 在直角梯形EABD 中,22AB a =,M 是AB 的中点,所以3DE a =,3EM a =,6MD a =,因此DM EM ⊥.因为CM ⊥平面EMD , 所以CM DM ⊥,因此DM ⊥平面EMC ,故DEM ∠是直线DE 和平面EMC 所成的角. 在Rt EMD △中,6MD a =,3EM a =,tan 2MDDEM EM∠==. 方法二:如图,以点C 为坐标原点,以CA ,CB 分别为x 轴和y 轴,过点C 作与平面ABC 垂直的直线为z 轴,建立直角坐标系C xyz -,设EA a =,则(2)A a 00,,,(020)B a ,,,EDCMAByzxED C MAB(20)E a a ,,.(022)D a a ,,,(0)M a a ,,.(I )证明:因为()EM a a a =--,,,(0)CM a a =,,, 所以0EM CM =, 故EM CM ⊥.(II )解:设向量001y z (),,n =与平面EMC 垂直,则EM ⊥n ,CM ⊥n , 即0EM =n ,0CM =n .因为()EM a a a =--,,,(0)CM a a =,,, 所以01y =-,02x =-, 即112(--),,n =,因为(22)DE a a a =--,,, 6cos 3DE DE DE <>==,n n n, DE 与平面EMC 所成的角θ是n 与DE 夹角的余角,所以tan 2θ=.21.本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.满分15分.(I )解:设点A 的坐标为1()x b ,,点B 的坐标为2()x b ,.由2214x y +=,解得21,221x b =±- 所以222121||21112S b x x b b b b =-=-≤+-= 当且仅当22b =时,.S 取到最大值1. (Ⅱ)解:由2214y kx b x y =+⎧⎪⎨+=⎪⎩得 222(41)8440k x kbx b +++-=2216(41)k b ∆=-+ ①|AB |=222212216(41)1||1241k b k x x kk -++-=+=+ ② 又因为O 到AB 的距离2||21||1b Sd AB k ===+ 所以221b k =+ ③ ③代入②并整理,得424410k k -+= 解得,2213,22k b ==,代入①式检验,△>0 故直线AB 的方程是2622y x =+或2622y x =-或2622y x =-+或2622y x =--. (22)本题主要考查函数的基本性质、方程与函数的关系等基础知识,以及综合运用所学知识、分类讨论等思想方法分析和解决问题的能力.满分15分. (Ⅰ)解:(1)当k =2时, 22()|1|20f x x x x =-++=① 当210x -≥时,x ≥1或x ≤-1时,方程化为22210x x +-= 解得132x -±=,因为13012-+<<,舍去, 所以132x --=. ②当210x -<时,-1<x <1时,方程化为210x += 解得12x =-, 由①②得当k =2时,方程()0f x =的解所以132x --=或12x =-. (II)解:不妨设0<x 1<x 2<2,因为22 1 ||1() 1 ||1x kx x f x kx x ⎧+->=⎨+≤⎩所以()f x 在(0,1]是单调函数,故()f x =0在(0,1]上至多一个解, 若1<x 1<x 2<2,则x 1x 2=-12<0,故不符题意,因此0<x 1≤1<x 2<2.由1()0f x =得11k x =-, 所以1k ≤-; 由2()0f x =得2212k x x =-, 所以712k -<<-; 故当712k -<<-时,方程()0f x =在(0,2)上有两个解. 因为0<x 1≤1<x 2<2,所以11k x =-,22221x kx +-=0 消去k 得 2121220x x x x --=即212112x x x +=, 因为x 2<2,所以12114x x +<.。
2006年慈溪中学保送生招生考试数学试题及答案
2006年慈溪中学保送生招生考试试题数 学说明:I. 本卷考试时间90分钟,满分100分。
II. 本卷分为试题(共2页)和答卷(共4页),答案必须做在答题卷上。
试 题一、 填空题(每题5分,共25分) 1.实数x 1,x 2满足x 1- x 2=3,则x 1,x 2的方差等于 ▲ 。
2. CD 为Rt △ABC 斜边上的高线,AC 、BC 为x 2-5x+2=0的两根,则AD ·BD 的值等于 ▲ 。
3.如图,△ABC 中,AB=AC=8,D 、E 、F 为BC 、AB 、AC 上的点,DE=DB ,DF=DC ,BE+CF=4,则BC= ▲ 。
4.如图,Rt △ABC 纸片中,∠C=90°,BC=1,AB=2,沿AD 对折,使点C 落在AB 边上,则tan α= ▲ 。
5.如图,在直角坐标系中,点P (3,3),两坐标轴的正半轴上有M 、N 两点,且∠MPN=45°,则△MON 的周长等于 ▲ 。
二、 选择题(每题5分,共25分)6.若关于x 的不等式组 有解,则函数y=(a-3)x 2-x-41图象与x 轴的交点个数为(▲)(A )0 (B )1 (C )2 (D )1或27.设a 、b 、c 、d 、e 的值均为0、1、2中之一,且a+b+c+d+e=6,a 2+b 2+c 2+d 2+e 2=10,则a 3+b 3+c 3+d 3+e 3的值为 (▲)(A )14 (B )16(C )18 (D )20 8.正五边形对角线长为2,则边长a 为(▲)(A )5-1 (B )5+1 (C )3-5 (D )25-39.如图,圆O 的圆心在梯形ABCD 的底边AB 上,并与其它三边均相切,若AB=10,AD=6,则CB 长(▲)(A )4 (B )5(C )6 (D )无法确定 10.平面直角坐标系中,已知点P 0(1,0),将点P 0绕原点O 按逆时针方向旋转30°得到P 1,延长OP 1到P 2,使OP 2=2OP 1;再将P 2绕点O 按逆时针方向旋转30°得P 3,然后延长OP 3到P 4,使OP 4=2OP 3;……;如此下去,则点P 2004的坐标为(▲)(A )(-22004,0) (B )(-21002,0) (C )(0,21002) (D )(21002,0)x ≥a+2x <3a-2 C (第3题)BDαC Ax(第5题)(第9题)三、 解答题(共50分) 11.(12分)设x 1、x 2是方程x 2-6x+a=0的两个根,以x 1、x 2为两边长的等腰三角形只可以画出一个,试求a 的取值范围。
2006-2007学年浙江省宁波市慈溪市七年级(下)期末数学试卷

2006-2007学年浙江省宁波市慈溪市七年级(下)期末数学试卷2006-2007学年浙江省宁波市慈溪市七年级(下)期末数学试卷一、填空题(共8小题,每小题5分,满分40分)1.(5分)计算:(﹣)0=_________.2.(5分)计算:(1)a3•a2=_________;(2)(a2)3=_________;(3)a3÷a2=_________.3.(5分)如图,在△ABC中,它的外角∠EAC=100°,∠C=60°,则∠B=_________度.4.(5分)写出方程2x﹣3y=7的两个解_________,_________.5.(5分)如图为一个可以自由转动的转盘,现转动转盘,当转盘停止转动时,指针可指到标有数字的区域,设指针指到数字为奇数区域的概率为P(A),指针指到数字为偶数区域的概率为P(B),则P(A),P(B)大小关系为P(A)_________P(B)(填“<”、“=”或“>”).6.(5分)已知3x﹣2y=5,3x+2y=12,则9x2﹣4y2=_________.7.(5分)举一个生活中的物体作平移运动的例子_________.8.(5分)节日期间,几名大学生合租了一辆车准备从市区到郊外游览,租金为500元,出发时又增加了4名同学,总人数达到了a名,则开始包车的几名学生平均每人可以比原来少分摊_________元钱(要求化简).二、选择题(共10小题,每小题4分,满分40分)10.(4分)下列图形中,是轴对称图形的有()11.(4分)(2006•柳州)在下列的计算中,正确的是()12.(4分)(2006•浙江)已知分式的值是零,那么x 的值是( )14.(4分)小明已有两根长度分别为5cm 和8cm 的木棒,他想把木棒首尾相接钉成一个三角形的木框,现在第三.CD .16.(4分)如图,在△ABC 和△DEF中,AB=DE ,∠B=∠E ,补充下列哪一个条件后,能直接应用“SAS ”判定△ABC ≌△DEF ( )17.(4分)有一对酷爱运动的年轻夫妇,给他们11个月大的婴儿拼排3块分别写有“20”、“08”和“北京”的字块,如图所示,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励.假设该婴儿不能辨别字块中的内容,但能将字块横着正排.现让该婴儿把三块字块任意排成一行,那么他能得到奖励的概率是( )CD .18.(4分)(2006•大兴安岭)为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么甲三、解答题(共8小题,满分0分) 1.把下列多项式分解因式: (1)x 2﹣4x+4;(2)4ax 2﹣ay 2.2.解下列方程(组):(1)(2).3.化简并求值:3(m+1)2﹣5(m﹣1)(m+1)+2m(m﹣1),其中m=3.4.计算:5.如图,分别按下列要求画出变换后的图形.(1)把△ABC向右平移3个单位得△A1B1C1(A与A1对应,B与B1对应);(2)以A1为旋转中心,将△A1B1C1逆时针旋转90°得△A1B2C2(B1与B2对应);(3)把A1B2C2的每一条边都扩大到原来的2倍得△DEF.6.已知:如图△ABC中,AD=AE,∠ADC=∠AEB,BE与CD相交于点O.(1)在不添加辅助线的情况下,我们可由已知条件得出一些结论,如△ABE≌△ACD,∠DOB=∠EOC,∠DOE=∠BOC,∠BDC=∠CEB等,请你写出除上述已列举外的其他4个结论.①_________≌_________;②_________=_________;③_________=_________;④_________=_________.(2)就你写出的其中一个结论,说明其成立的理由.7.已知:如图①,现有a×a,b×b的正方形纸片和a×b的长方形纸片各若干块.(1)图②是用这些纸片拼成的一个长方形,(每两个纸片之间既不重叠,也无空隙),利用这个长方形的面积,写出一个代数恒等式_________;(2)试选用图①中的纸片(每种纸片至少用一次)在下面的方框中拼成与图②不同的一个长方形,(拼出的图中必须保留拼图的痕迹),标出此长方形的长和宽,并利用拼成的长方形面积写出一个代数恒等式.8.学校书法兴趣小组准备到文具店购买A,B两种类型的毛笔,请你根据下面三位同学的对话,求出文具店的A,B两种类型毛笔的零售价各是多少?甲:文具店的销售方法是:一次性购买A型毛笔不超过20支,按零售价销售,超过20支时,超过部分每支比零售价低0.4元,其余部分仍按零售价销售,一次性购买B型毛笔不超过15支,按零售价销售,超过15支时,超过部分每支比零售价低0.6元,其余部分仍按零售价销售.乙:若全组共有20名同学,且每人各买1支A型毛笔和2支B型毛笔,共支付145元.丙:若每人各买2支A型毛笔和1支B型毛笔,共支付129元.2006-2007学年浙江省宁波市慈溪市七年级(下)期末数学试卷参考答案与试题解析一、填空题(共8小题,每小题5分,满分40分)1.(5分)计算:(﹣)0=1.)2.(5分)计算:(1)a3•a2=a5;(2)(a2)3=a6;(3)a3÷a2=a.3.(5分)如图,在△ABC中,它的外角∠EAC=100°,∠C=60°,则∠B=40度.4.(5分)写出方程2x﹣3y=7的两个解,.的二组解是:.5.(5分)如图为一个可以自由转动的转盘,现转动转盘,当转盘停止转动时,指针可指到标有数字的区域,设指针指到数字为奇数区域的概率为P(A),指针指到数字为偶数区域的概率为P(B),则P(A),P(B)大小关系为P(A)=P(B)(填“<”、“=”或“>”).=6.(5分)已知3x﹣2y=5,3x+2y=12,则9x2﹣4y2=60.7.(5分)举一个生活中的物体作平移运动的例子例如电梯上升下降.8.(5分)节日期间,几名大学生合租了一辆车准备从市区到郊外游览,租金为500元,出发时又增加了4名同学,总人数达到了a名,则开始包车的几名学生平均每人可以比原来少分摊元钱(要求化简).﹣==二、选择题(共10小题,每小题4分,满分40分)10.(4分)下列图形中,是轴对称图形的有()12.(4分)(2006•浙江)已知分式的值是零,那么x的值是()=014.(4分)小明已有两根长度分别为5cm和8cm的木棒,他想把木棒首尾相接钉成一个三角形的木框,现在第三.C D.16.(4分)如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能直接应用“SAS”判定△ABC≌△DEF ()17.(4分)有一对酷爱运动的年轻夫妇,给他们11个月大的婴儿拼排3块分别写有“20”、“08”和“北京”的字块,如图所示,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励.假设该婴儿不能辨别字块中的内容,但能将字块横着正排.现让该婴儿把三块字块任意排成一行,那么他能得到奖励的概率是()C D.的概率是18.(4分)(2006•大兴安岭)为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么甲三、解答题(共8小题,满分0分)1.把下列多项式分解因式:(1)x2﹣4x+4;(2)4ax2﹣ay2.2.解下列方程(组):(1)(2).)3.化简并求值:3(m+1)2﹣5(m﹣1)(m+1)+2m(m﹣1),其中m=3.4.计算:故答案为5.如图,分别按下列要求画出变换后的图形.(1)把△ABC向右平移3个单位得△A1B1C1(A与A1对应,B与B1对应);(2)以A1为旋转中心,将△A1B1C1逆时针旋转90°得△A1B2C2(B1与B2对应);(3)把A1B2C2的每一条边都扩大到原来的2倍得△DEF.6.已知:如图△ABC中,AD=AE,∠ADC=∠AEB,BE与CD相交于点O.(1)在不添加辅助线的情况下,我们可由已知条件得出一些结论,如△ABE≌△ACD,∠DOB=∠EOC,∠DOE=∠BOC,∠BDC=∠CEB等,请你写出除上述已列举外的其他4个结论.①△DBC≌△ECB;②∠ACD=∠ABE;③BD=CE;④OB=OC.(2)就你写出的其中一个结论,说明其成立的理由.7.已知:如图①,现有a×a,b×b的正方形纸片和a×b的长方形纸片各若干块.(1)图②是用这些纸片拼成的一个长方形,(每两个纸片之间既不重叠,也无空隙),利用这个长方形的面积,写出一个代数恒等式(a+b)(a+2b)=a2+3ab+2b2;(2)试选用图①中的纸片(每种纸片至少用一次)在下面的方框中拼成与图②不同的一个长方形,(拼出的图中必须保留拼图的痕迹),标出此长方形的长和宽,并利用拼成的长方形面积写出一个代数恒等式.8.学校书法兴趣小组准备到文具店购买A,B两种类型的毛笔,请你根据下面三位同学的对话,求出文具店的A,B两种类型毛笔的零售价各是多少?甲:文具店的销售方法是:一次性购买A型毛笔不超过20支,按零售价销售,超过20支时,超过部分每支比零售价低0.4元,其余部分仍按零售价销售,一次性购买B型毛笔不超过15支,按零售价销售,超过15支时,超过部分每支比零售价低0.6元,其余部分仍按零售价销售.乙:若全组共有20名同学,且每人各买1支A型毛笔和2支B型毛笔,共支付145元.丙:若每人各买2支A型毛笔和1支B型毛笔,共支付129元.参与本试卷答题和审题的老师有:郭静慧;399462;zhjh;cook2360;zhehe;玲;leikun;蓝月梦;leidan;自由人;kuaile;py168;wdxwzk;算术;MMCH;117173;CJX;haoyujun;开心;lanchong;csiya;zzz;xiu;lanyan;hnaylzhyk;wdxwwzy;HJJ;137-hui;心若在;wangming;zhangCF(排名不分先后)菁优网2013年5月16日。
慈溪中学保送生招生考试(含答案).

慈溪中学保送生招生考试英语试题Ⅰ、单项选择(共15小题,计15分从A、B、C、D四个选项中,选出可以填人空白处的最佳答案。
1.--This is _________ film I’ve told you about several times.--It’s great. I’ve never seen _______ more moving one.A. a; aB. the; aC. the; theD. a; the2.-- Linda, the new term is coming. Do you think you need a new school bag? --Yes. I’m going to buy ________ this afternoon.A. oneB. thisC. itD. that3.--What does the radio say?--It says there _______ this afternoon.A. is rainyB. is going to rainC. is going to have rainD. is going to be rain4.The little boy will not go to sleep _________________.A. until his mother comes backB. when his mother is coming backC. before his mother will come backD. whether his mother comes back5.He couldn’t _________ an answer when I asked him w hy he was late.A. open upB. try outC. look overD. come up with6.Do you know _____________ in a hundred years?A. what life will be likeB. what will life be likeC. how life will be likeD. how will life be like7.--How often do you have history lessons?--__________, Monday, Wednesday and Friday.A. Every dayB. Every other dayC. Every three daysD. Every a few days8.--I called you at eight o’clock yesterday evening, but there was no answer. --Oh, I’m sorry. I __________ dinner at my friend’s.A. haveB. hadC. was havingD. have had9. --Is England one of the members of APEC?--_________. And neither is France.A. Let me seeB. Yes, it isC. I hope soD. Of course not10.Great changes ________ in Zhejiang since 1979.A. have been taken placeB. have taken placeC. had been taken placeD. were taken place11._________ the man looks at his son! He thinks his son is getting more and more__________.A. How angry; carelesslyB. What angry; carelesslyC. How angrily; carelessD.What angrily; careless12.Day by day, the UN officials _______ discussing about Iran issue. But they wonder what todo with it.A. are busy withB. are interested inC. are excited atD. are amazed at13.The TV set _______ has gone wrong.A. I bought it last weekB. which I bought it last weekC. what I bought last weekD. I bought last week14.Today the forests have almost gone. People must _______ down too many trees.A. stop from cuttingB. be stopped from cuttingC. stop to cutD. be stopped to cut15.--You teach me English and I teach you Chinese.--_________.A. The same to youB. That’s a dealC. It’s a pityD. So do IⅡ、完形填空(共15小题,计15分阅读下面短文,掌握其大意,然后从A、B、C、D四个选项中选出可以填入空白处的最佳答案。
2007年慈溪中学保送生招生考试科学试题

2007年慈溪中学保送生招生考试科学试题本卷考试时间10 0分钟,满分13 0分。
本卷可能用到的相对原子质量:H—1,O—16,S—3 2,N—14,Fe—5 6,Na—2 3,Cu —6 4一、选择题(每小题4分,共10小题,共40分。
每小题只有一个正确选项)1.据报载,有一只鸭子特别有灵性,常跟着一老太太,老太太上哪它就上哪,老太太转个身它也照着做,如影随形,亦步亦趋。
这鸭子的行为与下列哪个选项最为接近( ) A.失去幼仔的母狗会给幼虎喂奶B.蜜蜂朝有花香的地方飞C.孔雀开屏、仙鹤起舞D.听到饲养员的叫声,小鸡会过来啄食2.如右图所示,一空心铝质小球悬浮在用新鲜南瓜制成的“容器”所盛的30%的蔗糖溶液中,一段时间后小球将( )A.上浮 B.停留在原来位置C.下沉D.无法判断3.在下图中,能够合理表示小麦种子萌发时胚乳(—)与胚(…)中有机物含量变化的曲线(横坐标为萌发时间,纵坐标为有机物含量)是( )4.空气是人类生存所必需的重要资源。
为改善空气质量而启动的“蓝天工程”得到了全民的支持。
下列措施不利于“蓝天工程”建设的是( )A.推广使用燃煤脱硫技术,防治SO2污染B.减少火力发电,充分利用风力、海洋潮汐发电C.研制开发燃料电池汽车,消除机动车尾气污染D.加大石油、煤炭的开采速度,增加化石燃料的供应量运用上表有关数据完成第5和6两题5.实验室欲配制12%稀硫酸500毫升,需要28%硫酸(计算结果保留l位小数)( )A.214.3 mL B.192.9 mL C.238.1mL D.235.2 mL6.将l0%的氨水与20%的氨水等体积混合时溶质质量分数( )A.15%B.>15%C.<15%D.上述情况均可能7.某同学用量筒量取酒精溶液。
他将装有酒精的量筒竖立放在水平桌面上,开始时俯视量筒内凹液面的最低处,读数为30毫升,倒出部分液体后,仍将量筒竖立放在水平桌面上,却仰视凹液面的最低处,读数为15毫升,则该同学实际倒出酒精溶液的体积( ) A.大于15毫升B.小于15毫升C.等于15毫升D.无法确定8.如图甲所示,某同学用天平测NaCl的质量,除了将砝码和被称物的位置放错之外其余操作都准确无误,现天平处于平衡状态,图乙表示出了游码在标尺上的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年慈溪中学保送生招生考试数学试题本卷考试时间90分钟,满分130分.一、选择题(每题6分,共30分)1.将正方形ABCD 折叠,使顶点A 与CD 边上的点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G(如图).如果DM :MC=3:2,则DE :DM :EM=(▲)(A)7:24:25 (B)3:4:5 (C)5:12:13 (D)8:15:172.假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学 需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为(▲)(A)8分钟 (B)7分钟 (C)6分钟. (D)5分钟3.已知:二次函数y=x 2+2x+a(a 为大于0的常数),当x=m 时的函数值y 1<0;则当x=m+2时的函数值y 2与0的大小关系为(▲)(A)y 2>0 (B)y 2<0 (C)y 2=O (D)不能确定4.记S=121221121212008200720072007-++++++ 则S 所在的范围为(▲)(A)0<S<1 (B)1<S<2 (C)2<S<3 (D)3<S<45.如图,点A 是函数y=x1的图象上的点,点B 、C 的坐标分别为B(-2,-2)、C(2,2).试利用性质:“函数y=x 1的图象上任意一点A 都满足|AB-AC|=22”求解下面问题:“作∠BAC 的内角平分线AE ,过B 作AE 的垂线交AE 于F ,已知当点A 在函数y=x1的图象上运动时,点F 总在一条曲线上运动,则这条曲线为(▲)(A)直线 (B)抛物线 (C)圆 (D)反比例函数的曲线二、填空题(每题6分,共36分)6.已知关于x 的不等式(2a-b)x≥a -2b 的解是x>5/2,则关于x 的不等式ax+b<0的解为 ▲ .7.已知右边方格纸中的每个小方格是边长为1的正方形,A 、B 两点在小方格的顶点上,位置如图所示.在小方格的顶点上确定一点C ,连结AB 、AC 、BC ,使△ABC 的面积为3个平方单位.则这样的点C 共有 ▲ 个.8.直角坐标系中,点A(0,0),B(2,0),C(0,23),若有一三角形与△AB C 全等,且有一条边与BC 重合,那么这个三角形的另一个顶点坐标是 ▲ .9.n个单位小立方体叠放在桌面上,所得几何体的主视图和俯视图均如图所示.那么n的最大值与最小值的和是▲ .10.对大于或等于2的自然数m的n次幂进行如右图方式的“分裂”,仿此,63的“分裂”中最大的数是▲ .11.甲,乙,丙3人用擂台赛形式进行训练,每局2人进行单打比赛,另1人当裁判,每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时发现甲共打了12局,乙共打了21局,而丙共当裁判8局.那么,整个比赛的第10局的输方一定是▲ .三、解答题(每小题16分,共64分)12.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交手点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形?并证明你的结论.13.已知函数y=x2+(b-1)x+c(b,c为常数),这个函数的图象与x轴交于两个不同的点A(x1,0)和B(x2,0).若x1,x2满足x2-x1>1(1)求证: b2≥2(b+2c);(2)若t<x1,试比较t2+bt+c与x1的大小,并加以证明。
14.有A、B、C、D、E 5位同学依次站在某圆周上,每人手上分别拿有小旗16、8、12、4、15面,现要使每人手中的小旗数相等.要求相邻的同学之间相互调整(不相邻的不作相互调整),设A给B有x1面(x1>0时即为A给B有x1面;x1<O时即为B给A有x1面.以下同),B 给C有x2面:C给D有x3面,D给E有x4面,E给A有x5面,问x1、x2、x3、x4、x5分别为多少时才能使调动的小旗总数|x1|+|x2|+|x3|+|x4|+|x5|最小?15.如图:已知a 为正常数,F 1(-202+a ,0),F 2(202+a ,0),过F 2作直线l ,点A ,B 在直线l 上,且满足AF 1-AF 2=BF 1-BF 2=2a ,M ,N 分别为△AF 1F 2,△B F 1F 2的内切圆的圆心.(1)设⊙M 与F 1F 2相切于点P 1,⊙N 与F 1F 2切于点P 2,试判断P 1与P 2的位置关系,并加以证明;(2)已知sin ∠BF 2F 1=8/9,且MN=9/2,试求a 的值慈溪中学2007年保送生招生考试数学标准答案及评分标准一、选择题(每题6分,共30分)1.D 2.C .3.A 4.A 5.C二、填空题(每题6分:共36分)6.x>-8 7.6 8.(2,23)或(3,3)或(-1,3)(全部正确才给分)9.23 10.41 11.甲三、解答题(共64分)12.(16分)证:(1)△ABC 是等腰直角三角形,∴∠MBE=45°.∴∠BME+∠MEB=135°(2分)又∵△DEF 是等腰直角三角形,∴∠DEF=45°∴∠NEC+∠ME B=135°,∴∠BME=∠NEC,(4分)而∠MBE=∠ECN=45°,∴△BEM∽△CNE (6分)(2)与(1)同理△BEM∽△CNE,BE /CN=EM/NE (10分)又∵BE=EC .(12分)∴EC/CN=EM/NE 则△ECN 与△MEN 中EC/CN =ME/EN ,又∠ECN=∠MEN=45°∴△ECN∽△MEN (16分)(如给出答案△MBE∽△MEN,同样给相应的分值)13.(16分).证:(1):由已知:x 1,2=24)1()1(2c b b --±--,又x 2-x 1>1,(3分) ∴14)1(2>--c b∴b 2-2b+1-4c>1即b 2>2(b+2c)。
(5分)(2)由已知x 2+(b-1)x+c=(x-x 1)(x-x 2) (8分)∴x 2+bx+c=(x-x 1)(x-x 2)+x∴t 2+bt+c=(t-x 1)(t-x 2)+t(12分)t 2+bt+c-x 1=(t-x 1)(t-x 2)+t-x 1=(t-x 1)(t-x 2+1)∵t<x 1 ∴ t-x 1<0 又x 2-x 1>1∴t<x 1<x 2-1∴t-x 2+1<0∴(t-x 1)(t-x 2+1)>0 (15分)即t 2+bt+c>x 1(16分)14.(16分)解:∵共有小旗面数;16+8+12+4+15=55面,要使每人手中的小旗面数相等,每人均为11面. 由题意:⎪⎪⎩⎪⎪⎨⎧=+=+=+=+11x -x 151 1x -x 4 1 1x -x 121 1x -x 854433221 ∴⎪⎪⎩⎪⎪⎨⎧==+=+=2-x x 6-x x 1x x 3x x 25242321∴|x 1|+|x 2|+|x 3|+x 4|+|x 5|=|x 2+3|+|x 2|+|x 2+1|+|x 2-6|+|x 2-2|=|x 2+3|+|x 2+1|+|x 2|+|x 2-2|+| x 2-6|(6分)设实数x 2在数轴上的对应点为P实数-3,-1,0,2,6在数轴上的对应点分别为P 1,P 2,P 3,P 4,P 5∴|x 1|+|x 2|+|x 3|+x 4|+|x 5|=|PP 1|+|PP 2|+|PP 3|+|PP 4|+|PP 5|(10分)当且仅当P 在线段P 1P 5上时|PP 1|+|PP 5|有最小值9:当且仅当P 在线段P 2P 4上时|PP 2|+|PP 4|有最小值3:当且仅当P 与点P 3重合时|PP 3|有最小值0(14分)即当且仅当P 与点P 3重合(x 2=0)时x 1+x 2+x 3+x 4+x 5=|PP 1|+|PP 2|+|PP 3|+|PP 4|+|PP 5|有最小值12。
当x 1=3,x 2=0,x 3=1,x 4=-6,x 5=-2时|x 1|+|x 2|+|x 3|+|x 4|+|x 5 |有最小值12(16分)15.(16分)证:(1)由题意:AC=AD ,∵AF 1-AF 2=2a∴CF 1-DF 2=2a又F 1C=F 1P 1 F 2D=F 2P 1∴P 1F 1-P 1F 2=2a (2分)同理P 2F 1-P 2F 2=2a∴P 1与P 2重合(3分)(2)由(1)知:MP 1⊥F 1F 2,NP 2⊥F 1F 2,P 1,P 2重合.∴M ,P 1,N 共线,且MN⊥F 1F 2(5分).连接MN ,NE ,MD ,则∠NED=∠MDE=90°过N 作NH⊥MD,H 为垂足,∵∠M P 1F 2=∠MD F 2=90°.∠HMN=∠B F 2F 1(9分) ∴sin∠HMN=sin∠B F 2F 1=8/9 又MN=9/2∴NH=MNs in∠HMN=4∴ED=4.(11分).而DF 2=F 2P 1=F 2E∴F 2P 1=2(14分)又由(1)P 1F 1-P 1F 2=2a .∴P 1F 1=2+2a ∴P 1F 1+P 1F 2=2+2+2a=2202 a (15分) 解得:a=4……(16分)。
