2017届天津市五区县高三上学期期末考试l理科数学试卷
【天津市五区县】2017届高三上学期期末考试(理)数学试卷-答案

天津市五区县2017届高三上学期期末考试(理)数学试卷答 案1~5.DACBD6~8.ACD9.810.24-11.32+12.4ln3-1314.(,e)-∞三、解答题:15.(本小题满分13分)解:(I)函数2()2cos cos cos212f x x x x a x x a =++=++π2sin(2)16x a =+++,……………………4分 故函数()f x 的最小正周期为πT =.………………………6分(II )由题意得πππ7π0,,2,2666x x ⎡⎤⎡⎤∈+∈⎢⎥⎢⎥⎣⎦⎣⎦,……………………10分 故min ()112f x a =-++=,所以2a =.……………………13分16.(本小题满分13分)解:(Ⅰ)由题意知,7名队员中分为两部分,3人为女棋手,4人为男棋手,设事件A =“恰有1位女棋手”,则()1334471235C C P A C ==,………………………4分 所以参加第一阶段的比赛的队员中,恰有1位女棋手的概率为1235.…………5分 (Ⅱ)随机变量X 的所有可能取值为0,2,4.其中()22344718035C C P X C ===, ()133134344716235C C C C P X C +===, ()0434471435C C P X C ===.………………………………9分所以,随机变量X 分布列为随机变量X 的数学期望()181613602435353535E X =⨯+⨯+⨯=.………………………………13分 17.(本小题满分13分)解:(Ⅰ)法一:∵~AGD CGE △△,知23DG AD AG GE EC GC ===,且AC =, 故35GC AC == 同理可得35GE DE ==,且3EC =,222GC GE EC +=,ED AC ⊥.………2分 又∵PA ⊥平面ABCD ∴PA ED ⊥……3分而PA AC A =∴ED ⊥平面PAC .ED ⊂平面PDE ,故平面PDE ⊥平面PAC ;……4分法二:∵PA ⊥平面ABCD ∴AB PA ⊥ 又∵AB AD ⊥,故可建立建立如图所示坐标系.由已知(0,2,0)D ,(2,1,0)E ,(2,4,0)C ,(0,0,)P λ(0λ>)∴(2,4,0)AC =,(0,0,)AP λ=,(2,1,0)DE =- ∴4400DE AC ⋅=-+=,0DE AP ⋅=.……3分,∴DE AC ⊥,DE AP ⊥,∴ED ⊥平面PAC,ED ⊂平面PDE ,平面PDE ⊥平面PAC ;……4分 (Ⅱ)(i )由(Ⅰ),平面PAC 的一个法向量是(2,1,0)DE =-,因为PAB △为等腰直角三角形,故2PA =,(2,1,2)PE =-. 设直线PE 与平面PAC 所成的角为θ,则sin cos ,PE DE θ=<>=8分 (ii )设平面PCD 的一个法向量为000(,,)n x y z =,(2,2,0)DC =,(0,2,2)DP =-由n DC ⊥,n DP ⊥∴0000220220x y y z +=⎧⎨-+=⎩,令01x =,则(1,1,1)n =--,………10分 ∴cos ,n DE <>==.………11分显然二面角A PC D --的平面角是锐角,∴二面角A PC D --.………13分(其他方法可酌情给分) 18.(本小题满分13分)解:(I )当2n ≥时,2n A n =,21(1)n A n -=-,两式相减:121n n n a A A n -=-=-;当1n =时,111a A ==,也适合21n a n =-,故数列{}n a 的通项公式为21n a n =-.………3分 (II )由题意知:2122n n n n a n c -==,12n n C c c c =+++,123135212222n n n C -=++++, 23411352122222n n C n +-=++++,两式相减可得:1231122221222222n n n C n +-=++++-,……… 4分 即123-111111121()2222222n n n C n +-=+++++-, -111121(1)2222n n n C n +-=+--,2332n n n C +=-.………7分 (III )21212121n n n b n n -+=++-,显然212122121n n n n -++>=+-, 即2n b >,122n n B b b b n =+++>;………9分 另一方面,21212222112212121212121n n n n n n n n -++=-++=+-+-+--+, 即122213b =+-,222235b =+-,…,11222121n b n n ⎛⎫=+- ⎪-+⎝⎭,2222222(2)(2)(2)22221335212121n B n n n n n =+-++-+++-=+-<+-++, 即:222n n B n <<+.………13分19.(本小题满分14分)解:(Ⅰ)由已知得2222262c a cb ab a b c ⎧+=⎪=⎨⎪=+⎩,解得21a b c =⎧⎪=⎨⎪=⎩所以椭圆C 的方程为22143x y +=.……………5分 (Ⅱ)由题意知12(2,0),(2,0)A A -,……………6分设00(,)P x y ,则100:(2)2A P y l y x x =++,得00(,(2))2y M m m x ++. 且由点P 在椭圆上,得22003(1)4x y =-.……………8分若以MP 为直径的圆过点2A ,则220A M A P ⋅=,……………9分 所以20000000(2,(2))(2,)(2)(2)(2)022y y m m x y m x m x x -+⋅-=--++=++ 2000000033(4)(2)(2)44(2)(2)(2)(2)(2)(2)022x x x m x m m x m x x --+--++=---+=++……………12分 因为点P 是椭圆C 上不同于12,A A 的点,所以02x ≠±. 所以上式可化为3(2)(2)04m m --+=,解得14m =.……………14分20.(本小题满分14分)解法一:(Ⅰ)2()2f x x x c '=-+,当[0,)x ∈+∞时2()20f x x x c '=-+≥ 所以:2min (2)0x x c -+≥,而22x x c -+在1x =处取得最小值,所以:120c -+≥,1c ≥;……………4分(Ⅱ)因为x α=为()f x 的极值点,所以21()20k f c ααα'==-+=,所以22c αα=-+,又因为()y f x m =-有不同的零点,αβ,所以()()f f αβ=, 即32321133c d c d ααααββ-++=-++, 整理得:21(23)()03αβαβ+--=,所以23αβ+=.……………9分(Ⅲ)满足条件的实数c 存在,由2()2f x x x c '=-+,知过00(,())A x f x 点与曲线相切的直线1l 为:000()()+()y f x x -x f x '=,且21002k x x c =-+ 将000()()+()y f x x -x f x '=与()y f x =联立即得B 点的横坐标,所以000()()+(())f x x -x f x f x '= 即:3223200000011(2)()33x x cx d x x c x x x x cx d -++=-+-+-++ 整理得:2001(23)()03x x x x +--= 由已知0x x ≠,所以0230x x +-=所以032x x =-,即B 点的横坐标为032x -所以过点B 的曲线的切线斜率为22()2k f x x x c '==-+200(32)2(32)x x c =---+2004(2)33x x c c =-++-1433k c =+-因此当且仅当330c -=时,1k 、1k 成比例,这时1c =即存在实数1c =,使12k k 为定值……………14分 解法二:(Ⅰ)2()2f x x x c '=-+,当[0,)x ∈+∞时2()20f x x x c '=-+≥, 所以2(2)c x x ≥--对任意的[0,)x ∈+∞恒成立,故2max [(2)]c x x ≥--, 即2max [(2)]1x x --=,故c 的取值范围是[1,)+∞;…………… 4分(Ⅱ)因为x α=为()f x 的极值点,且()y f x m =-有两个零点,()αβαβ≠, 所以()0f x m -=的三个实数根分别为,,ααβ, 由根与系数的关系得12313ααβαβ-++=+=-=;……………9分 (Ⅲ)满足条件的实数c 存在,因为2()2f x x x c '=-+,所以过00(,())A x f x 点且与曲线C 相切的直线1l 为:000()()+()y f x x -x f x '=,其中21002k x x c =-+.设1l 与C 交于另一点11(,)B x y ,则001,,x x x 必为方程000()()()()f x f x x x f x '=-+的三个实数根,由000()()()()f x f x x x f x '=-+,得32200001(2)()()3x x cx d x x c x x f x -++=-+-+ 因为上述方程的右边不含三次项和二次项, 所以0011313x x x -++=-=,所以1032x x =- 所以22111()2k f x x x c '==-+200(32)2(32)x x c =---+2004(2)33x x c c =-++-1433k c =+-.因此当且仅当330c -=时,1k 、1k 成比例,这时1c =,即存在实数1c =,使12k k 为定值.……………14分。
天津市五区县2017届高三上学期期末考试数学(理)试题 含答案

绝密★启用前天津市部分区2016~2017学年度第一学期期末考试高三数学(理科)试卷温馨提示:使用答题卡的区,学生作答时请将答案写在答题卡上;不使用答题卡的区,学生作答时请将答案写在试卷上.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第I卷1至2页,第Ⅱ卷2至4页.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并在规定位置粘帖考试用条形码。
答卷时,考生务必将答案涂写在答题卡上。
考试结束后,将本试卷和答题卡一并交回.祝各位考生考试顺利!第Ⅰ卷(选择题,共40分)注意事项:1.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件,A B互斥,那么()()()=+.P A B P A P B如果事件,A B相互独立,那么()()()=.P A B P A P B锥体的体积公式13V Sh =,其中S 表示锥体的底面面积,h 表示锥体的高。
柱体的体积公式V Sh =,其中S 表示柱体的底面面积,h 表示柱体的高。
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合2{1,4},{|log,}A B y y x x A ===∈,则A B =(A ){}1,4 (B ){}0,1,4 (C ){}0,2 (D ){}0,1,2,4(2)设变量x ,y 满足约束条件240,330,10.x y x y x y +-⎧⎪+-⎨⎪--⎩≤≥≤则目标函数2z x y =-的最小值为(A )165- (B)3- (C )0 (D )1(3)阅读右边的程序框图,运行相应的程序,则输出v 的值为(A )4 (B)5 (C)6 (D )7(4)已知ABC ∆是钝角三角形,若2,1==BC AC ,且ABC ∆3 则=AB(A 3 (B 7(C )22 (D )3(5)设{na }是公比为q 的等比数列,则“1q >” 是“{na }为单调递增数列”的(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(6)已知双曲线22221x y a b-=(0,0a b >>)的焦点到渐近线的距离为2,且双曲线的一条渐近线与直线230x y -+=平行,则双曲线的方程为(A )221164x y -=(B )22194x y -=(C )22149x y -=(D )22184x y -=(7)在ABC ∆中,D 在AB 上,:1:2AD DB =,E为AC 中点,CD 、BE 相交于点P ,连结AP .设AP xAB yAC =+,x y ∈R (),则x ,y 的值分别为 (A)11,23(B )12,33(C)12,55(D )11,36(8)已知2()(3)e x f x x=-(其中x ∈R ,e 是自然对数的底数),当10t >时,关于x 的方程12[()][()]0f x t f x t --=恰好有5个实数根,则实数2t 的取值范围是(A )(2e,0)- (B )(]2e,0- (C )32e,6e -⎡⎤-⎣⎦ (D )(32e,6e-⎤-⎦第Ⅱ卷(非选择题,共110分)注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上. 2.本卷共12小题,共110分.二、填空题:本大题共有6小题,每小题5分,共30分。
天津市五区县高三上学期期末考试数学理试题Word版含答案

( 19)(本小题满分 14 分)
已知椭圆
x2 C : a2
y2 b2
1 (a
b
0) 的左、右焦点分别为
F1 , F2 ,上顶点为 B ,若
BF1F2 的周长为 6 ,且点 F1 到直线 BF2 的距离为 b . (Ⅰ)求椭圆 C 的方程;
(Ⅱ)设 A1, A2 是椭圆 C 长轴的两个端点,点 P 是椭圆 C 上不同于 A1, A2 的任意一点,
解:( I)函数 f ( x) 2cos 2 x 2 3 sin xcos x a cos 2x 1 3 sin 2x a
2sin(2 x ) a 1 , 6
故函数 f (x) 的最小正周期为 T .
…………………… 4 分 ……………………… 6 分
( II)由题意得 x 0, , 2 x
7 ,
,
4x x2 , x 1,
若方程 f ( x) kx 有且仅有一个实数解,则实数 k 的
ex ,
x 1.
取值范围为 __________.
三、解答题:本大题共 6 小题,共 80 分 . 解答应写出文字说明,证明过程或演算步骤 . (15)(本小题满分 13 分)
已知函数 f x 2cos x(cos x 3sin x) a ( a R ) .
( A) 1, 4
( B) 0, 1, 4
(C) 0, 2 ( D) 0, 1, 2, 4
(2)设变量 x , y 满足约束条件
x 2y 4≤0, 3x y 3≥0, 则目标函数 z x y 1≤0.
x 2 y的最小值为
( A) 16 5
( B) 3
( C) 0
(3)阅读右边的程序框图,运行相应的程序,则输出
2017届高三上学期期末(理科)数学试卷

天津市红桥区2017届高三上学期期末数学(理科)试卷1.设集合{}0M x x x =≥∈R ,,{}21,N x x x <=∈R ,则M N =I ( ) A .[]0,1 B .()0,1 C .(]0,1 D .[)0,1 2.甲、乙两人射击比赛,两人平的概率是12,甲获胜的概率是13,则甲不输的概率为( ) A .25 B .56 C .16 D .133.某三棱锥的三视图如图所示,则该三棱锥的体积是( )A .13 B .12 C .1 D .324.已知双曲线()222210,0x y a b a b-=>>的两条渐近线与抛物线()220y px p =>的准线分别交于O 、A 、B 三点,O 为坐标原点.若双曲线的离心率为2,AOB △,则p =( ) A .1 B .32C .2D .35.若a 、b 为空间两条不同的直线,α、β为空间两个不同的平面,则直线a ⊥平面α的一个充分不必要条件是( )A .a β∥且αβ⊥B .a β⊂且αβ⊥C .a b ⊥且b α∥D .a β⊥且αβ∥6.已知α,()0,πβ∈,且()1tan 2αβ-=,1tan 7β=-,则2αβ-的值是( ) A .π4- B .3π4- C .π4- D .3π47.已知正方形ABCD 的面积为2,点P 在边AB 上,则PD PC •u u u r u u u r 的最大值为( )A B .32 C .2 D8.设方程()1e 110x m --+=的两根分别为1x ,2x ()12x x <,方程e 10x m --=的两根分别为3x ,4x ()34x x <.若10,2m ⎛⎫∈ ⎪⎝⎭,则()()4132x x x x +-+的取值范围为( )A .(),0-∞B .3,ln 5⎛⎫-∞ ⎪⎝⎭C .3ln ,05⎛⎫ ⎪⎝⎭D .(),1-∞-9.i 为虚数单位,复数2i 1i=+_________. 10.直线10ax y ++=被圆2220x y ax a -++=截得的弦长为2,则实数a 的值是_______.11.执行如图所示的程序框图,若输入的a 的值为3,则输出的i =__________.12.在ABC △中,已知角A ,B ,C 所对的边分别为a ,b ,c ,且()2cos cos c a B b A b -=,则sin sin A B =__________.13.已知实数x ,y 满足约束条件2211x y x y x y -≤⎧⎪-≥-⎨⎪+≥⎩,若目标函2z x ay =+,仅在点()3,4取得最小值,则a 的取值范围是__________.14.设函数()241,4log ,04x f x x x x ⎧+≥⎪=⎨⎪<<⎩若()()f a f b c ==,()0f b '<,则a ,b ,c 的大小关系是_________.15.(13分)设函数()2πsin co sin 4f x x sx x ⎛⎫=-- ⎪⎝⎭. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数π6f x ⎛⎫- ⎪⎝⎭在π0,2⎡⎤⎢⎥⎣⎦上的最大值与最小值. 16.(13分)如图,在直角梯形11AA B B 中,190A AB ∠=o ,11A B AB ∥,11122AB AA A B ===,直角梯形11AA C C 通过直角梯形11AA B B 以直线1AA 为轴旋转得到,且使得平面11AAC C ⊥平面11AA B B .点M 为线段BC 的中点,点P 是线段1BB 中点.(Ⅰ)求证:11AC AP ⊥;(Ⅱ)求二面角P AM B --的余弦值.17.(13分)在等差数列{}n a 中,13a =,其前n 项和为n S ,等比数列{}n b 的各项均为正数,11b =,公比为q ,且2212b S +=,22S q b =(Ⅰ)求n a 与n b ;(Ⅱ)设数列{}n c 满足1n nc S =,求{}n c 的前n 项和n T . 18.(13分)数列{}n a 的前n 项和为n S ,()*2n n S a n n -=∈N . (1)求证:数列{}1n a +成等比数列;(2)求数列{}n a 的通项公式;(3)数列{}n a 中是否存在连续三项可以构成等差数列?若存在,请求出一组适合条件的三项;若不存在,请说明理由.19.(14分)已知点)P 和椭圆C :22142x y +=. (1)设椭圆的两个焦点分别为1F ,2F ,试求12PF F △的周长及椭圆的离心率;(2)若直线l()200y m m -+=≠与椭圆C 交于两个不同的点A ,B ,设直线PA 与PB 的斜率分别为1k ,2k ,求证:120k k +=.20.(14分)已知函数()()()2212e x f x ax a x a a =++⎡⎤⎣⎦+-∈R .(1)当0a ≥时,讨论函数()f x 的单调性;(2)设()22ln bx g x x=,当1a =时,若对任意()10,2x ∈,存在()21,2x ∈,使()()12f x g x ≥,求实数b 的取值范围.。
天津五区联考2017-2018高三上学期期末数学(理)试题及答案

13.3
14. ,
1 1 3 e
三、解答题:本大题共 6 小题,共 80 分.解答应写出文字说明,证明过程或演算步骤. (15) (本小题满分 13 分) 解: (Ⅰ) f x cos x sin x 2 3 sin x cos x
2 2
cos 2 x 3 sin 2 x
由 g n 1 g n
2 n 1 7 2
n 3
2n 7 9 2n n 3 …………………………11 分 2n 2 2
得:当 9 2n 0 2 n 4 n N 时, g 2 g 3 g 4 g 5 ; 当 9 2n 0 n 5 n N 时, g 5 g 6 g 7 ; 所以对任意 n 2 ,且 n N 均有 g 5 g n ,故 k 5 .………………13 分
(18) (本小题满分 13 分) 解: (Ⅰ)设数列 an 的公比为 q ,则由条件得:
2 a3 2 a2 a4 ,
……………………………1分
又 a1 2 ,则 2 2q 2 2 2q 2q 3 4 q 2 1 2q 1 q 2 , 因为 1 q 0 ,解得: q 2 , 故 an 2 . (Ⅱ)由(Ⅰ)得: bn 2nan n 2 则 Sn 1 2 2 2 n 2
3 , 0 , 0 , C 0 ,1, 0 ,
由 AC 2 DE 3 得 E 0, 0 ,
3 , A 0 ,1, 3 …………6 分 2
依题意 AE 0 , 1,
天津市五区县2017-2018学年高三上学期期末数学试卷(理科) Word版含解析

2017-2018学年天津市五区县高三(上)期末数学试卷(理科)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|x2﹣x﹣2>0},B={x|1<x≤3},则(∁R A)∩B=()A.A、(1,2]B.[﹣1,2] C.(1,3]D.(﹣∞,﹣1)∪(2,+∞)2.设变量x,y满足约束条件,则目标函数z=x+y的最小值为()A.﹣3 B.﹣2 C.D.13.“辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为()A.0 B.1 C.9 D.184.设x∈R,则“x<1”是“x|x|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件5.如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC 的长为()A.5 B.4 C.D.36.若双曲线﹣=1的一条渐近线平行于直线x +2y +5=0,一个焦点与抛物线y 2=﹣20x的焦点重合,则双曲线的方程为( )( )A .﹣=1 B .﹣=1C .﹣=1D .﹣=17.已知定义在R 上的函数f (x )=x 2+|x ﹣m |(m 为实数)是偶函数,记a=f (loge ),b=f (log 3π),c=f (e m )(e 为自然对数的底数),则a ,b ,c 的大小关系( ) A .a <b <c B .a <c <b C .c <a <b D .c <b <a8.已知定义域为R 的奇函数f (x )的周期为4,且x ∈(0,2)时f (x )=ln (x 2﹣x +b ),若函数f (x )在区间[﹣2,2]上恰有5个零点,则实数b 应满足的条件是( )A .﹣1<b ≤1B .﹣1<b <1或b=C .<bD .<b ≤1或b=二、填空题:本大题共有5小题,每小题5分,共30分。
2017-2018年天津市部分区高三(上)期末数学试卷和答案(理科)
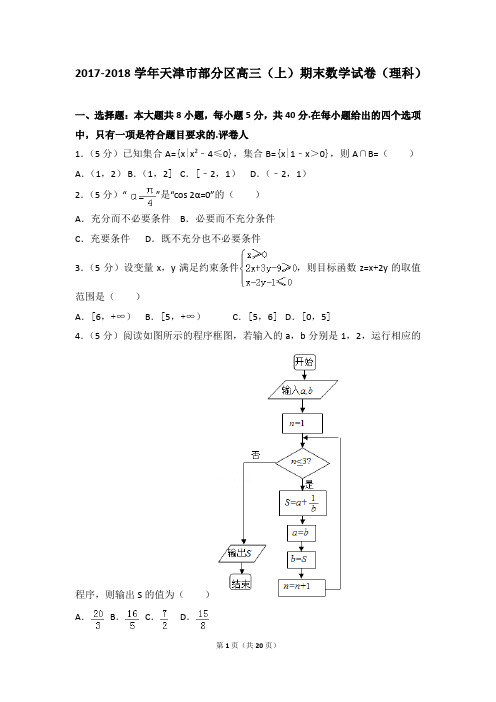
程序,则输出 S 的值为( A. B. C. D.
)
第 1 页(共 20 页)
5. (5 分)已知双曲线
(a>0,b>0)的一个焦点为 F(﹣2,0) ,且 )
双曲线的两条渐近线的夹角为 60°,则双曲线的方程为( A. B.
C.
或 x2
D.
或
6. (5 分) 在△ABC 中, 内角 A, B, C 所对的边分别是 a, b, c. 已知 sin C=sin 2B, 且 b=2,c= A. B. ,则 a 等于( C.2 D.2 )
(Ⅰ)求证:BD⊥平面 ACDE;
第 3 页(共 20 页)
(Ⅱ)求平面 BCD 与平面 BAE 所成角(锐角)的大小; (Ⅲ)若 F 为 AB 的中点,求直线 EF 与平面 BDE 所成角的大小.
18. (13 分)已知{an}是等比数列,满足 a1=2,且 a2,a3+2,a4 成等差数列. (Ⅰ)求{an}的通项公式; (Ⅱ)设 bn=2nan,数列{bn}的前 n 项和为 Sn,g(n)= N*) ,求正整数 k 的值,使得对任意 n≥2 均有 g(k)≥g(n) . 19. (14 分)设椭圆 M:x2+y2+2x﹣15=0 的圆心. (Ⅰ)求椭圆的方程; (Ⅱ)已知过椭圆右焦点 F2 的直线 l 交椭圆于 A,B 两点,过 F2 且与 l 垂直的直 线 l1 与圆 M 交于 C,D 两点,求四边形 ABCD 面积的取值范围. 20. (14 分)已知函数 f(x)=ln x+a(1﹣x) (a∈R) . (Ⅰ)讨论 f(x)的单调性; (Ⅱ)当 a=﹣ 时,令 g(x)=x2﹣1﹣2f(x) ,其导函数为 g′(x) .设 x1,x2 是 函数 g(x)的两个零点,判断 是否为 g′(x)的零点?并说明理由. (a>b>0)的左焦点为 F1,离心率为 .F1 为圆 (n≥2,n∈
天津五区县2017届高三一模理科综合试题及答案

天津市部分区2017年高三质量调查试卷(一)
理科综合化学部分参考答案
选择题共6题,每题6分,共36分
1.D 2.A 3.B 4.D 5.C 6.D
7.(14分,除注明外每空2分。
)
(1)第三周期第ⅥA族(1分)(1分)
(2)S2->O2->Na+(1分)Cl2+H2S=2HCl+S↓(合理即可)
(3)(1分)4AgBr+N2H4= 4Ag+N2↑+4HBr1:2
(4)氧化钠过氧化钠
(5)b
8.(18分,除注明外每空2分。
)
(1)羧基、硝基
(2)ac
(3)丙烯醇
(4)6(任写一种即可)
(5)(共4分,其中第一步1分,第二步条件和产物正确得2分,第三步条件和产物正确得1分。
若顺序颠倒不得分,条件或产物的结构简式写错不得分)
9.(18分,每空2分。
)
(1)2H+ + SnO=Sn2++H2O c Sn2++2e-= Sn
(2)①KMnO4或KClO3蒸馏烧瓶
②缺少温度计D与E之间缺少干燥装置
③Sn 4++4OH -=H 2SnO 3↓+H 2O
④92.0%
10.(14分,除标明外,每空2分)
(1) ①6a+b+2c 3
②>(1分) 由图可知,随着温度的升高,K 1增大、K 2减小,则△H 1>0、 △H 2<0,所以a >b
(2) b (1分)
(3) ①ad ②0.04 mol·L −1·min −1
1200 ③p 1>p 2>p 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津市五区县2016-2017学年度第一学期期末
考试
高三文科数学试卷
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷第1至2页,第Ⅱ卷3至8页。
全卷满分150,考试时间120分钟。
第I卷(选择题共4 0分)
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中.只有一项是符合题目要求的.
(l)已知集合{}{}
2
=∈>=∈-+<,则集合等于M x R x N x R x x
|2,|430
(A) {}|2x x < (B){}|22x x -≤≤ (C) {}|21x x -≤< (D){}|12x x <≤
(2)已知变量x ,y 满足约束条件10,0,20,y x y x y -≤⎧⎪
+≥⎨⎪--≤⎩
则z=x+2y 的最大值为
(A)6 (B)5 (C)4 (D)3 (3)阅读右边的程序框图,运行相应的程序,输出的结果为 (A)126 (B)127 (C) 63 (D) 64
(4)设,m n R ∈,则“3,3m n ≥≥”是“229m n +≥”的 ( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件
(5)若直线20x y a -+=与圆22(2)1x y -+=有公共点,则实数a 的取值范围是 ( )
(A) ⎡⎣
(B)(
(C) 22⎡---+⎣
(D)2⎡-+⎣
(6)将函数()3sin()2
3
x
f x π=+的图象向右平移3
π
个单位长度,再把图象上所有
点的横坐标 伸长到原来的2倍(纵坐标不变),得到()y g x =的图象,则
()y g x =的解析式为
( )
(A)()3sin()6
g x x π=+ (B)()3sin()3
g x x π
=+
(C)()3sin()4
3
x g x π
=+ (D)()3sin()4
6
x g x π
=+
(7)已知函数()x f x a x b =+-的零点0(,1)()x n n n Z ∈+∈,其中常数a ,b 满足
01b a <<<,则n 的值为 ( )
(A)2 (B)1 (C) -2 (D) -l (8)已如()f x 是定义在R 上的偶函数,且满足(2)()f x f x +=,当[]0,1x ∈时,()2f x x =.若在区间[-2,
3]上方程2()0ax a f x +-=恰有四个不相等的实数根,则实数a 的取值范围 是 ( )
(A)22
(,)53
(B) 2(,)5
+∞ (C) 2(0,)3
(D)2(0,)5
第Ⅱ卷
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.
(9)已知复数z 满足12i z i -+=⋅,则复数z=___________.
(10)已知一圆柱内接于球O ,且圆柱的底面直径与母线长均为2,则球O 的表面积为__________.
(11)若双曲线22
221x y a b
-=的左顶点与抛物线22(0)y px p =>的焦点的距离为4,
且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,2),则双曲线的焦距为_________.
(12)如图,△ABC 内接于O ,过BC 中点D 作平行于AC 的
直线l ,l 交AB
于E ,交O 在A 点处的切线于点P ,若PE=6 ,ED=3,则AE 的长为 ____________.
(13)已知1log ()log (0m m a m b
-=>≠∈且m 1,a,b R),则2a-b 的最大值 为__________.
(14)定义平面向量的一种运算:sin ,a b a b a b ⊗=,给出下列命题: ①a b b a ⊗=⊗;②()()a b a λλ⊗=b ⊗;③()()()a b c a c b c +⊗=⊗+⊗; ④若1122(,),(,)a x y b x y ==,则1221a b x y x y ⊗=-。
其中所有真命题的序号是___________.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
1 5.(本小题满分13分)
某中学田径队共有42名队员,其中男生2 8名、女生1 4名,采用分层抽样的方法选出6人参加一个座谈会.
(I)求运动员甲被抽到的概率以及选出的男、女运动员的人数; (Ⅱ)若从参加会议的运动员中选出2名运动员清扫会场卫生,用列举法求恰好有1名女队员的概率. 1 6.(本小题满分13分) 已知函数2()cos 2sin ()2
6x
f x x π
=--
(I)求()f x 的最大值;
(Ⅱ)设△ABC 的内角A,B,C 的对应边分别为a ,b ,c,且7,(2),6
2
A a f A π
==-
sin B C =,求△ABC 的面积.
17.(本小题满分13分) 已
知
四
棱
锥
A-BCDE
,
其
中
CD ,
1,2AB BC AC BE CD =====,CD ⊥平面ABC,BE ∥
F 为AD 的中点.
(I)求证:EF ∥平面ABC ; (Ⅱ)求证:平面ADE ⊥平面ACD ;
(Ⅲ)求直线AE 和平面BCDE 所成角的正弦值.
18.(本小题满分13分)
已知椭圆2222:1x y C a b +=的两焦点12(1,0),(1,0)F F -
(I)求椭圆C 的标准方程;
(Ⅱ)经过椭圆C 的上顶点B 的直线与椭圆另一个交点为A ,且满足
22BA BF ⋅=
,
求2ABF ∆外接圆的面积. 19.(本小题满分14分)
已知数列{}n a 前n 项和为n S ,首项为1a ,且1
,,2
n n a S 成等差数列. (I)求数列{}n a 的通项公式;
(Ⅱ)数列{}n b 满足221223log log n n n b a a ++=⋅,求证:12311111
2
n b b b b +++⋅⋅⋅+< 20.(本小题满分1 4分)
已知函数32()f x ax bx =+在点(3,(3))f 处的切线方程为122270x y +-=. (I)求函数()f x 的解析式;
(Ⅱ)若方程21
()2f x x m =-+有三个不同的解,求实数m 的取值范围;
(Ⅲ)若不等式23
()(1)0()2
f x x k x k R -++≥∈对于(,0)x ∈-∞恒成立,求实数k 的
取值范围.。
