数值计算课后答案2
《数值计算方法》习题答案

《数值计算方法》课后题答案详解吉 林 大 学第一章 习 题 答 案1. 已知(1)2,(1)1,(2)1f f f −===,求()f x 的Lagrange 插值多项式。
解:由题意知:()01201212001020211012012202121,1,2;2,1,1()()(1)(2)()()6()()(1)(2)()()2()()(1)(1)()()3(1)(2)(1)(2)()2162nj j j x x x y y y x x x x x x l x x x x x x x x x x l x x x x x x x x x x l x x x x x x x x L x y l x ==−=====−−−−==−−−−+−==−−−−−+−==−−−−+−==×+×−∴∑()2(1)(1)131386x x x x +−+×=−+2. 取节点01210,1,,2x x x ===对x y e −=建立Lagrange 型二次插值函数,并估计差。
解11201201210,1,;1,,2x x x y y e y e −−======1)由题意知:则根据二次Lagrange插值公式得:02011201201021012202110.510.520.51()()()()()()()()()()()()()2(1)(0.5)2(0.5)4(1)(224)(43)1x x x x x x x x x x x x L x y y y x x x x x x x x x x x x x x x x e x x e e e x e e x −−−−−−−−−−−−=++−−−−−−=−−+−−−=+−+−−+22)Lagrange 根据余项定理,其误差为(3)2210122()1|()||()||(1)(0.5)|3!61max |(1)(0.5)|,(0,1)6()(1)(0.5),()330.5030.2113()61()0.2113(0.21131)(0.21130.5)0.008026x f R x x e x x x x x x t x x x x t x x x x t x R x ξξωξ−+≤≤==−−≤−−∈′=−−=−+=−==≤××−×−=∴取 并令 可知当时,有极大值3. 已知函数y =在4, 6.25,9x x x ===处的函数值,试通过一个二次插值函数求的近似值,并估计其误差。
《数值计算方法》 课后题 答案(曾金平)湖南大学

= 0.105 × 10 2 − 0.144 × 10 2 + 0.657 × 10 1 − 1
= 0.167 × 101
g ( 2.19) = ((−0.81) × 0.219 × 101 + 3) × 0.219 × 101 − 1
= 0.123 × 10 1 × 0.219 × 10 1 − 1 = 0.169 × 101 1 1 即 f ( x) = 0.167 × 10 , g ( x) = 0.169 × 10
而当 x = 2.19 时 x 3 − 3 x 2 + 3 x − 1 的精确值为 1.6852,故 g ( x ) 的算法较正确。 8.按照公式计算下面的和值(取十进制三位浮点数计算) : (1)
∑3
i =1
6
1
i 6
;(2)
∑3
i =6
1
1
i
。
解: (1)
∑3
i =1 1
1
i
1 1 1 1 1 1 = + 2 + 3 + 4 + 5 + 6 = 0.333 + 0.111 + 0.037 + 0.012 + 0.004 + 0.001 3 3 3 3 3 3
xk
1 1.5 1.25 1.125 1.0625 1.09375 1.109375 1.1171875 1.11328125 1.115234375 1.1142578125 1.11376953125
f ( xk )
-0.1585 0.4962 0.1862 0.015051 -0.0718 -0.02835 -0.00664 0.004208 -0.001216 0.001496 0.001398 -0.000538
数值计算方法课后习题答案

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算方法答案

1数值计算方法习题一(2)习题二(6)习题三(15)习题四(29)习题五(37)习题六(62)习题七(70)2009.9,92习题一1.设x>0相对误差为2%,4x的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x xf x f xδδ∆=≈得(1)()f x=11()()*2%1%22x xδδδ≈===;(2)4()f x x=时444()()'()4()4*2%8%xx x x xxδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P关于1212.m nx a a a bb b=±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算(1)31.97+2.456+0.1352;(2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352≈21((0.3197100.245610)0.1352)fl fl⨯+⨯+=2(0.3443100.1352)fl⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl≈⨯+⨯= 21(0.3197100.259110)fl⨯+⨯=0.3456210⨯易见31.97+2.456+0.1352=0.345612210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?3解:设该正方形的边长为x,面积为2()f x x=,由(())(())'()()()()f x xf x f x xf x f xδδ∆=≈解得(())()()'()f x f xxxf xδδ≈=2(())(())22f x x f xx xδδ==0.5%5.下面计算y的公式哪个算得准确些?为什么?(1)已知1x<<,(A)11121xyx x-=-++,(B)22(12)(1)xyx x=++;(2)已知1x>>,(A)y=,(B)y=;(3)已知1x<<,(A)22sin xyx=,(B)1cos2xyx-=;(4)(A)9y=(B)y=解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算方法课后习题答案(李庆扬等) (修复的)

,。
第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++;[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算方法习题答案(第二版)(绪论)

数值分析(p11页)4 试证:对任给初值x 0,0)a >的牛顿迭代公式112(),0,1,2,......k ak k x x x k +=+= 恒成立下列关系式:2112(1)(,0,1,2,....(2)1,2,......kk k x k x x k x k +-=-=≥=证明:(1)(21122k k k k k kx a x x x x +-⎫⎛-=+==⎪ ⎝⎭(2) 取初值00>x ,显然有0>k x ,对任意0≥k ,a a x a x x a x x k k k k k ≥+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛+=+2121216 证明:若k x 有n 位有效数字,则n k x -⨯≤-110218, 而()k k k k k x x x x x 288821821-=-⎪⎪⎭⎫⎝⎛+=-+ nnk k x x 2122110215.22104185.28--+⨯=⨯⨯<-∴>≥ 1k x +∴必有2n 位有效数字。
8 解:此题的相对误差限通常有两种解法. ①根据本章中所给出的定理:(设x 的近似数*x 可表示为m n a a a x 10......021*⨯±=,如果*x 具有l 位有效数字,则其相对误差限为()11**1021--⨯≤-l a x x x ,其中1a 为*x 中第一个非零数)则7.21=x ,有两位有效数字,相对误差限为025.010221111=⨯⨯≤--x x e 71.22=x ,有两位有效数字,相对误差限为025.010221122=⨯⨯≤--x x e 3 2.718x =,有两位有效数字,其相对误差限为:00025.010221333=⨯⨯≤--x e x ②第二种方法直接根据相对误差限的定义式求解 对于7.21=x ,0183.01<-e x∴其相对误差限为00678.07.20183.011≈<-x e x 同理对于71.22=x ,有003063.071.20083.022≈<-x e x 对于718.23=x ,有00012.0718.20003.033≈<-x e x备注:(1)两种方法均可得出相对误差限,但第一种是对于所有具有n 位有效数字的近似数都成立的正确结论,故他对误差限的估计偏大,但计算略简单些;而第二种方法给出较好的误差限估计,但计算稍复杂。
数值计算课后规范标准答案2
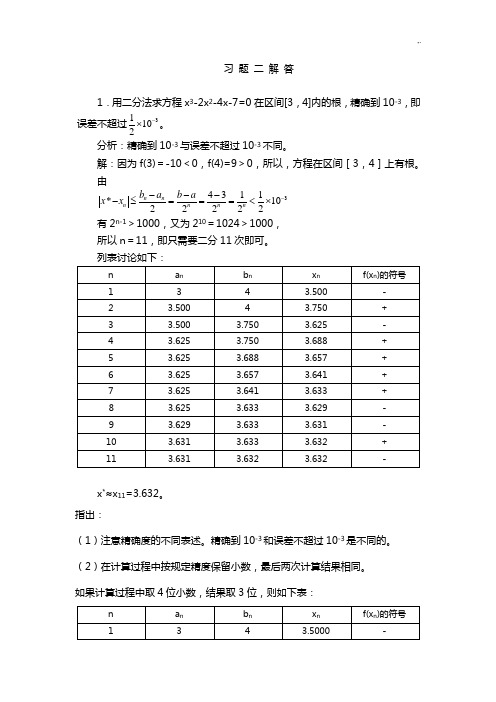
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
数值计算方法课后习题答案(李庆扬等) (修复的)

,。
第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++;[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n nn nnnb a b a x x -----≤===<⨯有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根;因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
解:令()1sin f x x x =--,因为(0)10sin 010,(1)11sin 1sin 10f f =--=>=--=-<,则(0)(1)0f f <,由零点定理,函数f(x)在[0,1]区间有一个根。
由41011*1022222n nn nnnb a b a x x -----≤===<⨯有2n-1>10000,又为210=1024,213=8192<10000,214=16384>10000 所以n =15,即需要二分15次。
指出:要证明的是有一个解而不是唯一解,因此不必讨论单调性。
3.试用迭代公式10220,1210k k k x x x x +==++,求方程32210200x x x ++-=的根,要求精确到510-。
分析:精确到510-即误差不超过51102-⨯解:令32()21020f x x x x =++- 列表进行迭代如下:指出:精确到510-可以从两个方面判定。
第一,计算过程中取小数到510-位,最后两个计算结果相同,终止计算。
第二,计算过程中取小数到610-,当511102k k x x -+-<⨯终止计算。
本题采用第一种方法。
4.将一元非线性方程20cos x x e -=写成收敛的迭代公式,并求其在005.x =附近的根,要求精确到210-。
解:20cos x x e -=改写为222110cos cos cos x xxx x x e ee=⇒=⇒-=,则21cos xx x x e=+-,设 21cos ()xx g x x e=+-有22224111)sin cos (sin cos )()()xxxxxx xe xex x g x e eeπ+--+'=+=-=-在005.x =处,因为05054051096151..)(.).g eπ+'=-=<所以迭代法121cos ()kkk k x x g x x e+=+-在005.x =的邻域内收敛。
列表迭代如下:此时0692069000614.cos ..e -=。
5.为求方程3210x x --=在015.x =附近的一个根,设将方程改为下列等价形式,并建立相应的迭代公式:12213223121121111121111311(),;(),();(),.()k kk kk k x x xx x x x x x x x x +++=+=+=+=+==--迭代公式迭代公式迭代公式 试分析每种迭代公式的收敛性,并取一种公式求出具有4位有效数字的近似值。
解:(1)因为211x x=+,所以迭代函数为211()g x x =+,则23212()()()g x xxx--'''===-,3322152151153375(.)...g -'=-⨯==<满足局部收敛性条件,所以迭代公式1211k kx x+=+具有局部收敛性。
(2)因为1231()x x =+,所以迭代函数为1231()()g x x =+,则12122332231221213331()()()()xg x x x x x x --'=+=+=+,223215150********.(.).(.)g ⨯'==<+满足局部收敛性条件,所以迭代公式12311()k kx x +=+具有收敛性。
(3)因为1211()x x =-,所以迭代函数为1211()()g x x =-,则13122111122()()()g x x x ---'=--=--,323211151********205(.)(.)..g -'=-==>⨯不满足收敛性条件,所以迭代公式11211()k k x x +=-不具有收敛性。
用迭代公式1211k kx x+=+列表计算如下:所以,方程的近似根为1465*.x ≈。
6.设23()()x x C x ϕ=+-,应如何取C 才能使迭代公式1()k k x x ϕ+=具有局部收敛性?解:设C 为常数,因为23()()x x C x ϕ=+-,所以12()x Cx ϕ'=+,要使迭代公式具有局部收敛性,需00121()x Cx ϕ'=+<,此时即有01121Cx -<+<,也即010Cx -<<。
即只要C 取满足如上条件的常数,就可以使得迭代公式具有局部收敛性。
指出:本题的一般形式为:设()()x x Cf x ϕ=+,应如何取C 才能使迭代公式1()k k x x ϕ+=具有局部收敛性?显然,()()x x Cf x ϕ=+是迭代格式1()k k x x ϕ+=相应的迭代函数,因此该迭代格式要求解的方程是()()()0x x x x Cf x f x ϕ=⇒=+⇒=。
也就是说,这是如何选择C ,构造一个求解方程f(x)=0的收敛的迭代格式的问题。
因为()()x x Cf x ϕ=+,所以()1()x Cf x ϕ''=+, 要使迭代格式收敛,需()1()1x Cf x ϕ''=+< 解之得2()0Cf x '-<<,即C 与()f x '异号,且()2Cf x '<。
下面的讨论利用了本题的特殊条件,求出了具体的结果:因为23()()x x C x ϕ=+-,所以当2(3)x x C x =+-时,有2(3)0C x -=,则x =23()()x x C x ϕ=+-的不动点为*x =。
而12()x Cx ϕ'=+, 根据局部收敛性定理,当1210C c ϕ'=+<⇒-<<;当(12(10C c ϕ'=+<⇒<<时,迭代格式收敛到。
7.用牛顿法求方程3310x x --=在初始值02x =邻近的一个正根,要求3110k k x x -+-<。
解: 因为3310x x --=所以有3()31f x x x =--,相应的迭代公式为3312231213333k k k k k k k x x x x x x x +--+=-=--取x 0=2为迭代的初始近似值。
迭代的结果列表如下:因为33210.0001102x x --=<⨯,符合计算的精度要求,所以*3 1.8794x x ≈=。
8.用牛顿法解方程10c x-=,导出计算数c 的倒数而不用除法的一种简单的迭代公式。
用此公式求0.324的倒数,设初始值03x =,要求计算有5位有效数字。
解:对于方程10c x -=,有1()f x cx =-,相应的迭代公式为212121k k k k k kc x x x x cx x +-=-=--。
应用该迭代公式求0.324的倒数,列表计算如下所以1308640324..≈。
指出: 如果将方程10c x -=改写为等价的10cx -=,则有1()f x cx =-,相应的迭代公式为111k k k cx x x cc+-=-=无法展开迭代。
9.设alimk →∞。
解:设a 为正实数,n 为自然数,由牛顿法,方程0()n f x x a =-=的解为11111()()(1)1[(1)]k k k k nnnk k k k n n k kn k n kk n kf x x x f x x a nx x ax nxnx n x anx a n x nx+----=-'--+=-=-+==-+此即求 由此,则111111[(1)][(1)] lim lim lim1[(1)(1)]lim1[(1)(1)]lim1[((1)()limnk n k k k k knkknkknkkan x n x axx n xn a n xn a n xa n n xn--→∞→∞→∞--→∞-→∞-→∞-+-+==--+-=--+-=---=111]2(1)(1)(1)lim22limn nkk kka n a nx x-++→∞→∞-⨯---====指出:本题中,表面上是k→∞的问题,但实际上却是kx→的问题,1,k kx x+才是极限过程中实际的变量。
本质上。
本题实际上是求极限11111[(1)][(1)] lim lim lim1[(1)]nk n k k k k knxan x n x axx n xn x ax--→∞→∞→∞--+-+==-+=由于讨论的是0型不定式,且不定式的分母上有2次的“0”因子,因此两次应用罗必塔法则。
解二:首先证明一个定理:定理:设**()0,()0f x f x'=≠,又设f(x)在*x的某个邻域内具有连续的二阶导数,则牛顿迭代法具有局部收敛性,且有。
