天津市部分区2018-2019学年高一上学期期末考试数学试卷含答案

合集下载

天津市部分区2022-2023学年高二下学期期末数学试题

【详解】ðU A = {1, 2} ，故 (ðU A) I B = {1, 2} I{0,1, 2} = {1, 2} .
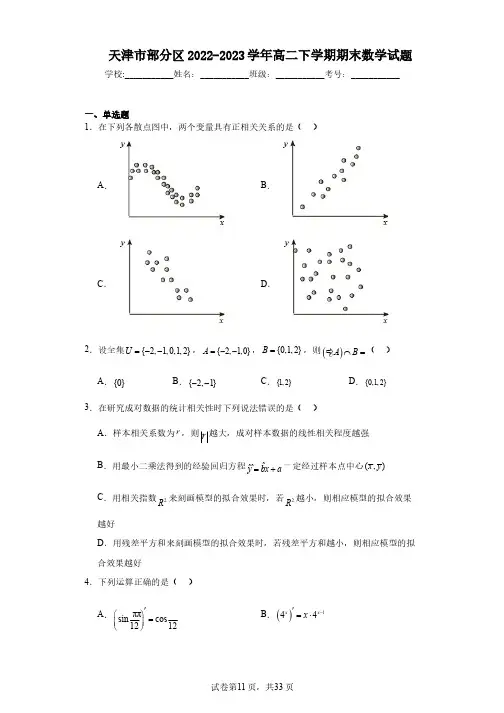
故选：C. 3．C 【分析】根据样本相关系数，回归直线方程，相关指数和残差的概念判断即可．
【详解】对于 A 选项，样本相关系数 r 来刻画成对样本数据的相关程度，当 r 越大，则成对样本数据的线性相关程度越强，故 A 正确；
天津市部分区 2022-2023 学年高二下学期期末数学试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题 1．在下列各散点图中，两个变量具有正相关关系的是（）
A．
B．
C．
D．
2．设全集U = {-2, -1, 0,1, 2} ， A = {-2, -1,0} ， B = {0,1, 2} ，则 (ðU A) Ç B = （）
的三位数，这样的三位数共有（）
A．24 个
B．36 个
C．48 个
D．54 个
8．已知每门大炮击中目标的概率都是 0.5，现有 10 门大炮同时对某一目标各射击一次．
记恰好击中目标 3 次的概率为 A；若击中目标记 2 分，记 10 门大炮总得分的期望值为
B，则 A，B 的值分别为（）
A． 15 ，5 128
【分析】求导
f ¢(x) =
2 x
，可得斜率 k
=
f ¢(1) = 2 ，进而得出切线的点斜式方程.
【详解】由
y
=
f
( x)
=
2 ln
x ，得
f
¢( x )
=
2 x
，
则曲线 y = 2 ln x 在点 (1, 0) 处的切线的斜率为 k = f ¢(1) = 2 ，

2019-2020学年人教A版天津市部分区高一上学期期末数学试卷及答案 (解析版)

2019-2020学年高一上学期期末数学试卷一、选择题1．已知全集U＝{1，2，3，4，5，6，7，8}，集合A＝{2，3，5，6}，集合B＝{1，3，4，6，7}，则集合A∩∁U B＝（）A．{2，5} B．{3，6} C．{2，5，6} D．{2，3，5，6，8} 2．下列函数中既是奇函数，又在R上单调递增的是（）A．B．y＝sin x C．y＝x3D．y＝lnx3．函数f（x）＝lnx+x﹣3的零点所在区间为（）A．（4，5）B．（1，2）C．（2，3）D．（3，4）4．在平面直角坐标系中，若角α以x轴的非负半轴为始边，且终边过点，则sinα的值为（）A．B．C．D．5．已知a＝log20.3，b＝20.3，c＝0.30.2，则a，b，c三者的大小关系是（）A．c＞b＞a B．b＞c＞a C．a＞b＞c D．b＞a＞c6．为了得到函数y＝sin（2x﹣）的图象，只需将函数y＝sin2x的图象上所有的点（）A．向左平移个单位B．向左平移个单位C．向右平移个单位D．向右平移个单位7．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，若，则不等式f（2x﹣1）＜0的解集为（）A．B．C．D．8．若α、β都是锐角，且sinα＝，cos（α+β）＝﹣，则sinβ的值是（）A．B．C．D．9．下列命题正确的是（）A．命题“∃x∈R，使得2x＜x2”的否定是“∃x∈R，使得2x≥x2”B．若a＞b，c＜0，则C．若函数f（x）＝x2﹣kx﹣8（k∈R）在[1，4]上具有单调性，则k≤2D．“x＞3”是“x2﹣5x+6＞0”的充分不必要条件10．已知函数在区间上单调递增，且存在唯一使得f（x0）＝1，则ω的取值范围为（）A．B．C．D．二、填空题11．幂函数f（x）的图象经过（2，4），则f（3）＝．12．函数的定义域为．13．已知lga+lg（2b）＝1，则a+b的最小值是．14．酒驾是严重危害交通安全的违法行为，为了保障交通安全，根据国家有关规定：100ml 血液中酒精含量达到20〜79mg的驾驶员即为酒后驾车，80mg及以上认定为醉酒驾车．假设某驾驶员喝了一定量的酒后，其血液中的酒精含量上升到了0.6mg/ml，如果在停止喝酒以后，他血液中酒精含量会以每小时20%的速度减少，那么他至少要经过t小时后才可以驾驶机动车．则整数t的值为（参考数据：lg2≈0.30，lg3≈0.48）三、解答题：本大题共5小题，共60分.解答应写出文字说明、证明过程或演算步骤. 15．设集合A＝{x|x2﹣x﹣6＞0}，B＝{x|﹣4＜3x﹣7＜8}．（1）求A∪B，A∩B；（2）已知集合C＝{x|a＜x＜2a+1}，若C⊆B，求实数a的取值范围．16．已知函数．（1）在给出的直角坐标系中，画出y＝f（x）的大致图象；（2）根据图象写出f（x）的单调区间；（3）根据图象写出不等式f（x）＞0的解集．17．已知sinα＝，α∈（，π），cosβ＝，β∈（0，）．（1）求cos（α﹣β）的值；（2）求tan（2β+）的值．18．已知函数．（1）判断f（x）的单调性，并用函数单调性的定义证明；（2）判断f（x）的奇偶性，并说明理由．19．已知函数．（1）求f（x）的最小正周期；（2）求f（x）在区间上的最大值和最小值；（3）若关于x的不等式mf（x）+3m≥f（x）在R上恒成立，求实数m的取值范围．参考答案一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.第I卷（选择题共40分）1．已知全集U＝{1，2，3，4，5，6，7，8}，集合A＝{2，3，5，6}，集合B＝{1，3，4，6，7}，则集合A∩∁U B＝（）A．{2，5} B．{3，6} C．{2，5，6} D．{2，3，5，6，8} 【分析】由全集U及B，求出B的补集，找出A与B补集的交集即可；解：∵全集U＝{1，2，3，4，5，6，7，8}，集合A＝{2，3，5，6}，集合B＝{1，3，4，6，7}，∴∁U B＝{2，5，8}，则A∩∁U B＝{2，5}．故选：A．2．下列函数中既是奇函数，又在R上单调递增的是（）A．B．y＝sin x C．y＝x3D．y＝lnx【分析】分别判断函数的奇偶性和单调性即可．解：A．f（x）是奇函数，在定义域（﹣∞，0）∪（0，+∞）上不单调，不满足条件．B．f（x）是奇函数，则R上不是单调函数，不满足条件．C．f（x）是奇函数，在R上是增函数，满足条件．D．函数的定义域为（0，+∞），为非奇非偶函数，不满足条件．故选：C．3．函数f（x）＝lnx+x﹣3的零点所在区间为（）A．（4，5）B．（1，2）C．（2，3）D．（3，4）【分析】根据对数函数单调性和函数单调性的运算法则，可得f（x）＝lnx+x﹣3在（0，+∞）上是增函数，再通过计算f（1）、f（2）、f（3）的值，发现f（2）•f（3）＜0，即可得到零点所在区间．解：∵f（x）＝lnx+x﹣3在（0，+∞）上是增函数f（1）＝﹣2＜0，f（2）＝ln2﹣1＜0，f（3）＝ln3＞0∴f（2）•f（3）＜0，根据零点存在性定理，可得函数f（x）＝lnx+x﹣3的零点所在区间为（2，3）故选：C．4．在平面直角坐标系中，若角α以x轴的非负半轴为始边，且终边过点，则sinα的值为（）A．B．C．D．【分析】利用三角函数定义直接求解．解：在平面直角坐标系中，角α以x轴的非负半轴为始边，且终边过点，∴，r＝＝1，∴sinα＝＝．故选：D．5．已知a＝log20.3，b＝20.3，c＝0.30.2，则a，b，c三者的大小关系是（）A．c＞b＞a B．b＞c＞a C．a＞b＞c D．b＞a＞c【分析】利用指数与对数函数的单调性即可得出．解：∵a＝log20.3＜0，b＝20.3＞1，0＜c＝0.30.2＜1，∴b＞c＞a．故选：B．6．为了得到函数y＝sin（2x﹣）的图象，只需将函数y＝sin2x的图象上所有的点（）A．向左平移个单位B．向左平移个单位C．向右平移个单位D．向右平移个单位【分析】由函数y＝A sin（ωx+φ）的图象变换规律，可得结论．解：∵y＝sin（2x﹣）＝sin[2（x﹣）]，∴将函数y＝sin2x的图象上所有的点向右平移个单位，即可得到函数y＝sin（2x﹣）的图象．故选：C．7．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，若，则不等式f（2x﹣1）＜0的解集为（）A．B．C．D．【分析】根据函数的奇偶性和单调性的性质将不等式进行转化求解即可．解：∵f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，∴若，则不等式f（2x﹣1）＜0等价为f（|2x﹣1|）＜f（），即|2x﹣1|＜，即﹣＜2x﹣1＜，得＜x＜，即不等式的解集为（，），故选：A．8．若α、β都是锐角，且sinα＝，cos（α+β）＝﹣，则sinβ的值是（）A．B．C．D．【分析】利用同角三角函数间的关系式的应用，可求得sin（α+β）与cosα的值，再利用两角差的正弦函数，可求得sinβ＝sin[（α+β）﹣α]的值．解：∵cos（α+β）＝﹣，α、β都是锐角，∴sin（α+β）＝＝；又sinα＝，∴cosα＝＝，∴sinβ＝sin[（α+β）﹣α]＝sin（α+β）cosα﹣cos（α+β）sinα＝×﹣（﹣）×＝．故选：A．9．下列命题正确的是（）A．命题“∃x∈R，使得2x＜x2”的否定是“∃x∈R，使得2x≥x2”B．若a＞b，c＜0，则C．若函数f（x）＝x2﹣kx﹣8（k∈R）在[1，4]上具有单调性，则k≤2D．“x＞3”是“x2﹣5x+6＞0”的充分不必要条件【分析】A由命题的否命题，既要对条件否定，也要对结论否定，注意否定形式，可判断；B由条件，注意举反例，即可判断；C由二次函数的图象，即可判断；D先求出不等式x2﹣5x+6＞0的解集，再由充分必要条件的定义，即可判断．解：对于A，命题“∃x∈R，使得2x＜x2”的否定是“∀x∈R，使得2x≥x2”，故A错误；对于B，由条件知，比如a＝2，b＝﹣3，c＝﹣1，则＝﹣＜＝，故B错误；对于C，若函数f（x）＝x2﹣kx﹣8（k∈R）在[1，4]上具有单调性，则≤1或≥4，故k≤2或k≥8，故C错误；对于D，x2﹣5x+6＞0的解集为{x|x＜2或x＞3}，故“x＞3”是“x2﹣5x+6＞0”的充分不必要条件，正确．故选：D．10．已知函数在区间上单调递增，且存在唯一使得f（x0）＝1，则ω的取值范围为（）A．B．C．D．【分析】由函数f（x）在[﹣，]上单调递增求出0＜ω≤，再由存在唯一使得f（x0）＝1求出≤ω＜3；由此求得ω的取值范围．解：由于函数f（x）＝sin（ωx+）（ω＞0）在[﹣，]上单调递增；x∈[﹣，]，ωx+∈[﹣ω+，ω+]，﹣≤﹣ω+且ω+≤，解得ω≤且ω≤，所以0＜ω≤；又存在唯一使得f（x0）＝1，即x∈[0，]时，ωx+∈[，ω+]；所以≤ω+＜，解得≤ω＜3；综上知，ω的取值范围是[，]．故选：B．二、填空题：本大题共4小题，每小题4分，共20分.11．幂函数f（x）的图象经过（2，4），则f（3）＝9 ．【分析】设幂函数f（x）＝x a，由幂函数f（x）的图象经过（2，4），解得f（x）的解析式，由此能求出f（3）．解：设幂函数f（x）＝x a，∵幂函数f（x）的图象经过（2，4），∴2a＝4，解得a＝2，∴f（x）＝x2，∴f（3）＝32＝9．故答案为：9．12．函数的定义域为（﹣1，4）．【分析】由分母中根式内部的代数式大于0且对数式的真数大于0联立不等式组求解．解：由，得﹣1＜x＜4．∴函数的定义域为（﹣1，4）．故答案为：（﹣1，4）．13．已知lga+lg（2b）＝1，则a+b的最小值是2．【分析】利用对数运算性质可得ab，再利用基本不等式的性质即可得出．解：∵lga+lg（2b）＝1，∴2ab＝10，即ab＝5．a，b＞0．则a+b≥2＝2，当且仅当a＝b＝时取等号．因此：a+b的最小值是2．故答案为：2．14．酒驾是严重危害交通安全的违法行为，为了保障交通安全，根据国家有关规定：100ml 血液中酒精含量达到20〜79mg的驾驶员即为酒后驾车，80mg及以上认定为醉酒驾车．假设某驾驶员喝了一定量的酒后，其血液中的酒精含量上升到了0.6mg/ml，如果在停止喝酒以后，他血液中酒精含量会以每小时20%的速度减少，那么他至少要经过t小时后才可以驾驶机动车．则整数t的值为 5 （参考数据：lg2≈0.30，lg3≈0.48）【分析】100ml血液中酒精含量达到60ml，由题意得则60（1﹣20%）t＜20由此利用对数的性质能求出整数t的值．解：某驾驶员喝了一定量的酒后，其血液中的酒精含量上升到了0.6mg/ml，则100ml血液中酒精含量达到60ml，在停止喝酒以后，他血液中酒精含量会以每小时20%的速度减少，他至少要经过t小时后才可以驾驶机动车．则60（1﹣20%）t＜20，∴0.8t＜，∴t＞＝﹣＝﹣＝≈＝4.8．∴整数t的值为5．故答案为：5．三、解答题：本大题共5小题，共60分.解答应写出文字说明、证明过程或演算步骤. 15．设集合A＝{x|x2﹣x﹣6＞0}，B＝{x|﹣4＜3x﹣7＜8}．（1）求A∪B，A∩B；（2）已知集合C＝{x|a＜x＜2a+1}，若C⊆B，求实数a的取值范围．【分析】（1）求出集合A，B，由此能求出A∪B，A∩B．（2）当C＝∅时，a≥2a+1，a≤﹣1，当C≠∅时，，由此能求出实数a的取值范围．解：（1）∵集合A＝{x|x2﹣x﹣6＞0}＝{x|x＞3或x＜﹣2}，B＝{x|﹣4＜3x﹣7＜8}＝{x|1＜x＜5}，∴A∪B＝{x|x＜﹣2或x＞1}，A∩B＝{x|3＜x＜5}．（2）∵集合C＝{x|a＜x＜2a+1}，C⊆B，∴当C＝∅时，a≥2a+1，a≤﹣1，当C≠∅时，，解得1≤a≤2，综上，实数a的取值范围是（﹣∞，﹣1]∪[1，2]．16．已知函数．（1）在给出的直角坐标系中，画出y＝f（x）的大致图象；（2）根据图象写出f（x）的单调区间；（3）根据图象写出不等式f（x）＞0的解集．【分析】根据各段函数的解析式作图即可解：（1）如图，（2）由图可知f（x）的单调递增区间为（﹣∞，﹣2），（0，1）；单调递减区间为（﹣2，0），（1，+∞）；（3）由图可知f（x）＞0时，x∈（﹣4，﹣1）．17．已知sinα＝，α∈（，π），cosβ＝，β∈（0，）．（1）求cos（α﹣β）的值；（2）求tan（2β+）的值．【分析】（1）由题意利用同角三角函数的基本关系，两角差的余弦公式，求得结果．（2）由题意利用同角三角函数的基本关系，两角和的正切公式，求得结果．解：（1）∵已知sinα＝，α∈（，π），∴cosα＝﹣＝﹣．∵cosβ＝，β∈（0，），∴sinβ＝＝，∵cos（α﹣β）＝cosαcosβ+sinαsinβ＝﹣•+•＝＝﹣．（2）由以上可得tanβ＝＝2，∴tan2β＝＝＝﹣，tan（2β+）＝＝＝﹣．18．已知函数．（1）判断f（x）的单调性，并用函数单调性的定义证明；（2）判断f（x）的奇偶性，并说明理由．【分析】（1）根据函数单调性的定义进行证明即可；（2）根据函数奇偶性的定义进行证明即可．解：（1）函数的定义域为R，设x1＜x2，则f（x1）﹣f（x2）＝﹣﹣+＝﹣＝＝，∵x1＜x2，∴＜，则﹣＜0，即f（x1）﹣f（x2）＜0，则f（x1）＜f（x2），即函数f（x）为增函数．（2）f（x）＝＝，则f（﹣x）＝＝＝﹣f（x），即f（x）是奇函数．19．已知函数．（1）求f（x）的最小正周期；（2）求f（x）在区间上的最大值和最小值；（3）若关于x的不等式mf（x）+3m≥f（x）在R上恒成立，求实数m的取值范围．【分析】（1）根据f（x）＝sin（2x﹣）可求最小正周期；（2）利用x∈以及正弦函数单调区间即可求出最大最小值；（3）令t＝sin（2x﹣），将不等式化成m≥＝1﹣对∀t∈[﹣1，1]恒成立，即可求出m取值范围．解：f（x）＝sin2x﹣cos2x＝2sin（2x﹣），（1）T＝＝π，即f（x）的最小正周期为π；（2）当x∈时，则2x﹣∈[﹣，π]，sin（2x﹣）∈[﹣，1]，所以f（x）∈[﹣，2]，即f（x）最大值为2，最小值为﹣；（3）mf（x）+3m≥f（x）即2m sin（2x﹣）+3m≥2sin（2x﹣），令t＝f（x）＝sin（2x﹣），则t∈[﹣1，1]，所以2t+3∈[1，5]根据题意得2mt+3m≥2t对∀t∈[﹣1，1]恒成立，即有m≥＝1﹣对∀t∈[﹣1，1]恒成立，因为1﹣最大为1﹣＝，所以m≥．。

天津市部分区2024_2025学年高二数学上学期期末考试试卷含解析

天津市部分区2024-2025学年高二上学期期末考试数学试卷一、选择题．在每小题给出的四个选项中，只有一项是符合题目要求的．1.双曲线﹣y2＝1的焦点坐标为（）A. （﹣3，0），（3，0）B. （0，﹣3），（0，3）C. （﹣，0），（，0）D. （0，﹣），（0，）【答案】C【解析】【分析】利用双曲线的标准方程干脆计算。

【详解】由双曲线﹣y2＝1可得：，则所以双曲线﹣y2＝1的焦点坐标为：（﹣，0），（，0）故选：C【点睛】本题主要考查了双曲线的简洁性质，属于基础题。

2.命题“∃x0∈（0，+∞），使得＜”的否定是（）A. ∃x0∈（0，+∞），使得B. ∃x0∈（0，+∞），使得C. ∀x∈（0，+∞），均有e x＞xD. ∀x∈（0，+∞），均有e x≥x【答案】D【解析】【分析】由特称命题的否定干脆写出结果即可推断。

【详解】命题“∃x0∈（0，+∞），使得＜”的否定是：“x∈（0，+∞），使得”故选：D【点睛】本题主要考查了特称命题的否定，属于基础题。

3.若复数（为虚数单位），则的共轭复数（）A. B. C. D.【答案】B【解析】因为，所以，应选答案B。

4.设R，则“＞1”是“＞1”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】【详解】试题分析：由可得成立，反之不成立，所以“”是“”的充分不必要条件考点：充分条件与必要条件5.设公比为﹣2的等比数列{a n}的前n项和为S n，若S5＝，则a4等于（）A. 8B. 4C. ﹣4D. ﹣8【答案】C【解析】【分析】由S5＝求出，再由等比数列通项公式求出即可。

【详解】由S5＝得：，又解得：，所以故选：C【点睛】本题主要考查了等比数列的前n项和公式及等比数列通项公式，考查计算实力，属于基础题。

6.已知函数f（x）＝lnx﹣，则f（x）（）A. 有微小值，无极大值B. 无微小值有极大值C. 既有微小值，又有极大值D. 既无微小值，又无极大值【答案】B【解析】【分析】求出，对的正负分析，即可推断函数的极值状况。

天津市部分区2019-2020学年度第一学期期中测试八年级数学试卷及答案

天津市部分区2019～2020学年度第一学期期中练习八年级数学参考答案一、选择题：1．A ；2．B ；3．C ；4．C ；5．C ；6．B ；7．D ；8．D ；9．B ；10．D ；11．B ；12．D二、填空题：13．030，060，090；14．六； 15．12； 16．AC=BD （答案不唯一）； 17．5，090；18．5.三、解答题：19．解：（1）图略 ……………………………………………………………2分 C 1（3，-2） ……………………………………………………………3分（2）图略 ………………………………………………………………5分 C 2（-3，2） …………………………………………………………6分20．解：设这个多边形的边数是n ， ……………………………………1分依题意得（n ﹣2）×180°=3×360°﹣180°， ……………………………………………3分n ﹣2=5，n=7． …………………………………………………………5分∴这个多边形的边数是7． ……………………………………6分21．解：∵︒=∠50B ，︒=∠60C .∴ 70BAC ∠=︒ ……………………………………………………………2分 ∵AD 为角平分线∴︒=∠=∠=∠3521BAC CAD BAD …………………………………3分 ∴00853550=+︒=∠+∠=∠BAD B ADE …………………………………4分 ∵BC AE ⊥∴090=∠AED∴000585-90==∠EAD …………………………………………………6分22．证明：∵BF=CE，∴BF+CF=CE+CF，即BC=EF ， …………………………………………2分在△ABC 和△DEF 中，AB=DE ，∠B=∠E, BC=EF∴△ABC≌△DEF（SAS ） …………………………………………4分∴∠A=∠D． ……………………………………………6分23．解：∵AB=AC，AC=CD ，BD=AD ，∴∠B＝∠C＝∠BAD,∠CAD＝∠CDA，（等边对等角）…………………2分设∠B＝x，则∠CDA＝∠BAD+∠B＝2x，从而∠CAD＝∠CDA＝2x，∠C＝x∴△ADC中，∠CAD+∠CDA+∠C＝2x+2x+x= 180° ………………………4分解得x= 36° ……………………………5分∴在△ABC中，∠B＝∠C＝36°，∠CAB＝108° …………………………6分24．证明：（1）∵AC∥DF，∴∠ACB=∠F，…………………………………………2分在△ABC和△DEF中，∴△ABC≌△DEF（AAS）；………………………………………4分（2）∵△ABC≌△DEF，∴BC=EF，…………………………………………………………6分∴BC﹣CE=EF﹣CE，即BE=CF．……………………………………………………8分25．解：（1）∵E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，∴DE=CE，……………………………………………………………1分OE=OE，∴Rt△ODE≌Rt△OCE，………………………………………2分∴OD=OC，∴△DOC是等腰三角形，……………………………………………3分∵OE是∠AOB的平分线，∴OE是CD的垂直平分线；…………………………………………4分（2）∵OE是∠AOB的平分线，∠AOB=60°，∴∠AOE=∠BOE=30°，………………………………………………5分∵EC⊥OB，ED⊥OA，∴OE=2DE，∠ODF=∠OED=60°，………………………………………6分∴∠EDF=30°，∴DE=2EF，∴OE=4EF．…………………………………………………………………8分。

天津市高一上学期期末数学试题(解析版)

数学试卷一､选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知，那么是（） cos tan 0θθ⋅>θA. 第一、二象限角B. 第二、三象限角C. 第三、四象限角D. 第一、四象限角【答案】A【解析】【分析】化简代数式，根据正弦值为正，得出终边所在象限.cos tan =sin θθθ⋅【详解】由可知同号，即，cos tan 0θθ⋅>cos ,tan θθcos tan =sin 0θθθ⋅>从而为第一、二象限角，故选A .θ故选：A【点睛】此题考查根据三角函数符号判断角的终边所在象限，关键在于熟记各个象限三角函数值的符号进行辨析.2.（） 253364a a a ÷=A .B. C. D. 43a 127a 712a 34a 【答案】C 【解析】【分析】根据指数幂的运算性质计算即可.【详解】. 235734612253364a aa a a +-==÷故选：C.3. 函数的零点是（） ()sin 1f x x =+A.B. ()π2πZ 2k k +∈()3π2πZ 2k k +∈C. D.()ππZ 2k k +∈()πZ k k ∈【答案】B【解析】【分析】令，再根据正弦函数的性质即可得解.()sin 10f x x =+=【详解】令，则，()sin 10f x x =+=sin 1x =-所以， ()3π2πZ 2x k k =+∈所以函数的零点是. ()sin 1f x x =+()3π2πZ 2k k +∈故选：B.4. 已知半径为的圆上，有一条弧的长是，则该弧所对的圆心角的弧度数为（）120mm 144mm A. 12B. 1.2C. 16D. 1.6【答案】B【解析】【分析】根据弧长公式即可得解.【详解】设该弧所对的圆心角的弧度数为，α则，解得.120144α= 1.2α=故选：B . 5. 设，，，则（）． 13log 2a =121log 3b =0.312c ⎛⎫= ⎪⎝⎭A.B. C. D. a b c <<b<c<a a c b <<b a c <<【答案】C 【解析】【分析】利用对数指数函数的单调性求出a,b,c 的范围即得解. 【详解】由题得， 1133log 2log 10a =<=， 112211log log 132b =>=， 0.30110122c ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭所以.a cb <<故选：C【点睛】本题主要考查指数对数函数的图象和性质，意在考查学生对这些知识的理解掌握水平. 6. 为了得到函数的图象，只需将函数的图象上所有的点（）()sin 21y x =+()sin 21y x =-A. 向左平移2个单位长度B. 向右平移2个单位长度C. 向左平移1个单位长度D. 向右平移1个单位长度【答案】C【解析】【分析】根据平移变换的原则即可得解.【详解】为了得到函数的图象，()()sin 21=sin 211y x x ⎡⎤=++-⎣⎦只需将函数的图象上所有的点向左平移1个单位长度即可.()sin 21y x =-故选：C .7. 设，，都是正数，且，那么（）a b c 346a b c ==A. B. C. D. 111c a b =+221c a b =+122c a b =+212c a b=+【答案】B【解析】【分析】令，根据指数与对数的关系将指数式化为对数式，再由换底公式及对数的运算346a b c M ===法则计算可得.【详解】解：由，，都是正数，令，则，，a b c 346a b c M ===()1M >3log a M =4log b M =，6log c M =所以，，， 1log 3M a =1log 4M b =1log 6M c=对于A ：，故A 错误； 111log 4log 3log 12log 6M M M M a b c+=+=>=对于B ：，22log 6log 36M M c ==()22212log 3log 4log 3log 4log 34log 36M M M M M M a b +=+=+=⨯=，所以，故B 正确； 221c a b=+对于C ：， ()222222log 32log 4log 3log 4log 34log 1442M M M M M M a b+=+=+=⨯=所以，故C 错误； 122c a b≠+对于D ：， ()221log 32log 4log 3log 4log 3824log 4M M M M M M a b +=+=+=⨯=所以，故D 错误； 212c a b≠+故选：B ．8. 函数的图象大致为 2sin ()1||x f x x =-A.B.C.D.【答案】A【解析】【分析】根据奇偶性排除B ，D ，取特殊值排除C ，即可得到答案.【详解】的定义域为关于原点对称 2sin ()1||x f x x =-(,1)(1,1)(1,)-∞--+∞ ()()2sin 2sin ()()1||1||x x f x f x x x --==-=----所以函数是奇函数，故排除B ，D()f x 因为，所以排除C 2sin 4(041||4f πππ==>-故选：A【点睛】本题主要考查了函数图像的识别，属于中等题.9. 下述四条性质：①最小正周期是，②图象关于直线对称，③图象关于点对称，④在ππ3x =π,012⎛⎫ ⎪⎝⎭上是增函数.下列函数同时具有上述性质的一个函数是（） ππ-,63⎡⎤⎢⎥⎣⎦A. B. πsin +26x y ⎛⎫= ⎪⎝⎭πsin 26y x ⎛⎫=- ⎪⎝⎭C. D. πcos 23y x ⎛⎫=+ ⎪⎝⎭πsin 26y x ⎛⎫=+ ⎪⎝⎭【答案】B【解析】【分析】根据条件判断选项中函数的周期性，单调性以及图像的对称性，从而得到结论.【详解】条件① ：的周期为，排除A ； πsin 26x y ⎛⎫=+ ⎪⎝⎭2π4π12=条件② ：当代入B ，函数取得最大值，满足关于对称；代入C ，函数取得最小值，满足关于π3x =π3x =对称；代入D ，函数值不是最大值也不是最小值，排除D ； π3x =条件③ ：代入B ，函数值为0，满足；代入C ，函数值为0，满足； π12x =条件④ ：在上，代入B ，是增函数；代入C ，单调ππ-,63⎡⎤⎢⎥⎣⎦πππ2622x ⎡⎤-∈-⎢⎥⎣⎦，ππ-,63⎡⎤⎢⎥⎣⎦[]π20π3x +∈，递减，不满足，排除C ；故选：B二､填空题：本大题共6小题，每小题5分，共30分.10. 若对数函数且）的图象经过点，则实数______.log (0a y x a =>1a ≠(4,2)=a 【答案】2【解析】【分析】直接将点代入计算即可.【详解】将点代入得，解得 (4,2)log ay=2log 4a =2a =故答案为：2.11. 已知角的终边经过点那么的值是_______.θ1(2tan θ【答案】【解析】【分析】直接利用三角函数的定义求解即可.【详解】因为角的终边经过点 θ1(),2所以为第二象限角，，θtan 0θ∴<由三角函数的定义可得，故答案为tan θ==【点睛】本题主要考查任意角的正切函数值,意在考查对基础知识的掌握情况，属于基础题. 12. 函数的定义域为_________.y =【答案】 3{|1}4x x <≤【解析】【分析】根据根式、对数的性质有求解集，即为函数的定义域. 0.5430log (43)0x x ->⎧⎨-≥⎩【详解】由函数解析式知：，解得， 0.5430log (43)0x x ->⎧⎨-≥⎩314x <≤故答案为：. 3{|1}4x x <≤13. 已知函数的部分图象如图所示，则___________. ()()sin 0,0,2πf x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭ϕ=【答案】π6【解析】【分析】根据图象可求得，再利用待定系数法求解即可.,A ωϕ【详解】由图可知， 3,π2T A ==所以，所以，2π2πT ω==1ω=所以，()()3sin f x x ϕ=+则，即， ππ3sin 066f ϕ⎛⎫⎛⎫-=-+= ⎪ ⎪⎝⎭⎝⎭πsin 06ϕ⎛⎫-+= ⎪⎝⎭所以，即， π2π,Z 6k k ϕ-+=∈π2π,Z 6k k ϕ=+∈又因，所以. π2ϕ<π6ϕ=故答案为：. π614. 函数在的值域是___________. π2cos 23y x ⎛⎫=- ⎪⎝⎭π5π,36x ⎡⎤∈⎢⎥⎣⎦【答案】[]2,1-【解析】【分析】根据余弦函数的性质结合整体思想即可得解. 【详解】因为，所以， π5π,36x ⎡⎤∈⎢⎥⎣⎦ππ4π2,333x ⎡⎤-∈⎢⎥⎣⎦所以， π1cos 21,32x ⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦所以函数在的值域是. π2cos 23y x ⎛⎫=- ⎪⎝⎭π5π,36x ⎡⎤∈⎢⎥⎣⎦[]2,1-故答案为：.[]2,1-15. 已知函数的零点个数为___________. ()4223,0274ln ,0x x f x x x x x +⎧-≤=⎨-+->⎩【答案】3【解析】【分析】分和两种情况讨论，时，函数零点的个数，即为函数0x ≤0x >0x >()2274ln f x x x x =-+-图象交点的个数，作出函数的图象，根据函数图象即2274,ln y x x y x =-+=2274,ln y x x y x =-+=可得解.【详解】当时，由，得， 0x ≤()4023x f x +=-=2log 34x =-当时，由，得，0x >()2274ln 0f x x x x =-+-=2274ln x x x -+=则时，函数零点的个数， 0x >()2274ln f x x x x =-+-即为函数图象交点的个数，2274,ln y x x y x =-+=如图，作出函数的图象，2274,ln y x x y x =-+=由图可知，两函数的图象有个交点，2即当时，函数有个零点， 0x >()2274ln f x x x x =-+-2综上所述，函数有个零点.()f x 3故答案为：.3三､解答题：本大题共3小题，共34分.解答应写出文字说明，证明过程或演算步骤. 16. 计算：（1）已知，求的值； 1sin 3α=-()()πcos 2sin 2πcos 2π5πsin 2αααα⎛⎫- ⎪⎝⎭--⎛⎫+⎪⎝⎭（2）求的值. 5551log 35log log 1450+--【答案】（1）19（2）2【解析】【分析】（1）根据诱导公式计算即可；（2）根据对数的运算性质计算即可.【小问1详解】 ()()πcos 2sin 2πcos 2π5πsin 2αααα⎛⎫- ⎪⎝⎭--⎛⎫+ ⎪⎝⎭. 2sin 1sin cos sin cos 9ααααα=⋅⋅==【小问2详解】5551log 35log log 1450+-. 51log 3550131214⎛⎫=⨯⨯-=-= ⎪⎝⎭17. 已知为第二象限角，为第一象限角，. α3sin ,5αβ=5cos 13β=（1）求的值；()sin αβ+（2）求的值.()tan 2αβ-【答案】（1） 3365-（2） 204253【解析】【分析】（1）先利用平方关系求出，再利用两角和的正弦公式即可得解； cos ,sin αβ（2）先利用二倍角的正切公式求出，再根据两角差的正切公式即可得解.tan 2α【小问1详解】因为为第二象限角，为第一象限角，， α3sin ,5αβ=5cos 13β=所以， 412cos ,sin 513αβ=-=所以. ()3541233sin 51351365αβ⎛⎫+=⨯+-⨯=- ⎪⎝⎭【小问2详解】， sin 3sin 12tan ,tan cos 4cos 5αβαβαβ==-==所以， 232tan 242tan 291tan 7116ααα-===---所以. ()241220475tan 22412253175αβ---==⎛⎫+-⨯ ⎪⎝⎭18. 已知函数 ()()2πcos 2cos2R 3f x x x x ⎛⎫=--∈ ⎪⎝⎭（1）求的最小正周期；()f x （2）求的单调递增区间.()f x 【答案】（1） πT =（2） π5ππ,π,Z 1212k k k ⎡⎤-++∈⎢⎥⎣⎦【解析】【分析】（1）先利用两角差的余弦公式和辅助角公式化简，再根据正弦函数的周期性即可得解；（2）根据正弦函数的单调性结合整体思想即可得解.【小问1详解】()2πcos 2cos23f x x x ⎛⎫=-- ⎪⎝⎭，13πcos 22cos 22cos 22223x x x x x x ⎛⎫=-+-=-=- ⎪⎝⎭所以；πT =【小问2详解】令， πππ2π22π232k x k -+≤-≤+得， π5πππ1212k x k -+≤≤+所以的单调递增区间为.()f x π5ππ,π,Z 1212k k k ⎡⎤-++∈⎢⎥⎣⎦。

天津市部分区2019-2020学年高一下学期期末考试物理试题+Word版含答案

天津市部分区2019 ~ 2020学年度第二学期期末考试高一物理温馨提示：本试卷分第卷（选择题）和第卷（非选择题）两部分，满分：100分，考试时间：60分钟。

第卷（选择题，共40分）一、单项选择题：（本题共5小题，每小题5分，共25分。

每小题给出的四个选项中，只有一个选项符合题意，有选错或不答的得0分。

）1.关于万有引力定律，下列说法正确的是A万有引力定律是卡文迪许提出的B万有引力定律是第谷提出的C万有引力定律是开普勒提出的D万有引力定律是牛顿提出的2.关于“点电荷”，所体现的物理思想方法是A等效替代B控制变量C建立模型D微元求和3.一航模兴趣小组设计出一架遥控飞行器，在一次试飞过程中，飞行器从地面由静止开始竖直加速上升高度为h，已知飞行器的动力系统所提供的升力恒为F，飞行器的质量为m，重力加速度为g。

则在这一过程中飞行器A所受恒定升力做功为FhB所受的重力做功为mghC恒定升力做功等于重力做功D动力系统的输出功率保持不变4.密立根油滴实验原理如图所示。

两块水平放置的金属板分别与电源的正负极相接，板间存在电压，形成竖直向下场强为E的匀强电场。

用喷雾器从上板中间的小孔注入大小、质量和电荷量各不相同的油滴。

通过显微镜可找到悬浮不动的油滴，若此悬浮油滴的质量为m，重力加速度为g。

下列说法正确的是A ．悬浮油滴带正电B ．悬浮油滴的电荷量为mgEC ．增大场强，悬浮油滴将向下运动D ．油滴的电荷量不一定是电子电量的整数倍5.2018年12月8日，肩负着亿万中华儿女探月飞天梦想的嫦娥四号探测器成功发射，“实现人类航天器首次在月球背面巡视探测，率先在月背刻上了中国足迹”。

已知月球的质量为M 、半径为R ，探测器的质量为m ，引力常量为G ，探测器围绕月球做半径为r 的匀速圆周运动时，探测器的AB C ．向心加速度为2GMr D ．向心加速度为2GMR二、不定项选择题：（本题共3小题，每小题5分，共15分。

在每小题给出的四个选项中，有多个选项符合题意。

天津市部分区2024-2025学年高三上学期11月期中考试语文试卷(含答案)

天津市部分区2024-2025学年度第一学期期中练习高三语文本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，练习用时150分钟。

使用答题卡的地区，将答案写在答题卡上；不使用答题卡的地区，将答案写在答题纸上。

第Ⅰ卷注意事项：本卷共11小题，每小题3分，共33分。

在每小题给出的四个选项中，只有一项是最符合题目要求的。

一、(9分)阅读下面的一段文字，完成1-2题。

国风音乐是指由现代与古典曲风融合而成的新音乐类型。

很多国风音乐喜欢用古诗词作歌词，或者巧妙地将古诗词化用在歌词中。

即使新创作的歌词，也大都喜欢使用富含古意的典故、意象。

如果把一首国风歌曲中的所有意象开来，就是一幅生动的图画。

听音乐时，人们会被各种意象带入一种“古风意境”，仿佛。

由于大量使用诗词古韵以及古典意象，使得国风音乐追求的是意境美、朦胧美，总基调一般是内敛的、含蓄的。

这使得国风音乐在情感表达上不像西方音乐那般直白，听众需要不断咀嚼歌词的含义，对作品进行抽丝剥茧般的欣赏，才能获得的审美体验。

1.依次填入文中横线上的词语，全都恰当的一项是A.铺陈身临其境与众不同B.铺展身临其境独一无二C.铺陈设身处地与众不同D.铺展设身处地独一无二2.文中画波浪线的句子有语病，下列修改最恰当的一项是A.由于大量使用的诗词古韵以及古典意象，使得国风音乐追求意境美、朦胧美，总基调一般是内敛的、含蓄的。

B.大量使用的诗词古韵以及古典意象，国风音乐的总基调一般是内敛的、含蓄的，追求的是意境美、朦胧美。

C.由于大量使用诗词古韵以及古典意象，使得国风音乐追求的是意境美，朦胧美，总基调一般是内敛的、含蓄的。

D.由于大量使用诗词古韵以及古典意象，国风音乐的总基调一般是内敛的、含蓄的，追求的是意境美、朦胧美。

3.下列文学常识对应关系的表述正确的一项是A. 《阿房宫赋》杜牧唐朝借古讽今B. 《答司马谏议书》王安石北宋奏章体C. 《大学之道》孟子战国散文D. 《大卫·科波菲尔》狄更斯俄国小说二、(9分)阅读下面的文字，完成4-6题。

2018-2019两年天津市中考数学试卷及答案解析

2018年天津市初中毕业生学业考试试卷数学第Ⅰ卷一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的）1. 计算2(3)-的结果等于（）A．5 B．5- C．9 D．9-2. cos30︒的值等于（）A．22 B．32C．1 D．33. 今年“五一”假期，我市某主题公园共接待游客77800人次，将77800用科学计数法表示为（）A．50.77810⨯ B．47.7810⨯ C．377.810⨯D．277810⨯4.下列图形中，可以看作是中心对称图形的是（）A． B． C. D．5.下图是一个由5个相同的正方体组成的立体图形，它的主视图是（）A ．B ． C.D ．6.65 ）A ．5和6之间B ．6和7之间C. 7和8之间 D ．8和9之间7.计算23211x x x x +-++的结果为（） A ．1 B ．3 C. 31x + D ．31x x ++ 8.方程组10216x y x y +=⎧⎨+=⎩的解是（） A ．64x y =⎧⎨=⎩ B ．56x y =⎧⎨=⎩ C. 36x y =⎧⎨=⎩ D ．28x y =⎧⎨=⎩ 9.若点1(,6)A x -，2(,2)B x -，3(,2)C x 在反比例函数12y x =的图像上，则1x ，2x ，3x 的大小关系是（）A ．123x x x <<B ．213x x x << C. 231x x x <<D ．321x x x <<10.如图，将一个三角形纸片ABC 沿过点B 的直线折叠，使点C 落在AB 边上的点E 处，折痕为BD ，则下列结论一定正确的是（）A．AD BD== B．AE ACC.ED EB DB+=+= D．AE CB AB11.如图，在正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP EP+最小值的是（）A．AB B．DE C.BD D．AF12.已知抛物线2=++（a，b，c为常数，0y ax bx c-，a≠）经过点(1,0) (0,3)，其对称轴在y轴右侧，有下列结论：①抛物线经过点(1,0)；②方程22ax bx c++=有两个不相等的实数根；③33-<+<.a b其中，正确结论的个数为（）A．0 B．1 C.2 D．3第Ⅱ卷二、填空题（本大题共6小题，每小题3分，共18分）13.计算432x x⋅的结果等于．14.计算63)(63)的结果等于．15.不透明袋子中装有11个球，其中有6个红球，3个黄球，2个绿球，这些球除颜色外无其他差别.从袋子中随机取出1个球，则它是红球的概率是．16.将直线y x=向上平移2个单位长度，平移后直线的解析式为．17.如图，在边长为4的等边ABC△中，D，E分别为AB，BC的中点，⊥于点F，G为EF的中点，连接DG，则DG的长为．EF AC18.如图，在每个小正方形的边长为1的网格中，ABC△的顶点A，B，C均在格点上.（1）ACB∠的大小为（度）；（2）在如图所示的网格中，P是BC边上任意一点.A为中心，取旋转角等于BACCP最短∠，把点P逆时针旋转，点P的对应点为'P.当'时，请用无刻度．．．的直尺，画出点'P，并简要说明点'P的位置是如何找到的（不要求证明）．三、解答题（本大题共7小题，共66分.解答应写出文字说明、演算步骤或推理过程.）19. 解不等式组31(1)413(2)x x x +≥⎧⎨≤+⎩请结合题意填空，完成本题的解答.（Ⅰ）解不等式（1），得．（Ⅱ）解不等式（2），得．（Ⅲ）把不等式（1）和（2）的解集在数轴上表示出来：（Ⅳ）原不等式组的解集为．20. 某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位：kg ），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：（Ⅰ）图①中m 的值为；（Ⅱ）求统计的这组数据的平均数、众数和中位数；（Ⅲ）根据样本数据，估计这2500只鸡中，质量为2.0kg 的约有多少只？21. 已知AB是O的直径，弦CD与AB相交，38∠=︒.BAC（Ⅰ）如图①，若D为AB的中点，求ABC∠和ABD∠的大小；（Ⅱ）如图②，过点D作O的切线，与AB的延长线交于点P，若∠的大小.//DP AC，求OCD22. 如图，甲、乙两座建筑物的水平距离BC为78m，从甲的顶部A处测得乙的顶部D处的俯角为48︒，测得底部C处的俯角为58︒，求甲、乙建筑物的高度AB和DC（结果取整数）.参考数据：tan48 1.11︒≈.︒≈，tan58 1.6023.某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.设小明计划今年夏季游泳次数为x（x为正整数）.（Ⅰ）根据题意，填写下表：游泳次数10 15 20 (x)150 175 …方式一的总费用（元）90 135 …方式二的总费用（元）（Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？（Ⅲ）当20x 时，小明选择哪种付费方式更合算？并说明理由. 24.在平面直角坐标系中，四边形AOBC是矩形，点(0,0)A，O，点(5,0)点(0,3)B.以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F.（Ⅰ）如图①，当点D落在BC边上时，求点D的坐标；（Ⅱ）如图②，当点D落在线段BE上时，AD与BC交于点H.①求证ADB AOB≌；△△②求点H的坐标.（Ⅲ）记K为矩形AOBC对角线的交点，S为KDE△的面积，求S的取值范围（直接写出结果即可）.25.在平面直角坐标系中，点(0,0)O，点(1,0)A.已知抛物线22y x mx m=+-（m是常数），定点为P.（Ⅰ）当抛物线经过点A时，求定点P的坐标；（Ⅱ）若点P在x轴下方，当45AOP∠=︒时，求抛物线的解析式；（Ⅲ）无论m取何值，该抛物线都经过定点H.当45AHP∠=︒时，求抛物线的解析式.试卷答案一、选择题1-5:CBBAA 6-10:DCABD 11、12：DC二、填空题13.72x 14. 3 15.611 16.2y x=+17.218. （Ⅰ）90︒；（Ⅱ）如图，取格点D，E，连接DE交AB于点T；取格点M，N，连接MN交BC延长线于点G；取格点F，连接FG交TC延长线于点'P ，则点'P 即为所求.三、解答题19. 解：（Ⅰ）2x ≥-；（Ⅱ）1x ≤；（Ⅲ）（Ⅳ）21x -≤≤.20. 解：（Ⅰ）28.（Ⅱ）观察条形统计图， ∵ 1.05 1.211 1.514 1.816 2.04 1.5251114164x ⨯+⨯+⨯+⨯+⨯==++++， ∴这组数据的平均数是1.52.∵在这组数据中，1.8出现了16次，出现的次数最多，∴这组数据的众数为1.8.∵将这组数据按从小到大的顺序排列，其中处于中间的两个数都是1.5，有1.5 1.5 1.52+=， ∴这组数据的中位数为1.5.（Ⅲ）∵在所抽取的样本中，质量为2.0kg 的数量占8%.∴由样本数据，估计这2500只鸡中，质量为2.0kg 的数量约占8%. 有25008%200⨯=.∴这2500只鸡中，质量为2.0kg 的约有200只。

天津市七区2022-2023学年高一上学期期末数学试题(解析版)

【小问1详解】
根据分段函数解析式可得，
易知；所以
即 .
【小问2详解】
①当时，，
解得，或（舍）.
②当时，，解得（舍）.
综上可得 .
即实数a的值为
【小问3详解】
画出函数图象如下所示：
所以，单调递增区间，单调递减区间，
18.已知指数函数（a＞0，且）的图象过点．
（1）求a的值；
∴ ，∴ ；
小问2详解】
，
，
∴ ，
，
.
17.已知函数
（1）求，的值；
（2）若，求实数a的值；
（3）直接写出的单调区间．
【答案】（1）；
（2）
（3）单调递增区间，单调递减区间，
【解析】
【分析】（1）根据分段函数定义直接代入计算即可；（2）分类讨论实数a的取值范围，解方程即可得出符合题意的a的值；（3）画出函数图象即可直接写出单调区间．
【详解】，
当且仅当 ,即时，取得最小值.
故答案为： .
15.有下列命题：
①函数的定义域为；
②不等式的解集为，则实数k的取值范围为；
③函数是定义在上的偶函数，当时，．则当x＜0时，．
其中正确命题的序号为______（把正确的答案都填上）．
【答案】①③
【解析】
【分析】对①②③逐一判断，①函数的定义域要满足分母不为0，对数函数的真数大于0，②对不等式的二次项系数分类讨论，分别求的满足条件的集合，即可求得实数k的取值范围，③有函数的奇偶性可知，又知当当时函数的解析式，即可求得当时函数的解析式.
（2）若，，求m＋n的值；
（3）求不等式的解集．

2023-2024学年天津市经开一中强基班高一(上)期中数学试卷【答案版】

2023-2024学年天津市经开一中强基班高一（上）期中数学试卷一、单选题（本大题共12小题，共36.0分。

每小题列出的选项中，选出符合题目的一项） 1．全称命题：∀x ∈R ，x 2+5x ＝4的否定是（） A ．∃x ∈R ，x 2+5x ＝4 B ．∀x ∈R ，x 2+5x ≠4 C ．∃x ∈R ，x 2+5x ≠4D ．以上都不正确2．若a ，b ，c ∈R ，a ＞b ，则下列不等式一定成立的是（） A ．a +c ＞b +cB ．ac ＞bcC ．ac ＜bcD ．a 2＞b 23．若a +2∈{1，3，a 2}，则a 的值为（） A ．﹣1或1或2B ．﹣1或1C ．﹣1或2D ．24．已知不等式x 2﹣2x ﹣3＜0的解集为A ，不等式x+3x−2＜0的解集为B ，则A ∩B 为（）A ．[﹣3，3]B ．（﹣3，3）C ．[﹣1，2]D ．（﹣1，2）5．若f （x ）对于任意实数x 都有2f(x)−f(1x )=2x +1，则f(12)=（）A ．3B ．4C ．83D ．436．已知p ：∃x ＜0，x +a ﹣1＝0，若p 的否定为真命题，则a 的取值范围是（） A ．a ＜1B ．a ≥﹣1C ．a ＞﹣1D ．a ≤17．已知函数f(x)={√x ，x ≥23−x ，x ＜2，则f （f （﹣1））等于（）A ．4B ．﹣2C ．√2D ．28．若一元二次不等式x 2+bx ﹣a ＜0的解集为{x |﹣2＜x ＜3}，则a +b ＝（） A ．﹣6B ．1C ．5D ．69．若定义在R 上的奇函数f （x ）在（﹣∞，0）单调递减，且f （2）＝0，则f(x)x＞0的解集（）A ．（﹣∞，﹣2）∪（0，2）B ．（﹣∞，﹣2）∪（2，+∞）C ．（﹣2，0）∪（0，2）D ．（﹣2，0）∪（2，+∞）10．若函数y ＝f （x ）是奇函数，且函数F （x ）＝af （x ）+bx +2在（0，+∞）上有最大值8，则函数y ＝F （x ）在（﹣∞，0）上有（） A ．最小值﹣8B ．最大值﹣8C ．最小值﹣4D ．最小值﹣611．若函数f （x ）是定义域为R ，且对∀x 1，x 2∈R ，且x 1＜x 2，有f （x 1）﹣f （x 2）＜x 2﹣x 1，不等式f （x ）﹣f （2﹣x ）+2x ＞2的解集为（）A ．（﹣1，+∞）B ．（0，+∞）C ．（1，+∞）D ．（2，+∞）12．已知函数f(x)=xx 2+2，下列关于f （x ）的性质，推断正确的有（） ①函数的定义域为R ； ②函数是偶函数；③函数f （x ）与f （x ﹣2）的值域相同； ④f （x ）在（0，1）上递增； ⑤f （x ）在[1，2]上有最大值13．A ．2B ．3C ．4D ．5二、填空题（本大题共6小题，共18.0分） 13．函数y =√7+6x −x 2的定义域是．14．已知幂函数f （x ）＝（m 2﹣2m ﹣2）x m 在（0，+∞）上单调递减，则m ＝． 15．已知f （x ）是偶函数，当x ＜0时，f （x ）＝x （x +1）．则当x ＞0时，f （x ）＝．16．已知函数f(x)={(a −3)x +5，x ≤12a x ，x ＞1是（﹣∞，+∞）上的减函数，那么a 的取值范围为．17．若关于x 的不等式x 2+mx ﹣4≥0在区间[1，4]上有解．则实数m 的最小值是． 18．已知x ，y 是正数，1x +2y =1，则2x+yxy+1的最小值为．三、解答题（本大题共5小题，共46.0分）19．（8分）已知集合A ＝{x |2﹣a ≤x ≤2+a }，B ＝{x |x ≤1或x ≥4}．（1）当a ＝4时，求A ∩B ；（2）若a ＞0，且“x ∈A ”是“x ∈∁R B ”的充分不必要条件，求实数a 的取值范围． 20．（8分）已知关于x 的不等式2kx 2+kx ﹣1＜0．（1）若不等式的解集为(−32，1)，求实数k 的值；（2）若不等式的解集为R ，求实数k 的取值范围．21．（8分）求关于x 的不等式ax 2﹣3x +2＞ax ﹣1（a ∈R ）的解集． 22．（10分）已知函数f(x)=ax+b x 2+4是定义在（﹣2，2）上的奇函数，且f(12)=217．（1）求函数f （x ）的解析式；（2）证明：函数f （x ）在区间（﹣2，2）上单调递增；（3）若f （a +1）+f （1﹣2a ）＞0，求实数a 的取值范围．23．（12分）已知f（x）是二次函数，且满足f（0）＝2，f（x+1）﹣f（x）＝2x+3．（1）求函数f（x）的解析式；（2）设函数g（x）＝f（x）﹣（2+t）x，求g（x）在区间[1，2]上的最小值h（t）的表达式．（3）在（2）的条件下，对任意的t∈[0，6]，存在m∈[0，2]，使得|h（t）|≤mk2+mk﹣8+m成立，求k的取值范围．2023-2024学年天津市经开一中强基班高一（上）期中数学试卷参考答案与试题解析一、单选题（本大题共12小题，共36.0分。

2018-2019学年天津市部分区七年级(上)期末数学试卷(解析版)

2018-2019学年天津市部分区七年级（上）期末数学试卷一、选择题（本大题共12小题，共36.0分）1.如果把得到10元钱记作+10元，那么花去6元钱记作（）A. 元B. 元C. 元D. 元2.下列说法中正确的是（）A. 的相反数是B. 的倒数2C.D.3.地球赤道周长约为40076000米，用科学记数法表示40076000的结果是（）A. B. C. D.4.由4个小立方体搭成如图所示的几何体，从正面看到的平面图形是（）A.B.C.D.5.下列说法不正确的是（）A. 两点之间的连线中，线段最短B. 若点B为线段AC的中点，则C. 若，则点P为线段为AB的中点D. 直线与射线不能比较大小6.下面说法：①-a一定是负数；②若|a|=|b|，则a=b；③一个有理数中不是整数就是分数；④一个有理数不是正数就是负数．其中正确的个数有（）A. 1个B. 2个C. 3个D. 4个7.已知a、b两数在数轴上的位置如图所示，将0、-a、-b用“＜”连接，其中正确的是（）A. B. C. D.8.下列说法正确的是（）A. 多项式是二次三项式B. 5不是单项式C. 多项式的次数是3D. 单项式的系数是，次数是69.已知代数式与的值相等，则x的值为（）A. B. 7 C. D.10.张磊比小海大10岁，5年前张磊的年龄是小海的年龄的2倍，小海现在的年龄为（）A. 10B. 15C. 20D. 2511.小刚从家跑步到学校，每小时跑12km，会迟到5分钟；若骑自行车，每小时骑15km，则可早到10分钟．设他家到学校的路程是xkm，则根据题意列出方程是（）A. B. C. D.12.已知线段MN=10cm，现有一点P满足PM+PN=20cm，有下列说法：①点P必在线段MN上；②点P必在直线MN上；③点P必在直线MN外；④点P可能在直线MN外，也可能在直线MN上．其中正确的说法是（）A. ①②B. ②③C. ③④D. ④二、填空题（本大题共6小题，共18.0分）13.延长线段AB到C，使BC=4，若AB=8，则线段AC的长为______．14.将3.6457用四舍五入法精确到十分位的近似数是______．15.“7减x差的比x的3倍大1”用方程表示为______．16.如图，已知∠AOC=90°，∠COB=α，OD平分∠AOB，则∠AOD的大小为______（度）17.如图，已知点D在点O的北偏西35°方向，如果∠DOE=80°，那么点E在点O的______方向．18.如图，已知OM，ON分别是∠BOC和∠AOC的角平分线，∠AOB=86°，（1）∠MON=______（度）；（2）当OC在∠AOB内绕点O转动时，∠MON的值______改变（填“会”或“不会”）．三、计算题（本大题共3小题，共20.0分）19.计算：（1）-14-（2-1）××[5+（-2）3]；（2）[1-（-+）×16]÷5．20.（1）化简：（3x2+1）+2（x2-2x+3）-（3x2+4x）；（2）先化简，再求值：m-（n2-m）+2（m-n2）+5，其中m=2，n=-3．21.国庆节期间，甲、乙两商场以同样价格出售相同的商品，并且各自推出不同的优惠方案：在甲商场累计购物超过250元后，超出部分打八五折；在乙商场累计购物超过100元后，超出部分打九五折．问：（1）购买多少元商品时（大于250元），两个商场的实际花费相同？（2）张华要购买500元的商品，李刚要购买300元的商品，他们分别选哪个商场购物实际花费会少些？说明理由．四、解答题（本大题共4小题，共26.0分）22.解方程：（1）2（x+3）-7=x-5（2x-1）；（2）-=-1．23.用方程解答下列问题（1）一个角的补角比它的余角的3倍少25°，求这个角的余角的度数．（2）甲乙两个工程队要开钻一条长560米的山洞．两工程队分别从山洞两头同时施工，甲队每天钻20米，16天后两队会合．求乙工程队每天钻山洞多少米？24.如图，已知点C、D在线段AB上，且AC：CB=2：3，点E是线段AC的中点，D是AB的中点，若ED=9cm，求AB的长度．25.如图，已知O为直线AB上的点，OC在∠BOD内，∠DOC：∠COB=2：3，OE平分∠AOD，∠EOC=78°，求∠BOD的度数．答案和解析1.【答案】B【解析】解：根据题意，花去6元钱记作-6元，故选：B．如果把得到记作“+”，那么花去记作“-”，据此可得．此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．2.【答案】A【解析】解：A、的相反数是-，正确；B、-2的倒数是-，错误；C、-24=-16，错误；D、23=8，错误；故选：A．根据有理数的乘方、倒数和相反数解答即可．此题考查有理数的乘方，关键是根据有理数的乘方、倒数和相反数解答．3.【答案】B【解析】解：40076000=4.0076×107．故选：B．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．4.【答案】C【解析】解：该几何体的主视图是故选：C．找到从正面看所得到的图形即可．本题考查了三视图的知识，主视图是从物体的正面看得到的视图．5.【答案】C【解析】解：A．线段公理，此项正确；B．中点的性质，中点将线段分成长度相等的两条线段，此项正确；C．A、B、P三点不一定在同一条直线上，因此点P不一定是线段AB的中点，此项错误；D．直线具有两边无限延伸性，射线具有一边无限延伸性，故直线与射线不能比较大小，此项正确；故选：C．分别根据直线、射线以及线段的定义和性质判断即可得出．此题主要考查了直线、射线以及线段的定义及相关性质，正确区分它们的定义和性质是解题关键．6.【答案】A【解析】解：①-a一定是负数，说法错误，如果a=-1，则-a=1；②若|a|=|b|，则a=b，说法错误，例如|3|=|-3|，但是3≠-3；③一个有理数中不是整数就是分数，说法正确；④一个有理数不是正数就是负数，说法错误，还有0，0既不是正数也不是负数；正确的个数有1个，故选：A．根据负数的定义和绝对值的定义可得①②错误；根据有理数的分类可得③正确，④错误．此题主要考查了绝对值、有理数的分类，关键是掌握0既不是正数也不是负数．7.【答案】A【解析】解：令b=-0.6，a=1.3，则-b=0.6，-a=-1.3，则可得：-a＜b＜0＜-b＜a．故选：A．根据a、b在数轴上的位置，可对a、b赋值，然后即可用“＜”连接．本题考查了有理数的大小比较及数轴的知识，同学们注意赋值法的运用，这可以给我们解题带来很大的方便．8.【答案】D【解析】解：A、多项式ab+c是二次二项式，故此选项错误；B、5是单项式，故此选项错误；C、多项式2x2+3y的次数是2，故此选项错误；D、单项式-x3y2z的系数是-1，次数是6，正确．故选：D．直接利用多项式的次数与项数确定方法和单项式得出与系数确定方法分别判断即可．此题主要考查了多项式的次数与项数和单项式得出与系数，正确把握相关定义是解题关键．9.【答案】A【解析】解：根据题意得：=，去分母得：2x-2=9x-3，移项合并得：7x=1，解得：x=，故选：A．根据题意列出方程，求出方程的解即可得到x的值．此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．10.【答案】B【解析】解：设小海现在的年龄为x岁，根据题意可得：2（x-5）=x+10-5，解得：x=15，答：小海现在的年龄为15岁．故选：B．直接利用张磊比小海大10岁，分别表示出5年前两人的年龄，进而得出答案．此题主要考查了一元一次方程的应用，正确得出等式是解题关键．11.【答案】D【解析】解：设他家到学校的路程是xkm，依题意，得：+=-．故选：D．设他家到学校的路程是xkm，根据时间=路程÷速度结合上课时间不变，即可得出关于x的一元一次方程，此题得解．本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．12.【答案】D【解析】解：∵MN=10cm，点P满足PM+PN=20cm，∴点P不可能在线段MN上，点P可能在直线MN外，也可能在直线MN上．故只有④说法正确．故选：D．根据线段的MN长度，及PM+PN的长度即可判断出P的位置．本题考查比较线段长度的知识，比较简单，这类题目一般不能具体确定P的位置，只是可能不能说必然．13.【答案】12【解析】解：如图，∵BC=4，AB=8，∴AC=AB+BC=12．故答案为：12．由已知条件可知，AC=AB+BC，代入求值即可．考查了两点间的距离，借助图形来计算，这样才直观形象，便于思维．灵活运用线段的和、倍转化线段之间的数量关系．14.【答案】3.6【解析】解：将3.6457用四舍五入法精确到十分位的近似数是3.6；故答案为：3.6．把3.6457精确到十分位就是对这个数的十分位后面的数进行四舍五入即可．此题考查了近似数，用到的知识点是近似数，一个数最后一位所在的数位就是这个数的精确度．15.【答案】（7-x）=3x+1【解析】解：依题意，得：（7-x）=3x+1．故答案为：（7-x）=3x+1．由7减x 差的比x的3倍大1，可得出关于x的一元一次方程，此题得解．本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．16.【答案】45°+【解析】解：∵∠AOC=90°，∠COB=α，∴∠AOB=∠AOC+∠COB=90°+α．∵OD平分∠AOB，∴∠AOD=∠AOB=（90°+α）=45°+．故答案为45°+．先用90°和α表示出∠AOB度数，再根据角平分线的定义求解∠AOD度数．本题主要考查了角平分线的定义，正确表示出角之间的关系是解题的关键．17.【答案】北偏东45°（或东北）【解析】解：∵D在点O的北偏西35°方向，∠DOE=80°，∴∠EOF=80°-35°=45°，即点E在点O的北偏东45°（或东北）方向上．故答案为：北偏东45°（或东北）．利用方向角的定义求解即可．本题主要考查了方向角，解答此类题需要从运动的角度，正确画出方位角，再结合角与角间的和差关系进行解答．18.【答案】43 不会【解析】解：（1）∵OM，ON分别是∠BOC和∠AOC的角平分线，∴∠MOC=∠OBC，∠NOC=∠AOC．∴∠MON=∠MOC+∠NOC=∠OBC+∠AOC=（∠OBC+∠AOC）=∠AOB=×86°=43°．故答案为43；（2）有（1）可知∠MON=∠AOB，即∠MON的度数始终等于∠AOB度数的一半，所以当OC在∠AOB内绕点O转动时，∠MON的值不会改变．故答案为不会．（1）根据角平分线的定义，及角的和差找到∠MON与∠AOB之间的关系即可求解；（2）求出∠MON与∠AOB的倍数关系即可说明问题．本题主要考查角平分线的定义，会运用整体思想找到∠MON与∠AOB的倍分关系是解题的关键．19.【答案】解：（1）原式=-1-××（5-8）=-1-×（-3）=-1+=-；（2）原式=（1-6+5-4）÷5=（-）×=-．【解析】（1）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可求出值；（2）原式先计算中括号中的乘法运算，再计算减法运算，最后算除法运算即可求出值．此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．20.【答案】解：（1）原式=3x2+1+2x2-4x+6-3x2-4x=2x2-8x+7；（2）原式=m+m+3m+5=4m-n2+5，当m=2，n=-3时，原式=4×2-9+5=4；【解析】（1）根据整式的运算法则即可求出答案．（2）先根据整式的运算法则将原式化简，然后将m与n的值代入即可求出答案．本题考查整式的运算，解题的关键是熟练熟练运用整式的运算法则，本题属于基础题型．21.【答案】解：（1）设购买x元商品时，两个商场的实际花费相同．由题意，得250+（x-250）×85%=（x-100）×95%+100 解得：x=325答：当购买325元商品时，两个商场的实际花费相同．（2）：当张华购买500元的商品时，在甲商场实际花费为：（500-250）×85%+250=462.5元在乙商场实际花费为：（500-100）×95%+100=480元∵462.5＜480∴张华选甲商场的实际花费较少当李刚购买300元的商品时，在甲商场实际花费为：（300-250）×85%+250=292.5元在乙商场实际花费为：（300-100）×95%+100=290元∵290＜292.5∴李刚选乙商场的实际花费较少．【解析】（1）：设购买x元商品时，满足题意，根据甲，乙两个商场的优惠方式列方程．（2）：分别讨论张华和李刚在两种商场优惠下的实际消费，最后比较哪一种更实惠．本题主要是应用题中的销售类，此题考查了关于优惠下的实际消费问题．22.【答案】解：（1）去括号得：2x+6-7=x-10x+5，移项得：2x-x+10x=5-6+7，合并同类项得：11x=6，系数化为1得：x=，（2）去分母得：4（2x-1）-3（x+1）=6（3x+1）-12，去括号得：8x-4-3x-3=18x+6-12，移项得：8x-3x-18x=6-12+4+3，合并同类项得：-13x=1，系数化为1得：x=-．【解析】（1）依次去括号，移项，合并同类项，系数化为1，即可得到答案，（2）依次去分母，去括号，移项，合并同类项，系数化为1，即可得到答案．本题考查了解一元一次方程，正确掌握解一元一次方程的方法是解题的关键．23.【答案】解：（1）设这个角的余角的度数为x，则这个角为90°-x，它的补角为90°+x．根据题意，得90°+x=3x-25°，解得x=57.5°．答：这个角的余角的度数是57.5°；（2）设乙工程队每天钻山洞x米．根据题意，得16（20+x）=560，解得x=15．答：乙工程队每天钻山洞15米．【解析】（1）设这个角的余角的度数为x，则这个角为90°-x，它的补角为90°+x，根据一个角的补角比它的余角的3倍少25°列出方程，解方程即可；（2）设乙工程队每天钻山洞x米．根据等量关系：（甲的工作效率+乙的工作效率）×工作时间=工作总量列出方程，解方程即可．本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．也考查了余角和补角．24.【答案】解：∵D是AB的中点，∴AD=AB，∵AC：CB=2：3，点E是线段AC的中点，∴DE=AD-AE=AB-×AB=9cm，∴AB=30cm．【解析】根据AC：CB=2：3，线段中点的性质，可得DE=AD-AE=AB-×AB=9cm，依此即可求解．本题考查两点间距离，线段的中点、线段的和差倍分定义等知识，熟知各线段之间的和差和倍分关系是解答此题的关键．25.【答案】解：∵∠DOC：∠COB=2：3，∴设∠DOC=2x，∠COB=3x，则∠BOD=5x，∵∠EOC=78°，∠EOC=∠EOD+DOC，∴∠EOD=78°-2x，∵OE平分∠AOD，∴∠AOD=2∠EOD=2（78°-2x），∵∠AOD+∠DOB=180°，∴2×（78°-2x）+5x=180°，解得：x=24°，∴∠BOD=120°．【解析】设∠DOC=2x，∠COB=3x，则∠BOD=5x，求得∠EOD=78°-2x，根据角平分线的定义得到∠AOD=2∠EOD=2（78°-2x），列方程即可得到结论．本题考查了角的计算，角平分线的定义，正确的识别图形是解题的关键．。

天津市部分区2023-2024学年高一上学期期中数学试卷(含答案)

参考答案
1、答案：C
解析：由题意可知 ,所以 .
故选：C.
2、答案：C
解析： ,
且 ,
,即 ,
所以“ ”是“ ”的充分必要条件.
故选：C.
3、答案：A
解析：在R上的偶函数, ,
.
故选:A.
4、答案：A
解析：由题意得函数在上单调递增,
因为 ,所以得： ,故A项正确.
故选：A.
5、答案：A
解析：前3年年产量的增长速度越来越快, 当时,总产量增长速度原来越快,图象上升的速度越来越快.
18、已知函数 , .
(1)若关于x的不等式对一切恒成立,求a的取值范围;
(2)若 ,解关于x的不等式 .
19、已知函数 ,a, , .证明：对 , , .
20、已知幂函数的图像过点 .
(1)求的解析式;
(2)设函数 .
①根据单调性的定义判断在区间上的单调性;
②判断的奇偶性,并加以证明.
所以得a的取值范围为： ,故选项C正确.
故选：C.
8、答案：D
解析：由题意得 ,从而可知： ,
化简得： ,解之得：或 ,
故解集为：或 ,故D项正确.
故选：D.
9、答案：D
解析：易知 ,所以的定义域为R,
又 ,且 ,
则函数为非奇非偶函数,故A、B错误;
由题意可知： ,
所以 ,
则的图象关于点成中心对称,故C错误,D正确.
的定义域 ,即定义域不关于原点对称,
所以为非奇非偶函数.
3、已知定义在R上的偶函数满足：当时, ,则的值为()
A.1B.3C.-2D.-3
4、若 ,则a,b,c的大小关系为()

天津市部分区2022-2023学年高一下学期期中数学试题及参考答案

天津市部分区2022-2023学年高一下学期期中数学试题及参考答案本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，共120分，考试用时100分钟。

祝各位考生考试顺利！第I 卷参考公式:●圆柱的体积公式V=Sh ，其中S 表示圆柱的底面面积，h 表示圆柱的高．●圆锥的体积公式V=31Sh ，其中S 表示圆锥的底面面积，h 表示圆锥的高．●棱锥的体积公式V=31Sh ，其中S 表示棱锥的底面面积，h 表示棱锥的高．●球的表面积公式S=4πR 2，其中R 表示球的半径．一、选择题：本大题共9小题，每小题4分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知向量a =(2,2)，b =(1,-1)，则=-b a （）A ．(3,0)B ．(3,1)C ．(1,3)D ．(-1,2)2．已知棱长为2的正方体的顶点都在球面上，则该球的表面积为（）A ．πB ．2πC ．4πD ．12π3．在△ABC 中，角A,B,C 所对的边分别为a,b,c ．若a=1，b=2，c=7，则C=（）A ．120°B ．90°C ．60°D ．45°4．已知点P(2,0)，Q(1,1)，向量EF =(λ,2)，若EF PQ ⋅=0，则实数λ的值为（）A ．21B ．21-C ．2D ．15．在△ABC 中，角A,B,C 所对的边分别为a,b,c ．若a=l ，b=2，B=4π，则A=（）A ．6πB ．3πC ．65πD ．6π或65π6．已知向量a =(-1,2)，b =(1,1)，则a 在b 上的投影向量为（）A ．22B ．(-1,2)C ．(22,22)D ．(2121，)7．陀螺是中国民间最早的娱乐工具之一，也称陀罗．图1是一种木陀螺，可近似地看作是一个圆锥和一个圆柱的组合体，其直观图如图2所示，其中A 是圆锥的顶点，B,C 分别是圆柱的上､下底面圆的圆心，且AB=1，AC=3，底面圆的半径为1，则该陀螺的体积是（）A ．πB ．2πC ．37πD ．310π8．已知向量a =(m,1)，b =(4,m)，若a 与b 方向相反，则=+b a （）A ．171022++m m B ．5C ．25D ．59．在△ABC 中，角A,B,C 所对的边分别为a,b,c ．已知△ABC 的面积为S ，2a+b=4，c(a +b -c)(sin A +sin B +sin C)=6S ，CA =3CD -2CB ，则CD 的最小值为（）A ．2B ．322C ．3D ．332第II 卷二、填空题：本大题共6小题，每小题4分，共24分．试题中包含两个空的，答对1个的给2分，全部答对的给4分．10．i 是虚数单位，复数ii+-12=____________．11．直线l 上所有点都在平面α内，可以用符号表示为____________．12．若A(1,1)，B(2,-1)，C(a,b)三点共线，则2a+b=____________．13．在长方体ABCD-A 1B 1C 1D 1中，AB=2，AD=1，AA 1=3，则异面直线A 1C 1与AD 1所成角的余弦值为____________．14．在△ABC 中，角A,B,C 所对的边分别为a,b,c ．已知a 2+b 2-c 2=ab ，则C=______________，若c=2，则△ABC 外接圆的半径为____________．15．如图，在边长为1的正方形ABCD 中，AE =AC 31;则BE DE ⋅=______________；若F 为线段BD 上的动点则FB FE ⋅的最小值为____________．三、解答题：本大题共5小题，共60分．解答应写出文字说明，证明过程或演算步骤.16．（本小题满分11分）已知向量a ，b 满足，=3，a 与b 的夹角为32π．（I +的值；（II ）若()()b a k b a -⊥+2，求实数k 的值．17．（本小题满分12分）如图，三棱锥S-ABC 的底面ABC 和侧面SAB 都是边长为2的等边三角形，D,E 分别是AB,AC 的中点，SD ⊥CD ．（I ）证明：BC //平面SDE ；（II ）求三棱锥S-ABC 的体积．18．（本小题满分12分）在△ABC 中，角A,B,C 所对的边分别为a,b,c ．已知a=3+3，c=6+2，A=32π．（I ）求C 的值；（II ）求b 的值．19．（本小题满分12分）如图，在长方体ABCD-A 1B 1C 1D 1中，AB=2，AD=AA 1=1．（I ）求证：B 1C ⊥BD 1（II ）求直线AB 1与平面ABC 1D 1所成角的正弦值．20．（本小题满分13分）在△ABC 中，角A,B,C 所对的边分别为a,b,c ．向量()b a m ,3=，()B A n cos ,sin =，且n m ∥．（I ）求B 的值；（II ）若a=2，b=7，求△ABC 的面积．参考答案一、选择题：本大题共9小题，每小题4分，共36分。