龙岩1月份质检理数(word)
福建省龙岩市长汀县第一中学等校2024--2025学年九年级上学期第一次月考化学试题(无答案)

2024~2025学年第一学期城区质量监测化学试题(满分:100分;考试时间:60分钟)注意事项:请将试题答案填写(填涂)在答题卡上。
第Ⅰ卷选择题第Ⅰ卷共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项符合题目要求。
1.翻译《化学鉴原》并创造出氢、氧、钠等化学元素汉语名称的我国近代化学先驱是()A.徐寿B.徐光启C.侯德榜D.沈括2.“化学推动科技进步,科技推动社会发展”,下列有关叙述与化学无关的是()A.建设高楼大厦使用了许多金属材料B.液氮用于磁悬浮列车C.我国首次实现了非人灵长类动物的体细胞克隆D.可燃冰将成为未来新能源3.规范的实验操作是实验成功的保证,下列实验操作正确的是()A.点燃酒精灯B.处理废液C.连接仪器D.倾倒液体4.下列实验现象的描述中,正确的是()A.木炭在氧气中剧烈燃烧,发出红光,放出热量,倒入澄清石灰水变浑浊B.红磷在氧气中燃烧更旺,产生大量的白烟,放出热量C.铁在氧气中剧烈燃烧,火星四射,生成四氧化三铁,放出大量的热量D.镁在空气中燃烧发出耀眼的白光,放热,生成黑色固体5.下图是水在电解过程中发生变化的微观示意图,下列说法正确的是()A.与负极相连玻璃管内产生的物质是乙B.实验说明水是由氢气和氧气组成C.反应产生的乙和丙的体积相同D.丙物质可以用作高能燃料6.下列有关化学实验操作中“先”与“后”的说法不正确的是()A.给试管中药品加热时,先使试管底部均匀受热,后固定加热B.排水法收集满气体后,先将集气瓶取出水面,后用玻璃片盖住瓶口C.连接玻璃导管和乳胶管时,先把导管口用水润湿,然后稍稍用力把导管插入乳胶管D.连接好气体发生装置,先检查装置的气密性,后装药品7.空气是一种重要的资源。
下列有关说法不正确的是()A.氧气是一种无色无味的气体,不易溶于水B.食品包装袋中充入氮气可延长食品保质期C.空气中氧气的质量分数约为21%D.稀有气体可用于制造多种用途的电光源8.化学兴趣小组的同学在完成跨学科实践活动后制作了净水器(如图所示),下列说法不正确的是()A.小卵石和石英砂能够除去一些难溶性杂质B.活性炭能除去水中的异味和颜色C.紫外灯的作用是杀菌消毒D.该装置能获得纯水9.实验室用一定质量的过氧化氢溶液制取氧气时,下列图像正确的是()A.B.C.D.10.如图所示实验方案能达到实验目的的是()A.测定空气中氧气含量B.验证二氧化锰是过氧化氢分解的催化剂C.探究水的组成元素D.验证蜡烛中含有碳、氢元素A.A B.B C.C D.D第Ⅱ卷非选题第Ⅱ卷共8题,共70分。
福建省龙岩市一级达标校2016-2017学年高二第二学期期末教学质量检查理科数学试卷(扫描版含答案)

福建省龙岩市一级达标校2016-2017学年高二第二学期期末教学质量检查理科数学试卷(扫描版含答案)龙岩市一级达标校2016-2017学年第二学期期末高二教学质量检查数学(理科)试题参考答案一、选择题(每小题5分,共60分)1.B2.A3.C4.C5.D6.B7.A8.C9.B10.A11.D12.D二、填空题(每小题5分,共20分)13.914.2715.a(45,81)16.m≤e+2三、解答题(共70分)17.(本小题满分12分)Ⅰ)列出列联表:男女合计课外体育不达标 60 90 150课外体育达标 30 20 50合计 90 110 200Ⅱ)依表格数据得跳远成绩的平均数x=70,短跑100米成绩的平均数y=66.b=(∑xy-5x·y)/(∑x^2-5x^2)=-5·70·66/2250=0.54b=y-b x=66-0.54·70=28.2所求的回归方程为y=0.54x+28.2.因为k=2200/33≈6.06<6.635,所以在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与性别有关。
17.(本小题满分12分)Ⅰ)解得z=1+i,所以ω=(2-i)/(2+i)=1-i。
OA=(1,-1),OB=(0,2)。
逆时针旋转5π/4可得到OA的位置,即θ的最小值为5π/4.Ⅱ)由已知可得n=10.设第r+1项的系数最大,则C(10,r+1)=2·C(10,r)。
2(r+2)/(r+1)≥10/(r+1),解得2≥r+1,即1≤r≤3.r=1,2,3.所以3≤n-r≤9,即n-r=3,4,5,6,7,8,9.解得x=1/3或x=-1/2.所求的三项式为3x^2-2x或2x^3-3x^2.答案不唯一。
注:原文章中,解答题的第17题和第18题没有明确区分,已修改。
所以r=7,即系数最大的项为T77.根据分式拆分,2x^2=x^2,化简得x=±24.解:(Ⅰ)由题意得y=(4+202)/(p-10-2p-x)=10+2p-x/(4+x+1)。
2023-2024学年福建省龙岩市新罗区铁山中学九年级(上)第一次月考数学试卷+答案解析

一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.若关于x 的方程是一元二次方程,则a 的取值范围是( )A. B.C.D.2.已知是关于x 的二次函数,则下列说法正确的是2023-2024学年福建省龙岩市新罗区铁山中学九年级(上)第一次月考数学试卷( )A. 有最大值4 B. 有最大值C. 有最小值4D. 有最小值3.方程的左边配成完全平方后所得方程为( )A.B.C.D.4.等腰三角形的一边长是3,另两边的长是关于x 的方程的两个根,则k 的值为( )A. 7B. 3C. 4D. 3或45.一元二次方程的根的情况是( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 无法确定6.若关于x 的一元二次方程的一个根是0,则a 的值为( )A. 1B.C.D. 07.某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数是若设主干长出x 个支干,则可列方程是( )A.B.C.D.8.一个菱形的边长是方程的一个根,其中一条对角线长为8,则该菱形的面积为( )A. 48B. 24C. 24或40D. 48或809.甲、乙两同学解方程,甲看错了一次项,得根2和7,乙看错了常数项,得根1和,则原方程为( )A.B. C. D.10.某建筑工程队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为440平方米.为了方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门.若设米,则可列方程( )A. B.C.D.二、填空题:本题共6小题,每小题3分,共18分。
11.已知关于x 的方程是一元二次方程,则m 的值为______.12.将抛物线向下平移3个单位长度,得到抛物线,则______,______.13.有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了______个人.14.若关于x 的一元二次方程有两个不相等的实数根,则点在第__________象限.15.已知:,且,则的值为______.16.如图,在中,,,,动点P 从点C 出发,沿CA 方向运动,速度是;同时,动点Q 从点B 出发,沿BC 方向运动,速度是,则经过______ s 后,P ,Q两点之间相距三、计算题:本大题共2小题,共12分。
福建省龙岩市八年级(上)第一次月考数学试卷
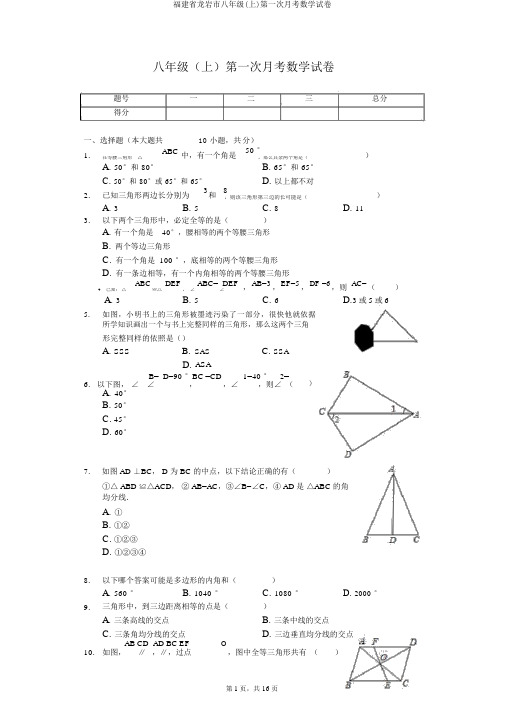
八年级(上)第一次月考数学试卷题号一二三总分得分一、选择题(本大题共10 小题,共分)1.ABC 中,有一个角是50 °)在等腰三角形△,那么其余两个角是(A. 50°和80°B. 65°和65°C. 50°和80°或65°和65°D. 以上都不对2. 已知三角形两边长分别为3和8),则该三角形第三边的长可能是(A. 3B. 5C. 8D. 113. 以下两个三角形中,必定全等的是()A. 有一个角是40°,腰相等的两个等腰三角形B.两个等边三角形C.有一个角是 100 °,底相等的两个等腰三角形D.有一条边相等,有一个内角相等的两个等腰三角形ABC DEF ABC= DEF ,AB=3 ,EF=5 ,DF =6 ,则AC= ()4. 已知:△≌△,∠∠A. 3B. 5C. 6D.3或5或65.如图,小明书上的三角形被墨迹污染了一部分,很快他就依据所学知识画出一个与书上完整同样的三角形,那么这两个三角形完整同样的依照是()A. SSSB.D. SAS C. SSA ASAB= D=90 °BC =CD 1=40 ° 2=)6. 以下图,∠ ∠,,∠,则∠ (A.40°B.50°C.45°D.60°7. 如图 AD ⊥BC, D 为 BC 的中点,以下结论正确的有()①△ ABD ≌△ACD,② AB=AC,③∠B=∠C,④ AD 是△ABC 的角均分线.A.①B.①②C.①②③D.①②③④8. 以下哪个答案可能是多边形的内角和()A. 560°B. 1040°C. 1080°D. 2000°9. 三角形中,到三边距离相等的点是()A. 三条高线的交点B. 三条中线的交点C. 三条角均分线的交点D. 三边垂直均分线的交点AB CD AD BC EF OA.2 对B.4 对C.6 对D.8 对二、填空题(本大题共 6 小题,共24.0 分)11.十边形的内角和的度数是 ______.12.一个等腰三角形的两边长分别为 2 和 5,则它的周长为______.13.把两根钢条 AD,BC 的中点连在一同,能够做成一个丈量工件内槽宽的工具(卡钳),如图,若测得AB=8 厘米,则槽宽为 ______厘米.14.如图,已知△ABC 的周长是 21,OB, OC 分别均分∠ABC 和∠ACB , OD⊥BC 于 D,且 OD=4,△ABC 的面积是 ______.15.如图,已知 AC =DB ,请增添一个条件,使△ABC≌△DCB,则需要增添的条件为 ______(填一个即可).16.如图,若 B, D ,F 在 AN 上, C, E 在 AM 上,且 AB=BC=CD=ED =EF ,∠A=20 o,则∠FEM =______.三、解答题(本大题共8 小题,共86.0 分)17.尺规作图题(不写作图步骤,但保存作图印迹).已知:如图∠MON( 1)求作:∠MON 的均分线 OC.( 2)依据作法,请说明所作的射线OC 就是∠MON 的平分线 OC.18.如图,已知点 B、E、C、F 在同一条直线上, AB∥DE,AC∥DF且 BE=CF .求证: AB=DE .19.已知一个多边形的内角和是它的外角和的3 倍,求这个多边形的边数.20.如图,△ABD、△AEC都是等边三角形,求证:B E=DC .21.已知: BE⊥CD ,BE=DE ,BC=DA,求证:①△ BEC≌△DEA ;② DF ⊥BC.22.已知:如图, BP, CP 是△ABC 的外角均分线,证明:点 P 必定在∠BAC 的角均分线上.23.如图,点 P 在 AB 上,∠1=∠2,∠3=∠4,求证:AC=AD .ABC为正三角形,如图(1 M是边BC上一点,点N是边CA上一点,24. 已知:△)点且 BM=CN, BN 与 AM 订交于 Q 点.( 1)猜一猜:在图( 1)中∠AQN 的度数.( 2)若 M ,N 两点分别在线段BC ,CA 的延伸线上,其余条件不变,如图(2)则( 1)中的结论能否仍旧建立?若建立,请赐予证明;假如不建立,请说明原因.答案和分析1.【答案】C【分析】解:当底角为 50°时,则顶角为:180°-50 °-50 °=80°,此时三角形的此外两个角的度数为 50°,80°;当顶角为 50°时,则底角为:=65°,此时三角形的此外两个角的度数为 65°,65°;综上可知其余两个角的度数为50°,80°或65°,65°.应选:C.分底角为 50°和顶角为 50°两种状况,再联合三角形内角和定理和等腰三角形的性质可求得答案.本题主要考察等腰三角形的性质,掌握等腰三角形的两底角相等是解题的关键,注意三角形内角和定理的应用,学会用分类议论的思想思虑问题.2.【答案】C【分析】解:依据三角形的三边关系,得第三边大于:8-3=5,小于:3+8=11.则此三角形的第三边可能是:8.应选:C.依据三角形的第三边大于两边之差,而小于两边之和求得第三边的取值范围,再进一步选择.本题考察了三角形的三边关系,即三角形的第三边大于两边之差,而小于两边之和,本题基础题,比较简单.3.【答案】C【分析】解:A 、不正确,没有指明该角是顶角仍是底角;C、正确,剖析得该 100 度角只好为顶角,切合判断 SAS;D、不正确,没有指明边与角详细是腰仍是底边,是顶角仍是底角.应选:C.依据全等三角形的判断方法及等腰三角形的性质对各个选项进行剖析,从而获得答案.本题考察了等腰三角形的性质和三角形的三边关系;给定等腰三角形的一角是锐角时,应分状况议论,AAA 不可以判断两个三角形全等.4.【答案】C【分析】解:∵△ABC ≌△DEF,∠ABC= ∠DEF,∴AC=DF=6 ,应选:C.依据全等三角形的性质解答即可.本题考察全等三角形的性质,重点是依据全等三角形对应边相等解答.5.【答案】D【分析】解:由图可知,三角形两角及夹边能够作出,因此,依照是 ASA .应选:D.图中三角形没被污染的部分有两角及夹边,依据全等三角形的判断方法解答即可.本题考察了全等三角形的应用,娴熟掌握三角形全等的判断方法是解题的关键.6.【答案】B【分析】解:∵∠B=∠D=90°在 Rt△ABC 和 Rt△ADC 中,∴Rt△ABC ≌Rt△ADC (HL )∴∠2=∠ACB=90°-∠1=50 °.应选:B.本题要求∠2,先要证明 Rt△ABC ≌Rt△ADC (HL ),则可求得∠2=∠ACB=90°-∠1 的值.本题考察全等三角形的判断和性质,三角形全等的判断是中考的热门,一般以考察三角形全等的方法为主,判断两个三角形全等,先依据已知条件或求证的结论确立三角形,而后再依据三角形全等的判断方法,看缺什么条件,再去证什么条件.7.【答案】D【分析】解:∵AD ⊥BC,D 为 BC 的中点,∴∠ADB= ∠ADC=90°,BD=BC ,在△ABD 和△ACD 中,∴△ABD ≌△ACD (SAS),∴AB=AC ,∠B=∠C,∠BAD= ∠CAD ,即 AD 是△ABC 的角均分线.应选:D.由 AD ⊥BC,D 为 BC 的中点,利用 SAS 可证明△ABD ≌△ACD ,而后利用全等三角形的性质即可求证出②③④.本题主要考察学生利用等腰三角形的性质来求证全等三角形的,本题的重点是利用 SAS 可证△ABD ≌△ACD ,而后即可得出其余结论,本题难度不大,是一道基础题.8.【答案】C【分析】解:判断哪个度数可能是多边形的内角和,我们主要看它能否能被180°整除.只有 1080°能被 180°整除.应选:C.依据多边形的内角和为(n-2)×180°来确立解决本题的方法,即判断哪个度数可能是多边形的内角和,就看它能否能被180°整除,从而依据这一方法解决问题.本题主要考察多边形的内角和定理,正确掌握多边形内角和定理是解题关键.9.【答案】C【分析】解:三角形中,到三边距离相等的点是三条角均分线的交点.应选:C.依据角均分线上的点到角的两边距离相等解答.本题考察了角均分线上的点到角的两边距离相等的性质,熟记性质是解题的重点.10.【答案】C【分析】解:∵AB ∥CD,AD ∥BC,∴四边形 ABCD 是平行四边形,由平行四边形的中心对称性,全等三角形有:△AOB ≌△COD,△AOD ≌△COB,△AOF ≌△COE,△DOF≌△BOE,△ABD ≌△CDB ,△ABC ≌△CDA 共 6 对.应选:C.依据平行四边形的中心对称性解答即可.本题考察了平行四边形的判断和性质,全等三角形的判断,主要利用了平行四边形的中心对称性.11.【答案】1440°【分析】解:十边形的内角和是(10-2)?180°=1440.°故答案为:1440°.n 边形的内角和是(n-2)?180°,代入公式就能够求出十边形的内角和.考察了多边形内角与外角,正确记忆多边形的内角和公式是解决本题的关键.12.【答案】12【分析】解:(1)若2 为腰长,5 为底边长,因为 2+2< 5,则三角形不存在;(2)若5 为腰长,则切合三角形的两边之和大于第三边.因此这个三角形的周长为 5+5+2=12.故答案为:12.求等腰三角形的周长,即是确立等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为 2 和 5,而没有明确腰、底分别是多少,因此要进行议论,还要应用三角形的三边关系考证可否构成三角形.本题考察了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,波及分类议论的思想方法.求三角形的周长,不可以盲目地将三边长相加起来,而应养成查验三边长可否构成三角形的好习惯,把不切合题意的舍去.13.【答案】8【分析】解:连结 AB ,CD,O为AD 和CB的中点,∴OC=OB,OA=OD ,∵∠COD=∠AOB∴△OCD≌△OAB ,即 CD=AB ,故 CD=AB=8cm ,故答案为 8.连结 AB ,CD,依据 O 为 AD 和 CB 的中点,且∠COD=∠AOB 即可判断本题考察了全等三角形在实质生活中的应用,考察了全等三角形的证明和对应边相等的性质,本题中求证△OCD≌△OAB 是解题的重点.14.【答案】42【分析】解:过 O 作 OE⊥AB 于 E,OF⊥AC 于 F,连结 OA ,∵OB,OC 分别均分∠ABC 和∠ACB ,OD⊥BC,∴OE=OD,OD=OF,即 OE=OF=OD=4,∴△ABC 的面积是:S△AOB+S△AOC+S△OBC=×AB×OE+ ×AC×OF+ ×BC×OD=×4×(AB+AC+BC )=×4×21=42,故答案为:42.过 O 作 OE⊥AB 于 E,OF⊥AC 于 F,连结 OA ,依据角均分线性质求出OE=OD=OF=4 ,依据△ABC 的面积等于△ACO 的面积、△BCO 的面积、△ABO 的面积的和,即可求出答案.本题考察了角均分线性质,三角形的面积,主要考察学生运用定理进行推理的能力.15.【答案】AB=DC【分析】解:增添AB=DC∵AC=DB ,BC=BC ,AB=DC∴△ABC ≌△DCB∴加一个适合的条件是AB=DC .故答案为:AB=DC本题考察三角形全等的判断方法;判断两个三角形全等的一般方法有:SSS、SAS、ASA 、AAS 、HL .增添时注意:AAA 、SSA 不可以判断两个三角形全等,不能增添,依据已知联合图形及判断方法选择增添的条件是正确解答本题的关键.16.【答案】100°【分析】解:∵∠A=20°,AB=BC ,∴∠A= ∠ACB=20°,∠CBD= ∠A+∠ACB=20°+20 °=40 °;∵BC=CD,∴∠CBD=∠CDB=40°,∴∠ECD=∠A+ ∠CDA=30°(外角定理);∵CD=DE,∴∠DCE=∠DEC=60°,∴∠EDF=∠A+ ∠AED=80°;又∵DE=EF,∴∠EDF=∠EFD=80°,∴∠FEM=∠A+ ∠EFD=20°+80 °=100 °.故答案为 100°.依据三角形内角和定理,三角形外角和内角的关系以及等腰三角形的性质,逐渐推出∠FEM 的度数.本题考察等腰三角形的性质、三角形内角和定理、三角形外角性质.此类题考生应当注意的是三角形内角和定理、外角性质的运用.17.【答案】解:(1)如图,射线OC 是∠MON 的均分线,(2)证明:如图,连结 OC、BC、 AC,依据作法可得 BC=AC, OA=OB,在△OAC 和△OBC 中,∵OA=OBAC=BCOC=OC∴△OAC≌△OBC( SSS),∴∠AOC=∠BOC ,即射线OC 是∠MON 的均分线.(1)依据角均分线的尺规作图可得;(2)连结 OC、BC、AC,利用“SSS”证明△OAC ≌△OBC 可得.本题主要考察作图-基本作图,解题的重点是掌握角均分线的尺规作图及全等三角形的判断与性质.18.【答案】证明:∵AB∥DE,AC∥DF,∴∠B=∠DEF ,∠ACB=∠F.∵BE=CF ,∴BC=EF .在△ABC 与△DEF 中,∠B=∠ DEFBC=EF∠ACB=∠F,∴△ABC≌△DEF( ASA),∴AB=DE .【分析】证明它们所在的三角形全等即可.依据平行线的性质可得∠B=∠DEF,∠ACB= ∠F;由BE=CF 可得 BC=EF.运用 ASA 证明△ABC 与△DEF 全等.本题考察全等三角形的判断与性质,属基础题.证明线段相等,往常证明它们所在的三角形全等.19.【答案】解:设这个多边形的边数为n,∵n 边形的内角和为(n-2) ?180 °,多边形的外角和为360 °,∴( n-2) ?180 °=360 °×3,解得 n=8.∴此多边形的边数为8.【分析】多边形的外角和是 360°,内角和是它的外角和的 3 倍,则内角和是3×360=1080度.n 边形的内角和能够表示成( n-2)?180°,设这个多边形的边数是 n,就获得方程,从而求出边数.依据正多边形的外角和求多边形的边数是常用的一种方法,需要熟记.20.【答案】证明:∵△ABD、△AEC都是等边三角形,∴AD =AB ,AE=AC,∠DAB=∠CAE=60 °,∴∠DAC=∠BAC +60 °,∠BAE=∠BAC+60 °,AD=AB∠ DAC=∠ AE=ACBAE,∴△DAC≌△BAE( SAS),∴BE=DC.【分析】利用△ABD 、△AEC 都是等边三角形,求证△DAC ≌△BAE ,而后即可得出BE=DC .本题考察学生对全等三角形的判断与性质和等边三角形的性质的理解与掌握,难度不大,是一道基础题.21.【答案】证明:(1)∵BE⊥CD,∴∠BEC=∠DEA =90 °,又∵BE=DE , BC=DA ,∴△BEC≌△DEA( HL );(2)∵△BEC≌△DEA ,∴∠B=∠D.∵∠D+∠DAE =90 °,∠DAE =∠BAF ,∴∠BAF+∠B=90 °.即 DF ⊥BC.【分析】(1)依据已知利用 HL 即可判断△BEC≌△DEA ;(2)依据第一问的结论,利用全等三角形的对应角相等可获得∠B=∠D,从而不难求得 DF⊥BC.本题主要考察学生对全等三角形的判断及性质的理解及运用,做题时要注意思虑,仔细找寻全等三角形全等的条件是解决本题的重点.22.【答案】证明:过点P分别作AM、BC、AN的垂线PE、PF 、PD, E、F、 D 为垂足,∵CP 是∠MCB 的均分线,∴PE=PD .同理: PF=PD.∴PE=PF.∴点 P 在∠BAC 的均分线上.【分析】过点 P 分别作 AM 、BC、AN 的垂线 PE、PF、PD,E、F、D 为垂足.依据角均分线的性质可得 PE=PD,PD=PF,从而可得出结论.23.【答案】解:解法一、∵∠1=∠2,∴∠DPB=∠CPB,又∵PB 是公共边,∠3= ∠4,∴△PDB≌△PCB,∴DB =CB,∵∠3=∠4,AB 是公共边,∴△ADB≌△ACB( SAS),∴AD =AC.解法二、连结DC,∵∠1=∠2,∠1+∠BPD =180 °,∠2+∠BPC=180 °,∴∠BPD=∠BPC,在△PBD 和△PBC 中∵∠ BPD=∠ BPCPB=PB∠ 3= ∠4,∴△PBD≌△PBC( ASA),∴DB =BC, PD=PC,∴AB 垂直均分DC,∴AD =AC.【分析】需证两次三角形全等,△PDB≌△PCB 和△ADB ≌△ACB ,分别利用 ASA ,SAS 证明.本题考察三角形全等的判断和性质,注意利用已知隐含的条件:公共边.24.【答案】解:(1)∠AQN=60°,原因以下:∵△ABC 为正三角形,∴AB=BC=AC,∠ABC=∠ACB=60 °,在△ABM 和△BCN 中 AB=BC∠ABC=∠ACBBM=CN∴△ABM≌△BCN( SAS)∴∠BAM=∠CBN,∵∠ABC=∠ABN +∠CBN=60 °,∴∠AQN=∠BAM +∠ABN=∠CBN+∠ABN =60 °;(2)不建立.∠AQN=120°,同( 1)易证△ABM ≌△BCN∴∠BAM=∠CBN,∴∠AQN=∠CBN +∠AMB=∠BAM+∠AMB=180 °-∠ABM=180 °-60 °=120 °.【分析】(1)依据全等三角形的判断和性质解答即可;(2)依据全等三角形的判断和性质解答即可.本题考察全等三角形的判断和性质,重点是依据 SAS 证明△ABM ≌△BCN .。
福建省龙岩第一中学2022-2023学年高三上学期第二次月考数学试题(解析版)

2023届福建省龙岩第一中学高三上学期第二次月考数学试题一、单选题1.已知{}1,0,1,3,5A =-,{}230B x x =-<,则R A B =ð( ) A .{}0,1 B .{}1,1,3-C .{}1,0,1-D .{}3,5【答案】D【分析】由题意求出B ,R B ð,由交集的定义即可得出答案.【详解】因为{}230B x x =-<32x x ⎧⎫=<⎨⎬⎩⎭, 所以R B =ð32x x ⎧⎫≥⎨⎬⎩⎭,所以A R B =ð{}3,5.故选:D. 2.若5:11xp x -≤+,则p 成立的一个充分不必要条件是( ) A .21x -<≤- B .12x -≤≤ C .15x ≤≤ D .25x <<【答案】D【分析】先求出分式不等式的解集,进而结合选项根据充分不必要条件的概念即可求出结果. 【详解】因为511xx -≤+,即51011x x x x -+-≤++,因此4201x x -≤+等价于()()42+10+10x x x -≤≠⎧⎨⎩,解得2x ≥或1x <-,结合选项可知p 成立的一个充分不必要条件是25x <<, 故选:D.3.已知函数()()2ln 16f x x x =++-,则下列区间中含()f x 零点的是( )A .()0,1B .()1,2C .()2,3D .()3,4【答案】C【分析】分别求出()0f 、()1f 、()3f 、()4f 的值,即可判断其正负号,利用零点存在定理则可选出答案.【详解】由题意知:()0ln1660f =-=-<,()231ln2+16ln3+462ln 32ln0e f f =-<-==-=<(), ()ln3+96ln3303f =-=+>,()ln4+166ln 40041f =-=+>. 由零点存在定理可知()f x 在区间()2,3一定有零点. 故选:C.4.如图是杭州2022年第19届亚运会会徽,名为“潮涌”,钱塘江和钱江潮头是会徽的形象核心,绿水青山展示了浙江杭州山水城市的自然特征,江潮奔涌表达了浙江儿女勇立潮头的精神气质,整个会徽形象象征着新时代中国特色社会主义大潮的涌动和发展.如图是会徽的几何图形,设弧AD 长度是1l ,弧BC 长度是2l ,几何图形ABCD 面积为1S ,扇形BOC 面积为2S ,若122l l =,则12S S =( )A .1B .2C .3D .4【答案】C【分析】通过弧长比可以得到OA 与OB 的比,接着再利用扇形面积公式即可求解 【详解】解:设AOD θ∠=,则12,l OA l OB θθ=⋅=⋅,所以122l OAl OB==,即2OA OB =, 所以12221222111222231122OA l OB l OB l OB l S S OB l OB l ⋅-⋅⋅-⋅===⋅⋅, 故选:C5.已知22sin sin ,cos cos 33αβαβ-=--=,且π,0,2αβ⎛⎫∈ ⎪⎝⎭,则ta n()αβ-的值为( )AB.CD.【答案】B【分析】将条件的两个式子平方相加可得()8922cos αβ--=,然后可得()5os 9c αβ-=,再由2sin sin 03αβ-=-<,π,0,2αβ⎛⎫∈ ⎪⎝⎭,可得()π,02αβ⎛⎫-∈- ⎪⎝⎭,从而可求出()in s αβ-=,由商式关系可求得()an t αβ-=【详解】由2sin sin 3αβ-=-,得22sin 2sin sin sin 49ααββ-+=,由2cos cos 3αβ-=,得22cos 2cos cos cos 49ααββ-+=,两式相加得,()8922cos αβ--=,所以可得()5os 9c αβ-=,因为2sin sin 03αβ-=-<,π,0,2αβ⎛⎫∈ ⎪⎝⎭,所以()π,02αβ⎛⎫-∈- ⎪⎝⎭,所以()in s αβ-=()an t αβ-=故选:B6.已知()()2222cos 1ln 4f x x x =-⋅,则函数()f x 的部分图象大致为( )A .B .C .D .【答案】A【分析】利用二倍角余弦公式化简()2f x 的表达式,令()20t x t =≠,可得()f x 的解析式,再判断函数()f x 的奇偶性,可排除选项C 、D ,最后根据0x +→时,()0f x <即可求解.【详解】解:()()()()22222cos 1ln 4cos 2ln 2f x x x x x =-⋅=⋅,令()20t x t =≠,则()2cos ln f t t t =⋅()0t ≠,所以()2cos ln f x x x =⋅()0x ≠,定义域关于原点对称,因为()()()()22cos ln cos ln f x x x x x f x -=-⋅-=⋅=,所以()f x 为偶函数,图象关于y 轴对称,故排除选项C 、D ;又0x +→时,因为2cos 0,ln 0x x ><,所以()2cos ln 0f x x x =⋅<,所以排除选项B ,选项A 正确; 故选:A.7.已知()22231,0log ,0x x x f x x x ⎧++≤⎪=⎨>⎪⎩,函数()()g x f x b =+有四个不同的零点1234,,,x x x x ,且满足:1234x x x x <<<.则下列结论中不正确的是( ) A .10b -<< B .341x x =C .3112x ≤< D .1232x x +=-【答案】A【分析】作出()f x 图象,利用函数有四个不同的交点求出10b -≤<,A 错误; 根据二次函数的对称轴求出1232x x +=-可判断D ;数形结合结合对数运算得到341x x =可判断B ;数形结合求出231log 0x -≤<,解得3112x ≤<,可判断C. 【详解】如图,作出()f x 图象,若y =-b 与()y f x =有四个交点,需01b <-≤,则10b -≤<,故A 错误;这四个交点的横坐标依次为1234,,,x x x x ,因为抛物线2231y x x =++的对称轴为34x =-,所以1232x x +=-,故D 正确;因为2324log log x x -=,即2324log log 0x x +=,所以341x x =,故B 正确;()(]323log 0,1f x x =-∈,即231log 0x -≤<,所以3112x ≤<,故C 正确.故选:A.8.已知13sin 2,ln 2,2a b c -===,则a ,b ,c 的大小关系是( ) A .c b a << B .a b c <<C .b a c <<D .b c a <<【答案】D【分析】判断sin2和2πsin3的大小,比较a 与34、b 与34、c 与34的大小可判断a 与b 大小关系及b 与c 大小关系,判断aca 与c 大小关系,从而可判断a 、b 、c 大小关系.【详解】2π3sin2sin34a =>=>, 4333344443e e 2e 2lne ln24⎛⎫=>⇒>⇒=> ⎪⎝⎭,即b 34<,∴a >b ;∵3131322264-⎛⎫== ⎪⎝⎭,3327464⎛⎫= ⎪⎝⎭,∴13324->,c b ∴>;∵62764=⎝⎭,6131162464-⎛⎫== ⎪⎝⎭,132->,a c ∴>; a cb ∴>>. 故选:D .【点睛】本题关键是利用正弦函数的值域求出sin2的范围,以34两个值作为中间值,比较a 、b 、c 与中间值的大小即可判断a 、b 、c 的大小.二、多选题9)A .2252cos cos 1212ππ⎛⎫- ⎪⎝⎭ B .1tan151tan15+︒-︒C.cos15︒︒ D .16sin10cos20cos30cos40︒︒︒︒【答案】ABD【分析】对于A ,采用降幂公式,结合特殊角三角函数,可得答案; 对于B ,根据特殊角三角函数,结合正切的和角公式,可得答案; 对于C ,根据辅助角公式,结合特殊角三角函数,可得答案; 对于D ,根据积化和差公式,结合特殊角三角函数,可得答案.【详解】对于A ,2251cos 1cos 55662cos cos 2cos cos12122266ππππππ⎛⎫++ ⎪⎛⎫-=-=- ⎪ ⎪⎝⎭⎪⎝⎭=,故A 正确; 对于B ,()1tan15tan 45tan15tan 4515tan 6031tan151tan 45tan15++==+==--,故B 正确;对于C ,13cos153sin152cos15sin1522⎛⎫-=- ⎪ ⎪⎝⎭()()()2sin30cos15cos30sin152sin 30152sin152sin 4530=-=-==-()212sin 45cos30cos 45sin 302222⎛⎫=-== ⎪ ⎪⎝⎭C 错误; 对于D ,16sin10cos 20cos30cos 40 ()116sin 30sin 10cos30cos 402⎡⎤=⨯+-⎣⎦ 8sin30cos30cos 408sin10cos30cos 40=-()18408sin 40sin 20cos 402⎡⎤=-⨯+-⎣⎦404sin 40cos 404sin 20cos 40=-+()1402sin804sin 60sin 202⎡⎤=-+⨯+-⎣⎦402sin8032sin 20=-+-404sin50cos303=-+ )cos 40sin 503=-+)cos 40cos 403=-+=D 正确;故选:ABD.10.已知0a >,0b >,且4a b +=,则下列结论正确的是( ) A .4ab ≤ B .111a b+≥ C .2216a b +≥ D .228a b +≤【答案】AB【分析】根据基本不等式进行逐一判断即可.【详解】A :因为0a >,0b >,所以4a b ab +≥≤,当且仅当2a b ==时取等号,故本选项正确;B :因为0a >,0b >,所以有11111()(2)(21444a b b a a b a b a b b a ++=+=++≥+=+,当且仅当2a b ==时取等号,故本选项正确;C :因为228a b +≥=,当且仅当2a b ==时取等号,所以本选项不正确;D :因为0a >,0b >,所以有22282a b a b +≤≤+≥,当且仅当2a b ==时取等号,所以本选项不正确,故选:AB11.已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称,则( )A .函数12f x π⎛⎫+ ⎪⎝⎭为奇函数B .函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增C .函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像关于6x π=对称,则a的最小值是3πD .若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ,则12x x -的最大值为2π【答案】AC【分析】根据题意得6πϕ=-,()3sin 26f x x π⎛⎫=- ⎪⎝⎭,再结合三角函数的图像性质依次分析各选项即可得答案.【详解】解:因为函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称,所以,2,Z 32k k ππϕπ⨯+=+∈,解得,Z 6k k πϕπ=-+∈,因为22ππϕ-<<,所以6πϕ=-,即()3sin 26f x x π⎛⎫=- ⎪⎝⎭,所以,对于A 选项,函数3sin 212f x x π⎛⎫+= ⎪⎝⎭,是奇函数,故正确;对于B 选项,当,32x ππ⎡⎤∈⎢⎥⎣⎦时,25,626x πππ-⎡⎤∈⎢⎥⎣⎦,由于函数sin y x =在5,26ππ⎡⎤⎢⎥⎣⎦上单调递减,所以函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递减,故错误;对于C 选项,函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像对应的解析式为()3sin 226g x x a π⎛⎫=-- ⎪⎝⎭,若()g x 图像关于6x π=对称,则22,Z 662a k k ππππ⨯--=+∈,解得,Z 62k a k ππ=-+∈, 由于0a >,故a 的最小值是3π,故正确; 对于D 选项,当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,672,66x πππ⎡⎤⎢⎥⎣⎦-∈,故结合正弦函数的性质可知,若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ,不妨设12x x <,则12x x -取得最大值时满足1266x ππ-=且25266x ππ-=, 所以,12x x -的最大值为3π,故错误.故选:AC12.已知1a b >>,则( ) A .ln ln a b b a > B .11ea ba b-<C .11e b a ->D .若m b b n =+,则m a a n >+ 【答案】BC【分析】根据各个选项中的不等式,通过构造新函数,利用导数判断其单调性,再结合特例法进行判断即可.【详解】因为1a b >>,所以ln ln ln ln b aa b b a b a>⇔>, 设函数ln ()(1)xf x x x=>,21ln ()x f x x -'=,当(1,e)x ∈时,()0f x '>,函数()f x 单调递增, 当(e,)x ∈+∞时,()0f x '<,函数()f x 单调递减, 所以A 选项错误;因为1a b >>,所以由111111eln ln ln ln a ba ab a b b a b a b -<⇔-<-⇔->-, 设函数1()ln g x x x =-,211()g x x x '=+,当,()0x ∈+∞时,()0g x '>,函数()g x 单调递增,所以B 选项正确;因为111eln 1ba a b->⇔>-,设函数1()ln 1h a a a ⎛⎫=-- ⎪⎝⎭,所以21()a h a a -'=,当()1,a ∞∈+时,()0'>h a ,函数()h a 单调递增, 当()0,1a ∈时,()0h a '<,函数()h a 单调递减,所以()(1)0h a h >=,即11ln 10ln 1a a a a ⎛⎫-->⇒>- ⎪⎝⎭,因为1a b >>,所以111111a b a b <⇒->-,因此11ln 11a a b>->-,所以C 选项正确. 令2,0b m ==,则有1n =-,又令3a =,所以01,2m a a a n ==+=, 显然不成立,所以D 选项错误, 故选:BC【点睛】方法点睛:不等式是否成立可以通过构造函数利用导数的性质来进行判断.三、填空题13.已知角θ的终边经过点(2,1)P -,则22cos 2sin cos 2θθθ-=___________.【答案】23【分析】利用三角函数定义求出tan θ,再利用二倍角公式化简,结合齐次式法计算作答.【详解】因角θ的终边经过点(2,1)P -,则1tan 2θ=-,所以2222222222112()cos 2sin cos 2sin 12tan 221cos 2cos sin 1tan 31()2θθθθθθθθθ-⨯----====----. 故答案为:2314.函数()xe f x x =的单调递减区间是__________.【答案】和(或写成和)【详解】试题分析:由题意得22(1)()x x x xe e e x f x x x-='-=,令()0f x '<,解得0x <或01x <<,所以函数的递减区间为和.【解析】利用导数求解函数的单调区间.15.已知函数(1)y f x =+的图象关于直线3x =-对称,且对R x ∀∈都有()()2f x f x +-=,当2(]0,x ∈时,()2f x x =+.则(2022)f =___________. 【答案】2-【分析】根据给定条件,推理论证出函数()f x 的周期,再利用周期性计算作答. 【详解】因函数(1)y f x =+的图象关于直线3x =-对称,而函数(1)y f x =+的图象右移1个单位得()y f x =的图象,则函数()y f x =的图象关于直线2x =-对称,即(4)()f x f x --=,而对R x ∀∈都有()()2f x f x +-=,则(4)()2f x f x --+-=,即R x ∀∈,(4)()2f x f x +=-+,有(8)(4)2f x f x +=-++[()2]2()f x f x =--++=,因此函数()y f x =是周期函数,周期为8,又当2(]0,x ∈时,()2f x x =+, 所以(2022)(25382)(2)2(2)242f f f f =⨯-=-=-=-=-. 故答案为:2-16.已知函数()sin cos (0,0)f x x a x a ωωω=+>>图像的两条相邻对称轴之间的距离小于,3f ππ⎛⎫= ⎪⎝⎭()6f x f π⎛⎫≤⎪⎝⎭,则ω的最小值为___________. 【答案】13【分析】先由对称轴间的距离确定了1ω>,再利用()6f x f π⎛⎫≤ ⎪⎝⎭得到2,Z 62k k πωπϕπ+=+∈,依次利用诱导公式与基本关系式求得tan 6πω⎛⎫⎪⎝⎭、cos 6πω⎛⎫ ⎪⎝⎭、sin 6πω⎛⎫⎪⎝⎭的a 关于表达式,求出a 的值,进而得到121,Z k k ω=+∈,即可得到结果. 【详解】()()sin cos f x x a x x ωωωϕ=+=+,tan a ϕ=, 因为两条相邻对称轴之间的距离小于π,即2T π<,故22T ππω=<,所以1ω>, 因为()f x 在6x π=处取得最大值,所以2,Z 62k k πωπϕπ+=+∈,即2,Z 26k k ππωϕπ=+-∈,所以1tan tan 2tan 2626tan 6k a ππωππωϕππω⎛⎫⎛⎫=+-=-== ⎪ ⎪⎛⎫⎝⎭⎝⎭ ⎪⎝⎭, 所以1tan 6a πω⎛⎫= ⎪⎝⎭,因为3f π⎛⎫= ⎪⎝⎭3πωϕ⎛⎫+=⎪⎝⎭,即sin 3πωϕ⎛⎫+= ⎪⎝⎭所以sin sin 2sin cos 3326266k πωπωππωππωπωϕπ⎛⎫⎛⎫⎛⎫⎛⎫+=++-=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以sin tan cos 666πωπωπω⎛⎫⎛⎫⎛⎫=⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又2222sin cos 166πωπω⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭,解得23a =,又0a >,所以a =1sin 62πω⎛⎫= ⎪⎝⎭,又tan 06πω⎛⎫> ⎪⎝⎭,所以2,Z 66k k πωππ=+∈,解得121,Z k k ω=+∈,又1ω>,所以ω的最小值为13.故答案为:13.四、解答题17.已知a ,b ,c 分别为ABC 内角A ,B ,C 的对边,且满足2225,sin 2sin 8b c a bc C B +-==. (1)求cos A ;(2)若ABC 的周长为6ABC 的面积.【答案】(1)516;(2【解析】(1)由余弦定理可求得cos A ;(2)根据正弦定理可得2c b =,再由已知和余弦定理可求得2b =,根据三角形的面积可求得答案.【详解】解:(1)因为22258b c a bc +-=,所以2225cos 216b c a A bc +-==;(2)因为sin 2sin C B =,所以2c b =.由余弦定理得2222152cos 4a b c bc A b =+-=,则a =,因为ABC 的周长为636b =2b =,所以ABC 的面积为122b b ⨯⨯【点睛】方法点睛:(1)在解三角形中,如果题设条件是关于边的二次形式,我们可以利用余弦定理化简该条件;(2)如果题设条件是关于边的齐次式或是关于内角正弦的齐次式,那么我们可以利用正弦定理化简该条件;(3)如果题设条件是边和角的混合关系式,那么我们也可把这种关系式转化为角的关系式或边的关系式.(4)与三角形有关的最值问题,我们可以利用基本不等式来求最值或利用正弦定理把边转化为关于角的三角函数式,再利用三角变换和正弦函数、余弦函数的性质求最值或范围.18.已知函数()2ππ2sin sin cos cos 44f x x x x x x ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭.(1)求()f x 的对称中心,并求当π0,2x ⎛⎫∈ ⎪⎝⎭时,()f x 的值域;(2)若函数()g x 的图像与函数()f x 的图像关于y 轴对称,求()g x 在区间()0,π上的单调递增区间.【答案】(1)对称中心:π1π,622k ⎛⎫-+ ⎪⎝⎭,k ∈Z ,值域:12⎛⎤- ⎥⎝⎦(2)5π11π,1212⎛⎫ ⎪⎝⎭【分析】(1)根据三角恒等变换,化简函数()f x ,再结合正弦型函数的对称中心公式,即可得到对称中心,结合正弦函数的图像即可求得其值域.(2)由(1)中()f x 的解析式,根据对称变换即可得到函数()g x 的解析式,再结合正弦型函数的单调区间即可求得结果.【详解】(1)因为函数()2ππ2sin sin cos cos 44f x x x x x x ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭222cos x x x x x x ⎫=+⎪⎪⎝⎭⎝⎭()221cos 2cos sin 22xx x x +=-+π1232x ⎛⎫++ ⎪⎝⎭令π2π,3x k k +=∈Z ,解得ππ62k x =-+,即对称中心π1π,622k k ⎛⎫-+∈ ⎪⎝⎭Z ,当π0,2x ⎛⎫∈ ⎪⎝⎭时,则ππ4π2,333x ⎛⎫+∈ ⎪⎝⎭,再结合三角函数图像可得()12f x ⎛⎤∈- ⎥⎝⎦所以,函数对称中心:π1π,622k ⎛⎫-+ ⎪⎝⎭,k ∈Z ,值域:12⎛⎤- ⎥⎝⎦.(2)因为函数()g x 的图像与函数()f x 的图像关于y 轴对称,则()()π1232g x f x x ⎛⎫=-=-++ ⎪⎝⎭,令ππ3π2π22π232k x k +≤-+≤+,k ∈Z ,解得7ππππ,1212k x k k -+≤≤-+∈Z 当1k =时,即为5π11π,1212⎛⎫ ⎪⎝⎭所以当()0,πx ∈时,()g x 的单调递增区间:5π11π,1212⎛⎫⎪⎝⎭.19.为进一步奏响“绿水青山就是金山银山”的主旋律,某旅游风景区以“绿水青山”为主题,特别制作了旅游纪念章,决定近期投放市场,根据市场调研情况,预计每枚该纪念章的市场价y (单位:元)与上市时间x (单位:天)的数据如下表:(1)根据上表数据,从下列函数中选取一个恰当的函数描述每枚该纪念章的市场价y 与上市时间x 的变化关系并说明理由:①(0)y ax b a =+≠,②()20y ax bx c a =++≠,③()log 0,0,1b y a x a b b =≠>≠,④(0)ay b a x=+≠; (2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低市场价;(3)利用你选取的函数,若存在()10,x ∈+∞,使得不等式()010f x k x -≤-成立,求实数k 的取值范围.【答案】(1)选择()20y ax bx c a =++≠,理由见解析(2)当该纪念章上市10天时,市场价最低,最低市场价为每枚70元 (3)k ≥【分析】(1)由表格数据分析变量x 与变量y 的关系,由此选择对应的函数关系;(2)由已知数据求出函数解析式,再结合函数性质求其最值;(3)不等式可化为()17010210x k x -+≤-,由条件可得()min 17010210x k x ⎡⎤-+≤⎢⎥-⎣⎦,利用函数的单调性求()17010210y x x =-+-的最小值,由此可得k 的取值范围. 【详解】(1)由题表知,随着时间x 的增大,y 的值随x 的增大,先减小后增大,而所给的函数(0)y ax b a =+≠,()log 0,0,1b y a x a b b =≠>≠和(0)ay b a x=+≠在(0,)+∞上显然都是单调函数,不满足题意,故选择()20y ax bx c a =++≠.(2)把()2,102,()6,78,()20,120分别代入2y ax bx c =++,得42102,36678,40020120,a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得12a =,10b =-,120c = ∴()221110120107022y x x x =-+=-+,,()0x ∈+∞. ∴当10x =时,y 有最小值,且min 70y =.故当该纪念章上市10天时,市场价最低,最低市场价为每枚70元. (3)令()()()1701010210f xg x x x x ==-+--(10,)x ∞∈+, 因为存在()10,x ∈+∞,使得不等式()0g x k -≤成立, 则()min k g x ≥.又()()17010210g x x x =-+-在(10,10+上单调递减,在()10++∞上单调递增,∴ 当10x =+()g x 取得最小值,且最小值为(10g +=∴k ≥20.己知函数21()2ln (21)(0)2f x x ax a x a =-+->.(1)若曲线(=)y f x 在点(1,(1))f 处的切线经过原点,求a 的值;(2)设2()2g x x x =-,若对任意(0,2]s ∈,均存在(0,2]t ∈,使得()()f s g t <,求a 的取值范围.【答案】(1)=4a ; (2)(0,1ln 2)-.【分析】(1)利用导数的几何意义求切线方程(含参数a ),由切线过原点求出a 的值; (2)利用导数研究()f x 的单调性并求出(0,2]上的最大值,由二次函数性质求()g x 在(0,2]上的最大值,根据已知不等式恒(能)成立求参数a 的范围.【详解】(1)由21()2ln (21)(0)2f x x ax a x a =-+->,可得2()21f x ax a x '=-+-.因为(1)2211f a a a '=-+-=+,13(1)21122f a a a =-+-=-,所以切点坐标为3(1,1)2a -,切线方程为:()311(1)2a y a x ⎛⎫--=+- ⎪⎝⎭, 因为切线经过(0,0),所以3112aa -=+,解得=4a . (2)由题知()f x 的定义域为(0,)+∞,21()[(21)2]f x ax a x x'=----,令()f x '=2(21)20ax a x ---=,解得1x a=-或=2x , 因为0,a >所以10a-<,所以12a-<, 令()0f x '>,即2(21)20ax a x ---<,解得:12x a-<<,令()0f x '<,即2(21)20ax a x --->,解得:1x a<-或2x >,所以()f x 增区间为(0,2),减区间为(2,)+∞.因为()22()211g t t t t =-=--,所以函数()g t 在区间(0,2]的最大值为0, 函数()f s 在(0,2)上单调递增,故在区间(0,2]上max ()(2)2ln 222f s f a ==+-, 所以2ln 2220a +-<,即ln 210a +-<,故1ln 2a <-, 所以a 的取值范围是(0,1ln 2)-.21.如图,在三棱柱111ABC A B C -中,1112,,AB AC AA AB AC A AB A AC ===⊥∠=∠,D 是棱11B C 的中点.(1)证明:1AA BC ⊥;(2)若三棱锥11B A BD -1A BD 与平面11CBB C 所成锐二面角的余弦值.【答案】(1)证明见解析【分析】(1)作出辅助线,由三线合一证明线线垂直,进而证明线面垂直,得到BC ⊥平面1AAO ,从而证明1AA BC ⊥;(2)作出辅助线,由三棱锥的体积求出1A H =用空间向量求解二面角;方法二:作出辅助线,找到二面角的平面角,再求解余弦值. 【详解】(1)取BC 中点O ,连接AO ,1AO ,1AC,因为AB AC =,所以AO BC ⊥,因为11A AB A AC ∠=∠,11,AB AC AA AA ==,所以11A AB A AC ≅,所以11A B AC =,所以1AO BC ⊥, 因为1AOAO O =,1,AO AO ⊂平面1AAO , 所以BC ⊥平面1AAO , 因为1AA ⊂平面1AAO , 所以1AA BC ⊥;(2)连接OD ,则平面1AAO 即为平面1AA DO , 由(1)知BC ⊥平面1AA DO ,因为BC ⊂平面ABC ,且BC ⊂平面11BCC B , 故平面1AA DO ⊥平面ABC ,平面1AA DO ⊥平面11BCC B ,过O 作1OM A D ⊥于M ,则OM ⊥平面ABC ,过1A 作1A H OD ⊥于H ,则1A H ⊥平面11BCC B ,因为11DO BB AA ∥∥知DO BC ⊥,在ABC中:2,AB AC BC ===所以1112BDB S DB DO =⋅△所以111111113B A BD A BDB BDB A A V V S h --==⋅==△,所以11A A H h = 法一:设MOD α∠=,则1DA H α∠=,在1Rt A HD △中11cos A H A D α===所以sin cos DM DO OM OD αα=⋅==⋅=又1A D M 为线段1A D 的中点,以O 为原点,分别以,,OA OB OM 分别为x ,y ,z 轴正方向建立空间直角坐标系,1(0,A B C A ⎝⎭,1,2222B D ⎛⎛ ⎝⎭⎝⎭, 设面1A BD 的法向量为()1111,,x n y z =,则有111111*********n BA xn BD x⎧⋅==⎪⎪⎨⎪⋅=-=⎪⎩,两式相减得:10x =,所以110=,令12z =,可得:1y = 所以1(0,7,2)n =,设面11CBB C 的法向量为()2222,,n x y z =,则有221122220202n CB n CB ⎧⋅==⎪⎨⋅=-=⎪⎩, 解得:20y =,令21z =,解得:2x =所以2(7,0,1)n=, 设锐二面角为θ,则有1212cos 4n n n n θ⋅===+⋅. 法二:过H 做HE BD ⊥,连接1A E ,1A H ⊥面11BCC B,1A H DB ∴⊥,则DB ⊥面1AHE ,1A E BD ∴⊥,则1A EH ∠即为所求二面角.在1Rt A DH △中,11A H A D =12DH =,在Rt DOB 中,2,DO OB DB == 由RtRt DEHDOB 可得:HE DHOB DB=,HE ∴=,则1A E =11cos HE A EH A E ∴∠===22.己知函数()e sin 1(0)x f x a x a =-->在区间(0,)π内有唯一极值点1x . (1)求实数a 的取值范围;(2)证明:()f x 在区间(0,)π内有唯一零点2x ,且212x x <. 【答案】(1)(1,)∈+∞a (2)证明见解析【分析】(1)根据极值点的定义,求导,进而求导函数的零点,研究零点左右与零大小关系,可得答案;(2)由(1)明确函数的单调区间,分别在两个单调区间上,利用零点存在性定理,证明零点唯一存在,根据单调性证明不等式成立. 【详解】(1)()e cos x f x a x '=-,①当01a <≤时,因为()0,x π∈,所以cos 1a x <,1e e x π<<,()0f x '>,()f x 在()0,π上单调递增,没有极值点,不合题意,舍去;②当1a >时,令()=()g x f x ',则()e sin x g x a x '=+,因为()0,x π∈,所以()0g x '>,所以()f x '在()0,π上递增,又因为(0)10f a '=-<,2e 02f ππ⎛⎫'=> ⎪⎝⎭,所以()f x '在()0,π上有唯一零点1x ,且10,2x π⎛⎫⎪⎝⎭∈,所以()10,x x ∈,()0f x '<;1,2x x π⎛⎫∈ ⎪⎝⎭,()0f x '>,所以()f x 在()0,π上有唯一极值点,符合题意. 综上,(1,)∈+∞a .(2)由(1)知1a >,所以,2x ππ⎡⎫∈⎪⎢⎣⎭时,()e cos 0x f x a x '=->,所以()10,x x ∈,()0f x '<,()f x 单调递减;()1,x x π∈,()0f x '>,()f x 单调递增,所以()10,x x ∈时,()(0)0f x f <=,则()10f x <,又因为()e 10f ππ=->, 所以()f x 在()1,πx 上有唯一零点2x ,即()f x 在(0,)π上有唯一零点2x .因为()112211112e sin 21e 2sin cos 1x xf x a x a x x =--=--,由(1)知()10f x '=,所以11e cos x a x =,则()112112e 2e sin 1x x f x x =--,构造2()e 2e sin 1,0,2t tp t t t π⎛⎫=--∈ ⎪⎝⎭,所以()2()2e 2e (sin cos )2e e sin cos t t t tp t t t t t '=-+=--,记()e sin cos ,0,2tt t t t πϕ⎛⎫=--∈ ⎪⎝⎭,则()e c o s s i n t t t t ϕ'=-+,显然()t ϕ'在0,2π⎛⎫⎪⎝⎭上单调递增,所以()(0)0t ϕϕ''>=,所以()t ϕ在0,2π⎛⎫ ⎪⎝⎭上单调递增,所以()(0)0t ϕϕ>=,所以()0p t '>,所以()p t 在0,2π⎛⎫⎪⎝⎭上单调递增,所以()(0)0p t p >=,所以()()1220f x f x >=,由前面讨论可知:112x x π<<,12x x π<<,且()f x 在()1,x x π∈单调递增,所以122x x >.【点睛】在利用导数证明不等式成立时,一定明确单调区间,在同一单调区间上,由函数值的大小关系,可得自变量的大小关系,探究函数的单调性,可通过研究导数过着导数中部分代数式所构成函数的单调性,求其最值,可得函数的单调性.。
2023-2024学年福建省龙岩市第一中学高三上学期第一次月考数学试题及答案

龙岩一中2024届高三上学期第一次月考数学试题(考试时间:120分钟 满分:150分)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一一次可使杂质含量减少1/4,要使产品达到市场要求,则至少应过滤的次数为(已知:lg2=0.3010,lg3=0.4771)( )目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知A B 、为实数集R 的非空集合,则A B ≠⊂的必要不充分条件可以是( )A .AB A ⋂=B .A ∩C R B =C .C R B ≠⊂C R AD .B ∪C R A=R三、填空题:本题共4小题,每小题5分,共20分.13.已知实数集R ,集合A ={x|log 2x<1},B ={x ∈Z |x 2+4≤5x},则(C R A)∩B = 15. 已知()24,1,log ,2,ax x f x x x +≤⎧=⎨≥⎩则()()0f f =______;若函数()f x 的值域为[)1,+∞,则a 的最小值为______.17.(本题满分10分)已知集合{}2680A x x x =-+<,{}22430B x x ax a =-+<.(1)若a =1,求(C R B )∩A ;(2)若a >0,设命题:p x A ∈,命题:q x B ∈,已知命题p 是命题q 的充分不必要条件,求实数a 的取值围.18. (本题满分12分)已知函数1(=21xf x a +-)是奇函数.(1)求a ;(2)若[](1ln 0f x x -⋅<),求x 的范围.19.(本题满分12分)已知函数232)1(31)(x k x x f +-=,kx x g -=31)(,且)(x f 在区间),2(+∞上为增函数.(1)求实数k 的取值范围;(2)若函数)(x f 与)(x g 的图象有三个不同的交点,求实数k 的取值范围.20. (本题满分12分)某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出()*x x N∈名员工从事第三产业,调整后他们平均每人每年创造利润为310500x a ⎛⎫- ⎪⎝⎭万元()0a >,剩下的员工平均每人每年创造的利润可以提高0.2%x .(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a 的取值范围是多少?21. (本题满分12分)已知函数())2log f x x =-是R 上的奇函数,()2g x t x a =--.(1)若函数()f x 与()g x 有相同的零点,求t 的值;(2)若123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x g x ≤,求t 的取值范围.22. (本题满分12分)已知函数()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦,a ∈R .(1)讨论函数()f x 单调性;(2)当0a =时,若函数()()()11g x f x m x =---在[)0,∞+有两个不同零点,求实数m 的取值范围.龙岩一中2024届高三上学期第一次月考数学参考答案题号123456789101112答案BBCDDDABABDCDBCDABD13.{2,3,4}143-15.2, -316.-1两个函数图象如下图所示:121,ln ln e 1x x <<=,又当1x <时,()f x 单调递增,所以又由{}2680(2,4)A x x x =-+<=,所以()[)3,4B A ⋂=R ð.. ........5分(2)当0a >时,可得(),3B a a =.因为命题p 是命题q 的充分不必要条件,则A ≠⊂B ,可得243a a≤⎧⎨≤⎩,等号不能同时成立,解得423a ≤≤,所以实数a 的取值范围为4,23⎡⎤⎢⎥⎣⎦ ......10分18. .......1分.....................6分 (用特殊值没检验的,扣2分)................8分.....................12分19.解:(1)由题意xk x xf )1()(2+-=' ∵)(x f 在区间),2(+∞上为增函数,≥0在区间(2,+∞)上恒成立..........2分即k+1≤x 恒成立,又2>x ,∴21≤+k ,故1≤k ∴k 的取值范围为1≤k ..........4分 ( 没有等号扣2分)(2)设312)1(3)()()(23-++-=-=kx x k x x g x f x h ,)1)(()1()(2--=++-='x k x k x k x x h ...........6分令0)(='x h 得k x =或1=x 由(1)知1≤k ,①当1=k 时,0)1()(2≥-='x x h ,)(x h 在R 上递增,显然不合题意...........7分②当1<k 时,)(x h ,)(x h '随x 的变化情况如下表:x ),(k -∞k )1,(k 1),1(+∞)(x h '+0—0+)(x h ↗极大值312623-+-k k ↘极小值21-k ↗由于021<-k ,欲使)(x f 与)(x g 的图象有三个不同的交点,即方程0)(=x h 有三个不同的实根,故需0312623>-+-k k ,即0)22)(1(2<---k k k ...........10分∴⎩⎨⎧>--<02212k k k ,解得31-<k ,综上,所求k 的取值范围为31-<k ...........12分20. 解:(1)由题意,得()()10100010.2%101000x x -+≥⨯,..................3分即25000x x -≤,又0x >,所以0500x <≤.即最多调整500名员工从事第三产业. ..........5分(2)从事第三产业的员工创造的年总利润为310500⎛⎫- ⎪⎝⎭x a x 万元,从事原来产业的员工的年总利润为110(1000)1500⎛⎫-+⎪⎝⎭x x 万元,..............7分21. 解:(1)因为())2log f x x =-是R 上的奇函数,所以()00f =,即log 0=解得1a =..................2分因为0x =是函数()f x 的零点,所以()010g t =-=,则1t =....................4分(2)由(1)可得())2log f x x =-,()121,221121,2x t x g x t x x t x ⎧-++≥⎪⎪=--=⎨⎪+-<⎪⎩, (6)分因为奇函数())2log log f x x ==()f x 在3,24⎡⎤-⎢⎥⎣⎦上是减函数,则()f x 在3,24⎡⎤-⎢⎥⎣⎦上的最大值为()2max 33log 144f x f ⎫⎛⎫⎛⎫⎪=-=-= ⎪ ⎪⎪⎝⎭⎝⎭⎭.......8分因为()121,2121,2x t x g x x t x ⎧-++≥⎪⎪=⎨⎪+-<⎪⎩,所以()gx 在31,42⎡⎤-⎢⎥⎣⎦上是增函数,在1,22⎡⎤⎢⎥⎣⎦上是减函数.则()g x 的最小值为34g ⎛⎫-⎪⎝⎭和()2g 中的较小的一个.因为33521442g t t ⎛⎫⎛⎫-=⨯-+-=- ⎪ ⎪⎝⎭⎝⎭,()22213g t t =-⨯++=-.所以()()min 23g x g t ==-.............10分因为123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x f x ≤,所以13t ≤-.解得4t ≥.故t 的取值范围为[)4,+∞.....................12分22. 解(1):因为()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦定义域为R ,所以()()()211e e x xf x x ax x x a --'=+=+,..........1分当0a >时,令()0f x ¢>,解得0x >或x a <-,令()0f x '<,解得0a x -<<,所以()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增,..........2分当0a =时()21e 0xf x x -'=≥恒成立,所以()f x 在R 上单调递增, ..........3分当a<0时,令()0f x ¢>,解得x a >-或0x <,令()0f x '<,解得0x a <<-,所以()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增,..........4分综上可得,当0a >时,()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增;当0a =时,()f x 在R 上单调递增;当a<0时,()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增;..........5分解(2):当0a =时,()()()()()211122e 11x g x f x m x x x m x -=---=-+---,所以()21e x g x x m -'=-,令()()21e x P x g x x m -'==-,则()()212e 0x P x x x -'=+>,所以()21e x g x x m -'=-在[)0,∞+上单调递增,所以()()0g x g m ''≥=-,①当0m -≥,即0m ≤时()()00g x g m ''≥=-≥,所以()g x 在[)0,∞+上单调递增,又()10g =,所以函数()g x 只有一个零点,不符合题意,舍去;..........6分②当0m -<,即0m >时()()00g x g m ''≥=-<,又()()211e 0m g m m m '+=+->,所以存在唯一的()00,1x m ∈+,使得()00g x '=,当()00,x x ∈时,'()0g x <,当()0,x x ∈+∞时,'()0g x >所以()g x 在()00,x 上单调递减,在()0,x +∞上单调递增,又()11g m '=-,当1m =时()10g '=,此时01x =,所以()()10g x g ≥=,函数()g x 只有一个零点,不符合题意,舍去;当1m ≠时()110g m '=-≠,01x ≠,此时有两个零点时,应满足()()0000g g x ⎧≥⎪⎨<⎪⎩,..........8分即()()()011200002e 1022e 110x m g x x x m x --⎧+-≥⎪⎨=-+---<⎪⎩,其中()()()()()0001112220000000022e 1122e e 11x x x g x x x m x x x x x ---=-+---=-+---()0132000222e 1x x x x -=-+-+-,..........9分设()()321222e 1x h x x x x -=-+-+-,()0,1x m ∈+,则()()()121e x h x x x x -'=+-,令()()()121e 0x h x x x x -'=+-=,解得1x =,所以当01x <<时()0h x '>,当11x m <<+时()0h x '<,所以()h x 在()0,1上单调递增,在()1,1m +上单调递减,所以()()10h x h ≤=,..........11分即()()()012000022e 110x g x x x m x -=-+---<恒成立,所以112e m -≥-且1m ≠...........12分【方法点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.龙岩一中2024届高三上学期第一次月考数学试题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一故选:D5.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量减少1/4,要使产品达到市场要求,则至少应过滤的次数为(已知:lg2=0.3010,lg3=0.4771)( )A.8B.9C.10D.11【答案】D【详解】设至少需要过滤n次,则10.0210.0014n⎛⎫⨯-≤⎪⎝⎭,即31420n⎛⎫≤⎪⎝⎭,所以3lg204nlg≤-,即lg2010.301010.42lg4lg320.30100.4471n+≥=≈-⨯-,又n N∈,所以11n≥,所以至少过滤11次才能使产品达到市场要求,故选D.【点睛】本题主要考查指数与对数的运算,考查学生的阅读能力,考查学生的建模能力,属于中档题.与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际【点睛】本题考查了比较大小的问题,考查了同构的思想,考查了利用导数求函数的单调区ln二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知A B 、为实数集R 的非空集合,则A B ≠⊂的必要不充分条件可以是( )⊂-x 121,ln ln e 1x x <<=,又当1x <时,()f x 单调递增,所以()()3233223ln 3ln ln ln e ex x x x x f x f x x ==⇒=,又2x 所以23ln x x =,332222ln 1ln ln x x x x x x m ===,21ln x x =确,故选:ABD三、填空题:本题共4小题,每小题5分,共20分.13.已知实数集R ,集合A ={x|log 2x<1},B ={x ∈Z |x 2+4≤5x},则(C R A)∩B = 【答案】{2,3,4}解析 由log 2x<1,解得0<x<2,故A =(0,2),故C R A =(-∞,0]∪[2,+∞),由x 2+4≤5x ,即x 2-5x +4≤0,解得1≤x ≤4,又x ∈Z ,所以B ={1,2,3,4}.15. 已知()24,1,log ,2,ax x f x x x +≤⎧=⎨≥⎩则()()0f f =______;若函数()f x 的值域为[)1,+∞,则a 的最小值为______.【答案】23- 【详解】()()()204log 42f f f ===,要使得函数()f x 的值域为[)1,+∞,则满足041a a ≤⎧⎨+≥,解得30a -≤≤,所以实数a 的最小值为3-.出文字说明、证明过程和演算步骤.17.(本题满分10分)已知集合{}2680A x x x =-+<,{}22430B x x ax a =-+<.(1)若a =1,求(C R B )∩A ;(2)若a >0,设命题:p x A ∈,命题:q x B ∈,已知命题p 是命题q 的充分不必要条件,求实数a 的取值围.17解:(1)当1a =时,{}2430(1,3)B x x x =-+<=,可得][(),13,=-∞⋃+∞R B ð,又由{}2680(2,4)A x x x =-+<=,所以()[)3,4B A ⋂=R ð.. ........5分(2)当0a >时,可得(),3B a a =.因为命题p 是命题q 的充分不必要条件,则A ≠⊂B ,可得243a a≤⎧⎨≤⎩,等号不能同时成立,解得423a ≤≤,所以实数a 的取值范围为4,23⎡⎤⎢⎥⎣⎦ (10)分18. (本题满分12分)已知函数1(=21x f x a +-)是奇函数.(1)求a ;(2)若[](1ln 0f x x -⋅<),求x 的范围........1分.....................6分 (用特殊值没检验的,扣2分).....................8分.....................12分19.(本题满分12分)已知函数232)1(31)(x k x x f +-=,kx x g -=31)(,且)(x f 在区间),2(+∞上为增函数.(1)求实数k 的取值范围;(2)若函数)(x f 与)(x g 的图象有三个不同的交点,求实数k 的取值范围.解:(1)由题意x k x x f )1()(2+-=' ∵)(x f 在区间),2(+∞上为增函数,≥0在区间(2,+∞)上恒成立..........2分即k+1≤x 恒成立,又2>x ,∴21≤+k ,故1≤k ∴k 的取值范围为1≤k ..........4分 ( 没有等号扣2分)(2)设312)1(3)()()(23-++-=-=kx x k x x g x f x h ,)1)(()1()(2--=++-='x k x k x k x x h ...........6分令0)(='x h 得k x =或1=x 由(1)知1≤k ,②当1=k 时,0)1()(2≥-='x x h ,)(x h 在R 上递增,显然不合题意...........7分②当1<k 时,)(x h ,)(x h '随x 的变化情况如下表:x ),(k -∞k )1,(k 1),1(+∞)(x h '+0—0+)(x h ↗极大值312623-+-k k ↘极小值21-k ↗由于021<-k ,欲使)(x f 与)(x g 的图象有三个不同的交点,即方程0)(=x h 有三个不同的实根,故需0312623>-+-k k ,即0)22)(1(2<---k k k ...........10分∴⎩⎨⎧>--<02212k k k ,解得31-<k ,综上,所求k 的取值范围为31-<k ...........12分20. (本题满分12分)某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出()*x x N∈名员工从事第三产业,调整后他们平均每人每年创造利润为310500x a ⎛⎫- ⎪⎝⎭万元()0a >,剩下的员工平均每人每年创造的利润可以提高0.2%x .(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a 的取值范围是多少?解:(1)由题意,得()()10100010.2%101000x x -+≥⨯,..................3分即25000x x -≤,又0x >,所以0500x <≤.即最多调整500名员工从事第三产业. ..........5分(2)从事第三产业的员工创造的年总利润为310500⎛⎫-⎪⎝⎭x a x 万元,从事原来产业的员工的年总利润为110(1000)1500⎛⎫-+ ⎪⎝⎭x x 万元,..............7分21. (本题满分12分)已知函数())2log f x x =是R 上的奇函数,()2g x t x a =--.(1)若函数()f x 与()g x 有相同的零点,求t 的值;(2)若123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x g x ≤,求t 的取值范围.解:(1)因为())2log f x x =是R 上的奇函数,所以()00f =,即log 0=解得1a =..................2分因为0x =是函数()f x 的零点,所以()010g t =-=,则1t =....................4分(2)由(1)可得())2log f x x =-,()121,221121,2x t x g x t x x t x ⎧-++≥⎪⎪=--=⎨⎪+-<⎪⎩,............6分因为奇函数())22log log f x x =-=()f x 在3,24⎡⎤-⎢⎥⎣⎦上是减函数,则()f x 在3,24⎡⎤-⎢⎥⎣⎦上的最大值为()2max 33log 144f x f ⎫⎛⎫⎛⎫⎪=-=-= ⎪ ⎪⎪⎝⎭⎝⎭⎭.......8分因为()121,2121,2x t x g x x t x ⎧-++≥⎪⎪=⎨⎪+-<⎪⎩,所以()g x 在31,42⎡⎤-⎢⎥⎣⎦上是增函数,在1,22⎡⎤⎢⎥⎣⎦上是减函数.则()g x 的最小值为34g ⎛⎫- ⎪⎝⎭和()2g 中的较小的一个.因为33521442g t t ⎛⎫⎛⎫-=⨯-+-=-⎪ ⎪⎝⎭⎝⎭,()22213g t t =-⨯++=-.所以()()min 23g x g t ==-.............10分因为123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x x ,所以13t ≤-.解得4t ≥.故t 的取值范围为[)4,+∞.....................12分22. (本题满分12分)已知函数()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦,a ∈R .(1)讨论函数()f x 单调性;(2)当0a =时,若函数()()()11g x f x m x =---在[)0,∞+有两个不同零点,求实数m 的取值范围.解(1):因为()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦定义域为R ,所以()()()211e e x xf x x ax x x a --'=+=+,..........1分当0a >时,令()0f x ¢>,解得0x >或x a <-,令()0f x '<,解得0a x -<<,所以()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增,..........2分当0a =时()21e 0xf x x -'=≥恒成立,所以()f x 在R 上单调递增, ..........3分当a<0时,令()0f x ¢>,解得x a >-或0x <,令()0f x '<,解得0x a <<-,所以()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增,..........4分综上可得,当0a >时,()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增;当0a =时,()f x 在R 上单调递增;当a<0时,()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增;..........5分解(2):当0a =时,()()()()()211122e 11x g x f x m x x x m x -=---=-+---,所以()21e x g x x m -'=-,令()()21e x P x g x x m -'==-,则()()212e 0x P x x x -'=+>,所以()21e x g x x m -'=-在[)0,∞+上单调递增,所以()()0g x g m ''≥=-,①当0m -≥,即0m ≤时()()00g x g m ''≥=-≥,所以()g x 在[)0,∞+上单调递增,又()10g =,所以函数()g x 只有一个零点,不符合题意,舍去;..........6分②当0m -<,即0m >时()()00g x g m ''≥=-<,又()()211e 0m g m m m '+=+->,所以存在唯一的()00,1x m ∈+,使得()00g x '=,当()00,x x ∈时,'()0g x <,当()0,x x ∈+∞时,'()0g x >所以()g x 在()00,x 上单调递减,在()0,x +∞上单调递增,又()11g m '=-,当1m =时()10g '=,此时01x =,所以()()10g x g ≥=,函数()g x 只有一个零点,不符合题意,舍去;当1m ≠时()110g m '=-≠,01x ≠,此时有两个零点时,应满足()()0000g g x ⎧≥⎪⎨<⎪⎩,..........8分即()()()011200002e 1022e 110x m g x x x m x --⎧+-≥⎪⎨=-+---<⎪⎩,其中()()()()()0001112220000000022e 1122e e 11x x x g x x x m x x x x x ---=-+---=-+---()0132000222e 1x x x x -=-+-+-,..........9分设()()321222e 1x h x x x x -=-+-+-,()0,1x m ∈+,则()()()121ex h x x x x -'=+-,令()()()121e0x h x x x x -'=+-=,解得1x =,所以当01x <<时()0h x '>,当11x m <<+时()0h x '<,所以()h x 在()0,1上单调递增,在()1,1m +上单调递减,所以()()10h x h ≤=,..........11分即()()()012000022e 110x g x x x m x -=-+---<恒成立,所以112e m -≥-且1m ≠...........12分【方法点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.。
精品解析:福建省龙岩第一中学2022-2023学年高一上学期第一次月考(实验班)化学试题(解析版)

D.200mL1mol∙L-1的乙醇(C2H5OH)溶液中所含有的H原子个数为1.2NA
【答案】C
【解析】
【详解】A.溶液体积未知,无法确定溶液中的微粒数目,故A错误;
B.温度和压强未知,无法确定气体的体积,故B错误;
C.18g 的物质的量为 =1mol,一个 含有10个电子,所以18g 中所含有的电子总数为10NA,故C正确;
14.已知 与浓盐酸在常温下能反应产生 。若用如图所示的实验装置来制备纯净、干燥的氯气,并与金属反应。每个虚线框表示一个单元装置,其中有错误的是()
A.①处和②处B.只有②处C.只有②处和③处D.②处、③处和④处
【答案】D
【解析】
【详解】① 与浓盐酸在常温下反应产生 ,①正确;
②浓盐酸易挥发,生成的氯气中混有 和水蒸气,应通入盛有饱和食盐水的洗气瓶除去 , 会与 溶液反应,故不能选择氢氧化钠溶液,②错误;
D.取少量晶体溶于水,用洁净的铂丝蘸取少量溶液在酒精灯火焰上灼烧,火焰呈黄色,不能证明晶体中无K+
【答案】B
【解析】
【详解】A.晶体加热后生成水,若无水硫酸铜变蓝,则证明晶体中含结晶水,故A正确;
B.向某无色溶液中加入浓NaOH溶液,加热试管,检验氨气,利用湿润的红色石蕊试纸,试纸变蓝,则说明原溶液中一定含NH4+,不是用蓝色石蕊试纸检验,故B错误;
【点睛】该类型的试题在判断时,关键是分析电解质的组成及其强弱。另外还需要注意的是,判断的是离子的浓度,还是离子的物质的量,因为物质的量还与溶液体积有关系。
11.NA表示阿伏加德罗常数。下列说法正确的是
A.0.5mol∙L-1的Na2SO4溶液中Na+的个数为NA
2019-2020学年福建省龙岩一中实验班高二(上)第一次月考数学试卷(含答案解析)

2019-2020学年福建省龙岩一中实验班高二(上)第一次月考数学试卷(含答案解析)2019-2020学年福建省龙岩一中实验班高二(上)第一次月考数学试卷一、选择题(本大题共12小题,共60.0分)1.已知数列√5,√11,√17,√23,…,则5√5是数列的第______项()A. 19B. 20C. 21D. 222.已知△ABC的内角A,B,C的对边分别为a,b,c,且(a+b)2=c2+ab,B=30°,a=4,则△ABC的面积为()A. 4B. 3√3C. 4√3D. 6√33.若a<b<0下列不等式中不成立的是的是()< bdsfid="77" p=""></b<0下列不等式中不成立的是的是()<>A. |a|>|b|B. 1a?b >1bC. 1a>1bD. a2>b24.在等差数列{a n}中,若a3+a11=6,则其前13项的和S13的值是()A. 32B. 39C. 46D. 785.在△ABC中,已知BC=2√3,AC=5,∠C=30°,则AB=()A. √7B. 2√3C. √19D. √37?10√36.设a>0,b>0,lg√2是lg4a与lg2b的等差中项,则2a +1b的最小值为()A. 2√2B. 3C. 4D. 97.已知实数?1,x,y,z,?4成等比数列,则xyz=()A. ?8B. ±8C. ?2√2D. ±2√28.若sin(θ+π4)=√26,则sin4θ+cos4θ=()A. 19B. 49C. 3281D. 49819.已知数列{a n}满足log2a n+1=log2a n+1,且a2+a4+a6=4,则log12(a5+a7+a9)的值为()A. ?5B. 15C. 5 D. ?1510.若实数x,y满足约束条件{x?3y+4≥03x?y?4≤0x+y≥0,则z=3x?2y的最大值是()A. 2B. 1C. 5D. 711.在△ABC中,角A,B,C的对边分别为a,b,c,若c2?a2?b22ab>0,则△ABC()A. 一定是锐角三角形B. 一定是直角三角形C. 一定是钝角三角形D. 是锐角或直角三角形12.设函数f(x)=(x?3)3+x?1,数列{a n}是公差不为0的等差数列,则f(a1)+f(a2)+?+f(a7)=14,则a1+a2+?+a7=()A. 0B. 7C. 14D. 21二、填空题(本大题共4小题,共20.0分)13.在△ABC中,若sin A∶sin B∶sin C=2∶3∶4,则cos C=_______.14.设等比数列{a n}的前n项的和为S n,且满足S2=3,S3?S1=6,则a6=________.15.已知变量x,y满足约束条件,目标函数z=2x+y的最小值为?5,则实数a=_____,此时,z=y?2的取值范围是___________.x?416.如图,四边形ABCD中,AD=DC=3,BC=5,AB=8,∠DCB=120°,则四边形ABCD的面积为______.三、解答题(本大题共6小题,共70.0分)17.已知函数f(x)=|x+m|+|2x?n|,m,n∈(0,+∞).(Ⅰ)若f(x)≥1恒成立,求2m+n的最小值;(Ⅱ)若m=2,n=3,求不等式f(x)>5的解集.18.已知数列{a n}满足a1=1,a2=1,且[3+(?1)n]a n+2?2a n+2[(?1)n?1]=0.2(1)求a3,a4,a5,a6的值及数列{a n}的通项公式;(2)设b n=a2n?1a2n,求数列{b n}的前n项和S n.19. 已知在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,已知∠B =π12,c =b(1+2cosA),求角A .20. 如图,在△ABC,B =π3,BC =2,点D 在边AB 上AD =DC ,DE ⊥AC ,E为垂足.(1)若△BCD 的面积为√33,求CD 的长;(2)若ED =√62,求角A 的大小.21. 锐角三角形△ABC 中,内角A ,B ,C 所对边分别为a ,b ,c 三角形的面积S =54√63,sinA =√638. (1)求ABAC 的值;(2)若c ?b =1,求三角形的周长.22.已知数列{a n}满足a1=12,1a n+1=1a n+2(n∈N?).(Ⅰ)求数列{a n}的通项公式;(Ⅱ)证明:a12+a22+a32+?+a n2<12.-------- 答案与解析 --------1.答案:C解析:解:由数列√5,√11,√17,√23,…,可得被开方数5,11,17,23,……,是首项为5,公差为6的等差数列{a n}∴a n=5+6(n?1)=6n?1.令6n?1=125,解得n=21.则5√5是数列的第21项.故选:C.利用等差数列的通项公式即可得出.本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于基础题.2.答案:C解析:【分析】本题考查正弦定理余弦定理和三角形面积公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.首先利用余弦定理求出B的值,进一步判定三角形为等腰三角形,进一步利用面积公式的应用求出结果.【解答】解:△ABC的内角A,B,C的对边分别为a,b,c,且(a+b)2=c2+ab,整理得a2+b2?c2=?ab,所以cosC=a2+b2?c22ab =?12,由于0<c< bdsfid="219" p=""></c<>3.由于B=30°,a=4,则△ABC为等腰三角形,所以b=4,所以S△ABC=12?4?4?√32=4√3.故选:C.3.答案:B解析:【分析】本题考查了不等式的基本性质,考查了推理能力与计算能力,属于基础题.根据不等式的性质,分别判断即可求出.【解答】解:∵a<b<0,< bdsfid="234" p=""></b<0,<>∴|a|>|b|,aab <b< bdsfid="237" p=""></b<>ab,即1b<1a,a2>b2,因此A,C,D正确,对于B:取a=?3,b=?2,a?b=?1,此时1a?b <1b,因此B不正确,故选B.4.答案:B解析:解:∵等差数列{a n}中,a3+a11=6,∴其前13项的和:S13=132(a1+a13)=132×6=39.故选:B.由等差数列前n项和公式及通项公式得S13=13(a3+a11),由此能求出结果.本题考查等差数列的前13项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.5.答案:A解析:【分析】本题考查余弦定理,属于基础题型,因为BC=2√3,AC=5,∠C=30°,由余弦定理可得AB2=AC2+BC2?2AC?BC?cos?C,代入即可求解;【解答】解:因为BC=2√3,AC=5,∠C=30°,则AB2=AC2+BC2?2AC?BC?cosC=52+(2√3)2?2×5×2√3×√3 2=7,所以AB=√7.故选A.6.答案:D解析:【分析】本题主要考查基本不等式的应用,利用等差中项的定义建立a,b 的关系是解决本题的关键,属于中档题.根据等差中项的定义建立a,b的关系,然后利用基本不等式进行求解即可.【解答】解:是lg4a与lg2b的等差中项,∴2lg√2=lg4a+lg2b,即lg2=lg(4a·2b),∴4a·2b=22a+b=2,即2a+b=1,∵2a1b=(2a+1b)×1=(2a+1b)(2a+b)=4+1+2ba +2ab,又∵a>0,b>0,∴2a +1b≥5+2√2ba2ab=9,当且仅当2ba =2ab,即a=b=13时取等号,∴2a +1b的最小值为9.故选:D.7.答案:A解析:【分析】本题考查等比数列的性质的运用,属于中档题,根据等比数列的性质得到xz的乘积等于y的平方,由此求出y的值,进而求出xyz的值.【解答】解:由等比数列的性质得,y2=xz=(?1)×(?4)=4,∴y=?2,或y=2(正数不合题意舍去),∴xyz=4×(?2)=?8.故选A.8.答案:D解析:【分析】本题考察了两角和与差的三角函数公式,属于基础题.【解答】解:∵sin(θ+π4)=√22(sinθ+cosθ)=√26,∴sinθ+cosθ=13,∴sinθ·cosθ=(sinθ+cosθ)2?12=?49,∴sin4θ+cos4θ=(sin2θ+cos2θ)2?2(sinθcosθ)2=1?2×(?49)2=4981.故选D.9.答案:A解析:【分析】本题考查了等比数列的定义及其性质、对数的运算性质,考查了计算能力,属于基础题.数列{a n}满足a n+1=2a n,因此数列{a n}是等比数列,公比q=2.再利用等比数列的性质、对数的运算性质即可得出.【解答】解:∵log2a n+1=log2a n+1,∴a n+1=2a n,∴数列{a n}是等比数列,公比q=2.∵a2+a4+a6=4,∴a5+a7+a9=q3(a2+a4+a6)=8×4=25,则log3(a5+a7+a9)=log1225=?5.故选:A.10.答案:C解析:【分析】本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解答】解:由实数x,y满足约束条件{x?3y+4?03x?y?4?0x+y?0作出可行域如图,联立{x +y =03x ?y ?4=0,解得C(1,?1),化目标函数z =3x ?2y 为y =32x ?12z ,由图可知,当直线y =32x ?12z 过C(1,?1)时,直线在y 轴上的截距最大,即z 有最大值5.故选:C .11.答案:C解析:【分析】本题考查余弦定理的运用,属于基础题.由题意结合余弦定理可得cosC <0,所以C 为钝角,即可求解.【解答】解:由c 2?a 2?b 22ab>0可得cosC =a2+b2?c22ab<0,又C ∈(0,π),故C 为钝角,所以三角形一定为钝角三角形.故选C .12.答案:D解析:解:由题意可得,[(a 1?3)3+a 1?1]+[(a 2?3)3+a 2?1]+?+[(a 7?3)3+a 7?1]=14,∴[(a 1?3)3+a 1?3]+[(a 2?3)3+a 2?3]+?+[(a 7?3)3+a 7?3]=0,根据等差数列的性质可得(a 4?3?3d)3+(a 4?3?2d)3+?+(a 4?3+3d)3+7(a 4?3)=0,[(a4?3?3d)3+(a4?3+3d)3]+[(a4?3?2d)3+(a4?3+2d)3]+[(a4?3+d)3+(a4?3?d)3]+(a4?3)3+7(a4?3)=0,化简可得(a4?3)[7(a4?3)2+84d2+7]=0,∴a4?3=0,即a4=3.∴a1+a2+?+a7=7a4=21,故选:D.由题意可得[(a1?3)3+a1?3]+[(a2?3)3+a2?3]+?+[(a7?3)3+a7?3]=0,再利用等差数列的性质求得a4=3,从而求得a1+a2+?+a7的值.本题主要考查等差数列的定义和性质的应用,属于中档题.13.答案:?14解析:【分析】由正弦定理可得,可设其三边分别为2k,3k,4k,再由余弦定理求得cos C的值.本题考查正弦定理、余弦定理的应用,设出其三边分别为2k,3k,4k,是解题的关键.【解答】解:因为sin A∶sin B∶sin C=2∶3∶4,所以a:b:c=2:3:4,令a=2k,b=3k,c=4k,(k>0)所以cosC=a2+b2?c22ab =4k2+9k2?16k22×2k×3k=?14.故答案为?14.14.答案:32解析:【分析】本题主要考查等比数列的通项公式及前n项的和为S n,属于基础题,【解答】解:设等比数列{a n}的公比为q,因为S2=3?a1+a2=3,所以a1+a1q=3,因为S3?S1=6?a2+a3=6,所以a1q+a1q2=6,所以q=2,a1=1,则a6=a1q5=32,故答案为32.15.答案:?3;[?12,1314]解析:【分析】本题主要考查线性规划的应用,根据目标函数z =2x +y 的最小值为?5,确定平面区域的位置,利用数形结合是解决本题的关键.作出不等式组对应的平面区域,利用目标函数z =2x +y 的最小值为?5,建立条件关系即可求出a 的值和z 的范围.【解答】解:目标函数z =2x +y 的最小值为?5,∴y =?2x +z ,要使目标函数z =2x +y 的最小值为?5,则平面区域位于直线y =?2x +z 的右上方,可以求得2x +y =?5,作出变量x ,y 满足约束条件对应的平面区域如图:则目标函数经过点A ,由{2x +y =?5x ?y +1=0,解得A(?2,?1),同时A 也在直线x +y ?a =0上,即?2?1?a =0,解得a =?3, z =y?2x?4表示点过(x,y)与点(4,2)直线斜率,由{x ?y +1=02x ?y ?1=0得(2,3),当过(2,3)和(4,2)时斜率最小?1 2,由{x +y +3=02x ?y ?1=0得(?23,?73),过(?23,?73)和(4,2)时斜率最大1314,故答案为?3;[?12,1314].16.答案:39√34解析:【分析】本题考查了余弦定理,三角形面积公式,以及特殊角的三角函数值,是基础题,连接BD ,在三角形DCB 中,由DC ,BC 以及cos∠DCB 的值,利用余弦定理求出BD 的长,在三角形ABD 中,利用余弦定理表示出cosA,将三边长代入求出cosA的值,利用同角三角函数间的基本关系求出sinA的值,四边形ABCD的面积由三角形BCD 面积与三角形ABD面积之和求出即可.【解答】解:如下图所示,连接BD,在△BCD中,DC=3,BC=5,∠DCB=120°,利用余弦定理得:BD2=DC2+BC2?2DC?BCcos∠DCB=9+25+15=49,∴BD=7,在△ABD中,AD=3,AB=8,BD=7,由余弦定理得:cosA=AD2+AB2?BD22AD·AB =9+64?492×3×8=12,∴sinA=√1?cos2A=√32,则S四边形ABCD=S△BCD+S△ABD=12×3×5×√32+12×3×8×√32=39√34.故答案为39√34.17.答案:解:(Ⅰ)|x+m|+|2x?n|=|x+m|+|x?n2|+|x?n2|≥|x+m|+|x?n2|≥|m+n2|=m+n2,故m+n2≥1,2m+n≥2,2m+n的最小值是2;(Ⅱ)①当x≤?2时,?x?2?2x+3>5,得x3,故x≤?2,②当?2<x<3< bdsfid="517" p=""></x<3<>2时,x+2?2x+3>5,得x<0,故?2<x<0,< bdsfid="521" p=""></x<0,<>③当x≥32时,x+2+2x?3>5,得x>2,故x>2,综上,不等式解集为(?∞,0)∪(2,+∞).解析:(Ⅰ)根据基本不等式的性质求出代数式的最小值即可;(Ⅱ)通过讨论x的范围,求出各个区间上的不等式的解集,取并集即可.本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道中档题.18.答案:解:(1)由[3+(?1)n]a n+2?2a n+2[(?1)n?1]=0,计算得a 3=3,a 4=14,a 5=5,a 6=18. 当n 为奇数时,a n+2=a n +2,即数列{a n }的奇数项成等差数列,公差为2,∴a n =a 1+n?12×2=n ;当n 为偶数时,a n+2=12a n ;即数列{an}的偶数项成等比数列,公比为12,∴a n =a 2(12)n?22=(12)n 2.∴数列{an}的通项公式为(2)由(1),知b n =a 2n?1a 2n =(2n ?1)(12)n ,∴S n =1×12+3×(12)2+5×(12)3+?+(2n ?3)×(12)n?1+(2n ?1)×(12)n ,① 12S n =1×(12)2+3×(12)3+5×(12)4+?+(2n ?3)×(12)n +(2n ?1)×(12)n+1,② 由①?②,得12S n =12+2[(12)2+(12)3+?+(12)n ]?(2n ?1)×(12)n+1 =12+12[1?(12)n?1]1?12(2n ?1)×(12)n+1=32?(2n +3)×(12)n+1,∴S n =3?(2n +3)(12)n .解析:本题考查等比数列和等差数列的通项和求和公式的运用,同时考查错位相减法求数列的和,考查运算能力,属于中档题.(1)通过n =1,2,3,4,计算可得a 3,a 4,a 5,a 6的值,讨论n 为奇数和偶数,由等差数列和等比数列的通项即可得到数列{a n }的通项公式;(2)求出b n =(2n ?1)·(12)n,运用错位相减法,即可得到数列{b n }的前n 项和S n .19.答案:解:在△ABC 中,∠A 、∠B、∠C 的对边分别为a 、b 、c ,已知∠B =π12,c =b(1+2cosA),由正弦定理可得:sinC =sinB(1+2cosA)=sin π12(1+2cosA),∴sin(π12+A)=sinπ12(1+2cosA),即sin π12cosA +cos π12sinA =sin π12+2sin π12cosA ,∴cosπ12sinA ?sinπ12cosA =sin π12,∴sin(A ?π12)=sin π12.解得A ?π12=π12.∴A =π6.解析:利用已知条件,通过正弦定理以及B 的大小,化简方程为A 的三角函数的形式,求解即可.本题考查正弦定理的应用,两角和与差的三角函数,三角函数的化简求值,基本知识的考查.20.答案:解:(1)由已知在△ABC,B =π3,BC =2,得S △BCD =12BC ?BD ?sinB =√33,又B =π3,∴BD =23.在△BCD 中,由余弦定理得:CD 2=BC 2+BD 2?2BC ?BD ?cosB =289,∴CD =2√73. (2)在△CDE 中CDsin∠DEC =DEsin∠DCE ,∵AD =DC ,∴A =∠DCE ,∴CD =AD =DE sinA =√62sinA ,在△BCD 中BCsin∠BDC =CDsinB ,又∠BDC =2A ,得2sin2A =CD sinπ3,CD =√3sin2A ,∴CD =√62sinA=√3sin2A ,解得:cosA =√22,所以A =π4.解析:(1)直接利用已知条件,根据三角形的面积公式和余弦定理求出结果, (2)进一步利用正弦定理求出结果.本题考查的知识要点:三角形面积公式的应用,正弦和余弦定理的应用.21.答案:解:由已知可得,S =12bcsinA =12bc ×√638=5√634,∴bc =20,∵sinA =√638且A 为锐角,∴cosA =18,(1)AB ????? ?AC ????? =bccosA =20×18=52;(2)∵c ?b =1,bc =20,∴c =5,b =4,由余弦定理可得,cosA =18=b 2+c 2?a 22bc =25+16?a 22×5×4,∴a =6∴三角形的周长a +b +c =5+4+6=15.解析:由已知及三角形的面积公式S =12bcsinA 可求bc ,由sin A 结合同角平方关系可求cos A ,(1)AB ????? ?AC=bccosA ,代入可求; (2)由c ?b =1可求b ,c ,由余弦定理可得,cosA =18=b 2+c 2?a 22bc可求a ,进而可求三角形的周长.本题主要考查了三角形的面积公式,余弦定理等知识的简单应用,属于基础试题.22.答案:解:(Ⅰ)由数列{a n }满足a 1=12,1a n+1=1a n +2(n ∈N ?).可知数列{1a n}为等差数列,且首项为12,公差为2,故a n =12n .(Ⅱ)证明:依题可知a n2=(12n )2=14?1n 2<14?1n ?1n?1=14(1n?1?1n),n >1,所以a 12+a 22+a 32+?+a n 2<14(1+1?12+12?13+?+1n?1?1n )=14(2?1n )=12?14n ,故a 12+a 22+a 32+?+a n 2<12.解析:(Ⅰ)求数列{a n}的通项公式;(Ⅱ)化简数列的通项公式,通过裂项相消法数列的和即可.本题考查数列求和,数列的递推关系式的应用,考查计算能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学教学质量检测试题 理
考试时间:120分钟;满分:150分
参考公式:
第I 卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有
一项是符合题目要求的,把答案填在答题卡的相应位置。
1.i 是虚数单位,复数
1i
i
+等于
( ) A .1-i B .1+i C .-1+i
D .i
2.下列命题中是假命题...
的是
( )
A .000000,,sin()sin sin x y R x y x y ∃∈-=-
B .000,sin cos 2x R x x ∃∈+=
C .,30x
x R ∀∈>
D .00,lg 0x R x ∃∈=
3.在ABC ∆中,90,C =︒且CA=CB=3,点M 满足2BM MA =,
则CM CB ⋅等于 ( )
A .2
B .3
C .4
D .6
4.已知函数2,1,
1,1,
x x y x x ⎧≥=⎨-<⎩图中表示的是给定x 的值,求其对应
的函数值y 的程序框图,在图中①处应填写 ( ) A .1?x < B .1?x ≤
C .1?x >
D .1?x ≥
5.若变量x 、y 满足约束条件0,
34,20,x y x y x -≤⎧⎪
+≤⎨⎪+≥⎩
则2z x y =-的最大值是
( )
A .-6
B .-1
C .2
D .4
7.函数lg ||
x y x
=
的图象大致是
( )
8.若110a b <<,则下列不等式:①||||a b >;②;a b a b +<
③2;b a a b +>④2
2a a b b
<-中,正确的不等式有 ( ) A .1个 B .2个 C .3个
D .4个
9.有下列数组排成一排:
则该数列中的第2012项是
( )
A .
57
7
B .
586
C .
595
D .
604
10.若直角坐标平面内两点P ,Q 满足条件:①点P 在函数()y f x =的图象上;②点P 关于
直线y x =的对称点Q 在函数()y g x =图象上,则称点对(P ,Q )是两个函数的一
第II 卷(非选择题,共100分)
二、填空题:本大题共5小题,每小题4分,共20分。
把答案填在答题卡的相应位置。
11
.函数3()log (31)f x x =
+-的定义域为 。
12.右图是一个几何体的三视图,根据图中数据,可得该
几何体的表面积是 。
13.若抛物线2
2(0)y px p =->的焦点与双曲线2
213
x y -= 的左焦点重合,则p 的值为 。
14.设(]2,[0,1]
()1,1,x x f x x e x
⎧∈⎪
=⎨∈⎪⎩(e 为自然对数的底数),则0
()e f x dx ⎰的值
为 。
三、解答题:本大题共6小题,共80分。
解答写在答题卡相应位置,应写出文字说明、证
明过程或演算步骤。
16.(本小题满分13分)
已知函数()cos
cos()cos()4242
x x x
f x ππ=---,将函数()(0,)f x +∞在的所有极值点从小到大排成一数列,记为{}.n a
(1)求数列{}n a 的通项公式;
(2)令1
1
n n n b a a +=
⋅,求数列{}n b 前n 项和.n T
17.(本小题满分13分)
如图,在多面体ABCDE 中,
1
,//,
1,22
C B B E
D
E C B B A B C B A E
⊥===,平面ABE ⊥平面BCDE 。
(1)求证:;CB AB ⊥
(2)若F 为AC 中点,DF//平面ABE ,求二面角
A CD
B --的余弦值。
18.(本小题满分13分)
已知F 为椭圆22:12x C y +=的右焦点,过F 且斜率为2
-的直线l 与C 交于P 、Q 两
19.(本小题满分13分)
为支持福利事业,解决残疾人就业问题,银行决定给某福利企业免息贷款46.8万元,用于经营某种商品,已知该种商品的进价为每件40元,每月销售量q (单位:百件)
与销售价P (单位:元/件)之间满足关系式2140,4058,
82,5881,
p p q p p -+≤≤⎧=⎨
-+<≤⎩该企业职工
每人每月工资为1200元,其它经营性费用为每月13200元.
(I )如果暂时不考虑还贷的前提下,当销售价P 为52元/件时,每月刚好收支平衡,求该企业的职工人数;
(Ⅱ)若该企业只有20名职工,在保证职工工资及其他经营性支出外,剩余的利润都用来偿还贷款,试问最早几年后可还清贷款?,并求此时每件商品的销售价格.
20.(本小题满分14分)
21.(奉小题满分14分)本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题
作答,满分14分,如果多做,则按照所做的前两题计分. (1)(本小题满分7分)选修4-2:矩阵与变换
变换T 1是将每个点绕原点O 沿顺时针旋转
2
π
的旋转变换,对应的变换矩阵是M 1,变换T 2对应的变换矩阵是211.01M ⎛⎫
= ⎪⎝⎭
(I )写出矩阵M 1;
(Ⅱ)求曲线sin y x =依次在T 1,T 2变换的作用下所得的曲线方程
斜角).
(I )写出圆C 的直角坐标方程;
(Ⅱ)当直线l 与圆C 无公共点时,求α的取值范围.。
