黑龙江哈三中2013届高三第二次高考模拟考试文数 Word版含答案
黑龙江哈三中2013届高三第二次模拟数学理科试题

2013年哈尔滨市第三中学第二次高考模拟考试理科数学本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,共24题,满分150分,考试时间120分钟。
注意事项1.答题前,考生先将自己的姓名、准考证号码填写清楚;2.选择题必须使用2B 铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,字迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不得折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 集合{||1|2}A x x =-<,1{|39}3x B x =<<,则A B = A .(1,2)B .(1,2)-C .(1,3)D .(1,3)-2.设S n 是公差为(0)d d ≠的无穷等差数列{}n a 的前n 项和,则“d < 0”是“数列{}n S 有最大项”的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件3.ΔABC 中,(cos ,sin )m A A =,(cos ,sin )n B B =-,若12m n ⋅=,则角C 为 A .3π B .23π C .6π D .56π4.已知11ea dx x =⎰,则61()x ax-展开式中的常数项为 A .20B .-20C .-15D .155.正三棱柱ABC —A 1B 1C 1的所有棱长都为2,则异面直线AB 1与BC 1所成角的余弦值为A .12B .14C .23D .46.已知函数()sin())(0,||)2f x x x πωφωφωφ=++><,其图象相邻的两条对称轴方程为0x =与2x π=,则A .()f x 的最小正周期为2π,且在(0,)π上为单调递增函数B .()f x 的最小正周期为2π,且在(0,)π上为单调递减函数C .()f x 的最小正周期为π,且在(0,)2π上为单调递增函数 D .()f x 的最小正周期为π,且在(0,)2π上为单调递减函数7.一个几何体的三视图及尺寸如右图所示,则该几何体的 外接球半径为A .12B .16C .174D 8.过抛物线22(0)y px p =>的焦点F 的直线l 与抛物线在第一象限的交点为A ,直线l 与抛物线的准线的交点为B ,点A 在抛物线的准线上的摄影为C ,若AF F B = ,36BA BC ⋅=,则抛物线的方程为A .26y x =B .23y x =C .212y x =D .2y =9.阅读右面的程序框图,输出结果s 的值为A .12B .16C .116D .1810.在平行四边形ABCD 中,AE EB = ,2CF FB =,连接CE 、DF 相交于点M ,若AM AB AD λμ=+,则实数λ与μ的乘积为A .14B .38C .34D .4311.已知函数32()132x mx m n x y +++=+的两个极值点分别为x 1,x 2,且1(0,1)x ∈,2(1,)x ∈+∞,记分别以m ,n 为横、纵坐标的点(,)P m n 表示的平面区域为D ,若函数log (4)(1)a y x a =+>的图象上存在区域D 内的点,则实数a 的取值范围为A .(1,3]B .(1,3)C . (3,)+∞D .[3,)+∞12.设点P 在曲线x y e =上,点Q 在曲线11(0)y x x=->上,则||PQ 的最小值为 A.1)2e - B1)e -C.2D第II 卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分。
黑龙江省哈尔滨市第三中学2013年高三第二次高考模拟考试文综试题
黑龙江省哈尔滨市第三中学2013年高三第二次高考模拟考试文科综合第Ⅰ卷(选择题共140分)本卷共35小题,每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目题意的。
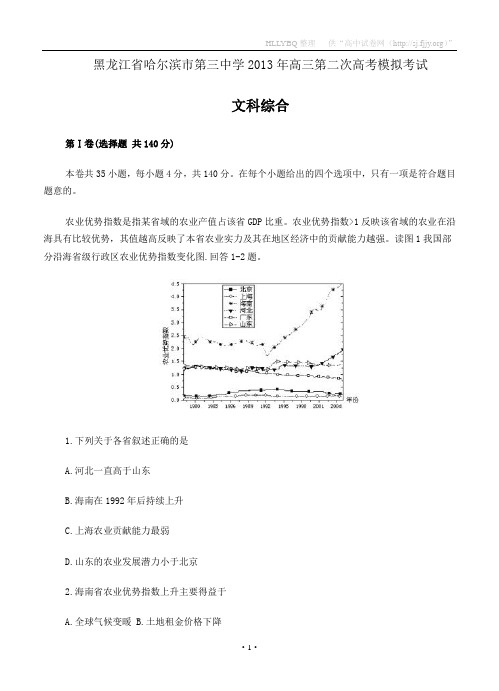
农业优势指数是指某省域的农业产值占该省GDP比重。
农业优势指数>1反映该省域的农业在沿海具有比较优势,其值越高反映了本省农业实力及其在地区经济中的贡献能力越强。
读图1我国部分沿海省级行政区农业优势指数变化图.回答1-2题。
1.下列关于各省叙述正确的是A.河北一直高于山东B.海南在1992年后持续上升C.上海农业贡献能力最弱D.山东的农业发展潜力小于北京2.海南省农业优势指数上升主要得益于A.全球气候变暖B.土地租金价格下降C.农业人口数量上升D.交通、科技和政策图2为某工业收益随空间变化曲线图,据此完成3-4题。
3.该工业可能是A.家具厂B.炼铝厂C.电子元件厂D.制糖厂4.图2中空间费用曲线由甲至丁先减后增的主导因素是A.地租费用、政策影响B.市场距离、工人工资C.工人工资、环境成本D.地租费用、交通费用图3为我国某城市功能分区的合理布局图,读图回答5-6题。
5.该城市的风向频率图可能是6.关于该城市功能区叙述错误的是A.①工业区的工业水污染较少B.②工业区的布置受交通通达度影响较大C.④住宅区平均房价高于③住宅区D.商业区的形成受行政因素影响最大人口红利是指一个国家的劳动年龄人口占总人口比重较大,抚养率比较低,为经济发展创造了有利的人口条件,人口红利拐点显现往往是人口红利消失的前兆,2012年我国劳动年龄人口在相当长时期里第一次出现了绝对下降。
图4为亚洲四个国家不同时期劳动年龄人口占总人口比重示意图.结合材料完成7-9题。
7.图4中甲乙丙丁所代表的国家分别是A. 日本越南中国印度B. 印度越南中国日本C. 印度越南日本中国D. 中国印度越南日本8.为了便于分析,人们认为总抚养比(14岁及以下少儿人口与65岁及以上老年人口之和除以15岁-64岁劳动年龄人口)小于50%的时期为人口红利期。
2013届高考语文模拟试卷及详细答案解析黑龙江哈三中2013届高三第二次模拟语文试题

2013年哈尔滨市第三中学第二次高考模拟考试语文试卷第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题。
在世界海权兴衰交替500余年的历史进程中,控制和利用海洋一直是世界大国追求的目标,海权构成了许多国家的战略追求,然而各国追求海权的历史命运却截然不同。
有的国家(英、美)通过发展海权实现了国家长久的强盛;有的(法、德)则惨遭失败乃至国运衰落;有的国家(英、美)的海权保持了长久的存在;有的(葡萄牙、西班牙、荷兰)则很快完成了从崛起到衰落的蜕变;还有的国家(如俄-苏)的海权追求一方面促进了国家崛起,但过度追求又埋下了国家衰落的根源。
海权在世界范围内兴起的历史机遇在于中世纪晚期出现的地理大发现,不同国家面对海洋的不同选择,尤其是东西方国家对历史机遇的不同把握,导致了不同的国家命运。
欧洲的一些国家抓住了历史机遇完成了国家崛起,而东方国家尤其是创造了郑和下西洋这一历史奇迹的中国,却与近代世界权势变革的历史机遇擦肩而过。
这一巨大差异无疑值得进行深刻反思。
世界历史表明,资本扩张与更新能力既是海权产生和发展的根本动力,也是决定海权能否长久存续与发展的支撑性要素。
同时,技术与制度创新能力、产业主导能力也是决定海权盛衰的重要因素。
在历史上,海上霸权国都分别主导了各自时代的技术革新,如葡萄牙的多桅帆船、荷兰的麦卡托航海图、英国的战列舰、美国的海军航空学等。
世界霸权国不仅是世界海军最强大的国家,同时也是世界经济领先产业的主导国。
由此可见,要成就大国海权,不仅需要足够强大的海军,而且还必须是世界科技的创新国,必须主导世界经济的领先产业。
因此,对于当下的中国而言,尤其要摆脱那种强调大国崛起离不开海权支撑,而忽视海权背后一系列复杂社会因素的简单化思维。
近年来,随着中国海洋安全环境的日趋复杂,中国的海军力量有了一定程度的发展,并积极应国际社会的要求实现了海军首次走出国门赴亚丁湾巡航。
而当前国际和国内社会,围绕中国海权发展动向及其可能产生的影响,均产生了激烈的争议。
2013哈三中二模文科数学及答案

2013年哈尔滨市第三中学第二次高考模拟考试数学试卷(文史类)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.)三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.2013年哈尔滨市第三中学第二次高考模拟考试数学试卷(文史类)答案及评分标准一、选择题:二、填空题:13. 1- 14. 2 15. []1,0 16. ]3,2三、解答题:17. (Ⅰ)整理得21=--n n a a ……………………………… 4分 又11=a 得12-=n a n ……………………………… 6分(Ⅱ) 由(1)知 )121121(21+--=n n b n …………………………… 8分所以12+=n n T n …………………………………… 12分18. (Ⅰ) 第六组08.0=p ···························2分 第七组06.0=p ··························4分 估计人数为180 ··························6分(Ⅱ) 设]190,185[组中三人为c b a ,,;]195,190[组中两人为n m ,则所有的可能性为()b a ,,()c a ,,()c b ,,()n m ,,()m a ,,()n a ,,()m b ,,()n b ,,()m c ,,()n c , ··························8分其中满足条件的为()b a ,,()c a ,,()c b ,,()n m ,···················10分故52104==p ··················· 12分19.(Ⅰ) ,//CD AB ,AD CD ⊥22===AB CD AD ,F 分别为CD 的中点,ABFD ∴为矩形,BF AB ⊥ ················· 2分 EF DC EC DE ⊥∴=, ,又EF AB CD AB ⊥∴,//⊥∴=AE E EF BF , 面BEF ,⊂AE 面ABE ,∴平面ABE ⊥平面BEF ····················· 4分(Ⅱ) EF DC EC DE ⊥∴=, ,又EF PD //,PD AB CD AB ⊥∴,//又PD AB ⊥,所以⊥AB 面PAD ,PA AB ⊥,⊥PA 面ABCD ··········6分 三棱锥PED B -的体积V =BCD E CED B V V --=22221=⨯⨯=∆BCD S ,到面BCD 的距离2a h =BCD E PED B V V --==]15152,1552[32231∈=⨯⨯a a ··········· 10分 可得]5152,552[∈a . ·············12 分 20. (Ⅰ)由已知⎪⎪⎩⎪⎪⎨⎧=+==+21143322222a c c b ab a 得42=a ,32=b ,方程为13422=+y x ···········3分 (Ⅱ)设),(),,(2211y x B y x A ,则)3,2(),3,2(2211y x Q y x P(1)当直线l 的斜率存在时,设方程为m kx y +=⎪⎩⎪⎨⎧=++=13422y x m kx y 联立得:0)3(48)43(222=-+++m kmx x k 有⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=+-=+>-+=∆22212212243)3(44380)43(48km x x k kmx x m k ①由以PQ 为直径的圆经过坐标原点O 可得:0432121=+y y x x · 整理得:04)(4)43(221212=++++m x x km x x k ②将①式代入②式得:22243m k =+, ··········· 6 分048,0,043222>=∆>∴>+m m k又点O 到直线m kx y +=的距离21km d +=2222222221223414334143433411mm kkm kkmkkx x kAB ⋅+=+⋅+=+-++=-+=·········· 8 分所以32322122===∆mm d AB S OAB ·········· 10 分 (2) 当直线l 的斜率不存在时,设方程为m x =(22<<-m ) 联立椭圆方程得:4)4(322m y -=代入0432121=+y y x x 得到04)4(3322=--m m 即552±=m ,5152±=y3212121=-==∆y y m d AB S OAB综上:OAB ∆的面积是定值3 ,又ODE ∆的面积33221=⨯⨯=,所以二者相等. ········· 12 分21. (Ⅰ)x x f x x x x f a ln )(,ln )(,0/-=-==, 1,0)(/==x x f ···········1分)上是增函数,在(10)(,0)(),1,0(/x f x f x >∈)上是减函数在(),(+∞<∞+∈,1)(,0)(,1/x f x f x ···········4分(Ⅱ)由原式b x x x ≥--⇔ln 11令xx xx g ln 11)(--=,可得)(x g 在(]1,0上递减,在[)+∞,1上递增∴0)1()(min ==g x g ·········7分即0≤b ·································8分(Ⅲ)由(Ⅱ)知xxx g ln 11)(+-=在(0,1)上单调递减∴11<<<y x e时,)()(y g x g >即yyx x ln 1ln 1+<+ ·································10分而11<<<y x e时,0ln 1,0ln 1>+∴<<-x x ··················11分 x yxy ln 1ln 1++<∴································12分22.(I )∵EC EF DE ⋅=2,∴C EDF ∠=∠,又∵C P ∠=∠,∴P EDF ∠=∠,∴EDF ∆∽PAE ∆∴EP EF ED EA ⋅=⋅又∵EB CE ED EA ⋅=⋅,∴EP EF EB CE ⋅=⋅···5分 (II )3=BE ,29=CE ,415=BPPA 是⊙O 的切线,PC PB PA⋅=2,4315=PA ·······10分23.(Ⅰ)圆C 的极坐标方程为:)4sin(22πθρ+= ········· 5 分(Ⅱ)圆心到直线距离为1,圆半径为2,所以弦长为2 ··········· 10分 24.(Ⅰ)0)(>x f 的解集为:),32()4,(+∞⋃--∞ ·········· 5分(Ⅱ)213-<a ·········· 10 分。
黑龙江哈三中2013届高三第二次高考模拟考试理科数学试题

2013年哈尔滨市第三中学第二次高考模拟考试理科数学本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,共24题,满分150分,考试时间120分钟。
注意事项1.答题前,考生先将自己的姓名、准考证号码填写清楚;2.选择题必须使用2B 铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,字迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不得折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 集合{||1|2}A x x =-<,1{|39}3x B x =<<,则A B = A .(1,2)B .(1,2)-C .(1,3)D .(1,3)-2.设S n 是公差为(0)d d ≠的无穷等差数列{}n a 的前n 项和,则“d < 0”是“数列{}n S 有最大项”的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件3.ΔABC 中,(cos ,sin )m A A =,(cos ,sin )n B B =-,若12m n ⋅=,则角C 为 A .3π B .23π C .6π D .56π4.已知11ea dx x =⎰,则61()x ax-展开式中的常数项为 A .20B .-20C .-15D .155.正三棱柱ABC —A 1B 1C 1的所有棱长都为2,则异面直线AB 1与BC 1所成角的余弦值为A .12B .14C .23D .46.已知函数()sin())(0,||)2f x x x πωφωφωφ=++><,其图象相邻的两条对称轴方程为0x =与2x π=,则A .()f x 的最小正周期为2π,且在(0,)π上为单调递增函数B .()f x 的最小正周期为2π,且在(0,)π上为单调递减函数C .()f x 的最小正周期为π,且在(0,)2π上为单调递增函数 D .()f x 的最小正周期为π,且在(0,)2π上为单调递减函数7.一个几何体的三视图及尺寸如右图所示,则该几何体的 外接球半径为A .12 B .16C .174D 8.过抛物线22(0)y px p =>的焦点F 的直线l 与抛物线在第一象限的交点为A ,直线l 与抛物线的准线的交点为B ,点A 在抛物线的准线上的摄影为C ,若AF FB = ,36BA BC ⋅=,则抛物线的方程为A .26y x =B .23y x =C .212y x =D .2y =9.阅读右面的程序框图,输出结果s 的值为A .12 B .16C .116D .1810.在平行四边形ABCD 中,AE EB = ,2CF FB =,连接CE 、DF 相交于点M ,若AM AB AD λμ=+,则实数λ与μ的乘积为A .14B .38C .34D .4311.已知函数32()132x mx m n x y +++=+的两个极值点分别为x 1,x 2,且1(0,1)x ∈,2(1,)x ∈+∞,记分别以m ,n 为横、纵坐标的点(,)P m n 表示的平面区域为D ,若函数log (4)(1)a y x a =+>的图象上存在区域D 内的点,则实数a 的取值范围为A .(1,3]B .(1,3)C . (3,)+∞D .[3,)+∞12.设点P 在曲线x y e =上,点Q 在曲线11(0)y x x=->上,则||PQ 的最小值为 A1)e - B1)e -CD第II 卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分。
东北三校2013届高三第二次高考模拟考试 文科数学 Word版含答案

2013年哈师大附中第二次高考模拟考试文科数学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分,考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正液、刮纸刀。
第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{|||3},||1}A x x B x y x =<==-,则集合为A .[0,3)B .[1,3)C .(1,3)D .(-3,1]2.已知i 为虚数单位,且15||22ai i +=则实数a 的值为 A .1B .2C .1或-1D .2或-23.双曲线2213y x -=的渐进线方程为 A .3y x =±B .33y x =±C .2y x =±D .233y x =±4.以下有关线性回归分析的说法不正确...的是 A .通过最小二乘法得到的线性回归直线过样本点的中心(,)x yB .用最小二乘法求回归直线方程,是寻求使()21niii y bx a =--∑最小的a 、b 的值C .相关系数r 越小,表示两个变量相关性越弱D .()2^21211ni i i ni i y y R y y==⎛⎫- ⎪⎝⎭=--∑∑与接近1.表示回归的效果越好 5.直角坐标系中坐标原点O 关于直线l:2tan 10x a y +-=的对称点为A (1,1),则tan2a 的值为A .43-B .43C .1D .456.已知点D 为等腰直角三角形ABC 斜边AB 的中点,则下列等式中不恒..成立的是 A .||||CA CBCD CA CB =+B .AC AC AB =C .BC BC BA =D .()()0CA CB CA CB +-=7.若S n 是等比数列{a n }的前n 项和,a 2 a 4= a 3, S 3 = 7则数列{a n }的公比q 的值为A .12B .12-或13C .12或13- D .138.三棱柱ABC-A 1B 1C 1的底面是边长为3的正三角形,侧棱AA 1⊥底面ABC ,若球O 与各三棱柱ABC-A 1B 1C 1各侧面、底面均相切,则侧棱AA 1的长为A .12B .32C .1D .39.下列判断中正确的是A .命题“若1a b -=,则2212ab +>”是真命题B .“114a b +=”的必要不充分条件是“12a b ==”C .命题“若12a a +=,则1a =”的逆否命题是“若1a =则12a a+≠”D .命题“2,12a R aa ∀∈+≥”的否定式“2,12a R a a ∃∈+<”10.某几何体的三视图如图所示,则该几何体的表面积为A .332+ B .832+C .662+D .1162+11.已知圆M 过定点(2,0),且圆心M 在24y x =抛物线上运动,若y 轴截圆M 所得弦为AB ,则弦长|AB|等于A .4B .3C .2D .与点M 位置有关12.当0a >时,函数2()(2)x f x x ax e =-的图像大致是第II 卷(非选择题,共90分)本卷包括必考题和选考题两部分。
2013年高考理科数学二模试题(哈三中有答案)

2013年高考理科数学二模试题(哈三中有答案)2013年哈尔滨市第三中学第二次高考模拟考试理科数学本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共24题,满分150分,考试时间120分钟。
注意事项1.答题前,考生先将自己的姓名、准考证号码填写清楚;2.选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,字迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不得折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第I卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合,,则A.B.C.D.2.设Sn是公差为的无穷等差数列的前n项和,则“dA.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件3.ΔABC中,,,若,则角C为A.B.C.D.4.已知,则展开式中的常数项为A.20B.-20C.-15D.155.正三棱柱ABC—A1B1C1的所有棱长都为2,则异面直线AB1与BC1所成角的余弦值为A.B.C.D.6.已知函数,其图象相邻的两条对称轴方程为与,则A.的最小正周期为,且在上为单调递增函数B.的最小正周期为,且在上为单调递减函数C.的最小正周期为,且在上为单调递增函数D.的最小正周期为,且在上为单调递减函数7.一个几何体的三视图及尺寸如右图所示,则该几何体的外接球半径为A.B.C.D.8.过抛物线的焦点F的直线l与抛物线在第一象限的交点为A,直线l 与抛物线的准线的交点为B,点A在抛物线的准线上的摄影为C,若,,则抛物线的方程为A.B.C.D.9.阅读右面的程序框图,输出结果s的值为A.B.C.D.10.在平行四边形ABCD中,,,连接CE、DF相交于点M,若,则实数λ与μ的乘积为A.B.C.D.11.已知函数的两个极值点分别为x1,x2,且,,记分别以m,n为横、纵坐标的点表示的平面区域为D,若函数的图象上存在区域D内的点,则实数a的取值范围为A.B.C.D.12.设点P在曲线上,点Q在曲线上,则的最小值为A.B.C.D.第II卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分。
2013年哈尔滨市第三中学第二次高考模拟考试 数学试卷(理工类)

2013年哈尔滨市第三中学第二次高考模拟考试数学试卷(理工类)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.)三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.2013年哈尔滨市第三中学第二次高考模拟考试数学试卷(理工类)答案及评分标准一、选择题:二、填空题: 13.1- 14. 2 15. []1,0 16. ]3,2三、解答题: 17. (Ⅰ)整理得21=--n n a a ……………………………… 4分又11=a 得12-=n a n ……………………………… 6分(Ⅱ)由(1)知)121121(21+--=n n b n …………………………… 8分所以12+=n nT n…………………………………… 12分 18. 解: (Ⅰ) 第六组08.0=p ···························2分 第七组06.0=p ···························4分 估计人数为180 ··························6分 (Ⅱ)X 可能的取值为0,1, 2, 3. ························7分 425)0(3935===C C x P4220)1(392514===C C C x P4215)2(391524===C C C x P 422)3(3934===C C x P所以X 的分布列·············10分)(X E =34. ····················· 12分 19.(Ⅰ),//CD AB ,AD CD ⊥22===AB CD AD ,F 分别为CD 的中点,ABFD ∴为矩形,BF AB ⊥ ················· 2分 EF DC EC DE ⊥∴=, ,又EF AB CD AB ⊥∴,// ⊥∴=AE E EF BF , 面BEF ,⊂AE 面ABE ,∴平面ABE ⊥平面BEF ····················· 4分(Ⅱ) EF DC EC DE ⊥∴=, ,又EF PD //,PD AB CD AB ⊥∴,//又PD AB ⊥,所以⊥AB 面PAD ,PA AB ⊥ ··················6分 法一:建系AB 为x 轴,AD 为y 轴,AP 为z 轴,)0,2,0(),0,0,1(D B ),0,0(a P ,)0,2,2(C ,)2,1,1(aE平面BCD 法向量1(0,0,1)n =,平面EBD 法向量)2,,2(2-=a a n ··········9分]22,21[452cos 2∈+=a θ,可得]5152,552[∈a . ·············12分 法二:连AC 交BF 于点K ,四边形ABCF 为平行四边形,所以K 为AC 的中点,连EK ,则PA EK //,⊥EK 面ABCD ,EK BD ⊥, 作BD KH ⊥于H 点,所以⊥BD 面EKH ,连EH ,则EH BD ⊥,EHK ∠即为所求 ············· 9分在EHK Rt ∆中,515221=⨯=HK ,]3,1[25512tan ∈==a aθ解得]5152,552[∈a ·············12 分 20. (Ⅰ)由已知⎪⎪⎩⎪⎪⎨⎧=+==+21143322222a c c b ab a 解得42=a ,32=b ,方程为13422=+y x ·······3 分 (Ⅱ) 设),(),,(2211y x B y x A ,则)3,2(),3,2(2211y x Q y x P (1)当直线l 的斜率存在时,设方程为m kx y +=⎪⎩⎪⎨⎧=++=13422y x mkx y 联立得:0)3(48)43(222=-+++m kmx x k 有⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=+-=+>-+=∆22212212243)3(44380)43(48k m x x k km x x m k ① 由以PQ 为直径的圆经过坐标原点O 可得:0432121=+y y x x ·整理得:04)(4)43(221212=++++m x x km x x k ②将①式代入②式得:22243m k =+, ··········· 6 分 048,0,043222>=∆>∴>+m m k又点O 到直线m kx y +=的距离21km d+=2222222221223414334143433411m m kk m kk m k k x x k AB ⋅+=+⋅+=+-++=-+=·········· 8 分所以32322122===∆mm d AB S OAB ·········· 10 分 (2) 当直线l 的斜率不存在时,设方程为m x =(22<<-m )联立椭圆方程得:4)4(322m y -=代入0432121=+y y x x 得到04)4(3322=--m m 即552±=m ,5152±=y3212121=-==∆y y m d AB S OAB 综上:OAB ∆的面积是定值3又ODE ∆的面积33221=⨯⨯=,所以二者相等. ·······12分 21. (Ⅰ) 由原式b x xx ≥--⇔ln 11, ················ 1分令xxx x g ln 11)(--=,可得)(x g 在(]1,0上递减,在[)+∞,1上递增,所以0)1()(min ==g x g即0≤b ···············3分(Ⅱ))0(,ln 2)(>-='x x ax x f x x a x f ln 2,0)(≥≥'得令,x x x h ln )(=设,时当e x =e x h 1)(max=e a 21≥∴当时,函数)(x f 在),0(+∞单调递增 ···············5分e a 210<<若,x a x g x x ax x g 12)(),0(,ln 2)('-=>-=a x x g 21,0)('==,0)(),,21(,0)(),21,0(//>+∞∈<∈x g a x x g a xax 21=∴时取得极小值即最小值时而当e a 210<< 021ln 1)21(<-=aa g , 必有根0)(/=x f ,)(x f 必有极值,在定义域上不单调··············8分 ea 21≥∴ ················9分(Ⅲ)由(I)知xxx g ln 11)(+-=在(0,1)上单调递减∴11<<<y x e 时,)()(y g x g >即y y x x ln 1ln 1+<+ ················ 10分 而11<<<y x e时,0ln 1,0ln 1>+∴<<-x x x y x y ln 1ln 1++<∴ ··············· 12分 22.(I )∵EC EF DE ⋅=2,∴C EDF ∠=∠,又∵C P ∠=∠,∴P EDF ∠=∠,∴EDF ∆∽PAE ∆∴EP EF ED EA ⋅=⋅又∵EB CE ED EA ⋅=⋅,∴EP EF EB CE ⋅=⋅···5分 (II )3=BE ,29=CE ,415=BP PA 是⊙O 的切线,PC PB PA ⋅=2,4315=PA ·······10分 23.(Ⅰ)圆C 的极坐标方程为:)4sin(22πθρ+= ·········5 分(Ⅱ)圆心到直线距离为1,圆半径为2,所以弦长为2 ··········· 10分24.(Ⅰ)0)(>x f 的解集为:),32()4,(+∞⋃--∞ ·········· 5分(Ⅱ)213-<a ·········· 10 分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年哈尔滨市第三中学第二次高考模拟考试数学试卷(文史类)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.)三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.2013年哈尔滨市第三中学第二次高考模拟考试数学试卷(文史类)答案及评分标准一、选择题:二、填空题:13. 1- 14. 2 15. []1,0 16. ]3,2三、解答题:17. (Ⅰ)整理得21=--n n a a ……………………………… 4分 又11=a 得12-=n a n ……………………………… 6分(Ⅱ) 由(1)知 )121121(21+--=n n b n …………………………… 8分所以12+=n n T n …………………………………… 12分18. (Ⅰ) 第六组08.0=p ···························2分 第七组06.0=p ··························4分 估计人数为180 ··························6分(Ⅱ) 设]190,185[组中三人为c b a ,,;]195,190[组中两人为n m ,则所有的可能性为()b a ,,()c a ,,()c b ,,()n m ,,()m a ,,()n a ,,()m b ,,()n b ,,()m c ,,()n c , ··························8分其中满足条件的为()b a ,,()c a ,,()c b ,,()n m ,···················10分故52104==p ··················· 12分19.(Ⅰ) ,//CD AB ,AD CD ⊥22===AB CD AD ,F 分别为CD 的中点,ABFD ∴为矩形,BF AB ⊥ ················· 2分 EF DC EC DE ⊥∴=, ,又EF AB CD AB ⊥∴,//⊥∴=AE E EF BF , 面BEF ,⊂AE 面ABE ,∴平面ABE ⊥平面BEF ····················· 4分(Ⅱ) EF DC EC DE ⊥∴=, ,又EF PD //,PD AB CD AB ⊥∴,//又PD AB ⊥,所以⊥AB 面PAD ,PA AB ⊥,⊥PA 面ABCD ··········6分 三棱锥PED B -的体积V =BCD E CED B V V --=22221=⨯⨯=∆BCD S ,到面BCD 的距离2a h =BCD E PED B V V --==]15152,1552[32231∈=⨯⨯a a ··········· 10分 可得]5152,552[∈a . ·············12 分 20. (Ⅰ)由已知⎪⎪⎩⎪⎪⎨⎧=+==+21143322222a c c b ab a 得42=a ,32=b ,方程为13422=+y x ···········3分 (Ⅱ)设),(),,(2211y x B y x A ,则)3,2(),3,2(2211y x Q y x P(1)当直线l 的斜率存在时,设方程为m kx y +=⎪⎩⎪⎨⎧=++=13422y x m kx y 联立得:0)3(48)43(222=-+++m kmx x k 有⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=+-=+>-+=∆22212212243)3(44380)43(48km x x k kmx x m k ①由以PQ 为直径的圆经过坐标原点O 可得:0432121=+y y x x · 整理得:04)(4)43(221212=++++m x x km x x k ②将①式代入②式得:22243m k =+, ··········· 6 分048,0,043222>=∆>∴>+m m k又点O 到直线m kx y +=的距离21km d +=2222222221223414334143433411mm kkm kkmkkx x kAB ⋅+=+⋅+=+-++=-+=·········· 8 分所以32322122===∆mm d AB S OAB ·········· 10 分 (2) 当直线l 的斜率不存在时,设方程为m x =(22<<-m ) 联立椭圆方程得:4)4(322m y -=代入0432121=+y y x x 得到04)4(3322=--m m 即552±=m ,5152±=y3212121=-==∆y y m d AB S OAB综上:OAB ∆的面积是定值3 ,又ODE ∆的面积33221=⨯⨯=,所以二者相等. ········· 12 分21. (Ⅰ)x x f x x x x f a ln )(,ln )(,0/-=-==, 1,0)(/==x x f ···········1分)上是增函数,在(10)(,0)(),1,0(/x f x f x >∈)上是减函数在(),(+∞<∞+∈,1)(,0)(,1/x f x f x ···········4分(Ⅱ)由原式b x x x ≥--⇔ln 11令xx xx g ln 11)(--=,可得)(x g 在(]1,0上递减,在[)+∞,1上递增∴0)1()(min ==g x g ·········7分即0≤b ·································8分(Ⅲ)由(Ⅱ)知xxx g ln 11)(+-=在(0,1)上单调递减∴11<<<y x e时,)()(y g x g >即yyx x ln 1ln 1+<+ ·································10分而11<<<y x e时,0ln 1,0ln 1>+∴<<-x x ··················11分 x yxy ln 1ln 1++<∴································12分22.(I )∵EC EF DE ⋅=2,∴C EDF ∠=∠,又∵C P ∠=∠,∴P EDF ∠=∠,∴EDF ∆∽PAE ∆∴EP EF ED EA ⋅=⋅又∵EB CE ED EA ⋅=⋅,∴EP EF EB CE ⋅=⋅···5分 (II )3=BE ,29=CE ,415=BPPA 是⊙O 的切线,PC PB PA⋅=2,4315=PA ·······10分23.(Ⅰ)圆C 的极坐标方程为:)4sin(22πθρ+= ········· 5 分(Ⅱ)圆心到直线距离为1,圆半径为2,所以弦长为2 ··········· 10分 24.(Ⅰ)0)(>x f 的解集为:),32()4,(+∞⋃--∞ ·········· 5分(Ⅱ)213-<a ·········· 10 分。
