高中数学必修四期末试题
(常考题)北师大版高中数学必修四第一章《三角函数》测试题(答案解析)(2)
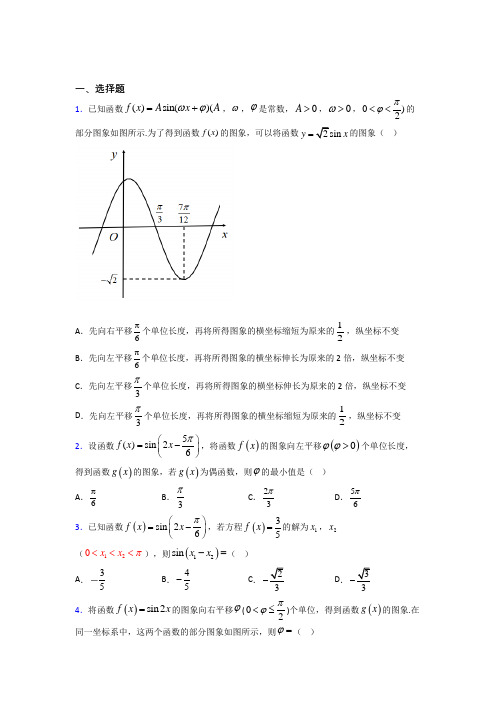
一、选择题1.已知函数()sin()(f x A x A ωϕ=+,ω,ϕ是常数,0A >,0>ω,0)2πϕ<<的部分图象如图所示.为了得到函数()f x 的图象,可以将函数2sin y x =的图象( )A .先向右平移6π个单位长度,再将所得图象的横坐标缩短为原来的12,纵坐标不变 B .先向左平移6π个单位长度,再将所得图象的横坐标伸长为原来的2倍,纵坐标不变 C .先向左平移3π个单位长度,再将所得图象的横坐标伸长为原来的2倍,纵坐标不变 D .先向左平移3π个单位长度,再将所得图象的横坐标缩短为原来的12,纵坐标不变2.设函数5()sin 26f x x π⎛⎫=- ⎪⎝⎭,将函数()f x 的图象向左平移()0ϕϕ>个单位长度,得到函数()g x 的图象,若()g x 为偶函数,则ϕ的最小值是( ) A .6πB .3π C .23π D .56π 3.已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭,若方程()35f x =的解为1x ,2x (120x x π<<<),则()12sin x x -=( ) A .35B .45-C .23-D .34.将函数()sin 2f x x =的图象向右平移ϕ(02πϕ<≤)个单位,得到函数()g x 的图象.在同一坐标系中,这两个函数的部分图象如图所示,则ϕ=( )A .6π B .4π C .3π D .2π 5.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称 C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 6.已知函数()tan()0,02f x x πωϕϕω⎛⎫=+<<< ⎪⎝⎭最小正周期为2π,且()f x 的图象过点,03π⎛⎫⎪⎝⎭,则方程()sin 2([0,])3f x x x π⎛⎫=+∈π ⎪⎝⎭所有解的和为( )A .76πB .56π C .2πD .3π 7.函数()3sin 22xf x x =-的部分图象大致为( ) A . B .C .D .8.现有四个函数:①y =x |sin x |,②y =x 2cos x ,③y =x ·e x ;④1y x x=+的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )A .①②③④B .①③②④C .②①③④D .③②①④9.:sin 31p x x +>的一个充分不必要条件是( ) A .02x π<<B .203x π<<C .32x ππ-<<D .566x ππ<<10.已知函数()tan()0,2f x x πωϕωϕ⎛⎫=+≠<⎪⎝⎭,点2,03π⎛⎫⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则ϕ=( ) A .6π B .6π-C .3π D .3π-11.将函数()3sin()2f x x =--图象上每一点的纵坐标不变,横坐标缩短为原来的13,再向右平移29π个单位得到函数()g x 的图象,若()g x 在区间,18πθ⎡⎤-⎢⎥⎣⎦上的最大值为1,则θ的最小值为( )A .12πB .6πC .3π D .18π 12.函数()()sin ln 0=->f x x x ωω只有一个零点,则实数ω的取值范围是( ) A .()0,πB .5,2⎫⎛⎪⎝⎭ππe C .50,2⎫⎛ ⎪⎝⎭πe D .5,2⎫⎛∞⎪⎝⎭π+e二、填空题13.已知函数cos ,[],y a x x ωππ=+∈-(其中,a ω为常数,且0>ω)有且仅有3个零点,则ω的最小值是_________. 14.以下关于函数()()21sin 324f x x x R π⎛⎫=-∈ ⎪⎝⎭的结论: ①()y f x =的图象关于直线2x π=-对称; ②()f x 的最小正周期是4π;③()y f x =在区间[]2,3ππ上是减函数; ④()y f x =的图象关于点,02π⎛⎫- ⎪⎝⎭对称.其中正确的结论是__________________(写出所有正确结论的序号).15.已知函数()f x x ω=-(0>ω)的图象关于点3,04π⎛⎫⎪⎝⎭对称,且()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,则ω的值为______.16.已知tan22α=,则sin()2πα+=_______. 17.函数()3sin 23f x x π⎛⎫=- ⎪⎝⎭的图象为C ,以下结论中正确的是______(写出所有正确结论的编号). ①图象C 关于直线1112π=x 对称; ②图象C 关于点2,03π⎛⎫⎪⎝⎭对称; ③函数()f x 在区间5,1212ππ⎛⎫-⎪⎝⎭内是增函数; ④由3sin 2y x =的图象向右平移3π个单位长度可以得到图象C . 18.已知如下变换:①将图象上各点的横坐标伸长到原来的2倍,纵坐标保持不变; ②将图象上各点的横坐标缩短到原来的12倍,纵坐标保持不变; ③将图像整体向右平移3π个单位长度; ④将图像整体向右平移6π个单位长度;⑤将图像整体向左平移3π个单位长度; ⑥将图像整体向左平移6π个单位长度; 要得到函数sin(2)3y x π=-的图象,只需将函数sin y x =的图象经过变换____________(填上你认为正确的一种情况即可,注意编号顺序) 19.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.20.在①()f x 的图像关于直线56x πω=对称,②()cos 3sin f x x x ωω=-,③()(0)f x f ≤恒成立这三个条件中任选一个,补充在下面问题中.若问题中的ω存在,求出ω的值,若ω不存在,请说明理由. 设函数()2cos()(0,0)2f x x πωϕωϕ=+>≤≤,________,是否存在正整数ω,使得函数()f x 在[0,]2π上是单调的?三、解答题21.已知函数()()1sin 226f x x x R π⎛⎫=+∈ ⎪⎝⎭. (1)填写下表,并用“五点法”画出()f x 在[0,]π上的图象;26x π+6π 136πxπ()f x(2)将()y f x =的图象向上平移1个单位,横坐标缩短为原来的2,再将得到的图象上所有点向右平移4π个单位后,得到()g x 的图象,求()g x 的对称轴方程. 22.已知函数21()3sin cos cos 2222x x x f x =++. (1)求函数()f x 的最小正周期;(2)将函数()y f x =的图象上的各点向左平移32π个单位,再保持纵坐标不变,横坐标缩短到原来的一半;得到函数()y g x =的图象,求函数()y g x =的最大值及取得最大值时x 的取值集合.23.已知函数()()2sin f x x ωϕ=+(0>ω,0ϕπ<<)的最大值和最小正周期相同,()f x 的图象过点()0,3,且在区间10,12⎡⎤⎢⎥⎣⎦上为增函数.(1)求函数()f x 的解析式;(2)若函数()()1g x f x =+在区间()0,b 上只有4个零点,求b 的最大值. 24.函数()sin()f x A x ωϕ=+(0,0,[0,2))A ωϕπ>>∈的图象如图所示:(1)求()f x 的解析式; (2)()f x 向左平移12π个单位后得到函数()g x ,求()g x 的单调递减区间;(3)若,2x ππ⎡⎤∈-⎢⎥⎣⎦且()32f x ≥,求x 的取值范围.25.已知712sin cos 2225ππαα⎛⎫⎛⎫---+= ⎪ ⎪⎝⎭⎝⎭,其中0,4πα⎛⎫∈ ⎪⎝⎭.(1)求tan α的值;(2)求3sin sin 3cos ααα-的值.26.已知函数()()sin f x A x =+ωϕ(0A >,0>ω)的图像是由3y x πω⎛⎫=+ ⎪⎝⎭的图像向右平移3π个单位得到的.(1)若()f x 的最小正周期为π,求()f x 的与y 轴距离最近的对称轴方程;(2)若()f x 在,2ππ⎡⎤⎢⎥⎣⎦上仅有一个零点,求ω的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】先根据函数图象求出函数()f x 的解析式,由三角函数图象的变换即可求解. 【详解】 由图可知,1741234A T πππ==-=,, 所以T π=,即2ππω=,解得2ω=.当712x π=时,73π22π,122k k Z πϕ⨯+=+∈, 所以 2,3k k Z πϕπ=+∈又2πϕ<,所以3πϕ=.所以()23f x x π⎛⎫=+ ⎪⎝⎭.将y x =的图象先向左平移3π个单位长度,得到)3y x π=+,.再将所得图象的横坐标缩短为原来的12,纵坐标不变,得到())3f x x π=+. 故选:D 【点睛】易错点点睛:图象变换的两种方法的区别,由sin y x =的图象,利用图象变换作函数()()()sin 0,0y A x A x R ωϕω=+>>∈的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象沿x 轴的伸缩量的区别.先平移变换再周期变换(伸缩变换),平移的量是|φ|个单位,而先周期变换(伸缩变换)再平移变换,平移的量是ϕω个单位. 2.A解析:A 【分析】根据题意有()5sin 226g x x ϕπ⎛⎫=+ ⎪⎝⎭-,若()g x 为偶函数则52()62k k Z πππϕ-=+∈,结合0ϕ>可得出答案. 【详解】 解:由题意可得()()55()sin 2sin 2266g x f x x x πϕϕϕπ⎛⎫⎛⎫=+=+-=+ -⎪⎪⎝⎭⎝⎭因为()g x 为偶函数,则52()62k k Z πππϕ-=+∈,即2()32k k Z ππϕ=+∈ 因为0ϕ>,所以当1k =-时ϕ取得最小值6π. 故选:A. 【点睛】应用函数奇偶性可解决的四类问题及解题方法(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解;(2)求解析式:先将待求区间上的自变量转化到已知区间上,再利用奇偶性求解,或充分利用奇偶性构造关于()f x 的方程(组),从而得到()f x 的解析式;(3)求函数解析式中参数的值:利用待定系数法求解,根据()()0f x f x ±-=得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值; (4)画函数图象和判断单调性:利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.3.B解析:B 【分析】求出函数()f x 在(0,)π上的对称轴,然后由正弦函数性质得1223x x π+=,这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭,而已知条件为23sin(2)65x π-=,再由正弦函数性质确定226x π-的范围,从而由平方关系求得结论.【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足:()262x k k Z πππ-=+∈,即()23k x k Z ππ=+∈,令0k =可得函数在区间()0,π上的一条对称轴为3x π=,结合三角函数的对称性可知1223x x π+=,则:1223x x π=-,()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意:0πx <<,则112666x πππ-<-<,23sin 265x π⎛⎫-= ⎪⎝⎭,120x x π<<<,则2226x πππ<-<,由同角三角函数基本关系可知:24cos 265x π⎛⎫-=- ⎪⎝⎭, 故选:B . 【点睛】关键点点睛:本题考查正弦函数的性质,考查平方关系.解题时根据自变量的范围求得此范围内函数的对称轴,从而得出两个变量12,x x 的关系,可化双变量为单变量,再根据函数值及函数性质确定出单变量的范围,从而求得结论.注意其中诱导公式的应用,目的是把求值式与已知条件中的角化为一致.4.C解析:C 【分析】由图可知,172482g f ππ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,根据函数图象的平移变化法则可知()()sin 2x g x ϕ=-,于是推出1717sin 22424g ππϕ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,即1722124k ππϕπ-=+或324k ππ+,k Z ∈,再结合02πϕ<≤,解之即可得ϕ的值.【详解】由图可知,17sin 224882g f πππ⎛⎫⎛⎫⎛⎫==⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因为()f x 的图象向右平移ϕ个单位,得到函数()g x 的图象,所以()()sin 2x g x ϕ=-,所以171717sin 2sin 22424122g πππϕϕ⎛⎫⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以1722124k ππϕπ-=+或17322124k ππϕπ-=+,k Z ∈,解得712k πϕπ=-或3k πϕπ=-,k Z ∈,因为02πϕ<≤,所以3πϕ=.故选:C 【点睛】本小题主要考查三角函数图象变换,属于中档题.5.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论. 【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫⎪⎝⎭对称,选项A 错误; 当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.6.A解析:A 【分析】先根据()f x 的最小正周期计算出ω的值,再根据图象过点,03π⎛⎫⎪⎝⎭结合ϕ的范围求解出ϕ的值,再根据条件将方程变形,先确定出tan 23x π⎛⎫+ ⎪⎝⎭的值,然后即可求解出方程的根,由此确定出方程所有解的和. 【详解】因为()f x 的最小正周期为2π,所以22πωπ==,又因为()f x 的图象过点,03π⎛⎫⎪⎝⎭,所以2tan 03πϕ⎛⎫+= ⎪⎝⎭, 所以2,3k k Z ϕππ+=∈,又因为02πϕ<<,所以3πϕ=且此时1k =,所以()sin 23f x x π⎛⎫=+ ⎪⎝⎭,即tan 2sin 233x x ππ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭, 即tan 2cos 21033x x ππ⎡⎤⎛⎫⎛⎫++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 又因为tan 203x π⎛⎫+= ⎪⎝⎭时,sin 203x π⎛⎫+= ⎪⎝⎭,cos 213x π⎛⎫+=± ⎪⎝⎭, 所以tan 2cos 210tan 2=0333x x x πππ⎡⎤⎛⎫⎛⎫⎛⎫++-=⇔+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 因为[]0,x π∈,所以72,333x πππ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦, 当tan 2=03x π⎛⎫+⎪⎝⎭时,23x ππ+=或223x ππ+=,解得3x π=或56x π=,所以方程()[]()sin 20,3f x x x ππ⎛⎫=+∈ ⎪⎝⎭所有解的和为57366πππ+=. 故选:A. 【点睛】关键点点睛:解答本题的关键是通过分析方程得到tan 2=03x π⎛⎫+ ⎪⎝⎭,此处需要注意不能直接约去tan 23x π⎛⎫+⎪⎝⎭,因为需要考虑tan 2=03x π⎛⎫+⎪⎝⎭的情况. 7.A解析:A 【分析】求得函数()y f x =的定义域,分析函数()y f x =的奇偶性,结合2f π⎛⎫⎪⎝⎭的值以及排除法可得出合适的选项. 【详解】 对于函数()3sin 22xf x x =-,20x -≠,得2x ≠±,所以,函数()y f x =的定义域为{}2x x ≠±.()()()sin 2sin 222x xf x f x x x --==-=----,函数()y f x =为奇函数,图象关于原点对称,排除B 、D 选项; 又02f ⎛⎫=⎪⎝⎭π,排除C 选项. 故选:A. 【点睛】本题考查利用函数的解析式选择图象,一般分析函数的定义域、奇偶性、单调性、零点以及函数值符号,考查分析问题和解决问题的能力,属于中等题.8.D解析:D 【分析】根据各函数的特征如函数值的正负,单调性、奇偶性,定义域、值域等进行判断. 【详解】左边第一个图象中0x <时,0y <,只有③满足,此时只有D 可选,实际上,左边第二个图象关于y 轴对称,是偶函数,只有②满足,而0x >时,10y x x=+>恒成立,只有最右边的图象满足,由此也可得顺序是③②①④,选D . 故选:D .【点睛】思路点睛:本题考查由函数解析式选择函数图象,解题时可两者结合,由函数解析式和图象分别确定函数的性质,如奇偶性、单调性、函数值的正负,特殊的函数值,变化趋势等等,两者对照可得结论.9.A解析:A 【分析】首先求解命题p 表示的集合,再根据集合关系表示充分不必要条件,判断选项. 【详解】:sin 2sin 13p x x x π⎛⎫+=+> ⎪⎝⎭,即1sin 32x π⎛⎫+> ⎪⎝⎭,解得:522,636k x k k Z πππππ+<+<+∈, 得22,62k x k k Z ππππ-+<<+∈,设22,62M x k x k k Z ππππ⎧⎫=-+<<+∈⎨⎬⎩⎭经分析,只有选项A 的集合是集合M 的真子集, 故选:A 【点睛】结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:(1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集; (2)p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集; (3)p 是q 的充分必要条件,则p 对应集合与q 对应集合相等;(4)p 是q 的既不充分又不必要条件, q 对的集合与p 对应集合互不包含.10.A解析:A 【分析】由正切函数的图象性质,得出相邻两个对称中心之间的距离为半个周期,可求出T ,然后由T πω=求出ω,然后再代点讨论满足题意的ϕ,即可得出答案. 【详解】由正切函数图象的性质可知相邻两个对称中心的距离为2T ,得72263T πππ⎛⎫=-= ⎪⎝⎭. 则由1T πω==得1ω=,即得1ω=±. 由2πϕ<,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则可得1ω=-,∴()()()tan tan f x x x ϕϕ=-+=--. 由2,32k k Z ππϕ-=∈得2,32k k Z ππϕ=-∈,因2πϕ<,可得6π=ϕ或3π-,当3πϕ=-时,()tan +3f x x π⎛⎫=- ⎪⎝⎭,由+,232k x k k Z πππππ-<<+∈,得5,66k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为5,,66k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由54,63ππ⎛⎫ ⎪⎝⎭7,66ππ⎛⎫ ⎪⎝⎭⊄,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上不是单调递减, 所以3πϕ=-不满足题意;当6π=ϕ时,()tan 6f x x π⎛⎫=-- ⎪⎝⎭,由,262k x k k Z πππππ-<-<+∈,得2,33k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为2,,33k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由25,3354,63ππππ⎛⎫⊂⎛⎫ ⎪⎝ ⎪⎝⎭⎭,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上单调递减, 所以6π=ϕ满足题意; 综上可得:6π=ϕ满足题意. 故选:A.【点睛】关键点睛:正切型函数的对称中心和单调性的问题,通常采用代入检验法,注意正切函数的对称中心为0,2k k Z π⎛⎫∈⎪⎝⎭,. 11.D解析:D 【分析】由题先求出()3sin 323g x x π⎛⎫=+- ⎪⎝⎭,可得3,3363x πππθ⎡⎤+∈+⎢⎥⎣⎦,要满足题意,则332ππθ+≥,即可求出.【详解】将()f x 横坐标缩短为原来的13得到3sin(3)2y x =--,再向右平移29π个单位得到()23sin 323sin 3293g x x x ππ⎡⎤⎛⎫⎛⎫---=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=,,18x πθ⎡⎤∈-⎢⎥⎣⎦,则3,3363x πππθ⎡⎤+∈+⎢⎥⎣⎦,要使()g x 在区间,18πθ⎡⎤-⎢⎥⎣⎦上的最大值为1,则332ππθ+≥,即18πθ≥,则θ的最小值为18π. 故选:D. 【点睛】本题考查正弦型函数的性质,解题的关键是通过图象变化得出()3sin 323g x x π⎛⎫=+- ⎪⎝⎭,再根据正弦函数的性质求解.12.C解析:C 【分析】函数()()sin ln 0=->f x x x ωω只有一个零点,等价于sin y x ω=与ln y x =图象只有一个交点,作出两个函数的图象,数形结合即可求解. 【详解】函数()()sin ln 0=->f x x x ωω只有一个零点, 可得sin ln 0x x ω-=只有一个实根,等价于sin y x ω=与ln y x =图象只有一个交点, 作出两个函数的图象如图所示,由sin y x ω=可得其周期2T πω=,当x e =时,ln 1y e ==sin y x ω=最高点5,12A πω⎛⎫⎪⎝⎭所以若恰有一个交点,只需要5ln 12πω>,即52e πω>, 解得:52e πω<,又因为0>ω,所以502eπω<<, 故选:C 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.二、填空题13.2【分析】根据函数为偶函数可知函数必有一个零点为可得根据函数的图象可知解得即可得解【详解】因为函数为偶函数且有且仅有3个零点所以必有一个零点为所以得所以函数的图象与直线在上有且仅有3个交点因为函数的解析:2 【分析】根据函数为偶函数可知函数必有一个零点为0x =,可得1a =-,根据函数cos y x ω=(0)>ω的图象可知222πππωω≤<⨯,解得24ω≤<即可得解.【详解】因为函数cos ,[],y a x x ωππ=+∈-为偶函数,且有且仅有3个零点, 所以必有一个零点为0x =, 所以cos00a +=,得1a =-,所以函数cos y x ω=(0)>ω的图象与直线1y =在[,]-ππ上有且仅有3个交点, 因为函数cos y x ω=(0)>ω的最小正周期2T πω=,所以2T T π≤<,即222πππωω≤<⨯,得24ω≤<,所以ω的最小值是2.故答案为:2 【点睛】关键点点睛:根据偶函数图象的对称性求出a 是解题关键.14.①②③【分析】利用正弦型函数的对称性可判断①④的正误;利用正弦型函数的周期公式可判断②的正误;利用正弦型函数的单调性可判断③的正误【详解】对于①所以的图象关于直线对称①正确;对于②的最小正周期是②正解析:①②③ 【分析】利用正弦型函数的对称性可判断①④的正误;利用正弦型函数的周期公式可判断②的正误;利用正弦型函数的单调性可判断③的正误. 【详解】 对于①,212sin 232243f πππ⎡⎤⎛⎫⎛⎫-=⨯--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以,()y f x =的图象关于直线2x π=-对称,①正确; 对于②,()f x 的最小正周期是2412T ππ==,②正确; 对于③,当23x ππ≤≤时,3154244x πππ≤-≤, 所以,函数()y f x =在区间[]2,3ππ上是减函数,③正确; 对于④,由①可知,④错误. 故答案为:①②③. 【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+形式,再求()sin y A ωx φ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可,注意要先把ω化为正数.15.【分析】根据函数图像的对称点得到的表达式根据在区间上单调得到的范围从而得到的范围再得到的值【详解】函数的图像关于点对称所以即得到在区间上单调所以即所以所以而所以故答案为:【点睛】本题考查根据余弦型函解析:23【分析】根据函数图像的对称点,得到ω的表达式,根据()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,得到T 的范围,从而得到ω的范围,再得到ω的值. 【详解】函数()f x x ω=-的图像关于点3,04π⎛⎫⎪⎝⎭对称,所以304πω⎛⎫-= ⎪⎝⎭,即342k ππωπ=+,k ∈Z ,得到4233k ω=+,k ∈Z , ()f x 在区间20,3π⎛⎫⎪⎝⎭上单调, 所以223T π≥,即43T π≥, 所以243ππω≥,所以32ω≤,而0>ω,所以0k =,23ω=. 故答案为:23. 【点睛】本题考查根据余弦型函数的对称中心求参数的值,根据余弦型函数的周期求参数的值,属于中档题.16.【分析】先切化弦再诱导公式化简后运用余弦二倍角公式得解【详解】故答案为:【点睛】本题考查同角三角函数的基本关系诱导公式二倍角公式同角三角函数的基本关系本身是恒等式也可以看作是方程对于一些题可利用已知解析:19-【分析】先切化弦,再诱导公式化简后,运用余弦二倍角公式得解. 【详解】2tan|cos |,|sin |2232ααα∴=∴== 22451sin()cos cos sin 222999παααα∴+==-=-=-故答案为:19-. 【点睛】本题考查同角三角函数的基本关系、诱导公式、二倍角公式.同角三角函数的基本关系本身是恒等式,也可以看作是方程,对于一些题,可利用已知条件,结合同角三角函数的基本关系列方程组,通过解方程组达到解决问题的目的. 应用诱导公式化简求值的关键是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解.转化过程中注意口诀“奇变偶不变,符号看象限”的应用.17.①②③【分析】利用整体代入的方式求出对称中心和对称轴分析单调区间利用函数的平移方式检验平移后的图象【详解】由题:令当时即函数的一条对称轴所以①正确;令当时所以是函数的一个对称中心所以②正确;当在区间解析:①②③ 【分析】利用整体代入的方式求出对称中心和对称轴,分析单调区间,利用函数的平移方式检验平移后的图象. 【详解】由题:()3sin 23x f x π⎛⎫=- ⎪⎝⎭,令2,32x k k Z πππ-=+∈,5,122k x k Z ππ=+∈, 当1k =时,1112π=x 即函数的一条对称轴,所以①正确; 令2,3x k k Z ππ-=∈,,62k x k Z ππ=+∈,当1k =时,23x π=, 所以2,03π⎛⎫⎪⎝⎭是函数的一个对称中心,所以②正确; 当5,1212x ππ⎛⎫∈- ⎪⎝⎭,,2223x ππ⎛⎫∈- ⎪⎝π⎭-,()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数,所以③正确;3sin 2y x =的图象向右平移3π个单位长度得到23sin 23sin 233y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,与函数()3sin 23x f x π⎛⎫=- ⎪⎝⎭不相等,所以④错误.故答案为:①②③ 【点睛】此题考查三角函数的图象和性质,利用整体代入的方式求解对称轴对称中心,求解单调区间,根据函数的平移变换求解平移后的函数解析式.18.②④或③②(填一种即可)【分析】利用三角函数图象变换可以先平移后伸缩也可以先伸缩后平移即可得到结论【详解】经过变换②可得到再经过变换④可得;或者经过变换③可得到再经过变换②可得故答案为:②④或③②(解析:②④或③②(填一种即可) 【分析】利用三角函数图象变换,可以“先平移,后伸缩”,也可以“先伸缩,后平移”即可得到结论. 【详解】sin y x =经过变换②可得到sin 2y x =,再经过变换④可得sin(2)3y x π=-;或者sin y x =经过变换③可得到sin()3y x π=-,再经过变换②可得sin 2y x =.故答案为: ②④或③②(填一种即可). 【点睛】本题考查三角函数图象变换,分辨清“先平移,后伸缩”,还是“先伸缩,后平移”是解题的关键,熟练掌握无论是哪种变换,切记每一个变换总是对x 而言,属于中档题.19.②③【分析】根据三角函数的零点性质三角函数对称和三角函数诱导公式依次判断每个选项得到答案【详解】①中是的两个零点即是的整数倍①错误;②中②正确;故④错误;③中③正确;所以正确命题序号是②③故答案为:解析:②③ 【分析】根据三角函数的零点性质,三角函数对称和三角函数诱导公式依次判断每个选项得到答案. 【详解】①中12,x x 是()f x 的两个零点,即12x x -是2π的整数倍,①错误; ②中06f π⎛⎫-= ⎪⎝⎭,②正确;故④错误; ③中4sin 24cos 2cos 23236y x x x ππππ⎛⎫⎛⎫⎛⎫=+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,③正确; 所以正确命题序号是②③. 故答案为:②③. 【点睛】本题考查了三角函数的对称,零点,诱导公式,意在考查学生对于三角函数知识的综合应用.20.见解析【分析】任选一个条件求出的取值结合单调性分析的情况即可得解【详解】若选①令代入解得因为所以当时当时若函数在上单调则有解得所以存在正整数时使得函数在上是单调的若选②所以当时若函数在上单调则有解得解析:见解析 【分析】任选一个条件求出ϕ的取值,结合单调性分析ω的情况即可得解. 【详解】若选①,令,x k k Z ωϕπ+=∈,代入56x πω=,解得5,6k k Z πϕπ=-∈, 因为02πϕ≤≤,所以当1k =时,6π=ϕ,()2cos()6f x x πω=+,当[0,]2x π∈时,[,]6626x πππωπω+∈+, 若函数()f x 在[0,]2π上单调,则有26πωππ+≤,解得503ω<≤, 所以存在正整数1ω=时,使得函数()f x 在[0,]2π上是单调的.若选②,()cos 2cos()3f x x x x πωωω==+,所以3πϕ=,当[0,]2x π∈时,[,]3323x πππωπω+∈+, 若函数()f x 在[0,]2π上单调,则有23πωππ+≤,解得403ω<≤, 所以存在正整数1ω=时,使得函数()f x 在[0,]2π上是单调的.若选③,因为()(0)f x f ≤恒成立,即max ()(0)2cos 2f x f ϕ===,所以cos 1ϕ=, 因为02πϕ≤≤,所以0ϕ=,()2cos f x x ω=,当[0,]2x π∈时,[0,]2x πωω∈,若函数()f x 在[0,]2π上单调,则有2πωπ≤,解得02ω<≤,所以存在正整数1ω=或2时,使得函数()f x 在[0,]2π上是单调的.【点睛】此题考查三角函数的综合应用,根据对称性单调性以及最值的关系求解参数,需要熟练掌握三角函数相关性质.三、解答题21.(1)答案见解析;(2)34k x ππ=+,k Z ∈. 【分析】(1)分别令x 等于0、6π、512π、23π、1112π、π,求得对应的纵坐标,确定点的坐标,列表、描点、作图即可;(2)利用放缩变换与平移变换法则可得到()15sin 4126g x x π⎛⎫=-+ ⎪⎝⎭,再令5462x k k Z πππ-=+∈,可得答案. 【详解】(1)由题意可得表格如下:26x π+6π 2π π32π 2π136πx6π 512π 23π 1112ππ()f x141212- 014(2)将()y f x =的图象向上平移1个单位得到1sin 2126y x π⎛⎫=++ ⎪⎝⎭的图象,再横坐标缩短为原来的12可得到1sin 4126y x π⎛⎫=++ ⎪⎝⎭的图象,再向右平移4π个单位可得115sin 41sin 412626y x x πππ⎛⎫⎛⎫=-++=-+ ⎪ ⎪⎝⎭⎝⎭的图象, 即()15sin 4126g x x π⎛⎫=-+ ⎪⎝⎭, 令5462x k πππ-=+,解得34k x k Z ππ=+∈,, 所以()g x 的对称轴方程是34k x ππ=+,k Z ∈. 【点睛】方法点睛:“五点法”作一个周期上的图象,主要把握三处主要位置点:1、区间端点;2、最值点;3、零点.22.(1)2π;(2)2,5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 【分析】(1)先利用二倍角公式化简,再用辅助角公式化为()f x sin 16x π⎛⎫=++ ⎪⎝⎭,即可求出()f x 的最小正周期;(2)利用图像变换得到()y g x =的解析式,利用换元法就可以得到()y g x =的最大值及取得最大值时 x 的取值 【详解】(1)∵函数1cos 1()22x f x x +=++ sin 16x π⎛⎫=++ ⎪⎝⎭∴函数的周期为2π(2)依题意:函数()f x sin 16x π⎛⎫=++ ⎪⎝⎭的图象上的各点向左平移32π个单位,得到y 3sin +1= -cos 1626x x πππ⎛⎫⎛⎫=++++ ⎪ ⎪⎝⎭⎝⎭;再保持纵坐标不变,横坐标缩短到原来的一半,得到y = -cos 216x π⎛⎫++ ⎪⎝⎭; 所以()cos 216g x x π⎛⎫=-++ ⎪⎝⎭令226t x k πππ=+=+,即5()12x k k Z ππ=+∈ 使函数()g x 取得最大值2,即max ()2g x =使函数()g x 取得最大值的集合为5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭.【注意】取得最大值的集合为7,12x x k k Z ππ⎧⎫=-∈⎨⎬⎩⎭也可以. 【点睛】 :(1)关于三角函数图像平移伸缩变换:先平移的话,如果平移a 个单位长度那么相位就会改变ωa ;而先伸缩势必会改变ω大小,这时再平移要使相位改变值仍为ωa ,那么平移长度不等于a ;(2)求y =Asin (ωx +φ)+B 的值域通常用换元法; 23.()2sin 3f x x ππ⎛⎫=+ ⎪⎝⎭;(2)296【分析】(1)根据条件先求ω,再根据()0f =ϕ,最后再验证ϕ值,确定函数的解析式;(2)根据条件求函数的零点,确定b 的最大值应是第5个零点. 【详解】 (1)函数的最大值是2,∴,函数的周期2T =,即22πωπω=⇒=,()02sin f ϕ==,且0ϕπ<<,3πϕ∴=或23π, 当3πϕ=时,()2sin 3f x x ππ⎛⎫=+⎪⎝⎭,当10,12x ⎡⎤∈⎢⎥⎣⎦时,5,3312x ππππ⎡⎤+∈⎢⎥⎣⎦ 0,2π⎡⎤⎢⎥⎣⎦,满足条件; 当23ϕπ=时,()22sin 3f x x ππ⎛⎫=+ ⎪⎝⎭,当10,12x ⎡⎤∈⎢⎥⎣⎦时,223,334x ππππ⎡⎤+∈⎢⎥⎣⎦ 3,22ππ⎡⎤⎢⎥⎣⎦,所以函数在区间10,12⎡⎤⎢⎥⎣⎦上为减函数,所以舍去, 所以函数()2sin 3f x x ππ⎛⎫=+ ⎪⎝⎭; (2)()2sin 103g x x ππ⎛⎫=++= ⎪⎝⎭,得1sin 32x ππ⎛⎫+=- ⎪⎝⎭, 72,36x k k Z ππππ+=+∈,解得:52,6x k k Z =+∈, 或112,36x k k Z ππππ+=+∈,解得:32,2x k k Z =+∈, 函数()()1g x f x =+在区间()0,b 上只有4个零点,∴这四个零点应是56,32,176,72,那么b 的最大值应是第5个零点,即296, 所以b 的最大值是296. 【点睛】关键点点睛:本题第一问注意求出两个ϕ 后需验证是否满足条件,第二个关键点是,注意()0,b 是开区间,开区间内只有四个零点,则b 的最大值是第5个零点.24.(1)()23f x x π⎛⎫=+ ⎪⎝⎭;(2),,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z ;(3){},66πππ⎡⎤-⋃⎢⎥⎣⎦. 【分析】(1)利用题中图象可知A =,44T π=,结合周期公式求得=2ω,再由3x π=代入计算得=3πϕ即得解析式;(2)根据三角函数平移的方法求得()g x ,再利用整体代入法求单调递减区间即可;(3)先由()32fx ≥可得sin 23x π⎛⎫+≥ ⎪⎝⎭,再由,2x ππ⎡⎤∈-⎢⎥⎣⎦得到23x π+的前提范围,结合正弦函数性质得到不等式中23x π+的范围,再计算x 范围即可.【详解】解:(1)由题中图象可知:A =,741234T πππ=-=, 2T ππω∴==,即2ω=,又由图象知,3x π=时,223k πϕππ⋅+=+,即23k πϕπ=+,k Z ∈,又02ϕπ≤<,∴=3πϕ,()23f x x π⎛⎫∴=+ ⎪⎝⎭;(2)()f x 向左平移12π个单位后得到函数()g x ,故()2221232g x x x x πππ⎡⎤⎛⎫⎛⎫=++=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由余弦函数性质知,令222,k x k k Z πππ≤≤+∈,得减区间,,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z , ∴()g x 的单调递减区间为,,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z ;(3)由题意知:()3232f x x π⎛⎫=+≥ ⎪⎝⎭,即sin 23x π⎛⎫+≥ ⎪⎝⎭, 由,2x ππ⎡⎤∈-⎢⎥⎣⎦,知[]0,x π∈,2,2333x ππππ⎡⎤+∈+⎢⎥⎣⎦,由正弦函数图象性质可知,22333x πππ≤+≤或2233x πππ+=+ 即06x π≤≤或x =π,又,2x ππ⎡⎤∈-⎢⎥⎣⎦,得x 的取值范围为{},66x πππ⎡⎤∈-⋃⎢⎥⎣⎦.【点睛】 方法点睛:求三角函数()()sin f x A x b ωϕ=++性质问题时,通常利用整体代入法求解单调性、对称性,最值等性质,或者整体法求三角不等式的解.25.(1)3tan 4α=;(2)3sin 3sin 3cos 25ααα=--.【分析】(1)利用诱导公式可得出12cos sin 25αα=,根据题意可得出关于cos α、sin α的值,求出cos α、sin α的值,利用同角三角函数的商数关系可求得tan α的值;(2)将所求代数式变形为()()3322sin sin sin 3cos sin 3cos sin cos αααααααα=--+,在分式的分子和分母中同时除以3cos α,利用弦化切可求得所求代数式的值. 【详解】 (1)712sin cos 2225ππαα⎛⎫⎛⎫---+= ⎪ ⎪⎝⎭⎝⎭,由诱导公式可得123sin cos cos sin 2522ππαααα⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭, 0,4πα⎛⎫∈ ⎪⎝⎭,cos sin 0αα∴>>,由已知可得2212cos sin 25cos sin 1cos sin 0αααααα⎧=⎪⎪+=⎨⎪>>⎪⎩,解得4cos 53sin 5αα⎧=⎪⎪⎨⎪=⎪⎩, 因此,sin 3tan cos 4ααα==; (2)()()3322sin sin sin 3cos sin 3cos sin cos αααααααα=--+()()332223sin tan 325sin sin tan 3tan 131cos cos cos ααααααααα===-⎛⎫-+⎛⎫-+ ⎪⎪⎝⎭⎝⎭.【点睛】方法点睛:三角函数求值问题中已知tan α,求关于sin α、cos α的代数式的值时,一般利用弦化切公式后直接代入tan α的值,在关于sin α、cos α的齐次式中,常常利用弦化切的方程转化为含tan α的代数式. 26.(1)12x π=-;(2)512ω≤<. 【分析】(1)由函数的()f x 的最小正周期求得ω,再根据图象的平移得出函数()f x 的解析式,由正弦函数的性质可得答案;(2)由图象平移得出:()33f x x ππω⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦,再由()f x 在,2ππ⎡⎤⎢⎥⎣⎦上仅有一个零点,建立不等式组,解之可得范围. 【详解】解:(1)因为()f x 的最小正周期为π,2ππω∴=,2ω∴=,()f x的图像是由3y x πω⎛⎫=+ ⎪⎝⎭的图像向右平移3π个单位得到,()33f x x ππω⎡⎤⎛⎫∴=-+ ⎪⎢⎥⎝⎭⎣⎦,即()23f x x π⎛⎫=- ⎪⎝⎭,令232x k ππ-=π+,k Z ∈,得()f x 的对称轴方程为212k x π5π=+,k Z ∈, 要使直线212k x π5π=+(k Z ∈)与y 轴距离最近,则须5212k ππ+最小,1k ∴=-,此时对称轴方程为12x π=-,即所求对称轴方程为12x π=-.(2)由已知得:()33f x x ππω⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦,令()0f x =得:33x k ππωωπ+-=,k Z ∈,即33k x πππωω+-=,k Z ∈,。
【沪科版】高中数学必修四期末一模试题含答案(3)

解析:①④.
【分析】
根据 为定值,求出 ,再对题目中的命题分析、判断正误即可.
【详解】
解:对于①,由 为定值,
3、给值求角:实质上可转化为“给值求值”即通过求角的某个三角函数值来求角(注意角的范围).
4.B
解析:B
【分析】
先化简函数,根据 在区间 上是增函数,则为函数含有零的增区间的子集,再根据区间 上恰好取得一次最大值,则取得最大值时对应的最小正数解属于 ,最后取交集.
【详解】
因为 ,
,
,
,
令 ,
则 ,
因为 在区间 上是增函数,
所以 ,
解得 ;
由题意知 时, 单调递减,所以 单调递增,
即 越大越费力, 越小越省力;①正确.
对于②,由题意知, 的取值范围是 ,所以②错误.
对于③,当 时, ,所以 ,③错误.
对于④,当 时, ,所以 ,④正确.
综上知,正确结论的序号是①④.
故答案为:①④.
【点睛】
此题考查平面向量数量积的应用,考查分析问题的能力,属于中档题
【点睛】
本题考查诱导公式进行化简求值,利用两角差的正弦公式进行化简求值,属于中档题.
16.3【分析】根据向量关系即可确定的形状再根据向量投影的计算公式即可求得结果【详解】因为圆O为△ABC的外接圆半径为2若故可得是以角为直角的直角三角形又因为且外接圆半径是故可得则故向量在向量方向上的投影
解析:3
【分析】
18.【解析】分析:先通过已知条件求出的值再求在方向上的投影详解:因为所以所以在方向上的投影为故答案为1点睛:(1)本题主要考查向量的运算和数量积考查向量的投影意在考查学生对这些基础知识的掌握水平和基本运
新人教A版高中数学必修四第二学期期末考试测试题(含答案)

山东省聊城四中第二学期高一期末考试数学试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,本试卷120分,考试时间100分钟。
2.答题前请将自己的学校、班级、姓名、考场号等填写在答题卷密封线内的相应栏目。
3.请将答案按题序号填写在答题卷上,考后仅收答题卷。
第Ⅰ卷(选择题 共48分)一、选择题:(本大题共12小题,每小题4分,共48分.在每小题给出的四个选项中,选择一个符合题目要求的选项.)1.5sin()6π-的值是A .B .12C .D .12- 2.已知(1,2),(5,4),(.3),(3,)A B C x D y -,且AB CD =,则,x y 的值分别为A 、-7,-5B 、-7,5C 、7,-5D 、7,5 3.下列给出的赋值语句中正确的是 ( )A . 4M =B .M M =-C 3B A ==D 0x y +=4.某经济研究小组对全国50个中小城市进行职工人均工资x 与居民人均消费水平y 进行了统计调查,发现y 与x 具有相关关系,其回归方程为ˆ0.3 1.65y x =+(单位:千元).某城市居民人均消费水平为6.60,估计该城市职工人均消费水平额占居民人均工资收入的百分比为 A .66%B .55.3%C .45.3%D .40%5.右图是某学校举行的运动会上,七位评委为某体操项目打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数及方差分别为( )A .84,4.84B .84,1.6C .85,1.6D .85,4 6.如图,已知正方形的面积为10,向正方形内随机地撒200颗黄豆,数得落在阴影外 的黄豆数为114颗,以此实验数据为依据, 可以估计出阴影部分的面积约为( ) A .5.3 B .4.3C .4.7D .5.77.已知)1,1(-A ,)5,2(B ,点P 在线段AB 上,且||3||=,则点P 的坐标为 ( )A .)4,1(-B .)313,23(C .)4,45(D .)213,411(8.函数x x y cos -=的部分图象是( )10.从分别写有A 、B 、C 、D 、E 的5张卡片中,任取2张,这2张上的字母恰好按字母顺序相邻的概率为( )A .51B .52C .103 D .107 11.要得到函数x y cos 2=的图象,只需将函数)42sin(2π+=x y 的图象上所有的点的( )A .横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动4π个单位长度; B .横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动8π个单位长度;C .横坐标缩短到原来的21倍(纵坐标不变),再向右平行移动4π个单位长度;D .横坐标缩短到原来的21倍(纵坐标不变),再向左平行移动8π个单位长度。
(完整版)高中数学必修四期末试题及答案,推荐文档

D. 24 25
14. 设向量 a=(m,n),b=(s,t),定义两个向量 a,b 之间的运算“ ”为 a b=(ms,nt).若向量
p=(1,2),p q=(-3,-4),则向量 q 等于( ).
A.(-3,-2)
B.(3,-2)
C.(-2,-3)
D.(-3,2)
二、填空题:本大题共 4 小题,每小题 4 分,共 16 分.把答案填在题中横线上.
第 4页
13.D
解析:因为 0<A< ,所以 sin A= 1+ cos2 A+ 4 ,sin 2A=2sin Acos A= 24 .
2
5
25
14.A
解析:设 q=(x,y),由运算“ ”的定义,知 p q=(x,2y)=(-3,-4),所以
q=(-3,-2).
二、填空题:
15. 3 .
5
1+4 3
10.B
解析:因为 cos x 的最大值和最小值分别是 1 和-1,所以函数 y=2cos x-1 的最大值、最小值分别是 1
和-3.
11.D
解析:易知 AB =(2,2), BC =(-1,c-2),由 AB ⊥ BC ,得 2×(-1)+2(c-2)=0,解得 c=3. 12.A 解析:画出函数的图象即知 A 正确.
).
3
A. 6
B. 3
C. 2 3
4. 若 cos >0,sin <0,则角 的终边在(
).
A.第一象限
B.第二象限 5. C.第三象限
sin 20°cos 40°+cos 20°sin 40°的值等于(
).
A. 1 4
B. 2
C. 1 2
D. 4
6. 如图,在平行四边形 ABCD 中,下列结论中正确的是(
(常考题)北师大版高中数学必修四第一章《三角函数》测试题(含答案解析)(1)

一、选择题1.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .D 2.设函数()3sin()10,2f x x πωϕωϕ⎛⎫=++><⎪⎝⎭的最小正周期为π,其图象关于直线3x π=对称,则下列说法正确是( )A .()f x 的图象过点30,2⎛⎫ ⎪⎝⎭; B .()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上单调递减; C .()f x 的一个对称中心是7,012π⎛⎫⎪⎝⎭; D .将()f x 的图象向左平移12ϕ个单位长度得到函数3sin 21y x =+ 的图象. 3.如果一个函数在给定的区间上的零点个数恰好为8,则称该函数为“比心8中函数”.若函数()2sin()1f x x ωπ=-,(0)>ω是区间[0,1]上的“比心8中函数”,则ω的取值范围是( ) A .4149,66⎡⎫⎪⎢⎣⎭B .4953,66⎡⎫⎪⎢⎣⎭C .3741,66⎡⎫⎪⎢⎣⎭D .[8,9)4.函数1sin3y x =-的图像与直线3x π=,53x π=及x 轴所围成的图形的面积是( ) A .23π B .πC .43π D .53π 5.已知函数sin()0,0,||2y A x b A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的图象上相邻的一个最大值点与对称中心分别为2,39π⎛⎫ ⎪⎝⎭,,018π⎛⎫⎪⎝⎭,则函数()f x 的单调增区间为( ) A .222,3939k k ππππ⎛⎫-+ ⎪⎝⎭,k Z ∈ B .242,3939k k ππππ⎛⎫--⎪⎝⎭,k Z ∈ C .227,318318k k ππππ⎛⎫++⎪⎝⎭,k Z ∈ D .272,318318k k ππππ⎛⎫--⎪⎝⎭,k Z ∈6.使函数())cos(2)f x x x θθ=+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π7.已知曲线1C :sin y x =,2C :cos 23y x π⎛⎫=-⎪⎝⎭,则下面结论正确的是( ) A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移12π个单位长度,得到曲线2CD .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移12π个单位长度,得到曲线2C8.已知奇函数()f x 满足()(2)f x f x =+,当(0,1)x ∈时,函数()2x f x =,则12log 23f ⎛⎫= ⎪⎝⎭( ) A .1623-B .2316-C .1623D .23169.有以下四种变换方式: ①向左平移12π个单位长度,再将每个点的横坐标伸长为原来的2倍;②向左平移6π个单位长度,再将每个点的横坐标伸长为原来的2倍; ③再将每个点的横坐标伸长为原来的2倍,再向左平移6π个单位长度; ④再将每个点的横坐标伸长为原来的2倍,再向右平移6π个单位长度; 其中能将函数sin 26y x π⎛⎫=- ⎪⎝⎭的图象变为函数sin y x =图象的是( )A .①③B .②③C .①④D .②④10.已知函数1,01()11sin ,14242x x f x x x π+≤≤⎧⎪=⎨+<≤⎪⎩,若不等式2()()20f x af x -+<在[]0,4x ∈上恒成立,则实数a 的取值范围为( )A .3a >B .23a <<C .22a >D .92a >11.函数()()sin ln 0=->f x x x ωω只有一个零点,则实数ω的取值范围是( ) A .()0,πB .5,2⎫⎛⎪⎝⎭ππe C .50,2⎫⎛ ⎪⎝⎭πeD .5,2⎫⎛∞ ⎪⎝⎭π+e 12.如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m ,转盘直径为110m 设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min .游客甲坐上摩天轮的座舱,开始转动t min 后距离地面的高度为H m ,则在转动一周的过程中,高度H 关于时间t 的函数解析式是( )A .()55cos 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭B .()55sin 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭C .()55cos 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭D .()55sin 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭二、填空题13.下列判断正确的是___________(将你认为所有正确的情况的代号填入横线上). ①函数1tan 21tan 2xy x+=-的最小正周期为π;②若函数()lg f x x =,且()()f a f b =,则1ab =; ③若22tan 3tan 2αβ=+,则223sin sin 2αβ-=;④若函数()2221sin 41x xy x ++=+的最大值为M ,最小值为N ,则2M N +=.14.已知函数cos ,[],y a x x ωππ=+∈-(其中,a ω为常数,且0>ω)有且仅有3个零点,则ω的最小值是_________.15.“一湾如月弦初上,半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.如图所示,月牙泉由两段在同一平面内的圆弧形岸连接围成.两岸连接点间距离为603米.其中外岸为半圆形,内岸圆弧所在圆的半径为60米.某游客绕着月牙泉的岸边步行一周,则该游客步行的路程为_______米.16.已知函数()()π5sin 24f x x x ⎛⎫=-∈ ⎪⎝⎭R ,对于下列说法:①要得到()5sin 2g x x =的图象,只需将()f x 的图象向左平移4π个单位长度即可;②()y f x =的图象关于直线3π8x =对称:③()y f x =在[]π,π-内的单调递减区间为3π7π,88⎡⎤⎢⎥⎣⎦;④5π8y f x ⎛⎫=+⎪⎝⎭为奇函数.则上述说法正确的是________(填入所有正确说法的序号). 17.已知函数()sin()f x A x ωϕ=+(其中0A >,0,0ωϕπ><<)的图象关于点M 5(,0)12π成中心对称,且与点M 相邻的一个最低点为2(,3)3π-,则对于下列判断: ①直线2x π=是函数()f x 图象的一条对称轴;②函数()3y f x π=-为偶函数;③函数1y =与35()()1212y f x x ππ=-≤≤的图象的所有交点的横坐标之和为7π.其中正确的判断是__________________.(写出所有正确判断的序号)18.已知函数f (x ),任意x 1,x 2∈,22ππ⎛⎫- ⎪⎝⎭(x 1≠x 2),给出下列结论:①f (x +π)=f (x );②f (-x )=f (x );③f (0)=1; ④1212()()f x f x x x -->0;⑤1212()()22x x f x f x f ++⎛⎫> ⎪⎝⎭.当()tan f x x =时,正确结论的序号为________.19.已知函数()2sin()(0)f x x ωϕω=+>满足()24f π=,()0f π=,且()f x 在区间(,)43ππ上单调,则ω的值有_________个.20.关于函数()()4sin 23f x x x R π⎛⎫=+∈ ⎪⎝⎭,有下列命题: ①函数()y f x =的表达式可以改写为4cos 26y x π⎛⎫=- ⎪⎝⎭; ②函数()y f x =是以2π为最小正周期的周期函数; ③函数()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称; ④函数()y f x =的图象关于直线6x π=-对称.其中正确的序号是______.三、解答题21.已知函数1()sin 22,23f x x x R π⎛⎫=-+∈ ⎪⎝⎭. (1)求()f x 的最小正周期; (2)求()f x 的单调递减区间; (3)求()f x 在区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值 22.如图,在矩形OABC 中,22OA OC ==,将矩形OABC 绕着顶点O 逆时针旋转,得到矩形OA B C ''',记旋转的角度为θ,0,2πθ⎛⎫∈ ⎪⎝⎭旋转前后两个矩形公共部分的面积为()S θ.(1)求3S π⎛⎫⎪⎝⎭; (2)若()72S θ=,求sin θ. 23.已知2sin ()cos(2)tan()(),sin()tan(3)f παπαπααπααπ-⋅-⋅-+=+⋅-+ (1)化简()f α;(2)若1(),8f α=且,42ππα<<求cos sin αα-的值; (3)求满足1()4f α≥的α的取值集合. 24.己知函数()sin 3cos (0, 0 )f x A x A x A ωωω=+>>,其部分图象如图所示.(1)求A 和ω的值;(2)求函数()y f x =在[]0,π的单调增区间.25.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><的部分图象如下图所示.(1)求函数()f x 的解析式,并写出函数()f x 的单调递增区间; (2)将函数()f x 图象上所有点的横坐标缩短到原来的14(纵坐标不变),再将所得的函数图象上所有点向左平移02m m π⎛⎫<< ⎪⎝⎭个单位长度,得到函数()g x 的图象.若函数()g x 的图象关于直线512x π=对称,求函数()g x 在区间7,1212ππ⎡⎤⎢⎥⎣⎦上的值域. 26.海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表: 时刻 0:00 1:00 2:00 3:00 4:00 5:00 水深5.0006.2507.1657.5007.1656.250(1)这个港口的水深与时间的关系可用函数(,)近似描述,试求出这个函数解析式;(2)一条货船的吃水深度(船底与水面的距离)为5米,安全条例规定至少要有1.25米的安全间隙(船底与洋底的距离),利用(1)中的函数计算,该船何时能进入港口?在港口最多能呆多久?【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++ ⎪⎝⎭为奇函数,所以6k πϕπ+=,sin 2sin 2sin 332k ππϕπ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.2.D解析:D 【分析】先根据对称轴及最小正周期,求得函数()f x 的解析式,再结合正弦函数的图象与性质,判断点是否在函数图象上可判断A ,求得函数的单调区间及对称中心即可判断选项BC ,由平移变换求得变化后的解析式并对比即可判断D. 【详解】函数()3sin()10,2f x x πωϕωϕ⎛⎫=++>< ⎪⎝⎭的最小正周期是π 所以22πωπ==,则()()3sin 21f x x ϕ=++,()()3sin 21f x x ϕ=++图象关于直线3x π=对称,对称轴为2,2x k k Z πϕπ+=+∈,代入可得2,32k k Z ππϕπ⨯+=+∈,解得,6k k Z πϕπ=-+∈,因为,22ππϕ⎛⎫∈- ⎪⎝⎭,所以当0k =时, 6πϕ=-, 则()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭, 对于A,当0x =时,()3103sin 11622f π=-+=-+=- ,所以错误; 对于B,()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭的单调递减区间为3222,262k x k k πππππ+-+∈Z ≤≤, 解得5,36k x k k Z ππππ+≤≤+∈,因为123ππ<,则()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上不是减函数,所以错误; 对于C ,773sin 213sin 11012126f ππππ⎛⎫⎛⎫=⨯-+=+=≠⎪ ⎪⎝⎭⎝⎭,所以7,012π⎛⎫ ⎪⎝⎭不是()f x 的一个对称中心,所以错误; 对于D ,1212πϕ=,将()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭的图象向左平移12π个单位长度得到可得3sin 213sin 21126y x x ππ⎡⎤⎛⎫=-++=+ ⎪⎢⎥⎝⎭⎣⎦,所以能得到3sin 21y x =+的图象,所以正确. 故选: D. 【点睛】本题考查了正弦函数的图象与性质的综合应用,关键点是根据已知条件先求出正弦函数的解析式,还要熟练掌握三角函数的性质才能正确的解题,属于中档题.3.A解析:A 【分析】根据题意问题转化为方程1sin()2x ωπ=在区间[0,1]上有8个解,根据正弦函数的图像与性质可求得1sin()2x ωπ=在区间[0,1]上取第8个解为416x ω=、第9个解为496x ω=,则4149166ωω≤<,解不等式即可. 【详解】根据题意,函数()2sin()1f x x ωπ=-,(0)>ω是区间[0,1]上零点个数为8,即方程1sin()2x ωπ=在区间[0,1]上有8个解, ∴26x k πωππ=+或52,6x k k Z πωππ=+∈, 当0k =时,1sin()2x ωπ=在区间[0,1]上取第1个解16x ω=,取第2个解56x ω=; 当1k =时,1sin()2x ωπ=在区间[0,1]上取第3个解136x ω=,取第4个解176x ω=; 当3k =时,1sin()2x ωπ=在区间[0,1]上取第7个解376x ω=,取第8个解416x ω=; 当4k =时,1sin()2x ωπ=在区间[0,1]上取第9个解496x ω=. 则4149166ωω≤<,解得414966ω≤<. 故选:A4.C解析:C 【分析】作出函数1sin3y x =-的图像,利用割补法,补成长方形,计算面积即可. 【详解】作出函数1sin3y x =-的图象,如图所示,利用割补法,将23π到π部分的图象与x 轴围成的图形补到图中3π到23π处阴影部分,凑成一个长为3π,宽为2的长方形,后面π到53π,同理;∴1sin3y x =-的图象与直线3x π=,53x π=及x 轴所围成的面积为24233ππ⨯=,故选:C. 【点睛】用“五点法”作()sin y A ωx φ=+的简图,主要是通过变量代换,设z x ωϕ=+,由z 取0,2π,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象. 5.A解析:A 【分析】由最大值点和对称中心的坐标可以求出()f x 的解析式,利用三角函数的性质,整体代换得出该复合函数的单调增区间. 【详解】图像上相邻的一个最大值点与对称中心分别为2,39π⎛⎫⎪⎝⎭,,018π⎛⎫⎪⎝⎭, 3A ∴=,0b =且124918T ππ=-,可得23T π=, 23Tπω∴==, 3sin(3)y x ϕ∴=+ 将2,39π⎛⎫⎪⎝⎭代入可得3sin(3)3y x ϕ=+=, 可得22,32k k Z ππϕπ+=+∈,且2πϕ<, 6πϕ∴=-,可得()3sin(3)6f x x π=-,令6232,22k x k k Z πππππ-+≤-≤+∈,可得222+9393k x k ππππ-≤≤,故选:A. 【点睛】方法点睛:根据图像求函数()sin()f x A x k ωϕ=++的解析式,根据最高点和对称中心的纵坐标可求出A 和k ,根据横坐标可求出周期T ,进而求出ω.求该函数的单调区间时,用整体代换的思想,借助正弦函数的单调区间,用解不等式的方法求复合函数的单调区间.6.B解析:B 【解析】1())cos(2))cos(2))2sin(2)26f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos2f x x =为减函数,符合题意,所以选B.7.C解析:C 【分析】由题意利用诱导公式得1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭,根据函数()cos y A x ωϕ=+的图象变换规律,得出结论. 【详解】已知曲线1sin cos :2C y x x π⎛⎫==-⎪⎝⎭,2cos 23:C y x π⎛⎫=-⎪⎝⎭, ∴把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,可得cos 22y x π⎛⎫=- ⎪⎝⎭的图象,再把得到的曲线向左平移 12π个单位长度,得到曲线2cos 2cos 263:2C x x πππ⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭的图象,故选C .【点睛】本题主要考查函数()cos y A x ωϕ=+的图象变换规律,属于基础题.8.B解析:B 【分析】由已知得到(2)()f x f x +=,即得函数的周期是2,把12(log 23)f 进行变形得到223()16f log -, 由223(0,1)16log ∈满足()2x f x =,求出即可. 【详解】(2)()f x f x +=,所以函数的周期是2.根据对数函数的图象可知12log 230<,且122log 23log 23=-;奇函数()f x 满足(2)()f x f x +=和()()f x f x -=-则2312222223(log 23)(log )(log 23)(log 234)()16f f f f f log =-=-=--=-, 因为223(0,1)16log ∈ 2231622323()21616log f log ∴-=-=-,故选:B . 【点睛】考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.9.A解析:A 【分析】直接利用三角函数图像的平移变换和伸缩变换求出结果. 【详解】对于①:sin 26y x π⎛⎫=-⎪⎝⎭向左平移12π个单位长度得到sin 2+=sin2126y x x ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,再将每个点的横坐标伸长为原来的2倍,得到sin y x =;故①正确;对于②:sin 26y x π⎛⎫=-⎪⎝⎭向左平移6π个单位长度得到sin 2+=sin 2+666y x x πππ⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,再将每个点的横坐标伸长为原来的2倍,得到sin 6y x π⎛⎫=+ ⎪⎝⎭;故②错误;对于③:sin 26y x π⎛⎫=-⎪⎝⎭将每个点的横坐标伸长为原来的2倍,得到sin 6y x π⎛⎫=-⎪⎝⎭,再向左平移6π个单位长度,得到sin sin 66y x x ππ⎛⎫=+-= ⎪⎝⎭;故③正确; 对于③:sin 26y x π⎛⎫=- ⎪⎝⎭将每个点的横坐标伸长为原来的2倍,得到sin 6y x π⎛⎫=-⎪⎝⎭,再向右平移6π个单位长度,得到sin sin()663y x x πππ⎛⎫=--=- ⎪⎝⎭;故④错误; 故选:A 【点睛】关于三角函数图像平移伸缩变换:先平移的话,如果平移a 个单位长度那么相位就会改变ωa ;而先伸缩势必会改变ω大小,这时再平移要使相位改变值仍为ωa ,那么平移长度不等于a .10.D解析:D 【分析】这是一个复合函数的问题,通过换元()t f x = ,可知新元的范围,然后分离参数,转为求函数的最大值问题,进而计算可得结果. 【详解】由题可知当[]0,1x ∈时,有[]()11,2f x x =+∈, 当4](1,x ∈时,0sin14xπ≤≤,即111()sin,12422x f x π⎡⎤=+∈⎢⎥⎣⎦ 所以当[]0,4x ∈时,1,22()f x ⎡∈⎤⎢⎥⎣⎦,令()t f x =,则1,22t ⎡⎤∈⎢⎥⎣⎦,从而问题转化为不等式220t at -+<在1,22t ⎡⎤∈⎢⎥⎣⎦上恒成立,即222t a t t t+>=+在1,22t ⎡⎤∈⎢⎥⎣⎦上恒成立, 由2y t t =+,1,22t ⎡⎤∈⎢⎥⎣⎦,设1212t t <<<()()()1212121212122220t t f t f t t t t t t t t t --=-+-=->, 所以2y t t =+在12t ⎡∈⎢⎣是单调递减函数,122t t <<<,()()()1212121212122220t t f t f t t t t t t t t t --=-+-=-<, 所以2y t t=+在2t ⎤∈⎦是单调递增函数,在1,22t ⎡⎤∈⎢⎥⎣⎦上先减后增,而2t t +在12t =时有最大值为92,所以92a >.【点睛】本题考查含参数的恒成立问题,运用到分离参数法求参数范围,还结合双勾函数的单调性求出最值, 同时考查学生的综合分析能力和数据处理能力.11.C解析:C 【分析】函数()()sin ln 0=->f x x x ωω只有一个零点,等价于sin y x ω=与ln y x =图象只有一个交点,作出两个函数的图象,数形结合即可求解. 【详解】函数()()sin ln 0=->f x x x ωω只有一个零点, 可得sin ln 0x x ω-=只有一个实根,等价于sin y x ω=与ln y x =图象只有一个交点, 作出两个函数的图象如图所示,由sin y x ω=可得其周期2T πω=,当x e =时,ln 1y e ==sin y x ω=最高点5,12A πω⎛⎫⎪⎝⎭所以若恰有一个交点,只需要5ln 12πω>,即52e πω>, 解得:52e πω<,又因为0>ω,所以502eπω<<, 故选:C 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.12.B解析:B 【分析】先判断游客进仓后第一次到达最高点时摩天轮旋转半周,大约需要10min ,结合摩天轮最高点距离地面高度为120m ,可得10t =时,120H =,再利用排除法可得答案. 【详解】因为游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min , 所以游客进仓后第一次到达最高点时摩天轮旋转半周,大约需要10min , 又因为摩天轮最高点距离地面高度为120m , 所以10t =时,120H =,对于A ,10t =时,55cos 106555cos 65651022H πππ⎛⎫=⨯-+=+= ⎪⎝⎭,不合题意;对于B ,10t =时,55sin 106555sin 651201022H πππ⎛⎫=⨯-+=+= ⎪⎝⎭,符合题意;对于C ,10t =时,355cos 106555cos65651022H πππ⎛⎫=⨯++=+= ⎪⎝⎭,不合题意; 对于D ,10t =时,355sin 106555sin65101022H πππ⎛⎫=⨯++=+= ⎪⎝⎭,不合题意; 故选:B. 【点睛】方法点睛:特殊法是“小题小做”的重要策略,排除法解答选择题是高中数学一种常见的解题思路和方法,这种方法即可以提高做题速度和效率,又能提高准确性,这种方法主要适合下列题型: (1)求值问题(可将选项逐个验证);(2)求范围问题(可在选项中取特殊值,逐一排除);(3)图象问题(可以用函数性质及特殊点排除);(4)解方程、求解析式、求通项、求前n 项和公式问题等等.二、填空题13.③④【分析】①化简可得即可求出;②由可能相等可判断;③利用同角三角函数关系可化简求出;④化简可得利用奇函数的性质可得【详解】对①则最小正周期为故①错误;对②若则可能相等故②错误;对③若则即即即即故③解析:③④ 【分析】①,化简可得tan 24y x π⎛⎫=+⎪⎝⎭,即可求出;②由,a b 可能相等可判断;③利用同角三角函数关系可化简求出;④化简可得24sin 141x xy x +=++,利用奇函数的性质可得.【详解】对①,tantan 21tan 24tan 21tan 241tan tan 24xx y x x x πππ++⎛⎫===+ ⎪-⎝⎭-⋅,则最小正周期为2π,故①错误;对②,若()()f a f b =,则,a b 可能相等,故②错误;对③,若22tan 3tan 2αβ=+,则2222sin 3sin 2cos cos αβαβ=+,即222222sin cos 3cos sin 2cos cos αβαβαβ=+,即22222222sin cos cos cos 3cos sin 3cos cos αβαβαβαβ+=+,即22cos 3cos βα=,即223sin sin 2αβ-=,故③正确;对④,()22221sin 4sin 14141x xx x y x x +++==+++,令()24sin 41x x g x x =++,则()()g x g x -=,故()g x 是奇函数,()()max min 0g x g x ∴+=,()()max min 112M N g x g x ∴+=+++=,故④正确.故答案为:③④. 【点睛】本题考查正切型函数的周期,考查同角三角函数的关系,考查奇函数的应用,解题的关键是正确利用三角函数的关键进行化简.14.2【分析】根据函数为偶函数可知函数必有一个零点为可得根据函数的图象可知解得即可得解【详解】因为函数为偶函数且有且仅有3个零点所以必有一个零点为所以得所以函数的图象与直线在上有且仅有3个交点因为函数的解析:2 【分析】根据函数为偶函数可知函数必有一个零点为0x =,可得1a =-,根据函数cos y x ω=(0)>ω的图象可知222πππωω≤<⨯,解得24ω≤<即可得解.【详解】因为函数cos ,[],y a x x ωππ=+∈-为偶函数,且有且仅有3个零点,所以必有一个零点为0x =, 所以cos00a +=,得1a =-,所以函数cos y x ω=(0)>ω的图象与直线1y =在[,]-ππ上有且仅有3个交点, 因为函数cos y x ω=(0)>ω的最小正周期2T πω=,所以2T T π≤<,即222πππωω≤<⨯,得24ω≤<,所以ω的最小值是2.故答案为:2 【点睛】关键点点睛:根据偶函数图象的对称性求出a 是解题关键.15.【分析】如图作出月牙湖的示意图由题意可得可求的值进而由图利用扇形的弧长公式可计算得解【详解】如图是月牙湖的示意图是的中点连结可得由条件可知所以所以所以月牙泉的周长故答案为:【点睛】关键点点睛:本题的 解析:(40303)π+【分析】如图,作出月牙湖的示意图,由题意可得3sin 2QPO ∠=,可求,QPO QPT ∠∠的值,进而由图利用扇形的弧长公式可计算得解. 【详解】如图,是月牙湖的示意图,O 是QT 的中点,连结PO ,可得PO QT ⊥,由条件可知603QT =,60PQ = 所以3sin QPO ∠=,所以3QPO π∠=,23QPT π∠=,所以月牙泉的周长(260303403033l πππ=⨯+⨯=+. 故答案为:(40303π+ 【点睛】关键点点睛:本题的关键是根据实际问题抽象出图象,再根据数形结合分析问题.16.②④【分析】结合三角函数的图象与性质对四个结论逐个分析即可得出答案【详解】①要得到的图象应将的图象向左平移个单位长度所以①错误;②令解得所以直线是的一条对称轴故②正确;③令解得因为所以在定义域内的单解析:②④ 【分析】结合三角函数的图象与性质对四个结论逐个分析即可得出答案. 【详解】①要得到()5sin 2g x x =的图象,应将()ππ5sin 25sin 248f x x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象向左平移π8个单位长度,所以①错误;②令ππ2π42x k -=+,k ∈Z ,解得3ππ82k x =+,k ∈Z ,所以直线3π8x =是()y f x =的一条对称轴,故②正确;③令ππ3π22π42π22k k x ≤+≤-+,k ∈Z ,解得3π7πππ88k x k +≤≤+,k ∈Z ,因为[]π,πx ∈-,所以()f x 在定义域内的单调递减区间为3π7π,88⎡⎤⎢⎥⎣⎦和5ππ,88⎡⎤--⎢⎥⎣⎦,所以③错误;④5π5ππ5sin 25sin 2884y f x x x ⎡⎤⎛⎫⎛⎫=+=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦是奇函数,所以该说法正确. 【点睛】本题考查了正弦型函数的对称轴、单调性、奇偶性与平移变换,考查了学生对()sin y A ωx φ=+的图象与性质的掌握,属于中档题.17.②③【分析】根据已知条件确定函数的解析式进一步利用整体思想确定函数的对称轴方程对称中心及各个交点的特点进一步确定答案【详解】函数(其中)的图象关于点成中心对称且与点相邻的一个最低点为则:所以进一步解解析:②③ 【分析】根据已知条件确定函数的解析式,进一步利用整体思想确定函数的对称轴方程,对称中心及各个交点的特点,进一步确定答案. 【详解】函数()()sin f x A x ωϕ=+(其中0A >,0,0ωϕπ><<)的图象关于点M 5,012π⎛⎫⎪⎝⎭成中心对称,且与点M 相邻的一个最低点为2,33π⎛⎫- ⎪⎝⎭,, 则:2543124T πππ-== ,所以T π=: ,326f x sin x π⎛⎫=+ ⎪⎝⎭(). 进一步解得:223A πωπ===, 由于()()sin f x A x ωϕ=+(其中0A >,0,0ωϕπ><<)的图象关于点M 5,012π⎛⎫⎪⎝⎭成中心对称,,所以:5212k k Z πϕπ⋅+∈=(), 解得:5,6k k Z πϕπ-∈= ,由于0ϕπ<<, 所以:当1k = 时,6πϕ=.所以: ①当2x π=时,33262f sin πππ⎛⎫=+=- ⎪⎝⎭().故错误. ②3232633f x sin x cos x πππ⎡⎤⎛⎫⎛⎫--+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=. 则3y f x π⎛⎫=- ⎪⎝⎭为偶函数,故正确. ③由于:351212x ππ-≤≤, 则:0266x ππ≤+≤,所以函数()f x 的图象与1y =有6个交点. 根据函数的交点设横坐标为123456x x x x x x 、、、、、, 根据函数的图象所有交点的横标和为7π.故正确. 故答案为②③ 【点睛】本题考查的知识要点:正弦型函数的解析式的求法,主要确定A ,ω、φ的值,三角函数诱导公式的变换,及相关性质得应用,属于基础题型.18.①④【分析】根据正切函数的周期判断①是否正确正切函数的奇偶性判断②是否正确由判断③是否正确由正切函数的单调性判断④是否正确由正切函数的图象判断⑤是否正确【详解】由于f(x)=tanx 的周期为π故①正解析:①④ 【分析】根据正切函数()tan f x x =的周期判断①是否正确,正切函数的奇偶性判断②是否正确,由tan 00=判断③是否正确,由正切函数的单调性判断④是否正确,由正切函数的图象判断⑤是否正确. 【详解】由于f (x )=tan x 的周期为π,故①正确; 函数f (x )=tan x 为奇函数,故②不正确; f (0)=tan 0=0,故③不正确;④表明函数为增函数,而f (x )=tan x 为区间,22ππ⎛⎫- ⎪⎝⎭上的增函数,故④正确;⑤由函数f (x )=tan x 的图象可知,设A =12()()2f x f x +,B =122x x f +⎛⎫⎪⎝⎭故函数在区间,02π⎛⎫- ⎪⎝⎭上有1212()()22x x f x f x f ++⎛⎫> ⎪⎝⎭, 在区间0,2π⎛⎫⎪⎝⎭上有1212()()22x x f x f x f ++⎛⎫<⎪⎝⎭,故⑤不正确. 故答案为:①④ 【点睛】本题考查了正切函数的图象和性质,属于中档题.19.9【分析】由在区间上单调可得故进一步求出范围即可【详解】由知故;又在区间上单调故即18符合条件的的值有9个故答案为:9【点睛】本题考查三角函数的图象与性质考查转化与化归思想考查逻辑推理能力运算求解能解析:9 【分析】 由()f x 在区间(,)43ππ上单调,可得342T ππ-,故6T π,进一步求出ω范围即可. 【详解】由()24f π=,()0f π=知,34244T kT πππ+=-=,k ∈N , 故312T k π=+,2(12)3k ω+=,k ∈N ; 又()f x 在区间(,)43ππ上单调,∴342T ππ-,故6T π,∴212T πω=,即2(12)123k +, ∴172k,k ∈N , 0k ∴=,1,2⋯,8符合条件的ω的值有9个. 故答案为:9. 【点睛】本题考查三角函数的图象与性质,考查转化与化归思想,考查逻辑推理能力、运算求解能力,属中档题.20.①③【分析】利用诱导公式化简函数判断①正误;求出函数周期判断②;求出函数的对称中心判断③;求出函数的对称轴判断④【详解】解:对于①所以①正确;对于②最小正周期所以②不正确;对于③因为所以为的对称中心解析:①③ 【分析】利用诱导公式化简函数()f x ,判断①正误;求出函数()f x 周期判断②;求出函数()f x 的对称中心判断③;求出函数()f x 的对称轴判断④. 【详解】解:对于①,()4sin 24cos 2323f x x x πππ⎛⎫⎛⎫=+=-- ⎪ ⎪⎝⎭⎝⎭4cos 24cos 2326x x πππ⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭,所以①正确;对于②,最小正周期222T πππω===,所以②不正确; 对于③,因为4sin 4sin 00633f πππ⎛⎫⎛⎫-=-+== ⎪ ⎪⎝⎭⎝⎭所以,,06π⎛⎫- ⎪⎝⎭为()f x 的对称中心,故③正确;对于④,()()4sin 23f x x x R π⎛⎫=+∈ ⎪⎝⎭的对称直线满足2,32x k k Z πππ+=+∈,6x π=-不满足条件,所以④不正确.故答案为:①③. 【点睛】本题考查正弦函数的性质,考查基本概念、基本知识的理解掌握程度,属于基础题.三、解答题21.(1)π;(2)()511,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(3)最小值为32;最大值为94. 【分析】(1)利用正弦型函数的周期公式可求得函数()f x 的最小正周期; (2)解不等式()3222232k x k k Z πππππ+≤-≤+∈,可得出函数()f x 的单调递减区间;(3)由44x ππ-≤≤求出23x π-的取值范围,利用正弦函数的基本性质可求得函数()f x 的最小值和最大值. 【详解】(1)因为1()sin 2223f x x π⎛⎫=-+ ⎪⎝⎭, 所以函数()f x 的最小正周期22T ππ==; (2)由()3222232k x k k Z πππππ+≤-≤+∈,得()5111212k x k k Z ππππ+≤≤+∈.即函数()f x 的单调递减区间为()511,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦; (3)因为44x ππ-≤≤,所以52636πππ-≤-≤x ,所以, 当232x ππ-=-即12x π=-时,函数()f x 取最小值,()min 13sin 2222f x π⎛⎫=-+= ⎪⎝⎭; 当236x ππ-=即4x π=时,函数()f x 取最大值,()max 19sin 2264f x π=+=. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).22.(1)36S π⎛⎫= ⎪⎝⎭;(2)1sin 3θ=. 【分析】(1)作出图形,可知公共部分区域为直角三角形,计算出两直角边的长,由此可求得该直角三角形的面积;(2)分6πθ=、06πθ<<、62ππθ<<三种情况讨论,求出()S θ的表达式,结合()728S θ=可求得sin θ的值. 【详解】 (1)当3πθ=时,A '点在矩形OABC 外部,公共部分形状为三角形,设A O BC D '⋂=,则6COD π∠=,3tan63CD CO π==, 则1133132236S CD CO π⎛⎫=⨯⨯=⨯⨯=⎪⎝⎭;(2)①当6πθ=时,点A '在线段BC 上,此时,223A C A O OC ''=-=,113136222S OC A C π⎛⎫'=⨯=⨯⨯=⎪⎝⎭; ②当06πθ<<时,公共部分为四边形,A '点在矩形OABC 内部,过点A '作线段AB 的平行线,分别交线段AO 、BC 于点E 、F ,设A B BC G ''⋂=,则有如下长度:2cos OE θ=,22cos AE θ=-,2sin A E θ'=,12sin A F θ'=-,()12sin tan FG θθ=-,则()OEA A FG OABC AEFB S S S S S θ''=---△△矩形矩形, 即()()()()111222cos 2cos 2sin 12sin 12sin tan 22S θθθθθθθ=⨯---⨯⨯-⨯-- ()2sin 12sin 45sin 2cos 2sin cos 2cos 2cos θθθθθθθθ--=--=,由题知45sin 2cos 8θθ-=,两边同时平方得221640sin 25sin 494cos 32θθθ-+=, 由22cos 1sin θθ=-,整理得2249sin 320sin 790θθ-+=,即()()3sin 183sin 790θθ--=,因为06πθ<<,所以1sin 2θ<,故1sin 3θ=;③当62ππθ<<时,公共部分为三角形,且()116228S S πθ⎛⎫<=⨯=< ⎪⎝⎭,不合题意; 综上所述,1sin 3θ=. 【点睛】关键点点睛:解决本题第二问的关键就是找出θ的临界情况,然后对θ的取值进行分类讨论,确定公共区域的形状,计算求出()S θ的表达式,结合已知条件求解sin θ的值.23.(1)()sin cos f ααα=;(2);(3)5,1212k k k Z ππαπαπ⎧⎫+≤≤+∈⎨⎬⎩⎭. 【分析】(1)利用诱导公式化简,即可求出()f α; (2)结合(1)得1()sin cos 8f ααα==,利用同角三角函数的关系,结合α的范围,即可得答案;(3)由题意可得1sin 22α≥,利用三角函数的图像与性质,即可求得α的范围. 【详解】(1)2sin cos tan ()sin cos (sin )(tan )f αααααααα⋅⋅==--; (2)由(1)可得1()sin cos 8f ααα==,则23(cos sin )12sin cos 4αααα-=-=, ,sin cos 42ππααα<<∴>,即cos sin 0αα-<cos sin 2αα∴-=-;(3)由题意得11()sin cos sin 224f αααα==≥,1sin 22α∴≥, 5222,66k k k Z πππαπ∴+≤≤+∈,即5,1212k k k Z πππαπ+≤≤+∈,所以α的取值集合为5,1212k k k Z ππαπαπ⎧⎫+≤≤+∈⎨⎬⎩⎭. 【点睛】本题考查诱导公式的应用、同角三角函数的关系、三角函数的图像与性质,考查分析理解,求值化简的能力,考查学生对基础知识的掌握程度,属基础题. 24.(1)1A =,2ω=;(2)0,12π⎡⎤⎢⎥⎣⎦和7,12ππ⎡⎤⎢⎥⎣⎦. 【分析】(1)根据辅助角公式和两角和的正弦公式化简得()2sin 3f x A x πω⎛⎫=+ ⎪⎝⎭,由函数图象可知()f x 的最大值为2,可求出A ,由图象可知43124T πππ=-=,结合2T πω=,即可求出ω的值;(2)由(1)得2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,利用整体代入法并结合正弦函数的单调性,即可求出()y f x =在[]0,π的单调增区间. 【详解】解:(1)由题可知,()sin cos (0,0)f x A x x A ωωω=+>>即1()2sin cos 2sin 223f x A x x A x πωωω⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭, 由图象可知,()f x 的最大值为2,则22A =,所以1A =, 由图象可知,43124T πππ=-=,则2T ππω==,所以2ω=; (2)由(1)得2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭, 令222,232k x k k πππ-+π≤+≤+π∈Z , 解得:5,1212k x k k Z ππππ-+≤≤+∈, 又因为[]0,x π∈,所以函数()y f x =在[]0,π的单调增区间为:0,12π⎡⎤⎢⎥⎣⎦和7,12ππ⎡⎤⎢⎥⎣⎦. 【点睛】思路点睛:本题考查由函数()sin y A ωx φ=+的部分图象求解析式,由函数图象的最大值求出A ,由周期2T πω=求出ω,从而可求出函数解析式,再利用整体代入法求正弦型函数的单调性,熟练掌握正弦函数的图象和性质是解题的关键. 25.(1)12()2sin 23f x x π⎛⎫=- ⎪⎝⎭,递增区间为74,4,33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦; (2)[]1,2-. 【分析】(1)由三角函数的图象,求得函数的解析式12()2sin 23f x x π⎛⎫=- ⎪⎝⎭,结合三角函数的性质,即可求解.(2)由三角函数的图象变换,求得2()2sin 223g x x m π⎛⎫=-+ ⎪⎝⎭,根据()g x 的图象关于直线512x π=对称,求得m 的值,得到()2sin 23g x x π⎛⎫=- ⎪⎝⎭,结合三角函数的性质,即可求解. 【详解】(1)由图象可知2A =,422433T πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦, 所以212T πω==,所以1()2sin 2f x x ϕ⎛⎫=+ ⎪⎝⎭,由图可求出最低点的坐标为,23π⎛⎫- ⎪⎝⎭,所以2sin 236f ππϕ⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭, 所以262k ππϕπ+=-+,所以22,3k k Z πϕπ=-+∈, 因为||ϕπ<,所以23πϕ=-,所以12()2sin 23f x x π⎛⎫=- ⎪⎝⎭,由1222,2232k x k k Z πππππ-+≤-≤+∈,可得744,33k x k k Z ππππ+≤≤+∈. 所以函数()f x 的单调递增区间为74,4,33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦.(2)由题意知,函数22()2sin 2()2sin 2233g x x m x m ππ⎡⎤⎛⎫=+-=-+ ⎪⎢⎥⎣⎦⎝⎭, 因为()g x 的图象关于直线512x π=对称, 所以5222,1232m k k Z ππππ⨯-+=+∈,即,62k m k Z ππ=+∈,因为02m π<<,所以6m π=,所以()2sin 23g x x π⎛⎫=-⎪⎝⎭. 当7,1212x ππ⎡⎤∈⎢⎥⎣⎦时,52,366x πππ⎡⎤-∈-⎢⎥⎣⎦,可得1sin 2,132x π⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦, 所以2sin 2[1,2]3x π⎛⎫-∈- ⎪⎝⎭,即函数()g x 的值域为[]1,2-. 【点睛】解答三角函数的图象与性质的基本方法:1、根据已知条件化简得出三角函数的解析式为sin()y A wx ϕ=+的形式;2、熟练应用三角函数的图象与性质,结合数形结合法的思想研究函数的性质(如:单调性、奇偶性、对称性、周期性与最值等),进而加深理解函数的极值点、最值点、零点及有界性等概念与性质,但解答中主要角的范围的判定,防止错解. 26.(1) 2.5sin()56y x π=+;(2)该船1:00至5:00和13:00至17:00期间可以进港,在港口最多能呆4个小时. 【分析】(1)由表格中数据可得, 2.5,5,12A B T ===,26T ππω==,取3x =代入可得2,k k Z ϕπ=∈,则解析式可得;(2)由(1)得计算2.5sin()5 6.256x π+≥解x 范围即可得结果.【详解】解:(1)由表格中数据可得, 2.5,5,12A B T ===. 因为0>ω,所以22126T πππω===. 因为3x =时y 取得最大值,所以32,62k k Z ππϕπ⨯+=+∈,解得2,k k Z ϕπ=∈.所以这个函数解析式为 2.5sin()56y x π=+(2)因为货船的吃水深度为5米,安全间隙至少要有1.25米, 所以2.5sin()5 6.256x π+≥,即1sin()562x π+≥, 所以522,666m x m m N πππππ+≤≤+∈,解得112512,m x m m N +≤≤+∈.取0,1,m m ==得15,1317x x ≤≤≤≤.。
高中数学必修四总复习测试题

高中数学必修四总复习测试题第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的.)1.化简sin()2απ+等于( ). A.cos α B.sin α C.cos α- D.sin α-2.已知M 是ABC ∆的BC 边上的一个三等分点,且BM MC <,若AB = a ,AC =b ,则AM 等于( ).A.1()3-a bB.1()3+a bC.1(2)3+b aD.1(2)3+a b3.已知3tan =α,则αααα22cos 9cos sin 4sin 2-+的值为( ). A.3 B.1021 C.31 D.301 4.化简=--+( ). A. B.0 C. D. 5.函数x x y 2cos 2sin =是( ). A.周期为4π的奇函数 B.周期为2π的奇函数 C.周期为2π的偶函数 D.周期为4π的偶函数 6.已知)7,2(-M ,)2,10(-N ,点P 是线段MN 上的点,且−→−PN −→−-=PM 2,则P 点的坐标为( ). A.)16,14(- B.)11,22(- C.)1,6( D.)4,2( 7.已知函数sin()y A x B ωφ=++(0,0,||2A ωφπ>><)的周期为T ,在一个周期内的图象如图所示,则正确的结论是( ). A.3,2A T ==π B.2,1=-=ωBC.4,6T φπ=π=-D.3,6A φπ== 8.将函数sin()3y x =-π的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移3π个单位,则所得函数图像对应的解析式为( ). A.1sin(26y x =-π B.1sin()23y x =-π C.1sin 2y x = D.sin(2)6y x =-π9.若平面四边形ABCD 满足0,()0AB CD AB AD AC +=-⋅=,则该四边形一定是( ).A.直角梯形B.矩形C.菱形D.正方形10.函数()sin 2cos2f x x x =-的最小正周期是( ).A.π2B.πC.2πD.4π11.设单位向量1e ,2e 的夹角为︒60,则向量1234e e +与向量1e 的夹角的余弦值是( ). A.43 B.375 C.3725 D.375 12.定义运算⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡df ce bf ae f e d c b a ,如⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡1514543021,已知αβ+=π,2αβπ-=,则=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡ββααααsin cos sin cos cos sin ( ). A.00⎡⎤⎢⎥⎣⎦ B.01⎡⎤⎢⎥⎣⎦ C.10⎡⎤⎢⎥⎣⎦D.11⎡⎤⎢⎥⎣⎦第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分. 把答案填在题中的横线上.) 13.︒75sin 的值为 .14.已知向量(2,4)=a ,(1,1)=b ,若向量()⊥+λb a b ,则实数λ的值是.15.︒︒︒80cos 40cos 20cos 的值为_____________________________. 16.在下列四个命题中:①函数tan()4y x π=+的定义域是{,}4x x k k π≠+π∈Z ; ②已知1sin 2α=,且[0,2]α∈π,则α的取值集合是{}6π;③函数x a x x f 2cos 2sin )(+=的图象关于直线8x π=-对称,则a 的值等于1-;④函数2cos sin y x x =+的最小值为1-.把你认为正确的命题的序号都填在横线上____________________.三、解答题(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程及演算步骤.) 17.(本小题满分10分)已知4cos()45x π+=,(,)24x ππ∈--,求xxx tan 1sin 22sin 2+-的值.18.(本小题满分12分)已知函数()sin sin()2f x x x π=++,x ∈R . (1)求)(x f 的最小正周期;(2)求)(x f 的的最大值和最小值; (3)若43)(=αf ,求α2sin 的值.19.(本小题满分12分)(1)已知函数1()sin()24f x x π=+,求函数在区间[2,2]-ππ上的单调增区间; (2)计算:)120tan 3(10cos 70tan -︒︒︒.20.(本小题满分13分)已知函数()sin()f x x ωφ=+(0>ω,0φ≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π.(1)求)(x f 的解析式; (2)若(,)32αππ∈-,1()33f απ+=,求5sin(2)3απ+的值.21.(本小题满分13分)已知a ,b ,c 是同一平面内的三个向量,其中)2,1(=a .(1)若||=c ,且//c a ,求c 的坐标;(2)若||=b ,且2+a b 与2-a b 垂直,求a 与b 的夹角θ.22.(本小题满分14分)已知向量33(cos ,sin )22x x =a ,(cos ,sin )22x x =-b ,且[0,]2x π∈,()2||f x =⋅-λ+a b a b (λ为常数),求:(1)⋅a b 及||+a b ; (2)若)(x f 的最小值是23-,求实数λ的值.参考答案一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的.)1.A 由诱导公式易得A 正确.2.C BC =- b a ,11()33BM BC ==- b a ,11()(2)33AM AB BM =+=+-=+ a b a b a .3.B αααααααααα222222cos sin cos 9cos sin 4sin 2cos 9cos sin 4sin 2+-+=-+10211tan 9tan 4tan 222=+-+=ααα. 4.B )()(=-=+-+=--+. 5.B x x x y 4sin 212cos 2sin ==,故是周期为2π的奇函数. 6.D 设),(y x P ,则)2,10(y x ---=,)7,2(y x ---=, −→−PN ⎩⎨⎧==⇒⎩⎨⎧--=-----=-⇒-=−→−.4,2),7(22),2(2102y x y y x x PM 7.C ⎩⎨⎧-==⇒⎩⎨⎧-=+-=+,1,3,4,2B A B A B A ππππ42)32(342=⇒=--=T T ,21422===πππωT ,623421πϕπϕπ-=⇒=+⨯. 8.A sin()sin()sin[(]sin(3336111))2232y x y y x x x πππππ=-→=→==-+--.9.C 0AB CD AB CD +=⇒=-⇒四边形ABCD 为平行四边形,()0AB AD AC DB AC DB AC -⋅=⋅=⇒⊥,对角线互相垂直的平行四边形为菱形.10.B ()sin 2cos 2)4f x x x x π=-=-,ππ==22T .11.D 1||1=e ,1||2=e ,2160cos ||||2121=︒⋅=⋅e e e e ,543)43(2121121=⋅+=⋅+e e e e e e ,37|43|21===+e e ,375|||43|cos 121121=⋅+=e e e θ.12.A ⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡002cos sin )cos()sin(sin sin cos cos sin cos cos sin sin cos sin cos cos sin ππβαβαβαβαβαβαββαααα.二、填空题(本大题共4小题,每小题4分,共16分. 把答案填在题中的横线上.) 13.426+ ︒︒+︒︒=︒+︒=︒30sin 45cos 30cos 45sin )3045sin(75sin 42621222322+=⨯+⨯=. 14.3- 30)4(2)4,2()1,1()()(-=⇒=+++=++⋅=+⋅⇒+⊥λλλλλλλ. 15.818120sin 8160sin 20sin 880cos 40cos 20cos 20sin 880cos 40cos 20cos =︒︒=︒︒︒︒︒=︒︒︒. 16.①③④ )(424Z k k x k x ∈+≠⇒+≠+πππππ,故①正确;1sin 2α=,且[0,2]6παπα∈⇒=或65πα=,故②不正确;函数)(x f 的图象关于直线8π-=x 对称1)4()0(-=⇒-=⇒a f f π,故③正确;22215cos sin 1sin sin (sin )24y x x x x x =+=-+=--+,451≤≤-y ,故④正确. 三、解答题(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程及演算步骤.) 17.解:∵)4,2(ππ--∈x , ∴)0,4(4ππ-∈+x ,∵54)4cos(=+x π, ∴53)4sin(-=+x π,4sin)4cos(4cos)4sin(]4)4sin[(sin ππππππx x x x +-+=-+=102722542253-=⋅-⋅-=, ∴102cos =x , ∴7528sin cos )sin (cos cos sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 22=+-=+-=+-x x x x x x xx x x x x x x .18.解:)4sin(2cos sin )2sin(sin )(ππ+=+=++=x x x x x x f ,(1))(x f 的最小正周期为ππ212==T ; (2))(x f 的最大值为2和最小值2-;(3)因为43)(=αf ,即167cos sin 2169)cos (sin 43cos sin 2-=⇒=+⇒=+αααααα,即1672sin -=α. 19.解:(1)由πππππk x k 2242122+≤+≤+-(Z k ∈)得ππππk x k 42423+≤≤+-(Z k ∈),当0=k 时,得223ππ≤≤-x , ]2,2[]2,23[ππππ-⊂-,且仅当0=k 时符合题意,∴函数)421sin()(π+=x x f 在区间]2,2[ππ-上的单调增区间是]2,23[ππ-. (2)︒︒-︒⋅︒⋅︒︒=-︒︒︒20cos 20cos 20sin 310cos 70cos 70sin )120tan 3(10cos 70tan ︒︒⋅︒︒-=︒︒-⋅︒⋅︒︒=20cos 20sin 70cos 70sin 20cos 10sin 210cos 70cos 70sin120cos 20sin 20sin 20cos -=︒︒⋅︒︒-=. 20.解:(1)∵图象上相邻的两个最高点之间的距离为π2,∴π2=T , 则12==Tπω, ∴)sin()(ϕ+=x x f ,∵)(x f 是偶函数, ∴)(2Z k k ∈+=ππϕ,又πϕ≤≤0, ∴2πϕ=, 则x x f cos )(=.(2)由已知得31)3cos(=+πα, ∵)2,3(ππα-∈, ∴)65,0(3ππα∈+, 则322)3sin(=+πα, ∴924)3cos()3sin(2)322sin()352sin(-=++-=+-=+παπαπαπα. 21.解:(1)设),(y x c =, ∵a c //,)2,1(=a , ∴02=-y x , ∴x y 2=,∵52||=, ∴5222=+y x , ∴2022=+y x , 即20422=+x x ,∴⎩⎨⎧==,4,2y x 或⎩⎨⎧-=-=,4,2y x∴)4,2(=或)4,2(--=(2)∵⊥+2-2, ∴)2(+0)2(=-⋅,∴023222=-⋅+b b a a , 即0||23||222=-⋅+b b a a , 又∵5||2=,45)25(||22==, ∴0452352=⨯-⋅+⨯b a , ∴25-=⋅b a , ∵5||=a ,25||=b , ∴125525||||cos -=⋅-=⋅=b a θ,∵],0[πθ∈, ∴πθ=. 22.解:(1)x xx x x 2cos 2sin 23sin 2cos 23cos=-=⋅, x x xx x x 222cos 22cos 22)2sin 23(sin )2cos 23(cos||=+=-++=+, ∵]2,0[π∈x , ∴0cos ≥x , x cos 2||=+.(2)2221)(cos 2cos 42cos )(λλλ---=-=x x x x f ,∵]2,0[π∈x , ∴1cos 0≤≤x ,①当0<λ时,当且仅当0cos =x 时,)(x f 取得最小值1-,这与已知矛盾;②当10≤≤λ,当且仅当λ=x cos 时,)(x f 取得最小值221λ--,由已知得23212-=--λ,解得21=λ; ③当1>λ时,当且仅当1cos =x 时,)(x f 取得最小值λ41-, 由已知得2341-=-λ,解得85=λ,这与1>λ相矛盾. 综上所述,21=λ为所求.。
【沪科版】高中数学必修四期末第一次模拟试卷(及答案)

一、选择题1.已知函数2()2sin cos (0)f x x x x ωωωω=->图像的相邻两条对称轴之间的距离为2π,则2f π⎛⎫= ⎪⎝⎭( )A .1B .1--C .0D .-2.函数()2cos ||cos 2f x x x =-在[,]x ππ∈-上的单调增区间为( ) A .,3ππ⎡⎤--⎢⎥⎣⎦和0,3π⎡⎤⎢⎥⎣⎦B .,03π⎡⎤-⎢⎥⎣⎦和,3ππ⎡⎤⎢⎥⎣⎦C .,06π⎡⎤-⎢⎥⎣⎦和,6ππ⎡⎤⎢⎥⎣⎦D .,6ππ⎡⎤--⎢⎥⎣⎦和06,π⎡⎤⎢⎥⎣⎦ 3.已知4sin cos 3θθ+=,,42ππθ⎛⎫∈ ⎪⎝⎭,则sin cos θθ-的值为( )A .13- B .13C .3-D .34.已知0,2x π⎛⎫∈ ⎪⎝⎭,3cos 45x π⎛⎫+= ⎪⎝⎭,则sin x 的值为( )A .BCD . 5.己知平面向量,a b 满足1a a b =-=,则32a b a b -++的最大值为( )A .4B .C .3+D .66.过点()3,1P 的直线l 与函数21()26x f x x -=-的图象交于A ,B 两点,O 为坐标原点,则()OA OB OP +⋅=( )A B .210C .10D .207.在直角梯形ABCD 中,0AD AB ⋅=,30B ∠=︒,AB =2BC =,13BE BC =,则( )A .1163AE AB AD =+ B .1263AE AB AD =+ C .5163AE AB AD =+ D .5166AE AB AD =+8.设O 是△ABC 20OB OC ++=,则∠BOC =( ) A .6π B .3π C .2π D .23π9.在平面直角坐标系中,AB 是单位圆上的一段弧(如右图),点P 是圆弧AB 上的动点,角α以Ox 为始边,OP 为终边.以下结论正确的是( )A .tan α<cos α<sin αB .cos α<tan α<sin αC .sin α<cos α<tan αD .以上答案都不对10.已知函数()cos2sin 2f x x x =-,将()y f x =的图象向左平移a (0a >)个单位长度可以得到一个奇函数的图象,将()y f x =的图象向右平移b (0b >)个单位长度可以得到一个偶函数的图象,则a b -的最小值等于( ) A .0B .8π C .4π D .2π 11.设函数()3sin()10,2f x x πωϕωϕ⎛⎫=++><⎪⎝⎭的最小正周期为π,其图象关于直线3x π=对称,则下列说法正确是( )A .()f x 的图象过点30,2⎛⎫ ⎪⎝⎭; B .()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上单调递减; C .()f x 的一个对称中心是7,012π⎛⎫⎪⎝⎭; D .将()f x 的图象向左平移12ϕ个单位长度得到函数3sin 21y x =+ 的图象. 12.将函数()3sin()2f x x =--图象上每一点的纵坐标不变,横坐标缩短为原来的13,再向右平移29π个单位得到函数()g x 的图象,若()g x 在区间,18πθ⎡⎤-⎢⎥⎣⎦上的最大值为1,则θ的最小值为( )A .12πB .6πC .3π D .18π 二、填空题13.若5,24ππα⎛⎫∈ ⎪⎝⎭,3cos 45πα⎛⎫-= ⎪⎝⎭,则cos2=α______.14.已知sin 3α=,()1cos 3αβ+=-,且,0,2παβ⎛⎫∈ ⎪⎝⎭,则sin β=_____.15.已知πsin(π)3sin()02αα+--=,则cos2α的值为________. 16.已知ABC ,点P 是平面上任意一点,且AP AB AC λμ=+(,λμ∈R ),给出以下命题: ①若1ABλ=,1ACμ=,则P 为ABC 的内心;②若1λμ==,则直线AP 经过ABC 的重心; ③若1λμ+=,且0μ>,则点P 在线段BC 上; ④若1λμ+>,则点P 在ABC 外; ⑤若01λμ<+<,则点P 在ABC 内. 其中真命题为______ 17.已知||1,||3,0OA OB OA OB ==⋅=|,点C 在AOB ∠内,且30AOC ∠=︒,设(,)OC mOA nOB m n R =+∈,则mn等于 . 18.已知非零向量m →,n →满足4m →=3n →,cos m →〈,13n →〉=.若n →⊥t m n →→⎛⎫+ ⎪⎝⎭,则实数t的值为_____________.19.已知函数cos ,[],y a x x ωππ=+∈-(其中,a ω为常数,且0>ω)有且仅有3个零点,则ω的最小值是_________. 20.设函数()3sin 23f x x π⎛⎫=-⎪⎝⎭的图象为C ,给出下列命题:①图象C 关于直线1112π=x 对称;②函数()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是减函数;③函数()f x 是奇函数;④图象C 关于点,03π⎛⎫⎪⎝⎭对称.其中,错误命题的是______. 三、解答题21.如图,在扇形OPQ 中,半径OP =1,圆心角3POQ π∠=,C 是扇形弧上的动点,矩形ABCD 内接于扇形.记POC α∠=,求当角α取何值时,矩形ABCD 的面积最大?并求出这个最大面积.22.在①2sin 3sin 2αα=,②6cos 2α=,③tan 22α=这三个条件中任选一个,补充在下面问题中,并解决问题. 已知10,,0,,cos()224ππαβαβ⎛⎫⎛⎫∈∈+=- ⎪ ⎪⎝⎭⎝⎭,_______,求cos β. 注:如果选择多个条件分别解答,按第一个解答计分.23.已知单位向量1e ,2e 的夹角为60︒,向量12a e e =+,21b e te =-,t R ∈. (1)若//a b ,求t 的值; (2)若2t =,求向量a ,b 的夹角.24.平面内给定三个向量(3,2),(1,2),(4,1)a b c ==-=,若()//(2)a kc b a +-,求实数k .25.函数()()()sin 0,0,0πf x A x A ωϕωϕ=+>><<的部分图象如图所示.(1)求函数()f x 的解析式;(2)求函数()f x 的单调递增区间,并求()f x 取最小值时的自变量x 的集合. 26.已知函数()12sin 26x f x π⎛⎫=+⎪⎝⎭,x ∈R . (1)用“五点法”画出函数()f x 一个周期内的图象; (2)求函数()f x 在[],ππ-内的值域; (3)若将函数()f x 的图象向右平移6π个单位长度,得到函数()g x 的图象,求函数()g x 在[],ππ-内的单调增区间.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】先将函数化简整理,根据相邻对称轴之间距离求出周期,确定1ω=,再求2f π⎛⎫ ⎪⎝⎭. 【详解】因为()21cos 22sin cos sin 22xf x x x x x ωωωωω-=-=- πsin 222sin 23x x x ωωω⎛⎫=+=+- ⎪⎝⎭由题意知()f x 的最小正周期为π22π⨯=,所以2π2πω=,即1ω=,所以()π2sin 23f x x ⎛⎫=+⎪⎝⎭π2sin 23f ππ⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭.故选:D. 【点睛】本题考查了三角函数的性质,关键点是根据已知条件先化简正弦函数的解析式,还要熟练掌握三角函数的性质才能正确的解题,属于中档题.2.A解析:A 【分析】先把函数解析式化简,然后令cos t x =,利用复合函数单调性求解即可 【详解】 当[]0,x π∈时,22()2cos ||cos 2=2cos (2cos 1)2cos 2cos 1f x x x x x x x =---=-++,令cos [1,1]t x t =∈-,,则cos t x =在[]0,x π∈上为减函数;而2221y t t =-++ 对称轴为12t =,∴2221y t t =-++在1[1,]2t ∈-上单增,在1[,1]2t ∈上单减, ∴()y f x =在0,3x π⎡⎤∈⎢⎥⎣⎦上为增函数,在,3x ππ⎡⎤∈⎢⎥⎣⎦上为减函数. 又()2cos ||cos 2f x x x =-为偶函数,其图像关于y 轴对称, ∴()y f x =在,3ππ⎡⎤--⎢⎥⎣⎦上为增函数,在,03π⎡⎤-⎢⎥⎣⎦上为减函数. 故()y f x =的单调增区间为,3ππ⎡⎤--⎢⎥⎣⎦和0,3π⎡⎤⎢⎥⎣⎦. 故选:A 【点睛】复合函数的单调性口诀:同增异减,其具体含义为: 内外函数的单调性相同(同),则复合函数为增函数(增); 内外函数的单调性相反(异),则复合函数为减函数(减).3.D解析:D 【分析】首先根据题意得到72sin cos 9θθ=,再计算()22sin cos 9θθ-=,根据,42ππθ⎛⎫∈ ⎪⎝⎭判断出sin cos θθ-的符号再进行开方计算即可得到答案. 【详解】 因为4sin cos 3θθ+=,所以()216sin cos 12sin cos 9θθθθ+=+=, 所以72sin cos 9θθ=, 所以()22sin cos 12sin cos 9θθθθ-=-=, 因为,42ππθ⎛⎫∈⎪⎝⎭,所以sin cos θθ>,即sin θcos θ0,所以sin cos θθ-= 故选:D . 【点睛】易错点睛:本题求sin cos θθ-的值时,采用的方法是先对其平方而后再开方,再开方时应注意根据θ的取值范围正确判断sin cos θθ-的符号,从而得到正确的答案.4.B解析:B 【分析】先求得πsin 4x ⎛⎫+ ⎪⎝⎭的值,然后利用ππsin sin 44x x ⎛⎫=+-⎪⎝⎭,展开后计算得出正确选项. 【详解】由于πππ3π0,,,2444x x ⎛⎫⎛⎫∈+∈ ⎪ ⎪⎝⎭⎝⎭, 所以π4sin 45x ⎛⎫+== ⎪⎝⎭.故ππsin sin 44x x ⎛⎫=+- ⎪⎝⎭ππππsin cos cos sin4444x x ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭43525210=⨯-⨯=,故选B. 【点睛】本小题主要考查同角三角函数的基本关系式,考查化归与转化的数学思想方法,属于基础题.5.B解析:B 【分析】利用1a a b =-=得到2cos ,b a b =〈〉,令[]cos ,,1,1t a b t =〈〉∈-,则2b t =,利用平面向量的运算法则得到29832a b a b t -+-=+,再利用基本不等式即可求解. 【详解】因为1a a b =-=, 所以22222cos ,1a a ba ab a b b =-=-〈〉+=,则2cos ,b a b =〈〉, 令[]cos ,,1,1t a b t =〈〉∈-, 所以2b t =, 则()23232a b a b-=-22124a a b t b =-+== ()2222a b a b a a b t b +=+=++418t t =+=+,所以29832a b a b t -+-=+,利用基本不等式知:2a b a b +≤+≤,≤=,=此时2t =±.则32a b a b -++的最大值为 故选:B. 【点睛】思路点睛:利用已知条件得到2cos ,b a b =〈〉,令[]cos ,,1,1t a b t =〈〉∈-,则2b t =,把问题化为了单一变量的函数问题,再利用平面向量的运算法则得到29832a b a b t -+-=+,最后利用基本不等式即可解决.6.D解析:D 【分析】判断函数()f x 的图象关于点P 对称,得出过点()3,1P 的直线l 与函数()f x 的图象交于A ,B 两点时,得出A ,B 两点关于点P 对称,则有 2OA OB OP +=,再计算()OA OB OP +⋅的值.【详解】()52121263x f x x x -==+-- ,∴函数21()26x f x x -=-的图象关于点()3,1P 对称,∴过点()3,1P 的直线l 与函数()2126x f x x -=-的图象交于A ,B 两点,且A ,B 两点关于点()3,1P 对称,∴ 2OA OB OP +=,则()()222223120OA OB OP OP +⋅==⨯+=.故选D . 【点睛】本题主要考查了函数的对称性,以及平面向量的数量积运算问题,是中档题.7.C解析:C 【分析】先根据题意得1AD =,3CD =,进而得2AB DC =,再结合已知和向量的加减法运算求解即可得的答案. 【详解】由题意可求得1AD =,3CD =,所以2AB DC =, 又13BE BC =, 则()1133AE AB BE AB BC AB BA AD DC =+=+=+++ 1111333AB AD DC ⎛⎫=-++ ⎪⎝⎭1111336AB AD AB ⎛⎫=-++ ⎪⎝⎭115116363AB AD AB AD ⎛⎫=-+=+ ⎪⎝⎭.故选:C. 【点睛】本题考查用基底表示向量,考查运算能力,是基础题.8.B解析:B 【分析】不妨设ABC 的外接圆的半径为1,作2=OF OB ,以,OC OF 为邻边作平行四边形COFE ,可得1,2,7===OC OF OE ,利用余弦定理,再利用两角和余弦公式可得3BOC π∠=【详解】不妨设ABC 的外接圆的半径为1,作2=OF OB ,以,OC OF 为邻边作平行四边形COFE ,+=OC OF OE ,所以1,2,7===OC OF OEcos sin∠==∠=EOC EOC ,22cos sin∠==∠=EOF EOF1cos cos()2∠=∠+∠==BOC COE EOF 3π∴∠=BOC故选:B 【点睛】本题考查了平面几何和向量的综合,考查了运算求解能力和逻辑推理能力,属于中档题目.9.D解析:D 【分析】根据三者的符号可得sin cos ,sin tan αααα>>,利用作差法可得tan ,cos αα大小关系不确定,从而可得正确的选项. 【详解】由题设可得AB 上的动点P 的坐标为()cos ,sin αα且()()1122cos ,sin ,cos ,sin A B θθθθ,其中122πθαθπ<<<<,12324ππθθπ<<<<, 注意到当13,4παθ⎛⎤∈ ⎥⎝⎦,tan 1α≤-,故按如下分类讨论: 若1324ππθα<<≤,则sin 0,cos 1,tan 1ααα>>-≤-, 故sin cos tan ααα>>.若234παθ<≤,则sin 0,cos 0,tan 0ααα><<,且20sin sin 2θα<≤<所以2222sin sin 1sin sin 1θθαα+-≤+-<,因为234πθπ<<,故20sin 2θ<<,故22211sin sin 12θθ-<+-<, 所以222sin sin 1θθ+-有正有负,所以2sin sin 1αα+-有正有负,而2sin sin 1tan cos cos ααααα+--=,cos 0α<,故tan cos αα-有正有负,故tan ,cos αα大小关系不确定.故选:D. 【点睛】方法点睛:三角函数式的大小比较,可先依据终边的位置判断出它们的符号,也可以利用作差作商法来讨论,注意根据三角函数值的范围确定代数式的符号.10.A解析:A 【分析】先整理函数,再根据平移后函数的奇偶性得到a ,b 的值,即可得结果. 【详解】解:函数()cos 2sin 224f x x x x π⎛⎫=-=+ ⎪⎝⎭,函数()24f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移a 个单位得到()224g x x a π⎛⎫=++ ⎪⎝⎭,又因为函数为奇函数,则242a k πππ+=+(k Z ∈),整理得28k a ππ=+(k Z ∈);函数()24f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移b 个单位得到()224h x x b π⎛⎫=-+ ⎪⎝⎭,由于得到的函数的图象为偶函数,2=4b k ππ-+-,=,()82k b k Z ππ+∈; 当0k =时,min 0a b -= 故选:A. 【点睛】本题考查了三角函数的平移变换和奇偶性,属于中档题.11.D解析:D 【分析】先根据对称轴及最小正周期,求得函数()f x 的解析式,再结合正弦函数的图象与性质,判断点是否在函数图象上可判断A ,求得函数的单调区间及对称中心即可判断选项BC ,由平移变换求得变化后的解析式并对比即可判断D. 【详解】函数()3sin()10,2f x x πωϕωϕ⎛⎫=++><⎪⎝⎭的最小正周期是π所以22πωπ==,则()()3sin 21f x x ϕ=++,()()3sin 21f x x ϕ=++图象关于直线3x π=对称,对称轴为2,2x k k Z πϕπ+=+∈,代入可得2,32k k Z ππϕπ⨯+=+∈,解得,6k k Z πϕπ=-+∈,因为,22ππϕ⎛⎫∈- ⎪⎝⎭,所以当0k =时, 6πϕ=-, 则()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭, 对于A,当0x =时,()3103sin 11622f π=-+=-+=- ,所以错误; 对于B,()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭的单调递减区间为3222,262k x k k πππππ+-+∈Z ≤≤, 解得5,36k x k k Z ππππ+≤≤+∈,因为123ππ<,则()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上不是减函数,所以错误; 对于C ,773sin 213sin 11012126f ππππ⎛⎫⎛⎫=⨯-+=+=≠⎪ ⎪⎝⎭⎝⎭,所以7,012π⎛⎫ ⎪⎝⎭不是()f x 的一个对称中心,所以错误;对于D ,1212πϕ=,将()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭的图象向左平移12π个单位长度得到可得3sin 213sin 21126y x x ππ⎡⎤⎛⎫=-++=+ ⎪⎢⎥⎝⎭⎣⎦,所以能得到3sin 21y x =+的图象,所以正确. 故选: D. 【点睛】本题考查了正弦函数的图象与性质的综合应用,关键点是根据已知条件先求出正弦函数的解析式,还要熟练掌握三角函数的性质才能正确的解题,属于中档题.12.D解析:D 【分析】由题先求出()3sin 323g x x π⎛⎫=+- ⎪⎝⎭,可得3,3363x πππθ⎡⎤+∈+⎢⎥⎣⎦,要满足题意,则332ππθ+≥,即可求出.【详解】将()f x 横坐标缩短为原来的13得到3sin(3)2y x =--,再向右平移29π个单位得到()23sin 323sin 3293g x x x ππ⎡⎤⎛⎫⎛⎫---=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=,,18x πθ⎡⎤∈-⎢⎥⎣⎦,则3,3363x πππθ⎡⎤+∈+⎢⎥⎣⎦,要使()g x 在区间,18πθ⎡⎤-⎢⎥⎣⎦上的最大值为1,则332ππθ+≥,即18πθ≥,则θ的最小值为18π. 故选:D. 【点睛】本题考查正弦型函数的性质,解题的关键是通过图象变化得出()3sin 323g x x π⎛⎫=+- ⎪⎝⎭,再根据正弦函数的性质求解.二、填空题13.【分析】由已知利用诱导公式求得然后分析角的范围得到的范围则答案可求【详解】∵即又∴则∴得∴故答案为:【点睛】角变换用已知角构造所求角是解决问题的关键如上:解析:2425-. 【分析】由已知利用诱导公式求得sin 2α,然后分析角α的范围,得到2α的范围,则答案可求. 【详解】∵3cos 45πα⎛⎫-= ⎪⎝⎭,2237cos 22cos 12144525ππαα⎡⎤⎛⎫⎛⎫⎛⎫∴-=--=⨯-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,即7sin 225α=, 又5,24ππα⎛⎫∈ ⎪⎝⎭,∴,44ππαπ⎛⎫-∈ ⎪⎝⎭,3cos cos 0445ππαα⎛⎫⎛⎫-=-=> ⎪ ⎪⎝⎭⎝⎭, 则,442πππα⎛⎫-∈ ⎪⎝⎭,∴3,24ππα⎛⎫∈ ⎪⎝⎭,得32,2παπ⎛⎫∈ ⎪⎝⎭,∴24cos 225α==-.故答案为:2425-. 【点睛】角变换用已知角构造所求角是解决问题的关键,如上:2=224ππαα⎛⎫-- ⎪⎝⎭14.【分析】由已知分别求得再由展开两角差的正弦得答案【详解】解:∵∴∴∴又∴则故答案为:【点睛】本题考查同角三角函数间的关系正弦的差角公式给值求值型的问题属于中档题解析:9【分析】由已知分别求得cos α,()sin αβ+,再由()sin sin βαβα=+-⎡⎤⎣⎦,展开两角差的正弦得答案. 【详解】解:∵sin 3α=,0,2πα⎛⎫∈ ⎪⎝⎭,∴1cos 3α==, ∴,0,2παβ⎛⎫∈ ⎪⎝⎭,∴()0,αβπ+∈,又()1cos 3αβ+=-,∴()sin 3αβ+==. 则()()()sin sin sin cos cos sin βαβααβααβα=+-=+-+⎡⎤⎣⎦1133339⎛⎫=⨯--⨯=⎪⎝⎭.故答案为:9. 【点睛】本题考查同角三角函数间的关系,正弦的差角公式,给值求值型的问题,属于中档题.15.【分析】根据利用诱导公式结合商数关系得到然后由求解【详解】因为所以解得所以故答案为:【点睛】本题主要考查诱导公式和二倍角公式以及同角三角函数基本关系式的应用还考查了运算求解的能力属于中档题解析:45-【分析】根据πsin(π)3sin()02αα+--=,利用诱导公式结合商数关系得到tan 3α=-,然后由222222cos sin cos 2cos sin cos sin ααααααα-=-=+求解. 【详解】因为πsin(π)3sin()02αα+--=, 所以sin 3cos 0αα--=, 解得tan 3α=-,所以222222cos sin cos 2cos sin cos sin ααααααα-=-=+,()()2222131tan 41tan 513αα---===-++-, 故答案为:45- 【点睛】本题主要考查诱导公式和二倍角公式以及同角三角函数基本关系式的应用,还考查了运算求解的能力,属于中档题.16.②④【分析】①可得在的角平分线上但不一定是内心;②可得在BC 边中线的延长线上;③利用向量线性运算得出可判断;④得出根据向量加法的平行四边形法则可判断;⑤令可判断【详解】①若则因为是和同向的单位向量则解析:②④ 【分析】①可得P 在BAC ∠的角平分线上,但不一定是内心;②可得P 在BC 边中线的延长线上;③利用向量线性运算得出=BP BC μ可判断;④得出()1CP CB AC λλμ=++-,根据向量加法的平行四边形法则可判断;⑤令1132=λμ=-,可判断. 【详解】 ①若1ABλ=,1ACμ=,则AB AC AP ABAC=+,因为,AB AC ABAC是和,AB AC 同向的单位向量,则P 在BAC ∠的角平分线上,但不一定是内心,故①错误;②若1λμ==,则AP AB AC =+,则根据平行四边形法则可得,P 在BC 边中线的延长线上,故直线AP 经过ABC 的重心,故②正确;③若1λμ+=,且0μ>,则()1=AP AB AC AB AB AC μμμμ=-+-+,即()==AP AB AB AC AC AB μμμ--+-,即=BP BC μ,则点P 在线段BC 上或BC 的延长线上,故③错误;④若1λμ+>,()()11AP AB AC AC λλλμ=+-++-,整理可得()1CP CB AC λλμ=++-,10λμ+->,根据向量加法的平行四边形法则可判断点P 在ABC 外,故④正确;⑤若01λμ<+<,则令1132=λμ=-,,则1132AP AB AC =-+,则根据向量加法的平行四边形法则可判断点P 在ABC 外,故⑤错误. 故答案为:②④. 【点睛】本题考查向量基本定理的应用,解题的关键是正确利用向量的线性运算进行判断,合理的进行转化,清楚向量加法的平行四边形法则.17.【详解】方法一:①又②③将②③代入①得:所以点在内所以方法二:以直线OAOB 分别为轴建立直角坐标系则设又得即解得故答案为:3解析:【详解】 方法一:3cos 2OA OC AOC OA OC⋅∠==⋅, ① 又()2OA OC OA mOA nOB m OA m ⋅=⋅+==, ②22222222||()||||23OC mOA nOB m OA n OB mnOA OB m n =+=++⋅=+, ③将②③代入①得:22323m n=+,所以229m n =,点C 在AOB ∠内, 所以3mn=. 方法二:以直线OA ,OB 分别为,x y 轴建立直角坐标系,则()(10,03A B ,, , 设()31cos30,sin 30=,2OC λλ⎫=︒︒⎪⎪⎝⎭,又()(()1,0OC mOA nOB m n m =+=+=,得()1,=2m λ⎫⎪⎪⎝⎭,即=12m λ⎧⎪⎪⎨⎪=⎪⎩, 解得3mn=. 故答案为:3.18.【分析】利用向量的数量积公式向量垂直的性质直接直解【详解】非零向量满足=⊥解得故答案为:【点睛】本题主要考查了向量的数量积公式向量垂直的性质等基础知识考查运算能力属于中档题 解析:4-【分析】利用向量的数量积公式、向量垂直的性质直接直解. 【详解】非零向量m →,n →满足4m →=3n →,cos m →〈,13n →〉=,n →⊥t m n →→⎛⎫+ ⎪⎝⎭,n →∴⋅22+||||cos ,||t m n t m n n t m n m n n →→→→→→→→→→⎛⎫+=⋅=<>+ ⎪⎝⎭223||||034t n n →→=⨯+=, 解得4t =-, 故答案为:4- 【点睛】本题主要考查了向量的数量积公式、向量垂直的性质等基础知识,考查运算能力,属于中档题.19.2【分析】根据函数为偶函数可知函数必有一个零点为可得根据函数的图象可知解得即可得解【详解】因为函数为偶函数且有且仅有3个零点所以必有一个零点为所以得所以函数的图象与直线在上有且仅有3个交点因为函数的解析:2 【分析】根据函数为偶函数可知函数必有一个零点为0x =,可得1a =-,根据函数cos y x ω=(0)>ω的图象可知222πππωω≤<⨯,解得24ω≤<即可得解.【详解】因为函数cos ,[],y a x x ωππ=+∈-为偶函数,且有且仅有3个零点,所以必有一个零点为0x =,所以cos00a +=,得1a =-,所以函数cos y x ω=(0)>ω的图象与直线1y =在[,]-ππ上有且仅有3个交点, 因为函数cos y x ω=(0)>ω的最小正周期2T πω=,所以2T T π≤<,即222πππωω≤<⨯,得24ω≤<,所以ω的最小值是2.故答案为:2 【点睛】关键点点睛:根据偶函数图象的对称性求出a 是解题关键.20.②③④【分析】根据函数的图象与性质分析函数的对称性奇偶性与单调性即可得出结论【详解】解:①由得令直线为函数图象的对称轴故图象C 关于直线对称故①正确;由得令得函数在区间内是增函数故②错误;故函数不是奇解析:②③④ 【分析】根据函数()3sin 23f x x π⎛⎫=- ⎪⎝⎭的图象与性质,分析函数的对称性,奇偶性与单调性,即可得出结论. 【详解】 解:①由232x k πππ-=+,Z k ∈,得25121x k ππ=+,Z k ∈, 令1k =,直线1112π=x 为函数图象的对称轴, 故图象C 关于直线1112π=x 对称,故①正确; 由222232k x k πππππ-+≤-≤+,k Z ∈,得5,1212x k k ππππ⎡⎤∈-++⎢⎥⎣⎦,k Z ∈, 令0k =,得函数()f x 在区间5,1212ππ⎛⎫-⎪⎝⎭内是增函数,故②错误; ()00f ≠,故函数()f x 不是奇函数,故③错误;由23x k ππ-=,k Z ∈,得612x k ππ=+,k Z ∈,图象C 不关于点,03π⎛⎫ ⎪⎝⎭对称,故④错误.故答案为:②③④. 【点睛】本题考查正弦函数的图象与性质,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力.三、解答题21.6πα=时,矩形ABCD 的面积,最大面积为3 【分析】由题意可得cos sin 3CD αα=-,sin BC α=,从而可得矩形ABCD 的面积为S CD BC =⋅(cos sin )sin 3ααα=-⋅sin(32)623πα=+-,再由03πα<<可得52666πππα<+<,由此可得262ππα+=时,S 取得最大值 【详解】在Rt OBC 中,sin BC α=,cos OC α=, 在Rt ADO 中,tan 33AD OD π==, 所以sin 333OD AD BC α===, 所以cos sin 3CD OC OD αα=-=-, 设矩形ABCD 的面积为S ,则S CD BC =⋅(cos sin )sin 3ααα=-⋅ 2sin cos sin 3ααα=-1sin 2cos 222323αα=+- sin(32)623πα=+-,由03πα<<,得52666πππα<+<,所以当262ππα+=,即6πα=时, max 3323S == 因此,当6πα=时,矩形ABCD 的面积,最大面积为36, 【点睛】关键点点睛:此题考查三角函数的应用,解题的关键是将四边形ABCD 的面积表示为S CD BC =⋅(cos )sinααα=-⋅2)6πα=+,再利用三角函数的性质可求得其最大值,属于中档题22 【分析】①②③任选一个条件,均可求出sin ,cos αα,求出sin()αβ+,利用()βαβα=+-,结合两角差的余弦公式,即可求解.【详解】 若选条件①因为2sin 3sin 2αα=,所以2sin 32sin cos ααα=⨯,即1cos 3α=. 因为0,2πα⎛⎫∈ ⎪⎝⎭,所以sin 3α== 因为1cos()4αβ+=-,由平方关系22sin ()cos ()1αβαβ+++=, 解得215sin ()16αβ+=. 因为0,,0,22ππαβ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,所以0αβ<+<π,所以sin()4αβ+=, 所以cos cos[()]βαβα=+-cos()cos sin()sin αβααβα=+++1143=-⨯=若选条件②因为cos23α=,所以21cos 2cos 123αα=-=. 由平方关系22sin cos 1αα+=,得28sin 9α=.因为0,2πα⎛⎫∈ ⎪⎝⎭,所以sin 3α=以下同①的解法. 若选条件③因为tan α=sin cos αα= 由平方关系22sin cos 1αα+=,解得sin 31cos 3αα⎧=⎪⎪⎨⎪=⎪⎩ 或sin 31cos 3αα⎧=-⎪⎪⎨⎪=-⎪⎩ 因为0,2πα⎛⎫∈ ⎪⎝⎭,所以sin 31cos 3αα⎧=⎪⎪⎨⎪=⎪⎩. 以下同①的解法. 【点睛】关键点点睛:本题根据不同的条件,利用三角恒等变换、同角三角函数的基本关系求出sin α,cos α,再利用1cos()4αβ+=-求出sin()αβ+,根据角的变换()βαβα=+-求解是关键,属于中档题.23.(1)1t =-;(2)23π. 【分析】(1)根据题意,设a kb =,则有122112()()e e k e te kte ke +=-=-+,分析可得11ktk =-⎧⎨=⎩,解可得t 的值;(2)根据题意,设向量a ,b 的夹角为θ;由数量积的计算公式可得a 、||b 以及a b , 由cos a b a bθ⋅=计算可得答案.【详解】(1)∵根据题意,向量12a e e =+,21b e te =-,若//a b ,则设a kb =, 则有122112()()e e k e te kte ke +=-=-+, 则有11ktk=-⎧⎨=⎩,解可得1t =-;(2)根据题意,设向量a ,b 的夹角为θ;若2t =,则212b e e =-,则2221||(2)3b e e =-=,则||3b =, 又由12a e e =+,则2212||()3a e e =+=,则||3a =,又由12213()(2)2a b e e e e =+-=-,则312cos 2||||3a b a b θ-===-⨯,又由0θπ,则23πθ=; 故向量a ,b 的夹角为23π. 【点睛】本题考查向量数量积的计算,涉及向量模的计算公式,属于基础题.24.1613k =-【分析】根据向量平行的坐标公式求解即可. 【详解】(3,2)(4,)(34,2)a kc k k k k +=+=++,2(2,4)(3,2)(5,2)b a -=--=-()//(2)a kc b a +-(34)2(2)(5)k k ∴+⨯=+⨯-解得1613k =- 【点睛】本题主要考查了由向量平行求参数,属于中档题.25.(1)()22sin 23f x x π⎛⎫=+ ⎪⎝⎭;(2)递增区间为7,,1212ππππ⎡⎤-+-+∈⎢⎥⎣⎦k k k Z ,x 的集合为5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭【分析】(1)先求出2A =,根据图形得出周期,可求出2ω=,再代入,06π⎛⎫⎪⎝⎭可求出ϕ;(2)令2222,232k x k k Z πππππ-+≤+≤+∈可求出增区间,当2322,32x k k Z πππ+=+∈时可得最小值. 【详解】(1)由图可知,2A =, 46124T πππ⎛⎫=--= ⎪⎝⎭,即T π=,22πωπ∴==,则()()2sin 2f x x ϕ=+,2sin 2066f ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,即,3k k Z πϕπ+=∈,则,3k k Z πϕπ=-∈,0πϕ<<,23πϕ∴=, ()22sin 23f x x π⎛⎫∴=+⎪⎝⎭; (2)令2222,232k x k k Z πππππ-+≤+≤+∈,解得27,121ππππ-+≤≤-+∈k x k k Z , 故()f x 的单调递增区间为7,,1212ππππ⎡⎤-+-+∈⎢⎥⎣⎦k k k Z ,当2322,32x k k Z πππ+=+∈,即25,1ππ=+∈x k k Z 时,()f x 取得最小值为2-, 此时x 的集合为5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 【点睛】方法点睛:根据三角函数()()sin f x A x =+ωϕ部分图象求解析式的方法: (1)根据图象的最值可求出A ; (2)求出函数的周期,利用2T πω=求出ω;(3)取点代入函数可求得ϕ.26.(1)答案见解析;(2)2⎡⎤⎣⎦;(3)5,6ππ⎡⎤-⎢⎥⎣⎦【分析】(1)利用五点法作图,按照列表、描点、连线的步骤作图即可; (2)根据x ππ-≤≤求出126x π+的范围,再利用正弦函数的性质求出1sin 26x π⎛⎫+ ⎪⎝⎭的范围即可求值域; (3)先求出()12sin 6212g x f x x ππ⎛⎫=+⎛⎫=-⎪⎝⎭ ⎪⎝⎭,再令12222122k x k πππππ-+≤+≤+, ()k Z ∈,不等式的解集与[],ππ-求交集即可.【详解】(1)利用五点法作图列表如下:126x π+ 02ππ32π 2πx3π-23π 53π 83π 113π()f x0 2 02-(2)因为x ππ-≤≤,所以123263x πππ-≤+≤, 所以31sin 1226x π⎛⎫-≤+≤ ⎪⎝⎭, 所以()12sin 2263x f x π⎛⎫=+≤⎪⎝⎭-≤, 函数()f x 在[],ππ-内的值域为3,2⎡⎤-⎣⎦(3)若将函数()f x 的图象向右平移6π个单位长度,得到函数()g x 的图象, 则()112sin 2sin 6266212g x x x x f ππππ⎡⎤⎛⎫⎛⎫=-+=+ ⎪ ⎪⎢⎥⎝⎭⎛⎫=- ⎪⎝⎝⎦⎭⎭⎣, 令12222122k x k πππππ-+≤+≤+()k Z ∈,解得:754466k x k ππππ-+≤≤+()k Z ∈, 当0k =时,7566x ππ-≤≤,当1k =时172966x ππ≤≤, 又因为[],x ππ∈-,所以56x ππ-≤≤, ()g x 在[],ππ-内的单调增区间为5,6ππ⎡⎤-⎢⎥⎣⎦,【点睛】关键点点睛:在求三角函数单调区间时,要把x ωϕ+看成一个整体让其满足正弦的单调区间,解出的x的范围即为所求三角函数的单调区间.。
(常考题)北师大版高中数学必修四第二章《平面向量》测试(包含答案解析)(1)

【分析】
设 , ,设 ,则 ,由 ,得到 , ,再利用 ,得到 ,再设 ,得到 ,根据 ,可解得结果.
【详解】
因为 ,所以可设 , ,
设 ,则 ,
由 ,得 ,所以 ,
由 ,得 ,化简得 ,所以 ,
所以由 ,得 ,
所以 ,
设 ,则 ,所以 ,
所以 ,
由 ,得 ,解得 ,
所以 ,
所以 ,
所以 ,
故答案为: .
15.已知正方形 的边长为4,若 ,则 的值为_________________.
16.已知圆 , 点为圆上第一象限内的一个动点,将 逆时针旋转90°得 ,又 ,则 的取值范围为________.
17.已知平面非零向量 ,满足 且 ,已知 ,则 的取值范围是________
18. 中, , ,且 ,则 ______.
6.C
解析:C
【详解】
由题意可得 ,所以 ,又因为 ,所以 ,选C.
7.B
解析:B
【分析】
根据方程有实根得到 ,利用向量模长关系可求得 ,根据向量夹角所处的范围可求得结果.
【详解】
关于 的方程 有实根
设 与 的夹角为 ,则
又
又
本题正确选项:
【点睛】
本题考查向量夹角的求解问题,关键是能够利用方程有实根得到关于夹角余弦值的取值范围,从而根据向量夹角范围得到结果.
此时,符合条件的点 有 个.
综上所述,满足题中条件的点 的个数为 .
故选:D.
【点睛】
本题考查符合条件的点的个数的求解,考查了平面向量加法法则的应用,属于中等题.
9.B
解析:B
【分析】
由 知, ,根据平面向量的线性运算可推出
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择题(共8小题,每小题4分,共32分)
1.向量a ,b 的坐标分别为(1,-1),(2,3),则a ﹒b
= ( ) A.5 B.4 C.-2 D.-1
2.已知sin A =21, 那么cos(
A -23π
)= ( ) A.-21 B. 21 C.-23 D. 2
3
3.已知角α的终边经过点(3,-4),则sin α+cos α的值为 ( ) A.-51 B. 51 C. ±51 D. ±51或±5
7
4.已知2
tan ,α
α则为第三象限角的值 ( )
A .一定为正数
B .一定为负数
C .可能为正数,也可能为负数
D .不存在
5.若向量()1,1a = ,()1,1b =- ,()1,2c =-
,则c = ( )
.A 1322a b -+ .B 1322a b - .C 3122a b - .D 3122
a b -+
6.要得到函数sin y x =-的图像,只需将函数cos y x =的图像( )
A .右移2π个单位
B .右移π个单位
C .左移2π
个单位 D .左移π个单位
7. 已知向量(1,2)a = ,2
(2,)b m = ,若a b ,则 m 的值为( ) A. 2或-1 B. -2或1 C. ±2 D. ±1 8.锐角α满足2tan()3cos(
)50tan()6sin()102
π
παβπαπβ--++=+++-=和,
则cos α的值为 ( )
D.13
二、填空题(共6小题,每小题4分,共24分)
9.向量 a ,b 满足︱a ︱=3,︱b ︱=4,︱a +b ︱=5,则︱a -b
︱=_____
10.cos 2x+cos 2(x+1200)+cos 2(x+2400)的值是________
11. 已知|a |=4,|b |=5, a 与b 的夹角为60°,且(k a +b )⊥(a -2b
), 则k = 12. 设0<α<π,且函数f (x )=sin (x +α)+cos (x -α) 是偶函数,则 α 的值为
13.已知2a b ==
,a 与b 的夹角为60︒,则a b + 在a 上的投影为 14、已知1
sin 3
m x m +=
-,1cos 3m x m -=-,则m=_______________
三.解答题(共4小题,其中15,16每题10分,17,18每题12分,共44分)
15.(本小题满分10分) 已知tan 2x =,求
)
(cos )sin(sin 1)
cos()cos()sin(222x x x x x x ---+++--+πππππ的值
16.(本小题满分10分)
已知矩形ABCD 中,3AB =,4BC =,1AB e AB = ,2AD e AD
=
. (1)若12AC xe ye =+
,求x 、y 的值; (2)求与的夹角的余弦值.
17.(本小题满分12分)
已知向量()x x x a cos sin ,2sin 1-+=→
,()x x b cos sin ,1+=→
函数()f x a b =⋅
.
(1)求()f x 的最大值及相应的x 的值;
(2)若58)(=
θf ,求πcos 224θ⎛⎫
- ⎪⎝⎭
的值.
18.(本小题满分12分)
已知函数2()2sin ()21,4
f x x x x R π
=+-∈.
(1)函数()()h x f x t =+的图象关于点(,0)6π
-对称,且(0,)t π∈,求t 的值;
(2)[,],()342
x f x m ππ
∈-<恒有成立,求实数m 的取值范围.
高中数学必修四试卷参考答案及评分标准
9.5 10.23 11.-10 12.4
3π 13. 3 三、解答题 15.解:x
x
x x x x x x x x x x sin cos )1sin 2(sin )1sin 2(cos cos sin sin 1cos cos sin 22
2=++=-+++ ……………… 6分 由
sin tan 2cos x
x x
=
= 得:原式
=1
2 ………………………………………… 10分
16.解:(1) 3AB =,4BC =∴ +==31e +42e ∴
x
=
3
,
y
=
4 …………………………………… 5分
(2)设与BD 的夹角为θ,由2143BD AD BA e e =+=-
,则5A C B D == ,
∴
()()
2212212134431697
cos 552525e e e e e e AC BD AC BD
θ+⋅--⋅====⨯⋅
∴
与BD 的夹角的余弦值为
7
25. …………………………………… 10分
17. 解: (1)因为(1sin2,sin cos )a x x x =+- ,(1,sin cos )b x x
=+
,所以
22()1sin2sin cos 1sin2cos2f x x x x x x =++-=+-
πs i n 21
4x ⎛
⎫=-+ ⎪⎝⎭ 当π
π22π42x k -=+,即3ππ8
x k =+(k ∈Z )时,()f x 1;…………6分
(
,0),26
k t k Z ππ
+-∈(2)由()1sin 2cos2f θθθ=+-及8
()5f θ=得3sin 2cos25
θθ-=,两边平方得
91sin 425θ-=
,即16sin 425θ=. ∴ππ16cos22cos 4sin 44225θθθ⎛⎫⎛⎫
-=-== ⎪ ⎪⎝⎭⎝⎭
. (12)
分
18.解: (Ⅰ)∵
2()2sin ()211cos(2)21
42f x x x x x ππ
=+-=-+-- ∴ ()()2sin(22)3h x f x t x t π
=+=+-,
∴
()
h x 的图象的对称中心
为 …………………………………… 4分
又已知点(,0)6π-为()h x 的图象的一个对称中心,∴()23
k t k Z ππ=
+∈ 而(0,)t π∈,∴3t π=或56π
. ……………………………………………6分
(Ⅱ)若[,]42x ππ∈时,22[,]363
x πππ
-∈,
()[1,2]f x ∈,由()33()3f x m m f x m -<⇒-<<+ ……………………………
10分
∴31
32m m -<⎧⎨
+>⎩,解得14m -<<, 即m 的取值范围是(1,4)-.……………… 12分。
