变位齿轮传动的受力分析及强度计算
变位齿轮计算公式

变位齿轮计算公式变位齿轮是一种特殊的齿轮传动装置,由于其特殊的设计结构,在很多工程领域中被广泛应用。
变位齿轮的计算涉及到很多参数和公式,下面将介绍1200字以上的变位齿轮计算公式。
1.变位齿轮的模数计算公式:变位齿轮的模数实际上是齿轮的基本参数之一,是计算齿轮尺寸和性能的重要依据。
模数的计算公式如下:m=(π*d)/(z+2)其中,m为模数,d为齿轮的总直径,z为齿数。
2.变位齿轮的齿宽计算公式:变位齿轮的齿宽决定了齿轮的受力和传动能力,齿宽的计算公式如下:bw = K * m其中,bw为齿宽,K为齿宽系数,m为模数。
3.变位齿轮的中心距计算公式:变位齿轮的中心距是指两个齿轮中心线之间的距离,中心距的计算公式如下:a=(m*(z1+z2))/2其中,a为中心距,m为模数,z1和z2分别为两个齿轮的齿数。
4.变位齿轮的齿数比计算公式:齿数比是指两个齿轮齿数的比值,齿数比的计算公式如下:i=z2/z1其中,i为齿数比,z1为主动齿轮的齿数,z2为从动齿轮的齿数。
5.变位齿轮的齿侧间隙计算公式:齿侧间隙表示两个齿轮侧面的距离,可以通过以下计算公式进行计算:cg = 0.25 * m * (z1 + z2) + c其中,cg表示齿侧间隙,m表示模数,z1和z2表示两个齿轮的齿数,c表示一个修正系数。
6.变位齿轮的分度圆直径计算公式:分度圆直径是指齿轮两齿间的直径,可以通过以下计算公式进行计算:d=m*z其中,d表示分度圆直径,m表示模数,z表示齿轮的齿数。
7.变位齿轮的螺旋角计算公式:螺旋角表示齿轮齿槽相对于圆柱面的旋转角度,可以通过以下计算公式进行计算:φ = tan^(-1)((cosα1/sinα1)+((z1+z2)/(2m*tanα1)))其中,φ表示螺旋角,α1表示变位齿轮的压力角,z1和z2分别表示两个齿轮的齿数,m表示模数。
8.变位齿轮的齿形因数计算公式:齿形因数是表示齿轮齿形的一个参数,可以通过以下计算公式进行计算:X = (2*m*(cosα1+cosα2))/(π*tan(α1+α2))其中,X表示齿形因数,m表示模数,α1和α2分别表示两个齿轮的压力角。
机械设计(6.14.1)--变位齿轮传动的强度计算

变位齿轮传动的受力分析和强度计算原理与标准齿轮的相同,其计算公式也与标准齿轮相同
齿轮啮合节点位置发生变化,Z H 有变化
2/
2cos tan H Z a a =2/2cos tan H t t Z a a =/a a =/t t a a =高高高高高高 高x Σ=x 1+x 2=0:
Z H 高高高高高高高高高高高高高
或/a a >/t t a a >/a a </t t
a a <高x Σ>0高高高高高高高高Z H 高高高εα高高高Z ε高高高
高Z H 高高高εα高高高Z ε高高高或齿面接触强度提高。
当xΣ<0(负传动)时,或齿面接触强度降低。
角变位传动即x Σ=x 1+x 2≠0 :
二、齿根弯曲强度齿根弯曲强度:
变位使齿形变化,齿根厚度和齿根圆角半径变化,引起计算系数Y Fa 和Y sa 的变化,影响齿根弯曲强度。
正变位齿轮的齿厚增大,Y Fa 减小,
齿根圆角半径减小,Y sa 增大。
正变位齿轮的齿根弯曲强度可有提高。
负变位使齿根弯曲强度降低。
变位使端面重合度系数εa 变化,Y ε也发生变化。
齿轮传动强度计算
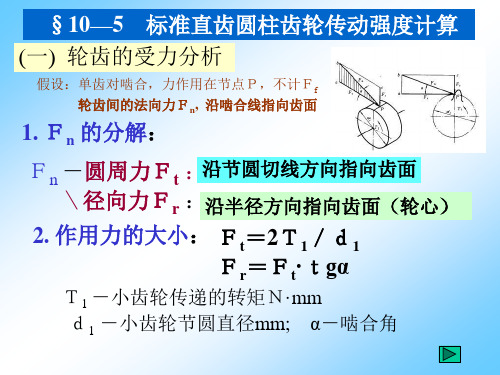
(一) 轮齿的受力分析
假设:单齿对啮合,力作用在节点P,不计Ff 轮齿间的法向力Fn, 沿啮合线指向齿面
1. Fn 的分解:
Fn -圆周力Ft :沿节圆切线方向指向齿面 \径向力Fr :沿半径方向指向齿面(轮心)
2. 作用力的大小: Ft=2T1/d1 Fr=Ft·tgα
N=60njLh
n——齿轮的转速(r/min)
j——齿轮转一周时,同一齿面参加啮合的次数
Lh——齿轮的工作寿命 Lh=年数×300×班数×8(h)
㈢ 齿轮精度的选择 (表10—8)
㈣ 齿轮设计基本步骤 选材料、精度、Z、φd
设计计算(d或m) →由接触、弯曲 设计出模数,依
(校核计算) 强度特点取其中 一个套标准。适
H 2.5Z E
KFt bd1
u 1 u
H
d1
2.323
2KT1
d
u
u
1
Z
E H
2
(四)齿轮传动强度计算说明
⒈ 因配对齿轮σH1 =σH2,按接触设计时取 [σH] 1 与[σH] 2的较小者代入设计公式
2. 硬齿面齿轮传动,材料、硬度一样,设计时
㈠齿轮传动的设计参数选择
⒈ 压力角α的选择: 一般齿轮 α=20°; 航空用齿轮α=25°
⒉ 齿数的选择:
d1一定,齿数Z1 ↑→重合度↑平稳性好 →m小→加工量↓,但齿轮弯曲强度差
闭式软齿面 :Z1宜取多→提高平稳性,Z1 =20~40 开式或闭式硬齿面:Z1宜取少→保证轮齿弯曲强度
Z1 ≥17 (ha*=1,C*=0.25)
齿轮传动(第11章)

K F FtYFa1YSa1Y F1 F 1 bm K F FtYFa 2YSa 2Y F2 F 2 bm
② 应力和许用应力的关系 两齿轮弯曲应力是否相同?许用应力呢?
F
K F Ft YFaYSaY [ F ] bm
39
③
设计计算时,因为 m 3
8
§11.2
齿轮传动的失效形式
1.轮齿折断
原因: • 齿根弯曲应力大; • 齿根应力集中。
9
1、轮齿折断
★ 疲劳折断 ★ 过载折断
全齿折断—常发生于齿宽较小的直齿轮
局部折断—常发生于齿宽较大的直齿轮,和斜齿轮
措施:选用合适的材料及热处理方法,使齿根芯部 有足够的韧性;采用正变位齿轮以增大齿根的厚度; 增大齿根圆角半径,消除齿根加工刀痕;对齿根进 行喷丸、碾压等强化处理; 提高齿面精度、增大 模数等
d1 sin 2
cos d1 d1 cos
O2
d N 2C 2 2 sin 2
1 1 1 2
d 2 z2 2 d2 u 1 d1 d1 z1
②
d'2 2
'
(从动)
2
②
u 1 1 2 d1 cos tan u
23
§11.4 齿轮传动的计算载荷
名义载荷:
Fn p L
pca K Fn L
计算载荷:
载荷系数:K K A Kv K K
24
1.使用系数KA
考虑齿以外的其他因素对齿轮传动 的影响,主要考虑原动机和工作机的影响
原动机 载荷状况 均匀平稳 轻微冲击 中等冲击 严重冲击 工作机器 … … … … 电机 1.0 … 1.1 … 1.25 1.5 1.75 2.0 内燃 机… 1.5 1.75 2.0 2.25 25
齿轮传动的强度设计计算

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中,由于赫兹应力是齿面间应力的主要指标,故把赫兹应力作为齿面接触应力的计算基础,并用来评价接触强度。
齿面接触疲劳强度核算时,根据设计要求可以选择不同的计算公式。
用于总体设计和非重要齿轮计算时,可采用简化计算方法;重要齿轮校核时可采用精确计算方法。
分析计算表明,大、小齿轮的接触应力总是相等的。
齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。
实际使用和实验也证明了这一规律的正确。
因此,在齿面接触疲劳强度的计算中,常采用节点的接触应力分析齿轮的接触强度。
强度条件为:大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力,即:⑴圆柱齿轮的接触疲劳强度计算1)两圆柱体接触时的接触应力在载荷作用下,两曲面零件表面理论上为线接触或点接触,考虑到弹性变形,实际为很小的面接触。
两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。
两圆柱体接触,接触面为矩形(2axb),最大接触应力σHmax位于接触面宽中线处。
计算公式为:接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径,(正号用于外接触,负号用于内接触)•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2)齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况,都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。
在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。
节点附近处的ρ虽然不是最小值,但节点处一般只有一对轮齿啮合,点蚀也往往先在节点附近的齿根表面出现,因此,接触疲劳强度计算通常以节点为最大接触应力计算点。
参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为,3)圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式,并考虑各载荷系数的影响,得到:接触疲劳强度的校核公式为:接触疲劳强度的设计公式为:•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力,N;•T1——端面内分度圆上的名义转矩,N.mm;•d1——小齿轮分度圆直径,mm;•b ——工作齿宽,mm,指一对齿轮中的较小齿宽;•u ——齿数比;•ψd——齿宽系数,指齿宽b和小齿轮分度圆直径的比值(ψd=b/d1)。
齿轮传动的作用力及计算

11-4直齿圆柱齿轮传动的作用力及计算载荷:一、齿轮上的作用力:为了计算齿轮的强度,设计轴和选用轴承,有必要分析轮齿上的作用力。
当不计齿面的摩擦力时,作用在主动轮齿上的总压力将垂直于齿面,(因为齿轮传动一般都加以润滑,齿轮在齿啮合时,摩擦系数很小,齿面所受的摩擦力相对载荷很小,所以不必考虑),即为P175图11-5b所示的F n(沿其啮合线方向),Fn可分解为两个分力:圆周力:Ft=2T1/d1 N径向力:Fr=Fttgα N而法向力:Fn=Ft/cosα NT1:小齿轮上的扭矩 T1=9550000p/n1 n·mmP:传递的功率(KW) d1:小齿轮分度圆直径 mmα:压力角 n1:小齿轮的转速(r·p·m)Ft1:与主动轮运动方向相反;Ft2与从动轮运动方向一致。
各力的方向 Fr:分别由作用点指向各轮轮心。
Fn:通过节点与基圆相切(由法切互为性质)。
根据作用力与反作用力的关系,主从动轮上各对的应力应大小相等,方向相反。
二、计算载荷:Fn是根据名义功率求得的法向力,称为名义载荷,理论上Fn沿齿宽均匀分布,但由于轴和轴承的变形,传动装置的制造安装误差等原因,载荷沿齿宽的分布并不均匀,即出现载荷集中现象(如P176图11-6所示,齿轮相对轴承不对称布置,由于轴的弯曲变形,齿轮将相互倾斜,这时,轮齿左端载荷增大,轴和轴承刚度越小,b越宽,载荷集中越严重。
此外,由于各种原动机和工作机的特性不同,齿轮制造误差以及轮齿变形等原因,还会引起附加动载荷。
精度越低,圆周速度V越大,附加载荷越大。
因此在计算强度时,通常以计算载荷K·Fn代替名义载荷Fn,以考虑上两因素的影响。
K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算:一、设计准则:齿轮强度计算是根据齿轮失效形式来决定的,在闭式传动中,轮齿的失效形式主要是齿面点蚀,开式传动中,是齿轮折断,在高速变截的齿轮传动中,还会出现胶合破坏,因胶合破坏的计算方法有待进一步验证和完善。
齿轮受力综合分析

齿轮受力综合分析齿轮是一种常用的机械传动元件,主要用于将一个轴上的动力或运动传递给另一个轴。
齿轮的工作原理是利用两个齿轮之间的啮合来传递动力和转矩,因此齿轮的强度和刚度是十分重要的。
齿轮传动在使用的过程中,由于外界的作用,会受到不同方向的力和力矩的作用,因此齿轮在设计时需要考虑各种力和力矩的综合作用。
齿轮的受力综合分析就是针对齿轮在使用过程中受到的各种力和力矩进行分析和计算,以确保齿轮能够安全、稳定地工作。
下面将介绍齿轮受力综合分析中需要考虑的各种因素。
1. 齿轮轴向力对于两个相啮合的齿轮,轴向力是沿着齿轮轴线方向上的力。
轴向力的大小和方向取决于齿轮在传递动力时所受的载荷和加速度,以及齿轮位置和啮合角度等因素。
一般情况下,齿轮所受的轴向力都会导致轴承的不必要负荷,因此在设计和制造齿轮时需要考虑这一因素。
齿轮切向力是指沿齿轮齿向方向的力,它与齿轮的强度和刚度密切相关。
齿轮工作时,由于啮合处的弯曲应力和拉伸应力的作用,会产生齿面接触处的切向力,这对齿轮的耐磨性和稳定性都有很大的影响。
因此,在设计齿轮时需要根据切向力的大小和方向制定相应的强度和刚度要求。
3. 齿轮弯曲应力齿轮在工作时会产生弯曲应力,主要集中在齿根和齿尖处。
由于齿轮的齿根处和齿谷处是应力集中部位,因此设计时需要特别注意这些位置的强度和刚度。
4. 齿轮振动齿轮振动是指齿轮在工作时由于啮合错位或不平衡造成的振动。
振动会导致齿面磨损加剧,甚至引起齿面的破坏。
因此在设计齿轮时需要考虑振动的影响,采取相应的措施进行消除或控制。
综合以上因素,在设计齿轮时需要根据所要传递的动力和转矩大小、啮合角度、齿数等因素,结合材料强度和制造工艺等因素进行综合分析和计算,以确保齿轮能够在安全、稳定的工作状态下工作。
齿轮传动受力分析

齿轮传动受力分析:力有三要素:大小、方向、作用点。
1、大小计算:见教科书公式2、作用点:分度圆上齿宽中部3、方向判断:分以下几种情况a)直齿轮:画受力分析图,根据力的平行四边形法则可知,对于主动轮,径向力指向圆心,周向力方向与外加转矩方向相反,外加转矩方向与转动方向一致,主动轮判断完毕后和它配合的从动轮的受力方向自然就知道了,因为二者是作用力与反作用力,简单地说,就是无论主动轮还是从动轮,其所受径向力指向各自的圆心,主动轮所受周向力是来自于从动轮的阻力,故其方向与主动轮的转向相反,从动轮所受的周向力来自于主动轮,是使从动轮转动的动力,与其转动方向相同。
直齿轮传动没有轴向力。
b)斜齿轮:斜齿轮传动同样受径向力、周向力,其方向的判断与直齿轮相同,所不同的是斜齿轮传动有轴向力的作用。
其方向的判断有两种方法:一种是画受力分析图,比较麻烦,另一种是用左右手法则判断,使用左右手法则时,通常用于主动轮上,即左旋齿轮用左手,右旋齿轮用右手,四指方向指向外加转矩方向,则大拇指方向即为轴向力方向(注意:是用于主动轮上)c)圆锥齿轮传动:圆锥齿轮传动同样受径向力、周向力和轴向力的作用。
径向力和周向力的方向判断也与直齿轮一样,其轴向力的作用方向小端指向大端。
d)蜗杆传动:蜗杆传动也受径向力、周向力和轴向力的作用。
径向力和周向力的方向判断仍然与直齿轮一样,其轴向力作用方向的判断和斜齿轮完全一样,一种是画受力分析图,另一种是用左右手法则判断,即在主动轮上,左旋用左手,右旋用右手,四指方向指向外加转矩方向,则大拇指方向即为轴向力方向,蜗杆传动中蜗杆是主动件。
在蜗杆传动中,蜗轮的周向力为蜗杆的轴向力,蜗轮的轴向力为蜗杆的周向力,二者为作用力与反作用力,大小相等方向相反。
相同点:以上几种传动中,主动轮的外加转矩方向均与其转动方向一致,周向力方向与其转动方向(或外加转矩方向)相反,径向力均指向各自的圆心。
◆这里要特别注意:一对相互啮合的斜齿轮,其旋向相反,即一个斜齿轮是左旋的,与其配合的另一个斜齿轮一定是右旋的,反之亦然。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变位齿轮传动的受力分析及强度计算的原理与标准齿轮传动的一样。
经变位修正后的轮齿齿形有变化,轮齿弯曲强度计算式中的齿形系数Y Fa及应力校正系数Y Sa,也随之改变,但进行弯曲强度计算时,仍沿用标准齿轮传动的公式。
变位齿轮的齿形系数Y Fa及应力校正系数Y Sa的具体数值可查阅有关资料。
在一定的齿数范围内(如80齿以内),正变位齿轮的齿厚增加(即Y Fa减小),尽管齿根圆角半径有所减小(即Y Sa有所增大),但Y Fa Y Sa的乘积仍然减小。
故对齿轮采取正变位可以提高其弯曲强度。
在变位齿轮传动中,分别以x2,x1代表大、小齿轮的变位系数,x∑代表配对齿轮的变位系数和,即x∑=x2+x1.对于x∑=0的高度变位齿轮传动,轮齿的接触强度未变,故高度变位齿轮传动的接触强度计算仍沿用标准齿轮传动的公式。
对于x∑≠0的角度变位齿轮传动,其轮齿接触强度的变化由区域系数Z H来体现。
角度变位的直齿圆柱齿轮传动的区域系数为:
角度变位的斜齿圆柱齿轮传动区域系数为:
式中αt、αt'分别为变位斜齿轮传动的端面压力角及端面啮合角。
角度变位齿轮传动的区域系数Z H的具体数值可查阅有关资料。
x∑>0的角度变位齿轮传动,节点的啮合角α'>α(或αt'〉αt)可使区域系数Z H减小,因而提
高了轮齿的接触强度。
渐开线齿轮传动可借适当的变位修正获得所需要的特性,满足一定要求。
为了提高外啮合齿轮传动的弯曲强度和接触强度,增强耐磨性抗胶合能力,推荐的变位系数列于下表中。
按表中所列变位系数设计制造的齿轮传动皆能确保轮齿不产生相切与干涉、端面重合度εa≥1.2
及齿顶厚s a≥0.25m n。
对于斜齿圆柱齿轮或直齿锥齿轮,按当量齿数z v查表,所得变位系数对斜齿圆柱齿轮为法向数值(x n1, x n2)。
但为使大、小齿轮轮齿的弯曲强度相近可对锥齿轮传动进行切向变位修正。
