SPSS软件应用具体操作及结果分析
SPSS软件在正交试验设计、结果分析中的应用
P O.0919 O.000 O.099 0.016 0.000 0.016
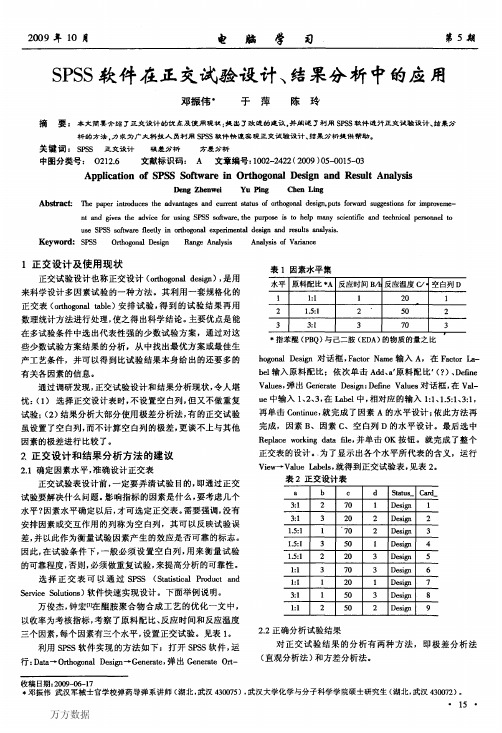
综合表6、7,可以得出:B。均数最大(8.333),且B3与 B,、B:之间存在显著性的差异(P<0.05),B。、B:之间不存在 显著性的差异(P=O.099>0.05)
同理,可以从另外的几张表格中分析可以得到:A:均数 最大(9.067),且A。、A:、A,之间均存在显著性差异;C:均 数最大(10.300),C。、C:、C,之间也都存在显著性差异。
总结论:中华芦荟丛生芽诱导的最佳培养基为:
A281C2,即6一BA:2.0rag/L:NAA:0.3rag/L:
· 16 ·
万方数据
2009年10月
电脑学 习
第5期
一个用VBA编写的Quine
蓝鹰‘
刘松
摘 要:本文介绍了一个在word
Word
递归定理
中图分类号:TP311.1
文献标识码: A 文章编号:1002-2422(2009)05-0017--01
A VBA Quine
Lan Ytng
Abstract:In this paper,a VBA Quine is presented.
Keyword:Qnl.e VBA Word
Recursion Theorem
2009年10月
电脑学 习
第5期
SPSS软件在正交试验设计、结果分析中的应用
邓振伟’
于萍 陈玲
摘 要:本文简要介绍了正交设计的优点及使用现状:提出了改进的建议.并阐述了利用SPSS软件进行正交试验设计、结果分
析的方法。力求为广大科技人员利用SPSS软件快速实现正交试验设计、结果分析提供帮助。
关键词:SPSS 正交设计 极差分析
SPSS软件在正交试验设计、结果分析中的应用

SPSS软件在正交试验设计、结果分析中的应用SPSS软件在正交试验设计、结果分析中的应用随着科学技术的飞速发展,正交试验设计在科学研究中的应用越来越广泛。
作为一种系统化的试验设计方法,正交试验设计在优化实验条件、提高实验效率、探索因素间相互作用等方面具有独特的优势。
而SPSS软件作为一种功能强大的统计分析工具,因其简单易学、数据处理能力强等特点,被广泛应用于正交试验设计及结果分析中。
本文将介绍SPSS软件在正交试验设计中的应用,并探讨其在结果分析中的优势。
一、SPSS软件在正交试验设计中的应用1. 正交试验设计的建立正交试验设计包括确定试验因素、确定水平数以及构建正交表格等步骤。
SPSS软件可以帮助实验者进行正交设计的建立。
首先,通过SPSS软件的数据管理功能,可以方便地建立试验因素、水平数等信息的数据框架。
然后,通过使用SPSS的数据编辑功能,可以轻松地输入试验因素的水平值。
最后,SPSS软件提供了正交试验设计模块,可以自动生成正交表格,并计算出试验所需的实验组合数。
通过SPSS软件的帮助,实验者可以快速、方便地完成正交试验设计的建立。
2. 数据的收集和整理正交试验设计所得到的数据需进行收集和整理,以便后续的结果分析。
SPSS软件提供了强大的数据处理功能,可以帮助实验者对数据进行收集和整理。
首先,SPSS软件提供了数据输入模块,可以方便地将实验数据输入到软件中。
其次,SPSS软件提供了数据清洗和转换的功能,可以对异常数据进行筛选和删除,并进行数据的转化、归一化等操作。
通过SPSS软件,实验者可以高效地对实验数据进行整理和准备,为后续的结果分析打下良好的基础。
3. 结果的分析与解释正交试验设计通过多因素的对比和交叉设计,可以更全面地了解各因素对实验结果的影响。
而SPSS软件作为一种统计分析工具,具备强大的数据分析能力,可以对正交试验设计所得到的数据进行有效的结果分析。
首先,SPSS软件提供了多种统计方法,如方差分析、回归分析等,可以对试验结果进行综合分析和比较。
如何用SPSS软件计算因子分析应用结果

如何用SPSS软件计算因子分析应用结果一、概述因子分析是一种在社会科学、心理学、经济学和许多其他领域广泛使用的统计分析方法。
这种方法的核心目的是简化数据集,通过找出潜在的结构或模式,将多个变量归纳为少数几个综合因子。
这些因子通常代表某种潜在的、不可直接观测的变量或特质,它们可以解释原始数据中的大部分变异。
SPSS,作为世界上最流行的统计分析软件之一,提供了强大的因子分析功能。
使用SPSS进行因子分析,研究者可以方便地得到因子载荷、因子得分、解释方差比例等关键信息,从而更深入地理解数据的内在结构和变量之间的关系。
本文将详细介绍如何使用SPSS软件进行因子分析,并解读分析结果。
我们将从数据准备开始,逐步讲解因子分析的步骤,包括选择适当的因子提取方法、旋转方法,以及如何解释和分析结果。
通过本文的学习,读者将能够掌握因子分析的基本方法,并能够独立运用SPSS软件进行有效的因子分析。
1. 简要介绍因子分析的概念及其在数据分析中的应用。
因子分析是一种在多元统计分析中广泛应用的技术,其主要目的是通过对大量变量间关系的研究,找出这些变量之间的潜在结构,或者说找出潜在的公共因子。
这些公共因子能够反映原始变量的大部分信息,并且彼此之间互不相关。
通过因子分析,研究者可以在减少变量数量的同时,保留原始数据中的关键信息,从而简化数据结构,方便后续的分析和解释。
在数据分析中,因子分析的应用非常广泛。
例如,在社会科学领域,研究者可能需要对大量的社会指标进行分析,以了解社会现象的本质。
这时,因子分析可以帮助他们找出这些指标背后的潜在结构,从而更深入地理解社会现象。
在市场营销领域,因子分析可以帮助研究者识别出消费者对不同产品的偏好模式,从而指导产品设计和市场定位。
在生物医学领域,因子分析可以用于基因表达数据的分析,帮助研究者找出影响特定生物过程的基因群。
在SPSS软件中,因子分析的实现相对简单,用户只需按照软件的操作步骤进行操作即可完成分析。
根据实验结果,进行多元方差分析SPSS操作步骤

根据实验结果,进行多元方差分析SPSS操作步骤多元方差分析(MANOVA)是一种统计方法,用于比较两个以上组之间在多个连续因变量上的差异。
SPSS是一款功能强大的统计分析软件,可以用于进行多元方差分析。
下面是进行多元方差分析的SPSS操作步骤:1. 打开SPSS软件,并导入实验数据。
2. 在菜单栏选择“分析”(Analyze),然后选择“一元方差分析”(General Linear Model)。
3. 在弹出的对话框中,将多个连续因变量添加到“因变量”(Dependent Variables)框中。
点击“添加”按钮,然后选择需要分析的连续因变量。
4. 将一个或多个离散自变量添加到“因子”(Factors)框中。
点击“添加”按钮,然后选择需要分析的离散自变量。
5. 点击“选项”(Options)按钮,可以进行一些附加的设置。
例如,可以选择是否计算效应大小、调整误差项或进行共同协方差矩阵的检验等。
6. 点击“确定”按钮,开始进行多元方差分析。
7. 分析结果会显示在SPSS的输出窗口中。
可以查看因变量之间的差异是否显著,以及不同组之间是否存在显著差异。
8. 为了更好地理解结果,可以进一步进行后续分析。
例如,可以进行事后比较(Post hoc tests)来确定具体哪些组之间存在显著差异。
请注意,进行多元方差分析前,需要确保数据满足一些假设条件,如正态性、方差齐性和无多重共线性等。
另外,为了减少假阳性结果,应谨慎解释显著性水平。
以上是根据实验结果进行多元方差分析SPSS操作的步骤。
希望对您有所帮助!如有需要,请随时与我联系。
SPSS统计软件使用指导

SPSS统计软件使用指导SPSS(统计软件包社会科学)是一个功能强大的统计分析软件,被广泛应用于社会科学领域的数据处理和统计分析。
本文将为您提供SPSS的简单使用指导。
一、数据导入与数据处理1. 数据导入:打开SPSS软件后,选择“文件”菜单中的“导入数据”,选择合适的数据类型(如Excel、CSV等),然后按照指引找到要导入的数据文件,并点击“打开”按钮导入数据。
2.数据处理:导入数据后,您可以使用SPSS进行数据清洗、数据变换和数据整合等操作。
例如,可以使用数据筛选功能去除缺失值,使用重编码功能对变量进行重新分组等。
二、数据描述统计1.频数统计:选择“分析”菜单中的“描述统计”→“频数”,将要分析的变量移至“变量列表”中,点击“统计”按钮,并选择要统计的指标(如中位数、均值等),最后点击“确定”按钮即可进行频数统计分析。
2.描述性统计:选择“分析”菜单中的“描述统计”→“描述统计”,将要分析的变量移至“变量列表”中,点击“统计”按钮,并选择要统计的指标(如均值、标准差等),最后点击“确定”按钮即可进行描述统计分析。
三、数据分析与模型建立1.相关分析:选择“分析”菜单中的“相关”→“双变量”,将要分析的变量移至“变量列表”中,点击“OK”按钮即可进行相关性分析。
2.回归分析:选择“分析”菜单中的“回归”→“线性”,将因变量和自变量移至相应的“因变量”和“自变量”框中,可以选择“统计”按钮进行相应的统计分析。
3.方差分析:选择“分析”菜单中的“比较组”→“方差分析”,将要分析的变量移至“因子”列表中以及自变量列表中,点击“OK”按钮即可进行方差分析。
四、结果输出与图表绘制1.结果输出:分析完成后,可以通过点击“结果”菜单中的“查看输出”来查看统计结果。
可以选择复制、粘贴或导出统计结果到其他软件进行进一步分析或报告。
2.图表绘制:选择“图形”菜单,其中包含了众多图表类型,如饼图、柱状图、折线图等。
SPSS软件在正交试验设计、结果分析中的应用

SPSS软件在正交试验设计、结果分析中的应用一、引言正交试验设计是一种经典的统计方法,用于探究多个因素对于试验结果的影响。
该方法将试验因素进行有序的组合,既能缩减试验次数,又能防止因素之间的互相影响。
而SPSS软件作为统计分析领域中的瑞士军刀,拥有强大的数据处理和分析功能,为探究者提供了便利的工具。
本文将探讨SPSS软件在正交试验设计与结果分析中的应用。
二、正交试验设计的基本原理正交试验设计遵循一定的规则和原则。
起首,需要明确要探究的因素,这些因素可以是试验操作,也可以是试验条件。
其次,确定各个因素的水平,水平的选择要充分思量试验的目标和探究对象。
然后,在确定因素和水平的基础上,构建正交试验设计表,以便按照设计表中的规则进行试验。
最后,依据试验结果,进行数据分析和结果诠释。
三、SPSS软件在正交试验设计中的应用1. 设计试验方案SPSS软件提供了一系列的数据输入工具和试验设计模块,可以援助探究者轻松地构建正交试验设计。
通过SPSS软件,可以灵活地选择因素和水平,并生成正交试验设计表。
同时,SPSS软件还提供了随机分组和重复设计等功能,以满足试验设计的要求。
2. 数据输入与整理SPSS软件支持多种数据输入方式,可以通过导入Excel表格、文本文件等格式的数据,或者直接在软件中手动输入数据。
在正交试验设计中,往往涉及大量的数据输入,SPSS软件的数据输入功能可以援助探究者快速、准确地输入数据。
同时,SPSS软件还提供了数据整理和清理功能,可以对异常值、缺失值等进行处理,使得数据更加可靠。
3. 数据分析与诠释SPSS软件的数据分析功能分外强大,可以进行多元方差分析、协方差分析、回归分析、相关分析等多种统计分析方法。
在正交试验设计中,可以使用SPSS软件进行多因素方差分析,以确定各个因素对试验结果的影响。
同时,SPSS软件还提供了图表制作功能,可以直观地展示分析结果。
四、SPSS软件在正交试验结果分析中的应用1. 参数预估SPSS软件可以通过正交试验设计的数据,进行参数预估和置信区间的计算。
SPSS相关分析实例操作步骤-SPSS做相关分析

SPSS相关分析实例操作步骤-SPSS做相关分析SPSS(Statistical Product and Service Solutions)是目前在工业、商业、学术研究等领域中广泛应用的统计学软件包之一。
Correlation是SPSS的一个功能模块,可以用于分析两个或多个变量之间的关系。
下面是SPSS进行相关分析的具体步骤:1. 打开SPSS软件,选择“变量视图”(Variable View),输入相关的变量名,包括数字型变量和分类变量。
2. 进入“数据视图”(Data View),输入数据,并保存数据集。
3. 打开菜单栏中的“分析”(Analyze),选择“相关”(Correlate),再选择“双变量”(Bivariate)。
4. 在双变量窗口中,选择包含需要分析的变量的变量名,并将其移至右侧窗口中的变量框(Variables)。
5. 如果需要控制其他变量的影响,可以选择“控制变量”(Options)。
6. 点击“确定”(OK)按钮后,SPSS将输出结果,并将其显示在输出窗口中。
相关系数(Correlation Coefficient)介于-1和1之间,可以用来衡量两个变量之间的线性关系的强度。
7. 如果需要对结果进行图形化展示,可以选择“图”(Plots),并选择适当的图形类型。
需要注意的是,进行相关分析时需要确保变量之间存在线性关系。
如果变量之间存在非线性关系,建议使用其他统计方法进行分析。
同时,SPSS进行相关分析的结果只能描述变量之间的关系,不能用于说明因果关系。
以上是SPSS做相关分析的具体步骤,希望能对大家进行SPSS 数据分析有所帮助。
学会使用SPSS进行数据处理和分析

学会使用SPSS进行数据处理和分析第一章:介绍SPSS及其基本功能SPSS(Statistical Package for the Social Sciences)是一款专业的统计软件,可广泛应用于社会科学、医学、教育、市场营销等领域的数据处理和分析。
SPSS具有强大的数据处理和展示功能,能够帮助用户进行数据清洗、统计描述、统计推断等分析工作。
本章将详细介绍SPSS的基本功能,包括数据导入导出、数据清洗和变量定义等。
第二章:数据导入与导出在使用SPSS进行数据处理和分析前,首先需要将原始数据导入到SPSS中。
SPSS支持多种数据格式的导入,如Excel、CSV、Txt等。
本章将介绍如何进行数据导入,并讲解一些常见的数据导入问题及解决方法。
此外,还将介绍如何将SPSS的分析结果导出到其他格式,如Excel、Word等,以便后续的数据展示和报告撰写。
第三章:数据清洗与变量定义数据清洗是数据处理的基础工作,对于原始数据中存在的异常值、缺失值、重复值等进行处理,以保证数据的准确性和可靠性。
本章将介绍如何使用SPSS进行数据清洗,包括识别与处理异常值、填补缺失值、删除重复值等。
同时,还将讲解如何进行变量的定义和测量水平的设置,以便后续的数据分析。
第四章:数据描述性统计数据描述性统计是对数据整体特征进行描述和总结的方法,可帮助研究者更好地理解数据。
本章将介绍如何使用SPSS进行数据描述性统计,包括计算变量的均值、标准差、频数分布等。
此外,还将讲解如何绘制直方图、散点图、箱线图等图表,以便更直观地展示数据的分布和关系。
第五章:统计推断与假设检验统计推断是在样本数据的基础上对总体参数进行推断的方法,常用于科学研究中的结论判定。
假设检验则用于判断样本数据与总体的差异是否显著。
本章将介绍如何使用SPSS进行统计推断和假设检验,包括T检验、方差分析、相关分析等。
同时,还将讲解如何解读统计结果并进行结果报告。
第六章:数据分析与建模数据分析是根据统计学原理对数据进行深度挖掘和解释的过程,而建模则是基于数据分析结果进行预测和决策的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS软件操作练习参考书:《生物统计学》张勤主编(第2版)一、均数差异显著性检验(一)单个样本t测验(二)独立样本测验(两个样本重组比较)(三)两个样本配对比较二、方差分析(一)单因素方差分析(样本量相等、样本量不等)三、相关回归分析相关分析:Analyze→Correlate→Bivariate(简单相关)相关回归:Analyze→Regression→Linear 注意:Dependent:因变量y Independent:自变量x 四、卡方测验(一)独立性:Date We ight→Cases→Frequency Variable(观察值)→ok Analyze→Descriptive Statistics→Crosstabs→Row(行)、Columns(列)→Statistics→Chi-Square(二)适合性测验:Date Weight→Cases→Frequency Variable(观察值)→ok Analyze→Nonparametric Tests→Chi-Squareic(注意比例的填写)五、两因素方差分析(一)两因素无重复值方差分析(二)两因素有重复值方差分析一、均数差异显著性检验(一)单个样本t测验P66 例5.1One-Sample Tes t-1.03516.316-1.00000-3.0486 1.0486Vitt df Sig. (2-tailed)M eanDifference Low er Upper95% ConfidenceI nterval of theDifferenceTest Value = 21由结果可知:t=-1.035 sig=0.316>0.05 该批罐头的平均维生素C与规定的21mg/g无显著差异。
注:Sig.(2-tailed) 双侧检验概率95% confidence.... 差值的95%置信下线和置信上线(二)独立样本测验(两个样本重组比较)P70 例5.3Independe nt Sample s Test.812.389-.92310.378-.81000.87744-2.76507 1.14507-.9239.363.379-.81000.87744-2.783251.16325E qual variancesassumedE qual variances not assum ed增重FSig.Levene's Test for E quality of Variancest dfSig. (2-tailed)M ean Difference Std. E rror DifferenceLow er Upper 95% Confidence I nterval of the Difference t-test for E quality of M eans由结果可知:两样本方差齐质性测验中 F=0.812 Sig=0.389>0.05 方差同质,因此选择t=-0.923 Sig=0.378>0.05 两种不同饲料对香猪生长无显著差异。
注:Levene ’e text for equality of Variances 两样本方差齐质性检验P73 例5.6Independe nt Sample s Test8.208.0102.07118.0537.500003.62169-.1089015.108902.07112.021.0617.500003.62169-.3894315.38943E qual variancesassumedE qual variances not assum ed增重FSig.Levene's Test for E quality of Variancest dfSig. (2-tailed)M ean Difference Std. E rror Difference Low er Upper 95% Confidence I nterval of the Difference t-test for E quality of M eans由结果可知方差同质测验结果 F=8.208 sig=0.010<0.05 说明方差不同质,因此应选择t=2.071 df=12.021 sig=0.061>0.05(三)两个样本配对比较P75 例5.7Paired Samples Te st812.50000546.25347193.12977355.820671269.179 4.2077.004正常饲料组 - VE缺乏组P air 1M ean Std. DeviationStd. E rrorM ean Low er Upper95% ConfidenceI nterval of theDifferenceP aired Differencest df Sig. (2-tailed)有结果可知,t=4.207 sig=0.004<0.01 用正常日粮饲喂的动物肝脏中的维生素A含量与用维生素E饲喂的动物肝脏中的维生素A的含量差异极显著。
注:Mean 差值均数Std.deviation差值的标准差Std.error mean 差值的标准误二、方差分析(一)单因素方差分析(样本量相等、样本量不等)P83 例6.1Te st of Homogeneity of Variance s 增重1.322316.302Levene Statistic df1df2Sig.注:Test homogenity of variance 变异的同质性测验方差同质测验结果 Sig=0.302>0.05 方差同质ANOVA增重2970.0003990.00010.219.0011550.0001696.8754520.00019Betw een Groups Within Groups TotalSum of Squares dfM ean SquareF Sig.F=10.219 Sig=0.001<0.05 差异显著 需进行多重比较 注:ANOV A 方差分析表Between... within...total...组间、组内、总变异 Sum of squares 离均差平方和 Mean square 均方Post Hot Tests 多重比较:最小显著差数法(LSD 法)在a=0.05时,饲料1与饲料2、3、4差异显著;饲料2与饲料3、4差异不显著;在a=0.01时饲料1与饲料2、3、4差异极显著;饲料2与饲料3、4差异不显著新复极差法(Duncan’s法)Homogeneous Subsets表在a=0.05时饲料2、3、4间差异不显著,饲料1与饲料2、3、4差异显著P97 3Sig=0.031<0.05 方差不同质(此时需对数据进行转换后在进行方差分析,详见书P290)F=7.252 Sig=0.001<0.01在a=0.05时,品种1与品种3差异显著,与品种2、4、5差异不显著;品种2与品种3差异显著、与品种4、5差异不显著;品种3与品1、2、4、5差异显著。
在a=0.01时.。
邓肯法P97 5方差同质测验结果:Sig=0.602>0.05 方差同质由方差分析表可知:F=18.070 Sig=0.000<0.01 差异极显著需进行多重比较多重比较结果:在a=0.05时地区2、3间差异不显著,地区1与地区2、3差异显著在a=0.01时地区2、3间差异不显著,地区1与地区2、3差异极显著SAS转换成SPSS单因素试验(各处理重复数相等)DATA E;INPUT TRS y@@;Cards;A1 15 A1 16 A1 15 A1 17 A1 18A2 45 A2 42 A2 50 A2 38 A2 39A3 30 A3 35 A3 29 A3 31 A3 35A4 31 A4 28 A4 20 A4 25 A4 30 A5 40 A5 35 A5 31 A5 32 A5 30 ;PROC anova;CLASS TR;Model y=TR;MEANS TR/T;RUN;LSD法:a=0.05时A3与A5差异不显著其他各组差异显著a=0.01时A3与A4 A5差异不显著其他各组差异极显著邓肯法:有方差同质表可知:Sig=0.168>0.05 方差同质由方差分析表可知:F=34.320 Sig=0.000<0.01 差异极显著需进行多重比较:LSD法:在a=0.05 A3与A5差异不显著其他各组差异显著在a=0.01 A3与A4 A5差异不显著其他各组差异极显著邓肯法:在a=0.05 A3与A5差异不显著其他各组差异显著在a=0.01 A3与A4 A5差异不显著其他各组差异极显著综上:A3与A5差异不显著A3与A4差异显著其他各组差异极显著二、相关回归分析相关分析:Analyze→Correlate→Bivariate(简单相关)相关回归:Analyze→Regression→Linear 注意:Dependent:因变量y Independent:自变量x P125 例9.1Correlations1.888**.0011010.888**1.0011010P earson CorrelationSig. (2-tailed)NP earson Correlation Sig. (2-tailed)N305天的产奶量X150天的产奶量Y305天的产奶量X150天的产奶量YCorrelation is significant at the 0.01 level (2-tailed).**.有结果可知,相关系数r=0.888 sig=0.001<0.01 所以存在极显著相关Mode l Summary.888a.788.7614.94143M odel 1RR SquareAdjusted R SquareStd. E rror of the E stimateP redictors: (Constant), 305天的产奶量Xa.R=0.888ANOVA b725.1581725.15829.698.001a195.342824.418920.5009Regression Residual TotalM odel 1Sum of Squares dfM ean SquareF Sig.P redictors: (Constant), 305天的产奶量X a. Depen dent Variable: 150天的产奶量Yb.有方差分析表可知 F=29.698 sig=0.001 <0.01 回归关系极显著存在由上表可知:a=-18.316 b=2.184 y=-18.316+2.184X对回归截距a 进行显著性测验:t=-1.228 sig=0.254>0.05 回归截距存在不显著/回归截距存在没有统计学意义对回归系数b 进行显著性测验:t=5.450sig=0.001<0.01 回归关系极显著存在P135 9.2Correlations 表Regreesion 表R=0.818 抽样误差Sig=0.004 <0.01体重和饲料消耗存在极显著相关; 有方差分析表可知,F=16.232 sig=0.004<0.01回归关系极显著存在; a=55.263 b=7.690 y=55.263+7.690X回归截距t=5.796 sig=0.000<0.01回归截距极显著存在 回归系数t=4.029 sig=0.004<0.01回归系数极显著存在 P144 3R=0.847 sig=0.002<0.01 胸围与体重存在极显著相关 体重Y 对胸围XF=20.393 sig=0.002<0.01 回归关系极显著存在a=-115.375 b=2.547 y=-115.375+2.547X对回归截距:t=-2.839 sig=0.022<0.05 回归截距显著存在对回归系数:t=4.516 sig=0.002<0.01 回归关系极显著存在胸围Y对体重XF=20.393 sig=0.002<0.01 回归关系极显著存在a=52.824 b=0.282 y=52.824+0.282X对回归截距假设性测验:t=12.362 sig=0.000<0.01回归截距极显著存在对回归系数假设性测验:t=4.516 sig=0.002<0.01 回归关系极显著存在P145.4由结果可知,相关系数R=0.939 抽样误差Sig=0.002<0.0 出生平均个体重与20日龄平均个体重相关关系存在极显著相关;由方差分析表可知,F=37.436 sig=0.002<0.01 回归关系极显著存在;a=2.189 b=2.129 y=2.189+2.129X对回归截距假设性测验t=4.592 sig=0.006<0.01回归截距极显著存在对回归系数假设性测验t=6.127 sig=0.002<0.01回归关系极显著存在SAS转换成SPSSSAS-线性回归SAS(一元线性回归与相关分析)DATA G;INPUT xy@@;CARDS;80 2350 86 2400 98 2720 90 2500 120 3150 102 2680 95 2630 83 2400 113 3080 105 2920 110 2960 100 2860 ;PROC REG CORRMODEL y x;RUN;Coefficientsa 582.185147.315 3.952.00321.712 1.485.97714.622.000(Constant)XM odel1B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.Dependent Variable: Ya.由结果可知,相关系数r=0.977 抽样误差Sig=0.000<0.05 X 和Y 相关关系存在极显著相关; 由方差分析表可知,F=213.808 sig=0.000<0.01 回归关系极显著存在; a=582.185 b=21.712 y=582.185+21.712X对回归截距假设性测验t=3.952 sig=0.003<0.01回归截距极显著存在 对回归系数假设性测验t=14.622 sig=0.000<0.01回归关系极显著存在四、卡方测验(一)独立性:Date Weight →Cases →Frequency Variable (观察值)→okAnalyze →Descriptive Statistics →Crosstabs →Row (行)、Column s(列)→Statistics →Chi-SquareP193 13.4两行两列抽烟与否 * 死亡与否 Cros stabulation Count11795010675434840217112981469不吸吸烟抽烟与否Total死亡存活死亡与否TotalChi-Square Tests1.728b 1.1891.4971.2211.6851.194.202.1111.7271.1891469P earson Chi-Square Continuity Correction a Likelihood Ratio Fisher's E xact Test Linear-by-Linear AssociationN of Valid CasesValue dfAsym p. Sig.(2-sided)E xact Sig.(2-sided)E xact Sig.(1-sided)Computed only for a 2x2 tablea. 0 cells (.0%) have expected count less than 5. The m inimum expected count is 46.80.b.由结果可知X 2 =1.497 df=1 Sig=0.221>0.05吸烟与死亡不产生显著关联注:Continuity correction 连续性矫正的X 2 Asymp.Sig (2。
