西电通院随机信 分析期中试卷
2002西安电子科技大学信号期中试题
■
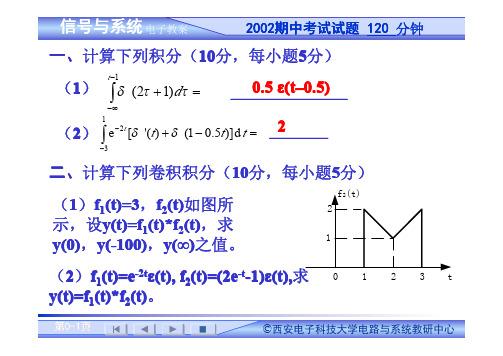
f2(t) 2 1
0
1
2
3
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2002期中考试试题 2002期中考试试题
10 y(t) f(t) 三、(10 10分)某连续系统输出y(t) y(t)与输入f(t) f(t)的关系为 y(t) = |f(t) – f(t – 1)| 试判别该系统是否线性系统?是否是时不变系统? (要求写出判别过程。)
10 四、(10 10分)已知某线性时不变系统的阶跃响应 g(t)=ε(t – 1)+ e – tε(t) f(t)=3e –∞<t< g(t)=ε (t),求当输入信号f(t)=3e2t(–∞<t<∞)时系 <t<∞ y (t)。 统的零状态响应yf(t)
第0-2页 0-2
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2002期中考试试题 2002期中考试试题
10 f(-0.5t+1) 五、(10 10分)已知f(-0.5t+1) f(-0.5t+1)的图形如图所示,试画出 f(t) f(t)的波形。 f(-0.5t+1)
3 1 -2 -1 -2 2 4 t
6 5 1 10 六、(10 10分)周期信号 f (t ) = 5 cos t + 10 sin t + 20 sin t 5 2 7 10 10 画出该周期信号10 10次谐波(含10 10次谐波)以下的单边 振幅频谱图与相位频谱图。
第0-3页 0-3
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2002期中考试试题 2002期中考试试题
西安电子科技大学 电院 《随机信号分析》大作业
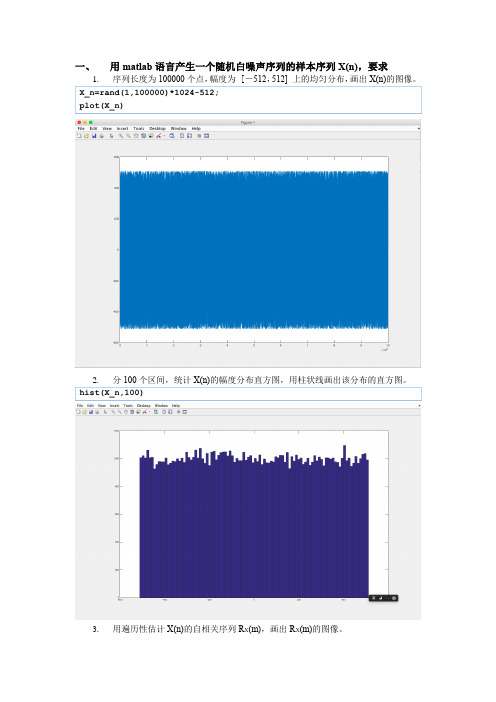
一、用matlab语言产生一个随机白噪声序列的样本序列X(n),要求
3.用遍历性估计X(n)的自相关序列R X(m),画出R X(m)的图像。
二、将一中产生的序列通过一个线性系统,其单位脉冲响应为h(n)=0.9n,n=0,
1,…,100
三、比较X(n)与Y(n)的幅度分布直方图,发生了什么变化。
分析其变化的原
因。
随机信号经过线性系统后,不会增加新的频率分量,但是输出的幅度和相位会发生变化。
白噪声X(n)的幅度基本相同,而Y(n)的幅度基本呈正态分布。
因为均匀白噪声是一种宽带非正态过程,所以通过一有限带宽线性系统后,输出Y(n)近似呈正态分布。
——via 1402011 赵春昊。
西安电子科技大学通信原理真题

2013西安电子科技大学通信工程学院考研专业课 ③ 历年真题 主编:@西电点儿敬告:1.本资料完全免费;2.请使用B5纸打印;3.建议双面打印;4.更多资料:/xduky。
准备考研,无论是哪个专业,真题都是最重要的,西电通院也是如此。
在做真题之前请务必了解试卷的题型结构及分值,为此,编者做了下表:通信原理部分信号与系统部分一、填空二、简答三、综合/计算一、选择二、填空三、计算题数分值题数分值1 2 3 4 5分值题数分值题数分值1 2 3 4 分值2011 10 10 5 25 8 88 8 840 4 16 4 1612 12 12 7 43 2010 10 10 5 25 8 88 8 840 4 16 4 1612 12 12 7 43 2009 10 10 5 25 8 88 8 840 4 16 4 1612 12 12 7 43 2008 10 10 5 25 8 88 8 840 4 16 4 1612 12 12 7 43 2007 10 10 5 25 8 88 8 840 4 16 4 1612 12 12 7 43 2006 10 10 5 25 8 69 9 840 4 16 4 1611 11 11 10 43 2005 10 10 5 25 8 88 8 840 4 16 4 1610 10 12 11 43 2004 10 10 4 20 9 99 9 945 4 16 4 1610 10 12 11 43 2003 10 10 4 20 9 99 9 945 4 16 4 169 9 13 12 43试卷分为两部分,通信原理、信号与系统,各占75分,从来没变过。
2003年的第一部分是信号与系统,第二部分是通信原理;而从2004年开始至今,第一部分是通信原理,第二部分是信号与系统。
至于各部分的题型与分值,上表已经很详细了,不做过多解释。
需要提一点,通信原理部分的第三大题“综合/计算”是指:2008和2009年试卷上写的是“计算题”,其余的年份写的是“综合题”,但是其中小题的类型却是一样的,都是“需要计算的综合题”,综合题一般集中在四、五、六、七、八、九章(以大纲章序号为准),有时会两章综合(如五八章、六八章)另外,专业课是可以使用计算器的,计算一些复杂的算式或者对数(如香农公式)很方便。
电子科技大学2009年随机信号分析试题B与标准答案

cos(2ωt + ωτ + 2θ ) f Ω ,= 0 Φ (ω , θ ) dθ d ω
∴R = X (t + τ , t ) = a2 2
a2 a2 E [ cos(2Ωt + Ωτ + 2Θ) + cos(Ωτ ) ] = E [ cos(Ωτ ) ] 2 2
∫
∞
−∞
cos(ω ′τ ) f Ω (ω ′)dω ′
第 页 共 5 页
2
学院_______________________
姓名____________
学号________________
任课老师____________
选课号______________
………….……密 …..……….封……..……线 ………..…以………..…内………....答 …………...题…………..无……. …….效…..……………..
∞ cos(ω ′τ )e − jωτ dτ f (ω ′)d ω ′ ∫−∞ ∫−∞ Ω
∞
∫
∞
−∞
π δ (ω − ω ′ ) + δ (ω + ω ′ ) f Ω (ω ′)d ω ′
由于 δ (ω ′), f Ω (ω ′) 为偶函数,所以
= π a2 ∫ δ (ω − ω ′ ) + δ (ω + ω ′ ) f Ω (ω ′)dω ′ 0
120 分钟) 考试形式: 一页纸开卷 10 卷面 成绩 分, 实验 期中 成绩 期末 成绩 0 平时 成绩
课程成绩构成:平时
分, 期末 实验 成绩
一
二
三
四
五
六
七
西电通信原理13试题带答案

西安电子科技大学考试时间 120 分钟试题(A)班级学号姓名任课教师一、选择(请将答案填写到下面表格中)(每题2分,共2×10=20分)1、多路信号复用方式中不含以下哪一种?()A. 频分复用B. 时分复用C. 码分复用D. 相分复用2、以下属于全双工通信的是:()A. 广播B. 对讲机C. 电话D.无线寻呼3、根据香农公式可知为了使信道容量趋于无穷大,不可以采取下列措施:( )A、噪声功率为零B、噪声功率谱密度始终为零C、信号发射功率为无穷大D、系统带宽为无穷大4、设某随参信道的最大多径时延差等于2ms,为了防止出现频率选择性衰落,该信道的相关带宽为:()A、500HzB、>500HzC、<500HzD、2KHz5、即使在“0”、“1”不等概率出现情况下,以下哪种码仍然不包含直流成分:( )第1页共6页第2页 共6页A 、AMI 码B 、双极性归零码C 、单极性归零码D 、差分码6、二进制数字基带传输系统的误码率计算公式为:( )A 、()()0/11/0P P P e +=B 、()()()()1/010/10P P P P P e +=C 、()()10P P P e +=D 、()()()()0/111/00P P P P P e +=7、功率利用率最低调制方式是:( )A 、2ASKB 、2FSKC 、2PSKD 、2DPSK8、对二进制频带传输系统而言,下列说法错误的是:( )A 、FSK 、PSK 、DPSK 的抗衰落性能均优于ASK ;B 、ASK 、PSK 、DPSK 的最佳判决门限比FSK 容易设置;C 、接收机的输入信噪比增加,解调的误码率一定下降;D 、ASK 、PSK 、DPSK 的频带利用率均高于FSK 。
9、为了防止ΔM 编码过程的过载现象出现,不可以采取以下哪种措施:( )A 、减小量化台阶B 、增大量化台阶C 、增大采样速率D 、减小采样周期10、按照A 律13折线编码实现PCM 编码时,第7段落的段落码为:( )A 、011B 、110C 、101D 、 111二、填空(每空2分,共2×10=20分)1、 频谱从零频附近开始的信号是 基带信号 。
电子科技大学随机信号分析中期考题2006随机(A)

1.设随机过程21)(cos )(2-Θ+=t t X ω,Θ 是随机变量,其特征函数为)(υφΘ。
证明:)(t X 是广义平稳随机过程的充要条件是0)4()2(==ΘΘφφ。
证明:(1))(t X 的均值为:()21()[()][cos ()]2111[1cos 2()][cos(22)]22211cos(2)[cos(2)]sin(2)[sin(2)]22X m t E X t E t E t E t t E t E ωωωωω==+Θ-=++Θ-=+Θ=Θ-Θ由上式可知,当且仅当0)]2sin()2[cos(][)2(2=Θ+Θ==ΘΘj E e E j φ时,()0X m t =,才与t 无关。
(2))(t X 的相关函数为:22(,)[()()]11[(cos ())(cos ())]2211[cos(222)cos(22)]22[cos(2)][cos(424)]811cos(2)cos(42)[cos(4)]881sin(42)][sin(4)]8X R t t E X t X t E t t E t t E E t t E t E ττωωτωωωτωωτωωτωτωωτωωτ+=+=++Θ-+Θ-=++Θ⨯+Θ+++Θ==++Θ-+Θ同理可得,当且仅当0)]4sin()4[cos(][)4(4=Θ+Θ==ΘΘj E eE j φ时,)cos(21),(ωττ=+t t R X 与t 无关。
2.设随机过程)sin()(0Θ+Ω=t A t X ,其中0A 为常数,ΘΩ和为相互独立的随机变量,Ω在]2010[ππ内均匀分布,Θ在]20[π内均匀分布。
证明:(1) )(t X 是广义平稳随机信号;(2) )(t X 的均值是各态历经的。
解: (1)00000[()][sin()][sin()cos()cos()sin())][sin()][cos()][cos()][sin())]0E X t E A t E A t A t A E t E A E t E =Ω+Θ=ΩΘ+ΩΘ=ΩΘ+ΩΘ= 202020(,)[()()][sin()sin()]cos()cos(22)2cos()2X R t t E X t X t A E t t t A E A E ττττττ+=+=Ω+Ω+ΘΩ+ΘΩ-Ω+Ω+Θ⎡⎤=⎢⎥⎣⎦Ω⎡⎤=⎢⎥⎣⎦所以)(t X 是广义平稳随机信号 (2)[]00000001[()][sin()]lim sin()lim sin()lim cos()|0TT T T T T A X t A A t A t dtT A A t d t t T T →+∞→+∞→+∞=Ω+Θ=Ω+Θ=Ω+ΘΩ=-Ω+Θ=ΩΩ⎰⎰时间平均等于统计平均,所以)(t X 的均值是各态历经的。
西电电院随机信号分析.

随机信号分析之简答题
1. 什么是随机过程非线性变换的变换法?
利用傅里叶变换或者拉普拉斯变换 ,将非线性函数变换成转移函数 ,将概率密度转换成特征函数 , 改变积分形式后再进行运算的方法就是变换法。
非线性变换的厄密特多项式法适用于何种随机过程?为什么?
适用于输入为正态随机过程。
因为输入随机过程为正态分布, 则可将用麦克劳林级数展开, 变成厄密特多项式, 由于分项积分容易计算, 正交性
重积分简化为一重积分。
此方法运算简便,因而广被引用。
普赖斯法适用的条件是什么?
普赖斯法适用于输入为平稳正态过程 , 且非线性函数经 k
缓变包络法适用的条件是什么?
缓变包络法适用于
2.
一维分布为瑞利分布 ,相位服从均匀分布
输出电压服从指数分布
N 次再积累输出,其输出随机变量服从何种分
加法器的输出电压服从 2N ,输出电压的均值为 2N ,方差为 4N 3. R (t 的一维概率分布服从何种分布?
服从
SNR<<1时, R (t 的一维概率分布近似为何种分布?
当信噪比时, R (t 的一维概率分布近似为何种分布? 近似为正态分布
By Elwin 2012年 11月 12日。
西电信号与系统期中试题

d dt
f
(t),
试画出f(t)和g(t)的波形.
f (2t-1)
f(t)
g(t)
1
t
t
t
o1 2
o1
o1
题 12 图
13、函数 f(t) = 1+sin(t) 的单边拉普拉斯变换
F(s)
;
1 s
1 s2
1
14、
已知
e jt f (t)
0
,| t | 1,
,否则
其频谱函数 F(jω) = 2Sa( 1)
Ⅰ、计算题(共20分)
1、 积分
(t
t0
)
(t
2t0 )dt
1,
(1/ 2, 0,
t0 0 t0 0) t0 0
k
k
2、 (i 3) (i 2) (i 2) (k 2)
i
i
2, k 0,1
3、
f1(k) (k 1) (k 2),
f2
(k
)
1,
k2
f (k) f1(t) * f2(t)
y(t) 2 cos( t )
43
n
3
/2
/4 2
3
18、描述某因果系统输出y(t)与输入f(t)的微分方程为
y"(t) 3y'(t) 2 y(t) f '(t) 4 f (t)
(1) 已知 f(t) = δ’(t), y(0-)=0, y’(0-)=1, 求系统的零输入响应yx(t)和零状态响应 yf1(t); (t≥0)
由LTI系统性质得
yzi 3 (t )
d [5et
dt
(t )]
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
8
1 3
exp(
x12
x22 12
x1x2 )
5)设马氏链的状态空间为 G {1,2,3},其一步转移概率为
0.3 0.7 0
P
0
0.2 0.8
0.7 0 0.3
(1) 当初始分布为时 P{X0 1} 1, P{X0 1} 0, P{X0 1} 0 ,经过两步转移
后,处于状态 2 的概率; (2) 求该马氏链的平稳分布。
3、填空 1)当随机过程 X (t) 表示施加在单位电阻上的电压信号时,则其均方值和方差分
别代表的物理意义是 瞬时功率统计平均值 和 瞬时交流功率统计平均值 。 P6 课本原文 2)除状态空间自身外,不含任何闭集的马氏链称为 不可约的马氏链 。 P63 不可约马氏链的定义 3)若随机过程 X (t) 的相关函数为 RX (t1,t2) ,其导数过程为Y (t) ,则和的互相关
族称为随机过程,简记为 X (,t) 或 X (t) 。族中每个函数称为该过程的一个样本, 它是随机过程一次试验的物理实现,是一个确知的时间函数。 2)泊松过程是宽平稳过程 错
E X (t) t ,而宽平稳随机过程要求均值为常数(与时间 t 无关)。
3)若齐次马氏链某状态的周期为 L,则从该状态出发,必然存在一条步长为 L 的路径,使得该状态返回自身。 错 马氏链某状态的周期定义为:从该状态出发能够返回此状态的所有步长 {n :n 1,pii 0的} 最大公约数 L。L 可能小于能够返回该状态的最小步长。
yx
对于连续的情况而言,即为 F(x, y) f (x, y)dxdy
yx
对于离散的情况而言,为 F(x, y) f (x, y)dxdy P(x, y)
( x, y )A
y (x, y)
A
0
x
FX (x1, x2, 2,6) 即为随机变量 X (2) 和 X (6) 的联合分布函数。
E Y (t) E[ A] E[0 sin(0t )] 0
RY (t1, t2 ) E[ A202 sin(0t1 ) sin(0t2 )]
02
E[
A2
]
E
cos
0
(t2
-t1
)
cos 2
0
(t2
+t1
)
2
02 cos 0(t2-t1) =02 cos(0 ), t2 t1
1
3
FX
( x1,
x2, 2,6)
P
X(2)
x1,
X(6)
x2
2 3
1
0
x1 5且1 x2 4, 2 x1 3且x2 4, 3 x1 5且4 x2 6
3 x1 5且x2 6, x1 5且4 x2 6,
x1 5且x2 6 其他
解析:本题的二维分布律如下
P X (6)
P60 例 1.27 所有可能步长为{4,6,8,10, },周期为 2,显然不存在步长为 2 的路 径,使得该状态返回自身。 4)无此题(试卷只有 1,2,3,5,6) 5)正态随机过程一二阶统计特性决定了其所有统计特性 对 正态随机过程的任意有限维概率密度函数由其均值函数与自相关函数完全确定。 而一个随机过程的有限维概率密度函数族决定了其所有统计特性。 6)有限状态马氏链中,至少有一个常返状态 对 对于有限状态马氏链,如果一个常返态都没有,则从任一状态 i 出发后经过有限 时间 Ti 后不再返回此状态。经过有限时间 Tmax max{T0,T1, ,Tn}之后,不再访问 该马氏链的任何状态,而这样的马氏链不可能状态有限。 7)两个联合平稳实随机过程的互相关函数必为偶函数 错 例如,第 4 大题中第 3)题 RXY ( )= 0 sin(0 ) ,此相关函数为奇函数。
1 5
+12
1 5
+22
1 5
=2
E
cos(0t1
)
cos(0t2
)
E
cos(0
(t2
t1
))
cos(0 2
(t1
t2
)
2
)
1 2
cos(0
)
0
1 2
cos(0
),
t2
t1
故RX
(t1,
t2
)
2
1 2
cos(0
)
cos(0
)
所以为 X (t) 平稳随机过程。
设 X (t) 的导数过程为Y (t) 0 Asin(0t ) 。
过程的均值为常数,相关函数只与时间间隔有关,所以其任意有限维概率密度函
数只与时间间隔有关。严平稳随机过程的定义为任意有限维概率密度函数只与时
间间隔有关而与时间起点的选择无关的随机过程,因此正态随机过程的宽平稳和
严平稳等价。
3)使用什么来完整描述随机过程的全部统计特性? 有限维分布函数族、有限维概率密度函数族,或有限维特征函数族。
cos
,其中 =t2
t1
3)有随机过程 X (t) Acos(0t ) ,其中 0 是常数, A 和 是相互独立的随
机变量, 服从[0, 2 ] 上的均匀分布, A 的分布律如下表所示:
A
-2
-1
0
1
2
PA
1/5
1/5
1/5
1/5
1/5
讨论 X (t) 与其导数过程的联合平稳性
解:
E A=(-2) 1 +(-1) 1 +0 1 +1 1 +2 1 =0
本题所对应的二维联合概率,只在点 (x1, x2 ) (2, 4),(3,6),(5,1) 处有值且为 1/3,而在其他
任何位置都为 0。所以当分布函数的积分范围包含这三点之中的一点时,概率为 1/3;包含 两点时,概率为 2/3;包含三点时,概率为 1,不包含任一点则概率为 0。
2)两个随机过程 (t) Asin(t ) 和(t) Bsin(t ) ,其中 A, B,,
函数
RXY
(t1,t2 )
等于
RX (t1, t2 t2
)
。
RXY
(t1, t2
)
ห้องสมุดไป่ตู้
E
X
(t1),Y
(t2
)
E
X
(t1),
lim
t0
X
(t2 +t)-X t
(t2 )
lim
t0
E
X
(t1),
X
(t2
+t)-X t
(t2
)
=
lim
t0
E
X
(t1),
X
(t2 +t) t
-E
X
(t1),
X (t2 t
p3 p1 p13 p2 p23 p3 p33 p3 0.7 p1 0 p2 0.3 p3
且有 p1 p2 p3 1,解之可得
p1 p2
8 7
/ /
23 23
p3 8 / 23
6)某电子系统受突发干扰的次数 N (t) 是泊松过程,干扰的到达率为 ,求: (1) t 5 和 t 10 时的平均干扰次数; (2)在 N(5) 3的条件下, N(10) 5 的概率;
333
3
E X (6) 1 1 1 4 1 6 11
33 3
3
RX
(2, 6)
E
X
(2) X
(6)
1 3
2
4
1 3
3
6
1 3
51
31 3
0
1
FX
( x,
2)
P(
X(2)
x)
3
2
3
1
x2 2 x3
3 x5 x5
0
1
FX
(
x, 6)
P(
X(6)
x)
3
2
3
1
x 1 1 x4
4 x6 x6
P28
4、计算 1)随机过程如右图所示,该过程仅由三个样本函数组成,而且每个样本函数均 等概发生。试求
(1) E X (2), E X (6), RX (2,6)
(2) FX (x,2), FX (x,6),FX (x1, x2,2,6)
解:
(1) (2)
E X (2) 1 2 1 3 1 5 10
解:
mX (t1) mX (t2 ) mX (t) 0
K
K11
K21
K12 K22
8 4
4 8
,
K
88 44
48
K
1
1/6 1 / 12
1 / 12 1 / 6
可以得到
fX
( x1,
x2;0,1 /
3)
2
1 K
1/2
exp
(x1, x2 )T
K 1( x1, 2
x2
)
期中考试试题解析
制作者 Imbamboo 2016.11
1、简述 1)何为宽遍历随机过程?研究此类随机过程的意义何在?
如果均方连续的平稳过程 X (t) 的均值函数和自相关函数都具有遍历性,则该过程 为宽遍历随机过程。 在实际应用中很难得到随机过程的概率分布,不能计算随机过程的统计平均,可
用此类过程的时间平均来替代统计平均(t 趋于无穷时取等号)。 2)为何正态随机过程宽平稳和严平稳等价? 正态随机过程的概率密度函数可以由其均值函数和自相关函数完全确定。宽平稳
解: (1)两步转移概率矩阵为
0.3 0.7 0 0.3 0.7 0 0.09 0.35 0.56
P(2)
P2
0
0.2
0.8
0
0.2 0.8 0.56 0.04
