第四章 电力声类比线路图
电力声 类比
电-力-声类比引言:电-力-声类比是应用电路理论来解决力学与声学问题。
定义:根据描述电振荡系统的微分方程和描述力学振动系统及声振动系统的微分方程在形式上的相似性,常将力学量和声学量与相应的电学量作类比,以便借助电路理论来分析力学振动和声振动的规律,称电-力-声类比。
类比方法有二种:一种为阻抗型类比,也称正类比;另一种为导纳型类比,也称反类比。
§5-1电路元件及基本的电振荡器在电学系统的分析中,经常用电路图来描述元件与元件之间的关系,从而研究电磁运动的规律。
通过电路分析,有时不必去求解微分方程,而能直接了解系统的工作情况和特点。
即使要作定量分析研究,通过形象的电路图,利用克希霍夫电路定律,再去建立微分方程,也要简单得多。
电路图最容易应用于集中参数的系统,因为集中参数元件的唯一变量是时间。
在电声学研究的系统中(如电声换能器),在低频时,大都近似地等效成集中参数系统,只要采用类比的办法,把力学或声学系统画成等效类比线路图,然后利用电路理论来研究系统的工作情况和特点。
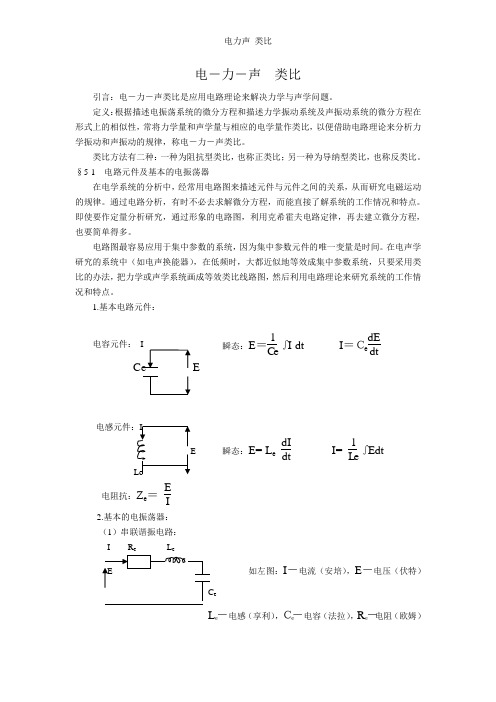
1.基本电路元件:电容元件:瞬态:E=1C e∫I dt I=CedEdtE瞬态:E= L edIdt I=1L e∫E dt电阻抗:Z e=EI2.基本的电振荡器:(1)串联谐振电路:I R L如左图:I-电流(安培),E-电压(伏特)eLe-电感(享利),Ce-电容(法拉),Re-电阻(欧姆)由上图可得:E = R eI + L e dI dt + 1C e ∫I dt对于作简谐变化的稳态电流值有:I = I 0 ej ωt 则:E =R e I + jωL e I + 1jωCe I=(R e + jωL e + 1jωCe ) I = Z e I式中Z e 为串联回路的阻抗I = E Ze即为熟知的欧姆定律 (2)并联谐振电路I '-为电流(安培),E '-为电压(伏特), E 'e' L e'-为电感(享利),Ce'-为电容(法特), ○ R e'-为电阻(欧姆)由上图可得:I '=E'Re' + 1L e ' ∫E 'dt +C e ' dE'dt对于作简谐变化的电压有:E '=E 0' ejωt 则:I '=E'Re' +1jωLe' E '+ jωC e 'E ' = (1Re' + 1jωLe1 + jωC e ')E ' = 1Ze' E '1Ze' =(1Re' +1jωLe' + jωC e ') = 1Re' + j(ωC e '-1 ωLe' )§5-2力学元件和基本的力学振动系统:1.力学元件:F 表示外力 F K 表示弹性力F R 表示阻力 M M 表示质点质量K M 表示弹性系数 C M 表示顺性系数R MC M =1KM又称为力顺 R M 表示阻力系数,又称为力阻由牛顿第二定律得:F = ma 即M M dv dt = F + F K + F R其中:①弹性力:F K 根据虎克定律有:F K =-K M ξ=-1CM ∫Vdt ξ为质点M M 离开平衡位置的位移,V 为质点振动速度,负号表示质点移的方向与弹性力方向相反②阻力: F R =-R M d ξdt =-R M V 式中负号表示阻力总是与系统的运动方向相反。
声学基础 电力声类比(2)

U
Ma
Ra
p
Ca
P0
Fundamentals of Acoustics
西北工业大学航海学院环境工程系
声学基础
一、画出类比线路图的方法
对于声学系统,运用声流线方法最 直接得到的是阻抗型类比线路。
Fundamentals of Acoustics
西北工业大学航海学院环境工程系
声学基础
一、画出类比线路图的方法
电路图的分析 力学系统的类比线路图 声学系统的类比线路图 阻抗型和导纳型类比线路图的互相转换 力学振动策动声振动的系统的类比线路图
Fundamentals of Acoustics
西北工业大学航海学院环境工程系
声学基础
一、画出类比线路图的方法
阻抗型电路图的分析
1. 电流线:电路图是以一条电流线连贯各个
Fundamentals of Acoustics
西北工业大学航海学院环境工程系
声学基础
一、画出类比线路图的方法
声学系统的分析
1. 声流线:声学元件是连通的。 2. 压强的相对性:在元件两端是压强差,对
应于大气压强的端点,认为是“接地”端。
3. 在远见交界处有流量守恒定律,即交界处
满足
∑U
i =1
声学基础
一、画出类比线路图的方法
阻抗型和导纳型类比线路图的互相转换 对同一个力学结构,在作阻抗型 和导纳型类比时表现的元件特性是互 易的。转换规律为:
Fundamentals of Acoustics
西北工业大学航海学院环境工程系
声学基础
一、画出类比线路图的方法
1. “电感”性元件——“电容”性元件; “电阻”性元件——“电导”性元件; “电感”性元件——“电容”性元件; “恒压”源——“恒流”源; 线路类型转换时注意各符号的转换。
初中物理--电路图详解

初中物理--电路图详解电路识别是初中物理电学的重点之一。
很多同学在学电学之初还是很感兴趣的,毕竟"电"跟我们生活密切相关么,电脑、电话、电视这些玩意儿天天挂在嘴边,早~就想知道什么是“电”了,这把真要解开电的奥秘了!好兴奋~!电学一开始,果然不负重望,老师一个劲儿的做实验,一会摩擦玻璃棒,一会摩擦橡胶棒,然后又搬来一个带金属箔的"小闹钟",上课就是看热闹,很开心;在加上这部分的考试作业主要考知识点,尽考些玻璃棒、橡胶棒都带什么电,是排斥还是吸引等鹦鹉学舌的问题,小case~。
上课又热闹看,下课作业不难,还能学知识,总体感觉电学真是8错。
可惜好景不长,进入电流电路后,初中物理三大猛药之一——电学的糖衣吃完了,开始动真格的了。
电学的各难点中,打前锋的就是电路识别,课上讲的很简单,电路就串联、并联就两种,看上去很清纯~。
但实际做题发现满不是那么回事儿,无数出题老师们殚精竭虑、前仆后继,把原本清纯可爱的串并联电路,设计成错综复杂电路怪物,再掺和进去电表和变阻器,使得电路的复杂度达到极致,不少同学学到这杯具了,之前的兴奋劲儿一扫而空,取而代之的是做错题的郁闷和对电路怪物的恐惧,更要命的是,过不了电路识别这一关,接下来的电学都得杯具:电路识别错,后面的计算判断都是无用功。
因此吧里同学跑上来求电路识别方法者层出不穷。
电路识别虽然是有些难度,但还是有章可循的,电路识别相关的包括二部分:电路图简化以及电路图、实物图互化。
这次我先介绍一个简化电路图的方法,我把它叫做标号法。
这种方法简单易学、练练就会、便于记忆,而且适用于所有电路,是居家旅行、特别是简化电路的杀手锏。
我朋友的孩子上学期初二学电学,概念啥的都没问题,但是就认不出复杂电路图,所以电学习题一做就错,班里都倒数了。
马上就要期末考试了,她妈妈请我去给她单独辅导一下,教给她一个识别电路的法子,当场学会,练习几道后就明白了,期末考试物理从70多提升到92。
声电类比

举例
例1 如图声学系统由两个 共鸣器连通组成。 共鸣器连通组成。
p Ma1 Ra1 Ca1 Ma2 Ra2 Ca2
从外加逾压引出一条声流 线,不分支穿过第一个短 穿出后, 管(Ma1 、 Ra1 ),穿出后,因 穿出后 流出的声体积流一部分使 第一个腔体C 第一个腔体 a1 内空气质量 发生变化, 发生变化,同时另一部分 还会使第二个短管中空气 产生振动, 产生振动,所以声流线要 分支,一支穿过C 分支,一支穿过 a1,终止 于腔壁(接地); );另一支穿过 于腔壁(接地);另一支穿过 第二个短管(M 第二个短管 a1 、 Ra1 ),再 再 p 穿过第二腔体C 穿过第二腔体 a2,终止于 腔壁(接地) 声流线如上图。 腔壁(接地),声流线如上图。 将声流线路径上声学结构 改为相应的电类比符号得 到类比电路如下图。 到类比电路如下图。
声学类比线路图
Za1
Za2
p
Ca
m
Rm
在阻抗型声学线路图和阻 抗型力学线路图之间加一 力声变量器(耦合),即 力声变量器(耦合),即 ), 可得到闭箱式扬声器的阻 抗型力—声线路图如下图 抗型力 声线路图如下图 所示。 所示。
m Rm
F
Cm
力学类比线路图
Za1 Za2
S:1
F
Cm
Ca
闭箱式扬声器的力—声类比等效线路图 闭箱式扬声器的力 声类比等效线路图
则最后得到
dU 1 Ma Udt = pa e jω t + RaU + dt Ca ∫
求解上式得到
(3)
p U= za
(4)
——声阻抗 声阻抗
p 1 za = = Ra + j (ω M a ) ω Ca U
声电类比

则最后得到
dU 1 Ma Udt = pa e jω t + RaU + dt Ca ∫
求解上式得到
(3)
p U= za
(4)
——声阻抗 声阻抗
p 1 za = = Ra + j (ω M a ) ω Ca U
单位:声欧姆, 声欧姆= 牛顿 单位:声欧姆,1声欧姆=1牛顿秒/米4
式(3)描述的声振动的微分方程与电振荡微分方程在形 式上完全类同。无疑表征了两种现象之间的某种共性, 式上完全类同。无疑表征了两种现象之间的某种共性,即 具有相似的运动规律。 具有相似的运动规律。
一、 类比电路元件
1. 赫姆霍兹共鸣器 由短管(半径为 ) 由短管(半径为a)与 体积为V 体积为 0的空腔连同而 成,是一种经典的声学 模型。 模型。 假设: 假设
(1) 共鸣器线度远小于声波波长,a, l0,V01/3<<λ 共鸣器线度远小于声波波长, λ (2) 短管体积远小于空腔体积,即Sl0 << V0 短管体积远小于空腔体积, (3) 腔体壁面为刚性 即腔内媒质振动时,腔壁不形变。 腔体壁面为刚性,即腔内媒质振动时 腔壁不形变。 即腔内媒质振动时,
i =1
举例
例1 如图声学系统由两个 共鸣器连通组成。 共鸣器连通组成。
p Ma1 Ra1 Ca1 Ma2 Ra2 Ca2
从外加逾压引出一条声流 线,不分支穿过第一个短 穿出后, 管(Ma1 、 Ra1 ),穿出后,因 穿出后 流出的声体积流一部分使 第一个腔体C 第一个腔体 a1 内空气质量 发生变化, 发生变化,同时另一部分 还会使第二个短管中空气 产生振动, 产生振动,所以声流线要 分支,一支穿过C 分支,一支穿过 a1,终止 于腔壁(接地); );另一支穿过 于腔壁(接地);另一支穿过 第二个短管(M 第二个短管 a1 、 Ra1 ),再 再 p 穿过第二腔体C 穿过第二腔体 a2,终止于 腔壁(接地) 声流线如上图。 腔壁(接地),声流线如上图。 将声流线路径上声学结构 改为相应的电类比符号得 到类比电路如下图。 到类比电路如下图。
浙教版科学八年级上册第四章电路探秘总复习课件(共56张PPT)

1、材料﹑粗细相同时,导体越长,电阻越大 2、材料﹑长度相同时,导体越粗,电阻越小
3、粗细﹑长度相同的导体, 电阻的大小与材
料有关。
R=ρ
L S
电阻率:20℃时,长1米,横截面积为1毫米2的材 料的电阻
二、不同材料的导体电阻
1、常见材料中,导电能力位于前三位的 依次是:银、铜、铝 2、导体的电阻率较小,绝缘体的电阻率很大 3、合金的电阻率比纯金属的大
I= —U R
U=IR
R= —U I
R跟U,I无关
伏安法测电阻
原理 电路图
U R= I
R
A
V
R′
变阻器的作用 调节定值电阻R两端的电压; 多次测量求平均值减小误差
保护电路 实验注意事项
串联电路特点 I1 = I2 = I
I1 R1 I2 R2 I
U1
电路的分支点 干 路
支路
将电路元件并列连接在电路两点间的电路 电流至少有两条回路 各支路间互不干涉
电流
电流的形成 电流的方向
电 单位
流 强
电 流
度
表
测量
的
使
用
一、电路中的电流
1、电流的形成: 正电荷、负电荷 电荷的定向移动形成电流
2、电流方向的规定 正电荷定向移动的方向为电流方向
如图所示闭合电路中,金
向左移动时,变阻器连入电路的电阻______, 电变流大表的示数______.(变填小:“变大”“变
小”“不变”)
1Ω 2Ω 2Ω 5Ω
欧姆定律
探究I
R不变时 改变U
与U、控制变量
R的
关系
改变R
U不变时
探究I与U的
关系
精品课件-电路与电子技术(季顺宁-第4章
P4 三相异步电动机控制电路的设计与制作
P4 三相异步电动机控制电路的设计与制作
MNL4
1.
(1) 线电压与相电压的关系:
(2) 线电流与相电流的关系:
① 数量关系: I线= I相
3
② 相位关系: 线电流在相位上滞后与之相对应的相电流
30°
4-1-12
P4 三相异步电动机控制电路的设计与制作
(3) 目前获得广泛应用的三相异步电动机, 它以三相交 流电作为电源。与单相电动机或其它电动机相比,三相异步电 动机具有结构简单、价格低廉、性能良好及使用和维护方便等 优点。
P4 三相异步电动机控制电路的设计与制作
2. 三相交流电的产生 三相交流电的产生就是指三相交流电动势的产生。三相交 流电动势由三相交流发电机产生,它是在单相交流发电机的基 础上发展而来的,如图4-1-1所示。 在发电机定子(固定不动 的部分)上嵌放了三相结构完全相同的线圈AX、BY、CZ(通称绕 组),这三相绕组在空间位置上各相差120°电角度,分别称为 A相、B相和C相。A、B、C三端称为首端,X、Y、Z则称为末端。 工厂或企业配电站内的三相电源线一般用黄、绿、红分别代表 A、B、C
② 中线(中性线或零线): (2)
① 相电压: ② 线电压: 相线与相线之间的电压。
P4 三相异步电动机控制电路的设计与制作
图4-1-2 三相电源Y形连接
P4 三相异步电动机控制电路的设计与制作
测试工作任务书
P4 三相异步电动机控制电路的设计与制作
P4 三相异步电动机控制电路的设计与制作
MNL2 三相电源的Y 1. 1) 三相电源电压的三角函数表达式为: eA=Em sinωt eB=Em sin(ωt-120°) eC=Em sin (ωt+120°)
高二物理竞赛电-力-声类比线路应用举例课件
cosh cosh j cos 1 Z1
2Z2
20
通频带条件为
1 1 Z1 1 2Z2
或:
1 Z1 0 4Z2
21
例题 8:
如图所示声学系统,假设其主导管截面积较大,故 主导管声质量很小,可近似认为是零。
求:截止频率
Ma Ma
Ca Ca
22
解:
Z1
0, Z2
jM a
1
Ca
Ma
Ra21
Ra21 2
M
2 a1
12
2
2
10
Zm Rm2 X m2
因: E Blv
故:
Ea
Bl
pa S Zm
如果pa对各频率都相同, 且要求传声器的频响均匀,
则必须使输入力阻抗 Zm 与频率无关
11
例4 耳机
Ma2, Ra2
Ma1, Ra1
V22
V21 V1
V3
12
例5 压差传声器
p1
Ca1
7
系统的阻抗型力-声线路图
8
统一为阻抗型的力学线路图
9
音膜-音圈系统的振动速度幅值为
式中
va
Fa Zm
pa S Zm
Zm Rm jX m
12
1 M a1Ca1
Rm
Rm
Ra21 2
S 2Ra1 / Ca21
M
2 a1
(12
2 )2
Xm
M m
1
Cm
S2
Ca1
M
2 a1
12
2
, 12
1 M aCa
15
例6 拾振器
e j(t 2 ) A
中考物理九年级电学等效电路图专题讲解(2021年整理)
(完整word)中考物理九年级电学等效电路图专题讲解(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word)中考物理九年级电学等效电路图专题讲解(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word)中考物理九年级电学等效电路图专题讲解(word版可编辑修改)的全部内容。
等效电路图谨记:电阻用电器是高山,导线是高速,电流表相当于导线,电压表相当于断路1.画出等效电路图:(1)当闭合S1、S2时;(2)当闭合S1、S3时。
2.(1)断开S1,闭合S2时;(2)闭合S1,断开S2时。
3.(1)当闭合开关S0、S1,断开开关S2时;(2)当闭合开关S2,断开开关S0、S1时。
1。
只闭合S l时;当S l、S2、S3都闭合时,将滑片P移动到b端;只闭合S2时;2。
只闭合开关S1时;只闭合开关S2时;开关S1、S2、S3都闭合时R1S1VSVAL1 L2S0S1S2R3R4VL1L2S1S23.只闭合开关S 1时;只闭合开关S 2时;只闭合开关S 3时4.闭合开关S 1、S 3时;闭合开关S 1、S 2、S 3时;闭合开关S 1、S 2、S 45.只闭合开关S1、S4时;只闭合S3时;只闭合S4、 S5时;只闭合S2、S3、S5时;6.只闭合开关S 1和S 2时;只闭合开关S 1时;只闭合开关S 3时S 1 R 3 R 1 S 2U V AR 2S 3 S 1 R 3 R 1S 2 U R 2S 3V A S 4。
高二物理竞赛阻抗型和导纳型类比线路图的互相转换课件
(2)将声流线穿过的声学元件符号改 成声学结构图
11
转换规律:
(1)
“电感”元件
“电容”元件
“电阻”元件
“电导”元件
“恒压源”元件
(2)
串联
“恒流源”元件 并联
(3) 串联中电压之和
并联中电流之和
12
例:
转换为:
13
变量器
一个能完成力—声阻抗变换的结构,称:变量器
p U
F2 S
S
F2
1 S2
阻抗型和导纳型类比线路 图的换
力线法:对力学系统最直接画出的是导纳型类比
声线法:对声学系统最直接画出的是阻抗型类比
在力-声共存的系统中,或电-力-声共存的系统中, 若画出混杂线路图(导纳型、阻抗型共存)处理很困难, 需要采用统一类型,因此需进行线路图类型转换。
因此,对有力、声共存的系统,在阻抗型力学线
路图和阻抗型声学线路图中间,要加入一个变量比为 1/S 的变量器。
由:
Za
1 S2
Zm
S:1 U
得:
Ma
Mm S2
Ra
Rm S2
F2
p
Ca CmS 2
F2 S :1 U
p
ZM
F2
Sp 1U
S2 p U
S 2Z A
S
16
即:
Za
1 S2
Zm
Zm S2Za
14
回顾 变压器
I1
1 : n I2
Z2 = n2 Z1
n:为匝数比
E1
E2
E1 1 I2 E2 n I1
Z2
E2 I2
nE1
1 n
I1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
������
M
������2������ ������������2
+
������������
������������ ������������
+
1 ��பைடு நூலகம்���
������
=
������������������������������������
将微扰动换成速度表达
M
������������ ������������
尤其是研究电声器件如传声器、扬声器,由于系统涉及到电力声三个振动系 统,运用电力声类比法,将极大提高研究的效率。
4.1 电力声类比
先以最简单的串联电路为分析例子,下图是一个基本的电路:
假设电动势是稳态谐振的E = ������������������������������������,这里采用复数形式是为了分析的简便。
第四章 电力声类比线路图
电学系统,力学系统,声学系统,虽然分属各个领域,研究不同的对象,但 是它们在数学上却具有相似的表达形式。而追溯数学的发展大多数要归功于物理 学的发展,因此数学上具有相似形式的物理过程,其本质上也必然有某些形式的 规律。
历史上,对力学振动的研究促进了人们对电磁振荡规律的认识。而近代电磁 学的发展很快,尤其是电路分析理论和电路图的运用,使得人们对电磁振荡的分 析大为简化。然而,物理学的发展告诉我们,这种借鉴式的研究不是单向的,对 电磁振荡的这种简单直接有效的分析方法,同样可以借鉴到力学系统与声学系统 的研究。
=
(������������������
+
������
+
1 ������������������)
再回到力学基本的受迫振动,如下图:
假设强迫力为������������ ������ ������������������ ,运动时候受到的阻力正比于速度,比例系数为������������ ,令
K = 1 那么系统的振动方程可以写出为
其力学系统与声学系统的等效线路图如下
按照������������/������������ = ������2将声学端折算到力学端有
从类比线路图可以看出,封闭箱的空气顺性������������⁄������2与扬声器单元的力顺是并 联的,它们的总力顺跟扬声器单元的振动质量就决定了封闭箱系统的谐振频率。
+
1 ������������������)
4.2 变量器
有上一节推导知道
������������
=
������������ ������
=
������������������
+
������
+
1 ������������������
������������
=
������������ ������
=
由电路元器件的性质可以写出电路方程
变换到频域里则有
L
������������ ������������
+
������������
+
1 ������
∫
������������������
=
������������ ������ ������������������
������������
=
������������ ������
+
������������������
+
1 ������
∫
������������������
=
������������ ������ ������������������
同样变换到频域,得到
������������
=
������������ ������
=
������������
+
������������������
+
������������
������������ ������������
+
1 ������
������
=
������������������������������������������
同样改写成速度的形式
M
������������ ������������
+
������������������
+
������������������
+
1 ������
∫
������������������)
=
������������������������������������
变换到频域有
������������
=
������������ ������
=
1 ������2
(������������
+
������������������
������������
+
������������������
+
1 ������������������
{ ������������
=
������������ ������
=
1 ������2
(������������
+
������������������
+
1 ������������������)
+
1 ������������������
同样的,假设有如下的声学系统
为了把这个系统看做集中参数系统,做如下假设
(1) 管腔的体积远远小于腔体体积
(2) 腔壁是刚性的
(3) 共振器的任何尺寸的线度均远远小于波长线度
经过适当的分析,可以写出管中空气柱的运动方程
M
������2������ ������������2
根据电力耦合因子 BL,力声耦合因子 S 可知
������������ = ������������������ { ������������ = ������������������ ������������ = ������������/������
推导得到
������������������������ = (������������)2 {������������������������ = (������������/������)2
������������/������������ = ������2
这样就得到了电力声阻抗的互相转化关系。
4.3 封闭式扬声器系统的类比线路图
上节得到了电力声之间阻抗互相转换的公式,因此在分析电声器件时候,可 以依据转化公式,将电学系统或者力学系统折算到声学系统中统一考量。可以大 大方便分析的程序。如下图的封闭箱
+
1 ������
∫
������������������
=
������������������������������������������
在声学系统中,讨论力 F 与速度 v 是没有意义的,而有现实意义的是愈压 p
与体积速度U = S������,那么上述方程改写为
1 ������2
(M
������������ ������������
