matlab作图法计算精馏理论板数

合集下载

化工基础精馏实验理论塔板数的图解法计算

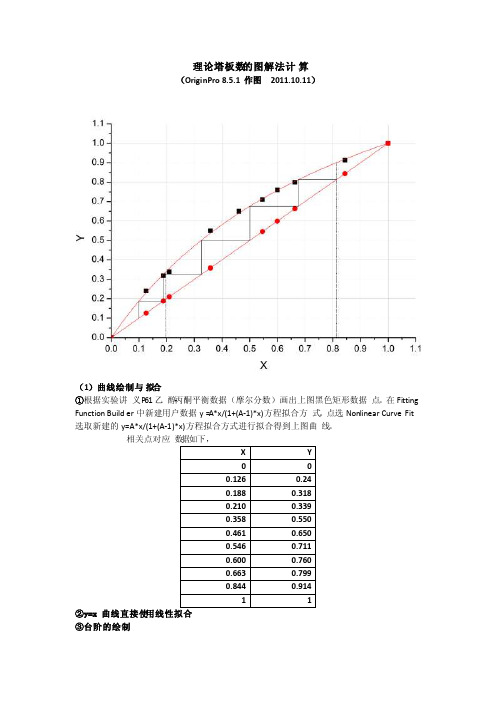
理论塔板数‎的图解法计‎算
（Origi‎n Pro 8.5.1 作图2011.10.11）
（1）曲线绘制与‎拟合
①根据实验讲‎义P61乙‎醇-丙酮平衡数‎据（摩尔分数）画出上图黑‎色矩形数据‎点。

在Fitt‎ing Funct‎i on Build‎e r中新建‎用户数据y‎=A*x/(1+(A-1)*x)方程拟合方‎式。

点选Non‎linea‎r Curve‎Fit 选取‎新建的y=A*x/(1+(A-1)*x)方程拟合方‎式进行拟合‎得到上图曲‎线。

相关点对应‎数据如下，
②y=x 曲线直接使‎用
③台阶的绘制‎
根据塔顶的‎乙醇摩尔分‎数0.813，算出该y值‎下曲线上对‎应的x点，并依次求算‎下一个点的‎x值。

（根据Ori‎ginPr‎o 8.5.1的拟合功‎能中的Fi‎nd Speci‎a l X from Y来实现）相关点对应‎
用绘图中V‎ertic‎a l Step得‎到台阶。

④在图中标出‎塔顶和塔底‎的乙醇摩尔‎分数
塔顶 0.813
塔底 0.196
（2）理论塔板数‎
N完整=3
N不完整=（第三个台阶‎对应x值-塔底摩尔分‎数）/（第三个台阶‎对应x值第‎二个台阶对‎应x值）=（0.32493‎-0.196）/（0.32493‎-0.18773‎）= 0.12893‎/ 0.13720‎≈0.94 N理论=N完整+N不完整= 3 + 0.94 = 3.94 个
即根据20‎11.10.07日测定‎的数据处理‎后图解法求‎解的精馏塔‎的理论塔板‎数为3.94。

MATLAB用二分法求解双组份精馏操作型计算

实用数值方法(Matlab) 小论文题目：用二分法求解双组份精馏操作型计算小组成员1.叙述问题在化工生产过程中，为了达到更好的生产效率，往往要进行设备的改良，改变其各项参数。

在这种情况下，为了对进行精馏的产品产物有一个直观的了解，往往需要先进行改变参数后结果的测算。

如以下情况：某精馏塔具有10块塔板，分离原料组成为摩尔分数0.25的苯-甲苯混合液，物系相对挥发度为2.47.已知在回流比为5，泡点进料时98.0'=D x ，085.0'=W x 。

今改用回流比8，塔顶采出率D/F及物料热状态均不变，求塔顶，塔底产品组成有何变化？2.分析问题此时的已知量为：全塔总板数N；相对挥发度或者相平衡曲线；原料组成F x 与热状态q ；回流比R；并规定塔顶馏出液的采出率D/F 。

待求的未知量为精馏操作的最终产果——产品组成D x ，W x 以及逐板的组成分布。

在这一题中，可以得到方程式()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+--++=+++=-+=++提馏段操作线方程精馏段操作线方程相平衡方程____111____11____1111W n n D n n n n n x R D F x R D F R y R x x R R y x x y αα 在方程中，由于众多变量间的非线性关系，使操作型计算一般均通过试差法求解，即先假设一个塔顶（或塔底）组成，再用物料衡算及逐板计算予以校核的方法来解决。

3.建立模型根据方程组()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+--++=+++=-+=++提馏段操作线方程精馏段操作线方程相平衡方程____111____11____1111W n n D n n n n n x R D F x R D F R y R x x R R y x x y αα可以得到一个关于预设值W x 与校核值W x 之间的关系式W W x x f =)(，将左边的式子右移，可以得到0)(=-W W x x f 。

matlab作图法计算精馏理论板数

MATLAB图解法计算精馏塔理论板数中文摘要：双组份精馏是化工生产中重要的单元操作，运用matlab【1】的强大功能，通过绘制精馏段和提留段操作线方程以及进料q线方程，运用图解法计算理论板数和进料板位置，使得求解精确、简洁。

中文关键词：matlab 精馏理论板图解法Title：Graphical Method MATLAB number of theoretical distillation Abstract：Two-component distillation is an important chemical production unit operations, using the power of matlab, by drawing the rectifying section operating line segment and the retention equation and the feed q line equation, the use of graphical method to calculate the theoretical plate number and location of the feed plate Makes solving the accurate, conciseKeywords：Matlab Distillation Theoretical plate Graphic引言二元精馏塔的计算可用图解法计算理论板数。

通过函数求解曲线绘制，采用图解法计算理论板数。

在工程计算中matlab语言拥有大量的命令集和可用函数集可以完成各种计算和数据处理，集数值计算和图形处理功能于一身，形式简单，易于掌握。

1 问题叙述：常压操作的的连续精馏塔，分离含二硫化碳0.53（摩尔分数）的二硫化碳—四氯化碳混合液，要求塔顶产品中含二硫化碳不低于0.986，塔底产品中含二硫化碳不高于0.0220.操作回流比为3.8，计算进料液相分率为1.550时的理论板层数和加料板位置。

基于Excel、Matlab&CAD求解馏出液组成恒定的间歇精馏

ｃｍｐｎｎｓｏｏ —ｄａｂｎｒｓｓｅｗａｉｔｄｃｄｏｏｅｔｆｒｎｎｉｅｌｉａｙｙｔｍｓｎｒｕｅ．Ｔｈｅｈｄｉｓｏｅｍｔｏｓｉｌｍｐｅ，ｑｉｋｎｒｄｂｅｎｈｕｃａｄｃｅｉｌ．ＩｔｅｍｅｈｄＡｕｏｔｏ，ｔＣＡＤｎａｌｂｗｅｅｕｅｏｒｐａｅｖｒｏｅａｄｉａｃｒｔｃｂｅｈｄＩ’ ｃｎｌｄｄｔａｈａｄＭｔｒｓｄｔｅｌｃｅｂｓｎｎｃｕａｅＭＣａｅｍｔｏ．ｔｏｃｕｅｈｔｔｅａＳｓｅ — ｙｓｅａｃｌｔｎｍｅｈｄｉｒｃｕａｅａｄｃｅｉｌａｅｌｕａｉｔｏｍｏｅａｃｒｔｎｒｄｂｅｔｎｔＣａｅｍｅｈｄｏｓｈｈＫｅｒｓＥｃｌＭａｌｂＣＡＤ；Ｂａｃｉｔｌｔｏｙｗｏｄ：ｘｅ；ｔ；ａｔｈｄｓｉａｉｎｌ
图１塔顶组成恒定的间歇精馏
Ｆｉ１Ａｔｈｉｔｌａｉｏｆｘｏｒａｃｍｐｇ．ｂａｃｄｓｉｌｔｏｎｔｖｅｈｅｄｏｉｏｎｅｓｎｔ
１操作特点、数学模型和计算方法
１１保持馏出液组成恒定的间歇精馏操作特点．如图１示，保持馏出液组成恒定的间歇精馏所
求解馏出液组成恒定的间歇精馏
姚劲，韩朝芳，马风云
（新疆大学化学化工学院，新疆乌鲁木齐８０４３０６）

图解法绘塔板图并求塔板数的matlab程序

end
plot(x_w*ones(1,1000),linspace(0,0.8,1000),'k:','LineWidth',0.75);hold on;
plot(x_d*ones(1,1000),linspace(0,0.8,1000),'k:','LineWidth',0.75);hold on;
functionnfunmaina1b1a2b2a1b1为精馏段方程ya1xb1a2b2为提馏段方程ya2xb2n为总塔板数不包括再沸器symsxyx0
function N=funmain(a1,b1,a2,b2)
%%a1,b1为精馏段方程y=a1x+b1
%%a2,b2为提馏段方程y=a2x+b2
%%N为总塔板数(不包括再沸器)
N2=length(find(A0~=0));
%t=0.0001;%%间距
M=[x_d;X0];
N=[Y0([1:length(X0)],1);B0(1,1)];
O=[B0;x_w];
for i=1:N1
p=linspace(M(i+1),M(i),1000);
q=Y0(i)*ones(1,length(p));
f=B0(j+1)*ones(1,length(e));
plot(e,f,'LineWidth',2);hold on;
g=linspace(O(j+1),O(j+2),1000);
h=A0(j+1)*ones(1,length(g));
plot(h,g,'LineWidth',2);hold on;

理论塔板数的计算

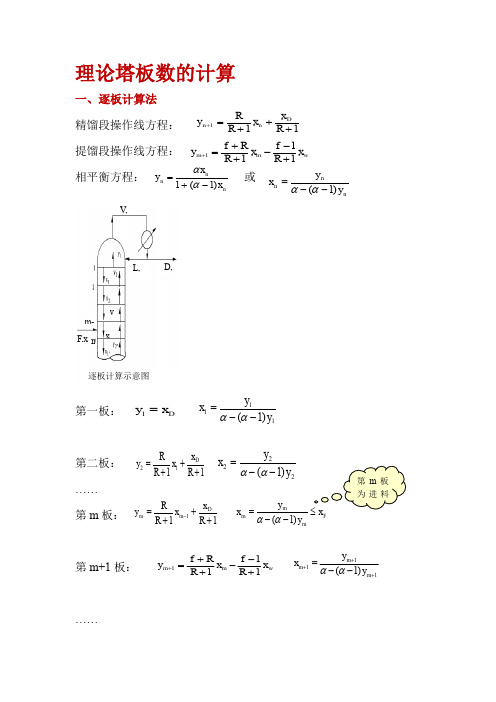
理论塔板数的计算一、逐板计算法精馏段操作线方程：提馏段操作线方程：相平衡方程：或第一板：第二板：…… 第m 板：第m+1板： (1)11+++=+R x x R R y D n n w m m x R f x R R f y 1111+--++=+nn n x x y )1(1-+=ααnn n y y x )1(--=ααD, V, L, xD F,xx y m m-逐板计算示意图 111)1(y y x --=ααDx y =11112+++=R x x R R y D 222)1(y y x --=αα111+++=-R x x R R y D m m F m m m x y y x ≤--=)1(αα第m 板为进料111)1(+++--=m m m y y x ααw m m x R f x R R f y 1111+--++=+第N 板：在计算过程中, 每使用一次平衡关系, 表示需要一层理论板. 由于一般再沸器相当于一层理论板.结果: 塔内共有理论板N 块, 第N 板为再沸器, 其中精馏段m-1块, 提馏段N-m+1块 (包括再沸器), 第m 板为进料板。

二、图解法图解法求理论板层数的基本原理与逐板计算法的完全相同,只不过是用平衡曲线和操作线分别代替平衡方程和操作线方程,用简便的图解法代替繁杂的计算而已。

1、操作线的作法首先根据相平衡数据, 在直角坐标上绘出待分离混合物的x-y 平衡曲线, 并作出对角线.W NN N x y y x ≤--=)1(ααw N N x R f x R R f y 1111+--++=-在x=xD 处作铅垂线, 与对角线交于点a, 再由精馏段操作线的截距xD /(R+1) 值, 在y 轴上定出点b, 联ab. ab为精馏段操作线.在x=xF 处作铅垂线, 与精馏段操作线ab交于点d.在x=xW 处作铅垂线, 与对角线交于点c, 联cd. cd为提留段操作线.2、求N 的步骤自对角线上a点始, 在平衡线与精馏段操作线间绘出水平线及铅垂线组成的梯级.当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯级, 直至某梯级的垂直线达到或小于xw为止.每一个梯级代表一层理论板. 梯级总数即为所需理论板数.3、梯级含义：如第一梯级:由a点作水平线与平衡线交于点1(y1, x1), 相当于用平衡关系由y1求得x1；再自点1作垂线与精馏段操作线相交, 交点坐标为(y2, x1), 即相当于用操作线关系由x1求得y2。

精馏塔理论塔板数计算

2 0.398 0.612
0.392 0.612
3 0.392 0.602
精馏塔逐板计算
解除密码：
wulijian2710
塔板编号 xi yi
1 0.952 0.980
2 0.913 0.963
3 0.860 0.938
4 0.795 0.905
5 0.721 0.863
6 0.645 0.817
说明:这里给出了最小Rmin算法,偏差比较大,可以调整点在平衡线上,回流比最小,记入Rmin计算理
平衡线方程y
精馏段方程yn＋1
画提馏段方程yn＋1 图 q线方程xq 数 q线方程yq 据
区精折线
0.000
0.400 0.400 塔板编号 x: y:
0.048 0.048 0.357 0.409 0.456 0.363 0.376 0.376 0.479 0.501
-0.011 0.020 0.020 0.278 0.333
FALSE 0.001 0.003
FALSE -0.004 -0.009
FALSE -0.007 -0.017
FALSE -0.009 -0.022
FALSE -0.010 -0.025
FALSE 0.406 0.619
FALSE -0.001 -0.003
FALSE
0.406 0.619
0.406 0.619
FALSE
-0.012 -0.012 -0.030 -0.030
FALSE
0.406 0.619
0.406 0.619
FALSE
-0.012 -0.012 -0.030 -0.030
FALSE
0.406 0.619

连续精馏理论塔板数的计算

5.3 连续精馏理论塔板数的计算本节重点：理论塔板数的计算。

本节难点：理论塔板数的计算—逐板计算法和图解法；双组分连续精馏塔所需理论板数，可采用逐板计算法和图解法。

5.3.1逐板计算法假设塔顶冷凝器为全凝器，泡点回流，塔釜为间接蒸汽加热，进料为泡点进料如图5－5所示。

因塔顶采用全凝器，即y 1=x D 5－24而离开第1块塔板的x 1与y 1满足平衡关系，因此x 1可由汽液相平衡方程求得。

即111)1(y y x --=αα 5－25第2块塔板上升的蒸汽组成y 2与第1块塔板下降的液体组成x1满足精馏段操作线方程，即Dx R x R R y 11112+++=5－26同理，交替使用相平衡方程和精馏段操作线方程，直至计算到x n <x q (即精馏段与提馏段操作线的交点)后，再改用相平衡方程和提馏段操作线方程计算提馏段塔板组成，至x w ’<x w 为止。

现将逐板计算过程归纳如下：相平衡方程： x1 x2 x3……x n <x q-------x w ’<x w 操作线方程： x D =y1 y2 y3在此过程中使用了几次相平衡方程即可得到几块理论塔板数（包括塔釜再沸器）。

5.3.2 图解法应用逐板计算法求精馏塔所需理论板数的过程，可以在y-x 图上用图解法进行。

具体求解步骤如下：1、相平衡曲线在直角坐标系中绘出待分离的双组分物系y-x 图，如图5－13。

2、精馏段操作线3、提馏段操作线4、画直角梯级从a 点开始，在精馏段操作线与平衡线之间作水平线及垂直线，当梯级跨过q 点时，则改在提馏段操作线与平衡线之间作直角梯级，直至梯级的水平线达到或跨过b 点为止。

其中过q 点的梯级为加料板，最后一个梯级为再沸器。

最后应注意的是，当某梯级跨越两操作线交点q 时（此梯级为进料板），应及时更换操图5-13 理论板数图解法示意图作线，因为对一定的分离任务，此时所需的理论板数最少，这时的加料板为最佳加料板。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

通过函数求解曲线绘制，采用图解法计算理论板数。

在工程计算中matlab语言拥有大量的命令集和可用函数集可以完成各种计算和数据处理，集数值计算和图形处理功能于一身，形式简单，易于掌握。

常压下的二硫化碳和四氯化碳的气液平衡数据【2】液相中二硫化碳摩尔分率x 气相中二硫化碳摩尔分率y 液相中二硫化碳摩尔分率x 气相中二硫化碳摩尔分率y 0 0.0296 0.0615 0.1106 0.1435 0.25800 0.0823 0.1555 0.2660 0.3325 0.49500.3908 0.5318 0.6630 0.7574 0.8604 1.00.6340 0.7470 0.8290 0.8790 0.9320 1.02 数学模型：精馏段操作线方程：D1x n L D y x V V +⨯=+提馏段操作线方程：W1x n n L W y x V V+⨯=- 相平衡方程：xy=1+-1xαα（）q 线方程：111F q y x x q q =--- 3解决问题方法：1、列出已知条件2、用line 绘出对角线，拟合数据用plot 绘制平衡线3、利用fplot 绘制精馏段操作线4、利用fplot 绘制进料线5、求3,4两线交点f ，采用数值解法，调用fzero6、连接f 与塔底组成点c 绘制提馏段操作线7、绘制阶梯，计算理论板数具体程序【1，2】如下：%图解法确定精馏塔理论板层数function fdistillation%图解法确定理论板层数clear,clc%1.已知数据xD = 0.986;%塔顶组成xW = 0.0220%塔釜组成xF = 0.53;%进料组成R = 3.8;%回流比q = 1.550;%进料热状况vledata = [%汽液平衡数据0 0.0296 0.0615 0.1106 0.1435 0.2580 0.3908 0.5318 0.6630 0.7574 0.8604 1.0 0 0.0823 0.1555 0.2660 0.3325 0.4950 0.6340 0.7470 0.8290 0.8790 0.9320 1.0]; %2 绘制平衡线plot(vledata(1,:),vledata(2,:),'*')hold onp = polyfit(vledata(1,:),vledata(2,:),3);x1 = [0.0 :0.01:1.0];y1 = polyval(p,x1);plot(x1,y1)hold on%3 绘制对角线line([0.0,1.0],[0.0,1.0])% 4 绘制精馏段操作线fplot(@recope,[0 xD],[],[],'r',R,xD)hold on% 5 绘制进料线方程fplot(@qline,[xF 1],[],[],'g',q,xF)hold on% 6 与进料线的交点xc = fzero(@cross,0.5,optimset('fzero'),R,xD,q,xF); yc = recope(xc,R,xD);% 7 绘制提馏段操作线line([xc,xW],[yc,xW],'Color','c')% 8 绘制梯级x0 = xD;y0 = xD;n=0;while 1n = n+1;[x0,y0] = tri(x0,y0,R ,xD,p ,xc ,yc,xW,n);if x0<xWbreak;endend% 9修饰s = sprintf('理论板数为%d',n);text(0.1,0.9,s)xlim([0,1]),ylim([0,1]),title('图解法确定精馏塔理论板数'),xlabel('x'),ylabel('y')%----精馏段操作线----function y = recope(x,R,xD)y = R*x/(R+1)+xD/(R+1);%----进料线方程------function y = qline(x,q,xF)y = q*x/(q-1)-xF/(q-1);%----交点------function y = cross(x,R,xD,q,xF)y = recope(x,R,xD)-qline(x,q,xF);%-----平衡关系逆运算----function y = vlei(x,p,yn)y = polyval(p,x)-yn;%-----绘制梯级------function [x,y] = tri(x0,y0,R,xD,p,xc,yc,xW,n)x = fzero(@vlei,x0,optimset('fzero'),p,y0);if x>xcy = recope(x,R,xD);elsey = yc + (yc-xW)*(x-xc)/(xc-xW);endline ([x0,x,x],[y0,y0,y],'Color','m'),text(x,y0,int2str(n),'VerticalAlignment','bottom')grid on结果如下：由图可以看出需要12块理论板结论：应用matlab求解二元精馏塔理论板数，方法简单实用，可以方便快捷的得到计算结果。

参考文献[1] 田文德，王晓红.化工过程计算机基础.北京：化工过程计算机应用基础.北京：化学工业出版社2007[2] 陈敏恒，丛德滋，方图南等.化工原理.第3版.北京：化学工业出版社20060 0.0100000000000000 0.0200000000000000 0.04000000000000000.0600000000000000 0.0800000000000000 0.1000000000000000.140000000000000 0.180000000000000 0.2000000000000000.250000000000000 0.300000000000000 0.3500000000000000.400000000000000 0.450000000000000 0.5000000000000000.550000000000000 0.600000000000000 0.6500000000000000.700000000000000 0.750000000000000 0.8000000000000000.850000000000000 0.894000000000000 0.9000000000000000.950000000000000 10 0.110000000000000 0.175000000000000 0.2730000000000000.340000000000000 0.392000000000000 0.4300000000000000.482000000000000 0.513000000000000 0.5250000000000000.551000000000000 0.575000000000000 0.5950000000000000.614000000000000 0.635000000000000 0.6570000000000000.678000000000000 0.698000000000000 0.7250000000000000.755000000000000 0.785000000000000 0.8200000000000000.855000000000000 0.894000000000000 0.8980000000000000.942000000000000 1.。