四年级上册(三单元2:三位数乘两位数)——“结构图”2013.10
三位数乘两位数思维导图
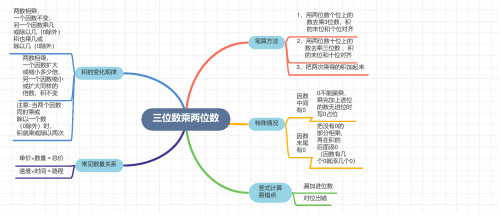
三位数乘两位数笔算方法1,用两位数个位上的 数去乘3位数,积 的末位和个位对齐2,用两位数十位上的 数去乘三位数 ,积 的末位和十位对齐3,把两次乘得的积加起来特殊情况因数中间有00不能漏乘,乘完加上进位的数无进位时写0占位因数末尾有0把没有0的部分相乘,再在积的后面添0(因数有几个0就添几个0)竖式计算易错点漏加进位数对位出错积的变化规律两数相乘,一个因数不变,另一个因数乘几或除以几(0除外)积也乘几或除以几(0除外)
两数相乘,一个因数扩大或缩小多少倍,另一个因数缩小或扩大同样的倍数,积不变注意::当两个因数同时乘或除以一个数(0除外)时,积就乘或除以两次常见数量关系
单价×数量=总价速度×时间=路程。
【典例精讲】第4讲 三位数乘两位数-四年级上册数学精品讲义(思维导图+知识梳理+例题精

第4讲三位数乘两位数(思维导图+学问梳理+例题精讲+易错专练)一、思维导图二、学问点梳理学问点一:三位数乘两位数的笔算方法1、先用两位数个位上的数去乘三位数,积的末位和两位数的个位对齐;2、再用两位数十位上的数去乘三位数,积的末位和两位数的十位对齐;3、最终把两次乘得的积加起来。
学问点二:因数中间或末尾有0的计算方法1、因数末尾有0的乘法的简便算法:先把末尾0前面的数相乘,再看两个因数末尾一共有几个0,就在积的末尾添几个0。
2、当三位数中间有0时,用其次个因数每一位上的数依次乘三位数上每一位上的数,包括0都要乘。
学问点三:积的变化规律1、一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)2、一个因数乘(或除以几),另一个因数除以(或乘)相同的数,积不变,留意除数不能为0。
学问点四:三位数乘两位数的实际应用1、单价、数量和总价的数量关系每件商品的价钱,叫做单价;买了多少,叫做数量;一共用的价钱,叫做总价。
单价×数量=总价单价=总价÷数量数量=总价÷单价2、速度、路程和时间的数量关系一共行了多长的路,叫做路程;每小时(或每分钟等)行的路程,叫做速度;行了几小时(或几分钟等),叫做时间。
速度×时间=路程速度=路程÷时间时间=路程÷速度三、例题精讲考点一:三位数乘两位数的笔算【典型一】病题门诊部。
【分析】依据两位数乘三位数乘法的笔算法则进行推断即可。
【解答】解:【典型二】学校购买16套民族服装。
每件上衣68元,每条裤子57元,一共用去多少元?【分析】先用加法求出每套服装的价钱,再依据单价×数量=总价,把数据代入计算即可解【解答】解:(57+68)×16=125×16=2000(元)答:一共花了2000元。
【典型三】绿水青山就是金山银山,生态环境爱护是功在当代、利在千秋的事业。
武警右玉中队接力植树66年,先后义务植树造林127公顷,黄沙地见证“橄榄绿”。
《三位数乘两位数》单元知识结构图

内容目标
知识技能
数学素养ห้องสมุดไป่ตู้
数与代数
三位数乘两位数
会笔算三位数乘两位数,能口算、估算简单的乘法算式,估计积的大致范围;掌握积的变化规律,并在具体问题中加以应用。解决生活中两种常见的数量关系。
培养学生初步的观察能力、基本数感。初步建立数学模型思想,通过建模,使学生初步感受数学与实际生活的联系,学以致用。
养成学生良好的做题习惯,以及良好做事习惯。通过生活实际问题的解决,激发学习数学的爱好兴趣,能主动用学过的数学知识解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
核心问题:先算什么? 核心目标:使学生掌握用一位数乘两位数(积在100以内)或几百几十的数的口算方法 主题研讨结构图
四年级数学(上册)三单元“三位数乘两位数”(一) 制作人:王立峰2013.10.8 研究主题:拓展笔算乘法模型 核心问题: ①你能把这两个竖式合在一起吗?
②第二次乘得的积写在哪儿?
③(先算什么)竖式里个位在哪儿?
核心目标:理解竖式算理,熟练计算 已有的知识经验: 1.末尾有0的口算
20×80=2×8×100=1600
2.学生已经掌握的两位数乘两
位数的笔算方法。
3.已有的位值观念 口算例1 (1课时) 例1因数中间、末尾没有0教参目标
1.使学生掌握用一位数乘两位数(积在100以内)或几百几十的数的口算方法。
2.使学生能根据两位数乘两位数的笔算方法,推出并掌握三位数乘两位数的笔算方法。
3.使学生知道速度的表示法,经历从实际问题中抽象出时间、速度和路程之间的关系,并应用这种关系解决问题的过程。
4.使学生掌握乘法的估算方法。
在解决具体问题的过程中,能应用合适的方法进行核心问题:要乘几次,每次乘得的积个位在哪儿? 核心目标:建“三位数乘两位数”笔算模型 三位
数乘
两位数
三单元 三位数乘两位数 (9课时) 16×3=48 30+18 1 6 × 3 4 8 160×3=480 16×3×10 1 6 × 3 4 8 48×10=480 口算模型 笔 算 1 4 5 × 1 2 2 9 0 1 4 5 0 1 7 4 0
师:145先和2乘:145×2=290 师:竖式的个位在哪儿?因数12中2是个位,第一次乘得的积290个位对齐写在竖式下面 师:145第二次和谁相乘 生:1 ……10 师:145和十位上的1相乘,145×10=1450 或145×1(十)=145(十) 师:第二次乘得的积145(十),应和十位对齐 哪一位乘得的积就和哪一位对齐 160×3=480 300+180
例2因数中间、末尾有0的 核心问题:(先算什么)竖式里个位在哪儿? 核心目标:建“因数末尾有0”笔算模型。
主题研讨结构图
四年级数学(上册)三单元“三位数乘两位数”(二) 制作人:王立峰2013.10.8 160×30=480
16×3×100 1 6
× 3 4 8
48×100=4800 1 6 0 × 3 0 4 8 0 0 1 6 0 3 0 × 4 8 0 0 个 位 10
10 × 10 0 1 6 0 3 0 × 个 位 4 8 1 6
3 × 个
位
(16×3=48) (10×10=100) 160×30=(16×3)×(10×10)=48×100=4800 个 位
核心问题:个位在哪儿?
在这个乘法竖式里我们只算其中的一部分16×3,而对于因数末尾0的处理,则采取了一种简便方式“添0”,它源自因数末尾有0口算方法的运用 在竖式里突出对口算模型的运用(先算什么再算什么)
三位数乘两位数(笔算)
例3速度、时间和路程之间的关系 例4:积的变化规律 核心问题:速度、时间和路程之间有什么样的关系? 核心目标:建“时间×速度=路程”数学模型,并应用其解决问题。
核心问题:你发现了什么?
核心目标:掌握积的变化规律(规律本身很难理解,运用就更难了,理解这样的规律需要函数思想) 主题研讨结构图
四年级数学(上册)三单元“三位数乘两位数”(三) 制作人:王立峰2013.10.8 三单元
三位数乘两位数 四年级同学去秋游。
每套车票和门票49元,一共需要104套票。
估算一下,大约应该准备多少钱买票? 104×49≈5000元 100 50
竖式计算,应该准备多少钱买票? 104×49≈5096元
1 0 4 × 4 9
9 3 6 4 1 6 5 0 9 6 为什么估算的钱不够买票?
(讨论) 生:我们把数估小了
师:把哪个数估小了 生:104应该估成110 师:那我们像这样再估算一下… 重新估算一下,大约应该准备多少钱买票?
104×49≈5500元 在解决实际问题时,我们的
①实际情境 ②尝试估算 ③准确计算 ④遭遇问题 ⑤解决问题 ⑥总结提升 核心问题:为什么估算的钱不够买票? 核心目标:使学生掌握符合实际的的估算方法。
例5:估算 抽象数学还要回到实际生活中去,怎么回?具体问题具体分析,数学上的“四舍五入”到了生活中,有时会产生一些矛盾,解决矛盾的办法就是“符合实际”
,无论是估算、还是准确计算都是在解决实际问题……
1 6 0 3 0 × 4 8 0 0
个 位
10 10
× 10 0
1 6 0 3 0
× 个 位
4 8 1 6 3 × 个 位
(16×3=48)
(10×10=100)
160×30=(16×3)×(10×10)=48×100=4800
个 位
核心问题:个位在哪儿?
例2因数中间、末尾有0的 核心问题:(先算什么)竖式里个位在哪儿? 核心目标:建“因数末尾有0”笔算模型。
160×30=480 16×3×100 1 6 × 3 4 8 48×100=4800 1 6 0
× 3 0 4 8 0 0 1 6 0 3 0 × 4 8 0 0 个
位 10
10
× 10 0
1 6 0 3 0 × 个 位 4 8 1 6 3 × 个 位 (16×3=48) (10×10=100) 160×30=(16×3)×(10×10)=48×100=4800 个 位 核心问题:个位在哪儿?
在这个乘法竖式里我们只算其中的一部分16×3,而对于因数末尾0的处理,则采取了一种简便方式“添0”,它源自因数末尾有0口算方法的运用 在竖式里突出对口算模型的运用(先算什么再算什么)
三位数乘两位数(笔算)
核心问题:为什么估算的钱不够买票? 四年级同学去秋游。
每套
车票和门票49元,一共需要
104套票。
估算一下,大约应该准备多少钱买票? 104×49≈5000元 100 50 竖式计算,应该准备多少钱买票? 104×49≈5096元
1 0 4 × 4 9 9 3 6 4 1 6 5 0 9 6
为什么估算的钱不够买票?
(讨论)
生:我们把数估小了 师:把哪个数估小了 生:104应该估成110
师:那我们像这样再估算一下…
重新估算一下,大约应该准备多少钱买票? 104×49≈5500元
110 50 在解决实际问题时,我们的估算应符合实际……
①实际情境 ②尝试估算 ③准确计算
④遭遇问题
⑤解决问题
⑥总结提升 抽象数学还要回到实际生活中去,怎么回?具体问题具体分析,数学上的“四舍五入”到了生活中,有时会产生一些矛盾,解决矛盾的办法就是“符合实际”
,无论是估算、还是准确计算都是在解决实际问题……。
