08届高三年级理科数学第三次质量检测试卷
2008年高三教学质量检测数学试卷(理)

7 、 已 知 集 合 A n | 0 n 10, n N , 从 A 中 任 取 3 个 不 同 元 素 分 别 作 为 圆 方 程
( x a ) 2 ( y b) 2 r 2 中 的 a, b, r 。 则 使 圆 心 与 原 点 的 连 线 恰 好 垂 直 于 直 线 l : x 3 y 1 0 的概率为________.
17、 (本题满分 12 分) (1)、 (解法一) : (如图)以 DA 为 x 轴,以 DC 为 y 轴, 以 DD1 为 z 轴, 建立空间直角坐标系。 A1 D D1 B1 C C1
AB 3, AE 2 EB, EB 1, AE 2 ,则 E (1,2,0) , A 1 ,0 ,0
2 的实数 a 的取值范
4、设 S n 为等差数列 a n 的前 n 项和,若 S 5 10, S10 5 ,则公差为 ___________ . 5、已知直线 a, b 及平面 ,下列命题中: ①
a b a b a // ;② a ; b b //
因为 AD DD1 1 ,所以 AE D1 E 而 AD1 角的大小为
2 , ,-----------------------------------------------4 分
2 , 所以△ AD1 E 为正三角形, D1 AE /
3
,从而异面直线 AD1 与 EC 所成
S1 S 2 S n 为 A 的“优化和” ;现有 2007 项的数列 ( a1 , a 2 , , a 2007 ) 的“优化和”为 n
2008 , 则 有 ( ) 2008 项 的 数 列 (1, a1 , a 2 , , a 2007 ) 的 “ 优 化 和 ” 为
2008学年高三第三次月考理科

福建省福州三中2007—2008学年高三第三次月考数学试题(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分共150分,考试时间120分钟。
注意事项:(1)答第I 卷前,考生务必将自己的姓名、考生号码、考试科目用铅笔涂写在答题卡上。
(2)每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
第I 卷(选择题共60分一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合1{10}{0}1M x x N xx=+>=>-,,则M N =( )A .{11}x x -≤<B .{1}x x >C .{11}x x -<<D .{1}x x ≥- 2.函数41xy =+的反函数是( )A .4log 1y x =+B .4log (1)y x =+C .4log 1y x =-D .4log (1)y x =-3.已知i z i -=+⋅)1(那么复数z 对应的点位于复平面内的( )A .第一象限B .第二象限C .第三象限D .第四象限4.设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩<,则的值为, ( )A .0B .1C .2D .3 5.函数xxa y x=(01)a <<的图象的大致形状是( )A .B .C .D .6.若q p x q x p 是则,2|1:|,0)1lg(:<-<-的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.已知函数321()22f x x x m =-+的图象上A 点处的切线与直线30x y -+=的夹角为45°,则A 点的横坐标为( )A .0B .1C .0或16D .1或168.不等式411x x ≤--的解集是 ( ) A .(][),13,-∞-+∞ B .[)[)1,13,-+∞C .[]1,3-D . ()[),31,-∞-+∞9.二次函数),1()0()(),2()2()(f f a f x f x f x f <≤-=+且满足则实数a 的取值范围是( )A .0a ≥B .0a ≤C .04a ≤≤D .0a ≤或4a ≥10.已知,,a b R a b ∈>,又∞→n lim 1n n n a b a ++>∞→n lim n nn ab a +-1,则a 的取值范围是( )A .1a >B .11a -<<C .1a >D .1a >或10a -<<11.已知()f x 是R 上的奇函数,对x R ∈都有(4)()(2)f x f x f +=+成立,若(1)2f =,则(2005)f 等于 ( )A .2005B .2C .1D .1a >12.已知)(x f 是定义在R 上的奇函数,其图象关于1=x 对称且021=⎪⎭⎫⎝⎛f ,则方程()0=x f 在()0,5内解的个数的最小值是( )A .4B .5C .6D .7第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上. 13.函数22112x x y +-⎛⎫=⎪⎝⎭的值域是__________________。
安徽省合肥市2008年高三第三次教学质量检测(数学理)

合肥市2008年高三第三次教学质量检测数学试题(理)(考试时间:120分钟满分:150分)参考公式:如果事件A 、B 互斥,那么)()()(B P A P B A P +=+如果事件A 、B 相互独立,那么)()()(B P A P B A P ⋅=⋅如果事件A 在一次试验中发生的概率是 p ,那么n 次独立重复试验中事件A 恰好 发生k 次的概率()kn kk n n p p C k P --=1)(球的表面积公式24R S π=(其中R 表示球的半径) 球的体积公式334R V π=(其中R 表示球的半径)线性回归方程中a 、b 的值由下列公式给出()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=---=∑∑∑∑====xb y a xn x yx n y x x x y y x x b ni i ni ii ni i ni i i 1221121第Ⅰ卷(选择题 共55分)注意事项:1.选择题用答题卡的考生,答第Ⅰ卷前,考生务必将自己的姓名、准考证号、试题科目用2B 铅笔涂写在答题卡上。
2.选择题用答题卡的考生,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷和答题卷的选择题栏中;不用答意卡的考生,每小题选出答案后,填在答题卷相应的选择题栏中。
3.考试结束,监考人将答题卷和答题卡一并收回,第Ⅰ、Ⅱ卷不收回。
一、选择题 本大题共11小题,每小题5分,共55分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案代号填涂在答题卡上。
1.函数x x y cos sin 21-=的最小正周期为π21⋅A π.Bx C 2. π4.D2.已知全集U=R ,集合{}1|≥=x x M ,⎭⎬⎫⎩⎨⎧≥-+=021|x x x N ,则()N M C U }2|.{<x x A }2|.{≤x x B }21|.{≤≤-x x C }21|.{<≤-x x D3.若函数()96,22+-+=y y x y x f 是定义在⎪⎪⎩⎪⎪⎨⎧<-≤≤≤≤=1}25020|),{(x y y x y x D 上,的函数,则函数z ),(y x f的值域是]2,0.[A )3,217.(B )3,210.(C ]13,2.(D4.若函数)(x f 是定义在R 上的奇函数,当0<x 时,x x f 3)(=,则)91(1--f的值是 A .-2 B .221.-C 21.D 5.侧棱长为4,底面边长为3的正三棱柱的各顶点均在同一个球面上,则该球的表面积为π76.A π68.B π20.C π9.D6.某调查者从调查中获知某公司近年来科研费用支出(i x )万元与公司所获得利润(i y )万元的统计资料如下表:序号 科研费用支出i x 利润i y i x i y2i xl 2 3 4 5 6 5 11 4 5 3 2 31 40 30 34 25 20 155 440 120 170 75 40 25 121 16 25 9 4 合计301801000200则利润(i y )对科研费用支出(i x )的线性回归方程为202.+=∧x y A220ˆ.+=x yB 042ˆ. +-=x yC 402ˆ.+=x yD 7.设πθ20<≤,θθsin cos 331i ii+=++,则θ的值为 32.πA 2.πB 3.πC 6.πD 8.设,0>a ,0>b ,0>c 下列不等关系不恒成立的是1411.23-+>++c c c c A||||||.c b c a b a B -+-≤-C .若14=+b a ,则8.611>+ba)(0.2R x c bx ax D ∈≥-+9.已知函数)(x f 的定义域为R ,)('x f 为)(x f 的导函数,函数)(x f y =的图象如图所示,1)3(1)2(,==-f f 则不等式1)(>x f 的解集为)3,2.(-A )2,.(--∞B),3.(+∞C),3()2,.(+∞--∞ D10.已知平面上不共线的四点O ,A ,B ,C .若,023=+-OC OB OA 则=BCAB31.A21.B C .1 D .211.函数)(x f y =的定义域为),(+∞-∞且具有以下性质:;0)()(=--x f x f ①;1)()2(=⋅+x f x f ②)(x f y =③在[0,2]上为单调增函数,则对于下述命题:(1))(x f y =的图象关于原点对称 (2))(x f y =为周期函数且最小正周期是4 (3))(x f =γ在区间[2,4]上是减函数正确命题的个数为A .0个B .1个C .2个D .3个第Ⅱ卷(非选择题 共95分)注意事项:第Ⅱ卷共2页,共95分。
安徽省皖南八校2008届高三第三次联考(数学理)

安徽省皖南八校2008届高三第三次联考理科数学考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
2.答题前,考生务必将密封线内的项目填写清楚。
3.请将各卷答案填在试卷后面的答题卡上。
第Ⅰ卷 (选择题 共55分)一、选择题:本大题共11小题,每小题5分,共55分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知3sin 25a π-=(),则2tan a 等于 A .169B .916C .43D .342.{}21log A a=,(1+),{1|02x B x x -⎫=≤⎬-⎭,若A B ⊆,则实数a 的取值范围是 A .(1,2)B .(1,3)C .(2,3)D .(2,4)3.设m ,n 为两条不同直线αβ,为两个不同平面,则下列命题正确的是A .m ∥n ,m ∥α,n ∥β,则α∥βB .m ∥n ,m ⊥α,n ⊥β,则α∥βC .m ∥α,n ∥β,α∥β,则m ∥nD .m ∥n ,m ⊥α,α∥β,则n ∥β 4.已知i 是虚数单位,m ∈R ,且2i 1i m -+是纯虚数,则2i 2im m -+2008()等于 A .1B .-1C .iD .-i5.在大小相同的6个球中,有2个红球,4个黄球.若从中任意选取3个,则所选的3个球中至少有1个红球的概率是 A .12B .23C .34D .456.若直线40mx ny +-=(0m >,0n >)始终平分圆22420x y x y +--=,则12m n+ 的最小值是AB .3C .D .27.将式子x x+-6(2展开整理后,含4x 项的系数为 A .0B .36C .48D .-308.已知| p | | q | =3,p ,q 的夹角为4π,如图所示,若 AB =5p + 2q ,AC =p —3 q ,且D 为BC 的中点,则AD 的长度为A .152B C .7 D .89.如图,设地球半径为R ,点A 、B 在赤道上,O 为地心,点C 在北纬60°的纬线('O 为其圆心)上,且点A 、C 、'O 、O 共面,若AOB ∠=90°,则异面直线A B 与O C 所成角的余弦值为A BC .4D .410.已知1F 、2F 几分别是双曲线22221x y a b-=(a >0,b >0)的左、右焦点,P 是双曲线的准线上一点,若120PF PF ⋅=且123PF PF ab ⋅=,则双曲线的离心率是AB .2C .2D .5411.定义:设函数()f x 的定义域为R ,若存在正常数M ,使得()f x M x ≤对一切实数x 均成立,则称()f x 为F 函数.给出下列函数: ①2()f x x =,②()22x xxf x -=+,③()sin cos f x x x =-),④()4sin cos 22f x ππ=其中是F 函数的有 A .1个B .2个C . 3个D .4个第Ⅱ卷 (非选择题 共95分)二、填空题:本大题共4小题,每小题4分,共16分。
修改版2008届高三调研考试数学试题(理科)答案及评分标准校对版
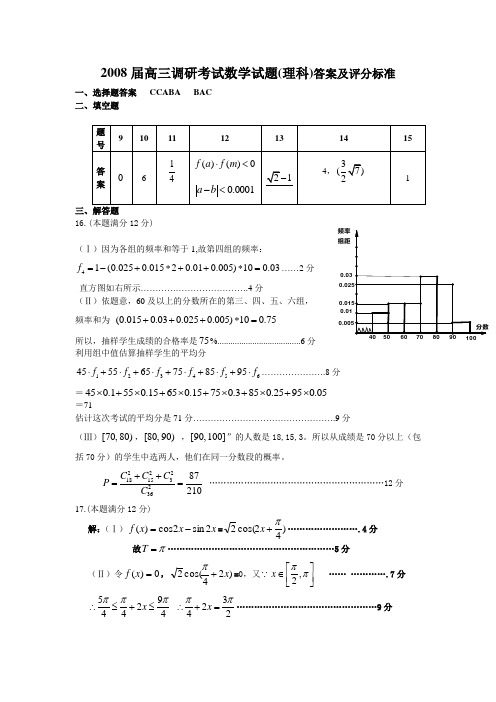
0.030.01频率组距2008届高三调研考试数学试题(理科)答案及评分标准一、选择题答案 CCABA BAC 二、填空题三、解答题16.(本题满分12分)(Ⅰ)因为各组的频率和等于1,故第四组的频率:41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组, 频率和为 (0.0150.030.0250.005)100.75+++*=所以,抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分=450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯ =71估计这次考试的平均分是71分………………………………………….9分(Ⅲ)[70,80),[80,90) ,[90,100]”的人数是18,15,3。
所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
22218153236C C C P C ++==87210 ……………………………………………………12分 17.(本题满分12分)解:(Ⅰ)x x x f 2sin 2cos )(-==)42cos(2π+x …………………….4分故π=T …………………………………………………5分 (Ⅱ)令0)(=x f ,)24cos(2x +π=0,又 ,2x ππ⎡⎤∈⎢⎥⎣⎦…… ………….7分 592444x πππ∴≤+≤ 3242x ππ∴+=…………………………………………9分故58x π=函数)(x f 的零点是58x π= ……………. 12分 18.(本题满分12分)证(Ⅰ)因为AB ⊥侧面11BB C C ,故1AB BC ⊥ 在1BC C 中,1111,2,3BC CC BB BCCπ===∠=由余弦定理有1BC == 故有 222111BC BC CC C B BC += ∴⊥而 BC AB B = 且,AB BC ⊂平面ABC∴1C B ABC ⊥平面(Ⅱ)由11,,,,EA EB AB EB ABAE A AB AE ABE ⊥⊥=⊂平面从而1B E ABE ⊥平面 且BE ABE ⊂平面 故1BE B E ⊥不妨设 CE x =,则12C E x =-,则221BE x x =+-又1123B C C π∠= 则2211B E x x =++在1Rt BEB 中有 22114x x x x +++-+= 从而1x =±(舍负)故E 为1CC 的中点时,1EA EB ⊥法二:以B 为原点1,,BC BC BA 为,,x y z 轴,设CE x =,则11(0,0,0),(1),(2B E x B A -- 由1EA EB ⊥得 10EA EB ⋅=即11(1,2)(,0)2211(1)(2)022x x x x x x x --=⎫--=⎪⎪⎭化简整理得 2320x x -+= 1x = 或 x = 当2x =时E 与1C 重合不满足题意EC 1B 1A 1CBA111当1x =时E 为1CC 的中点 故E 为1CC 的中点使1EA EB ⊥(Ⅲ)取1EB 的中点D ,1A E 的中点F ,1BB 的中点N ,1AB 的中点M 连DF 则11//DF A B ,连DN 则//DN BE ,连MN 则11//MN A B 连MF 则//MF BE ,且MNDF 为矩形,//MD AE 又1111,A B EB BE EB ⊥⊥ 故MDF ∠为所求二面角的平面角在Rt DFM 中,111(22DF A B BCE==∆为正三角形)111222MF BE CE === 1tan 2MDF ∴∠== 法二:由已知1111,EA EB B A EB ⊥⊥, 所以二面角11A EB A --的平面角θ的大小为向量11B A与EA 的夹角因为11B A BA ==1(2EA=-- 故 11112cos tan 3EA B A EA B A θθ⋅==⇒=⋅.19. (本题满分14分)解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线.…………………….2分∴PQ 是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF =.…………4分 故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x =>.…………………………………………………….7分(Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y…………………………………………………….8分则⎪⎩⎪⎨⎧==)2(4)1(422BB AA x y x y(1)—(2)得k y y B A 4=+,即ky M 2=,……………………………………9分代入方程)1(-=x k y ,解得122+=kx M .所以点M的坐标为222(1,)k k+.……………………………………10分同理可得:N 的坐标为2(21,2)k k +-.直线MN 的斜率为21kkx x y y k N M N M MN -=--=,方程为 )12(1222---=+k x kkk y ,整理得)3()1(2-=-x k k y ,………………12分 显然,不论k 为何值,(3,0)均满足方程,所以直线MN 恒过定点R (3,0). (14)20. (本题满分14分) .解:11n na kn a +=+ 故2211a a k a ==+,.……………………………………1分 又因为()211111,,2n n n n n a a a a a a n N n +--+==+∈≥则3121a a a a =22a +,即3322221,21,2a aa k a k a a =+=+∴=又.………………………3分 所以212,1k a k k +==∴=, ……………………………………4 (2)11,n na n a +=+ 121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅⋅⋅⋅⋅=()1...21!n n n ⋅-⋅⋅⋅= ……………………………………6 因为()()11!n n a x g x n -=-=1n nx -所以,当1x =时,()()()11123 (2)n n f x f n +==++++=.................................7 当1x ≠时,()21123...n f x x x nx -=++++. (1)()1x ⋅得()()23123...1n n xf x x x x n x nx -=++++-+……(2) ()()()()2112:11...n n x f x x x x nx ---=++++-=11nn x nx x--- ()()2111nn x nx f x xx -∴=--- ……………………………9 综上所述:2(1),12()1,1(1)1n nn n x f x x nx x x x+⎧=⎪⎪=⎨-⎪-≠⎪--⎩ ……………………………10 (3)因为()()()212221211212nnn n f n -∴=-=-+-- 又()333n g n=,易验证当1,2n =,3时不等式不成立; ……………………………11 假设()3n k k =≥,不等式成立,即()3121kkk >-+ 两边乘以3得:()()111331232131222k k k k k k k k k +++>-+=⋅++--+又因为()()()131222233223220k k k k k k k k k +--⋅+=--+=-+>所以()11113213122221k k k k k k k k k ++++>⋅++--+>⋅+即1n k =+时不等式成立.故不等式恒成立. (14)21. (本题满分14分) 解:(Ⅰ)()ln(1)(1),x f x a e a x =+-+(1)()(1)011x xx xae a e f x a e e-+-'∴=-+=<++恒成立,………………………… 所以函数()f x 在(,)-∞+∞上是单调减函数. …………………………4分(Ⅱ) 证明:据题意1,12233(()),(,()),(,())A x f x B x f x C x f x 且x 1<x 2<x 3,由(Ⅰ)知f (x 1)>f (x 2)>f (x 3), x 2=231x x +…………………………6分 12123232(,()()),(,()()BA x x f x f x BC x x f x f x ∴=--=--12321232()()[()()][()()]BA BC x x x x f x f x f x f x ∴⋅=--+--…………………8分123212320,0,()()0,()()0x x x x f x f x f x f x -<->->-<0,(,)2BA BC B ππ∴⋅<∴∠∈即⊿ABC 是钝角三角形……………………………………..9分(Ⅲ)假设⊿ABC 为等腰三角形,则只能是BA BC =即2132()()()f x f x f x =+3212132ln(1)2(1)[ln(1)(1)(1)()x x x a e a x a e e a x x ⇔+-+=++-++ 321222ln(1)2(1)[ln(1)(1)2(1)x x x a e a x a e e a x ⇔+-+=++-+3212ln(1)ln(1)(1)x x x e e e ⇔+=++31332122122(1)(1)(1)2x x x x x x x x x e e e e e e e e +⇔+=++⇔+=++3212x x x e e e ⇔=+ ① …………………………………………..12分而事实上, 3122xx x e e e +≥= ②由于31xxe e <,故(2)式等号不成立.这与(1)式矛盾. 所以⊿ABC 不可能为等腰三角形..14分222212123232()[()()]()[()()]x x f x f x x x f x f x -+-=-+-即:2221321232[()()][()()]x x x x f x f x f x f x -=-∴-=-。
08届高中毕业班第三次理科综合能力测试

08届高中毕业班第三次理科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷共300分,考试时间为150分钟。
第Ⅰ卷(选择题,共126分)可能用到的相对原子质量:H ~1,C ~12,N ~14,O ~16,Na ~23,S ~32,Cl ~35.5一、选择题(本题包括13小题。
每小题只有一个....选项符合题意) 1.英国的一项研究宣称:已经可以将从人类胚胎中分离出来的干细胞培养成原始生殖细胞。
今后这项研究的发展能使人类面临下列哪个方面的伦理道德的问题 ( )A .用于治疗性克隆研究的卵细胞将不再来自捐赠者B .来自女性的体细胞可以培育出卵细胞C .来自同性别的两个个体可共同生育具备双方遗传物质的后代D .不能产生生殖细胞的不育患者将能够生育具有自己遗传基因的后代2.将一个刚出芽的马铃薯块茎切成大致相同的6块,每块均带有芽眼。
取6个同样大小、质地相同的花盆,分别装满同样的泥土,将每块分别埋于6个花盆的沙土中5 cm 深处,按下表要求连续管理培植20天。
下列有关该实验的叙述中,错误的是( )A .6号花盆的马铃薯将死亡,因为没有水B .5号花盆中的马铃薯最终死亡,原因是根细胞缺氧C .如经过较长时间后3号长出了幼苗,预计会出现“黄化”现象,因光照较弱,不能形成大量的叶绿素D .1号花盆和4号花盆对照,可以证明马铃薯块茎的萌发与温度的关系3.乙酰胆碱(Ach )是一种神经递质。
欲研究Ach 浓度与反应时间的关系(简图如下),在除去突触小泡的前提下自①处注入不同浓度的Ach ,②处给予恒定刺激,③、④处分别为灵敏感应时间测量点。
测得不同浓度Ach 条件下③、④两处感受到信号所用时间如下表所示。
下列各项叙述正确的是( )A B .实验中除去突触小泡的目的是防止实验结果受到相关因素的干扰 C .表中数据说明高浓度Ach 能促进兴奋在神经纤维上的传导D .表中数据说明Ach 浓度的增加对兴奋在神经元之间的传递无明显影响4.下图表示人体内某些淋巴细胞的分化和某种免疫过程,数字表示过程,字母表示细胞或物质。
四川省绵阳市高2008级第三次诊断性考试(数学理)

四川省绵阳市高2008级第三次诊断性考试数 学(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷,全卷150分。
第Ⅰ卷1至2页,第Ⅱ卷3至10页,考试结束后,将第Ⅱ卷和答题卡两部分一并交回。
第Ⅰ卷(选择题,共60分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用4B 或5B 铅笔涂写在答题卡上。
2.每小题选出答案后,用4B 或5B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上。
参考公式:如果事件A 、B 互斥,那么P(A+B)=P(A)+P(B);如果事件A 、B 相互独立,那么)()()(B P A P B A P ∙=∙;如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中恰好发生k 次的概率:kn k k n n P P C k P --∙∙=)1()(;正棱锥、圆锥的侧面积公式cl S 21=锥侧,其中c 表示底面周长,l 表示斜高与母线长;球的体积公式334R V π=球,其中R 表示球的半径。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上。
1.复数212⎪⎭⎫⎝⎛+i i 的虚部为( B )A .-2B .2C .-2iD .2i2.下列各选项中,与︒2008sin 最接近的是( A )A .-21 B .21 C .22-D .223.对平面α和异面直线l 1,l 2,下面四个命题中正确的是( D )A .若α⊂1l ,则l 2与α相交B .若α⊂1l ,则l 2一定不垂直于αC .若直线l 1’,l 2’是l 1,l 2在α内的射影,则l 1’,l 2’是相交直线D .若21l l ⊥,且l 1与α成︒45的角,则l 2与α所成的最大角是︒45 4.已知a,b 是非零向量,且3),(π=b a ,则向量||||b b a a p +=的模为( B )A .2B .3C .2D .35.设实数a,b 满足a<b,b+b<0,ab>0,则下列不等式一定成立的是( C )A .ba ab > B .2211ba>C .ba a->11 D .ba ab2211>6.若对于任意实数x ,有x 3=a 0+a 1(3-x)+a 2(3-x)2+a 3(3-x)3,则a 0+a 2=( D )A .36B .18C .10D .47.已知:集合⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎩⎨⎧≥+≤-=u y x y x y x G 2),(,集合}2|),{(22=+=y x y x H ,“命题:G y x ∈),(”是“命题:H y x ∈),(”的必须而不充分条件,则u 的取值范围是( A )A .2≤u B .2-≤u C .2≤u D .2-≤u8.已知lga<0,则函数f(x)=a |logax|的图象是( D)9.直三棱柱ABCD-A 1B 1C 1的底面是︒=∠90BAC 的等腰三角形,M AA AB ,21==是CC 1的中点,设三棱柱的外接球球心为O ,则点O 到面A 1B 1M 的距离等于(A )A .55 B .105 C .510 D .101010.设F 1,F 2分别是椭圆)0(12222>>=+b a by ax 的左、右焦点,与直线y=b 相切的⊙F 2交椭圆于点E ,E 恰好是直线EF 1与⊙F 2的明点,则椭圆的离心率为( C )A .23 B .33 C .45 D .3511.定义f(M)=(m,n,p),其中M 是ABC ∆内一点,m 、n 、p 分别是MBC ∆、MCA ∆、MAB ∆的面积已知ABC ∆中,),,21()(,30,32y x N f BAC AC AB =︒=∠=∙,则yx41+的最小值是( D )A .8B .9C .16D .18 12.若*221,555N n a a a nn ∈+++=λ,且a 1、a 2、…、}4,0{∈n a ,则λ一定不属于...( C ) A .)1,0[ B .]1,0( C .⎪⎭⎫⎢⎣⎡54,51 D .⎥⎦⎤ ⎝⎛54,51 第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分。
2008年临沂高三教学质量检查考试三理

2008年临沂市高三教学质量检查考试(三)数学(理工农医类)本试卷分为选择题和非选择题两部分,满分l50分。
考试时间l20分钟 参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 如果事件A ,B 互斥,那么P(A+B)=P(A)+P(B). 如果事件A ,B 相互独立,那么P(A ·B)=P(A)·P(B) 用最小二乘法求线性回归方程系数公式∑∑==---=ni ini i ix xy y x xb121)())((ˆ, x b y a-=ˆ 第Ⅰ卷 (选择题 共60分)一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数2)1(2i i++的虚部是 A .一l B .21-C .21D .12.设函数)2lg(-=x y 的定义域为集合M ,集合N={}M x x y y ∈=,2,则M ∩N= A .MB .NC .[0,+∞)D .φ3.已知命题P :α∃∈R ,使函数)cos()(α+=x x f 是奇函数;命题Q :x ∀∈R ,012≥+-x x 恒成立,则下列命题是真命题的是A .Q P ∧⌝B .⌝∧⌝Q PC .Q P ⌝∨⌝D .Q P ⌝∨4.△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =1,∠B=45°,△ABC 的面积S=2,则b=A .1B .3C .5D .425.已知某几何体的三视图如图,正视图与侧视图为全等的图形.根据图中标出的数据,可得该几何体的体积为A .63 B .33 C .23D .36.已知点P(x ,y )的坐标满足条件⎪⎩⎪⎨⎧≥≥≤+,1,,4x x y y x 则22y x +的最大值为A .10B .8C .10D .167.如果执行下边的程序框图,那么输出的C=A .3B .5C .8D .138.要从10名女生与5名男生中选取6人组成兴趣小组,如果按性别分层抽样,则能组成兴趣小组的概率为A .61525410C C C B .61535310C C C C .615615A CD .61525410A A C 9.已知直线a y x =+与圆422=+y x 交于A ,B 两点,O 是坐标原点,向量OB OA ,满+=+,则实数a 的值为A .2B .一2C .6或6-D .2或-210.已知双曲线12222=-by a x 与抛物线x y 82-=有相同的焦点,x y 3=是其一条渐近线,则双曲线的方程为A .1322=-y xB .1322=-y x C .112422=-y xD .141222=-y x 11.若三角形内切圆半径为r ,三边长分别为a ,b ,c ,则三角形的面积)(21c b a r S ++=;类比知,若四面体内切球半径为R ,其四个面的面积分别为S 1,S 2,S 3,S 4,则四面体的体积V=A .R(S 1+S 2+S 3+S 4)B .21R(S 1+S 2+S 3+S 4) C .31R(S 1+S 2+S 3+S 4) D .41R(S 1+S 2+S 3+S 4) 12.已知M 是△ABC 内一点,且32=∙,∠BAC=30°,定义=)(m f (m ,n ,p),其中m ,n ,p 分别为△MBC ,△MCA 和△MAB 的面积,若),,21()(y x p f =,则yx 41+的最小值为A .9B .18C .16D .20第Ⅱ卷 (非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把正确答案填在答题纸给定的横线上. 13.某人5次上班途中所花时间(单位:分钟)分别为x ,y ,10,11,9,已知这组数据平均数为10,方差为2,则y x -的值为 .14.曲线22x y =和直线1+=x y 所围成的区域为M ,在其内部有一小区域N ,为了估计N 的面积,向区域M 进行投点实验,结论表明落在区域N 的点是落在区域M 的41,那么区域N 的面积约为 .15.关于x 的不等式a a x x ≥-+-1的解集为R ,则实数a 的取值范围是 . 16.已知奇函数)(x f y =满足)()1(x f x f -=+,且当x ∈[-1,0]时,943)(+=xx f ,则=)5(log 31f .三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤 17.(本小题满分12分)已知函数a x x x f ++=2sin 3cos 2)(2,a ∈R .(Ⅰ)若x ∈[0,π],求)(x f 的单调增区间;(Ⅱ)若)(x f 的最大值为4,写出使)1(<x f 成立的x 的取值集合. 18.(本小题满分12分)如图,ACDE 是矩形,△ABC 是直角三角形且AC=BC ,F 是BC 中点,沿AC 将△ABC 折起,使得二面角B —AC —D 为直二面角.(Ⅰ)求证:BE//平面ADF ; (Ⅱ)设λ=ACCD,问λ为何值时,直线AB 与CE 所成角为60°?19.(本小题满分12分)某学校对高三(1)班的50位同学进行成绩分析,随机抽取8位同学的数学,物理试卷,将他们的数学成绩从小到大排序分别是:60,65,70,75,80,85,90,95,物理成绩从小到大排序分别是:72,77,80,84,88,90,93,95.(Ⅰ)若规定85分以上(含85分)为优秀,求这8位同学中恰有3位同学的数学成绩和物理成绩均优秀的概率;(Ⅱ)若这8位同学的数学,物理成绩事实上对应于下表:与x 的线性回归方程(系数精确到0.01);否则,说明理由; (Ⅲ)若某同学的数学成绩为72分,请你预测该同学的物理成绩. 参考数据:5.77=,=y =85,∑=≈-812)(i ix1050,∑=≈-812456)(i i y y ,∑=≈--81688))((i i iy y x x.20.(本小题满分12分)已知函数x kx e x f x,)(-=∈R . (Ⅰ)试确定函数)(x f 的单调区间;(Ⅱ)若)(x f 在区间(0,2)内恰好有两个零点,求实数k 的取值范围. 21.(本小题满分12分)已和直线l :b kx y +=与椭圆1222=+y x 相交于A 、B 两点,O 为坐标原点. (Ⅰ)当k =0,0<b<1时,求△AOB 的面积S 的最大值;(Ⅱ)若⊥,求证直线l 与以原点为圆心的定圆相切,并求该圆的方程. 22.(本小题满分14分)已知曲线C :1=xy ,过C 上一点A ),(n n n y x 作一斜率为21+-=n n x k 的直线交曲线C 于另一点A ),(111+++n n n y x ,点列A n (n=1,2,3,…)的横坐标构成数列{n x },其中7111=x . (Ⅰ)求n x 与1+n x 的关系式; (Ⅱ)求证:⎭⎬⎫⎩⎨⎧+-3121n x 是等比数列;(Ⅲ)求证1)1()1()1()1(33221<-+⋅⋅⋅+-+-+-n nx x x x .(n ∈N ,n ≥1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
08届高三年级理科数学第三次质量检测试卷本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷为1—8题,共40分,第II 卷为9—21题,共110分。
全卷共计150分。
考试用时120分钟.一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合要求的.1.已知集合A={}4,3,2,1,那么A 的真子集的个数是( ) A .3 B .16 C .15 D .42.已知向量)3,(),2,4(x b a ==向量,且a ∥b ,则x = ( )A .9B .6C .5D .13.函数12sin cos y x x=++的最大值是 ( )A 1B 1C .1D . 1- 4. 若5522105)1(...)1()1()1(-++-+-+=+x a x a x a a x ,则0a = ( ) A .32 B .1 C .-1 D .-325.若函数ln y x ax =-的减区间为(1,0)-,则a 的值是 ( )A.01a <<B.01<<-aC. 1a =-D. 1a = 6. 在ABC ∆中,“A>B ”是“sin sin A B >”成立的 ( )A .充要条件B .2充分部必要条件C .必要不充分条件D .既不充分也不必要条件7.设等比数列{}n a 的公比为q ,前n 项和为s n ,若s n+1,s n ,s n +2成等差数列,则公比q 为 ( )A .2-=qB .1=qC.12=-=q q 或D .12-==q q 或8.已知函数()d cx bx ax x f +++=23的图象如右图,则 ( )A . ()0,∞-∈bB .()1,0∈bC .()2,1∈bD .()+∞∈,2b二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.计算2111333324()3a b a b ---÷-= (其中0,0a b >>) ;10.曲线sin y x =在点(3π)处的切线方程为 ;11.从10名女生和5名男生中选出6名组成课外学习小组,如果按性别比例分层抽样,则组成此课外学习小组的概率是 ;12.在的面积则中,若ABC BC AB A ABC ∆===∠∆,7,5,1200= ;13.(坐标系与参数方程选做题)以极坐标系中的点 1 , 6π⎛⎫ ⎪⎝⎭为圆心,1为半径的圆的方程是 ;14.(不等式选讲选做题)不等式|4||x x -+-<的解集是 ;15.(几何证明选讲选做题),,,D EF AD C O EF O AB 于于切圆的直径是圆⊥2,6,AD AB ==则AC 长为_______.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)在△ABC 中,角A 、B 、C 所对边分别为a ,b ,c ,已知11tan ,tan 23A B ==,且最长边的边长为l.求:(I )角C 的大小;(II )△ABC 最短边的长.17. (本小题满分12分)在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是32.,每次命中与否互相独立. (Ⅰ) 求油罐被引爆的概率.(Ⅱ) 如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望;18. (本小题满分14分)BAOFCED 第15题设S n 是正项数列}{n a 的前n 项和,且4321412-+=n n n a a S , (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)n n n n n b a b a b a T b +++== 2211,2求已知的值19. (本小题满分14分)据调查,某地区100万从事传统农业的农民,人均收入3000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有x (x >0)万人进企业工作,那么剩下从事传统农业的农民的人均收入有望提高2x %,而进入企业工作的农民的人均收入为3000a 元(a >0)。
(I )在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入,试求x 的取值范围;(II )在(I )的条件下,当地政府应该如何引导农民(即x 多大时),能使这100万农民的人均年收入达到最大。
20.(本小题满分14分)设21,x x 是函数322()(0)32a b f x x x a x a =+->的两个极值点,且2||||21=+x x (Ⅰ)求a 的取值范围;(Ⅱ)求证:||b ≤21.(本小题满分14分)已知二次函数t t t t y l c bx ax x f .20(8:,)(212≤≤+-=++=其中直线为常数);2:2=x l .若直线l 1、l 2与函数f (x )的图象以及l 1,y 轴与函数f (x )的图象所围成的封闭图形如阴影所示. (Ⅰ)求a 、b 、c 的值(Ⅱ)求阴影面积S 关于t 的函数S (t )的解析式;(Ⅲ)若,ln 6)(m x x g +=问是否存在实数m ,使得y=f (x )的图象与y=g (x )的图象有且只有两个不同的交点?若存在,求出m 的值;若不存在,说明理由.参考答案一.选择题:CBBA CAAA二.填空题:9、6a-;10、203x yπ-=;11、43105615C CC⋅60143=;12、4315;13、2cos6πρθ⎛⎫=-⎪⎝⎭;14、59{}64x x<<;15、三.解答题:16.解:(I)tanC=tan[π-(A+B)]=-tan(A+B)11tan tan231111tan tan123A BA B++=-=-=---⨯∵0Cπ<<,∴34Cπ=……………………5分(II)∵0<tanB<tanA,∴A、B均为锐角, 则B<A,又C为钝角,∴最短边为b ,最长边长为c……………………7分由1tan3B=,解得sin B=……………………9分由sin sinb cB C=,∴1sinsinc BbC⋅===………………12分17.解:(I)“油罐被引爆”的事件为事件A,其对立事件为A,则P(A)=C5415313132⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛…………4分∴P(A)=1-2432323131325415=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛∙C答:油罐被引爆的概率为232243 (6)分(II)射击次数ξ的可能取值为2,3,4,5,…………7分P(ξ=2)=94322=⎪⎭⎫⎝⎛,P(ξ=3)=C27832313212=...,P(ξ=4)=C274323132213=⎪⎭⎫⎝⎛..,P(ξ=5)=C913131324314=⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛.…………10分故ξ的分布列为:E ξ=2×94+3×278+4×274+5×91=2779 …………12分 18.解(Ⅰ)当n = 1时,21111113,424a s a a ==+-解出a 1 = 3 , …………1分又4s n = a n 2 + 2a n -3①当2n ≥时 4s n -1 = 21-n a + 2a n-1-3②①-② 221142()n n n n n a a a a a --=-+-, 即0)(21212=+----n n n n a a a a …………3分∴)2)((11=--+--n n n n a a a a ,2011=-∴>+--n n n n a a a a (2≥n )…………5分}{n a 数列∴是以3为首项,2为公差的等差数列12)1(23+=-+=∴n n a n …………7分(Ⅱ)123252(21)2n n T n =⨯+⨯+++⋅③又23123252(21)2(21)2n n n T n n +=⨯+⨯+-⋅++④ …………9 分④-③ 13212)12()222(223++++++-⨯-=n n n n T …………11分112)12(2286++⋅++⨯-+-=n n n …………13分22)12(1+-=+n n …………14分19. 解:(I )由题意得(100-x )·3000·(1+2x%)≥100×3000,即x 2-50x ≤0,解得0≤x≤50, ……………………4分 又∵x >0 ∴0<x≤50; ……………………6分 (II )设这100万农民的人均年收入为y 元,则y= (100-x )×3000×(1+2x %)+3000ax 100 = -60x 2+3000(a +1)x +300000100=-35[x -25(a +1)]2+3000+475(a +1)2 (0<x ≤50) ………………9分(i )当0<25(a +1)≤50,即0<a ≤1,当x=25(a +1)时,y 最大; ………………11分(ii )当25(a +1)>50,即a >1,函数y 在(0,50]单调递增,∴当x=50时,y 取最大值。
…………13分答:在0<a ≤1时,安排25(a +1)万人进入企业工作,在a >1时安排50万人进入企业工作,才能使这100万人的人均年收入最大 ………………14分20.解证:(I )易得22')(a bx ax x f -+=…………………………………………1分)(,21x f x x 是 的两个极值点,0)(,'21=∴x f x x 是的两个实根,又a >0abx x a x x -=+<-=2121,0……………………………………………………3分∴1212||||||x x x x +=-∵2||||21=+x x , )1(44444232222a a a a b a a b -=-==+∴,即1002≤<∴≥a b ……………………………………………7分(Ⅱ)设,44)(322a a a g b -==则)32(4128)(2'a a a a a g -=-= 由''22()0,0,()0133g a a g a a ><<<<≤得由得 ………………10分 ∴()g a 在2(0,)3上单调递增;在2(,1)3上单调递减………………12 分 ∴23x =时,()g a 取得极大值也是最大值 max 216[()]()327g a g ∴==,b ∴≤14分 22.(本小题满分14分)解:(I )由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16则220188080416,4c a a b c b c ac b a⎧⎪==-⎧⎪⎪⋅+⋅+==⎨⎨=⎪-⎪⎩=⎪⎩解之得:, ∴函数f (x )的解析式为x x x f 8)(2+-=…………………………4分(Ⅱ)由⎪⎩⎪⎨⎧+-=+-=xx y t t y 8822得,8,,0)8(8212t x t x t t x x -==∴=---∵0≤t ≤2,∴直线l 1与f (x )的图象的交点坐标为()8,2t t t +-…………………………6分由定积分的几何意义知:222220()[(8)(8)][(8)(8]t tS t t t x x dx x x t t dx =-+--++-+--+⎰⎰23322220[(8)(4)][(4)(8)]33ttx x t t x x x t t x =-+--++-+--+⋅32440101633t t t =-+-+………………………………9分(Ⅲ)令.ln 68)()()(2m x x x x f x g x ++-=-=ϕ因为x >0,要使函数f (x )与函数g (x )有且仅有2个不同的交点,则函数m x x x x ++-=ln 68)(2ϕ的图象与x 轴的正半轴有且只有两个不同的交点)0()3)(1(2682682)(2'>--=+-=+-=∴x xx x x x x x x x ϕ∴x=1或x=3时,0)('=x ϕ当x ∈(0,1)时,)(,0)('x x ϕϕ>是增函数; 当x ∈(1,3)时,)(,0)('x x ϕϕ<是减函数 当x ∈(3,+∞)时,)(,0)('x x ϕϕ>是增函数∴;7)1()(-=m x ϕϕ极大值为153ln 6)3()(-+=m x ϕϕ极小值为……………12分 又因为当x →0时,-∞→)(x ϕ;当+∞→+∞→)(x x ϕ时,所以要使0)(=x ϕ有且仅有两个不同的正根,必须且只须⎩⎨⎧>=⎩⎨⎧<=0)1(0)3(0)3(0)1('ϕϕϕϕ或 即⎩⎨⎧>-=-+⎩⎨⎧<-+=-070153ln 60153ln 607m m m m 或, ∴m=7或.3ln 615-=m ∴当m=7或.3ln 615-=m 时,函数f (x )与g (x )的图象有且只有两个不同交点。
