通用版2017届高三数学二轮复习第一部分重点保分专题检测(四)空间几何体的三视图表面积与体积文
高考数学二轮复习学案:第二部分专项二专题四1第1讲空间几何体的三视图、表面积与体积含答案
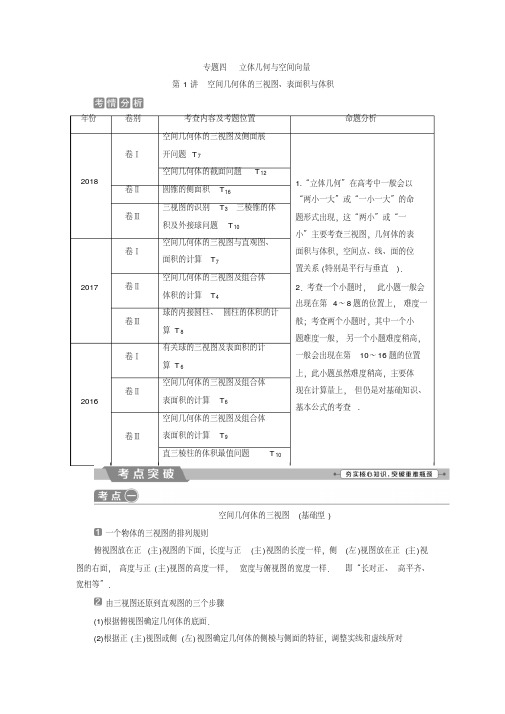
27 A. 2 π
27 3 B. 2 π
C.27 3π
D .27π
【 解析 】 因为三棱锥 P-ABC 中,△ ABC 为等边三角形, PA=PB
=PC =3,所以 △ PAB≌△ PBC ≌△ PAC .因为 PA⊥ PB,所以 PA⊥PC,
PC⊥ PB.以 PA,PB ,PC 为过同一顶点的三条棱作正方体 (如图所示 ), 则正方体的外接球同时也是三棱锥 P-ABC 的外接球.因为正方体的体
专题四 立体几何与空间向量 第 1 讲 空间几何体的三视图、表面积与体积
年份 2018 2017 2016
卷别 卷Ⅰ 卷Ⅱ 卷Ⅲ 卷Ⅰ 卷Ⅱ 卷Ⅲ 卷Ⅰ 卷Ⅱ
卷Ⅲ
考查内容及考题位置 空间几何体的三视图及侧面展 开问题 ·T 7 空间几何体的截面问题 ·T 12 圆锥的侧面积 ·T16 三视图的识别 ·T3 三棱锥的体 积及外接球问题 ·T 10 空间几何体的三视图与直观图、 面积的计算 ·T7 空间几何体的三视图及组合体 体积的计算 ·T4 球的内接圆柱、 圆柱的体积的计 算 ·T 8 有关球的三视图及表面积的计 算 ·T 6 空间几何体的三视图及组合体 表面积的计算 ·T6 空间几何体的三视图及组合体 表面积的计算 ·T9 直三棱柱的体积最值问题· T 10
3
3
6
S=
4πr 2=
2
π 3
.故选
C.
【 答案 】 C
求解多面体的内切球的问题, 一般是将多面体分割为以球心为顶点, 面的棱锥,利用多面体的体积等于各棱锥的体积之和求内切球的半径.
命题角度三 与球有关的最值问题
多面体的各面为底
(2018 ·高考全国卷 Ⅲ )设 A,B,C,D 是同一个半径为 4 的球的球面上四点, △ ABC
2017高考数学(理)(新课标版)考前冲刺复习讲义:第2部分专题4第1讲空间几何体含答案

第1讲空间几何体空间几何体的三视图自主练透夯实双基1.一个物体的三视图的排列规则俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.2.由三视图还原几何体的步骤一般先由俯视图确定底面,再利用正视图与侧视图确定几何体.[题组通关]1.(2016·高考天津卷)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为()B [解析] 由几何体的正视图和俯视图可知该几何体为图①,故其侧(左)视图为图②。
2.已知长方体的底面是边长为1的正方形,高为错误!,其俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,则该长方体的正视图的面积等于()A.1 B。
错误!C.2 D.2错误!C [解析]依题意得,题中的长方体的侧视图的高等于错误!,正视图的长是2,因此相应的正视图的面积等于错误!×错误!=2,故选C.由三视图还原到直观图的思路(1)根据俯视图确定几何体的底面.(2)根据正(主)视图或侧(左)视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.(3)确定几何体的直观图形状.空间几何体的表面积与体积高频考点多维探明1.柱体、锥体、台体的侧面积公式(1)S柱侧=ch(c为底面周长,h为高);(2)S锥侧=错误!ch′(c为底面周长,h′为斜高);(3)S台侧=错误!(c+c′)h′(c′,c分别为上下底面的周长,h′为斜高).2.柱体、锥体、台体的体积公式(1)V柱体=Sh(S为底面面积,h为高);(2)V锥体=错误!Sh(S为底面面积,h为高);(3)V台=错误!(S+错误!+S′)h(S,S′分别为上下底面面积,h为高)(不要求记忆).由空间几何体的结构特征计算表面积与体积如图,在棱长为6的正方体ABCD。
2017届高三数学高考二轮复习(书讲解课件)第一部分 专题四 第一讲 空间几何体
第十四页,编辑于星期六:一点 十七分。
第一讲 空间几何体
考点一 空间几何体与三视图
课前自主诊断 课堂对点补短 限时规范训练 上页 下页
考点一 考点二
考点三
[经典结论·全通关] 一个物体的三视图的排列规则 俯视图放在正视图的下面,长度与正视图的长度一样,侧视图放 在正视图的右面,高度与正视图的高度一样,宽度与俯视图的宽 度一样.即“长对正、高平齐、宽相等”.
=BC2,所以 AB⊥AC,所以 AB⊥平面 CC1A1A.
过点 B1 作平行于平面 ABC 的平面分割几何体,则该几何体的体
积 V=VABC-EB1F+VB1-FEA1C1=12×3×4×2+13×4×3
×3=24.
第二十七页,编辑于星期六:一点 十七分。
第一讲 空间几何体
课前自主诊断 课堂对点补短 限时规范训练
考点二
试题
通解
根据三视图可得该几何体的直观图如图中几
上页 下页
优解
考点一 考点二
考点三
何体 A1ABB1C1C 所示,且 AA1,BB1,CC1 都与平面 ABC 垂直,所以平面 AA1B1B,平 面 BB1C1C,平面 CC1A1A 都与平面 ABC 垂 直,又 AB2+AC2=BC2,所以 AB⊥AC,所 以 AB⊥平面 CC1A1A.连接 AB1,CB1 分割几何体,则该几何体的 体积 V=VB1-ABC+VB1-CAA1C1=13×2×12×3×4+13
A.4π
B.92π
C.6π
D.323π
第十二页,编辑于星期六:一点 十七分。
第一讲 空间几何体
考点三
课前自主诊断
课堂对点补短
限时规范训练 上页 下页
试题 解析
《三维设计》2017届高三数学(理)二轮复习(通用版)第一部分拉分题压轴专题(一)选择题第12题、填空题第

压轴专题(一) 选择题第12题、填空题第16题抢分练一、选择题1.(2016·山东高考)若函数y =f (x )的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y =f (x )具有T 性质,下列函数中具有T 性质的是( )A .y =sin xB .y =ln xC .y =e xD .y =x 32.设数列{a n }的前n 项和为S n ,且a 1=a 2=1,{nS n +(n +2)a n }为等差数列,则a n =( )A.n2n -1 B.n +12n -1+1C.2n -12n -1D.n +12n +13.已知变量x ,y 满足约束条件⎩⎨⎧x +2y ≥1,x -y ≤1,y -1≤0,若z =x -2y 的最大值与最小值分别为a ,b ,且方程x 2-kx +1=0在区间(b ,a )上有两个不同实数解,则实数k 的取值范围是( )A .(-6,-2)B .(-3,2) C.⎝ ⎛⎭⎪⎫-103,-2 D.⎝ ⎛⎭⎪⎫-103,-3 4.(2016·海口调研)在平面直角坐标系xOy 中,点P 为椭圆C :y 2a 2+x 2b 2=1(a >b >0)的下顶点,M ,N 在椭圆上,若四边形OPMN 为平行四边形,α为直线ON 的倾斜角,α∈⎝ ⎛⎦⎥⎤π6,π4,则椭圆C 的离心率的取值范围为( )A.⎝ ⎛⎦⎥⎤0,63B.⎝ ⎛⎦⎥⎤0,32C.⎣⎢⎡⎦⎥⎤63,32 D.⎣⎢⎡⎦⎥⎤63,223 5.(2016·石家庄质检)已知定义在(0,2]上的函数f (x )=⎩⎪⎨⎪⎧1x-3,x ∈(0,1],2x -1-1,x ∈(1,2],且g (x )=f (x )-mx 在(0,2]内有且仅有两个不同的零点,则实数m 的取值范围是( )A.⎝ ⎛⎦⎥⎤-94,-2∪⎝ ⎛⎦⎥⎤0,12B.⎝ ⎛⎦⎥⎤-114,-2∪⎝ ⎛⎦⎥⎤0,12 C.⎝ ⎛⎦⎥⎤-94,-2∪⎝ ⎛⎦⎥⎤0,23 D.⎝ ⎛⎦⎥⎤-114,-2∪⎝ ⎛⎦⎥⎤0,23 6.(2016·重庆模拟)设D ,E 分别为线段AB ,AC 的中点,且=0,记α为的夹角,则下述判断正确的是( ) A .cos α的最小值为22 B .cos α的最小值为13 C .sin ⎝ ⎛⎭⎪⎫2α+π2的最小值为825D .sin ⎝ ⎛⎭⎪⎫π2-2α的最小值为7257.(2016·浙江高考)已知实数a ,b ,c ,( ) A .若|a 2+b +c |+|a +b 2+c |≤1,则a 2+b 2+c 2<100 B .若|a 2+b +c |+|a 2+b -c |≤1,则a 2+b 2+c 2<100 C .若|a +b +c 2|+|a +b -c 2|≤1,则a 2+b 2+c 2<100 D .若|a 2+b +c |+|a +b 2-c |≤1,则a 2+b 2+c 2<1008.(2016·全国乙卷)已知函数f (x )=sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝ ⎛⎭⎪⎫π18,5π36上单调,则ω的最大值为( )A .11B .9C .7D .59.(2016·沈阳质检)已知函数y =x 2的图象在点(x 0,x 20)处的切线为l ,若l 也与函数y =ln x ,x ∈(0,1)的图象相切,则x 0必满足( )A .0<x 0<12 B.12<x 0<1 C.22<x 0< 2 D.2<x 0< 310.(2016·东北四市联考)已知在区间[-4,4]上f (x )=⎩⎪⎨⎪⎧log 2(x +5)+43(x +1),-4≤x ≤-1,2|x -1|-2,-1<x ≤4,g (x )=-18x 2-x +2(-4≤x ≤4),给出下列四个命题:①函数y =f [g (x )]有三个零点; ②函数y =g [f (x )]有三个零点; ③函数y =f [f (x )]有六个零点; ④函数y =g [g (x )]有且只有一个零点. 其中正确命题的个数是( ) A .1 B .2 C .3 D .4 二、填空题11.(2016·南昌模拟)正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C 间的距离为2,此时四面体ABCD 外接球的表面积为________.12.(2016·合肥质检)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且b =1,c =2,∠C =60°,若D 是边BC 上一点且∠B =∠DAC ,则AD =________.13.(2016·全国丙卷)已知直线l :mx +y +3m -3=0与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别作l 的垂线与x 轴交于C ,D 两点.若|AB |=23,则|CD |=________.14.(2016·石家庄二模)已知向量a ,b ,c 满足|a |=2,|b |=a ·b =3,若(c -2a )·(2b -3c )=0, 则|b -c |的最大值是________.15.(2016·浙江高考)如图,在△ABC 中,AB =BC =2,∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD =DA ,PB =BA ,则四面体PBCD 的体积的最大值是________.16.设函数f (x )=(x -2)2(x +b )e x ,若x =2是f (x )的一个极大值点,则实数b 的取值范围为________.17.(2016·广州模拟)已知函数f (x )=⎩⎨⎧1-|x +1|,x <1,x 2-4x +2,x ≥1,则函数g (x )=2|x |f (x )-2的零点个数为________.18.(2016·安徽十校联考)已知S n 为数列{a n }的前n 项和,a 1=1,2S n =(n +1)a n ,若存在唯一的正整数n 使得不等式a 2n -ta n -2t 2≤0成立,则实数t 的取值范围为________.19.(2016·兰州模拟)已知F 1,F 2为双曲线x 216-y 2=1的左、右焦点,点P i (x i ,0)与点P ′i (x ′i ,0)(i =1,2,3,…,10)满足=0,且x i <-4,过P i 作x 轴的垂线交双曲线的上半部分于Q i 点,过P′i 作x 轴的垂线交双曲线的上半部分于O′i 点,若|F 1Q 1|+| F 1Q 2|+…+| F 1Q 10|=m ,则| F 1Q ′1|+| F 1Q ′2|+…+| F 1Q ′10|=________.20.(2016·河南八市联考)如图放置的边长为1的正方形P ABC 沿x 轴滚动,点B 恰好经过原点.设顶点P (x ,y )的轨迹方程是y =f (x ),则对函数y =f (x )有下列判断:①函数y =f (x )是偶函数;②对任意的x ∈R 都有f (x +2)=f (x -2);③函数y =f (x )在区间[2,3]上单调递减;④⎠⎛02f (x )d x =π+12.其中判断正确的序号是________.答 案一、选择题1.解析:选A 若y =f (x )的图象上存在两点(x 1,f (x 1)),(x 2,f (x 2)),使得函数图象在这两点处的切线互相垂直,则f ′(x 1)·f ′(x 2)=-1.对于A :y ′=cos x ,若有cos x 1·cos x 2=-1,则存在x 1=2k π(k ∈Z ),x 2=2k π+π(k ∈Z )时,结论成立;对于B :y ′=1x ,若有1x 1·1x 2=-1,即x 1x 2=-1,∵x >0,∴不存在x 1,x 2,使得x 1x 2=-1;对于C :y ′=e x ,若有e x 1·e x 2=-1,即e x 1+x 2=-1,显然不存在这样的x 1,x 2;对于D :y ′=3x 2,若有3x 21·3x 22=-1,即9x 21x 22=-1,显然不存在这样的x 1,x 2.综上所述,选A.2.解析:选A 设b n =nS n +(n +2)a n ,则b 1=4,b 2=8,又{b n }为等差数列,所以b n =4n ,所以nS n +(n +2)a n =4n ,所以S n +⎝ ⎛⎭⎪⎫1+2n a n =4.当n ≥2时,S n -S n -1+⎝ ⎛⎭⎪⎫1+2n a n -⎝ ⎛⎭⎪⎫1+2n -1a n -1=0,所以2(n +1)n a n =n +1n -1a n-1,即2·a n n =a n -1n -1,又因为a 11=1.所以⎩⎨⎧⎭⎬⎫a n n 是首项为1,公比为12的等比数列,所以a nn =⎝ ⎛⎭⎪⎫12n -1(n ∈N *),所以a n =n 2n -1(n ∈N *),故选A. 3.解析:选C 作出可行域,如图所示,则目标函数z =x -2y 在点(1,0)处取得最大值1,在点(-1,1)处取得最小值-3,∴a =1,b =-3,从而可知方程x 2-kx +1=0在区间(-3,1)上有两个不同实数解.令f (x )=x 2-kx +1,则⎩⎪⎨⎪⎧f (-3)>0,f (1)>0,-3<k2<1,Δ=k 2-4>0⇒-103<k <-2,故选C.4.解析:选A 因为OP 在y 轴上,在平行四边形OPMN 中,MN ∥OP ,因此M ,N 的横坐标相等,纵坐标互为相反数,即M ,N 关于x 轴对称,|MN |=|OP |=a ,可设M (x ,-y 0),N (x ,y 0),∴y 0=a 2.把点N 的坐标代入椭圆方程得|x |=32b ,点N ⎝ ⎛⎭⎪⎫32b ,a 2.因为α是直线ON 的倾斜角,因此tan α=a 2÷32b =a 3b .又α∈⎝ ⎛⎦⎥⎤π6,π4,因此33<tan α≤1,33<a 3 b ≤1,即33≤b a <1,13≤b 2a 2<1,e =1-⎝ ⎛⎭⎪⎫b a 2∈⎝ ⎛⎦⎥⎤0,63,选A.5.解析:选A 由函数g (x )=f (x )-mx 在(0,2]内有且仅有两个不同的零点,得y =f (x ),y =mx 在(0,2]内的图象有且仅有两个不同的交点.当y =mx 与y =1x -3,x ∈(0,1]相切时,mx 2+3x -1=0,Δ=9+4m =0,m =-94,由图可得当-94<m ≤-2或0<m ≤12时,函数g (x )=f (x )-mx 在(0,2]内有且仅有两个不同的零点,选项A 正确.6.7.解析:选D 对于A ,取a =b =10,c =-110, 显然|a 2+b +c |+|a +b 2+c |≤1成立,但a 2+b 2+c 2>100,即a 2+b 2+c 2<100不成立. 对于B ,取a 2=10,b =-10,c =0, 显然|a 2+b +c |+|a 2+b -c |≤1成立,但a 2+b 2+c 2=110,即a 2+b 2+c 2<100不成立. 对于C ,取a =10,b =-10,c =0, 显然|a +b +c 2|+|a +b -c 2|≤1成立,但a 2+b 2+c 2=200,即a 2+b 2+c 2<100不成立. 综上知,A 、B 、C 均不成立,所以选D.8.解析:选B由题意得⎩⎨⎧-π4ω+φ=k 1π,k 1∈Z ,π4ω+φ=k 2π+π2,k 2∈Z ,则ω=2k +1,k ∈Z ,φ=π4或φ=-π4.若ω=11,则φ=-π4,此时f (x )=sin(11x -π4),f (x )在区间⎝ ⎛⎭⎪⎫π18,3π44上单调递增,在区间⎝ ⎛⎭⎪⎫3π44,5π36上单调递减,不满足f (x )在区间⎝ ⎛⎭⎪⎫π18,5π36上单调;若ω=9,则φ=π4,此时f (x )=sin ⎝ ⎛⎭⎪⎫9x +π4,满足f (x )在区间⎝ ⎛⎭⎪⎫π18,5π36上单调递减,故选B.9.解析:选D 由题令f (x )=x 2,f ′(x )=2x ,f (x 0)=x 20,所以直线l 的方程为y=2x 0(x -x 0)+x 20=2x 0x -x 20,因为l 也与函数y =ln x (x ∈(0,1))的图象相切,令切点坐标为(x 1,ln x 1),y ′=1x ,所以l 的方程为y =1x 1x +ln x 1-1,这样有⎩⎨⎧2x 0=1x 1,1-ln x 1=x 20,所以1+ln 2x 0=x 20,x 0∈(1,+∞).令g (x )=x 2-ln 2x -1,x ∈(1,+∞),显然该函数的零点就是x 0,又因为g ′(x )=2x -1x =2x 2-1x ,所以g (x )在(1,+∞)上单调递增,又g (1)=-ln 2<0,g (2)=1-ln 22<0,g (3)=2-ln 23>0,从而2<x 0<3,选D.10.解析:选D 如图,画出函数f (x ),g (x )的草图,①设t=g(x),则由f[g(x)]=0,得f(t)=0,则t=g(x)有三个不同值,且这三个值都在g(x)的值域内,由于y=g(x)是减函数,所以f[g(x)]=0有3个解,所以①正确;②设m=f(x),若g[f(x)]=0,即g(m)=0,则m=x0∈(1,2),所以f(x)=x0∈(1,2),由图象知对应f(x)=x0∈(1,2)的解有3个,所以②正确;③设n=f(x),若f[f(x)]=0,即f(n)=0,n=x1∈(-3,-2)或n=0或n=x2=2,而f(x)=x1∈(-3,-2)有1个解,f(x)=0对应有3个解,f(x)=x2=2对应有2个解,所以f[f(x)]=0共有6个解,所以③正确;④设s=g(x),若g[g(x)]=0,即g(s)=0,所以s=x3∈(1,2),则g(x)=x3,因为y=g(x)是减函数,所以方程g(x)=x3只有1个解,所以④正确.二、填空题11.解析:由题知,求四面体ABCD的外接球的表面积可转化为求长、宽、高分别为1、1、3的长方体的外接球的表面积,其半径R=1212+12+(3)2=52,所以S=4πR2=5π.答案:5π12.解析:在△ABC中,由正弦定理可得bsin ∠B=csin ∠C,sin ∠B=b sin ∠Cc=34,且∠B<∠C,则∠B为锐角,cos ∠B=134.在△ADC中,由正弦定理得ADsin ∠C=b sin ∠ADC=bsin (∠DAC +60°)=bsin (∠B +60°),则AD =b sin ∠C sin (∠B +60°)=3234×12+134×32=13-13.答案:13-1313.解析:由直线l :mx +y +3m -3=0知其过定点(-3,3),圆心O 到直线l 的距离为d =|3m -3|m 2+1.由|AB |=23得⎝ ⎛⎭⎪⎪⎫3m -3m 2+12+(3)2=12,解得m =-33.又直线l 的斜率为-m =33,所以直线l 的倾斜角α=π6.画出符合题意的图形如图所示,过点C 作CE ⊥BD ,则∠DCE =π6.在Rt △CDE 中,可得|CD |=|AB|cos π6=23×23=4.答案:414.解析:设a 与b 的夹角为θ,则a ·b =|a ||b |cos θ, ∴cos θ=a ·b |a ||b |=32×3=22, ∵θ∈[0,π],∴θ=π4. 设=a ,=b ,c =(x ,y ),建立如图所示的平面直角坐标系.则A (1,1),B (3,0),∴c -2a =(x -2,y -2),2b -3c =(6-3x ,-3y ), ∵(c -2a )·(2b -3c )=0,∴(x -2)·(6-3x )+(y -2)·(-3y )=0. 即(x -2)2+(y -1)2=1. 又知b -c =(3-x ,-y ), ∴|b -c |=(x -3)2+y 2≤(3-2)2+(0-1)2+1=2+1,即|b -c |的最大值为2+1. 答案:2+115.解析:在△ABC 中,AB =BC =2,∠ABC =120°, ∴AC =22+22-2×2×2×⎝ ⎛⎭⎪⎫-12=2 3.设CD =x ,则AD =23-x ,∴PD =23-x , ∴V P BCD =13S △BCD ·h ≤13×12BC ·CD ·sin 30°·PD =16x (23-x )≤16⎝⎛⎭⎪⎫x +23-x 22=16×⎝⎛⎭⎪⎫2322=12, 当且仅当x =23-x ,即x =3时取“=”, 此时PD =3,BD =1,PB =2,满足题意. 故四面体PBCD 的体积的最大值为12. 答案:1216.解析:由条件得,f (x )=[x 3+(b -4)x 2+(4-4b )x +4b ]e x ,则f ′(x )=[x 3+(b -1)x 2+(-4-2b )x +4]e x ,易知f ′(2)=0恒成立,满足题意.记g (x )=x 3+(b -1)x 2+(-4-2b )x +4,则g ′(x )=3x 2+2(b -1)x +(-4-2b ),又x =2是f (x )的一个极大值点,所以g ′(2)<0,所以2b +4<0,解得b <-2.答案:(-∞,-2)17.解析:由g (x )=2|x |f (x )-2=0得f (x )=⎝ ⎛⎭⎪⎫12|x |-1,作出y =f (x ),y =⎝ ⎛⎭⎪⎫12|x |-1的图象,由图象可知共有2个交点,故函数的零点个数为2.答案:218.解析:n ≥2时,a n =S n -S n -1=(n +1)a n 2-na n -12, 整理得a n n =a n -1n -1,又a 1=1,故a n =n , 不等式a 2n -ta n -2t 2≤0可化为n 2-tn -2t 2≤0,设f (n )=n 2-tn -2t 2,由于f (0)=-2t 2≤0,由题意可得⎩⎪⎨⎪⎧f (1)=1-t -2t 2≤0,f (2)=4-2t -2t 2>0,解得-2<t ≤-1或12≤t <1.答案:(-2,-1]∪⎣⎢⎡⎭⎪⎫12,1 19.解析:因为=0,所以点P i ,P ′i 关于坐标原点对称,又由题可知| F 1Q i |=| F 2Q ′i |,因为| F 1Q 1|+| F 1 Q 2|+…+| F 1 Q 10|=m ,根据双曲线定义可知,| F 1 Q ′i |-| F 2 Q ′i |=2a =8,所以| F 1 Q ′1|+| F 1 Q ′2|+…+| F 1 Q ′10|=(8+| F 1 Q 1|)+(8+| F 1 Q 2|)+…+(8+| F 1 Q 10|)=80+m .答案:80+m20. 解析:从函数y=f(x)的图象可以判断出,图象关于y轴对称,每4个单位图象重复出现一次,且在区间[2,3]上随x增大,图象是往上的,所以①②正确,③错误;又函数图象与直线x=0,x=2,x轴围成的图形由一个半径为2、圆心角为π4的扇形,一个半径为1、圆心角为π2的扇形和一个直角边长为1的等腰直角三角形组成,其面积S=18×π×2+14×π+12=π+12,④正确.答案:①②④。
全国通用2017年高考数学大二轮专题温习第二编专题整合冲破专题五立体几何第一讲空间几何体的三视图表面

专题五立体几何第一讲空间几何体的三视图、表面积与体积适考素能特训理一、选择题1.在一个几何体的三视图中,正视图和俯视图如下图,那么相应的侧视图能够为( )答案D解析由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如下图,可知侧视图为等腰三角形,且轮廓线为实线,应选D.2.[2016·重庆测试]某几何体的三视图如下图,那么该几何体的体积为( )A.23B.43C.53D.73答案B解析依题意,题中的几何体是由一个直三棱柱与一个三棱锥所组成的,其中该直三棱柱的底面是一个直角三角形(腰长别离为一、2)、高为1;该三棱锥的底面是一个直角三角形(腰长别离为一、2)、高为1,因此该几何体的体积为12×2×1×1+13×12×2×1×1=43,选B.3.[2016·唐山统考]三棱锥P-ABC中,PA⊥平面ABC且PA=2,△ABC是边长为3的等边三角形,那么该三棱锥外接球的表面积为( )A.4π3B.4πC.8πD.20π答案 C解析 由题意得,此三棱锥外接球即为以△ABC 为底面、以PA 为高的正三棱柱的外接球,因为△ABC 的外接圆半径r =32×3×23=1,外接球球心到△ABC 的外接圆圆心的距离d =1,所之外接球的半径R =r 2+d 2=2,因此三棱锥外接球的表面积S =4πR 2=8π,应选C .4.[2016·武昌调研]某几何体的三视图如下图,那么该几何体的表面积为( )A .18+2πB .20+πC .20+π2D .16+π答案 B 解析 由三视图可知,那个几何体是一个边长为2的正方体割去了相对边对应的两个半径为一、高为1的14圆柱体,其表面积相当于正方体五个面的面积与两个14圆柱的侧面积的和,即该几何体的表面积S =4×5+2×2π×1×1×14=20+π,应选B . 5.[2016·陕西质检]某几何体的三视图如下图,该几何体的体积为( )A .43B .52C .73D .3 答案 A 解析 依照几何体的三视图,得该几何体是下部为直三棱柱,上部为三棱锥的组合体,如下图.那么该几何体的体积是V 几何体=V 三棱柱+V 三棱锥=12×2×1×1+13×12×2×1×1=43.故应选A .6.已知边长为1的等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C -AB -D 的余弦值为33,假设A 、B 、C 、D 、E 在同一球面上,那么此球的体积为( ) A .2πB .823πC .2πD .23π 答案 D 解析 如图,取AB 的中点为M ,连接CM ,取DE 的中点为N ,连接MN ,CN ,可知∠CMN 即为二面角C -AB -D 的平面角,利用余弦定理可求CN =32=CM ,因此该几何体为正四棱锥,半径R =22,V =43πR 3=2π3,应选D .二、填空题7.[2016·广西南宁检测]设甲、乙两个圆柱的底面积别离为S 1、S 2,体积别离为V 1、V 2.假设它们的侧面积相等且V 1V 2=32,那么S 1S 2的值是________. 答案 94解析 设甲、乙两个圆柱的底面半径别离为r 1,r 2,高别离为h 1,h 2,那么有2πr 1h 1=2πr 2h 2,即r 1h 1=r 2h 2,又V 1V 2=πr 21h 1πr 22h 2,∴V 1V 2=r 1r 2,∴r 1r 2=32,那么S 1S 2=⎝ ⎛⎭⎪⎫r 1r 22=94. 8.[2016·山西太原一模]已知在直角梯形ABCD 中,AB⊥AD,CD⊥AD,AB =2AD =2CD =2,将直角梯形ABCD 沿AC 折叠成三棱锥D -ABC ,当三棱锥D -ABC 的体积取最大值时,其外接球的体积为________.答案 43π 解析 当平面DAC⊥平面ABC 时,三棱锥D -ABC 的体积取最大值.现在易知BC⊥平面DAC ,∴BC⊥AD,又AD⊥DC,∴AD⊥平面BCD ,∴AD⊥BD,取AB 的中点O ,易患OA =OB =OC=OD =1,故O 为所求外接球的球心,故半径r =1,体积V =43πr 3=43π. 9.[2016·云南玉溪一模]表面积为60π的球面上有四点S 、A 、B 、C ,且△ABC 是等边三角形,球心O 到平面ABC 的距离为3,假设平面SAB⊥平面ABC ,那么三棱锥S -ABC 体积的最大值为________.答案 27解析 设球O 的半径为R ,那么有4πR 2=60π,解得R =15.由于平面SAB⊥平面ABC ,因此点S 在平面ABC 上的射影D 在AB 上,如图,当球心O 在三棱锥S -ABC 中,且D 为AB 的中点时,SD 最大,三棱锥S -ABC 的体积最大.设O′为等边三角形ABC 的中心,那么OO′⊥平面ABC ,即有OO′∥SD.由于OC =15,OO′=3,那么CO′=CO 2-OO′2=23,那么DO′=3,那么△ABC 是边长为6的等边三角形,那么△ABC 的面积为12×6×33=9 3.在直角梯形SDO′O 中,作OM⊥SD 于M ,那么OM =DO′=3,DM =OO′=3,∴SD=DM +MS=3+152-32=33,因此三棱锥S -ABC 体积的最大值为13×93×33=27. 三、解答题10.[2016·达州一模]已知几何体A -BCED 的三视图如下图,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A -BCED 的体积为16.(1)求实数a 的值;(2)将直角三角形△ABD 绕斜边AD 旋转一周,求该旋转体的表面积.解 (1)由该几何体的三视图知AC⊥平面BCED ,且EC =BC =AC =4,BD =a ,体积V =13×4×a +4×42=16,因此a =2. (2)在Rt △ABD 中,AB =42,BD =2,因此AD =6,过点B 作AD 的垂线BH ,垂足为点H ,易患BH =423, 该旋转体由两个同底的圆锥组成,圆锥底面半径为BH =423. 因此圆锥底面周长为c =2π·423=82π3,两个圆锥的母线长别离为42和2,故该旋转体的表面积为S =12×82π3(2+42)=32π+82π3. 11.[2016·河北五校联盟质检] 如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD ,Q 为AD 的中点,PA =PD =2,BC =12AD =1,CD =3,M 是棱PC 的中点.(1)求证:PA∥平面MQB ;(2)求三棱锥P -DQM 的体积.解 (1)证明:连接AC ,交BQ 于点N ,连接MN ,CQ ,∵BC∥AD 且BC =12AD , 即BC∥AQ,BC =AQ ,∴四边形BCQA 为平行四边形,且N 为AC 的中点,又点M 是棱PC 的中点,∴MN∥PA,又∵PA ⊄平面MQB ,MN ⊂平面MQB ,那么PA∥平面MQB.(2)连接DM ,那么V P -DQM =V M -PDQ ,∵平面PAD⊥底面ABCD ,CD⊥AD,∴CD⊥平面PAD ,∴点M 到平面PAD 的距离为12CD , ∴V P -DQM =V M -PDQ =13S △PDQ ·12CD =13·12·QD·PQ·12CD =14. 12.[2016·鹰潭二模]如图1所示,直角梯形ABCD ,∠ADC=90°,AB∥CD,AD =CD =12AB =2,点E 为AC 的中点,将△ACD 沿AC 折起,使折起后的平面ACD 与平面ABC 垂直(如图2),在图2所示的几何体D -ABC 中.(1)求证:BC⊥平面ACD ;(2)点F 在棱CD 上,且知足AD∥平面BEF ,求几何体F -BCE 的体积. 解 (1)证明:在图1中,由题意知,AC =BC =22, 因此AC 2+BC 2=AB 2,因此AC⊥BC因为E 为AC 的中点,连接DE ,那么DE⊥AC,又平面ADC⊥平面ABC ,且平面ADC∩平面ABC =AC ,DE ⊂平面ACD ,从而ED⊥平面ABC , 因此ED⊥BC又AC⊥BC,AC∩ED=E ,因此BC⊥平面ACD.(2)取DC 的中点F ,连接EF ,BF ,因为E 是AC 的中点,因此EF∥AD,又EF ⊂平面BEF ,AD ⊄平面BEF ,因此AD∥平面BEF ,由(1)知,DE 为三棱锥B -ACD 的高,因为三棱锥F -BCE 的高h =12DE =12×2=22,S △BCE =12S △ABC =12×12×22×22=2, 因此三棱锥F -BCE 的体积为:V F -BCE =13S △BCE ·h=13×2×22=23.。
2017届高三数学二轮复习(通用版)第一部分课件 重点保分题题型专题(十四) 点、直线、平面之间的位

平面图形的折叠问题 [典例] (2016·全国甲卷)如图,菱形 ABCD 的对角线 AC 与 BD 交于点 O,点 E,F 分别在 AD,CD 上,AE=CF,EF 交 BD 于点 H.将△DEF 沿 EF 折到△D′EF 的位置.
(1)证明:AC⊥HD′; (2)若 AB=5,AC=6,AE=54,OD′=2 2,求五棱锥 D′ABCFE 的体积.
图① 因为 AE=EC,D 为 AC 的中点, 所以 DE⊥AC.
第十页,编辑于星期六:一点 十四分。
同理可得 BD⊥AC. 又 BD∩DE=D, 所以 AC⊥平面 BDEF. 因为 FB⊂平面 BDEF,所以 AC⊥FB. (2)如图②,设 FC 的中点为 I,连接 GI,HI.在△CEF 中,
第二十页,编辑于星期六:一点 十四分。
[解] (1)证明:由已知得 AC⊥BD,AD=CD. 又由 AE=CF 得AADE=CCDF,故 AC∥EF. 由此得 EF⊥HD,故 EF⊥HD′,所以 AC⊥HD′. (2)由 EF∥AC 得ODHO=AADE=14. 由 AB=5,AC=6 得 DO=BO= AB2-AO2=4. 所以 OH=1,D′H=DH=3. 于是 OD′2+OH2=(2 2)2+12=9=D′H2, 故 OD′⊥OH.
第十五页,编辑于星期六:一点 十四分。
解:(1)证明:设 BD 的中点为 O,连接 AO,EO,
∵AB=AD,∴AO⊥BD. 又 E 为 BC 的中点,∴EO∥CD. ∵CD⊥BD,∴EO⊥BD. 又 OA∩OE=O,∴BD⊥平面 AOE. 又 AE⊂平面 AOE,∴AE⊥BD.
第十六页,编辑于星期六:一点 十四分。
第二十二页,编辑于星期六:一点 十四分。
2017年全国高考数学考前复习专题4.1立体几何和答案

【知识网络】【考点聚焦】对知识的考查要求依次分为了解、理解、掌握三个层次(在下表中分别用A、B、C 表示).一.空间几何体的结构、三视图及表面积与体积1.【原题】(必修2第15页练习第4题)如图是一个几何体的三视图,想象它的几何结构特征,并说出它的名称.正视图侧视图【原题解读】(1)知识上;需要明确三视图的原则即;主俯长对正,主侧高对齐,俯侧宽相等。
(2)思路方法上;需要经历由三视图对原几何体的直观想象,操作确认(由三视图画出直观图),思辨论证(由所画的直观图,再看是否能获得对应的三视图)。
(3)考察空间想象能力及推理论证能力。
变式.【2014湖北高考】在如图所示的空间直角坐标系xyzO 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C. ④和③D.④和②【答案】D【解析】设)2,2,2(2,0,0(DCBA,0,2,2(),),1,2,1(),在坐标系中标出已知的四个点,根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②,故选D.2. 【原题】(必修2第28页习题1.3第3题) 如图将一个长方体沿相邻三个面的对角线截出一个棱锥,求棱锥的体积与剩下的几何体体积的比。
【原题解读】本题以最为熟悉的几何体长方体为背景,进行截取并求体积。
可采用分解的思想,即求出长方体和三棱锥的体积,而剩下体积可减出。
从而求出体积比。
体现了基本运算能力、空间想象能力和分解与组合的思想。
变式.【2015高考新课标2】一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A .81B .71C .61D .51【答案】D3.【原题】(必修2第29习题1.3 B组1)如图是一个奖杯的三视图,是根据奖杯的三视图计算它的表面积和体积(尺寸如图,单位:cm,π取3.14,结果分别精确到1cm²,1cm³,可用计算器)。
2017届高三数学文二轮复习第一部分检测基础送分 专题检测四 空间几何体的三视图、表面积与体积 含解析 精品

专题检测(四) 空间几何体的三视图、表面积与体积一、选择题1.如图所示是一个物体的三视图,则此三视图所描述物体的直观图是( )2.(2016·广州模拟)一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的四分之一圆周和两条半径,则这个几何体的体积为( )A.312π B.36π C.34π D.33π 3.某几何体的三视图如图所示,则该几何体的体积为( )A.13+2π B.13π6 C.7π3 D.5π24.(2016·江西两市联考)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )A .2 B.92 C.32D .35.(2016·山东高考)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )A.13+23πB.13+23πC.13+26π D .1+26π 6.(2016·安徽江南十校联考)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )A .4π+16+4 3B .5π+16+4 3C .4π+16+2 3D .5π+16+2 37.(2016·昆明七校调研)一个正三棱柱被平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.15B.16C.17D.188.(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15. 9.(2016·江西赣州二模)某几何体的正视图和侧视图如图(1),它的俯视图的直观图是矩形O 1A 1B 1C 1,如图(2),其中O 1A 1=6,O 1C 1=2,则该几何体的侧面积为( )A .48B .64C .96D .12810.等腰△ABC 中,AB =AC =5,BC =6,将△ABC 沿BC 边上的高AD 折成直二面角B -AD -C ,则三棱锥B -ACD 的外接球的表面积为( )A .5π B.203π C .10π D .34π11.(2016·唐山模拟)三棱锥P-ABC 中,P A ⊥平面ABC 且P A =2,△ABC 是边长为3的等边三角形,则该三棱锥外接球的表面积为( )A.4π3B .4πC .8πD .20π 12.(2016·海口调研)一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )A.33B.17C.41D.42二、填空题13.(2016·四川高考)已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.14.如图是某空间几何体的三视图,则该几何体的体积为________.15.(2016·海口调研)半径为2的球O中有一内接正四棱柱(底面是正方形,侧棱垂直底面).当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是________.16.(2016·山西质检)某几何体的三视图如图所示,当xy取得最大值时,该几何体的体积是________.一、选择题1.解析:选D 先观察俯视图,由俯视图可知选项B 和D 中的一个正确,由正视图和侧视图可知选项D 正确.2.解析:选A 由题意可知,该几何体是14个圆锥,圆锥的底面半径是1,高是3,故该几何体的体积V =13×14×π×12×3=312π.3.解析:选B 由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体,其体积为π×12×2+12×13π×12×1=13π6.4.解析:选D 由三视图判断该几何体为四棱锥,且底面为梯形,高为x ,∴该几何体的体积V =13×12×(1+2)×2×x =3,解得x =3.5.解析:选C 由三视图知,该四棱锥是底面边长为1,高为1的正四棱锥,结合三视图可得半球半径为22,从而该几何体的体积为13×12×1+12×43π×⎝⎛⎭⎫223=13+26π.故选C.6.解析:选D 由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×12×2×3=23;半圆柱的侧面积为π×4=4π,两个底面面积之和为2×12×π×12=π,所以几何体的表面积为5π+16+23,故选D.7.解析:选A 依题意,剩余部分所表示的几何体是从正三棱柱ABC- A 1B 1C 1 (其底面边长是2)中截去三棱锥E A 1B 1C 1 (其中E 是侧棱BB 1的中点),因此三棱锥E A 1B 1C 1的体积为=13×34×22×1=33,剩余部分的体积为V =-=34×22×2-33=533,因此截去部分体积与剩余部分体积的比值为15,选A. 8.解析:选D 由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥.设正方体的棱长为1,则三棱锥的体积为V 1=13×12×1×1×1=16,剩余部分的体积V 2=13-16=56.所以V 1V 2=1656=15.9.解析:选C 由几何体的三视图可知该几何体为一个四棱柱.因为它的俯视图的直观图是矩形O 1A 1B 1C 1,其中O 1A 1=6,O 1C 1=2,所以俯视图的直观图的面积为12,由平面图形的直观图与原图形面积的关系可知俯视图的面积为242,易知俯视图是边长为6的菱形,又几何体的高为4,所以该几何体的侧面积为4×6×4=96.故选C.10.解析:选D 依题意,在三棱锥B-ACD 中,AD ,BD ,CD 两两垂直,且AD =4,BD =CD =3,因此可将三棱锥B ACD 补形成一个长方体,该长方体的长、宽、高分别为3、3、4,且其外接球的直径2R =32+32+42=34,故三棱锥B -ACD 的外接球的表面积为4πR 2=34π,选D.11.解析:选C 由题意得,此三棱锥外接球即为以△ABC 为底面,以P A 为高的正三棱柱的外接球,因为△ABC 的外接圆半径r =32×3×23=1,外接球球心到△ABC 的外接圆圆心的距离d =1,所以外接球的半径R =r 2+d 2=2,所以三棱锥外接球的表面积S =4πR 2=8π,故选C.12.解析:选C 依题意,题中的几何体是四棱锥E -ABB 1A 1,如图所示(其中ABCD -A 1B 1C 1D 1是棱长为4的正方体,C 1E =1),EA =32+42+42=41,EA 1=12+42+42=33,EB =32+42=5,EB 1=12+42=17,AB =BB 1=B 1A 1=A 1A =4,因此该几何体的最长棱的棱长为41,选C.二、填空题13.(2016·四川高考)已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.解析:由三视图可得三棱锥如图所示,则V =13×⎝⎛⎭⎫12×23×1×1=33. 答案:3314.解析:由三视图可知,该几何体是棱长为2,2,1的长方体挖去一个半径为1的半球,所以长方体的体积为2×2×1=4,半球的体积为12×43π×13=2π3,所以该几何体的体积是4-2π3.答案:4-2π315.解析:依题意,设球的内接正四棱柱的底面边长为a 、高为h ,则有16=2a 2+h 2≥22ah ,即4ah ≤162,该正四棱柱的侧面积S =4ah ≤162,当且仅当h =2a =22时取等号.因此,当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是 4π×22-162=16(π-2).答案:16(π-2)16.解析:由题意可知,该几何体为如图所示的四棱锥P -ABCD ,CD=y2,AB =y ,AC =5,CP =7,BP =x ,∴BP 2=BC 2+CP 2,即x 2=25-y 2+7,x 2+y 2=32≥2xy ,则xy ≤16,当且仅当x =y =4时,等号成立.此时该几何体的体积V =13×2+42×3×7=37.答案:37。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题检测(四) 空间几何体的三视图、表面积与体积
一、选择题
1.如图所示是一个物体的三视图,则此三视图所描述物体的直观图是( )
2.(2016·广州模拟)一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的四分之一圆周和两条半径,则这个几何体的体积为( )
A.
312π B.36π C.34π D.33
π 3.某几何体的三视图如图所示,则该几何体的体积为( )
A.13+2π
B.13π6
C.7π3
D.5π2
4.(2016·江西两市联考)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )
A .2 B.92 C.3
2
D .3
5.(2016·山东高考)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
A.13+23π
B.13+23π
C.13+26π D .1+2
6
π 6.(2016·安徽江南十校联考)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )
A .4π+16+4
3 B .5π+16+4
3
C .4π+16+2 3
D .5π+16+23
7.(2016·昆明七校调研)一个正三棱柱被平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
A.15
B.16
C.17
D.18
8.(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )
A.18
B.17
C.16
D.15
. 9.(2016·江西赣州二模)某几何体的正视图和侧视图如图(1),它的俯视图的直观图是矩形O 1A 1B 1C 1,如图(2),其中O 1A 1=6,O 1C 1=2,则该几何体的侧面积为( )
A .48
B .64
C .96
D .128
10.等腰△ABC 中,AB =AC =5,BC =6,将△ABC 沿BC 边上的高AD 折成直二面角
B AD
C ,则三棱锥B AC
D 的外接球的表面积为( )
A .5π B.20
3
π C .10π D .34π
11.(2016·唐山模拟)三棱锥PABC 中,PA ⊥平面ABC 且PA =2,△ABC 是边长为3
的等边三角形,则该三棱锥外接球的表面积为( )
A.4π
3
B .4π
C .8π
D .20π 12.(2016·海口调研)一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )
A.
33 B.
17 C.
41 D.
42
二、填空题
13.(2016·四川高考)已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.
14.如图是某空间几何体的三视图,则该几何体的体积为________.
15.(2016·海口调研)半径为2的球O中有一内接正四棱柱(底面是正方形,侧棱垂直底面).当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是________.16.(2016·山西质检)某几何体的三视图如图所示,当xy取得最大值时,该几何体的体
积是________.
一、选择题
1.解析:选D 先观察俯视图,由俯视图可知选项B 和D 中的一个正确,由正视图和侧视图可知选项D 正确.
2.解析:选A 由题意可知,该几何体是1
4个圆锥,圆锥的底面半径是1,高是
3,
故该几何体的体积V =13×1
4
×π×12×
3=312
π.
3.解析:选B 由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体,其体积为π×12×2+
12×13π×12×1=13π
6
.
4.解析:选D 由三视图判断该几何体为四棱锥,且底面为梯形,高为x ,∴该几何体的体积V =13×1
2
×(1+2)×2×x =3,解得x =3.
5.解析:选C 由三视图知,该四棱锥是底面边长为1,高为1的正四棱锥,结合三视图可得半球半径为22,从而该几何体的体积为13×12×1+12×43π×⎝ ⎛⎭⎪⎪⎫223=13+26π.故选
C.
6.解析:选D 由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×1
2
×2×
3=2
3;半圆柱
的侧面积为π×4=4π,两个底面面积之和为2×1
2×π×12=π,所以几何体的表面积为5π+
16+2
3,故选D.
7.解析:选A 依题意,剩余部分所表示的几何体是从正三棱柱ABC A 1B 1C 1 (其底面边长是2)中截去三棱锥E A 1B 1C 1 (其中E 是侧棱BB 1的中点),因此三棱锥E A 1B 1C 1的体积为
=13×34×22×1=3
3
,剩余部分的体积为V =
-
=
3 4
×22×2-
3
3
=
53
3
,因此截去部分体积与剩余部分体积的比值为
1
5
,选A.
8.解析:
选D 由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥.设正方体的棱长为1,则三棱锥的体积为V1=
1
3
×
1
2
×1×1×1=
1
6
,
剩余部分的体积V2=13-
1
6
=
5
6
.
所以
V1
V2=
1
6
5
6
=
1
5
.
9.解析:选C由几何体的三视图可知该几何体为一个四棱柱.因为它的俯视图的直观图是矩形O1A1B1C1,其中O1A1=6,O1C1=2,所以俯视图的直观图的面积为12,由平面图形的直观图与原图形面积的关系可知俯视图的面积为242,易知俯视图是边长为6的菱形,又几何体的高为4,所以该几何体的侧面积为4×6×4=96.故选C.
10.解析:选D 依题意,在三棱锥BACD中,AD,BD,CD两两垂直,且AD=4,BD=CD=3,因此可将三棱锥BACD补形成一个长方体,该长方体的长、宽、高分别为3、3、4,且其外接球的直径2R=32+32+42=34,故三棱锥BACD的外接球的表面积为4πR2=34π,选D.
11.解析:选C 由题意得,此三棱锥外接球即为以△ABC为底面,以PA为高的正三棱柱的外接球,因为△ABC的外接圆半径r=
3
2
×3×
2
3
=1,外接球球心到△ABC的外接圆圆心的距离d=1,所以外接球的半径R=r2+d2=2,所以三棱锥外接球的表面积S
=4πR 2=8π,故选C.
12.解析:选C 依题意,题中的几何体是四棱锥E ABB 1A 1,如图所示(其中ABCD A 1B 1C 1D 1是棱长为4的正方体,C 1E =1),
EA =32+42+42=41,EA 1=12+42+42=33,EB =
32+42=5,EB 1=
12+42=
17,AB =BB 1=B 1A 1=A 1A
=4,因此该几何体的最长棱的棱长为
41,选C.
二、填空题
13.(2016·四川高考)已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.
解析:由三视图可得三棱锥如图所示,则V =13×⎝ ⎛⎭
⎪
⎫12×2
3×1×1=
33
. 答案:
33
14.解析:由三视图可知,该几何体是棱长为2,2,1的长方体挖去一个半径为1的半球,所以长方体的体积为2×2×1=4,半球的体积为12×43π×13=2π
3,所以该几何体的体
积是4-2π
3
.
答案:4-2π
3
15.解析:依题意,设球的内接正四棱柱的底面边长为a 、高为h ,则有16=2a 2+h 2
≥2
2ah ,即4ah ≤16
2,该正四棱柱的侧面积S =4ah ≤16
2,当且仅当h =
2a =22
时取等号.因此,当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是 4π×22-16
2=16(π-
2).
答案:16(π-
2)
16.解析:由题意可知,该几何体为如图所示的四棱锥P ABCD ,CD =y
2
,AB =y ,AC =5,CP =
7,BP =x ,∴BP 2=BC 2+CP 2,即x 2=25
-y 2+7,x 2+y 2=32≥2xy ,则xy ≤16,当且仅当x =y =4时,等号成立.此时该几何体的体积V =13×2+42
×3×
7=3
7.
答案:37。
