统计学计算题例题
统计学计算题整理

:典型计算题一1、某地区销售某种商品的价格和销售量资料如下:根据资料计算三种规格商品的平均销售价格。
解:36==∑∑ffxx (元)点评: 第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格。
第二,所给资料是组距数列,因此需计算出组中值。
采用加权算术平均数计算平均价格。
第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算。
2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少?解:%110%105%116===计划相对数实际相对数计划完成程度。
即1992年计划完成程度为110%,超额完成计划10%。
点评:此题中的计划任务和实际完成都是“含基数”百分数,所以可以直接代入基本公式计算。
3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少?解: 计划完成程度%74.94%95%90==计划相对数实际相对数。
即92年单位成本计划完成程度是94.74%,超额完成计划5.26%。
点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少?解:计划完成程度%110%51%161=++=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少?解:计划完成程度%74.94%51%101=--=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少? 解:103%=105%÷(1+x ) x=1.9%即产值计划规定比上期增加1.9%.点评:计划完成程度=103%,实际完成相对数=105%,设产值计划规定比上期增加x ,则计划任务相对数=1+x ,根据基本关系推算出x.7、某煤矿某月计划任务为5400吨,各旬计划任务是均衡安排的,根据资料分析本月生产情况.解:从资料看,尽管超额完成了全期计划(5400=104%),但在节奏 性方面把握不好。
统计学计算题

第三章统计整理例 1、某厂工人日产量资料如下:(单位:公斤)162 158 158 163 156 157 160 162 168 160164 152 159 159 168 159 154 157 160 159163 160 158 154 156 156 156 169 163 167试根据上述资料,编制组距式变量数列,并计算出频率。
解:将原始资料按其数值大小重新排列。
152158 159154 154 156 156 156 156 157 157 158 158 159 159 159 159 160 160 160 162 162 163 163 163 164 167168 168 169最大数=169,最小数=152,全距=169-152=17n=30, 分为 6 组例 2、某企业 50 个职工的月工资资料如下:113 125 78 115 84 135 97 105 110 130105 85 88 102 101 103 107 118 103 87116 67 106 63 115 85 121 97 117 10794 115 105 145 103 97 120 130 125 127122 88 98 131 112 94 96 115 145 143试根据上述资料,将50 个职工的工资编制成等距数列,列出累计频数和累计频率。
解:将原始资料按其数值大小重新排列。
63 97 117 118工人按日产量分组(公斤)152-154155-157158-160161-163164-166 工人数(人)361151比率(频率)(%)10.0020.0036.6016.7067 78 84 85 85 87 88 88 94 94 96 97 97 98 101 102 103 103 103 105 105 105 107 110 112 113 115 115 115 115 116 118 120 121 122 125 125 127 130 130 131 135 143 145 145按工资额分组(元)60-70 70-80 80-90频数216工人数频率( %)4212频数239向上累计频率( %)4618频数504847向下累计频率(%)1009694例 3、有 27 个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3试编制分布数列。
统计学计算题例题
第四章1。
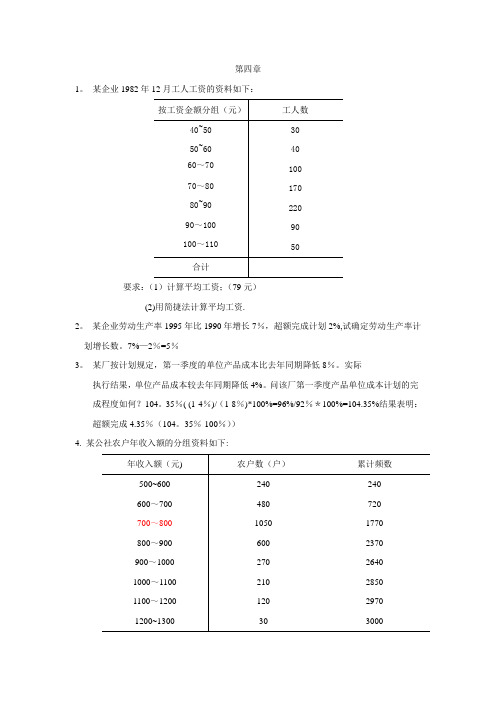
某企业1982年12月工人工资的资料如下:要求:(1)计算平均工资;(79元)(2)用简捷法计算平均工资.2。
某企业劳动生产率1995年比1990年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%—2%=5%3。
某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何?104。
35%( (1-4%)/(1-8%)*100%=96%/92%*100%=104.35%结果表明:超额完成4.35%(104。
35%-100%))4. 某公社农户年收入额的分组资料如下:要求:试确定其中位数及众数。
中位数为774.3(元)众数为755。
9(元)求中位数:先求比例: (1500—720)/(1770-720)=0。
74286分割中位数组的组距:(800-700)*0。
74286=74.286加下限700+74。
286=774。
286求众数:D1=1050—480=570D2=1050-600=450求比例:d1/(d1+d2)=570/(570+450)=0。
55882分割众数组的组距:0。
55882*(800-700)=55。
882加下限:700+55.882=755。
8825.1996年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:.64。
43(件/*140+85*60)/)6。
根据表中资料计算中位数和众数。
中位数为733.33(元)众数为711。
11(元)求中位数:先求比例:(50-20)/(65-20)=0。
6667分割中位数组的组距:(800—600)*0。
6667=66。
67 加下限:600+66.67=666。
677。
某企业产值计划完成103%,比去年增长5%.试问计划规定比去年增长 多少?1。
94%(上年实际完成1。
03/1.05=0。
981 本年实际计划比上年增长(1-0。
统计学计算题例题(含答案)
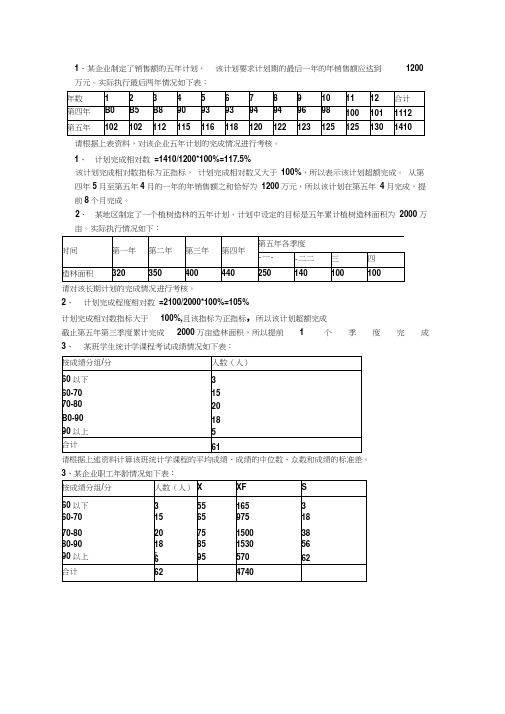
1、某企业制定了销售额的五年计划,该计划要求计划期的最后一年的年销售额应达到1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、计划完成相对数=1410/1200*100%=117.5%该计划完成相对数指标为正指标,计划完成相对数又大于100%,所以表示该计划超额完成。
从第四年5月至第五年4月的一年的年销售额之和恰好为1200万元,所以该计划在第五年4月完成,提前8个月完成。
2、某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为2000万亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、计划完成程度相对数=2100/2000*100%=105%计划完成相对数指标大于100%,且该指标为正指标,所以该计划超额完成截止第五年第三季度累计完成2000万亩造林面积,所以提前1个季度完成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
4、某学校有5000名学生,现从中按重复抽样方法抽取250名同学,调查其每周观看电视的小时数的情4> 样本平均数X= Sxf/Sf-l250/250-5样 ________ __________二>/刀(好予f/(工f—1)二V 1136/249二2. 14抽样平均误差U二s/ Vn=0.14因为F (t) =95%,所以日.96抽样极限误差△二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在(4.73,5.27)小时之间,概率保证程度为95%5、某企业对全自动生产线上的产品随机抽取1000件进行检验,发现有45件是不合格的,设定允许的极限误差为 1.32%。
请对全部产品的合格率进行区间估计。
5、样本合格率p=955/1000=95.5% 抽样平均误差u二V pChp)/n= 0.66%因为△=1.32%,所以t= A/ u =2所以F.(.t)-95. 45%区间下限二95. 5%-l. 32%=94. 18%区间上限二95. 5%+l. 32%二96. 82%所以我们以95. 45%的概率估计全部产品和合格率是在(94.18%, 96. 82%)之间。
统计学计算题
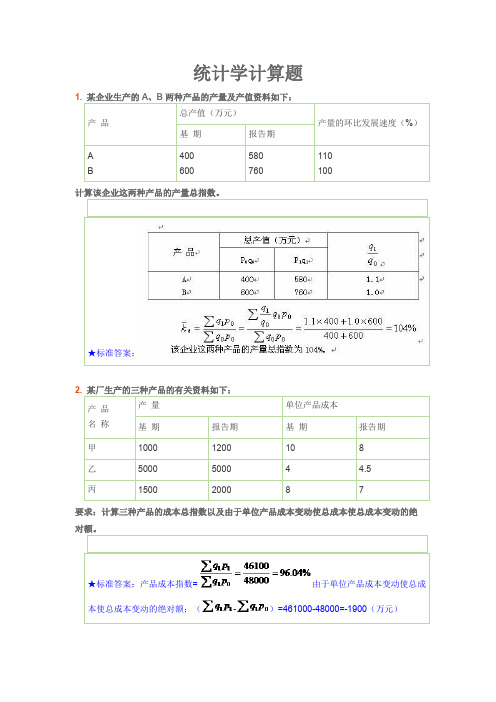
统计学计算题要求:计算三种产品的成本总指数以及由于单位产品成本变动使总成本使总成本变动的绝=本使总成本变动的绝对额;(-)★标准答案:4. 某厂三个车间一季度生产情况如下:第一车间实际产量为200件,完成计划95%;第二件,完成计划105%,请车间实际产量280件,完成计划100%;第三车间实际产量650根据资料计算:(1)产量计划平均完成百分比;8. 某市场上某种蔬菜早市每斤0.25元,中午每斤0.2元,晚市每斤0.1元,现在早、中、9. 某商店出售某种商品第一季度价格为6.5元,第二季度价格为6.25元,第三季度为6元,第四季度为6.2元,已知第一季度销售额3150元,第二季度销售额3000元,第三季度销10. 某厂生产某种机床配件,要经过三道工序,各加工工序的合格率分别为95.74%,★标准答案:试根据上表已知数据计算空格中的数字(保留一位小数并分别说明⑵、⑹、⑻、⑼栏是何试计算:(1)三种商品的销售额总指数(2)三种商品的价格综合指数和销售量综合指数18. 某自行车车库4月1日有自行车320辆,4月6日调出70辆,4月18日进货120辆,419. 某厂开展增产节约运动后,1月份总成本为10000元,平均成本为10元,2月份总成本为3000元,平均成本为8元,3月份总成本为35000元,平均成本为7.2元,试问,第试计算该地区三种水果的价格指数及由于价格变动对居民开支的影响。
2003年年末定额流动资金占有额为320万元。
根据上表资料,分别计算该企业定额流动资24. 某市2002年社会商品零售额12000万元,2003年增加为15600万元。
物价指数提高要求:(1)计算并填列表中所缺数字。
(2)计算该地区1997—2001年间的平均国民生产总值。
要求:⑴填满表内空格31.★标准答案:3(1)计算平均每个小组的日产量;★标准答案:计算平均每个小组的日产量(产量。
要求:(1)分别计算2000年、2001年的进出口贸易差额;(2)计算2001年进出口总额比例相对数及出口总额增长速度;(3)分析我国进出口贸易状况。
统计学计算题8个例题及答案

统计学计算题8个例题及答案
1.给定一组数据,X=(13,12,13,13,10,13,11),求它的众数:
答:13(众数是出现次数最多的值)
2.给定一组数据,X=(1,2,3,4,5,6,7),求它的中位数:
答:4(中位数是将一组数据按照大小顺序排列后位于正中间的一个数)
3.给定一组数据,X=(1,2,3,4,5,6,7),求它的样本标准差:
答:(样本标准差S=√ [(∑(Xi−X平均数)2)/ (n−1)],其中,Xi代表样本的每一项,X平均数是样本的平均值,n是样本的总观测值数量)
4.给定一组数据,X=(1,2,3,4,5,6,7,8,9),求它的方差:
答:(方差σ^2=∑(Xi−X平均数)^2/n,其中,Xi代表样本的每一项,X平均数是样本的平均值,n是样本的总观测值数量)
5.给定一组数据,X=(21, 25, 28, 31, 34, 37, 40),求它的算术平均数:
答:31(算术平均数是将样本中数据求和,再除以样本的个数得到的数)
6.给定一组数据,X=(1,2,3,4,5,6,7,8,9),求它的期望:
答:5(期望是一组数据根据概率分布定义出的一种数学期望)
7.给定一组数据,X=(3,4,5,7,12,15,18),求它的方差:
答:(方差σ^2=∑(Xi−X平均数)^2/n,其中,Xi代表样本的每一项,X平均数是样本的平均值,n是样本的总观测值数量)
8.给定一组数据,X=(7,7,7,7,8,8,9),求它的众数:
答:7(众数是出现次数最多的值)。
统计学计算题例题及计算分析

计算分析题解答参考1.1.某厂三个车间一季度生产情况如下:车间计划完成百分比(%)实际产量(件)f单位产品成本(元/件)x第一车间第二车间第三车间9010511019831522015108合计――733 ――计算一季度三个车间产量平均计划完成百分比和平均单位产品成本。
解:平均计划完成百分比=实际产量/计划产量=733/(198/0.9+315/1.05+220/1.1)=101.81%平均单位产量成本 X=∑xf/∑f=(15*198+10*315+8*220)/733=10.75(元/件)1.2.某企业产品的有关资料如下:产品单位成本(元/件)x98年产量(件)f99年成本总额(元)m甲乙丙25283215001020980245002856048000合计-3500 101060 试分别计算该企业产品98年、99年的平均单位产品成本。
解:该企业98年平均单位产品成本 x=∑xf/∑f=(25*1500+28*1020+32*980)/3500=27.83(元/件)该企业99年平均单位产品成本x=∑xf /∑(m/x)=101060/(24500/25+28560/28+48000/32) =28.87(元/件)1.3.1999年某月甲、乙两市场三种商品价格、销售量和销售额资料如下:商品品种价格(元/件)x甲市场销售量(件)f乙市场销售额(元)m甲乙丙10512013770090011001260009600095900合计――2700 317900 试分别计算三种商品在两个市场上的平均价格。
解:三种商品在甲市场上的平均价格x=∑xf/∑f=(105*700+120*900+137*1100)/2700=123.04(元/件)三种商品在乙市场上的平均价格x=∑m/∑(m/x)=317900/(126000/105+96000/120+95900/137)=117.74(元/件)2.1.某车间有甲、乙两个生产小组,甲组平均每个工人的日产量为22件,标准差为3.5件;乙组工人日产量资料:日产量(件)工人数(人)10-12 13-15 16-18 19-21 10 20 30 40试比较甲、乙两生产小组中的哪个组的日产量更有代表性?解:∵X甲=22件σ甲=3.5件∴V甲=σ甲/ X甲=3.5/22=15.91%列表计算乙组的数据资料如下:日产量组中值(件)x 工人数(人)fxf(x-x)2(x-x)2f1110110363601420280918017305100020408009360合计1001700-900∵x乙=∑xf/∑f=(11*10+14*20+17*30+20*40)/100=17(件)σ乙=√[∑(x-x)2f]/∑f =√900/100 =3(件)∴V乙=σ乙/ x乙=3/17=17.65%由于V甲<V乙,故甲生产小组的日产量更有代表性。
统计学计算题例题(课件)

【例1】:某企业生产A 产品的工人有1000人,某日采用不重复抽样从中随机抽取100人调查他们的当日产量,样本人均产量为35件,产量的样本标准差为4.5件。
请以95.45%的置信度估计该日人均产量的置信区间。
解:①计算抽样平均误差()件4269.0100010011005.411222≈⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-≈⎪⎭⎫ ⎝⎛--=N n n s N n N n x σμ ②计算抽样极限误差由9545.01=-)(α,查正态概率表得2=Z(件)8538.04269.02=⨯==∆x x Z μ③确定置信区间 估计区间上限:85.358538.035=+=U X (件) 估计区间下限:15.348538.035=-=L X (件)故,可以95.45%的置信度断言,该日人均产量在34.15~35.85件之间。
【例2】某企业生产某种产品的工人有1000人,某日采用不重复抽样从中随机抽取100人调查他们的当日产量,要求在95﹪的概率保证程度下,估计该厂全部工人的日平均产量和日总产量。
解: ()()()件件47.69941441126100126002==--====∑∑∑∑f f x x s f xf x ()件614.01000100110047.6122=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=N n n s x μ()件203.1614.096.1=⨯=⋅=∆x x Z μ则该企业工人人均产量及日总产量的置信区间为:()()203.11261000203.11261000,203.1126203.1126+≤≤-+≤≤-X N X即该企业工人人均产量在124.797至127.203件之间,其日总产量在124797至127303件之间,估计的可靠程度为95﹪。
【例2变形】工人日产量在118件以上者为完成生产定额任务,要求在95﹪的概率保证程度下,估计该厂全部工人中完成定额的工人比重及完成定额的工人总数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章1. 某企业1982年12 月工人工资的资料如下:按工资金额分组(元)工人数40~503050~604060~7010070~8017080~9022090~10090100~11050合计要求:(1)计算平均工资;(79 元)(2)用简捷法计算平均工资。
2. 某企业劳动生产率1995 年比1990 年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%-2%=5%3. 某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何?104.35%((1-4%)/(1-8%)*100%=96%/92%*100%=104.35% 结果表明:超额完成4.35%(104.35%-100%))4. 某公社农户年收入额的分组资料如下:年收入额(元)农户数(户)累计频数500~600240240600~700480720700~80010501770800~9006002370900~100027026401000~110021028501100~120012029701200~1300303000合计要求:试确定其中位数及众数。
中位数为774.3(元)众数为755.9(元)求中位数:先求比例: (1500-720) / (1770-720) =0.74286 分割中位数组的组距: ( 800-700)*0.74286=74.286 加下限 700+74.286=774.286 求众数:D1=1050-480=570 D2=1050-600=450求比例: d1/(d1+d2)=570/ ( 570+450)=0.55882 分割众数组的组距: 0.55882*( 800-700) =55.882 加下限: 700+55.882=755.882(55*300+65*200+75*140+85*60 ) / ( 300+200+140+60 )6. 某地区家庭按人均月收入水平分组资料如下:根据表中资料计算中位数和众数。
中位数为(元) 众数为 (元)求中位数: 先求比例:(50-20)/ (65-20)=0.6667 分割中位数组的组距: (800-600) *0.6667=66.67 加下限: 600+66.67=666.677. 某企业产值计划完成 103%,比去年增长 5%。
试问计划规定比去年增长 多少? 1.94%(上年实际完成 1.03/1.05=0.981本年实际计划比上年增长5.1996年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:该企业工人平均劳动生产率。
(1-0.981)/0.981=0.019/0.981=1.937% )8. 甲、乙两单位工人的生产资料如下:试分析:(1)哪个单位工人的生产水平高?(2)哪个单位工人的生产水平整齐?x甲1.5(件/ 人)x乙1.8(件/ 人)V甲44.7% V乙33.3%9.在计算平均数里,从每个标志变量中减去75 个单位,然后将每个差数缩小10 倍,利用这个变形后的标志变量计算加权算术平均数,其中各个变量的权数扩大7 倍,结果这个平均数等于0.4 个单位。
试计算这个平均标志变量的实际平均数,并说明理由。
79 10.某地区1998~1999 年国内生产总值资料如下表:(单位:亿元)1998 年1999 年国内生产总值3640544450 试计算 1998年和 1999年第一产业、 其中:第一产业81578679第二产业、 第三产业的结构相对指标 第二产业 1380117472 和比例相对指标。
第三产业1444718319结构相对指标 第一产业第二产业 第三产业1998年22.4%37.9% 39.7% 1999年19.5%39.3% 41.2% 比例相对指标第一产业:第二产业: 第三产业1998年1 :1.7 : 1.8 1999年1:2 :2.1.某产品资料如下:等级 单价(元 /斤)收购量(斤) 收购额(元)一级品 1.202000 2400二级品 1.053000 3150 三级品0.940003600要求:按加权算术平均数、加权调和平均数计算该产品的平均收购价格。
1.03(元 /斤)12. 根据某一个五年计划规定,某种工业产品在该五年计划的最后一年生产试根据表列资料计算该产品计划完成程度及提前完成五年计划的时间。
112.5% 4 个月 又五天13. 某厂的劳动生产率(按全部职工计算) ,计划在去年的基础上提高 8%,计划执行的结果仅 提高 4%。
试计算劳动生产率的计划完成程度。
96.3%14. 某企业工人完成产量定额资料如下:要求:分别计算各月份的众数和中位数。
7 月份:中位数为122.33(%)众数为122.14(%)8 月份:中位数为114.08(%)众数为111.9(%)15. 某种商品在两个地区销售情况如下:试分别计算甲、乙两个地区该商品的平均价格。
(甲、乙两个地区该商品的平均价格分别为:1.20(元/ 件)1.23(元/ 件))16. 有人提出有三种萍果,一种是每元买2斤,一种是每元买3斤,一种是每元买4 斤,现在各买1元,用了3元,买了9斤,当然是每元平均买了3 斤,可是用调和平均数计算每元只买了2.7斤[即:3/(1/2+1/3+1/4 )=2.7 斤],少了0.3斤,因而否定调和平均数,你怎样回答这个问题?17. 兹有某地区水稻收获量分组资料如下:耕地面积(亩)水稻收获量(千克/亩)150~17518175~20032200~22553225~25069250~27584275~300133300~325119325~35056要求:( 1)计算中位数及众数;中位数 283.3(千克 / 亩) 众数 294.4(千克 / 亩) ( 2)计算算术平均数;算术平均数277.4(千克 / 亩)( 3)计算全距、 平均差和标准差; 全距 275(千克 / 亩) 平均差 41.3(千克 / 亩) 标准差 千克 /亩)( 4)比较算术平均数、中位数、众数的大小,说明本资料分布的偏斜特征。
为左偏1)全距( 2)平均差( 3)标准差,并比较哪一组的平均数代表性大?第一组 第二组1)全距 100(件) 6(件) 2)平均差 27.7(件) 1.7(件) 3)标准差31.6(件)2(件)试计算各门市部完成零售计划的平均百分比。
106.4%20. 某无线电厂生产某型号收音机,按计划规定, 1992 年每台成本要求在1991年 84元的基础上降低 2.94元,而 1992年的实际每台成本为 80.85元。
试计算单位成 本计划完成程度指标。
99.74% 21.在计算平均数里,从每个标志变量中减去 120 个单位,然后将每个差数缩小 10 倍,利 用 这个变形后的标志变量计算加权算术平均数,其20个门市部门,它们的商品零售计划完成情况如下表:50.918. 某车间有两个小组,每组都是 第一组: 20 40 60 70 第二组: 67 68 69 70 7 个工人,各人日产的件数如下:80 100 12071 72 73这两个组每人平均日产件数都是70件,试计算工人日产量的变异指标:19. 某零售商业企业包括中各个变量的权数缩小5倍,结果这个平均数等于0.5 个单位。
试计算这个平均标志变量的实际平均数,并说明理由。
12522. 某商业企业1992 年的营业额计划完成105%,比上年增长10%。
试计算该企业计划规定比上年的增长程度。
4.76%23. 某商品在三个农村集市贸易市场上的单位价格和贸易额资料如下表:试计算该商品的市场平均价格。
1.27(元/ 件)24. 某企业164 人的日产量资料如下:按日产量分组(千克)工人人数(人)60 以下1060~701970~805080~903690~10027100~11014110 以上8合计164试确定其中位数与众数。
中位数80.83(千克)众数76.89(千克)25. 根据某一个五年计划规定,某种工业产品在该五年计划的最后一年生产量达到803 万吨,该产品在五年计划最后两年的每月实际产量如下完成五年计划的时间。
124.16% 8 个月又7 天试计算该厂各生产车间和全厂产量计划完成百分比。
甲 110% 乙 90%105% 全厂 101.8%27. 某地区粮食生产资料如下:耕地按亩产分组(斤)耕地面积(万亩)750 以下 4.0 750—— 800 8.3 800—— 850 10.7 850—— 900 31.7 900—— 950 10.8 950—— 1000 10.0 1000 以上4.5 合计80试计算该地区粮食耕地亩产众数和中位数。
中位数 877(斤 / 亩) 众数亩)28. 某采购供应站工作人员工资分组如下:工资分组(元)工作人员数50—— 60 10 60—— 70 20 70—— 80 110 80—— 90 90 90—— 10015 100—— 1105 合计250要求:试用上述资料单位:万元 26.某企业 6 月份生产情况如下表:875(斤/(1)计算算术平均数X A;78.8(元)(2)计算全距R、平均差A D 、标准差σ;全距60(元)平均差7.46(元)标准差9.36(元)(3)计算标准差系数Vσ;离散系数11.88%(4)计算众数Mo ;78.18(元)(5)用皮克逊关系式换算出中位数Me。
78.59(元)29. 设第一组工人的平均工龄为6年,第二组为8年,第三组为10 年。
第一组工人人数占工人总数的30%,第二组占工人总数的50%。
要求:试计算这三组工人的平均年龄。
7.8(年)30. 指出下面的统计分析报告摘要错在哪里?并把它改写.(1)本厂按计划规定,第一季度的单位产品成本应比去年同期降低10%,实际执行结果,单位产品成本较去年同期降低8%,仅完成产品成本计划的80%。
(8%/10%=80% )102.2%(2)本厂的劳动生产率(按全部职工计算),计划在去年的基础上提高8%,计划执行的结果仅提高了4%,劳动生产率的计划任务仅实了一半。
(即4%/8%=50% )96.3%31. 某厂两个车间生产同一产品的产量和成本资料如下:1)计算产量结构相对指标。
2)各车间单位成本不变,全厂单位成本下降20 元,试分析原因。
1977 年1978 年甲车间40% 60%乙车间60% 40%32. 区分下列统计指标是属于总量指标、相对指标、还是平均指标。
(1)某年某市人口出生率,死亡率;(2)某年全国粮食总产量;(3)某年全国工业总产量;4)资金利润率;5)某市某年的工业产品产值;6)某月份某工厂工人出勤率;7)商品流通费率;(注:流通费用率= 流通费用额/实际销售额)8)某市某年的工业净产值;9)某地区按人口平均计算的国民收入;10)某年华东地区粮食产量为华北地区粮食产量的82%;11)某个时期某种商品的价格;12)单位产品成本;13)某年某月某日的全国人口数;14)粮食单位面积产量。
