比例和反比例 测试题
小学数学“正比例和反比例”过关测试题(3套)

比习题精编1一、对号入座。
1.( )÷10=0.6=( )%=( ):( )=()9 2.把158:43化成最简单的比是( );43千克: 400克的比值是( )。
3.甲乙两数的比是3:5,甲数是乙数的( )%,乙数是甲数的( )%,甲数与两数和的比是( )。
4.一杯400克的糖水,含糖率是20%,糖与糖水的比是( ),再加入20克糖,糖与糖水的比是( )。
5.把3:8的前项加上6,要使比值不变,后项可以乘( )或加( )二、慎重选择。
1.如果减数相当于被减数的53,那么差与减数的比是( )。
A 2:3B 2:5C 3:5D 3:22.同一段路程,甲车行完要4小时,乙车行完要6小时,甲、乙两车速度的最简比是( )A 4:6B 6:4C 2:3D 3:23.甲乙两个正方体棱长的比是1:2。
它们的表面积的比是( ),体积比是( );A 1:2B 1:4C 1:6D 1:84.一个三角形三个内角的度数比是2:3:5,这是()三角形。
A 锐角B 钝角C 直角 D无法确定五、解决问题。
1.一种药水是把药粉和水按照1∶100的比例配成的.要配成这种水4040千克,需要药粉多少千克?2.一个长方形周长50米,长与宽的比是3∶2,这个长方形的面积是多少?3.建筑工人用2份水泥、3份沙子和5份石子配置一种混凝土.配置6000千克这种混凝土,需要水泥、沙子和石子各多少千克?4.加工一批零件,已完成个数与零件总个数的比是1:3。
如果再加工15个,那么完成个数与剩下的个数同样多,这批零件共有多少个?5.画一个长3厘米,宽2厘米的长方形,把这个长方形按2:1放大后,画下来。
想一想:这两个长方形的面积的比是多少?比例尺习题精编2一、对号入座。
1.在比例尺是1:4000000的地图上,图上距离1厘米表示实际距离()千米。
也就是图上距离是实际距离的1,实际距离是图上距离的()倍。
()0 20 402.一幅图的比例尺是,那么图上的1厘米表示实际距离();实际距离50千米在图上要画()厘米。
反比例函数单元测试题及答案

第17 章反比例函数综合检测题一、选择题(每小题 3 分,共30 分)1、反比例函数y=n 5图象经过点(2,3),则n 的值是().xA、-2B、-1C、0D、1k2、若反比例函数y=(k≠0)的图象经过点(-1,2),则这个函数的图象一定经过点().xA、(2,-1)B、(-1 1,2)C、(-2,-1)D、(2 2,2)3、(08 双柏县) 已知甲、乙两地相距s (km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h)与行驶速度v (km/h)的函数关系图象大致是()t/hO v/(km/h) O t/hv/(km/h) Ot /hv/(km/h)t/hO v/(km/h)A.B.C.D.4、若y 与x 成正比例,x 与z 成反比例,则y 与z 之间的关系是().A、成正比例B、成反比例C、不成正比例也不成反比例D、无法确定k5、一次函数y=kx-k,y 随x 的增大而减小,那么反比例函数y=x满足().A、当x>0 时,y>0 B、在每个象限内,y 随x 的增大而减小C、图象分布在第一、三象限D、图象分布在第二、四象限6、如图,点P 是x 轴正半轴上一个动点,过点P 作x 轴的垂y1线PQ 交双曲线y=x 于点Q,连结OQ,点P 沿x 轴正方向运动时,QRt△QOP 的面积().A、逐渐增大B、逐渐减小C、保持不变D、无法确定7、在一个可以改变容积的密闭容器内,装有一定质量m 的某种气体,当改变容积V 时,气体的密度ρ也随之改变.m o p xρ与V 在一定范围内满足ρ=V气体的质量m 为().,它的图象如图所示,则该A、1.4kg B、5kg C、6.4kg D、7kg8、若A(-3,y 1),B(-2,y2),C(-1,y 3)三点都在函数y=-y 2,y 3的大小关系是().A、y1>y 2>y 3B、y1<y2<y3C、y 1=y 2=y 3D、y1<y3<y21的图象上,则y 1,x1 9、已知反比例函数y=2 m的图象上有A(x1,y1)、B(x 2,y 2)两点,当x 1<x2<0 时,xy 1<y 2,则m 的取值范围是().A、m<0B、m>0C、m<1D、m>1 2 210、如图,一次函数与反比例函数的图象相交于A、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围是().A、x<-1B、x>2C、-1<x<0 或x>2D、x<-1 或0<x<2二、填空题(每小题 3 分,共30 分)1 1. 某种灯的使用寿命为1000小时,它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为.12、已知反比例函数ky 的图象分布在第二、四象限,则在一次函数yxkx b 中,y 随x 的增大而(填“增大”或“减小”或“不变”).b 313、若反比例函数y=和一次函数y=3x+b 的图象有两个交点,且有一个交点的纵坐x标为6,则b=.214、反比例函数y =(m+2)x m-10 的图象分布在第二、四象限内,则m 的值为.15、有一面积为S 的梯形,其上底是下底长的关系是.1,若下底长为x,高为y,则y 与x 的函数3a16、如图,点M 是反比例函数y=x(a≠0)的图象上一点,过M 点作x 轴、y 轴的平行线,若S 阴影=5,则此反比例函数解析式为.217、使函数y=(2m2-7m-9)x m-9 m+19 是反比例函数,且图象在每个象限内y 随x 的增大而减小,则可列方程(不等式组)为.k18、过双曲线y=(k≠0)上任意一点引x 轴和y 轴的垂线,所得长方形的面积为.x419. 如图,直线y =kx(k >0)与双曲线y交于 A (x 1,y 1),xB(x 2,y 2)两点,则2x1y2-7x2y1=.20、如图,长方形AOCB 的两边OC、OA 分别位于x 轴、20y 轴上,点 B 的坐标为B(-,5),D 是AB 边上的一点,3将△ADO 沿直线OD 翻折,使 A 点恰好落在对角线OB 上的点E 处,若点 E 在一反比例函数的图象上,那么该函数的解析式是.三、解答题(共60 分)21、(8 分)如图,P 是反比例函数图象上的一点,且点P 到x轴的距离为3,到y 轴的距离为2,求这个反比例函数的解析式.22、(9 分)请你举出一个生活中能用反比例函数关系描述的实例,写出其函数表达式,并画出函数图象.举例:函数表达式:k23、(10 分)如图,已知A(x 1,y 1),B(x2,y 2)是双曲线y=x的两点,连结OA、OB.在第一象限内的分支上(1)试说明y 1<OA <y1+k;y 1(2)过 B 作BC⊥x 轴于C,当m=4 时,求△ BOC 的面积.24、(10 分)如图,已知反比例函数y=-8与一次函数xy=kx +b 的图象交于A、B 两点,且点 A 的横坐标和点 B 的纵坐标都是-2.求:(1)一次函数的解析式;(2)△AOB 的面积.k25、(11 分)如图,一次函数y=ax+b 的图象与反比例函数y=x的图象交于M 、N 两点.(1)求反比例函数与一次函数的解析式;(2)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.k26、(12 分)如图,已知反比例函数y=x的图象与一次函数y=ax +b 的图象交于M(2,m)和N(-1,-4)两点.(1)求这两个函数的解析式;(2)求△ MON 的面积;(3)请判断点P(4,1)是否在这个反比例函数的图象上,并说明理由.参考答案:一、选择题1、D ;2、A;3、C;4、B;5、D ;6、C7、D;8、B;9、D;10、D.二、填空题1 1 、y =1000x3s;12 、减小;13、5 ;14、-3 ;15、y =2 x;16、y21 5 m=-; 17、9m 19112 ; 18、|k|; 19、 20; 20、y =-.x2 m7 m 9> 0x三、解答题 6 21、 y =-.x22、举例:要编织一块面积为 2 米 的矩形地毯,地毯的长x (米)与宽 y (米)之间的函2数关系式为 y = ( x > 0).x 1 3 x , 1 2 , 224 y,421,3(只要是生活中符合反比例函数关系的实例均可) 画函数图象如右图所示.23、( 1)过点 A 作 AD ⊥x 轴于 D ,则 OD = x 1,AD =y 1,因为点 A ( x 1 , y 1)在双曲线 y= k上 ,故 x =xk ,又在 Rt △ OAD 中, AD < OA < AD + OD ,所以 y 1 y 1<OA < y 1+k ;y 1(2)△ BOC 的面积为 2.24、( 1)由已知易得 A (- 2,4), B ( 4,- 2),代入 y = kx + b 中,求得 y =- x + 2; (2)当 y = 0 时, x = 2,则 y =- x + 2 与 x 轴的交点 M (2, 0),即 |OM| = 2,于是 S △ AOB1 =S △ AOM + S △ BOM = 21 |OM| · |y A |+ 21 |OM|·|y B |= 21× 2× 4+ 2× 2× 2= 6.25、( 1)将 N (- 1,- 4)代入 y = k,得 k =4.∴反比例函数的解析式为 y = x4. 将 Mx4(2,m )代入 y = x2 a b 2, ,得 m = 2.将 M ( 2,2),N (- 1,- 4)代入 y = ax +b ,得ab4.a 2 ,解得b2 .∴一次函数的解析式为 y = 2x - 2.(2) 由图象可知,当 x <- 1 或 0< x <2 时,反比例函数的值大于一次函数的值.26、解 ( 1)由已知,得- 4=k 4 ,k = 4,∴ y = 1x 4 .又∵图象过 M ( 2, m )点,∴ m =22a b 2a2=2,∵ y = ax + b 图象经过 M 、N 两点,∴, 解之得, ∴y = 2x - 2.ab4 b2(2)如图,对于 y = 2x - 2,y = 0 时, x = 1,∴ A ( 1, 0), OA =1,∴ S △ MON = S △ MOA + S △22NOA = 1 OA ·MC + 21 OA · ND =21 × 1× 2+ 21×1× 4= 3.2(3) 将点 P ( 4, 1)的坐标代入 y = 4,知两边相等,∴ P 点在反比例函数图象上.x。
反比例函数单元测试题(含答案)

反比例函数练习题一. 选择题1. 函数y m x m m =+--()2229是反比例函数,则m 的值是( )A. m =4或m =-2B. m =4C. m =-2D. m =-1 2. 下列函数中,是反比例函数的是( ) A. y x =-2 B. y x =-12 C. y x =-11 D. y x =123. 函数y kx =-与y k x=(k ≠0)的图象的交点个数是( ) A. 0 B. 1 C. 2 D. 不确定 4. 函数y kx b =+与y k x kb =≠()0的图象可能是( )A B C D5. 若y 与x 成正比,y 与z 的倒数成反比,则z 是x 的( )A. 正比例函数B. 反比例函数C. 二次函数D. z 随x 增大而增大6. 下列函数中y 既不是x 的正比例函数,也不是反比例函数的是( )A. y x =-19B. 105=-x y :C. y x =412 D.152xy =- 二. 填空题7. 一般地,函数__________是反比例函数,其图象是__________,当k <0时,图象两支在__________象限内。
8. 已知反比例函数y x=2,当y =6时,x =_________。
9. 反比例函数y a x a a =---()3224的函数值为4时,自变量x 的值是_________。
10. 反比例函数的图象过点(-3,5),则它的解析式为_________11. 若函数y x =4与y x =1的图象有一个交点是(12,2),则另一个交点坐标是_________。
三. 解答题12. 直线y kx b =+过x 轴上的点A (32,0),且与双曲线y k x =相交于B 、C 两点,已知B 点坐标为(-12,4),求直线和双曲线的解析式。
13. 已知一次函数y x =+2与反比例函数y k x =的图象的一个交点为P (a ,b ),且P 到原点的距离是10,求a 、b 的值及反比例函数的解析式。
小学六年级数学比例和反比例 测试题含答案及知识点
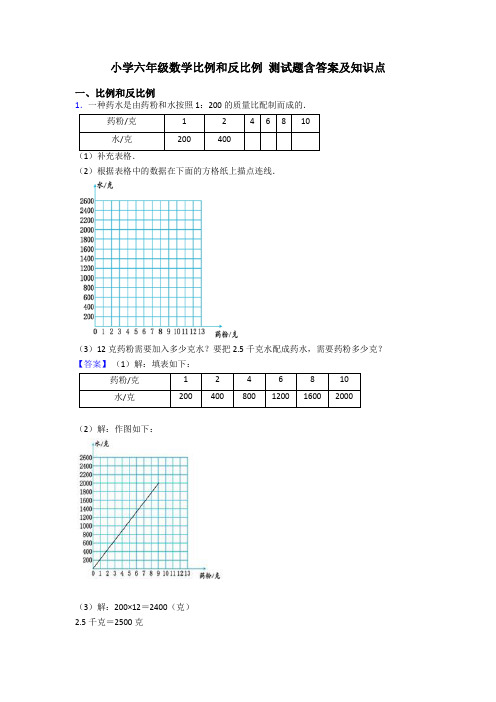
小学六年级数学比例和反比例测试题含答案及知识点一、比例和反比例1.一种药水是由药粉和水按照1:200的质量比配制而成的.药粉/克1246810水/克200400(1)补充表格.(2)根据表格中的数据在下面的方格纸上描点连线.(3)12克药粉需要加入多少克水?要把2.5千克水配成药水,需要药粉多少克?【答案】(1)解:填表如下:药粉/克1246810水/克200400800120016002000(2)解:作图如下:(3)解:200×12=2400(克)2.5千克=2500克2500× =12.5(克)答:12克药粉需要加水2400克,要把2.5千克水配成药水,需要药粉12.5克.【解析】【分析】(1)根据条件“ 一种药水是由药粉和水按照1:200的质量比配制而成的”可知,用药粉:水=1:200,据此列比例解答,然后填表即可;(2)根据统计表中的数据,在统计图中先描点,然后再连线,图中的统计图纵轴每格代表200克,据此作图;(3)根据条件可知,1克药粉要加入200克水,用药粉的质量×200=水的质量,据此用乘法计算;要把2.5千克水配成药水,需要药粉多少克,先统一单位,1千克=1000克,然后用水的质量×药粉占水的分率=药粉的质量,据此列式解答。
2.如果10千克菜籽可以榨6.5千克菜油,那么有这种菜籽360千克,可以榨多少千克油?(用比例解)【答案】解:设可以榨x千克油。
10:6.5=360:x10x=6.5×360x=2340÷10x=234答:可以榨油234千克。
【解析】【分析】菜籽的重量和榨油的质量的比值是不变的,二者成正比例,设出未知数,根据正比例关系列出比例,解比例求出可以榨油的重量即可。
3.把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如下表。
分的杯数/杯6543每杯的果汁量/mL100120()200(2)分的杯数和每杯的果汁量有什么关系?为什么?(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?【答案】(1)150(2)解:成反比例,因为每杯的果汁量×分的杯数=果汁总量。
第二十六章反比例函数 达标测试卷(含答案)

第二十六章反比例函数一、选择题(每小题3分,共30分)1.下列函数中,属于反比例函数的是( )A .y =3xB .y =-2x C .y =x 2+3 D .x +y =522.已知双曲线y =kx 经过点(-2,5),则下列各点在该双曲线上的是( )A .(-5,-2)B .(1,10)C .(5,2)D .(10,-1) 3.对于反比例函数y =2x ,下列说法正确的是( )A .点(-2,1)在它的图象上B .它的图象位于第一、三象限C .它的图象经过原点D .当x >0时,y 随x 的增大而增大4.已知反比例函数y =k -3x ,当x >0时,y 随x 的增大而增大,则k 的取值范围是( )A .k <3B .k ≤3C .k >3D .k ≥35.如图是反比例函数y 1=kx 和一次函数y 2=mx +n 的图象,若y 1<y 2,则相应的x的取值范围是( )A .1<x <6B .x <1C .x <6D .x >1(第5题) (第7题)6.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后汽缸内气体的体积和气体对汽缸壁所产生的压强,如下表:体积x /mL 100 80 60 40 20 压强y /kPa6075100150300则可以反映y 与x 之间的关系的式子是( )A.y=3 000x B.y=6 000xC.y=3 000x D.y=6 000x7.如图,反比例函数y=4x和y=2x在第一象限内的图象分别是C1和C2,设点P在C1上,P A⊥x轴于点A,交C2于点B,则△POB的面积为() A.1 B.2 C.4 D.无法计算8.函数y=kx(k≠0)与y=-kx2+k(k≠0)在同一直角坐标系中的图象可能是() 9.如图,O为坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=kx(x<0)的图象经过顶点B,则k的值为() A.-12 B.-27 C.-32 D.-36(第9题) (第10题)10.如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=kx的图象交于C,D两点,过点C作CE⊥y轴于点E,过点D作DF⊥x 轴于点F,连接CF,DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于k2,其中正确的有()A.2个B.3个C.4个D.5个二、填空题(每小题3分,共15分)3 11.已知函数y =(m -1)x |m |-2是反比例函数,则m =________.12.已知点A (1,y 1),B (2,y 2)是双曲线y =5x 上的点,则y 1________y 2(填“>”“<”或“=”).13.近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y 与镜片焦距x 之间的函数关系式为________________.14.反比例函数y =kx 的图象经过点A (2,1),若y ≤1,则x 的取值范围为________________.15.如图,点A 在反比例函数y =6 2x (x >0)的图象上,以OA 为直径的圆交该双曲线于点C ,交y 轴于点B ,若CB ︵=CO ︵,则点A 的坐标为__________.三、解答题(一)(每小题8分,共24分)16.已知反比例函数y =kx 的图象经过点P (1,6). (1)求k 的值;(2)若点M (-2,m ),N (-1,n )都在该反比例函数的图象上,试比较m ,n 的大小.17.如图,直线y =x +m 与双曲线y =kx 相交于A (2,1)和B 两点.(1)求m与k的值;(2)求点B的坐标;(3)直线y=-2x+4m经过点B吗?请说明理由.18.已知y是x+1的反比例函数,且当x=-2时,y=-3.(1)求y与x的函数关系式;(2)当x=12时,求y的值.四、解答题(二)(每小题9分,共27分)19.如图,一次函数y=kx+b与反比例函数y=6x(x>0)的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出kx+b-6x<0中的x的取值范围;(3)求△AOB的面积.20.制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作.操作8 min时,材料温度降为600 ℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系(如图),已知某材料初始温度是26 ℃.(1)分别求出该材料煅烧和锻造时y关于x的函数解析式,并写出自变量x的取值范围.(2)根据工艺要求,当材料温度低于400 ℃时,须停止操作,那么锻造的操作时间有多长?21.如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=mx(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的解析5式.五、解答题(三)(每小题12分,共24分)22.如图,正比例函数y=2x的图象与反比例函数y=kx的图象交于A,B两点,过点A作AC⊥x轴于点C,连接BC.若△ABC的面积为2.(1)求k的值;(2)①点A的坐标为________,点B的坐标为________;②当kx≤2x时,x的取值范围为________________;(3)在x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.23.如图,已知一次函数y=32x-3的图象与反比例函数y=kx的图象交于点A(4,n),与x轴交于点B.(1) 填空:n的值为________,k的值为________;(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;(3)观察反比例函数y=kx的图象,当y≥-2时,请直接写出自变量x的取值范围.7答案一、1.B 2.D 3.B 4.A 5.A 6.D 7.A 8.B 9.C 点拨:∵A (-3,4),∴OA =32+42=5.∵四边形OABC 是菱形,∴AB =OA =5,AB ∥OC , 则点B 的横坐标为-3-5=-8,纵坐标为4, 即点B 的坐标为(-8,4),将点B (-8,4)的坐标代入y =k x ,得4=k-8,解得k =-32.故选C.10.C二、11.-1 12.> 13.y =100x 14.x <0或x ≥2 15.(3,2 6)三、16.解:(1)∵反比例函数y =k x 的图象经过点P (1,6), ∴6=k1,解得k =6.(2)∵k =6>0,∴当x <0时,y 随x 的增大而减小, ∵-2<-1,∴m >n .17.解:(1)将A (2,1)的坐标代入y =x +m ,得1=2+m ,解得m =-1.将A (2,1)的坐标代入y =k x ,得1=k2,解得k =2. (2)由(1)知m =-1,k =2,联立⎩⎪⎨⎪⎧y =x -1,y =2x ,解得⎩⎨⎧x 1=2,y 1=1,⎩⎨⎧x 2=-1,y 2=-2, ∴点B 的坐标为(-1,-2). (3)经过,理由略. 18.解:(1)设y =kx +1(k ≠0). 把x =-2,y =-3代入,得-3=k-2+1,解得k =3,故y 与x 的函数关系式为y =3x +1.9 (2)把x =12代入y =3x +1,得y =312+1=2.四、19.解:(1)分别把A (m ,6),B (3,n )的坐标代入y =6x (x >0)得6=6m ,n =63,解得m =1,n =2, 所以A 点坐标为(1,6),B 点坐标为(3,2), 把A (1,6),B (3,2)的坐标代入y =kx +b ,得 ⎩⎨⎧k +b =6,3k +b =2,解得⎩⎨⎧k =-2,b =8,所以一次函数的解析式为y =-2x +8. (2)当0<x <1或x >3时,kx +b -6x <0.(3)设一次函数y =-2x +8的图象与x 轴,y 轴分别交于点D ,C, 当x =0时,y =8,则C 点坐标为(0,8), 当y =0时,-2x +8=0,解得x =4, 则D 点坐标为(4,0),所以S △AOB =S △COD -S △AOC -S △BOD =12×4×8-12×8×1-12×4×2=8.20.解:(1)设该材料锻造时y 关于x 的函数解析式为y =k x (k ≠0),则600=k8,∴k=4 800,∴y =4 800x .当y =800时,800=4 800x ,解得x =6, ∴点B 的坐标为(6,800).设该材料煅烧时y 关于x 的函数解析式为y =ax +b (a ≠0),将点A (0,26),B (6,800)的坐标代入得⎩⎨⎧b =26,6a +b =800,解得⎩⎨⎧a =129,b =26,∴y =129x +26.∴该材料锻造时y 关于x 的函数解析式为y =4 800x (x ≥6),煅烧时y 关于x 的函数解析式为y =129x +26(0≤x <6).(2)把y =400代入y =4 800x ,得x =12,12-6=6(min),∴锻造的操作时间有6 min.21.解:∵点B (2,n ),P (3n -4,1)在反比例函数y =mx (x >0)的图象上,∴⎩⎨⎧2n =m ,3n -4=m ,解得⎩⎨⎧m =8,n =4,∴反比例函数的解析式为y =8x ,B (2,4),P (8,1). 如图,过点P 作PD ⊥BC 于D ,并延长交AB 于点P ′.在△BDP 和△BDP ′中,⎩⎨⎧∠PBD =∠P ′BD ,BD =BD ,∠BDP =∠BDP ′=90°,∴△BDP ≌△BDP ′,∴DP ′=DP .易知DP =8-2=6,∴DP ′=6.∵BC ⊥x 轴,PP ′⊥BC , ∴PP ′∥x 轴,∴易得P ′(-4,1).将B (2,4),P ′(-4,1)的坐标代入y =kx +b ,得⎩⎨⎧2k +b =4,-4k +b =1,解得⎩⎪⎨⎪⎧k =12,b =3,∴一次函数的解析式为y =12x +3.五、22.解:(1)由题意知点A 与点B 关于原点对称,∴OA =OB ,∴S △AOC =S △BOC =12S △ABC =12×2=1, ∴12|k |=1,∵k >0,∴k =2. (2)①(1,2);(-1,-2) ②x ≥1或-1≤x <0(3)存在.由(2)可得AB 2=(-1-1)2+(-2-2)2=20.设D (m ,0),则AD 2=22+(1-m )2=m 2-2m +5, BD 2=22+(m +1)2=m 2+2m +5,当△ABD 为直角三角形时,可分以下三种情况:11当∠BAD =90°时,AB 2+AD 2=BD 2,即20+m 2-2m +5=m 2+2m +5,解得m =5;当∠ABD =90°时,AB 2+BD 2=AD 2,即20+m 2+2m +5=m 2-2m +5,解得m =-5, 当∠BDA =90°时,AD 2+BD 2=AB 2,即m 2-2m +5+m 2+2m +5=20,解得m =±5. ∴点D 的坐标为(-5,0),(-5,0),(5,0)或(5,0).23.解:(1)3;12(2)对于y =32x -3,令y =0,则32x -3=0,解得x =2,∴B (2,0). 如图,过点A 作AE ⊥x 轴于E ,过点D 作DF ⊥x 轴于F .∵A (4,3),B (2,0),∴OE =4,AE =3,OB =2, ∴BE =OE -OB =4-2=2.∴在Rt △ABE 中,AB =AE 2+BE 2=32+22=13.∵四边形ABCD 是菱形,∴AB =CD =BC =13,AB ∥CD ,∴∠ABE =∠DCF , ∵AE ⊥x 轴,DF ⊥x 轴,∴∠AEB =∠DFC =90°,在△ABE 与△DCF 中,⎩⎨⎧∠AEB =∠DFC ,∠ABE =∠DCF ,AB =DC ,∴△ABE ≌△DCF ,∴CF =BE =2,DF =AE =3, ∴OF =OB +BC +CF =2+13+2=4+13,∴点D 的坐标为(4+13,3).(3)当y ≥-2时,自变量x 的取值范围是x ≤-6或x >0.。
正比例反比例练习试题

正比例反比例练习题1、圆的面积和圆的半径成正比例。
()2、圆的面积和圆的半径的平方成正比例。
()3、圆的面积和圆的周长的平方成正比例。
()4、正方形的面积和边长成正比例。
()5、正方形的周长和边长成正比例。
()6、长方形的面积一定时,长和宽成反比例。
()7、长方形的周长一定时,长和宽成反比例。
()8、三角形的面积一定时,底和高成反比例。
()9、梯形的面积一定时,上底和下底的和与高成反比例。
()10、圆的周长和圆的半径成正比例。
()二:选择题。
1.根据表格判断数量间的比例关系。
时间(小时) 2 3 5 7 8 ...路程(千米)100 150 250 350 400 ...时间与路程()A.成正比例.B.成反比例.3.不成比例.2.圆柱体底面积与高()A.成正比例.b.成反比例.c.不成比例圆柱体底面积300 200 150 120 100圆柱的高 2 3 4 5 6三.看图填空.1.根据规律判断比例关系,并填空。
X 2 3 5 () 10 ...y ()4.5 7.5 12 ()...X与Y成().A.正比例B.反比例.X 2 3 5 ()10 ...Y () 4 2.4 12 () ...X与Y()A.正比例.B.反比例3.选择填空.A除以B=C,当C一定时A和B();当A一定时B和C();当B一定时A和C()A.成正比例.b.成反比例。
四.判断对错.1.路程一定,速度和时间成正比例。
()2.一堆煤的总量不变,烧去的煤与剩下的煤成反比例。
()3.花生的出油率一定,花生的重量与榨出花生油的重量成正比例。
()4.平行四边形的面积不变,它的底与高成反比例。
()五、选择题。
1.长方形的________,它的长和面积成正比例。
A.周长一定。
B.宽一定。
C.面积一定。
2.圆柱体体积一定,______和高成反比例。
A.底面半径.B.底面积.C.表面积.六.应用题。
1.工厂制作一种零件,现在每个零件所用的时间由革新前的8分钟减少到3分钟,原来制造60个的时间现在能生产多少个?(用比例方法解答)2.一个晒盐场用500千克的海水可以晒15千克盐;照这样的计算,用100吨海水可以晒多少吨盐?(用比例方法解答)正比例和反比例”过关测试题一、对号入座1、35:()=20÷16==()%=()(填小数)2、因为X=2Y,所以X:Y=():(),X和Y成()比例。
反比例函数》单元测试题(含答案)-

反比例函数》单元测试题(含答案)-1.给定双曲线经过点(-2,3),求解析式。
解析:双曲线的一般式为y=k/x,代入点(-2,3)可得3=k/(-2),解得k=-6,所以双曲线的解析式为y=-6/x。
2.已知y与x成反比例,且y=1时,x=4,求x=2时的y 值。
解析:由反比例函数的定义可知,y1*x1=y2*x2,代入y=1,x=4可得1*4=y2*2,解得y2=2,所以当x=2时,y=2.3.已知反比例函数和正比例函数的图象都经过点A(-1,-2),求它们的解析式。
解析:正比例函数的图象为直线y=kx,代入点A可得-2=k*(-1),解得k=2,所以正比例函数的解析式为y=2x。
反比例函数的图象为双曲线y=k/x,代入点A可得-2=k/(-1),解得k=2,所以反比例函数的解析式为y=2/x。
4.某厂有1500吨煤,求这些煤能用的天数y与每天用煤的吨数x之间的函数关系式。
解析:假设每天用煤的吨数为x,那么1500吨煤能用的天数为y=1500/x,所以函数关系式为y=1500/x。
5.若点(3,6)在反比例函数y=k/x(k≠0)的图象上,那么下列各点在此图象上的是()解析:由反比例函数的图象可知,其图象为双曲线,因此点(3,6)在图象上,而点(-3,-6)、(2.-9)、(2.9)、(3.-6)不在图象上。
6.已知反比例函数的图象过(2,-2)和(-1,n),求n的值。
解析:反比例函数的图象为双曲线,过点(2,-2)和(-1,n)的双曲线有两个分支,分别为y=k/x和y=-k/x,因此可列出方程组-2=k/2和n=-k/-1,解得k=4,n=4,所以n的值为4.7.反比例函数y=k^3/x的图像经过(-,5)点、(a,-3)及(10,b)点,求k、a、b的值。
解析:代入三个点可得5=k^3/-,-3=k^3/a^3,b=k^3/10,解得k=∛(-50),a=∛(k^3/-3),b=10∛(-50)。
反比例函数单元测试题二及答案

第17章反比例函数综合检测题一、选择题(每小题3分,共30分) 1、反比例函数y =xn 5+图象经过点(2,3),则n 的值是( ). A 、-2 B 、-1 C 、0 D 、12、若反比例函数y =xk(k ≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ).A 、(2,-1)B 、(-21,2) C 、(-2,-1) D 、(21,2) 3、(08双柏县)已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )4、若y 与x 成正比例,x 与z成反比例,则y 与z 之间的关系是().A 、成正比例B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5、一次函数y =kx -k ,y 随x 的增大而减小,那么反比例函数y =xk 满足( ).A 、当x >0时,y >0B 、在每个象限内,y 随x 的增大而减小C 、图象分布在第一、三象限D 、图象分布在第二、四象限6、如图,点P 是x 轴正半轴上一个动点,过点P 作x 轴的垂 线PQ 交双曲线y =x1于点Q ,连结OQ ,点P 沿x 轴正方向运动时, Rt △QOP 的面积( ).A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定 7、在一个可以改变容积的密闭容器内,装有一定质量m 的某种气体,当改变容积V 时,气体的密度ρ也随之改变. ρ与V 在一定范围内满足ρ=Vm,它的图象如图所示,则该 气体的质量m 为( ).A 、1.4kgB 、5kgC 、6.4kgD 、7kg 3,y 1),B (-2,y 2),C (-1,y 3)三点都在函数y =-x 1的y 1,y 2,y 3的大小关系是( ). y 3 B 、y 1<y 2<y 3 C 、y 1=y 2=y 3 D 、y 1<y 3<y 2 y =xm 21-的图象上有A (x 1,y 1)、B (x 2,y 2)两点,12时,y 1<y 2,则m 的取值范围是( ). A 、m <0 B 、m >0 C 、m <21 D 、m >2110、如图,一次函数与反比例函数的图象相交于A 、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围是( ). A . B . C . .A 、x <-1B 、x >2C 、-1<x <0或x >2D 、x <-1或0<x <2 二、填空题(每小题3分,共30分)11.某种灯的使用寿命为1000小时,它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 .12、已知反比例函数xky =的图象分布在第二、四象限,则在一次函数b kx y +=中,y 随x 的增大而 (填“增大”或“减小”或“不变”).13、若反比例函数y =xb 3-和一次函数y =3x +b 的图象有两个交点,且有一个交点的纵坐标为6,则b = . 14、反比例函数y =(m +2)x m 2-10的图象分布在第二、四象限内,则m的值为 .15、有一面积为S 的梯形,其上底是下底长的31,若下底长为x ,高为y ,则y 与x 的函数关系是 . 16、如图,点M 是反比例函数y =xa(a ≠0)的图象上一点, 过M 点作x 轴、y 轴的平行线,若S 阴影=5,则此反比例函数解析 式为 .17、使函数y =(2m 2-7m -9)x m2-9m +19是反比例函数,且图象在每个象限内y 随x 的增大而减小,则可列方程(不等式组)为 .18、过双曲线y =xk(k ≠0)上任意一点引x 轴和y 轴的垂线,所得长方形的面积为______.19. 如图,直线y =kx(k >0)与双曲线xy 4=交于A (x 1,y 1), B (x 2,y 2)两点,则2x 1y 2-7x 2y 1=___________.20、如图,长方形AOCB 的两边OC 、OA 分别位于x 轴、 y 轴上,点B 的坐标为B (-320,5),D 是AB 边上的一点, 将△ADO 沿直线OD 翻折,使A 点恰好落在对角线OB 上的 点E 处,若点E 在一反比例函数的图象上,那么该函数的解析 式是 .三、解答题(共60分) 21、(8分)如图,P 是反比例函数图象上的一点,且点P 到x 轴的距离为3,到y 轴的距离为2,求这个反比例函数的解析式. 22、(9分)请你举出一个生活中能用反比例函数关系描 述的实例,写出其函数表达式,并画出函数图象. 举例:函数表达式:23、(10分)如图,已知A (x 1,y 1),B (x 2,y 2)是双曲线y =xk在第一象限内的分支上的两点,连结OA 、OB .(1)试说明y 1<OA <y 1+1y k;(2)过B 作BC ⊥x 轴于C ,当m =4时, 求△BOC 的面积.24、(10分)如图,已知反比例函数y =-x8与一次函数 y =kx +b 的图象交于A 、B 两点,且点A 的横坐标和点B 的 纵坐标都是-2. 求:(1)一次函数的解析式; (2)△AOB 的面积.25、(11分)如图,一次函数y =ax +b 的图象与反比例函数y =xk的图象交于M 、N 两点.(1)求反比例函数与一次函数的解析式; (2)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.26、(12分)如图, 已知反比例函数y =xk的图象与一次函 数y =a x +b 的图象交于M (2,m )和N (-1,-4)两点. (1)求这两个函数的解析式; (2)求△MON 的面积;(3)请判断点P (4,1)是否在这个反比例函数的图象上, 并说明理由.参考答案:一、选择题 1、D ; 2、A ; 3、C ; 4、B ; 5、D ; 6、C 7、D ; 8、B ; 9、D ; 10、D .二、填空题 11、y =x 1000; 12、减小; 13、5 ; 14、-3 ;15、y =xs23 ; 16、y =-x 5; 17、⎩⎨⎧---=+-0972119922>m m m m ; 18、|k|; 19、 20; 20、y =-x12.三、解答题21、y =-x6. 22、举例:要编织一块面积为2米2的矩形地毯,地毯的长x (米)与宽y (米)之间的函数关系式为y =2(x >0). (只要是生活中符合反比例函数关系的实例均可)画函数图象如右图所示. 23、(1)过点A 作AD ⊥x 轴于D ,则OD =x 1,AD =y 1,因为点A (x 1,y 1)在双曲线y =x k 上,故x 1=1y k,又在Rt △OAD 中,AD <OA <AD +OD ,所以y 1<OA <y 1+1y k; (2)△BOC 的面积为2. 24、(1)由已知易得A (-2,4),B (4,-2),代入y =kx +b 中,求得y =-x +2;(2)当y =0时,x =2,则y =-x +2与x 轴的交点M (2,0),即|OM|=2,于是S △AOB =S △AOM +S △BOM =21|OM|·|y A |+21|OM|·|y B |=21×2×4+21×2×2=6. 25、(1)将N (-1,-4)代入y =xk,得k =4.∴反比例函数的解析式为y =x 4.将M (2,m )代入y =x4,得m =2.将M (2,2),N (-1,-4)代入y =ax +b ,得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y =2x -2.(2)由图象可知,当x <-1或0<x <2时,反比例函数的值大于一次函数的值.26、解(1)由已知,得-4=1-k ,k =4,∴y =x4.又∵图象过M (2,m )点,∴m =24=2,∵y =a x +b 图象经过M 、N 两点,∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y =2x -2. (2)如图,对于y =2x -2,y =0时,x =1,∴A (1,0),OA =1,∴S △MON =S △MOA +S △NOA =21OA ·MC +21OA ·ND =21×1×2+21×1×4=3. (3)将点P (4,1)的坐标代入y =x4,知两边相等,∴P 点在反比例函数图象上.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比例和反比例测试题
一、比例和反比例
1.如图是某地区6~~12岁儿童平均体重情况:
看图回答问题:
(1)从统计图中可以看出,随年龄的增长,平均体重有什么变化?
(2)从统计图中可以看出,女生在哪个年龄段平均体重增加最快?
(3)平均体重的增加与年龄增长成正比例吗?
(4)从图中,你还能得到哪些信息?
【答案】(1)解:随着年龄的增加折线的数值在增大,所以平均体重是在增加。
(2)解:女生体重的折线在11﹣12岁时最陡,说明这一时期变化的最快,所以11﹣12岁时女生的平均体重变化的最快。
(3)解:男生6岁时的平均体重是19.3千克,体重与年龄的比值是:19.3:6≈3.2;
当男生7岁时平均体重是21千克,体重与年龄的比值是:21:7=3;
比值不相同,所以体重的增加与年龄的增长不成正比例。
(4)解:由图可知:11岁之前,男生和女生体重的增长速度相当,但11﹣﹣12岁女生体重增长的速度要快于男生
【解析】【分析】(1)观察复式折线统计图可知,两条折线都是上升趋势,说明:随着年龄的增加,折线的数值在增大,所以平均体重是在增加;
(2)观察女生的折线可知,女生体重的折线在11~12岁时最陡,说明这一时期变化的最快,所以11~12岁时女生的平均体重变化的最快;
(3)根据题意可知,可以求出体重与年龄的比值,然后对比比值,比值不相等,则不成正比例;
(4)观察统计图可知,11岁之前,男生和女生体重的增长速度相当,但11~12岁女生体重增长的速度要快于男生,据此解答.
2.服装厂加工一批服装,计划每天加工120套,50天可以完成。
实际每天加工了150套,多少天可以加工完?(用比例解)
【答案】解:设x天可以加工完。
150x=120×50
x=6000÷150
x=40
答:40天可以加工完。
【解析】【分析】这批服装的总数不变,每天加工的套数与加工的天数成反比例,设出未知数,根据总套数不变列出比例,解比例求出实际加工的天数即可。
3.兄弟俩在玩跷跷板,哥哥体重30千克,坐的地方距支点10分米,弟弟体重20千克,他坐的地方距支点多远才能保持跷跷板的平衡?
【答案】解:30×10÷20=15(分米)
答:他坐的地方距支点15分米才能保持跷跷板的平衡。
【解析】【分析】根据题意可知:哥哥的体重×坐的地方距支点的长度=弟弟的体重×他坐的地方距支点的长度,用哥哥的体重×坐的地方距支点的长度÷弟弟的体重=他坐的地方距支点的长度,据此解答.
4.小明打算12天看完一本故事书,平均每天看15页。
如果要提前2天看完,平均每天应看多少页?(用比例知识解)
【答案】解:设平均每天应看x页,则
(12-2)x=12×15
x=18
答:平均每天应看15页。
【解析】【分析】根据故事书的总页数不变可得等量关系式:实际看的天数×实际平均每天应看多少页=计划看的天数×计划平均每天看多少页,据此代入数据列方程解答即可。
5.在下面的方格纸上画一画。
(每一个小方格的边长代表1cm)
画一个长方形,周长是32cm,长与宽的比是5∶3。
【答案】解:32÷2=16(cm),16÷(5+3)=2(cm),
长方形的长:5×2=10(cm),宽:3×2=6(cm)
【解析】【分析】用长方形的周长除以2求出长与宽的和,然后把长与宽的和按5:3的比分配后分别求出长和宽,然后画出指定长和宽的长方形。
6.乐乐买了一个军舰模型,包装盒上写着“按1:400制作”,他量了一下,模型长45cm。
这艘军舰实际有多长?
【答案】解:设这艘军舰实际长xcm.
x=45×400
x=18000
18000cm=180m
答:这艘军舰实际长180米.
【解析】【分析】先设出未知数,然后根据1:400的比列出比例,解比例求出实际的长度,注意换算单位.
7.圆的周长和它的面积成正比例。
()
【答案】错误
【解析】【解答】圆的周长=2πr,圆的面积=πr2,因为圆的面积÷圆的周长=,没有定值,所以圆的周长和面积不成正比例,原题说法错误.
故答案为:错误.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此判断.
8.正方形的周长和边长成________比例。
【答案】正
【解析】【解答】解:正方形的周长=边长×4,即可得:正方形的周长÷边长=4,所以正方形的周长和边长成正比例。
故答案为:正。
【分析】正方形的周长=边长×4。
正比例:两种相关联的量,一种量变化,另一种量也随着相同变化,如果两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做正比例的量,它们的关系叫做正比例的关系。
9.如果,那么与成________比例;如果,那么和成________比例。
【答案】正;反
【解析】【解答】解:因为,所以=8,所以x与y成正比例;因为,所以xy=8,x和y成反比例。
故答案为:正;反。
【分析】根据等量关系判断x和y的商一定还是乘积一定,如果商一定就成正比例,如果
乘积一定就成反比例。
10.某种型号的铁丝,它的长度与质量()
A. 成正比例
B. 成反比例
C. 不成比例
【答案】 A
【解析】【解答】解:某种型号的铁丝,它的长度与质量成正比例关系。
故答案为:A。
【分析】因为铁丝的型号被确定了,那么它的横截面积也就确定了,横截面积一定时,它的体积和长度成正比,而质量=体积×重度,重度是一定的,所以质量和体积成正比,综上长度与质量成正比例关系。
11.下面各选项中,成反比例的量是()
A. 时间一定,路程和速度
B. 烧煤的总量一定,每天烧煤量和所烧的天数
C. 车轮半径一定,行驶的路程和车轮的转数
D. 小明的身高与所跳的高度
【答案】 B
【解析】【解答】选项A,因为路程÷速度=时间,所以当时间一定,路程和速度成正比例;
选项B,因为每天烧煤量×所烧的天数=烧煤的总量,所以当烧煤的总量一定,每天烧煤量和所烧的天数成反比例;
选项C,因为行驶的路程÷车轮的转数=车轮的周长2πr,所以当车轮半径一定,行驶的路程和车轮的转数成正比例;
选项D,小明的身高与所跳的高度没有必要的关联,不成比例。
故答案为:B。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的积一定,这两种量叫做成反比例的量,它们的关系叫做反比例关系,据此判断。
12.X、Y是两种相关联的量,同时X=Y(X、Y≠0),那么X和Y成( )。
A. 正比例
B. 反比例
C. 不成比例
【答案】 A
【解析】【解答】解:X、Y是两种相关联的量,同时X=Y(X、Y≠0),那么X和Y成正比例。
故答案为:A。
【分析】如果x和y成正比例,那么y=kx(其中k为常数),据此作答即可。
13.把一个圆柱体切割后拼成一个长方体,它的表面积()。
A. 增加了
B. 减少了
C. 不变
【答案】 A
【解析】【解答】解:把一个圆柱体切割后拼成一个长方体,它的表面积增加了。
故答案为:A。
【分析】把一个圆柱切割后拼成一个长方体,表面积会增加两个长方形的面。
14.圆柱的侧面展开后是一个正方形,它的高是37.68m,它的底面半径是()m。
A. 4
B. 6
C. 8
D. 12
【答案】 B
【解析】【解答】解:37.68÷3.14÷2=6(m)
故答案为:B。
【分析】因为侧面展开后是一个正方形,那么这个圆柱的高与底面周长相等,用底面周长除以3.14,再除以2即可求出底面半径。
15.将一个棱长2分米的正方体木块削成一个最大的圆柱,圆柱的体积是()立方分米.
A. 6.28
B. 3.14
C. 25.12
D. 12.56
【答案】 A
【解析】【解答】2÷2=1(分米)
3.14×12×2
=3.14×2
=6.28(立方分米)
故答案为:A.
【分析】将一个棱长2分米的正方体木块削成一个最大的圆柱,圆柱的底面直径和高是正方体的棱长,先求出圆柱的底面半径,用底面直径÷2=底面半径,然后用公式:V=πr2h,据此列式解答.。
